Abstract
This paper presents an experimental research that proposes to determine the influence of process parameters on CO2 laser cutting of 8 mm thick Hardox 400 steel, for which Kerf has a minimum value. The experimental research was conducted according to a complete factorial plan with laser power, assistant gas pressure and cutting speed as the input parameters, and cutting width as the dependable variable. The Design of Experiment (DOE) consisted of 27 references and was completed with four replicas to determine the variation of the Kerf average. Functional, linear and quadratic relations were determined, which describe the Kerf dependence on the cutting parameters in order to establish the most influential parameter. The results show that the independent parameter with the most significant influence was the laser power, with minimum Kerf obtained if the laser power and the assistant gas pressure were adjusted to average values. The interaction between laser power and auxiliary gas pressure at constant cutting speed was investigated to improve Kerf and reduce the laser processing cost. The study offers the right combination of process parameters that leads to a minimum value of the cutting width.
1. Introduction
The extension of laser beam cutting (LBC) as a cutting process in industrial processes is due to the advantages it generates. Laser beam processing allows for cutting a wide range of materials with different mechanical properties. The optimization of the cutting parameters, which results from the concentration of the laser beam in a very small point, on the surface of the material to be processed, will lead to faster processing of various materials with lower processing costs.
The use of laser in cutting and processing metallic materials has been researched in many specialized works. Tatzel et al. showed the effect of the focusing position on the induced heat affecting the laser-cut edges of 3-mm-thick stainless steel. The process parameters observed during cutting were speed, assistant gas pressure and focusing position. The latter has proven to be an important parameter if a high processing quality is to be achieved [1]. Levichev et al. shows that continuous heating of the semifinished part during oxygen-assisted cutting decreases the quality and generates material losses to thick metal plates, where the cutting speed is low. The cutting experiments took place on a soft steel with a thickness of 15 mm using a 4 KW power laser. Three methods were used to obtain high quality of the cut surface: optimizing the input parameters for preheated areas, using active cooling to eliminate heat excess and using active cooling to avoid heated regions [2]. Madic et al. showed that the optimization of laser cutting parameters is necessary to obtain a quality cut at low cost, using a CO2 laser on a soft material. This paper aims to calculate the cutting parameters to maximize the speed of melt removal taking into account the iterative algorithm [3]. Moradi et al. used a post-processing method by additive deposition for the parts manufacturing. The input parameters used in the experiment were: focal position, laser power and scanning speed. These were processed using statistical software to determine the regression functions of the cutting width. By optimizing the process parameters, an adequate quality of Kerf results [4]. Pramanik et al. studied the effects of cutting angle, Z distance, laser power, scanning speed and pulsation frequency to observe the cutting width and surface roughness Ra of a 1-mm-thick titanium part with engineering and medical applications [5]. Darwish et al. investigated the effect of the nozzle (size, diameter) on a high-pressure gas jet to improve laser cutting. The Schlieren view shows that the outlet jet from the supersonic nozzle has a constant flow, better dynamic properties and a gas flow with a longer length than the gas jet from the conical nozzle [6]. Jiang et al. analyzed the influence of the process parameters: cutting speed, laser power, sheet thickness, and distance between nozzle and part on the temperature in the cutting region for the Al 6061–T6 alloy. The results showed that the thickness of the sheet determined the values of the input parameters, while the change in power density led to a variation of the temperature in the cutting area, which means that power is the most influential factor on the quality of the cut surface [7]. Eltawahni et al. showed that CO2 laser cutting is an economical manufacturing process for stainless steel. By applying the Box–Behneken design, the cutting experiment was designed according to the input parameters: laser power, cutting speed, auxiliary gas pressure, focusing position and nozzle diameter, to mathematically model the cutting width, Ra surface roughness and operating cost. Mathematical optimization has indicated the best conditions for laser cutting to achieve high quality and low cost [8]. Nath et al. recommended laser cutting of combined materials due to the properties of nickel and stainless steel. The study shows the effect of laser power and scanning speed on width, depth of cut and thermal stress. The effect of heat generated by the laser beam indicates that the cutting width and depth proportionally vary to the laser power, thermal stress is dependent on process parameters, and increased speed means a small cutting width, i.e., economy of molten material [9]. Sibalija et al. used as influencing factors: assistant gas pressure, focusing position, laser power and cutting speed to determine the properties of the cut area using the artificial neural network (ANN) model in order to optimize the cutting parameters. The (ANN) responses and the validation of the results show that the selected parameters determine improved cutting characteristics with an impact on the quality of the cut area and the mechanical aspects [10]. Savanth et al. used a YAG laser to apply a Colmonoy-5 layer on carbon steel plates. Laser power processing and scanning speed parameters were varied to observe their effect on microstructural characteristics: microhardness and wear. It was determined that the laser power has a great influence on the HV microhardness, and the simultaneous combination of factors, namely, low laser power and high scanning speed, leads to an increased wear resistance [11]. Kang et al. researched ultra-fast 10 ps pulse lasers to fabricate sharp-edged cutting tools by heat treatment. Thus, it is necessary to round the edges of the cut edges of the WC-Co alloy with the help of the laser due to the high precision and the low heat accumulation. The experiments were performed on the free surfaces of the tools used for cutting which modified the laser parameters: wavelength, fluency and pressure of the assistant gas. The analysis of the tools does not show a change in hardness, and in terms of surface quality results in a very low Ra roughness of 0.15 µm for wavelengths other than 1064 nm (IR) and 532 nm (VIS) [12]. Elsheikh et al. used a CO2 laser that emits a pulsed light beam onto the methyl polymethacrylate sheets to study the cutting width. The authors optimized the cutting parameters, respectively speed, auxiliary gas pressure, laser power and material thickness. With the help of a microscope they measured the upper and lower cutting width and the Kerf taper, these being considered as output parameters for the cutting process. The influence of the cutting parameters on Kerf was statistically analyzed with ANOVA dispersion technique. The obtained results show that any increase of the values of the cutting parameters generates a larger cutting width and the increase of the laser speed and power leads to the increase of the Kerf taper [13]. Hajad et al. indicated a method of optimizing the laser cutting path to accumulate minimal heat by using a genetic algorithm with neighborhood search. This technique is useful for hardening the surface in the welding process where the working distance and heat accumulation must be optimized to obtain quality parts [14]. Seong et al. highlighted the behavior of the gas flow in the subsonic and supersonic nozzle by analysis with the Nomarsk interferometer. The process of cutting 60 mm thick stainless steel sheets took place with the help of a 6 KW laser. The experiments were performed to observe the effect of the geometric configuration of the nozzles. By varying the stand-off distance, the ability to eliminate the formed melt was determined. The results show that the supersonic nozzle has a capacity to remove the melt at a greater distance [15].
Anghel et al. conducted CO2 laser cutting research on 304 stainless steel to obtain miniatural gears. The cutting experiments were designed according to the Box–Behnken design and performed based on the response technique, with 29 references evaluated by the RSM (response surface) model. The varied parameters were laser power, cutting speed, focal position and cutting gas pressure, while the output parameter measured and calculated the surface roughness Ra. With the help of ANOVA it was established that the focal position is the most influential parameter [16]. Chen et al. presented the optimization of the hardness of the carbon steel material AISI 1045 under the influence of the input parameters: laser power, scanning speed and focusing distance. They found that the hardness of the hardened surface after laser cutting improved from 200 HV to 660 HV. RSM models are able to interpret hardened width (HW), hardened hardness (MH) and hardness gradient (HG) [17]. Li et al. showed that when laser cutting thin sapphire sheets with the help of a Bessel beam, a zero taper and a higher roughness were obtained [18]. Subasi et al. used a laser beam guided by a water jet to process the nickel alloys used in the aerospace industry, in the technological process of micro-drilling. The improvement consisted of eliminating the burrs of the cut surfaces, reducing the taper and reducing the area affected by the laser heat [19]. Das Partha et al. optimized the cutting parameters (cutting speed, gas pressure, pulse width, pulse frequency) of two laser sources, solid Nd- YAG and gas CO2 in pulsed mode. The optimization method is based on several criteria, superiority and inferiority, to identify the most suitable combination, which ensures low Ra value, reduced cutting width and slope [20]. Cheng et al. presented a low-cost method of manufacturing PMMA (polymethyl methacrylate) nozzles, based on laser cutting and PDMS (polydimethylsiloxane) bonding [21]. Powell et al. experimentally investigated the CO2 laser cutting of soft steel sheets with a thickness of 15–20 mm. There is a decrease in the quality of the cut edge to thicknesses between 15 and 20 mm [22]. Dontu [23], Savii [24] and Draganescu [25] contributed to the expansion of the CO2 and Nd-YAG laser application in industrial engineering activities, as well as applications in the production processes of laser cutting, drilling and welding in the manufacture of industrial products. Genna et al. studied the interaction between the cutting parameters and the part parameters depending on the type of chosen material—AlMg3, St37–2 and AlSI 304—in order to vary the kerf width. The auxiliary gases used were N2 and O2. The results show that the Kerf width increases as the cutting speed decreases, due to the higher accumulated energy [26]. Son et al. presented the influence of laser parameters on Kerf in the case of SS41 and SUS 304 metal sheets used in engineering applications. The ANOVA method established the most significant parameters used in the experiments: laser power and cutting speed [27]. Tahir et al. researched UHSS ultrahard steel in nitrogen and oxygen-assisted laser processing. The results observed after cutting and analysis indicate a better cutting width for nitrogen, and better hardness and perpendicularity of the cut edge when using oxygen as an assistant gas [28]. El Aoud et al. demonstrated that CO2 laser technology is advantageous for cutting sheets of Ti-6Al-4V titanium alloys and pure titanium. For both types of material, the most influential cutting parameter is the laser power in case of cutting width disturbance. In this study, Kerf is inversely proportional to the cutting speed [29]. Chatterjee et al. showed laser piercing for Ti6Al4V alloy in order to obtain quality holes. The analysis of variance indicates that the most influential input parameter is the laser power on the area affected by HAZ heat and the conicity of the processing [30].
Gvozdev et al. presented a mathematical model that describes the influence of laser cutting parameters on the surface roughness, HAZ and the deviation from the rectilinearity of the cut surface. Nomograms are constructed indicating the selection of cutting regimes in case of minimizing the responses for carbon steel sheets with thicknesses of 6, 10 and 14 mm [31]. Patel et al. studied the effect of the input parameters (laser power, gas pressure, cutting speed, nozzle diameter) on the cutting quality for H400 materials. They concluded that the minimum Kerf was obtained at a pulse frequency of 25 Hz, while maximum Kerf was obtained at a laser pulse frequency of 20 Hz [32]. Patel et al. showed the influence of the cutting parameters (cutting speed, laser power, frequency, pressure) to identify the responses due to laser cutting (taper, Ra and HAZ) of En-31 molded steel. Mathematical models were developed using the method of response surfaces and it was identified that the best roughness is obtained when selecting process parameters at average values [33]. Prajapati et al. investigated the effect of laser installation parameters such as laser power, gas pressure, cutting speed and thickness in the case of cutting experiments designed after the Taguchi L27 model on roughness. The statistical analysis was performed using the ANOVA variant. The sensitive parameters identified are the cutting speed and the thickness of the part [34]. El Aoud et al. used 3-mm-thick Ti sheets to investigate laser cutting. The cutting parameters, laser power, cutting speed and gas pressure ran according to an experimental plan given by Taguchi’s method in order to analyze the microstructure of the cut edge and optimize the roughness. The conclusion indicated the optimal cutting condition was obtained at laser power P = 3 KW, cutting speed v = 2.400 mm/min and gas pressure p = 8 bar [35]. Boujelbene et al. studied CO2 laser cutting on Ti sheet with thickness g = 2 mm. Taguchi’s method was implemented to minimize roughness and identify optimal cutting parameters. It turned out that the roughness increases when the thermal energy is increased by the laser and decreases at the high cutting speed [36]. Zhou et al. studied the laser polishing of S136D die-cast steel using an L16 orthogonal experimental plane. Experiments have shown a tendency for surface roughness to vary with laser energy density using a moving laser heat source [37]. From the above literature it appears that numerous investigations were performed to identify the effects of process parameters on Kerf responses, hardness, roughness and taper [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. In addition, other research included the focusing position, nozzle geometry, stand-off distance on the gas jet, temperature of the cutting area, melting depth, thermal stresses, HAZ [6,15,21], and laser fusion deposition technique [11]. Further, some studies methods used modern design and optimization, genetic algorithm, iterative, artificial neural network model, superiority and inferiority criteria [3,10,14,20].
Most research focuses on various metallic materials, alloys, groups of materials with different physical, chemical and thermal properties. The presented studies conducted numerous experimental investigations in order to identify the effects of laser cutting parameters on process responses. At present, there is a diversity of research aimed at finding a suitable combination of the main parameters that affect the quality of cutting. In the previous approaches the most common use of materials in the case of laser heating is found on stainless steel, Ti, mild steel, alloys and reduced on hard and ultra-hard steel. In this study we selected the H400 steel material in the laser manufacturing process due to its extensive capacity for use and exploitation over time, surface conditions and absorbability. H400 is an insufficiently used steel from a technical point of view, and is little used in the laser processing process, which is why it was chosen as a study material. Linear (L) and quadric (Q) prediction models, and regression (L) and (Q) models, respectively, were developed using the response surfaces, which were then compared for adequacy and in the ranking of the cutting factors. A number of physical quantities were calculated that accompany the interaction between radiation and substance as a result of the transformation of light energy into caloric energy.
H400 steel can be heat-processed with laser, needs minimal subsequent post-laser processing, and is often used after cutting mechanical machining operations can be performed. The selection criterion is based on the fact that the material is suitable for mechanical processing for different types of parts that must meet wear resistance in operation; it is a a high-quality material used in the machine building industry and is superior to ordinary hot rolled steels. It behaves very well in operation, and the processed parts are very well manifested in the coal mining industry. Due to its wear resistance properties, the material is used in the oil shale industry, stone quarries, civil engineering and road construction. H400 is an economical, high-quality material that is durable and resistant to abrasion and corrosion. It is superior to OL, Dillidur and Weldox rolled steel. The main destination of H400 steel is for the production of mechanical parts whose strength is very high; in the machine building industry it is used to make crushing machines, metal waste compactors and sandblasting machines.
CO2 laser cutting is a manufacturing process based on focusing light energy in a spot with a diameter of 0.2 mm. Laser beam melts the material due to the incident intensity in a range of 105–106 W/cm2. The characteristics of the laser beam and the projection on the part have been set in order to reduce the local heat and stress. From the laser spot starts a beam of rays with very small divergence (<2°) which cuts the material by heat processing, resulting in a conical surface. The light generated by the laser attacks the material and crosses it through a stationary piercing, after which the cut is made in a straight profile until it enters the contour of the piece. The H400 steel plate is heated with the laser light beam until the initialization of the oxidation and melting reaction. There is a surplus of heat due to the thermochemical reaction that accompanies the laser thermal cutting. The manufacture of parts by laser cutting is done with the help of the computer based on the execution drawing. Laser cutting is improved with the help of spotlights, which generate melts of different sizes, depending on the laser power. The energy from the laser is transferred and absorbed by the metal increasing the temperature of the cutting area and forming the melt.
The thermal laser cutting process is assisted by the oxygen jet that coaxially accompanies the laser light from the cutting head, through the nozzle, until it enters the material. The role of the gas jet is to protect the laser beam from dust particles; it is used to meet the material and cause the iron to burn. The gas flows through the nozzle, removing the molten mass of material from the slit. Due to the heat distribution, there is a thermal stress in the material of the cut surfaces. When laser light interacts with the substance, a collision process takes place between the incident photons and the electrons of the steel. In this process, part of the photon energy is taken up by free electrons from the metal, in the form of kinetic energy, and the other part is taken up by the ions of the network that vibrate with higher amplitude, which leads to increased internal energy and its transformation into heat.
Depending on the laser parameters and the physical and chemical properties of the material, the position of spot f can be chosen after several tests. The technological process of cutting can be explained based on the interaction between energy-carrying radiation and matter. The cutting of allied and non-allied steels takes place when the preheating temperature is reached (1200 °C). The laser spot advances with speed v, and the part is cut as it moves. The spot moves on the established trajectory from the execution drawing, electronically transmitted from ByVision software to the cutting head. The shorter the stand-off distance, the higher the pressure of the gas jet on the part. Temperature is a status parameter that influences the cut. Laser melting gives rise to an oxidation reaction between iron and oxygen. Slot dimensions are influenced by pressure and temperature due to heat flow. The size of the 0.2 mm laser spot produces a larger slit due to the working pressure and temperature of the thermal energy reaction. Oxygen produces a crack as a result of the combustion reaction. High pressure removes the molten material and creates a slit. The increase in temperature due to laser energy and chemical reaction influences the cut. The cut edges are burned, oxidized and corroded, so oxygen pressure causes the cutting of edges. The temperature also rises due to friction between the gas and the contact surface. The intensity of the chemical reaction in the material is influenced by the laser power and the pressure of the assistant gas. The melting mass is determined by the power and pressure of the cutting gas. The gas jet has more energy than the energy of the melt, so destruction of the surface is achieved. As a result of chemical reactions, oxides appear on the cutting surface, material and in the atmosphere [38].
When heating a metal target with a circular spot of diameter d, the working temperature is given by the relation:
where A is the absorbsion coefficient, dimensionless; p is the laser power (W); k is the thermal conductivity of the material (W/m·K); d is the spot diameter (mm).
The novelty of this research consists in the fact that for the studied material no recommendations regarding the working regime were found in the literature. In order to understand the processes that take place inside the material, the authors considered it necessary to mathematically model aspects related to the cutting width. The obtained results allowed the determination of the optimal variant of the input parameters which leads to obtaining a minimum cutting width. The cost of processing H400 steel by CO2 laser cutting was also established.
2. Materials and Methods
The material used in cutting experiments was high-hardness steel H400. There are few studies to discover the qualities and uses of steel, which is why it was chosen as a study material in CO2 laser cutting experiments. Prior to processing, the material was carefully studied to ensure it was not damaged nor oxidized, because this would inhibit its ability to absorb laser light. The chemical composition of the processed material is specified in Table 1.

Table 1.
Chemical composition H400 [39].
The alloying element silicon has a melting point of 1414 °C, which burns more than manganese, which has a melting point of 1244 °C. In addition, carbon helps to increase the hardness of the material to a certain concentration. Laser treatment changes the chemical composition of the material in the cutting area. Manganese increases the tendency to overheat while carbon reduces the intensity of the oxidation reaction. The laser-treated surface contains MnC and SiC carbides. The chromium and nickel content make the material corrosion-resistant. Laser treatment of this material increases the hardness on the cut surface. The parts made of this steel are intended for the industrial, extractive, and automotive fields.
The problem of identifying the sensitive parameters that reduce the cut has been solved experimentally using RSM (model of response surfaces). The intelligent production in the manufacture of H400 parts considers the design potential of the experiment and its directing from the computer of the laser installation that has the capacity of self-positioning, self-adjustment, self-determination, and self-measurement. Two steel plates were prepared in the laboratory, which were subjected to a robust factorial plan complete with 27 independent experiments that were conducted four times. The design of the complete factorial plan is robust and respects the recommendations of the cutting technology, the distance from the edges and the distance between the parts equal to the thickness of the material. For the experimental design, a model was chosen with all the interactions between the three influencing factors that provide relevant information about the cutting process. The project has two constant parameters at a time and a variable parameter to determine the effect, the correlation coefficient and the estimated average of Kerf. The way in which the cutting process varies is ensured by performing four subsequent identical experiments. Dimensional accuracy is ensured when we select cutting parameters within the tolerances. DOE renders an execution of the experimental project that changes a factor at each step. In designing the experiment each factor must be run at the maximum and minimum level to calculate the effect as accurately as possible. The experimental design is suitable for the H400 experiment for the following reasons: the design of the experiment consists of 27 different experiments that lead us to look for the most appropriate parameters to minimize Kerf. The input values of the important parameters result from the criteria imposed on the experiment and the Kerf taxonomy. The set of the optimum point chosen can subsequently save time and reduce the processing cost in the manufacture of approximately identical parts by setting the laser machine to execute a certain number of products using the operation of multiplication and copying, ensuring production. Moreover, under laser cutting conditions, the cutting speed is used at the maximum level to have a low heat flux and reduced interaction time, resulting in a reduced melt mass so that the gas flux eliminates drops in smaller numbers. The DOE generates an orthogonal matrix that can be discussed and evaluated mathematically and theoretically based on data obtained for Kerf.
The dimensions of the semi-finished product used in the experiment are 300 mm, 220 mm and 8 mm for length, width and thickness, respectively. The 5.181 kg plate was cut, as shown in Figure 1, to perform a complete factorial experiment, based on an experimental plan, to determine the optimal value of the input parameters that influence the cutting width.
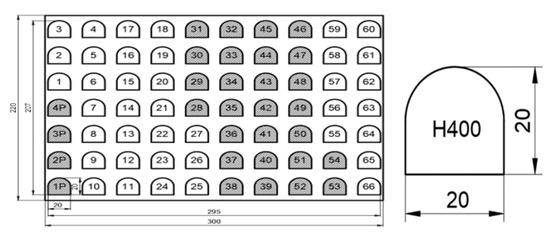
Figure 1.
Cutting plan and dimensions of the semi-finished product.
The factorial design consists of 27 tests, followed by four replicas. There were two semi-finished products containing 135 pieces. Test processing was done to determine the combinations of parameters that provide the least satisfactory results, especially that still ensure cutting. The extreme combinations were tested, and the average values of laser power, gas pressure and cutting speed were chosen. Following the experimental design, design 33 was built which offers all possible combinations of the values of the cutting parameters. The complete factorial plan allows the study of the common influence of the input parameters on the variation of the cutting width. The complete design of the independent test block was established with respect to the single central test point, maintaining a balance of increase and decrease in the values of the independent parameters, resulting in an orthogonal matrix.
The piece with a contour consisting of three straight segments and a circular profile, was designed to be cut to the dimensions: length 20 mm, width 20 mm, with a semi-circular side, from a 20 mm side square, effective area 0.00036 m2 and mass 0.02803 kg. The sketch of the resulting piece is shown in Figure 1.
A complete factorial experiment was performed to determine the most suitable combinations that decrease the cutting width and improve the production cost. The ByAutonom 4020/6000 W laser cutting equipment, manufacturer: Bystronic Switzerland, was used to cut H400 sheets (Figure 2).

Figure 2.
Laser ByAutonom 4020.
The wavelength of the CO2 laser beam is 10.6 µm. The diameter of the laser beam D at the entrance to the lens is 20 mm, and the diameter of the spot is 0.2 mm. The conical nozzle through which the gas is directed has a diameter of 1.5 mm. Starting from the source, the laser beam reaches the lens with focal length of 190.5 mm, and is concentrated in the focus of the lens, where the incident intensity on the piece increases 103–104 times, compared to the value recorded before entering the lens, approximately 162.5 × 105 W/cm2. The focusing position of the laser spot was kept constant at +1 mm above the upper level of the blank, taking into account that the assistant gas is O2.
The research of the influencing factors on the dependent variable, the cutting width, was based on performing preliminary tests to identify the central point, then the cutting experiments were run, the selection of parameters being a condition to obtain correct results. After these tests, the reference values were established: laser power p = 5000 W, auxiliary gas pressure p = 0.50 bar and cutting speed v = 1800 mm/min. The factorial experiment has three influencing factors, and each factor has three levels. Compared to the central values, the experiment predicted the variation of the input parameters as follows: laser power ± 100 W, auxiliary gas pressure ± 0.05 bar, cutting speed ± 100 mm/min, so that the levels for laser power reached the values of 4900 W, 5000 W and 5100 W; the auxiliary gas pressure was 0.45, 0.50 and 0.55 bar; the cutting speed was 1700, 1800 and 1900 mm/min. The process parameters of the laser installation are shown in Table 2.

Table 2.
Working parameters of ByAutonom 4020 equipment.
A mixed experimental design with independently run experiments was prepared with three input levels for laser power, auxiliary gas pressure and cutting speed. The size of the experiment is a block containing 27 independent experiments. You can easily see how the input parameters have been changed. The 27 parts were divided into three series. For each series, a value of the laser power (4900, 5000 and 5100 W) was maintained, while the values of the gas pressure (0.45, 0.50 and 0.55 bar), respectively of the cutting speed (1700, 1800 and 1900 mm/min) were modified.
In the stationary piercing stage (initial piercing of the laser material in pulsed regime) the working parameters are different, compared to those used in the actual experiment, in which dynamic piercing is used. The cutting gas pressure is 0.7 bar, higher than the maximum pressure used in the cutting experiments, and the focusing position f = 0 mm, which means that the laser spot is positioned on the surface of the material. In addition, through a stationary piercing, a conical channel with a diameter larger than the cutting width was drilled. After drilling, the laser entered the straight profile at a distance of about 10 mm until it reached the contour of the part.
In addition to process factors (laser power, auxiliary gas pressure and cutting speed), the cutting width is also influenced by uncontrollable factors: material condition, chemical composition, heat propagated in the material and temperature. The laser beam interacts with the part determining the geometry of the cutting slot. One aspect to consider in the laser beam at the top is that it does not have the same intensity at all points, the distribution being given by the Gaussian curve. The intensity of the oxidation reaction can ensure an improved cutting width. To improve laser cutting, the light rays refracted by the lens meet above the steel material and form the laser spot by interference.
The front inclination of the cut determines the taper in the processing of the parts. The first test piece was 1P, processed as follows: At first a perforated channel with a diameter of 1.07 mm outside the part was created, and after, the laser entered a straight line with a length of 10 mm for processing the first part. Four sample pieces were cut, and subsequently 27 pieces for which the cutting width was measured. An important role in establishing the geometry of the slot and the conical have the cutting fronts created by the laser spot. As the rays leave at an angle of divergence, it follows that the vertical section through the material has the shape of a trapezoid with bases Ks and Ki, whose height is 8 mm. How each process parameter influences the cutting width is analysed using the statistical model of prediction and regression calculation. The laser beam exposed to the material for a long time heats the cutting area, achieving larger cutting widths than usual. The state of sudden heating and cooling of the part determines the appearance of a temperature gradient in the plate.
UNIOR 701 caliber (from Unior Tools manufacturer) was used to measure the slit at the straight side. In the experiment it was used to measure the cut through the material by probing, based on the pass-by-pass principle. Laser piercing is the first contact between radiation and material. A conical channel is produced, because the geometry of the laser beam has a conical appearance, while around it the cut edges are burnt by the oxidation reaction. With the help of a Celestron digital microscope, the plate channel was studied for parts 1 and 28 (replica of part 1), in which minimum values of the input parameters were used (Figure 3a,b).
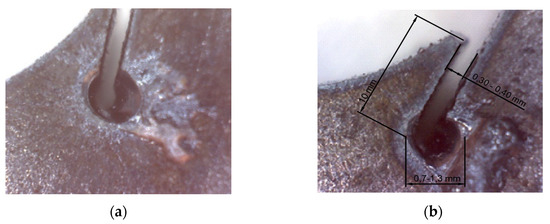
Figure 3.
(a) Part 1 with the pierced channel; (b) Part 28 with the perforated channel.
The shape at the entrance of the channel is a circular surface, surrounded by melt. As the laser penetrates the material, the diameter of the bore decreases. The melt around the channel was removed from the slit at first on the top edge. There is melting on the bottom edge of the metal sheet due to the removal of hot drops on the bottom edge. The material is melted locally and cut due to the focused laser energy.
The spot of the laser beam produces in the material a liquid portion (melt) which is removed with the help of the assistant gas, thus forming the gap between the piece and the waste plate. The melt acquires an approximate spherical shape. Centrifugal, superficial and inertia forces act on the melt. Centrifugal force (Fcf) occurs due to heating and increased thermal agitation of the liquid melt. Surface forces (Fs) act to reduce the potential energy in the surface layer, keeping the melt to a minimum volume. The force of inertia (Fi) occurs as a result of the tendency to increase the liquid volume and the tendency of detachment of small droplets from the melt [33].
Heat accumulation helps to process the material by laser cutting. H400 steel has increased thermal resistance, reducing heat dissipation, which shows us a giant energy available in the processing area. The high energy density required by laser cutting of Hardox steels means increased energy consumption and thus reduced cutting efficiency and increased processing costs. Mainly the research methods include: CO2 laser is suitable for cutting H400 steels, because the laser beam has a power of over 4 KW with an average and maximum level, good quality and high cutting efficiency; DOE is used in robust experiments of laser cutting; metal sheets and parts are researched to set Kerf to the right profile; the experimental design was run at three levels of cutting parameters resulting in 27 references; the measurement of Kerf responses was done with the slit by probing the slot based on the passing principle/does not pass; and the experimental data were mathematically and statistically processed using the RSM response surfaces given by the linear (L) and quadratic (Q) model.
3. Results
During the study, the cut parts and steel scrap plates were carefully analysed. The followed parameters were cutting width, dimensional accuracy and surface quality. The sequence consisted of checking the plates and the cut parts (surface, thickness and dimensions). The following conclusions were drawn:
- The parts have unevenness at the entrance and exit of the laser, places where a portion with wrinkles affected by heat is formed at a distance of up to 3.22 mm, measured from the exit of the contour;
- The quality of the cut surface is higher on the semi-circular profile compared to the linear profile. The cut surface has a concave appearance in the middle of the piece;
- The surface of the part is damaged at the corners where the laser changes its cutting direction in the area of 90° angles. On the side surfaces, the pieces have unevenness, more accentuated towards the corners. The position of the ridges on the cut surface is vertical and coincides with the direction of the laser beam. Some ridges/striations show bends due to slipping of the melt and resolidification of the surface. On the rectilinear sections of the linear contour of the parts, the surfaces are smooth with small irregularities. The upper part of the cut part has no molten material, which means a good setting of the cutting parameters, except for the area where the laser comes out of the worksheet (the lower part of the piece). This is due to the lower piercing speed of the laser at the exit of the material, which explains the formation of melt on the lower edge of the sheet. For the same reason, another cutting defect was observed on the cut surfaces, in the form of a notch, located between two ridges;
- Analysing the stationary piercing on the upper face of the sheet, it results that the largest diameter of the perforation is at piece 8 (3.54 mm), for which the laser power was 4900 W, the assist gas pressure 0.55 bar and the cutting speed 1800 mm/min, while for the rest of the parts the penetration is very small (maximum 1 mm).
Table 3 shows the cutting defects found on the cut parts, the values of the input parameters, and the value of the response of the cutting width, for the 27 pieces of the experimental plan. Parts 9 and 18 are largely affected by steeper and thicker unevenness and penetrations towards the bottom. In all cases, the parts have a small penetration at the lower level, about 0.75 mm. The metal sheet of Hardox expanded in thickness, where the laser acted, due to the heat flow that passes through the material. It has no melt deposited on the bottom edge, which means that the selection of the cutting parameters was correct. Dimensional measurements show differences, from part to part, due to heating, burning and deformation of the plate. The laser attacks the surface, and there is surface damage to the lower corners of the part. Due to the melting of the material, the surface of the part is not perfectly smooth. In the laser input and output areas there are high values of Ra roughness.

Table 3.
Observations on the parts. Input and output parameter values.
In order to obtain finished products with a smooth surface, free of unevenness and roughness, the parts must undergo further mechanical processing to remove the solidified melt. Setting the cutting parameters (laser power, gas pressure, cutting speed) to average values results in a minimum cutting width; 37% of the parts have a minimum cutting width of 0.30 mm. The parts in the third series were made at a temperature of over 100 °C, which led to an increase in cutting width. The evaluation of the cutting width was performed with the Statistics 7.0 program by analysing and interpreting the predictability model and determining the cutting width by the regression analysis method.
The experiment results are:
- The parts were processed by laser cutting following the complete experimental factorial design (DOE);
- Series 1 of the experiment conducted at minimum laser power, with maximum cutting speed, has a higher cutting width, under the conditions of using the auxiliary gas at average to maximum values;
- Series 2 which uses an average power of 5000 W achieves a good cut with a qualitative aspect, without structural defect of the parts. The cutting width reaches the lowest value in six experimental cases. The combination of medium power, low pressure and medium speed indicates the best result of the cutting width. In addition, the average power combined with the average pressure and any value of the cutting speed, indicates a cutting width of 0.30 mm;
- If the laser power increases, it causes an increased energy density of the laser beam. The heat absorption in the steel sheet increases and the melt increases its volume, which determines a large cutting width;
- Series 3 indicates a generally increased cutting width involving high consumption and costs. The cutting width increases with the evolution of laser power up to 5100 W;
- The cutting width decreases if a laser spot with moderate energy is used. This causes a local heat that melts a very small volume of material and after a very short time it dissipates quickly through the material;
- If the cutting speed decreases, the time of interaction between the spot and the material increases, having as an effect a longer irradiation of the material, high heat absorption, increased melted volume and finally, the cutting width deteriorates;
- If the cutting speed is increased, the spot-part interaction time decreases, resulting in reduced heat absorption of the H400 plate and a decrease in the cutting width;
- If low assist gas pressure values are used, the cutting width is affected.
From the calculations, a cutting width of 0.37 mm is obtained, a good result that falls within the limits of the experimental data. Next, the individual influence of laser power and gas pressure on Kerf was studied.
The graphs are built to find the dependence of the cutting width on the laser power. Series 1 was run at 4900 W in three references, 5000 W in three experiments and 5100 W in three cases, at the same time with the low pressure of 0.45 bar kept constant. Nine values for the cutting width resulted. The coefficient of determination R2 = 0.33 is low. For series 2, the procedure was similar, slightly increasing the gas pressure to 0.50 bar (Figure 4).
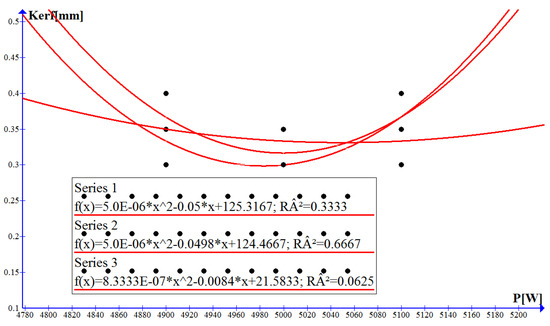
Figure 4.
Influence of laser power on cutting width.
The Pearson coefficient R2 = 0.66 shows that the cutting width depends on 66% laser power. The functional relationship between the cutting width and the laser power is approximated by the polynomial:
The best dimensions of the slot width are obtained at average values of laser power equal to 5000 W and cutting gas pressure of 0.50 bar. The speed between values of 1800 and 1900 mm/min ensures a better quality of the cut surface, smaller cutting width, if we consider an average laser power level 5000 W, and an average pressure of 0.50 bar. If the pressure is increased to 0.55 bar the results become unsatisfactory. Series 1 was chosen for all minimum levels of the independent parameters (4900 W; 0.45 bar; 1700 mm/min), at the average levels of the cutting parameters (5000 W; 0.50 bar; 1800 mm/min) and at the level of maximum input parameters (5100 W; 0.55 bar; 1900 mm/min). With the help of the Graph 4 program, the dependence of the cutting width was obtained depending on the assistant gas pressure and the functional relationship between them (Figure 5). The minimum pressure is obtained using Fermat’s theorem and is equal to 0.508 bar. The Karl–Pearson coefficient is equal to 1 which indicates that there is a strong link between the cutting width and the assist gas pressure. The parts manufactured by laser processing are geometrically characterized by a minimum width of 0.30, under the conditions of setting the input parameters at 5000 W, 0.50 bar and 1800 mm/min.
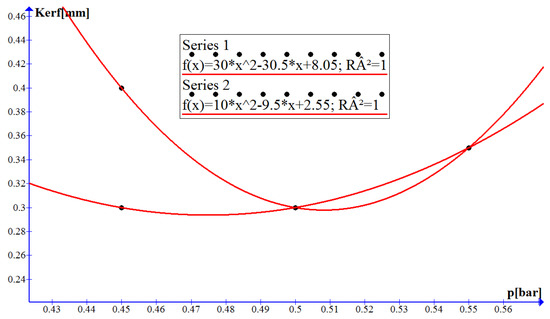
Figure 5.
Influence of auxiliary gas pressure on cutting width.
Series 2 was obtained under the following experimental conditions: (5000 W; 1900 mm/min; 0.45 bar), (5000 W; 1900 mm/min; 0.50 bar) and (5000 W; 1900 mm/min; 0.50 bar). Very good cutting widths were obtained for the pressure range (0.47–0.48 bar). The minimum of the function is 0.479 bar characterized by a cutting width of 0.31 mm. The optimal cutting conditions are described by the variation of the cutting width as a function of the auxiliary gas pressure for H400 using the polynomial:
For series 1 (laser power 4900 W), the measurements made on the cutting width highlighted three pieces with 0.30 mm, three pieces with 0.35 mm and three pieces with 0.40 mm. It is observed that under conditions of minimum gas pressure, laser power and speed, a maximum cutting width is obtained, and for the combination of minimum power, maximum pressure and speed a minimum cutting width (0.30 mm) results. Series 2 with pieces numbered from 10 to 18, has six pieces with minimum values of cutting width (0.30 mm), due to preheating of the sheet. Series 3 with parts 19 to 27 has a single piece with a cutting width equal to 0.30 mm (piece 25), because the sheet was heated during previous processing.
We therefore conclude that the parameters used in series 1 and 2 are indicated as a priority in the technological process of cutting in order to have a minimum cutting width, material savings, low energy consumption and implicitly low processing costs.
The input data needed to determine the cost of the laser manufacturing process were centralized in Table 4, with the prices being of the manufacturers. The study aims to determine the cost of the manufacturing process, which is of interest to manufacturers of such facilities, but especially to users. The first column of the table contains the cost elements identified in the processing. The second column indicates the calculation relationship. All costs were expressed in Euro/hour.

Table 4.
Determination of the cost of the laser cutting machining process.
The range of variation of the cutting width allows the evolution of the processing cost between certain limits. The consumptions in the table are specific to the installation used for laser processing.
The analysis of the experiment shows a good arrangement of the block of parts. An important parameter used in cutting is the assist gas pressure. For this reason, an important result is the identification of the function of approximating the cutting width in relation to the oxygen gas pressure. In this case, the dependent variable is the cutting width. The initial function depends on the set of xi points, according to Table 5. The values considered were: (4900 W; 0.45 bar; 1700 mm/min), (5000 W; 0.50 bar; 1800 mm/min) and (5100 W; 0.55 bar; 1900 mm/min).

Table 5.
Interpolation points and value of the function f(x).
The Lagrange interpolation polynomial that corresponds to a functional relation f in nodes x0, x1, x2 is given by the relation:
The polynomial passes through the points (0.45; 0.40), (0.50; 0.30), (0.55; 0.35) being described by a parabola. The Lagrange interpolation polynomial is obtained from the basic Lagrange polynomials and the value of the function f at points xi. The mathematical expression has the following form:
The interpolation approximation criterion presents the best possible approximation of the function f(x) by the interpolation polynomial L(x). The interpolation method establishes a functional link between the interpolation support consisting of the assisting gas pressure data set and the cutting width. The estimation error calculated as the difference between the actual function and the Lagrange function is 4.25%.
To calculate the external parameters of the laser beam, it is important to know the radiation strength, spot diameter and optical properties of the material. The physical phenomena that take place following the laser–material interaction are based on the transformation of laser energy into thermal energy. The increase in local temperature and the distribution of laser-induced heat change the thermal state of the metal by heating-melting-vaporization. The intensity of the incident radiation at the moment of penetration in the material is given by the relation:
The intensity of incident radiation entering the material at depth x follows the relation [35]:
where R is the coefficient of reflexion; A is the absorption coefficient.
The temperature inside the material developed by the absorption of laser radiation is a parameter that indicates the heat input required for heating with phase transformations of the target until melting. The absorption coefficient for metals is 10–15% for the CO2 laser wavelength of 10.6 µm [32]. The reflection coefficient depends on the wavelength; in the case of the CO2 laser it is 0.9. Draganescu et al. indicated that at 0.2% C, the thermal conductivity is 39 W/m*K [33]. Thus, we obtain the values of the physical quantities studied given in Table 6.

Table 6.
Values of intensity and temperature depending on the laser output power.
The dimensions of the target are larger in relation to the radius of the laser spot which generates a constant flow of energy while creating cuts of material, delimiting the slot. The cutting width dependence on the temperature and the incident intensity, under conditions of maximizing oxygen gas pressure and cutting speed, for the three levels of laser power used in the experiment are shown in Figure 6 and Figure 7.
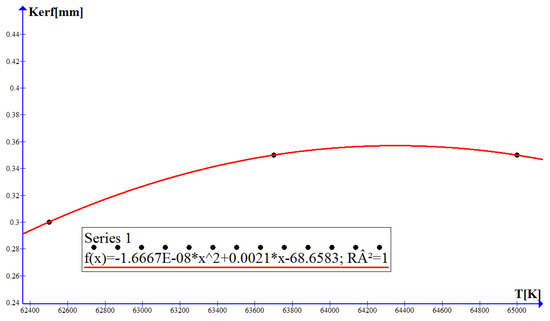
Figure 6.
Dependence of cutting width as a function of temperature.
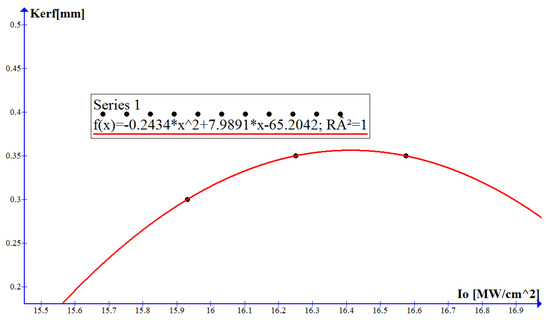
Figure 7.
Dependence of cutting width depending on the incident laser intensity.
The quadratic regression model of the cutting width as a function of the temperature produced by the laser in the material has the form:
The quadratic regression model of the cutting width as a function of the incident intensity produced by the laser radiation at the entrance to the material has the expression:
The second-order model of quadratic regression was developed for the cutting width by accessing data from independent experiments. The coefficient of determination R2 was calculated to verify that the data anticipated by the regression model are appropriate. When using the Graph program, the coefficient of determination is 1, which means that the mathematical accuracy of the regression is the most appropriate. When the temperature and power density increase, an increase in the cutting width is observed. The cutting width decreases as the temperature in the material and the incident intensity decrease.
If the laser power increases, the cutting width is disturbed due to the energy density. The situation leads to a longer interaction time between the laser radiation and the substance, and the slit increases due to thermal erosion. Specifically, the cutting efficiency of the laser beam decreases with the increase of energy received from the laser, due to losses through thermal conduction. Kerf was evaluated, and the results show a section of the slit as a V-profile, almost straight edges, parallel or A-shaped. In most cases, the top width is larger compared to its size at the bottom edge. Moreover, a sufficient amount of laser energy is absorbed more intensely at the upper edge of the Kerf profile. This energy is transformed into heat, thermal energy that melts a very small portion of the material locally, strongly heats the cut surfaces by changing the metallographic structure of the surfaces, the local change of the material characteristics. The local heat generated in the material, in the area affected by the laser, can trigger chemical reactions very quickly. As a result of the thermal action of the laser and the chemical reaction under the influence of an oxygen jet, changes in the size of the cutting width occur, so that at the lower edge of the material, an increased Kerf results due to burning and melting of cut material. In the process of interaction of laser radiation with the substance there is a temperature gradient through the cut that determines the heat in the slot.
The diffusion of heat through the sheet is based on the fact that, under the influence of the laser pulse, the optical energy is instantly transformed into heat. The incident intensity of the laser beam decreases as it enters the material. The gradient of laser radiation intensity can be explained by the fact that the material is resistant, the layers of molten material have different temperatures and the accumulated heat is removed from the slit more difficultly. The temperature difference between the two surfaces of the plate explains that the melt loses mass as it discharges to the bottom edge. The range of variation of the radiation intensity has a higher temperature of the molten area on the surface of the material, and a lower temperature on the lower surface of the steel plate, resulting in a smaller melting area.
In this study, the cutting width was determined as a function of laser power, gas pressure, material temperature and the incident intensity of laser radiation. The measured results are represented graphically in Figure 3 and Figure 4 showing a low Kerf at values close to 5000 W and gas pressures in the range of 0.47–0.48 bar. As can be seen from Figure 5 and Figure 6, in the case of the assisting gas pressure of 0.55 bar and a speed of 1900 mm/min, Kerf is the lowest. The same result happens at a temperature of 6.25 × 104 K and a minimum incident intensity of 15.931 × 106 W/cm2. The Kerf cutting width compared to the laser power, the assisting gas pressure, the working temperature and the incident intensity for the H400 sheet with a thickness of 8 mm has a square shape. These curves have a maximum for Kerf processing at oxygen gas pressures and cutting speed under maximizing conditions and a minimum that was reached at selected cutting pressures and inputs at average values. The average cost is for the CO2 laser installation applied to the 8 mm sheet for H400 at the value of 13.245 Euro/h. The function of approximating the cutting width according to the important cutting parameter, the low pressure of the assistant gas, run at three levels used in the experiment (0.45, 0.50, 0.55) bar is a Lagrange polynomial of quadratic order. The channel/cut is well formed during the O2 laser cutting of the steel when the input parameters are set to medium values and low power densities that cause lower surface and material temperatures, the important role being played by the minimum thermal energy that forms melt of minimal geometric dimensions and moving on the side walls along the cutting front. The evaluation of the influence of the input factors, laser power and gas pressure, but also of the physical quantities detached from the laser melting on the slit showed that under laser processing conditions, the distribution of these inlets in the slot have different parabolic shapes. The interaction between the input factors can create a minimal melt that removed from the slot will ensure a small cutting width between the piece and the sheet. There is a good agreement between the experimental model and the calculated one of the assistant gas pressure.
4. Discussion
4.1. Linear Predictive Model
The linear predictive model shown in Figure 8a shows that, during the cutting of the parts, the laser power was progressively changed to the values of 4900 W, 5000 W and 5100 W. A set value of the laser power outside the range of 4900–5100 W, indicates an increase in cutting width. The simultaneous variation of two parameters of influence (laser power, auxiliary gas pressure) on the cutting width, determines the most appropriate influence of the predictive factors if the level of the cutting speed is maintained at a constant value. The linear prediction graph rendered by the RSM method shows a 2D surface with the interaction between the laser power and the assistant gas pressure. The cutting width can be evaluated, following the interaction between two influencing factors, as follows:
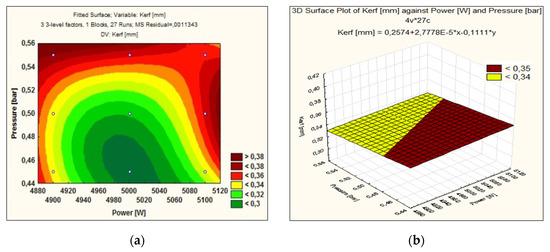
Figure 8.
(a) Linear predictive model of influence factors; (b) Linear dependence of cutting width as a function of laser power and gas pressure.
- When the laser power has values in the range 4980–5040 W while the assist gas pressure is in the range 0.45–0.48 bar, a cutting width of less than 0.3 mm results;
- The minimum gas pressure of 0.45 bar at the same time as the maximum power of 5100 W, has a cutting width <0.34 mm;
- The assist gas pressure at the average level, at the same time as maximum values of the laser power, shows a cutting width >0.38 mm. The same result is obtained when the laser power is maintained at the minimum value of 4880 W, at the same time as the oxygen gas pressure is located at the maximum value of 0.55 bar;
- If the laser power is the minimum of 4900 W and the assisting gas pressure is in the range 0.45–0.53 bar a cutting width <0.34 mm results;
- The change of the cutting gas pressure values compared to the values within the range 0.44–0.48 bar, at the same time as that of the laser power located in the range 4980–5040 W, determines a significant increase of the Kerf parameter;
- The laser power 5000 W, at the same time with the cutting gas pressure 0.45 bar ensures the best Kerf below 0.3 mm.
The linear prediction graph anticipates that the best results of the cutting width are obtained at low values of the assist gas pressure (0.45–0.48 bar) with values of the laser power in the range (4980–5040 W). The average value of the laser power leads to a better absorbability of the laser energy by the material, small amount of molten material, optimal heat distribution efficiency and low processing cost. A low value of the laser power negatively influences the melting process.
The linear mathematical model (Figure 8b) for the cutting width is given by the regression calculation in case of the interaction between the laser power (P) and the assistant gas pressure (p) by the relation:
In the ANOVA linear regression function, the interaction effect of the laser power term is higher than that of the assisting gas pressure (0.1111). It means that the most significant factor in determining the cutting width is the laser power. The positive sign indicates in the linear equation that the laser power is an influencing factor that determines the increase of the cutting width and the minus sign shows that the gas pressure acts in the direction of decreasing Kerf. The interaction of laser power and cutting gas pressure will change the geometry produced in the slit; the two independent factors optimized validate the quality of Kerf. Regression analysis studies the effect of each controllable factor on the Kerf response during laser cutting. This demonstrates that the laser parameters used in cutting have an influential effect on the results of the experiment. The line graph in Figure 8b shows the following:
- At a maximum power of 5100 W and a minimum assisting gas pressure 0.45 bar an average cutting width of 0.35 mm is obtained;
- At a minimum power of 4900 W and a minimum assisting gas pressure 0.45 bar a cutting width of approximately 0.34 mm results;
- The cutting width increases linearly with the laser power because the laser energy supplied to the material causes an excess heat, which changes the size of the cutting width under low pressure conditions. The cutting width decreases linearly with the increase of the auxiliary gas pressure at the same time with the laser power level of minimum up to the value of 0.33 mm;
- The cutting width 0.33 mm is obtained at power value of 4900 W and auxiliary gas pressure of 0.55 bar;
- The cutting width increases to values close to 0.34 mm when the gas pressure is maximum 0.55 bar and the laser power increases to a maximum value of 5100 W. Increasing the density of the energy flow contributes to the increase of the melting mass, the heat entering the material increases, which is why the width of Kerf increases;
- There is a similarity between the prediction and the linear regression model at gas pressure values of 0.52 bar at the same time as the laser power of 5000 W. The response surface graph for the linear regression model is a flat surface describing the cutting width perturbation. There are differences for average values of laser power and low pressure between the anticipated and the calculated model. Such differences occur due to the deviation of the values from the measurements compared to the average value. A possible cause may be the degree of heating of the steel plate. Another cause may be the low speed level, which causes a longer irradiation time of the steel plate, having the effect of increasing the cutting width. Increasing the cutting speed to the maximum level causes a short irradiation time and a lower heat absorption, and finally a minimum cutting width.
There is a similarity between the prediction and the linear regression model at gas pressure values of 0.52 bar and laser power of 5000 W. The regression model is different from the anticipated one due to the estimation of the cutting width. Possible causes would be technical, standard error, standard deviation, plate temperature gradient, pressure gradient and melt mass. The mathematical model more accurately estimates the width cut by its small variations and errors to an average value. The predictive model indicates lower values of the cut width due to the correlation between the laser energy and the heat flow distribution through the material at high values of the cutting speed. The disturbed values of the cutting width are obtained when the values of the laser power are antagonistic to those of the assist gas pressure. The two investigated models lead to the same value of the cutting width <0.34 mm, a good agreement due to the influence factors set at values close to the environment.
4.2. Quadratic Predictive Model
The 3D diagram in Figure 9 provides a clear picture of how the prediction factors, laser power and gas pressure affect the cutting width of Hardox 400 steel parts. It is observed that the smallest values of cutting width are obtained when the laser power is 5000 W, and the assist gas pressure has a low value located in the range 0.45–0.46 bar. The values increase with the distance (somewhat circular, semi-elliptical) from the area characterized by average power values and low pressure values. The highest values of the cutting width (over 0.38 mm) are obtained, on the one hand, for small values of the laser power, 4900 W, at the same time with increased values of the cutting gas pressure of about 0.55 bar, and on the other hand, at high laser power values 5100 W and gas pressure value of 0.50 bar.
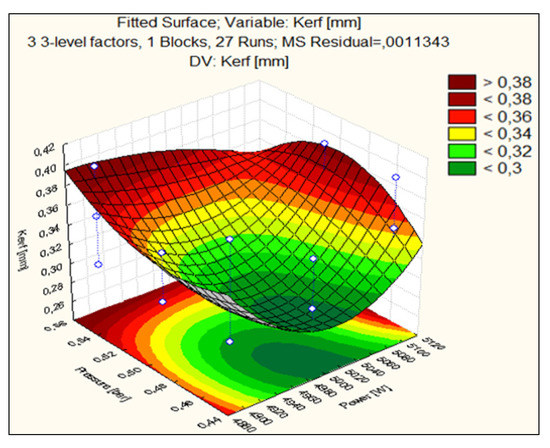
Figure 9.
Prediction of the dependence of the cutting width on the laser power and the assist gas pressure.
Specifically, the best cutting width (0.30 mm) is obtained for laser power 5000 W and auxiliary gas pressure 0.46 bar. For the response confidence interval of ±1 mm (width = 0.26–0.28 mm), the graph shows values of the laser power between 4980 and 5020 W, at the same time as the gas pressure between 0.45 and 0.48 bar. The response surface combines the shape of a classical paraboloid (in the centre) with a hyperbolic paraboloid (at the extremes) and shows that the cutting width has a variation of the shape of the Gaussian bell, with the tip on the average axis of laser power. If the laser power is maintained at average values and the gas pressure increases, the bell rises, which means that the cutting width increases. The predicted graph indicates a significant influence of the input parameters (power and pressure) on the cutting width using the RSM model.
The estimated square model of the cutting width, depending on the laser power and the assist gas pressure, using the regression technique is represented by the polynomial in Figure 10
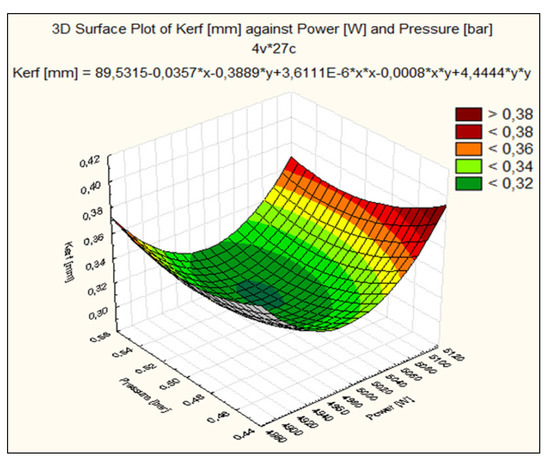
Figure 10.
Graph of the quadric dependence of the cutting width on the laser power and the assist gas pressure.
The term of the square laser power effect is greater than the term of the assistant gas pressure effect with the experimentally used data. It results that the significant factor is the laser power. The term containing the square of the laser power is positive, which means that the dominant effect of the laser power is to increase the value of the Kerf response, while the positive sign of the term containing the square of the pressure shows that the dominant effect of the second influencing factor, gas pressure, is of Kerf increasing. Furthermore, it can be seen that the important factors that interact with each other affect Kerf. From this identification it is found that the most influential factor on the kerf is the laser power, and the second significant factor is the assist gas pressure. The coefficient of the model is 89.5315, the correlation coefficient of the interaction between laser power and pressure is 0.0008, which indicates an effect conjugated with a Kerf reduction influence, and the linear correlation coefficients of laser power and gas pressure are low which shows a decrease Kerf take together with the level of independent factors.
By analysing Figure 9 the following aspects were deduced:
- The cutting width is a quadratic surface, resulting from the interaction between laser power and auxiliary gas pressure;
- The low value of the cutting width, below 0.32 mm, is obtained when the cutting gas pressure is 0.50 bar, and the gas pressure 5000 W;
- The shape of the Kerf variation in the RSM model is a paraboloid representing a quadratic surface that indicates a more pronounced influence of the laser power than the gas pressure. The Kerf graph depending on the laser power is steeper and longer compared to the graph representing Kerf depending on the cutting gas pressure which is less deformed, that is a curve less pronounced;
- The damaged values of the cutting width, over 0.38 mm, are obtained at 5100 W laser power and 0.45 bar gas pressure;
- From the spectral analysis of the colors (green to red) corresponding to the cutting width, there is an increase from the set values (average power and pressure) to the extremities;
- Comparing the quadratic model with the prediction given in Figure 9, we find that the minimum cutting width moves from minimum values of gas pressure to average values. The agreement between predictability and the statistical mathematical model for laser power is good, but there are significant differences in gas pressure. The explanation can be attributed to the increase in gas flow that increases the contact surface so that the cutting width increases. As the cutting gas pressure decreases, the area affected by the gas decreases and the cutting width is minimized. The gas jet is high (length at the outlet of the nozzle) when the pressure increases, the material melts in larger quantities, which leads to an increase in the cutting width, while an average jet of gas affects the steel plate less.
The variation of the laser power has as effect the change of temperature and implicitly of the viscosity of the melt. In the case of very narrow cuts, the operation of removing the melt is more difficult. The cutting gas pressure is influenced by the length of the gas flow, which determines a cutting force exerted on the cut surface. Changing the assistant gas flow has effects on Kerf geometry. The low cutting speed causes a significant accumulation of laser energy in the cutting area, which implies a larger cutting width. The cutting width on the top side is larger than the one on the bottom side as it is closer to the laser spot and captures a larger amount of energy. The heat is transmitted inwards with a negative heat gradient. The cutting width on the lower side is larger than on the upper side due to changes in the cutting parameters. There is a pressure gradient towards the outlet, as the amount of heat absorbed increases. Cylindrical cases are rare and depend on the structure of the material. The geometry of the beam changes in the material due to the section variation. The cut in the material is U-shaped due to the decrease of the transmitted energy, so that, at the bottom, the molten material is stationary. As the beam advances in the material it loses energy, so at certain depths the melting time is different.The cutting surface is parabolic, concave and test-tube-bottom shaped. Laser power is a physical quantity that influences the density of energy absorbed by the material. Energy density is closely related to power density and interaction time. If the laser power remains constant, the laser intensity in the material varies with the change of section. Oxygen gas pressure can influence the cutting width due to gas flow, gas flow length and nozzle diameter. The combination of laser power—gas pressure assistant can improve the cutting width.
The surface methodology of the Kerf response was developed and influenced by the laser power and the assist gas pressure. Graphs with response areas were obtained for the linear (L) and quadric (Q) models to predict and calculate the global Kerf. Laser power and gas pressure were chosen on the X and Y axes. The Kerf response for the straight profile is made on the Z axis. The prediction graph (L) due to the effects of the interaction between laser power and gas pressure is a curved flat surface. The linear shape of the Kerf answer is given by Equation (10). The graph (L) resulting from the mathematical modeling of the answer is a linear surface indicating the Kerf force. In conditions of average power and average pressure Kerf reaches the value of 0.34 mm. There is a good agreement between the prediction and the linear mathematical model for average values of laser power and gas pressure. The Kerf prediction graph contains the interaction effects of the laser power and the assist gas pressure. Kerf decreases sharply at average values of 5000 W of laser power compared to the average values of gas pressure, but also at minimum laser power with maximum gas pressure. The Kerf response surface contains several interaction effects due to input factors, and the surface area reaches the Kerf value. The prediction graph (Q) is a curved area at maximum values of laser power and gas pressure. The Kerf minimum is achieved at sensible variations compared to the average level of laser power and low gas pressure. The developed mathematical RSM (Q) model shows that the average gas pressure and the average laser power have a Kerf size reduction effect. The curve due to the effects of laser power is steeper than due to the effect of working gas pressure, which means that laser power had a greater effect in reducing Kerf, being the most significant parameter. The gas pressure had a lower effect in terms of Kerf size compared to laser power. These quadratic models of predictability and regression can reduce the cost of the experiment and the working time. The minimum Kerf < 0.32 mm is obtained at p = 5000 W and the pressure of 0.45 bar, and the maximum Kerf > 0.38 mm results at the maximum power of 5100 W and the cutting gas pressure equal to 0.45 bar. The quadratic model is more complete than the linear model because it contains quadratic interactions of process parameters, linear interactions, and interactions of each type, so it is possible to obtain a better cutting width for Kerf in the case of the straight cut profile. Square RSM (Q) graphs predict and estimate Kerf for average values of laser power and are significantly different for cutting gas pressure due to instability of cutting flow. In any case, maximised laser power and gas pressure damage Kerf due to the accumulation of caloric energy, and the increased gas flow maximises Kerf at minimum values of the energy received from the laser. Kerf is optimized when the technical characteristics chosen are the gas pressure in the range (0.44–0.52 bar) at the same time with the laser power around (4920–5080 W). The quadric model is a restricted mathematical analysis model that requires that the parameters of studied cutting, laser power and gas pressure tend to the average values used in the experiment. As there is relatively good comparative agreement between prediction (Q) and regression (Q), it is possible that other external factors influence the process: temperature in the material, heat gradient, state of the material and chemical composition.
Statistical models were developed to validate the Kerf regression equations (linear and quadratic). The effect of each input parameter, the interaction between the parameters, the standard deviation, the Student’s t-test and the probability of error are presented in Table 7.

Table 7.
Statistical data regarding the effects of influencing factors on cutting width.
From Table 7 provided by the Statistics 7.0 program results: the coefficient of determination R2 = 0.74211, the adjustment coefficient Adj = 0.16184 and the standard deviation STD = 0.01122. The average cutting width is 0.348 mm resulting from a complete factorial experiment with 27 trials. There is a 7421% chance that the influencing factors and their interactions will determine the cutting width. The adjustment coefficient helps to detail the process and the influence of the independent parameters. The normal distribution of the cutting width is within a maximum of two standard deviations from the central mean (media): cnf. limit (–95%) = µ-2σ = 0.322 mm and cnf. limit (+95%) = µ + 2σ = 0.374 mm. The Student’s t-test (t) equal to 31.01196 and the probability p < 0.05 (corresponding to the average, on the first line of the table) show that the relationship between the influencing factors and the cutting width is appreciable. The value distribution of the cutting width is normal, the distribution graph is plotted by the Gaussian curve, and the maximum height is the arithmetic mean µ = 0.348 mm.
For verification, the initial experiment was replicated four times, at equal intervals. The average cutting width for each replica was calculated. The following values were obtained: µ1 = 0.335 mm, µ2 = 0.338 mm, µ3 = 0.317 mm, µ4 = 0.348 mm. Notice that replica 3 has the best average. For the 3rd replica we have: , standard deviation: , and tcrit = 1.706, critical intervals , probability p = 0.95, significance level 1 – p = 0.05, number of the block n = 27, number of freedon degrees df = n – 1 = 26. The t-test parameter of the Student distribution belongs to the critical region, and the H0 hypothesis is rejected, so that the average cutting width of the initial design differs significantly from the average of three replicates. In conclusion, there is a statistically significant difference between the two averages. In the case of reply 4, an uncontrolled disturbing factor intervened, which altered to some extent the experimental results. Table 7 uses the significance of the indices: (1) laser power, (2) gas pressure, (3) cutting speed. Q and L also refer to the term square and linear. 1L by 2Q means the influence of linear power combined with square gas pressure. The effect determines the correlation coefficient of the shear parameters in determining the polynomial that describes the Kerf answer.
The parameter of the Student’s t-test distribution belongs to the critical region, and the H0 hypothesis is rejected, so that the average cutting width of the initial design differs significantly from the average of three replicates. In conclusion, there is a statistically significant difference between the two averages. In the case of reply 4, an uncontrolled disturbing factor intervened, which altered to some extent the experimental results. Table 8 uses the significance of the indices (1) laser power, (2) gas pressure, (3) cutting speed. In addition, Q and L refer to the square and linear term. 1L by 2Q means the influence of linear power combined with square gas pressure. The effect determines the correlation coefficient of the cutting parameters in determining the polynomial that describes the Kerf answer.

Table 8.
Influence of laser power and assisting gas pressure at CO2 laser cutting.
The developed regression models have acceptable values of standard deviation. Due to the high standard error, the probability of error is high. The probability p > 0.05 shows that the terms of the model are not significant (Table 8). The statistical table reduced after the comparison p > t, to establish the significance of each influencing factor and the interactions between them, shows that the input parameters randomly influence the cutting process. In Table 8 the project has no interaction with significant influence on the Kerf response. The experimental data are adequate for the regression model. The correlation model was used to determine the most influential input parameter on Kerf. In this study the linear and quadratic regression model is the most appropriate. The graphs show the effect of the interaction between the influencing factors, the laser power and the cutting gas pressure in establishing the Kerf variation.
The novelty of the paper consists in the use of a material for which in the specialized literature there were no references related to the cutting width for CO2 laser processing. In addition, the influence of incident intensity and material temperature on Kerf was established. In addition to the technical aspects presented, the study presents the determination of the processing cost for laser cutting. The results complete other research on other steel grades [25]. The study is more deepened if we take into account the energy of the laser beam. The melting efficiency which takes into account Kerf is mathematically expressed [40]:
where σcut is the cutting efficiency (how many mm2 are cut with 1 Joule) (mm2/J); σmelt is the melting efficiency (mm3/J).
The mathematical modeling of the laser thermal manufacturing is based on the following reasoning: at the interaction of laser radiation with the part material the light energy is instantly transformed into thermal energy, strongly heating a volume V forming the melt [23]. The amount of heat required for heating is Q, and the elementary variation dQ:
The absorbed heat flux q entering the elementary surface is in a Gaussian relation with the characteristics of the laser beam by the relation.
The heat in the melt is achieved by decreasing the temperature along the Oz axis, the temperature gradient during t period is:
The radial coordinate r can be calculated by the mathematical relation:
where q0 is the heat flux absorbed in the center of the circular region (W/cm2); r0 is the laser beam radius on the material (mm); c is the specific heat (J/kgxK); zm is the melting heat (µm); ρ is the material density (kg/m3).
5. Conclusions
This paper investigates the process of manufacturing CO2 laser cutting parts from H400 material. The experimental research was designed according to an experimental plan that was replicated four times to observe the variation of the Kerf mean response. The study investigates the coefficients of controllable parameters to establish the significance and influence of each input factor. The independent parameters selected during the cutting experiments are laser output power, auxiliary gas pressure and cutting speed. Based on the independent experiments, their observations and analysis, the following conclusions were drawn:
- An important role in the melting of the material is the heat gradient that influences the cutting, having an unstable role in the upper and lower face of the semi-finished product, which influences the hydrodynamic processes in the melt;
- The cutting width is dependent on the assisting gas pressure through a quadratic interpolation function;
- The incident laser intensity, the working temperature and the laser intensity at the output of the material are physical quantities analytically determined;
- The quadratic prediction shows that a cutting width of 0.3 mm is obtained at the laser power inlet level in the range (4980–5020 W) and the cutting gas pressure in the range (0.47–0.51 bar);
- Contrary to prediction, the square regression response surface model indicates a cutting width <0.32 mm, if the laser power is 5000 W and the assisting gas pressure is 0.5 bar. A relatively good agreement was obtained between the predictive model and the regression mathematical model;
- The regression graph, indicated by the RSM response area, shows a Kerf value affected as the laser power is 5100 W and the gas pressure in the range (0.46–0.48 bar), but also in the case of laser power of 4900 W and low gas pressure of 0.45 bar, resulting in a Kerf >0.40 mm. It is observed that the edges of the laser power adjustment range at the same time with low gas pressure indicate a negatively affected Kerf;
- Opposite extreme values, laser power and gas pressure, increase the width of the Kerf;
- The term laser power, in the linear (Equation (10)) and quadric (Equation (11)) polynomials, has the higher effect showing that laser power is the most influential input factor;
- The prediction linear model of the cutting width is in relative agreement with the calculated polynomial model, the laser power being the most significant parameter in determining the cutting width. The calculated linear model indicates a Kerf of 0.33 mm for the power of 4900 W and the gas pressure of 0.45 bar. The differences between the linear and quadric result are due to the heating of the material during processing;
- The quadric model is more accurate because it takes into account the interactions between laser power and auxiliary gas pressure, at a constant level at the cutting speed. It also takes into account the combined action of the parameters on Kerf, while the linear model takes into account the independent action of one factor or the other;
- Pressure is the second significant factor in relations (Equations (10) and (11)). This influences the cutting process through the pressure gradient that eliminates the melt, hot drops and heat transfer through the slot;
- High power causes an increased power density, which induces a higher amount of heat in the material, resulting in increased Kerf.
Response surface models for the evaluation of the Kerf cutting width at the straight profile using the full factorial design L27 were considered appropriate. The empirical data developed are used to predict and calculate the global mean of the Kerf response using the linear (L) and quadric (Q) response area model. From the response graph (Q) it could be seen that the laser power had a more pronounced effect in reducing the Kerf size compared to the pressure. To obtain a small Kerf it is necessary to select an average value of the gas pressure observed using the regression model (Q). In the case of the calculated linear model (L) it is observed that a low Kerf is obtained at the low value of the laser power and the increased gas pressure. These models can be used successfully to anticipate Kerf at the right profile in the case of CO2 laser cutting of the H400 sheet. The RSM model can be used to predict Kerf under the influence of other cutting parameters to optimize Kerf at the right profile. A minimum straight profile Kerf of 0.33 mm is obtained when cutting parameters such as gas pressure and laser power are maintained at 0.55 bar and 4900 W, as indicated by model (L). A minimum kerf of 0.30 mm can be obtained when we maintain the laser power at 5000 W and the cutting gas pressure at 0.50 bar. As a result, we propose to use the combination of values: laser power p = 5000 W, auxiliary gas pressure p = 0.50 bar at constant cutting speed v = 1900 mm/min to obtain a fine cut.
Author Contributions
Conceptualization, C.C.G.; methodology, C.C.G., C.G. and C.R.; software, C.R. and C.C.G.; validation, C.G., C.R. and C.C.G.; formal analysis, D.C.; investigation, C.C.G.; resources, C.R.; data curation, C.R.; writing—original draft preparation, C.C.G., C.R. and C.G.; writing—review and editing, C.C.G. and C.G.; visualization, D.C. and C.R.; supervision, C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The experimental research used in this study was conducted with the support of SC BYSTRONIC Brasov, the authors thank for the technical support provided in conducting this experiment with CO2 laser. Figure 3a,b was made at the Oltenia Energy Complex, Measurement Laboratory of the Rovinari Thermal Power Plant.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tatzel, L.; Leon, F.P. Impact of the thermally induced focus shift on the quality of a laser cutting edge. J. Laser Appl. 2020, 32, 022022. [Google Scholar] [CrossRef]
- Levichev, N.; Rodrigues, G.C.; Dewil, R.; Duflou, J.R. Anticipating heat accumulation in laser oxygen cutting of thick metal plates. J. Laser Appl. 2020, 32, 022018. [Google Scholar] [CrossRef] [Green Version]
- Madic, M.; Mladenovic, S.; Gostimirovic, M.; Radovanovic, M.; Jankovic, P. Maximization of material removal rate in CO2 laser cutting of mild steel. J. Eng. Manuf. 2020, 134, 1323–1332. [Google Scholar] [CrossRef]
- Moradi, M.; Moghadam, M.K.; Shamsborhan, M.; Bodaghi, M.; Falavandi, H. Post-processing of FDM 3D-printed polylactic acid parts by laser beam cutting. Polymers 2020, 12, 550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pramanik, D.; Kuar, A.S.; Sarkar, S.; Mitra, S. Enhancement of sawing strategy of multiple surface quality characteristics in low power fiber laser micro cutting process on titanium alloy sheet. Opt. Laser Technol. 2020, 122, 105847. [Google Scholar] [CrossRef]
- Darwish, M.; Mrna, L.; Orazi, L.; Reggiani, B. Modeling and analysis of the visualized gas-assisted laser cutting flow from both conical and supersonic nozzles. Int. J. Adv. Manuf. Technol. 2020, 106, 4635–4644. [Google Scholar] [CrossRef]
- Jiang, D.; Panjehpour, A.; Niazi, S.; Akbari, M. Laser Cutting of Al 6061-T6 Aluminium Alloy Sheet: Effect of Cutting Condition and Sheet Thickness on the Temperature and Edge Cut Quality. Lasers Eng. 2020, 45, 293–308. [Google Scholar]
- Eltawahni, H.A.; Hagino, M.; Benyounis, K.Y.; Inoue, T.; Olabi, A.G. Effect of CO2 laser cutting process parameters on edge quality and operating cost of AISI316L. Opt. Laser Technol. 2012, 44, 1068–1082. [Google Scholar] [CrossRef] [Green Version]
- Nath, S.; Das, A.; Inaba, K.; Karmakar, A. simulation of laser cutting on functionally graded material used in aviation industry. In Proceedings of the Asme Gas Turbine India Conference, Chennai, India, 5–6 December 2019. [Google Scholar]
- Sibalija, T.; Petronic, S.; Milovanovic, D. Experimental optimization of nimonic 263 laser cutting using a particle swarm approach. Metals 2019, 9, 1147. [Google Scholar] [CrossRef] [Green Version]
- Savanth, T.; Singh, J.; Gill, J.S. Laser power and scanning speed influence on the microstructure, hardness, and slurry erosion performance of Colmonoy-5 claddings. J. Mater. Des. Appl. 2020, 234, 947–961. [Google Scholar] [CrossRef]
- Kang, Y.Y.; Derouach, H.; Berger, N.; Herrmann, T.; L’huillier, J. Experimental research of picosecond laser based edge preparation of cutting tools. J. Laser Appl. 2020, 32, 022043. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Deng, W.; Showaib, E.A. Improving laser cutting quality of polymethylmethacrylate sheet: Experimental investigation and optimization. J. Mater. Res. Technol. 2020, 9, 1325–1339. [Google Scholar] [CrossRef]
- Hajad, M.; Tangwarodomnukun, V.; Jaturanonda, C.; Dumkum, C. Laser cutting path optimization with minimum heat accumulation. Int. J. Adv. Man. Technol. 2019, 105, 2569–2579. [Google Scholar] [CrossRef]
- Seong, Y.O.; Jae, S.S.; Taek, S.K.; Hyunmin, P.; Lim, L.; Chin-Man, C.; Jonghwanm, L. Effect of nozzle types on the laser cutting performance for 60-mm-thick stainless steel. Opt. Laser Technol. 2019, 119, 105607. [Google Scholar]
- Anghel, C.; Gupta, K.; Jenb, T.C. Analysis and optimization of surface quality of stainless steel miniature gears manufactured by CO2 laser cutting. Optik 2020, 203, 164049. [Google Scholar] [CrossRef]
- Chen, C.; Zeng, X.; Wang, Q.; Lian, G.; Huang, X.; Wang, Y. Statistical modelling and optimization of microhardness transition through depth of laser surface hardened AISI 1045 carbon steel. Opt. Laser Technol. 2020, 124, 105976. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Wang, J.; Allegre, O.; Guo, W.; Gao, W.; Jia, N.; Li, L. Stealth dicing of sapphire sheets with low surface roughness, zero kerf width, debris/crack-free and zero taper using a femtosecond Bessel beam. Opt. Laser Technol. 2020, 135, 106713. [Google Scholar] [CrossRef]
- Subasi, L.; Diboine, J.; Gunaydin, A.; Tuzemen, C.; Ozaner, O.C.; Martin, R. Water jet guided laser microdrilling of aerospace alloys: Correlation of material properties to process time and quality. J. Lasers Appl. 2021, 33, 012015. [Google Scholar] [CrossRef]
- Das Partha, P.; Chakraborty, S. Application of superiority and inferiority multi-criteria ranking method for parametric optimization of laser cutting processes. Pro. Int. Opt. Sust. 2020, 4, 409–427. [Google Scholar]
- Cheng, E.; Yang, X.; Yin, Z.; Hu, W.; Li, L. Low cost and simple PMMA nozzle fabrication by laser cutting and PDMS curing bonding. Int. J. Prec. Eng. Manuf. 2021, 22, 139–146. [Google Scholar] [CrossRef]
- Powell, J.; Frass, K.; Menzies, I.A. 2.5 Kw laser cutting of steels. Factors affecting cut quality in sections up to 20 mm. In Proceedings of the Fourth International Symposium on Optical and Optoelectronic Applied Sciences and Engineering, The Hague, The Netherlands, 30 March–3 April 1987; Volume 0801.
- Dontu, O. Laser Processing Technologies; Technical Publishing House: Bucharest, Romania, 1985; pp. 74–80; 89–91. [Google Scholar]
- Savii, G. Lasers; Facla Publishing House: Timisoara, Romania, 1981; pp. 82–88; 117–127. [Google Scholar]
- Draganescu, V.; Velculescu, V.G. Laser Thermal Processing; Academy Publishing House: Bucharest, Romania, 1986; pp. 70–88; 130–138. [Google Scholar]
- Genna, S.; Menna, E.; Rubino, G.; Tagliaferri, V. Experimental investigation of industrial laser cutting: The effect of the material selection and the process parameters on the kerf quality. Appl. Sci. 2020, 10, 4956. [Google Scholar] [CrossRef]
- Son, S.; Lee, D. The effect of laser parameters on cutting metallic materials. Materials 2020, 13, 4596. [Google Scholar] [CrossRef]
- Tahir, A.F.M.; Rahim, E.A. A study on the laser cutting quality of ultra-high strength steel. J. Mech. Eng. Sci. 2016, 10, 2146–2159. [Google Scholar]
- El Aoud, B.; Boujelbene, M.; Bayraktar, E.; Ben Salem, S. Optimization of kerf quality during CO2 laser cutting of titanium alloy sheet Ti-6Al-4V and pure titanium Ti. In Mechanics of Composite, Hybrid and Multifunctional Materials; Springer: Berlin/Heidelberg, Germany, 2019; Volume 5, pp. 213–219. [Google Scholar]
- Chatterjee, S.; Mahapatra, S.S.; Mondal, A.; Abhishek, K. An experimental study on drilling of titanium alloy using CO2 laser. In Proceedings of the ASME 2017 Gas Turbine India Conference, Bangalore, India, 7–8 December 2017; American Society of Mechanical Engineers: New York, NY, USA; p. V002T10A006. [Google Scholar]
- Gvozdev, A.E.; Golyshev, I.V.; Minayev, I.V.; Sergeyev, A.N.; Sergeyev, N.N.; Tikhonova, I.V.; Khonelidze, D.M.; Kolmakov, A.G. Multiparametric Optimization of Laser Cutting of Steel Sheets. Inorg. Mater. App. Res. 2015, 6, 305–310. [Google Scholar] [CrossRef]
- Patel, J.M.; Patel, D.M. Parametric investigation in CO2 laser cutting Quality of Hardox-400 materials. Int. J. Eng. Sci. Tech. 2011, 3, 5979–5984. [Google Scholar]
- Patel, A.; Bhavsar, S.N. Experimental investigation to optimize laser cutting process parameters for difficult to cut die alloy steel using response surface methodology. Mater. Today Proc. 2021, 43, 28–35. [Google Scholar] [CrossRef]
- Prajapati, B.D.; Patel, R.J.; Khatri, B.C. Parametric Investigation of CO2 Laser Cutting of Mild Steel and Hardox-400 Material. Int. J. Emerg. Tech. Adv. Eng. 2013, 3, 204–208. [Google Scholar]
- El Aoud, B.; Boujelbene, M.; Boudjemline, A.; Bayraktar, E.; Salem, S.B.; Elbadawi, I. Investigation of cut edge microstructure and surface roughness obtained by laser cutting of titanium alloy Ti-6Al-4V. Mater. Today Proc. 2021, 44, 2775–2780. [Google Scholar] [CrossRef]
- Boujelbene, M.; El Aoud, B.; Bayraktar, E.; Elbadawi, I.; Chaudhry, I.; Khaliq, A.; Ayyaz, A.; Elleuch, Z. Effect of cutting conditions on surface roughness of machined parts in CO2 laser cutting of pure titanium. Mater. Today Proc. 2021, 44, 2080–2086. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, H.; Zhao, Z.; Li, K.; Yin, J. Numerical Simulation and Verification of Laser-Polishing Free Surface of S136D Die Steel. Metals 2021, 11, 400. [Google Scholar] [CrossRef]
- Ursu, I.; Mihailescu, I.N.; Prokhorov, A.M.; Konov, V.I. The Interaction of Laser Radiation with Metals; Academy Publishing House: Buchharest, Romania, 1986; pp. 60–75; 205–209. [Google Scholar]
- Available online: https://www.ssab.com/Products/Brands/Hardox/Products/Hardox-400 (accessed on 12 March 2021).
- Pocorni, J.; Petring, D.; Powell, J.; Deichsel, E.; Kaplan, A.F.H. The effect of laser type and power on the efficiency of industrial cutting of mild and stainless steels. ASME. J. Manuf. Sci. Eng. 2016, 138, 031012. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).