Abstract
To understand the hydraulic vibration characteristics in a traditional hydropower system and identify possible exciting sources that may induce serious hydraulic vibrations in the flow passage, experimental tests and numerical calculations were conducted for different operating conditions. The experimental results show that the pressure fluctuations are mainly related to the vortex rope phenomena in the draft tube, and the dominant frequency of pressure fluctuation is 0.2~0.4 times the runner rotational frequency (fn). The numerical results show all the attenuating factors are negative, which indicates the system itself is stable on the condition that all the hydraulic elements have steady operating performance. The free vibration analyses confirm that the frequency range of the vortex rope in the draft tube partly overlaps the natural frequencies of the hydropower system. Apart from the vortex rope, the runner rotational frequency is another common frequency that is approximately equal to the frequency of the 10th vibration mode. From the vibration mode shapes, it is inferred that a small disturbance in its frequency close or equal to a specific natural frequency of the vibration mode could induce large pressure oscillations in the tail tunnel. In light of the system’s response to different forcing frequencies, the vortex rope formed under off-design conditions and runner rotational frequency is verified to be the potential exciting source of a traditional hydropower system, and the frequency 0.2 fn is much more dangerous than other disturbances to the system.
1. Introduction
Nowadays, the increasing global demands for electricity and environmental protections are gradually bringing about the transformation of energy structure such that clean and renewable energy covers an increasing proportion of energy consumption [1]. In this aspect, hydropower plays an irreplaceable role in the clean and renewable energy system, and attracts much attention [2]. Hydraulic turbines are designed for working at the rated head and rated discharge, which is defined as the best efficiency point (BEP), while the current tendency for hydropower plants is that they are undertaking increasing power frequency regulation tasks in the electric grid, and turbines are required to work at off-design conditions more than before [3]. Vibrations exist in various fields, including hydropower stations, and vibration mitigations have been extensively investigated by researchers [4,5]. Recently, more hydraulic vibration phenomena in hydropower systems have been reported accompanied by obvious pressure oscillations along with their hydro-mechanical systems, and even severe accidents, such as local structural damages and power swings, have happened [6].
When turbines operate under off-design conditions, pressure fluctuations due to rotor–stator interaction (RSI), rotating stall, vortex rope, and other flow instabilities might be induced, and accompanying vibration phenomena may be generated [7,8]. Numerous studies, including model experimental tests and numerical simulations, have been conducted to investigate the pressure fluctuations under various off-design conditions. With an overall literature review, it was pointed out that pressure fluctuations in the turbine caused by transient processes would result in fatigue development in the runner, and then shorten the life span of the runner [9]. Based on CFD simulations and validated by experiments, rotor–stator interactions (RSI) were reported to be the primary cause of pressure fluctuation in the vaneless space, and the geometric and operating parameters of the unit were the main affecting factors [10,11,12]. Moreover, vortex rope in the draft tube was an unavoidable problem that formed under off-design conditions, and this would cause low-frequency but high-amplitude pressure fluctuations in the draft tube that propagate upstream and downstream [13,14]. Qin et al. discovered that the Thoma number influenced not only pressure fluctuation amplitude but also the distribution of the frequency components of pressure fluctuation in the draft tube [15]. Yu et al. discovered that there is a close relation between vortex rope and cavitation in the draft, such tube that the cavitation increases the vortex production as well as the pressure fluctuation frequency induced by vortex rope [16]. Apart from traditional hydraulic turbines, for a pump-turbine operating under off-design conditions, especially in S-shaped regions, pressure fluctuation in the flow passage is also attracting increasing attention [17,18,19]. Through numerical simulations of a pump-turbine working in an off-design way, it has been reported that the low-frequency pressure fluctuations originate from the rotation of vortices in the draft tube; further, the number of runner blades had an impact on the dominant frequency of pressure fluctuations in the draft tube [20,21]. The vibration affected the security of the hydropower station, and various strategies used to suppress vortex rope oscillation in the turbine flow passage have been explored [22,23]. In view of the pressure fluctuation caused by the vortex rope under off-design conditions, a novel passive control method using an adjustable diaphragm is introduced in decelerating swirling flow; further, the water injection method was proposed to mitigate the pressure fluctuation and change the velocity field in the flow passage, and correlation between the water jet discharge and vortex rope has been investigated [24,25]. However, the experimental method is restricted owing to its high costs and security risk, and the numerical simulation, including the one-dimensional method of characteristics (1D-MOC) and three dimensional (3D) numerical simulations [26] based on computational fluid dynamics (CFD), sometimes requires plenty of computation time, since the process of convergence to a stable state is very slow for long-distance water conveyance systems [27,28].
Hydraulic vibration is a periodic hydraulic transient that exists in various water conveyance systems and may result in instabilities and local destructions [29,30]. With complex condition switches under frequency regulation tasks, both the initial and boundary conditions become extremely complicated, especially for off-design conditions. If frequencies of exciting sources are coincident with the natural frequencies of the hydropower system and continuous working, hydraulic resonance will inevitably develop, and severe pressure oscillations may occur. Consequently, intense flow-induced pressure oscillations may lead to strong vibrations and structural damages [31]. As hydraulic turbines are subjected to increasing off-design operating conditions, the resonance may originate from the vortex rope in the draft tube when its frequency is approximately close to the intrinsic frequency of the water oscillation [32]. However, the exciting sources of hydraulic vibration in hydropower systems have not yet been revealed, and it is imperative to have a clear understanding of the exciting sources of hydraulic vibration in hydropower systems so as to ensure safety and stability during the operating process.
In this paper, pressure fluctuations in the turbine are analyzed, and possible exciting sources that may induce hydraulic vibration in hydropower systems are identified. Firstly, experimental tests were carried out for three off-design conditions by utilizing a reduced scale model runner to monitor pressure fluctuation characteristics in the spiral case, vaneless space, draft tube cone, and draft tube elbow. Secondly, based on transfer matrix and hydraulic impedance methods, free vibration analyses were performed to assess the vibration characteristics, including natural frequencies with attenuating factors of each order, and corresponding vibration mode shapes. Finally, the pressure fluctuations were analyzed in both the time domain and the frequency domain. Then, by comparing the frequency characteristics of pressure fluctuations with natural frequencies of the hydropower system, the correlations between flow instabilities in the hydraulic turbine and hydraulic vibration were revealed, and possible exciting sources were identified.
2. Research Object Description
The research project in this paper involved two turbines with a capacity of 1015 MW per unit. This set up consists of two parallel water diversion penstocks and tail branches, a downstream surge tank, and a D-shaped tail tunnel with a maintenance tail gate shaft located next to the tail water. Figure 1 is a sketch of the plan layout and detailed division information of the hydropower system.
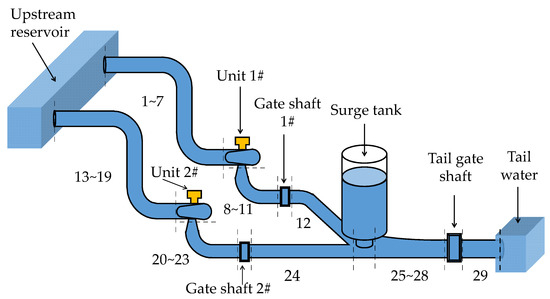
Figure 1.
Sketch of the plan layout of the hydropower system.
Table 1 lists the details of each pipe segment, including length and equivalent diameter, in the hydropower system.

Table 1.
Basic parameters of the pipe in the hydropower system.
The specific parameters of the prototype turbine are as follows: the rated output Pr = 1015 MW, the rated head Hr = 202 m, the rated discharge Qr = 545.49 m3/s, and the rated rotational speed nr = 111.1 r/min. The maximum and minimum head of the prototype turbine are Hmax = 243.1 m and Hmin = 163.9 m, respectively. The test rig consists of a spiral casing, a scaled model turbine runner with 15 blades, and a draft tube.
Figure 2 shows the comprehensive characteristic curves of the turbine. Here, Q11 and n11 stand for the unit discharge and unit speed, respectively, which are defined as and . From Figure 2, the optimal operating conditions for the turbine are guide vane opening a = 18.8°, unit speed n11 = 53.07 r/min, unit flow rate Q11 = 0.579 m3/s, and peak efficiency = 95.07%.
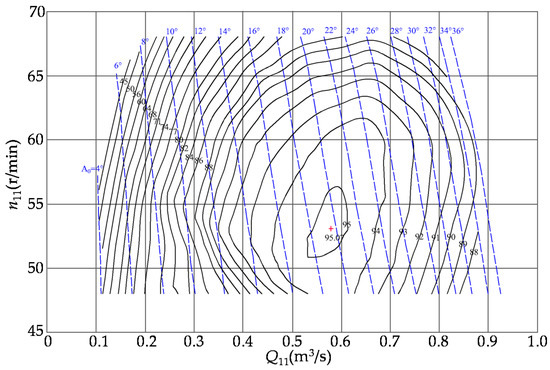
Figure 2.
Comprehensive characteristic curves of the turbine.
3. Materials and Mathematical Model
3.1. Governing Equations
For a single pressurized pipe, as shown in Figure 3, the simplified governing equations for the internal steady-oscillatory flow, including the momentum equation and continuity equation, can be deduced by simplifying differential equations of transient flow [33]. The two governing equations are as below,
where , , H is the instantaneous pressure head, Q is the instantaneous discharge, and are the average value, and and are the fluctuation value from the average. x is length to the inlet, t is the time, g is the gravity acceleration, f is the friction factor, A is the cross-sectional area of the pipe, D is the diameter of the pipe, and a is the wave speed.
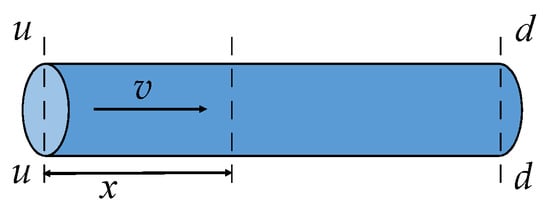
Figure 3.
Single characteristic computing pipe.
By substituting the instantaneous items into Equations (1) and (2), and removing the average items, the following form of equations can be obtained and written as
where , , , , , , L, C, and R are defined as the hydraulic inductance, hydraulic capacitance, and hydraulic resistance of the fluid in the pressurized pipe, respectively.
Application of the Laplace transformation yields the following subsidiary equation,
where is the transformation of , . s = σ + iω, s is the complex frequency, σ is coefficient of attenuation, and ω is angular frequency.
Assuming the oscillatory pressure head and discharge at the upstream end are known, the complex oscillatory pressure head and discharge are expressed as
where is the characteristic impedance of the pipe, is the complex propagation constant, and x is the length from the inlet.
3.2. Transfer Matrix and Hydraulic Impedance Methods
The transfer matrix is a square matrix that relates two state vectors at any point of the pipe by introducing matrix form. Hydraulic impedance is defined as the ratio of the complex head to the complex discharge at the same cross-section. Expressions of some commonly used hydraulic elements have already been established [33,34]. Generally, for various complicated pressurized water conveyance systems, hydraulic vibration analyses are realized by combining the transfer matrix and hydraulic impedance. Two kinds of matrices are commonly used.
3.2.1. Field Matrix
The field transfer matrix connects state vectors at adjacent cross-sections in the same pipe, and as previously deduced, the field matrix of a single pressurized pipe with a length of l is
3.2.2. Point Matrix
The point transfer matrix relates the left and right state vectors of local discontinuity, such as a junction, valve, turbine, etc. The point matrices of several common hydraulic elements are presented below.
For a series junction connecting two pipes, neglecting the minor losses and obeying the relationship QD1 = QU2, HD1 = HU2, the point matrix is,
The equations for a hydraulic machine operating at a fixed speed can be expressed in a simplified matrix form if there is no excitation pressure head and flow rate at the turbine point,
where M is the slope of the head–discharge curve, and the value of M is usually assumed to be a real constant for pumps and turbines if the opening of guide vanes remains constant in the transient regime.
For a throttled surge tank installed in the system shown in Figure 4, the equation of motion is applied to the fluid in the pipeline between the upstream and downstream ends, and the friction term is linearized while the mean flow conditions are subtracted.
where k, As, and l are the head loss coefficient, cross-sectional area, and water depth in the surge tank, respectively.
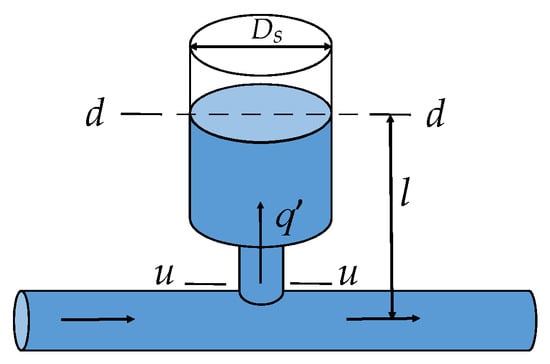
Figure 4.
Sketch of the throttled surge tank.
Based on the continuity equation , the Laplace transformation of hd can be derived, .
Applying the Laplace transformation to Equation (9), the impedance formula can be wrtiten,
Therefore, the matrix of a throttled surge tank is
For the parallel system in Figure 5 with no forcing function, the field matrix of path j is expressed as . Then, the overall field transfer matrix of the whole parallel system is
where , and are , , and , respectively.
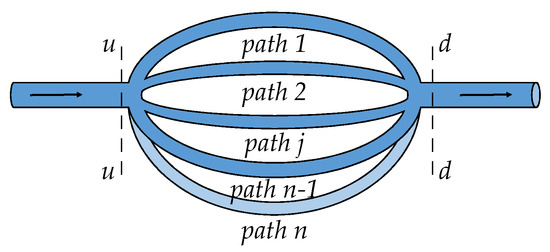
Figure 5.
Parallel system.
3.3. Hydraulic Vibration Analysis
3.3.1. Free Vibration Analysis
Free vibration is the residual oscillation in the absence of an external disturbance, and the aim of conducting free vibration analysis is to obtain the complex frequencies of a given system, as well as the corresponding vibration mode shapes. With some commonly used hydraulic elements, the characteristic equations of the whole pressurized water conveyance system can be derived, and the overall matrix that relates the boundary data at two terminal points of the system is expressed as
For the condition wherein the upstream is a reservoir and the outlet is a tailwater, and water elevation remains constant, HU = 0, HD = 0, which means the impedance values at the inlet and outlet are both zero. Hence, the characteristic equation of the system is written as below,
By solving Equation (14), we can obtain the complex frequency sk (k = 1,2,3,…).
3.3.2. Forced Vibration Analysis
A periodic external disturbance that continues acting on a certain boundary, and which can generate steady oscillatory flow, is recognized as forced vibration. The purpose of forced vibration analysis is to investigate the system’s response to a known forcing function that existed all the time. In a fully developed forced vibration, the whole system oscillates with the frequency of the forcing function, and the complex frequency only contains an imaginary part, s = iωk, the attenuate factor, while σ = 0 means the vibration amplitude was independent of time.
3.4. Mathematical Model of Pressurized Flow in the System
For the hydropower system shown in Figure 1, based on the transfer matrix and hydraulic impedance method, the overall transfer matrix of the entire system was built. The format of the overall transfer matrix connecting the oscillatory pressure head and discharge at the upstream and downstream end of the system is,
where (i = 25, 26, 27, 28, 29) is the field matrix of the pipe numbered i in the main tail tunnel, is the point matrix of the gate shaft, is the point matrix of the surge tank located at the branch, and is the field matrix of two parallel branches. The corresponding hydraulic vibration analysis process is presented in Figure 6.
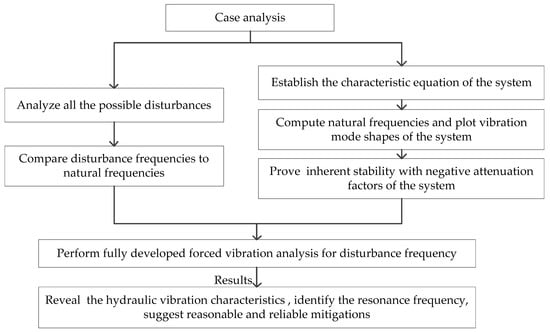
Figure 6.
Hydraulic vibration analysis method.
4. Results and Discussions
In the experiment, twelve pressure-monitoring points, designated as CH0~CH12, were evenly arranged in the flow passage as shown in Figure 7. In detail, CH0 and CH1 were located in the spiral casing, CH2~CH5 were located in the vaneless space, CH6~CH9 were located in the draft tube cone, and CH10~CH11 were located in the draft tube elbow.
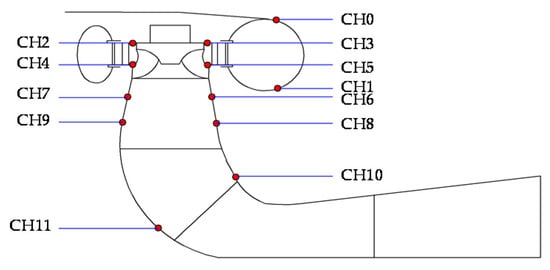
Figure 7.
Locations of pressure-monitoring points.
The fluctuation peak ΔH/H was calculated by processing the pressure signal at the confidence level of 97%, and its definition is
where H is the rated head of the turbine, pi is the instantaneous pressure, and is the average pressure.
Three off-design operating conditions are selected in this paper to study the regularity of the pressure fluctuation. Details of operating points for the model runner are listed in Table 2.

Table 2.
Details of operating conditions.
4.1. Pressure Fluctuation in the Flow Passage
The pressure fluctuations at points CH0~CH11 under condition S01, S02, and S03 were monitored and recorded. Table 3 lists the pressure fluctuation peaks in the time domain at points CH0~CH11, and it is clear that the pressure fluctuations in the spiral case are relatively small compared to other points. The corresponding dominant frequencies are listed in Table 4, and 0.2fn is the frequency with the greatest number of occurrences in the vaneless space and draft tube. Consequently, the pressure fluctuations in the vaneless space and draft tube are analyzed in the following section.

Table 3.
Pressure fluctuation peaks in time domain under different operating conditions.

Table 4.
f/fn in frequency domain at different monitoring points.
4.1.1. Pressure Fluctuation in Vaneless Space
Figure 8 shows the pressure fluctuation characteristics in the vaneless space (CH2 and CH4). The time domain characteristics show that the fluctuation peak monitored under mode S02 was the largest compared to S01 and S03. The frequency domain characteristics indicate that under mode S01 with smaller guide vane openings, a blade frequency of 15fn was manifested, caused by rotor–stator interaction, and with guide vane openings increasing, the runner rotational frequency reached 1.0fn at point CH4 under S02. A frequency of 0.2fn, affected by vortex rope in the draft tube, persists in all operating modes.
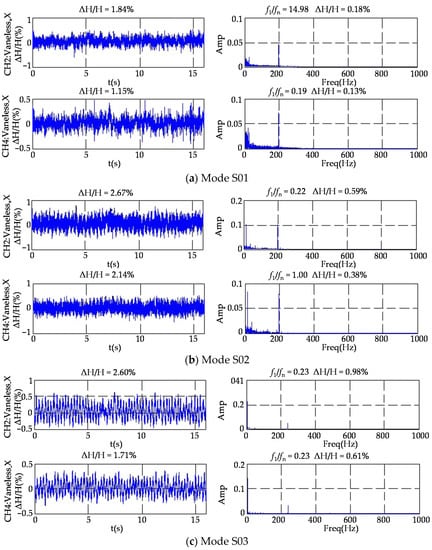
Figure 8.
Pressure fluctuations in vaneless space.
4.1.2. Pressure Fluctuation in the Draft Tube
When turbines work under off-design conditions, the rotational velocity component of fluid in the runner outlet will probably cause vortex rope accompanied by low-frequency and large-amplitude pressure fluctuations in the draft tube. According to the empirical formula, the estimated frequency range of vortex rope is f = (0.167~0.5) fn, and the frequency of 0.2~0.4fn captured in the experiment is in the range of the estimated frequency. Figure 9 shows the pressure fluctuations in the draft tube (CH6) under S01, S02, and S03. The time domain characteristics illustrate that the pressure fluctuation in the draft tube cone is the highest compared to other regions. From the frequency domain characteristics, we can infer that 0.2fn is the leading frequency that occurred in all conditions. Additionally, frequencies of 1.6fn and 1.5fn, measured at the inlet of the draft tube only, occurred in S01, and these may propagate from the upstream region affected by RSI.
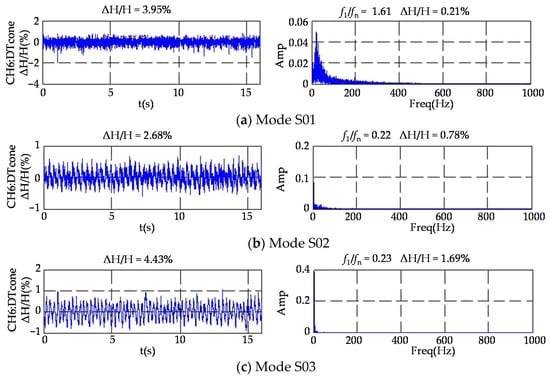
Figure 9.
Pressure fluctuations in the draft tube.
4.2. Numerical Computation
4.2.1. Natural Frequencies
On the derivation of the mathematical model used for hydraulic vibration analysis, as mentioned above, further free vibration analyses were performed. The complex frequency mainly depends on the length of the system and the wave speed; as a result, for a traditional pressurized hydropower system, the hydraulic vibration characteristics can be revealed at a typical designed operating point. For this research project, the boundary conditions were Hu = 806.8 m and Hd = 597.42 m, and both turbines worked at the rated head and discharge. Then, by solving the characteristic Equation (14), the complex frequencies were calculated and are listed in the Case 1 column in Table 5. Taking the effect of wave speed on numerical computation into consideration, the column Case 2 lists the results by adding a 10% increase to the wave speed.

Table 5.
Complex frequencies of the hydropower system.
The data in Table 5 show that the frequencies of the first three orders have few relationships to wave speed, whereas for orders higher than 3, the frequencies are affected by the wave speed distinctly, and with increasing orders, the deviation between two frequencies corresponding to the same order becomes obvious. For the frequency 7.4851 of 8 order in Case 1 is approximately equal to the frequency of 7 order in Case 2 if ignoring the difference after the decimal point, so it is unnecessary to perform free vibration analysis on higher orders because of the clearly error induced by value of wave speed, and herein, only frequencies lower than fn should be reserved in Table 5. Further, all attenuating factors in Table 5 are negative, which means that all vibration modes would attenuate with time until a steady state is achieved, and the possibility of self-excited resonance can be excluded.
4.2.2. Mode Shapes
The vibration mode shapes are calculated with an assumed initial oscillatory discharge value QU = 1.0 m3/s at the upstream end. The rotational frequency of the prototype runner is fn = 1.852 Hz, and ω = 11.63 rad/s. According to the empirical formula, the estimated frequency range of vortex rope was f = (0.167~0.5) fn = 0.309~0.926 Hz, and ω = 1.94~5.82 rad/s. Based on the above analysis, only orders whose angular frequency is in the range of vortex rope frequency (4th, 5th, 6th) and close to the runner rotational frequency (10th) are selected for plotting in Figure 10, including oscillatory discharge and oscillatory pressure head, and the abscissa is the distance from the inlet, while the black line is the head and the red line is the flow rate. For frequencies approximately equal to those of the 4th, 5th, and 10th orders, a small disturbance could cause intense pressure oscillation in the tail tunnel. However, for the sixth order, there was no obvious pressure oscillation in the tail tunnel shown in Figure 10c. The mode shapes reveal the modulus of oscillatory value along the pipeline at different frequencies, and the amplitude of pressure fluctuation is at a minimum at the node and a maximum at the antinode. The locations of the node and antinode of the flow are opposite to those in the head. Since the upstream and downstream are reservoirs with a constant water level, the oscillatory head is zero at both ends and in all vibration modes.
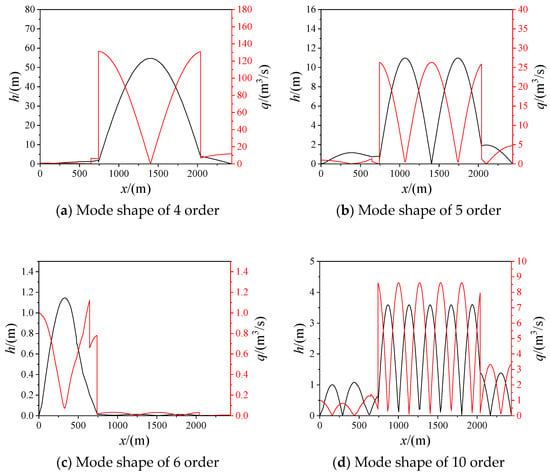
Figure 10.
Vibration mode shapes.
4.3. Comparative Analysis
The estimated frequency range of the vortex rope overlaps the 4th, 5th, and 6th orders, and the rotational frequency of the prototype runner is close to the frequency of the 10th mode. For the prototype turbine, the frequencies of 0.2~0.4fn measured for the vortex rope and the runner rotational frequency are emphasized here. Forced vibration was performed at three frequencies (0.2fn, 0.4fn, and fn) of oscillating discharge at the turbine point as the forcing function, with an expression , and the system’s responses are shown in Figure 11.
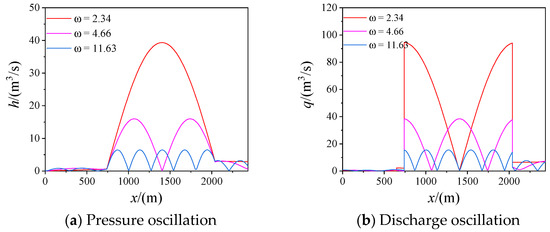
Figure 11.
System’s response to the forcing function.
It is shown in Figure 11 that if the frequency of disturbance close is to the 4th, 5th, or 10th mode, a small disturbance would cause intense pressure oscillation in the tail tunnel, and the response to 0.2fn is the highest. On the contrary, the response to the runner rotational frequency is the lowest. It is clear that the oscillatory crest value of both pressure and discharge decreases as the disturbance’s frequency increases, which indicates that the lower frequency vibration is more severe and should be avoided, because severe pressure oscillation can burst or collapse the pipe due to pressure in excess of the designed pressure. The pressure fluctuation in the tail tunnel shown in Figure 11 is much higher than that in the upstream part of the system. For the blade frequency of 15fn with an extremely short exciting period, it is unnecessary to carry out targeted analyses, since the natural frequency of the higher order is not exact owing to the error in the estimated wave speed, and the corresponding higher-order vibration usually manifests as energy dissipation. It is confirmed that the leading frequencies of the vortex rope and the runner rotational frequency are closely related to natural frequencies, which may induce huge pressure fluctuations and even resonance along the water conveyance line. Under the actual operating conditions, real-time monitoring should concentrate on the frequency characteristics of vortex rope in the draft tube and pressure fluctuation in the vaneless space, in case these equal the natural frequency of the system.
5. Conclusions
In this paper, the pressure fluctuations in a reduced-scale model turbine test rig under three sets of off-design conditions are tested. According to the time domain and frequency domain analysis, the leading frequencies of pressure pulsation throughout the flow passage are obtained. Then, the natural frequencies are calculated, and the vibration mode shapes corresponding to various frequencies are revealed for the whole hydraulic system, based on detailed free vibration analysis. It was found that the leading frequencies of the vortex rope in the draft tube partially overlap the natural frequencies, including the fourth, fifth, and sixth modes. It is concluded from the forced vibration analysis that if the frequency of the vortex rope is close to these modes and continues acting as a forcing disturbance, intense pressure fluctuation inevitably occurs, and a frequency of 0.2fn in the vortex rope is the most dangerous disturbance, as this will cause huge pressure fluctuations in the water conveyance line. Besides this, the runner rotational frequency cannot be ignored either, as this may cause severe pressure fluctuations in the tail tunnel. According to the computation results, when the disturbance frequencies are similar to certain natural frequencies, vibration mitigations actions should be taken during the operating stage.
Hydraulic vibration analysis can provide a reference to recognize disturbances during the design stage in order to avoid severe pressure fluctuation, and even resonance, during the operation stage. A future study will focus on the exploration of vibration reduction methods, and on exactly identifying the disturbance by decomposing the pressure signal in the flow passage into synchronous and asynchronous parts. The study will also focus on the wide application of hydraulic vibration theory to various kinds of water conveyance systems.
Author Contributions
Conceptualization, A.S. and J.Z.; methodology, A.S. and J.Z.; software, A.S. and J.Z.; validation, J.Z.; formal analysis, A.S. and J.Z.; investigation, A.S. and J.Z.; resources, Y.C. and F.C.; data curation, J.Z.; writing—original draft preparation, A.S. and J.Z.; writing—review and editing, A.S. and J.Z.; visualization, Y.C.; supervision, J.Z.; project administration, Y.C. and F.Y. and H.S.; funding acquisition, Y.C. and F.Y. and H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors wish to thank the support given by College of Water Conservancy and Hydropower Engineering, Hohai University and Huadong Engineering Corporation Limited.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, X.; Chen, Z.; Fan, X.; Cheng, Z. Hydropower development situation and prospects in China. Renew. Sustain. Energy Rev. 2018, 82, 232–239. [Google Scholar] [CrossRef]
- Bilgili, M.; Bilirgen, H.; Ozbek, A.; Ekinci, F.; Demirdelen, T. The role of hydropower installations for sustainable energy development in Turkey and the world. Renew. Energy 2018, 126, 755–764. [Google Scholar] [CrossRef]
- Trivedi, C.; Gogstad, P.J.; Dahlhaug, O.G. Investigation of the unsteady pressure pulsations in the prototype Francis turbines—Part 1: Steady state operating conditions. Mech. Syst. Signal Process. 2018, 108, 188–202. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Kozik, J.; Piech, K.; Gutten, M.; Caesarendra, W.; Liu, H.; Brumercik, F.; Irfan, M.; Faizal Khan, Z. Detection of Deterioration of Three-phase Induction Motor using Vibration Signals. Meas. Sci. Rev. 2019, 19, 241–249. [Google Scholar] [CrossRef]
- Li, D.; Fu, X.; Zuo, Z.; Wang, H.; Li, Z.; Liu, S.; Wei, X. Investigation methods for analysis of transient phenomena concerning design and operation of hydraulic-machine systems—A review. Renew. Sustain. Energy Rev. 2019, 101, 26–46. [Google Scholar] [CrossRef]
- Müller, A.; Favrel, A.; Landry, C.; Yamamoto, K.; Avellan, F. On the physical mechanisms governing self-excited pressure surge in Francis turbines. IOP Conf. Ser. Earth Environ. Sci. 2014, 22. [Google Scholar] [CrossRef]
- Trivedi, C. Time-dependent inception of vortex rings in a Francis turbine during load variation: Large eddy simulation and experimental validation. J. Hydraul. Res. 2019, 58, 790–806. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, Q.; Ma, Z.; Wang, X. Transient vibration analysis of unit-plant structure for hydropower station in sudden load increasing process. Mech. Syst. Signal Process. 2019, 120, 486–504. [Google Scholar] [CrossRef]
- Trivedi, C.; Gandhi, B.; Michel, C.J. Effect of transients on Francis turbine runner life: A review. J. Hydraul. Res. 2013, 51, 121–132. [Google Scholar] [CrossRef]
- Goyal, R.; Gandhi, B.K.; Cervantes, M.J. Transient Pressure Measurements in the Vaneless Space of a Francis Turbine during Load Acceptances from Minimum Load. J. Phys. Conf. Ser. 2018, 1042. [Google Scholar] [CrossRef]
- Guo, L.; Liu, J.; Wang, L.; Qin, D.; Wei, X. Pressure fluctuation propagation of a pump turbine at pump mode under low head condition. Sci. China Technol. Sci. 2014, 57, 811–818. [Google Scholar] [CrossRef]
- Zuo, Z.; Liu, S.; Sun, Y.; Wu, Y. Pressure fluctuations in the vaneless space of High-head pump-turbines—A review. Renew. Sustain. Energy Rev. 2015, 41, 965–974. [Google Scholar] [CrossRef]
- Cheng, H.; Zhou, L.; Liang, Q.; Guan, Z.; Liu, D.; Wang, Z.; Kang, W. A method of evaluating the vortex rope strength in draft tube of Francis turbine. Renew. Energy 2020, 152, 770–780. [Google Scholar] [CrossRef]
- Kumar, S.; Cervantes, M.J.; Gandhi, B.K. Rotating vortex rope formation and mitigation in draft tube of hydro turbines—A review from experimental perspective. Renew. Sustain. Energy Rev. 2021, 136. [Google Scholar] [CrossRef]
- Qin, D.; Xu, Y.; Liu, W.; Wei, X.; Zhao, Y.; Meng, X. Experimental study of the influence of Thoma number and model testing head on pressure fluctuation in draft tube of a Francis turbine. IOP Conf. Ser. Earth Environ. Sci. 2016, 49. [Google Scholar] [CrossRef]
- Yu, A.; Zou, Z.; Zhou, D.; Zheng, Y.; Luo, X. Investigation of the correlation mechanism between cavitation rope behavior and pressure fluctuations in a hydraulic turbine. Renew. Energy 2020, 147, 1199–1208. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, W.; Cheng, Y.; Yang, Z.; Chen, Q.; Yang, J. Mechanism of Fast Transition of Pressure Pulsations in the Vaneless Space of a Model Pump-Turbine During Runaway. J. Fluid Eng. 2019, 141. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Z.; Zhu, B.; Zhang, F. Pressure fluctuation and flow instability in S-shaped region of a reversible pump-turbine. Renew. Energy 2020, 154, 826–840. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Y.; Yang, Z.; Chen, Q.; Liu, D. Influence of rotational inertia on the runner radial forces of a model pump-turbine running away through the S-shaped characteristic region. IET Renew. Power Gener. 2020, 14, 1883–1893. [Google Scholar] [CrossRef]
- Li, D.; Sun, Y.; Zuo, Z.; Liu, S.; Wang, H.; Li, Z. Analysis of Pressure Fluctuations in a Prototype Pump-Turbine with Different Numbers of Runner Blades in Turbine Mode. Energies 2018, 11, 1474. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Qin, Y.; Li, Z.; Wei, X.; Qin, D. Mechanism of high amplitude low frequency fluctuations in a pump-turbine in pump mode. Renew. Energy 2018, 126, 668–680. [Google Scholar] [CrossRef]
- Su, W.-T.; Binama, M.; Li, Y.; Zhao, Y. Study on the method of reducing the pressure fluctuation of hydraulic turbine by optimizing the draft tube pressure distribution. Renew. Energy 2020, 162, 550–560. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, R.-Z.; Yu, A.; Lu, L.; Luo, X.-W. Suppression of vortex rope oscillation and pressure vibrations in Francis turbine draft tube using various strategies. J. Hydrodyn. 2021. [Google Scholar] [CrossRef]
- Bosioc, A.I.; Tănasă, C. Experimental study of swirling flow from conical diffusers using the water jet control method. Renew. Energy 2020, 152, 385–398. [Google Scholar] [CrossRef]
- Tănasă, C.; Bosioc, A.; Muntean, S.; Susan-Resiga, R. A Novel Passive Method to Control the Swirling Flow with Vortex Rope from the Conical Diffuser of Hydraulic Turbines with Fixed Blades. Appl. Sci. 2019, 9, 4910. [Google Scholar] [CrossRef]
- Kan, K.; Zheng, Y.; Chen, H.; Zhou, D.; Dai, J.; Binama, M.; Yu, A. Numerical simulation of transient flow in a shaft extension tubular pump unit during runaway process caused by power failure. Renew. Energy 2020, 154, 1153–1164. [Google Scholar] [CrossRef]
- Yin, C.; Yang, J.; Zeng, W.; Cheng, Y. Simulation of the simultaneous load rejection processes of two parallel pump turbines using a 1D–3D approach. IOP Conf. Ser. Earth Environ. Sci. 2019, 240. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Y.; Yang, Z.; Chen, Q.; Liu, D. Water column separation in pump-turbine after load rejection: 1D-3D coupled simulation of a model pumped-storage system. Renew. Energy 2021, 163, 685–697. [Google Scholar] [CrossRef]
- Palikhe, S.; Zhou, J.; Bhattarai, K.P. Hydraulic Oscillation and Instability of a Hydraulic System with Two Different Pump-Turbines in Turbine Operation. Water 2019, 11, 692. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, Y. Discussion on Stochastic Analysis of Hydraulic Vibration in Pressurized Water Diversion and Hydropower Systems. Water 2018, 10, 353. [Google Scholar] [CrossRef]
- Landry, C.; Favrel, A.; Müller, A.; Nicolet, C.; Avellan, F. Local wave speed and bulk flow viscosity in Francis turbines at part load operation. J. Hydraul. Res. 2016, 54, 185–196. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Dou, H.-S.; Wu, S.; Chen, T. Numerical prediction and similarity study of pressure fluctuation in a prototype Kaplan turbine and the model turbine. Comput. Fluids 2012, 56, 128–142. [Google Scholar] [CrossRef]
- Wiley, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients; Springer: Berlin, Germany, 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).