A Novel Advancing Signal Processing Method Based on Coupled Multi-Stable Stochastic Resonance for Fault Detection
Abstract
1. Introduction
- A novel advancing signal processing method based on coupled multi-stable stochastic resonance is proposed to detect the faults of motor bearings;
- The output signal-to-noise ratio (SNR) for system parameters and coupling coefficients are analyzed in depth;
- The SOA is used to adaptively optimize and determine the system parameters of the SR by using the subsampling technique;
- The actual vibration data of induction motor bearings are used to prove the effectiveness of the proposed CMSR system.
2. Theoretical Background
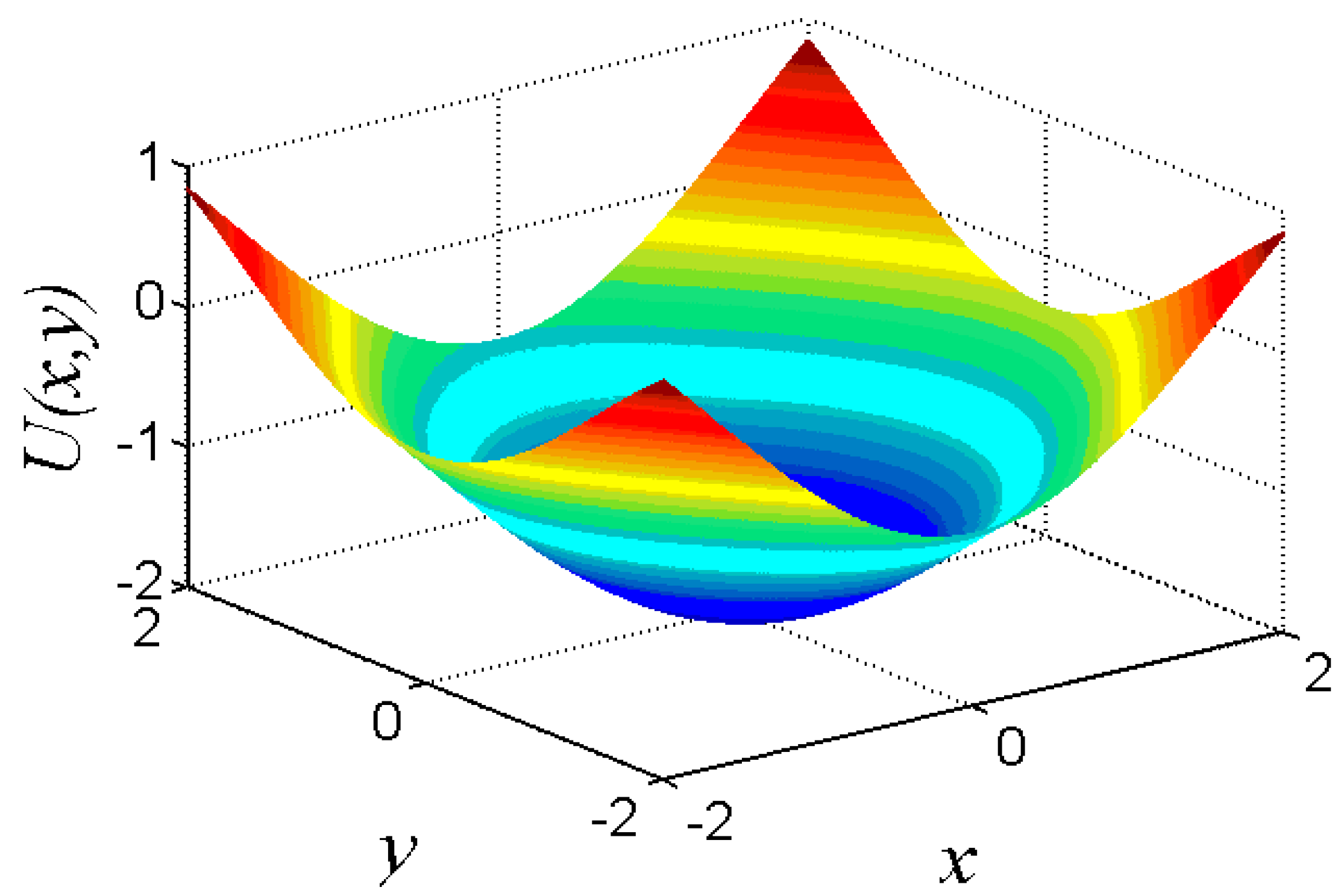
2.1. First-Order MSR System Model
2.2. Mode of CMSR System
2.3. System Measurement Index
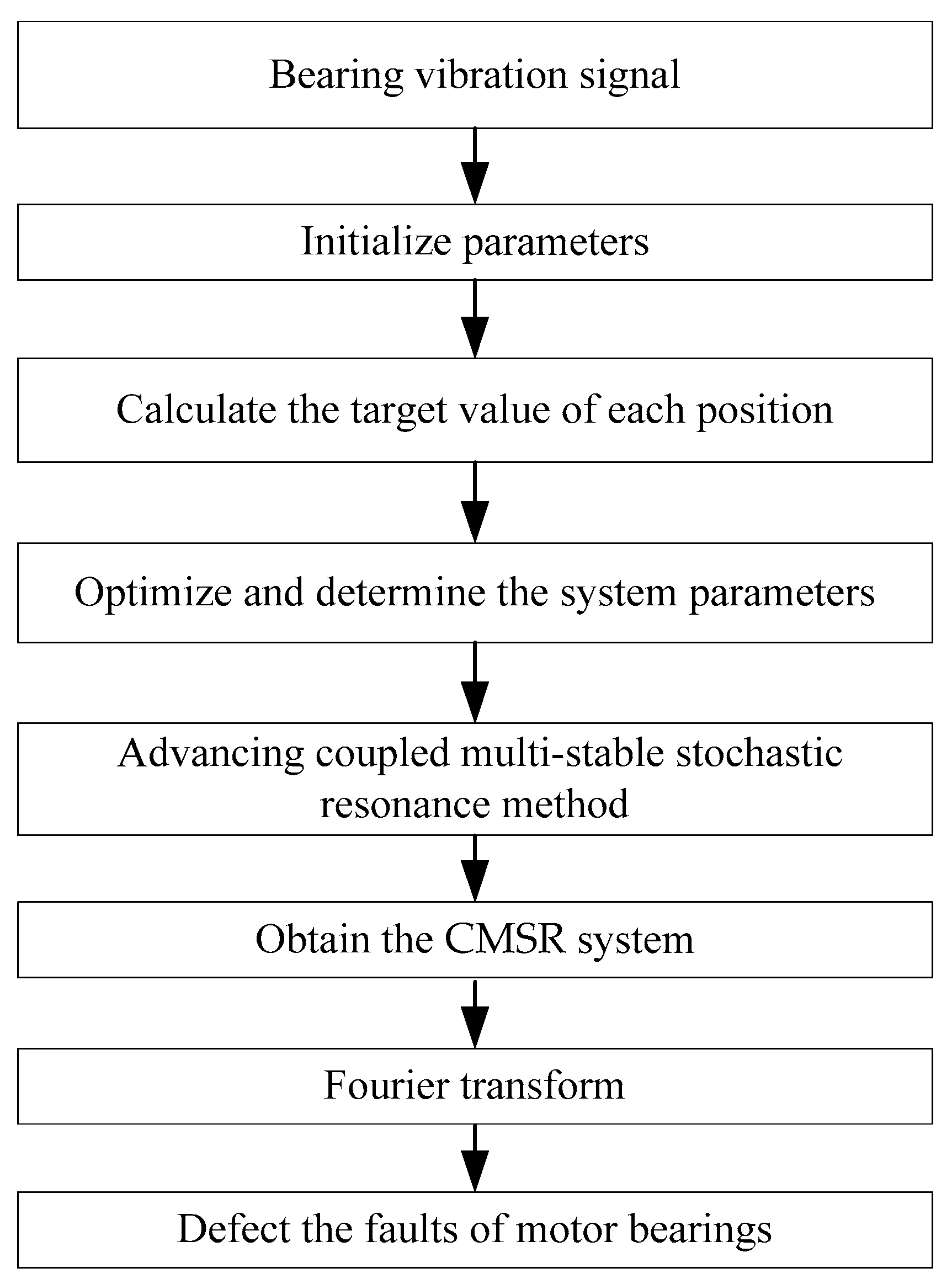
2.4. The Flow of the CMSR System
- Signal preprocessing. The envelope signal obtained after filtering and demodulating the collected bearing vibration signal is recorded as , , , S is the input signal;
- Parameter initialization. Number of iterations, population size, and range of parameters are determined;
- Calculate the target value of each position using the output SNR formula;
- Parameter optimization. The SNR is considered as the fitness function of the seeker optimization algorithm (SOA) to adaptively optimize and determine the system parameters of the SR by using the subsampling technique;
- If the set value is equal to the current number of iterations, output the best system parameters a, b, r, R and enter the next step; otherwise, return to the previous step;
- Signal detection. Import the pre-processed signal into the CMSR system with the determined parameters to get the output signal Scale recovery of signal frequency and amplitude ;
- Fault detection. Fourier transform of x to complete fault detection.
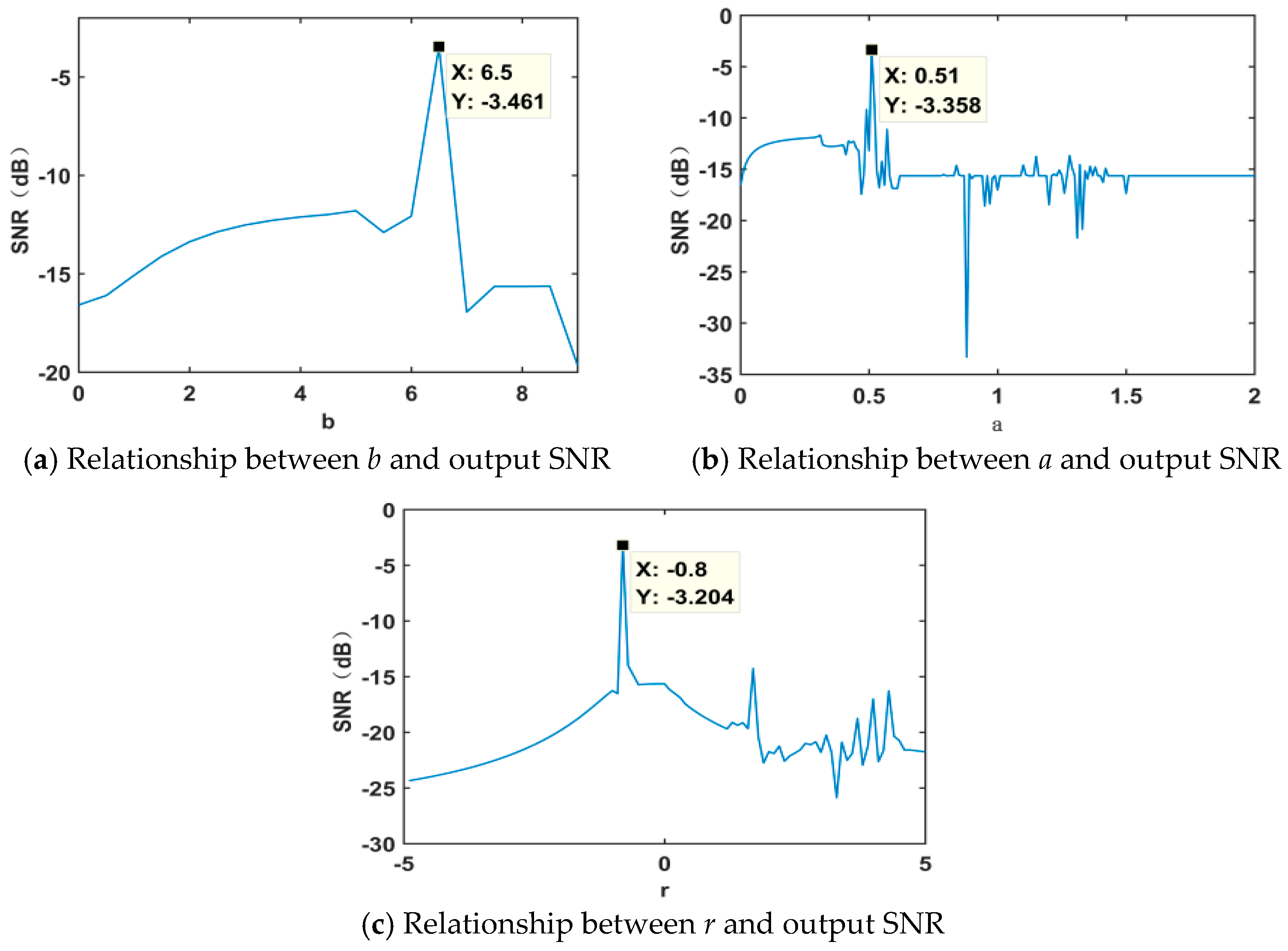
3. System Parameter Analysis
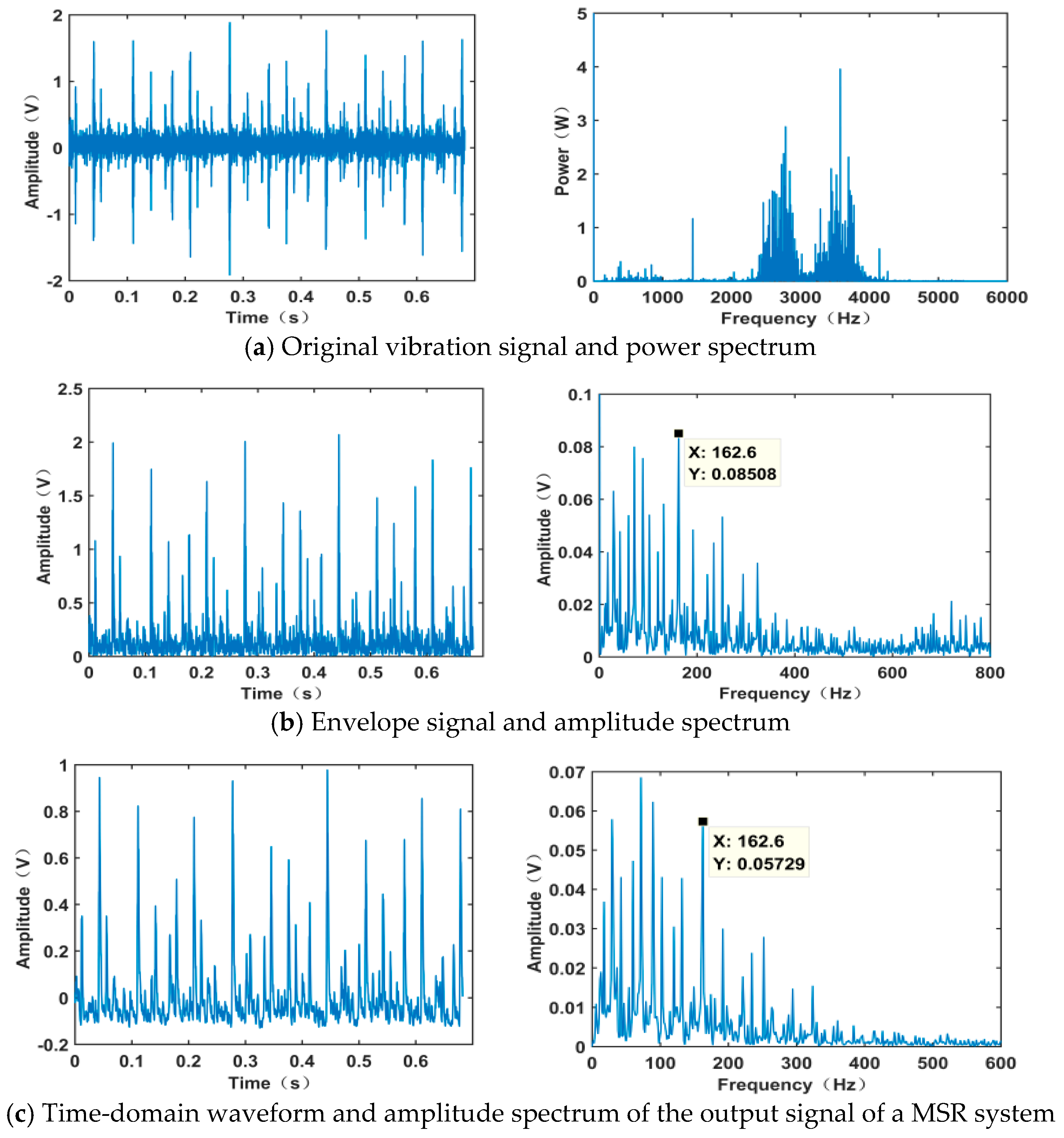
4. Engineering Application
5. Conclusions
- The CMSR system can detect weak high-frequency signals by combining the variable-scale method;
- With the output SNR as the fitness function of the SOA the parameters of the CMSR system can be determined;
- The engineering data-processing results show that the CMSR system has better filtering performance, higher output SNR, and more effective detection results than traditional SR methods, which has broader prospects for weak signal processing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, L.; Yuan, Y.; Wang, H.; Zhao, X.; Zheng, J. A New Second-Order Tristable Stochastic Resonance Method for Fault Diagnosis. Symmetry 2019, 11, 965. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, W.; Lou, S. Adaptive blind extraction of rolling bearing fault signal based on equivariant adaptive separation via independence. J. Electron. Inf. Technol. 2020, 42, 2471–2477. [Google Scholar]
- Jin, T.; Yang, X.; Xia, H.; Ding, H. Reliability index and option pricing formulas of the first hitting time model based on the uncertain fractional-order differential equation with Caputo type. Fractals 2020. [Google Scholar] [CrossRef]
- Luo, Z.; Lu, X.; Zhou, Y. EEG feature extraction based on brain function network and sample entropy. J. Electron. Inf. Technol. 2021, 43, 412–418. [Google Scholar]
- AlShorman, O.; Irfan, M.; Saad, N.; Zhen, D.; Haider, N.; Glowacz, A.; AlShorman, A. A review of artificial intelligence methods for condition monitoring and fault diagnosis of rolling element bearings for induction motor. Shock Vib. 2020, 2020, 8843759. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Nasiri, S.; Weinberg, K. Prediction of fracture in sandwich-structured composite joints using case-based reasoning approach. Procedia Struct. Integr. 2018, 13, 168–173. [Google Scholar] [CrossRef]
- Jin, T.; Ding, H.; Xia, H.; Bao, J. Reliability index and Asian barrier option pricing formulas of the uncertain fractional first-hitting time model with Caputo type. Chaos Solitons Fractals 2021, 142, 110409. [Google Scholar] [CrossRef]
- Gui, W.; Lu, Q.; Su, M. A firewoks algorithm-back propagation fault diagnosis algorithm for system-level fault diagnosis. J. Electron. Inf. Technol. 2020, 42, 1102–1109. [Google Scholar]
- Zhao, H.; Li, H.; Jin, Y.; Dang, X.; Deng, W. Feature extraction for data-driven remaining useful life prediction of rolling bearings. IEEE Trans. Instrum. Meas. 2021. [Google Scholar] [CrossRef]
- AlShorman, O.; Alkahatni, F.; Masadeh, M.; Irfan, M.; Glowacz, A.; Althobiani FKozik, J.; Kozik, J.; Glowacz, W. Sounds and Acoustic emission-based early fault diagnosis of induction motor: A review study. Adv. Mech. Eng. 2021, 13, 1687814021996915. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, X.; Du, Y.; Zheng, Y.; Cao, Z. Path planning of coastal ships based on optimized DQN reward function. J. Mar. Sci. Eng. 2021, 9, 210. [Google Scholar] [CrossRef]
- Glowacz, A.; Tadeusiewicz, R.; Legutko, S.; Caesarendra, W.; Irfan, M.; Liu, H.; Brumercik, F.; Gutten, M.; Sulowicz, M.; Daviu, J.A.A.; et al. Fault diagnosis of angle grinders and electric impact drills using acoustic signals. Appl. Acoust. 2021, 179, 108070. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Q.; Luo, J.; Xu, Y.; Zhang, X. An enhanced Bacterial Foraging Optimization and its application for training kernel extreme learning machine. Appl. Soft Comput. 2020, 86, 105884. [Google Scholar] [CrossRef]
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A Math. Gen. 1981, 14, L453–L457. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Leng, Y.G.; Leng, Y.S.; Wang, T.Y.; Guo, Y. Numerical analysis and engineering application of large parameter stochastic resonance. J. Sound Vib. 2006, 292, 788–801. [Google Scholar] [CrossRef]
- Li, T.; Zhou, M. ECG classification using wavelet packet entropy and random forests. Entropy 2016, 18, 285. [Google Scholar] [CrossRef]
- Tan, J.; Chen, X.; Wang, J.; Chen, H.; Cao, H.; Zi, Y.; He, Z. Study of frequency-shifted and re-scaling stochastic resonance and its application to fault diagnosis. Mech. Syst. Signal Process. 2009, 23, 811–822. [Google Scholar] [CrossRef]
- Wang, J.; He, Q.; Kong, F. An improved multiscale noise tuning of stochastic resonance for identifying multiple transient faults in rolling element bearings. J. Sound Vib. 2014, 333, 7401–7421. [Google Scholar] [CrossRef]
- Shi, P.M.; Ding, X.J.; Han, D.Y. Study on multi-frequency weak signal detection method based on stochastic resonance tuning by multi-scale noise. Measurement 2014, 47, 540–546. [Google Scholar] [CrossRef]
- Zhao, H.; Li, D.; Deng, W.; Yang, X. Research on vibration suppression method of alternating current motor based on fractional order control strategy. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2017, 231, 786–799. [Google Scholar] [CrossRef]
- Zheng, J.; Yuan, Y.; Zou, L.; Deng, W.; Guo, C.; Zhao, H. Study on a Novel Fault Diagnosis Method Based on VMD and BLM. Symmetry 2019, 11, 747. [Google Scholar] [CrossRef]
- Li, T.; Shi, J.; Zhang, D. Color image encryption based on joint permutation and diffusion. J. Electron. Imaging 2021, 30, 013008. [Google Scholar] [CrossRef]
- Cai, X.; Zhao, H.; Shang, S.; Zhou, Y.; Deng, W.; Chen, H.; Deng, W.Q. An improved quantum-inspired cooperative co-evolution algorithm with muli-strategy and its application. Expert Syst. Appl. 2021, 171, 114629. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Luo, J.; Zhang, Q.; Jiao, S.; Zhang, X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019, 492, 181–203. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Gao, X.; Zhao, H. An enhanced MSIQDE algorithm with novel multiple strategies for global optimization problems. IEEE Trans. Syst. Man. Cybern. Syst. 2020. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; He, Z. Multi-stable stochastic resonance and its application research on mechanical fault diagnosis. J. Sound Vib. 2013, 332, 5999–6015. [Google Scholar] [CrossRef]
- Han, D.; An, S.; Shi, P. Multi-frequency weak signal detection based on wavelet transform and parameter compensation band-pass multi-stable stochastic resonance. Mech. Syst. Signal. Process. 2016, 70, 995–1010. [Google Scholar] [CrossRef]
- Lu, S.; He, Q.; Kong, F. Effects of underdamped step-varying second-order stochastic resonance for weak signal detection. Digit. Signal Process. 2015, 36, 93–103. [Google Scholar] [CrossRef]
- Lei, Y.; Qiao, Z.; Xu, X.; Lin, J.; Niu, S. An underdamped stochastic resonance method with stable-state matching for incipient fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2017, 94, 148–164. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, M. Detection of bearing fault signals based on coupled Bistable system stochastic resonance. J. China Univ. Metrol. 2014, 25, 51–56. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Li, M.; Zhang, Y. A novel adaptive stochastic resonance method based on coupled bistable systems and its application in rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 128–145. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, D.; Zhang, T. The analysis of stochastic resonance and bearing fault detection based on linear coupled bistable system under lévy noise. Chin. J. Phys. 2018, 56, 2718–2730. [Google Scholar] [CrossRef]
- Jin, T.; Ding, H.; Li, B.; Xia, H.; Xue, C. Valuation of interest rate ceiling and floor based on the uncertain fractional differential equation in Caputo sense. J. Intell. Fuzzy Syst. 2021, 40, 5197–5206. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Zhou, Y.; Chen, H.; Deng, W. Quantum differential evolution with cooperative coevolution framework and hybrid mutation strategy for large scale optimization. Knowl. Based Syst. 2021, 224, 107080. [Google Scholar] [CrossRef]
- Shao, H.; Chen, J.; Jiang, H.; Yang, Y.; Wu, Z. Enhanced deep gated recurrent unit and complex wavelet packet energy moment entropy for early fault prognosis of bearing. Knowl. Based Syst. 2019. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Zhao, H.; Song, Y. A novel gate resource allocation method using improved PSO-based QEA. IEEE Tran. Intell. Transp. Syst. 2020. [Google Scholar] [CrossRef]
- Jin, T.; Xia, H.; Chen, H. Optimal control problem of the uncertain second-order circuit based on first hitting criteria. Math. Methods Appl. Sci. 2021, 44, 882–900. [Google Scholar] [CrossRef]
- Hu, B.; Guo, C.; Wu, J.; Tang, J.; Zhang, J.; Wang, Y. An adaptive periodical stochastic resonance method based on the grey wolf optimizer algorithm and its application in rolling bearing fault diagnosis. J. Vib. Acoust. 2019, 141, 041016. [Google Scholar] [CrossRef]
- Wu, D.; Liao, Y.; Hu, C.; Yu, S.; Tian, Q. An enhanced fuzzy control strategy for low-level thrusters in marine dynamic positioning systems based on chaotic random distribution harmony search. Int. J. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Jin, T.; Yang, X. Monotonicity theorem for the uncertain fractional differential equation and application to uncertain financial market. Math. Comput. Simul. 2021, 190, 203–221. [Google Scholar] [CrossRef]
- Xu, P.; Jin, Y. Stochastic resonance in multi-stable coupled systems driven by two driving signals. Phys. A Stat. Mech. Appl. 2018, 492, 1281–1289. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, G. The optimization of wireless sensor network topology based on FW-PSO algorithm. J. Electron. Inf. Technol. 2021, 43, 396–403. [Google Scholar]
- Dai, C.; Chen, W.; Zhu, Y.; Zhang, X. Seeker optimization algorithm for optimal reactive power dispatch. IEEE Trans. Power Syst. 2009, 24, 1218–1231. [Google Scholar]
- Buchner, A.; Hadrath, S.; Burkard, R.; Kolb, F.; Ruskowski, J.; Ligges, M.; Grabmaier, A. Analytical Evaluation of Signal-to-Noise Ratios for Avalanche- and Single-Photon Avalanche Diodes. Sensors 2021, 21, 2887. [Google Scholar] [CrossRef]
- Jin, T.; Zhu, Y. First hitting time about solution for an uncertain fractional differential equation and application to an uncertain risk index model. Chaos Solitons Fractals 2020, 137, 109836. [Google Scholar] [CrossRef]
- Peterson, B.J.; Reichle, R.; Pandya, S.; O’Mullane, M.G.; Mukai, K. Consideration of signal to noise ratio for an imaging bolometer for ITER. Rev. Sci. Instrum. 2021, 92, 043534. [Google Scholar] [CrossRef]
- Loparo, K.A. Case Western Reserve University Bearing Data Center. Available online: https://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website (accessed on 10 January 2021).





| Inner Diameter (mm) | Outer Ring Diameter (mm) | Pitch Diameter (mm) | Roller Diameter (mm) | Roller Number | Angular Contact Angle |
|---|---|---|---|---|---|
| 25.001 | 51.999 | 39.04 | 7.94 | 9 | 0 |
| Objects | Theoretical Value | Obtained Value | Error |
|---|---|---|---|
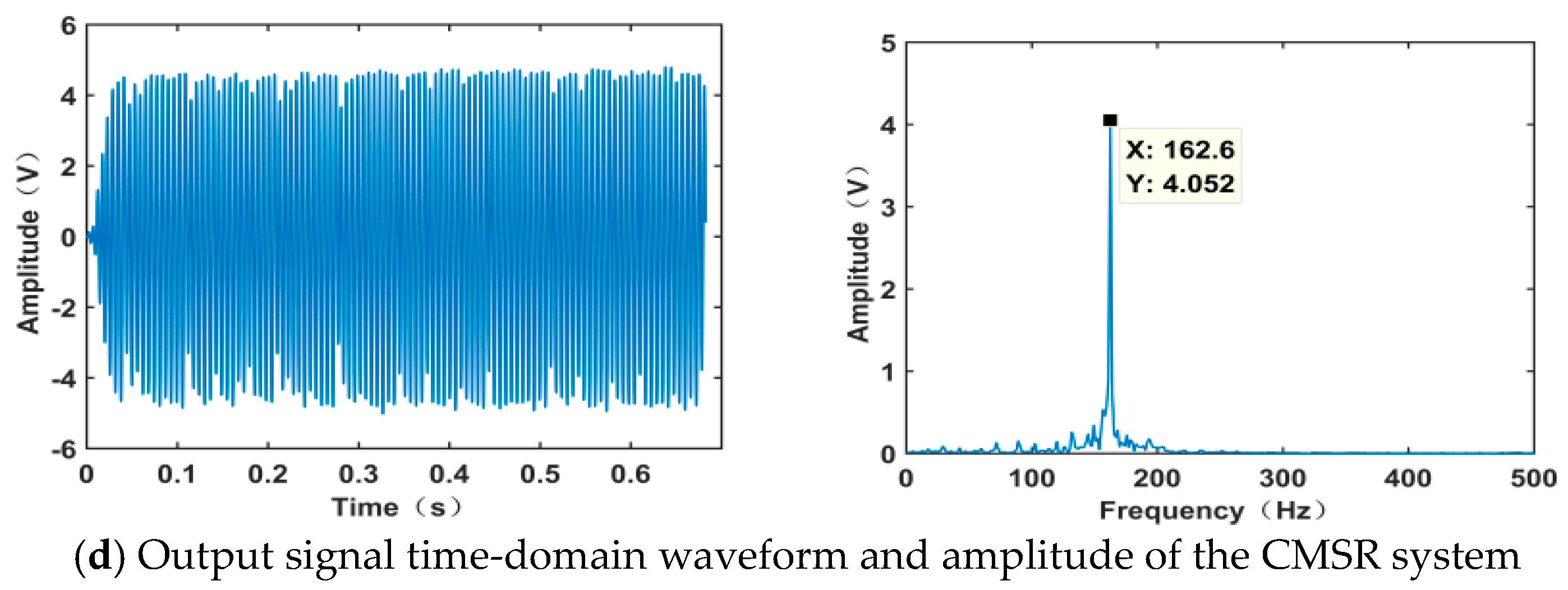
| Inner race | 162.2 Hz | 162.6 Hz | 0.4 Hz |
| Rolling element | 141.1 Hz | 140.6 Hz | 0.5 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Guan, Y.; Chen, H.; Deng, W. A Novel Advancing Signal Processing Method Based on Coupled Multi-Stable Stochastic Resonance for Fault Detection. Appl. Sci. 2021, 11, 5385. https://doi.org/10.3390/app11125385
Cui H, Guan Y, Chen H, Deng W. A Novel Advancing Signal Processing Method Based on Coupled Multi-Stable Stochastic Resonance for Fault Detection. Applied Sciences. 2021; 11(12):5385. https://doi.org/10.3390/app11125385
Chicago/Turabian StyleCui, Hongjiang, Ying Guan, Huayue Chen, and Wu Deng. 2021. "A Novel Advancing Signal Processing Method Based on Coupled Multi-Stable Stochastic Resonance for Fault Detection" Applied Sciences 11, no. 12: 5385. https://doi.org/10.3390/app11125385
APA StyleCui, H., Guan, Y., Chen, H., & Deng, W. (2021). A Novel Advancing Signal Processing Method Based on Coupled Multi-Stable Stochastic Resonance for Fault Detection. Applied Sciences, 11(12), 5385. https://doi.org/10.3390/app11125385








