1. Introduction
Wind power is the second largest source of renewable energy after solar technology. The global popularity of wind power has risen significantly due to the need to harness electrical power in order to limit and end the necessity of fossil fuels [
1,
2]. Variable-speed horizontal-axis Wind Turbines (WTs) represent the most important Wind Energy Conversion System (WECS). Moreover, for effective and reliable power conversion, suitable technical and technological solutions have to be properly implemented and exploited in WECSs.
Technological advances in WECSs have encouraged the installation of wind farms. Owing to their large size and requirement of high wind speeds, these installations are located in offshore areas. However, offshore WECSs result in disadvantages such as high installation costs, continuous supervision, and Operation and Maintenance (O & M), which in turn affect their degree of reliability and availability. O & M costs for offshore WTs have been found to be nearly 30–40% of the comprehensive life costs of WECSs [
1], thus increasing the final production costs of the generated electricity.
Reducing O&M costs and increasing the plant availability are the key points in operating and generating power from WECSs [
1,
3]. The optimal conversion cost of WECS operation can be achieved in two ways: (i) by using efficient design techniques to prevent the unbalancing of loads and maintaining a rated power output throughout the operation, which can be achieved via appropriate modelling and monitoring strategies of the WT system; (ii) by developing suitable fault diagnosis techniques that prevent unnecessary O&M and shutdown periods due to failures. Technological advancements have been proposed and implemented in order to achieve effective designs for different models of WTs in recent years. However, the existence of faults is inevitable in the operation of WECSs, like any other industrial system. Electromechanical devices, actuators and sensors represent the most common components affected by faults in a WECS [
1,
3]. Any faulty event in the WECS results in a deviation of the system from its objectives and causes possible damage to the process components. Moreover, a fault will deteriorate the performance of the overall plant, resulting in the unscheduled shutdown of the WECS. To remain operative and competitive, there is a high demand for improving the reliability and availability of WTs with reduced unplanned downtimes in the electricity market, thus limiting O&M and significantly reducing the final cost of energy.
To this end, Fault Detection and Isolation (FDI) for WTs has been successfully exploited, together with Fault Tolerant Control (FTC) strategies, see e.g., [
3,
4]. In general, FDI relies on three methods, i.e., parity equations, parameter estimation approaches and observer/filter methods [
5]. In particular, model-based FDI schemes for WTs exploited sliding mode approaches, as shown e.g., in [
6], linear observers [
7], and Kalman filters [
8]. However, these methods usually assume that an accurate mathematical description of the monitored process is available, as well as for the sources of uncertainty and disturbance. Therefore, any inaccurate information during faults may result in degradation of system performance and can cause instability during post-fault operation. This issue is of great significance in safety-critical systems such as WTs, having several sources of noise and uncertainties. Therefore, it is required to develop robust and reliable FDI strategies in a WECS to ensure its safe operation.
Robust FDI strategies can be also based on data-driven solutions, as they are able to learn from experience, i.e., from the information brought by the input and the output measurements of the monitored process. Therefore, in contrast to model-based techniques, data-driven approaches for WTs can exploit e.g., fuzzy logic [
9,
10], neural networks [
11,
12,
13,
14], neuro-fuzzy [
15], or mixed solutions [
16].
With reference to this paper, the topic of the FDI for a WT system is analysed. In particular, the design of simple and viable solutions to FDI are considered here, with respect for example, to more complex methodologies relying on convolutional neural networks or support vector machines. In fact, as already remarked above, the FDI modules provide the direct reconstruction of the fault signals affecting the process, which represents the most robust and reliable fault indicator, as remarked e.g., in [
5]. Moreover, the FDI design addressed in the paper is also enhanced by the procedure for deriving the fault reconstructors that are estimated via data-driven approaches.
In more detail, the first data-driven strategy proposed in this work exploits Takagi-Sugeno (TS) fuzzy prototypes [
17], which are estimated via a fuzzy clustering algorithm and from the data-driven identification developed in [
18]. As alternative tool, a second approach is also proposed, which uses Neural Networks (NNs) to derive the nonlinear dynamic relations between the input and output measurements of WT process and the faults affecting the plant. The selected structures belong to the feed-forward Multi-Layer Perceptron (MLP) NN class that includes also Auto-Regressive with eXogenous (ARX) inputs in order to model nonlinear dynamic links among the data. In this way, the training of these Nonlinear ARX (NARX) prototypes for fault estimation can exploit standard back-propagation training algorithms, as recalled e.g., in [
19].
The designed FDI schemes are tested via a high-fidelity simulator of a WT process, which describes its behaviour in healthy and faulty conditions. This simulator, which represents a well-established benchmark [
20], includes the presence of uncertainty, disturbance and model-reality mismatch effects, thus allowing to verify the reliability and robustness characteristics of the proposed FDI methodologies. Moreover, this work has validated the efficacy of the designed FDI techniques by exploiting a more realistic scenario, which consists of a hardware-in-the-loop (HIL) tool.
The same authors have already investigated similar topics in previous papers. For example, this study analyses the solutions addressed e.g., in [
21], but taking into account a more realistic real-time system illustrated in
Section 4. The fuzzy methodology was also proposed by the same authors in [
22], which considered the development of recursive algorithms for the implementation of adaptive laws relying on Linear Parameter Varying (LPV) systems. However, the approach considered in this paper estimates the FDI models by means of off-line procedures. Moreover, this study improves the solutions achieved e.g., in [
23], but applied to a wind farm. The paper [
24] proposed the design of a FTC using the input-output data from a single WT, by exploiting the results obtained in [
25]. On the other hand, this work considers the verification and the validation of the developed FDI methodologies by exploiting a HIL tool, proposed considered in a preliminary paper by the same authors [
26].
It is worth highlighting the main aims of the article.
The paper proposes two data-driven techniques for the FDI of a WT system;
the developed FDI strategies are based on the direct reconstruction of the fault functions affecting the monitored process. In this way, the diagnostic residuals are represented by the estimated fault signals;
the residual generators are organised into a bank structure in order to accomplish the fault isolation task. Their structures rely on Fuzzy Systems (FSs) in the form of TS models and dynamic NNs;
a fault sensitivity analysis enhances the design of the residual generators, by a proper selection of their inputs;
the developed FDI schemes are applied to a WT benchmark first; moreover, the verification of their robustness and reliability features is performed using a HIL tool representing the realistic behaviour of a WT process.
The paper has the following structure.
Section 2 briefly summarises the WT simulator, as it represents a well-established benchmark [
3,
20].
Section 3 describes the FDI strategies based on FS and NN structures, detailed in
Section 3.1.
Section 4 analyses the obtained results via extended simulations, whilst
Section 4.1 illustrates the HIL tool describing the behaviour of the WT process. Comparisons and further discussions are also drawn. Finally,
Section 5 concludes the work by summarising the main achievements of the paper, as well as suggesting interesting issues for further research and future investigations.
2. Wind Turbine Benchmark
This section illustrates the WT benchmark considered in this work. In particular,
Section 2.1 recalls the realistic measurements that are acquired from the WT model for FDI purpose, whilst
Section 2.2 summarises the fault scenario. Moreover,
Section 2.3 sketches the procedure exploited for the selection of the input and output measurements that feed the residual generators for FDI, as recalled in
Section 3.
2.1. WT Benchmark Model
The WT simulator considered in this work was presented in [
3,
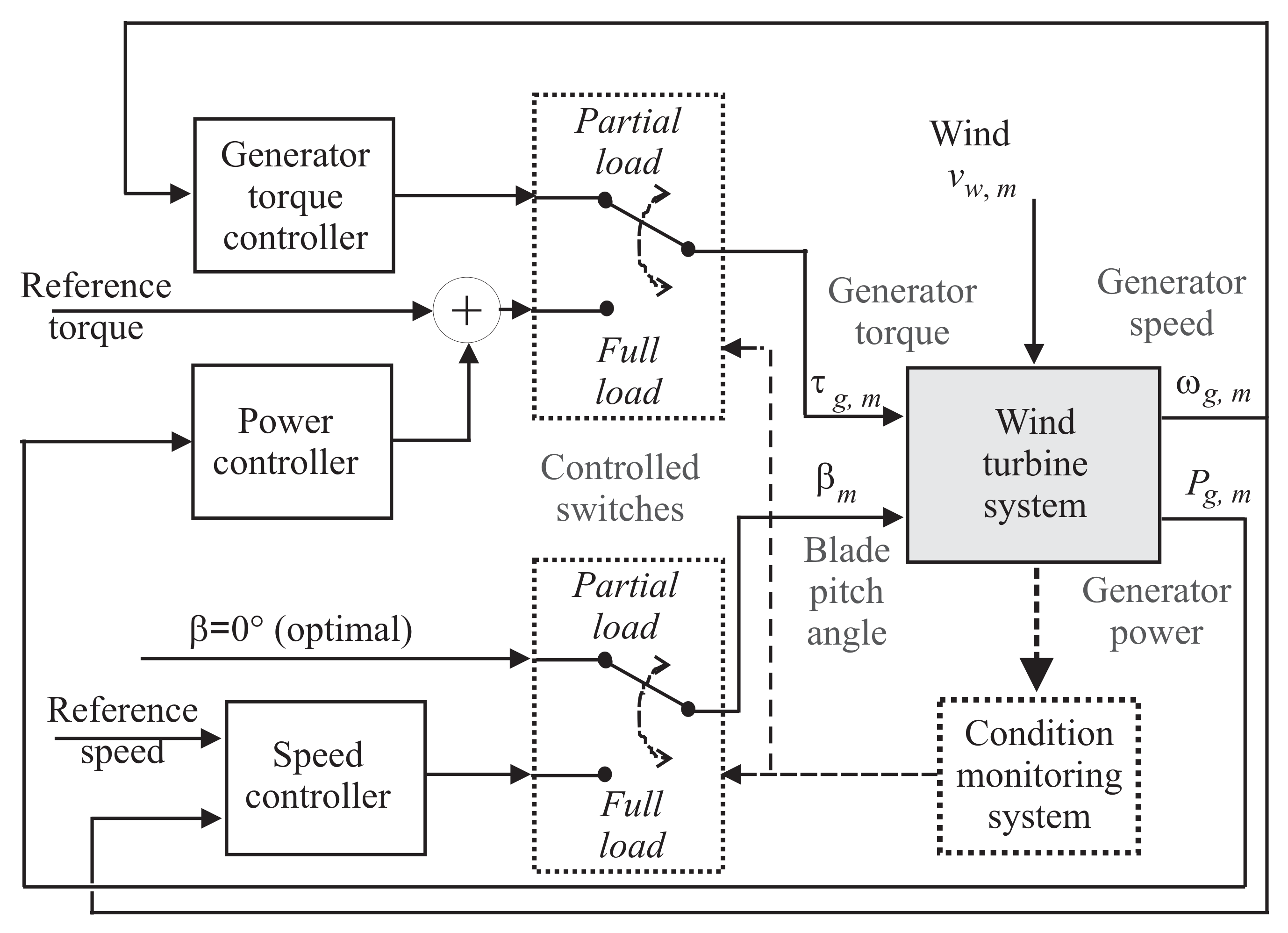
20] and motivated by an international competition. Despite its simple structure, it is able to describe quite accurately the actual behaviour of a three-blade horizontal-axis WT that is working at variable-speed and controlled by means of the pitch angle of its blades. The plant includes several interconnected subsystems, namely the wind process, the WT system, the controllers, and the condition monitoring module. The WT block includes the WT aerodynamics, the drive-train, the electric generator/converter, the sensor and the actuator systems, which are not detailed here. The overall scheme is sketched in
Figure 1, which represents the FDI target of this work. The diagram of
Figure 1 includes also the switching control strategy driving the WT system in partial and full load working conditions [
20]. These operating regions will be exploited for the generation of the estimation and validation data sequences, as remarked in
Section 4.
The nominal operating conditions of the WT are selected to satisfy different demands below and above a certain wind speed. The control task is thus split into the partial and full load controllers, as shown in
Figure 1. The condition monitoring system depicted in
Figure 1 determines the actual working point of the WT plant and drives the controlled switches accordingly.
The measurements that are available from the WT benchmark for FDI purpose come directly from several sensors or, in one case, they are obtained via estimation. In particular, for each of the three blades, a redundant couple of sensors measures the current pitch angle
. Then, a couple of sensors measures the speed of the rotor
and another one the speed of the generator
. A single sensor is available for the wind speed at hub height
, and another one for the generator torque
. The wind measurements are estimated exploiting the hub anemometer.
Table 1 reports a summary of the measured variables. The model of the measurements consists of the sum of the actual value with a white Gaussian noise process [
20].
2.2. WT Fault Scenario
The benchmark model implements different kinds of actual faults, namely sensor, actuator and system faults. Regarding the sensor faults, they affect the measurements of the pitch angles and the measurements of the rotor speed, in form of a fixed value or a scaling error. They represent a common fault scenario of WTs, but their severity is low and they are easily identified. In particular, electrical or mechanical faults in the pitch sensors, if not handled, result in the generation of a wrong pitch reference for the controller with the consequence of a loss in the generated power. The speed of the rotor is measured by means of two redundant encoders, an offset faulty signal can affect these measurements when the encoder does not detect the updated marker, while a gain factor faulty signal represents the reading of excessive markers in each loop, due to dirt on the rotating part.
The considered actuator faults are modelled either as a fixed value or changed dynamics of the transfer function. They affect the converter torque and the pitch actuator. In the former case, the fault is located in the electronics of the converter, while in the latter case the fault affects hydraulic circuit: it represents the pressure drop in the hydraulic supply system (e.g., due to a leakage in hose or a blocked pump) or the excessive air content in the oil that causes the variation of the compressibility factor.
Finally, the considered system fault concerns the drive-train, in form of a slow variation of the friction coefficient in time due to wear and tear (months or year, but for benchmarking reason in the model it has been accelerated up to some seconds). It results in a combined faulty signal affecting the rotor speed and the generator speed.
Table 2 summarises the considered faults, with a brief description of their typology and topology.
This scenario comprising the 9 faulty situations is considered in
Section 2.3, which describes the procedure for determining the input and output measurements acquired from the WT process and mainly affected by these faults.
2.3. Fault Sensitivity Analysis
The paper proposes to exploit this tool, which was suggested earlier by the authors for a different application, see e.g., [
27], as it simplifies the design of the bank of fault estimators. Moreover, it enhances the identification of the dynamic FS and NN prototypes recalled in
Section 3.1. This analysis must be preliminarily performed on the WT simulator. In particular, as already remarked, it is used to select the input and output measurements
and
of the process that feed the dynamic FIS or NN of the bank of
Figure 2.
In practice, the faults considered in the WT benchmark have been injected into the simulator, assuming that only a single fault may occur. Then, the Relative Mean Square Errors (RMSE) index computed by considering the fault-free and faulty measured signals is computed, so that, for each fault, the most sensitive signal and is determined.
In particular, the fault sensitivity analysis relies on a selection algorithm using the normalised sensitivity function
in the form of Equation (
1):
with:
and:
The factor
represents the effect of the considered fault case on the generic measured signal
, with
its sample number. The subscripts ‘
f’ and ‘
n’ indicate the faulty and the fault-free case, respectively. Therefore, the signals mainly affected by the considered fault generate a value of
equal to 1. On the other hand, values of
closer to zero indicate that
is not affected by the fault. Those signals corresponding to significantly higher values of
are thus selected as the most sensitive measurements to the fault cases, and will be used to feed the residual generator modules of the bank reported in
Figure 2.
As already remarked, the WT benchmark is able to generate different typical fault cases affecting the sensors, the actuators and the process components. This scenario with the 9 faults is illustrated by means of
Table 3, which reports the input and output measurements acquired from the WT process signals and mainly affected by these faults.
Table 3 thus summarises the results of this fault sensitivity analysis for the case of the WT simulator.
For FDI purpose, the WT benchmark of
Figure 1 can be described as a nonlinear continuous-time dynamic model represented by the function
of Equation (
4) with state vector
and fed by the driving input vector
:
Equation (
4) highlights that the WT simulator allows to measure the state vector signals, i.e., the rotor speed, the generator speed and the generated power of the WT process:
The driving input vector is represented by the following signals:
that includes the acquired measurements of the pitch angles from the three WT blades and the measured generator/converter torque. These signals are acquired with sample time
T in order to obtain
N data indicated as
and
with index
that are exploited to design the FDI strategies addressed in this work.
Note finally that this tool represents one of the key features of the proposed strategy to FDI. In fact, the fault reconstructors exploited for FDI can be estimated by using a smaller number of inputs, thus leading to a noteworthy simplification of the overall complexity, while decreasing the computational cost of the identification and training algorithms.
3. Data-Driven Strategies for Fault Diagnosis
This section recalls the FDI strategy proposed in this study that relies on FS and NN tools, as summarised in
Section 3.1. These architectures are able to represent NARX models exploited for estimating the nonlinear dynamic relations between the input and output measurements of the WT process and the fault signals. In this sense, these NARX prototypes will be employed as fault estimators for solving the problem of the fault diagnosis of the WT system.
Under these assumptions, the fault estimators derived by means of data-driven approaches represent the residual generators
, which provide the on-line reconstruction
of the actual fault signals
summarised in
Table 3, as represented by Equation (
5):
where the term
represents the estimated fault vector of
Table 3, with
.
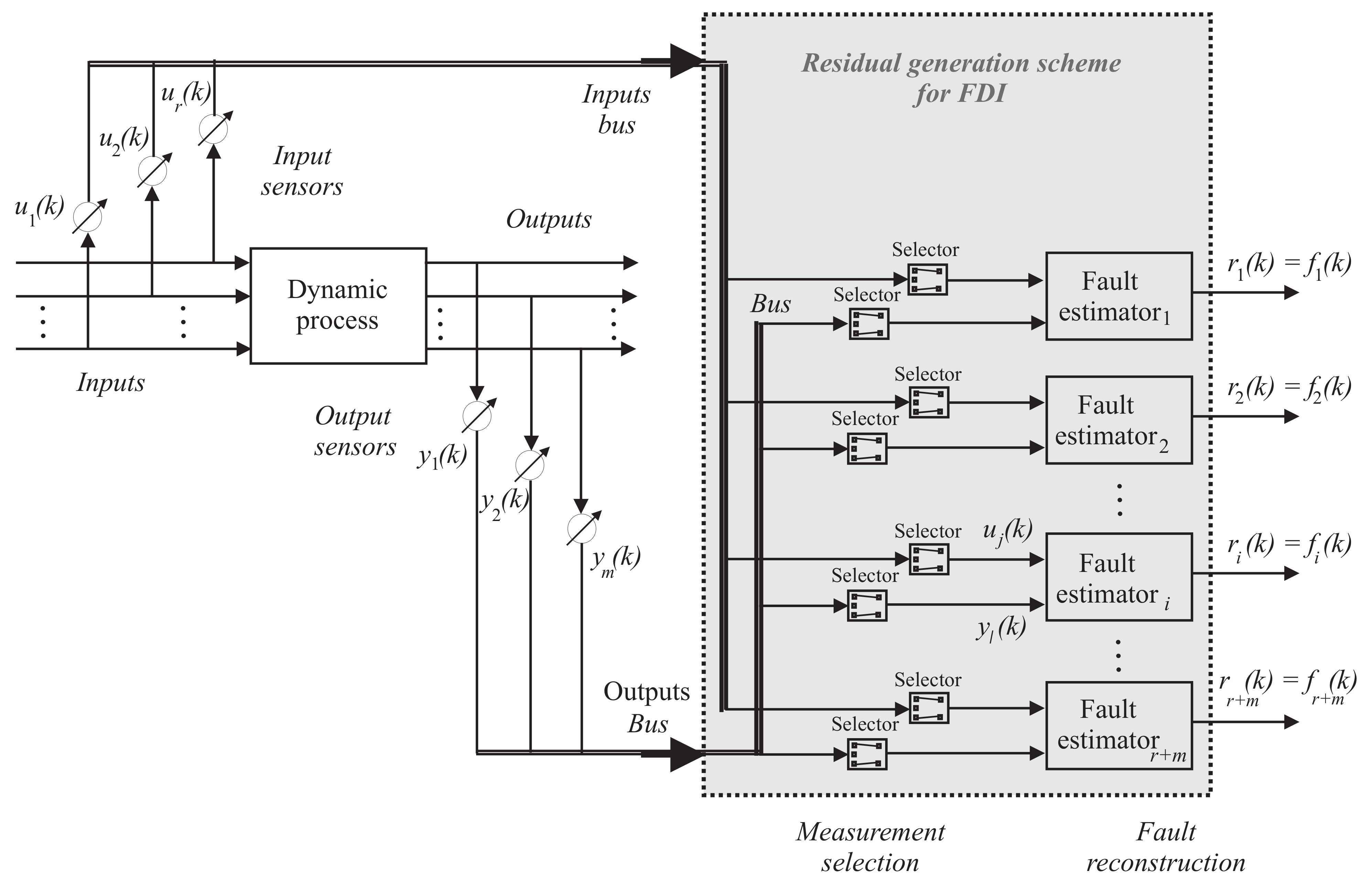
The FDI scheme exploiting the proposed fault estimators as residual generators is sketched in
Figure 3. Note that, as already highlighted, this scheme is also able to solve the fault isolation task [
5].
Figure 2 shows that the general residual generator exploits the input and output measurements acquired from the process under diagnosis,
and
, properly selected according to the fault sensitivity analysis shown in
Table 3. The fault detection problem can be easily achieved by means of a simple threshold logic applied to the residuals themselves, as described in [
5]. This issue will not be considered in this paper.
Once the fault detection phase has been solved, the fault isolation stage is directly obtained via the bank of estimators of
Figure 2. In this case, the number of estimators of
Figure 2 is equal to the faults to be detected, i.e., 9, which is much lower than the number of input and output measurements,
, acquired from the WT process.
This condition provides several degrees of freedom, as the
i-th fault reconstructor
is a function of the input and output signals
and
. These signals are thus selected in order to be sensitive to the specific fault
, as highlighted in
Table 3. This procedure enhances also the design of the fault reconstructors, as it reduces the number of possible input and output measurements,
and
, which have to be considered for the identification procedure reported in
Section 3.1.
The sensitivity analysis already represented in
Table 3 has to be performed before the derivation of the fault estimators. Therefore, once the input-output signals are selected, according to
Table 3, the FSs and the NNs used as fault reconstructors can be developed, as summarised in
Section 3.1.
Fault Estimators via FS and NN Tools
This section recalls the procedure for developing the fault estimators modelled as TS FSs. In this way, the unknown dynamic relations between the selected input and output measurements of the WT plant and the faults are represented by means of FSs, which rely on a number of rules, antecedent and consequent functions. These rules are used to represent the inference system for connecting the measured signals from the WT system to its faults, in form of IF ⟹ THEN relations, implemented as Fuzzy Inference System (FIS), see e.g., [
17].
According to this modelling strategy, the general TS fuzzy prototype has the form of Equation (
6):
Using this approach, in general, the i-th fault signal is reconstructed by using suitable data taken from the WT process under diagnosis. In this case, the fault function is represented as a weighted average of affine parametric relations (consequents) depending on the input and output measurements collected in . These weights are the fuzzy membership degrees depending on the system inputs.
The parametric relations of the consequents are affine functions of the unknown variables
and
, which are estimated by means of an identification approach. The rule number is assumed equal to the cluster number
exploited to partition the data via a clustering algorithm with respect to regions where the parametric relations (consequents) are valid [
17].
Note that the system under diagnosis corresponds to a WT plant, which is described by a dynamic model. Therefore, the vector
in Equation (
6) contains both the current and the delayed samples of the system input and output measurements. Therefore, the consequents include discrete-time linear Auto-Regressive with eXogenous (ARX) input structures of order
o. This regressor vector is described in form of Equation (
7):
where
and
represent the
l-th and
j-th components of the actual WT input and output vectors
and
. These components are selected according to the results reported in
Table 3.
The consequent affine parameters of the
i-th model of the Equation (
6) can be organised into a vector:
where the coefficients
are usually associated to the delayed output samples, whilst
to the input ones.
The approach proposed in this paper for the derivation of the generic
i-th fault FIS approximator starts with the fuzzy clustering of the data
and
from the WT process. This paper exploits the well-established Gustafson-Kessel (GK) algorithm [
17]. Moreover, the estimation of the FIS parameters is solved as a system identification problem from the noisy data of the WT process. Once the data are clustered, the identification strategy proposed in this work uses the methodology developed by the authors in [
28].
Another point not addressed in this work concerns the selection of the optimal cluster number
. This issue was investigated and developed by the authors in [
28], which leads to the estimation of the membership degrees
required in Equation (
6) and solved as a curve fitting problem [
17].
This paper considers an alternative data-driven approach, which exploits NNs used as fault approximators in the scheme of
Figure 2. Therefore, in the same way of the FSs, a bank of NNs is employed to reconstruct the faults affecting the WT system using a proper selection of the input and the output measurements. This NN structure consists of a feed-forward MLP architecture with 3 layers of neurons [
19].
However, as MLP NNs represent static relations, the paper suggests to implement these structures with a tapped delay line. Therefore, this quasi-static NN represents a powerful way for estimating nonlinear dynamic regressions between the input and output measurements from the WT process and its fault functions. This solution allows to obtain another Nonlinear ARX (NARX) description among the data. Moreover, when properly trained, these NARX NNs are able to reconstruct the fault function
using a suitable selection of the past measurements of the WT system inputs and outputs
and
, respectively. The example of the general solution is sketched in
Figure 3, which can be implemented by means of FIS or NARX NN structures.
Similarly to the fuzzy scheme, with reference to the
i-th fault reconstructor, a bank of NARX NNs is exploited, where the generic NARX system models the relation of Equation (
9):
the signal
represents the estimate of the general
i-th fault in
Table 3, whilst
and
indicate the components of the measured inputs and outputs from the WT process. These signals are selected again by means of the solution of the fault sensitivity problem reported in
Table 3. The accuracy of the fault reconstruction depends on the number of neurons per layer, their weights and their activation functions.
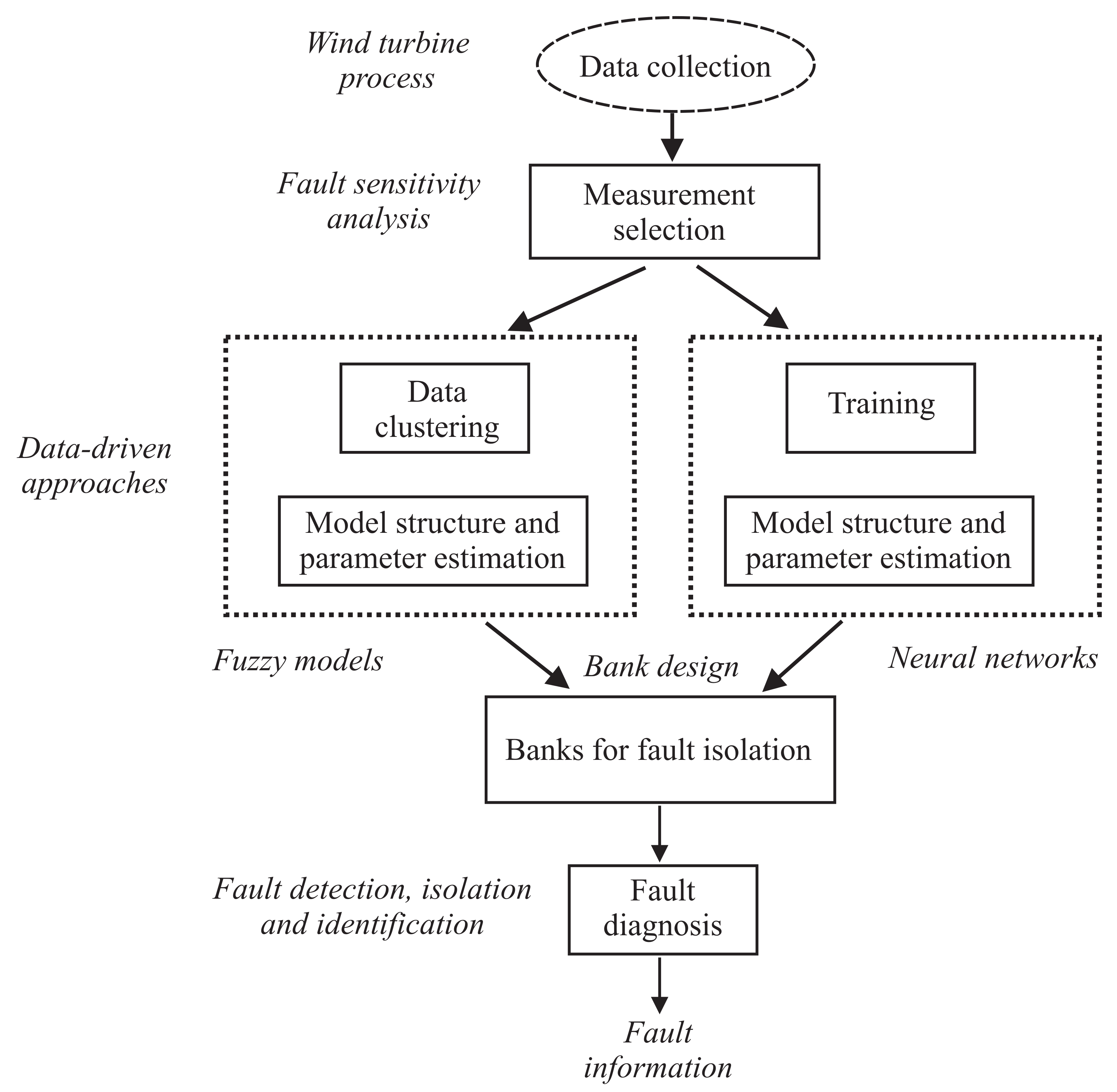
In order to summarise the overall procedure exploited for the implementation of the FDI schemes,
Figure 4 reports the different phases involved in the proposed methods and a summary of the complete design flows.
In particular, once the measurements have been selected according to the procedure addressed in
Section 2.3, the design of the FIS requires the clustering of the data into
regions, the selection of the model structure (order
o) and the estimation of the consequent parameters
and
, as well as the membership functions
in Equation (
6). The data are usually divided into three sets, i.e., the training, the validation and the test sets. This solution leads to improve the estimation capabilities of the identified fuzzy prototypes. The FIS models can be thus organised into the bank structure that allows for fault isolation. Moreover, the fault identification is also accomplished.
On the other hand, the same procedure can be performed for the NARX NN models. After the measurement selection, the data are divided into the training, the validation and the test sets. Also in this case, this partition improves the generalisation capabilities of these systems. The derivation of the NARX NN prototypes requires the selection of the delays
and
in Equation (
9), as well as the the number of neurons per layers. Once these NARX NN models are estimated, they can be organised into the bank structure for achieving the fault identification task.
The results of the selection of the optimal structure of the fault reconstructors for FDI and the achieved performances will be shown in
Section 4.
4. Simulation Results, Experimental Validation, Comparisons and Discussion
With reference to the WT benchmark of
Section 2, the simulations are driven by different wind sequences generated in a random way. They represent real measurements of wind speed sequences from typical WT operating conditions, with ranges varying from 5 m/s to 20 m/s. This scenario was modified by the authors with respect to the benchmark earlier proposed in [
20]. The simulations consist of 4400 s, with single fault occurrences and a number of samples
440,000 for a sampling frequency of 100 Hz. Almost all fault signals are modelled as step functions lasting for 100 s with different commencing times. Further details can be found in [
20,
29].
The first part of this section reports the results achieved by means of the fuzzy prototypes used as fault reconstructors according to
Section 3.1. In particular, the fuzzy
c-means and the GK clustering algorithms were exploited. A number of clusters
and a number of delays
were estimated. The membership functions of the TS FS and the parameters of the consequents
and
were derived for each cluster by following the procedure developed by the same authors in [
30]. The TS FSs of Equation (
6) were thus determined and 9 fault reconstructors were organised according to the scheme of
Figure 2.
The performances of the 9 TS FSs when used as fault estimators were evaluated again according to the RMSE index, computed as the difference between the reconstructed
and the actual
signals for each of the fuzzy estimators. These values were reported in
Table 4.
Indeed, the RMSE values reported in
Table 4 represent an average of the results obtained from a campaign of 1000 simulations, as the benchmark exploited in this work changes the parameters of the WT model at each run. Moreover, the model-reality mismatch, the measurement errors, uncertainty and disturbance effects are described as Gaussian processes with suitable distributions, as remarked in
Section 2. Therefore,
Table 4 reports also the values of the standard deviation (std. dev.) of the estimation errors achieved by the FS fault estimators.
Note that these reconstructed signals
can be directly used as diagnostic residuals in order to detect and isolate the faults affecting the WT. Moreover, each TS FS of Equation (
6) is fed by 3 inputs (according to
Table 3), with a number of delayed inputs and outputs
and
clusters.
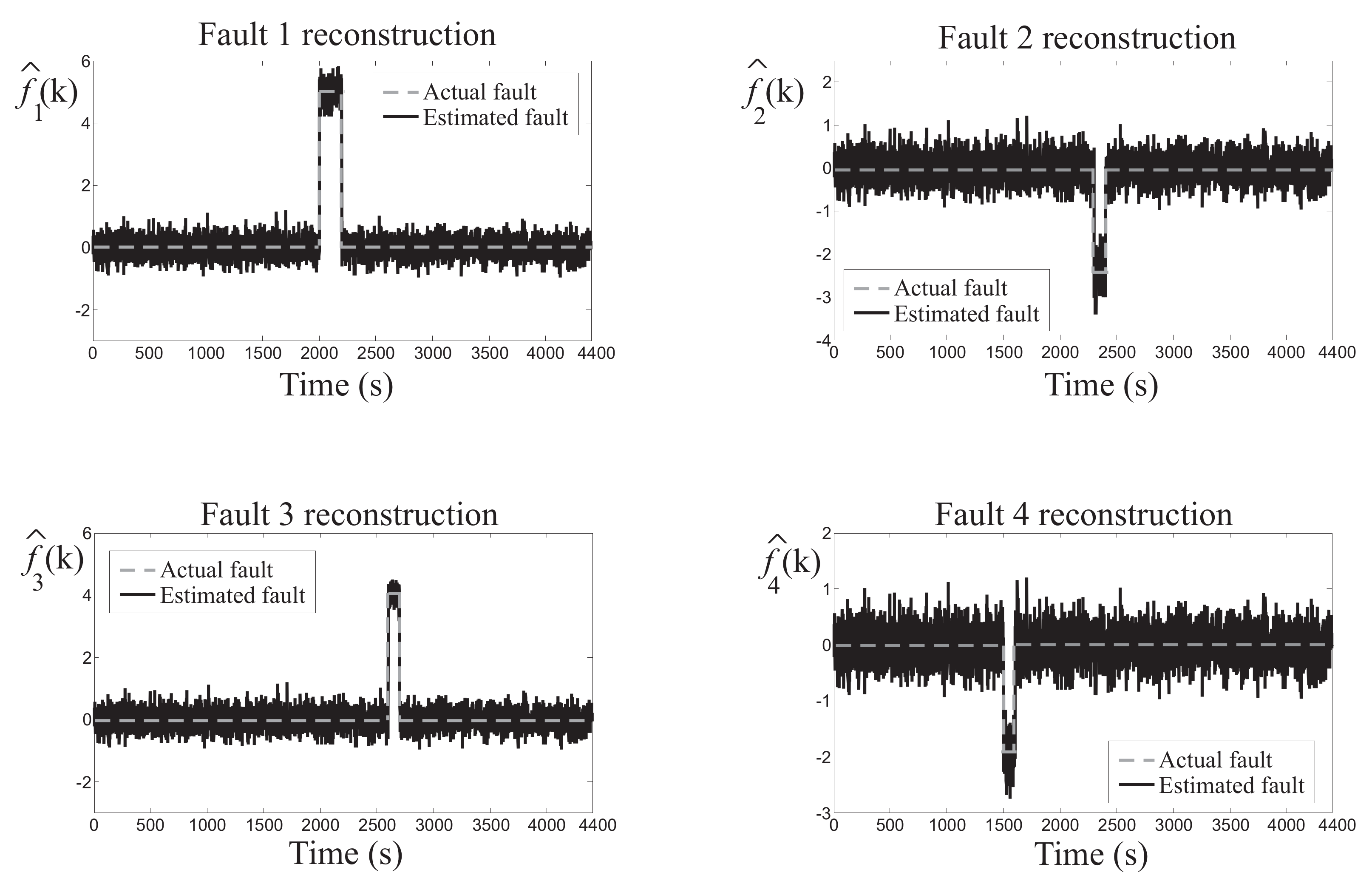
As an example,
Figure 5 shows the results regarding the fault cases 1, 2, 3, and 4 of the WT plant recalled in
Section 2.
In particular,
Figure 5 reports the estimated faults
provided by the FSs in faulty conditions (black continuous line). They are compared with respect to the actual faults (grey dashed line). The fault detection task can be easily accomplished as the residuals are significantly different from zero in faulty conditions. Note also that the reconstructed fault functions
are different from zero also in fault-free conditions due to the measurement errors and the model-reality mismatch. This aspect serves to highlight the accuracy of the reconstructed signals provided by the estimated fuzzy models.
As for the FSs, 9 NARX NNs summarised in
Section 3.1 were trained to provide the reconstruction of the 9 faults affecting the WT plant. In particular, the NARX were implemented as MLP NNs with 3 layers: the input layer consisted of 3 neurons, the hidden one used 10 neurons, whilst one neuron for the output layer.
delays were used in the relation of Equation (
9). Moreover, sigmoidal activation functions were used in both the input and the hidden layers, and linear functions for the output layers. With reference to
Table 3, the NARX NNs were fed by 9 signals, representing the delayed inputs and outputs from the WT process.
As for the FSs, the prediction accuracy of the NARX NN was analysed by means of the RMSE index, and its average values summarised in
Table 5.
As for the TS FS case,
Table 5 reports also the values of the standard deviation (std. dev.) of the estimation errors achieved by the NARX NN fault estimators.
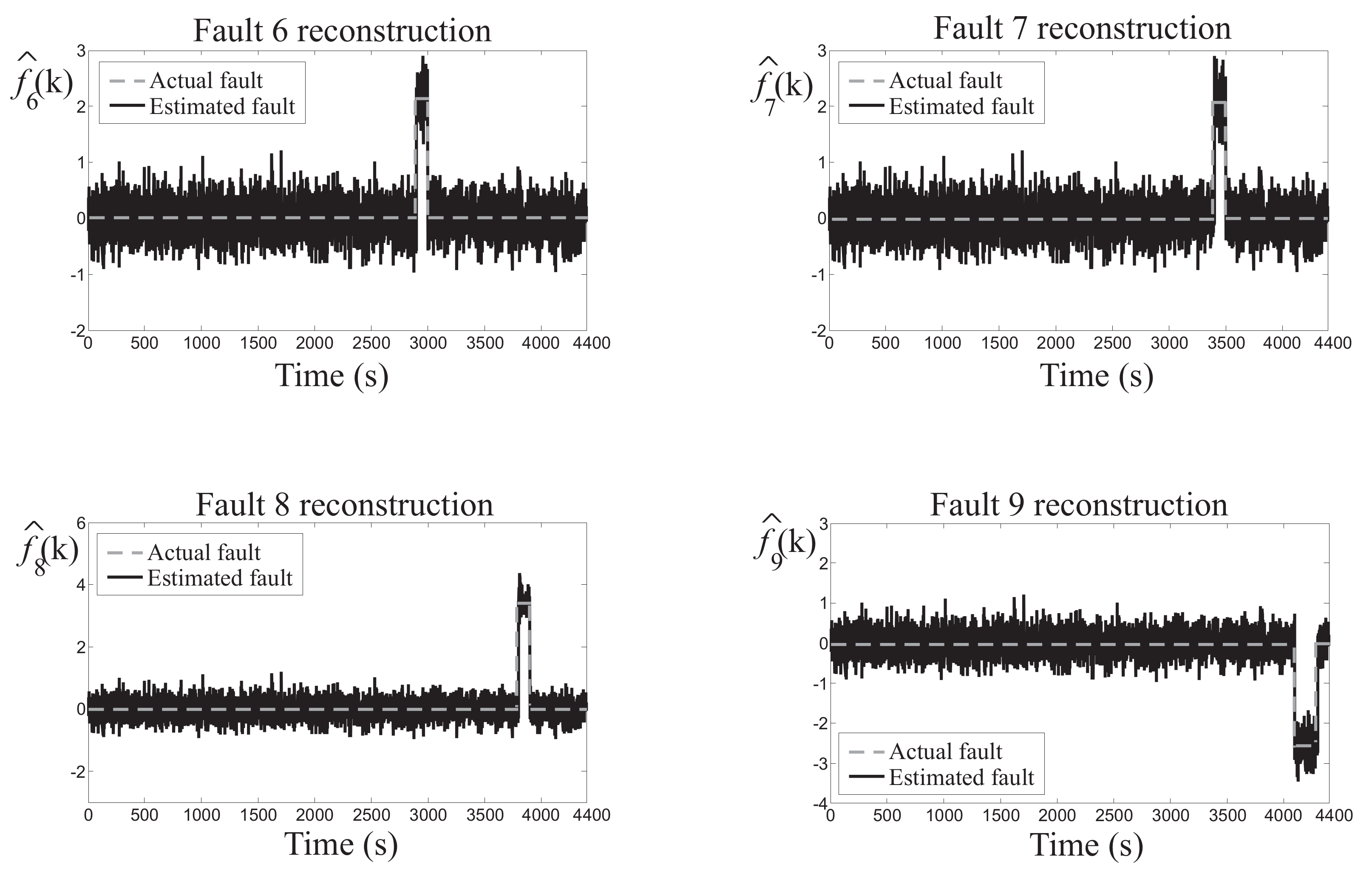
As an example,
Figure 6 depicts some of the residual signals
(black continuous line) provided by the NARX NNs for the fault conditions 6, 7, 8, and 9, and compared to the actual fault signals (grey dashed line).
Also in this case, the results obtained by the NARX NNs serve to highlight the efficacy of the developed solution, taking into account disturbance and uncertainty affecting the WT system.
4.1. HIL Validation
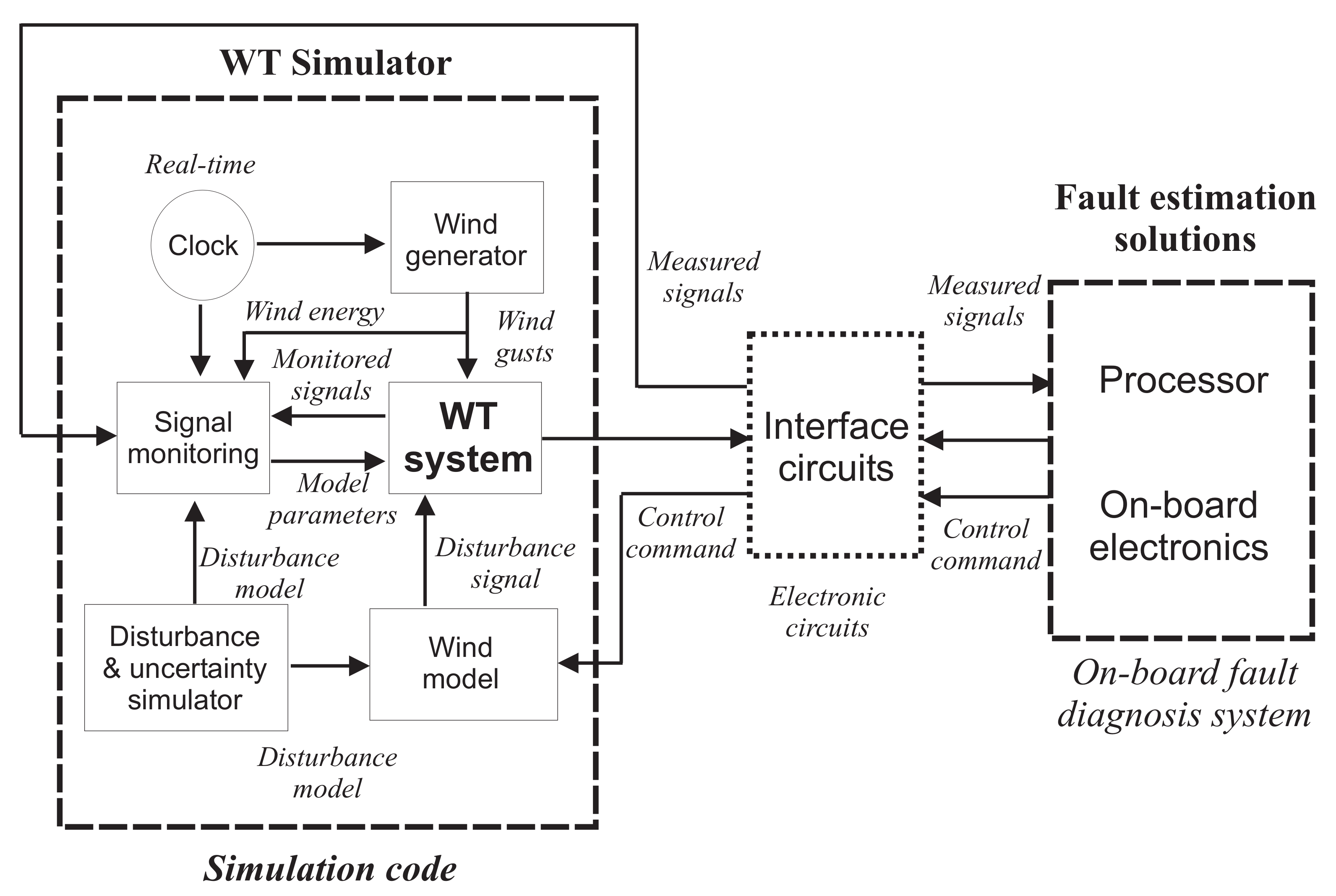
In order to validate the developed FDI solutions in more realistic working situations, the WT process and the designed algorithms have been implemented and executed by means of a HIL tool. This test-bed allows to reproduce experimental tests that are oriented to the verification of the results achieved in simulations. This test-bed is sketched in
Figure 7, which highlights 3 main modules.
The WT simulator that was used to describe the system dynamics, its actuator, measurement sensors, and the WT controllers were implemented in the LabVIEW environment. Realistic effects such as uncertainty, measurement errors, disturbance and the model-reality mismatch were also included, as recalled
Section 2. The overall system is converted into the C++ code running on a standard PC, which allows also to test and monitor the signals generated by the proposed fault diagnosis strategies.
The FDI schemes summarised in
Section 3.1 were also compiled as executable code and implemented in an AWC 500 industrial system that features typical WT requirements. This industrial module receives the signals acquired from the PC simulating the realistic WT plant that represent the monitored signals reported in
Table 3. Therefore, the on-board electronics elaborate these signals according to the FDI algorithms and produce the monitoring signals transmitted back to the WT simulator running on the PC.
An intermediate module represents the interface circuits providing the communications between the PC with the WT simulator and the on-board electronics running the fault diagnosis algorithms. In this way, it manages the signals and exchanges the data between the WT simulator and the AWC 500 system.
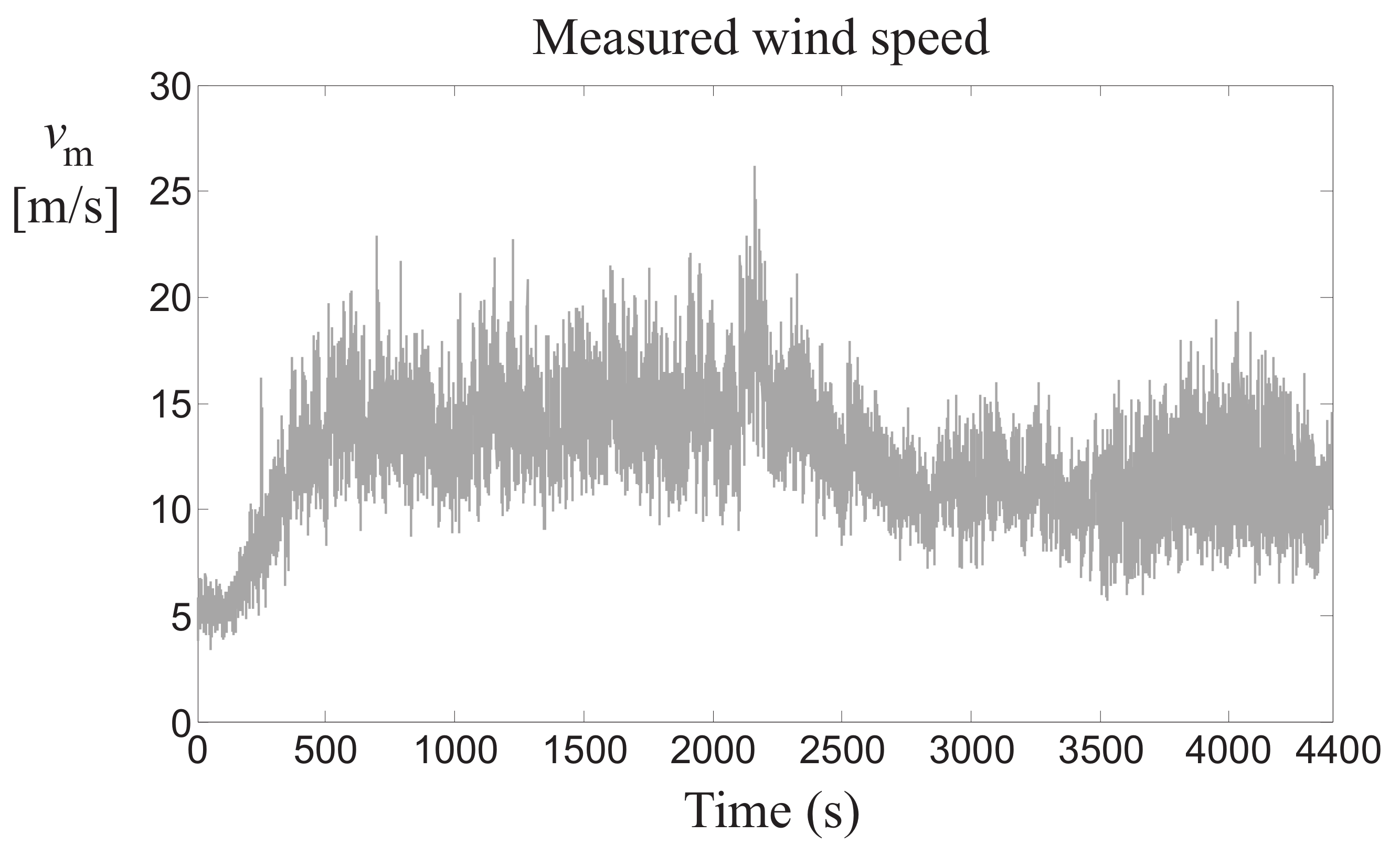
In the following, the data sequences generated by the WT simulator are briefly described. With reference to the WT benchmark model of
Section 2 and its HIL implementation, all simulations are driven by realistic wind sequences, as depicted in
Figure 8.
Figure 8 shows an example of the realistic acquisition of wind speed data from a WT, as described in [
20,
26]. It should represent a good coverage of typical operating conditions, as it ranges from 5 to 20 m/s, with a few spikes at 25 m/s.
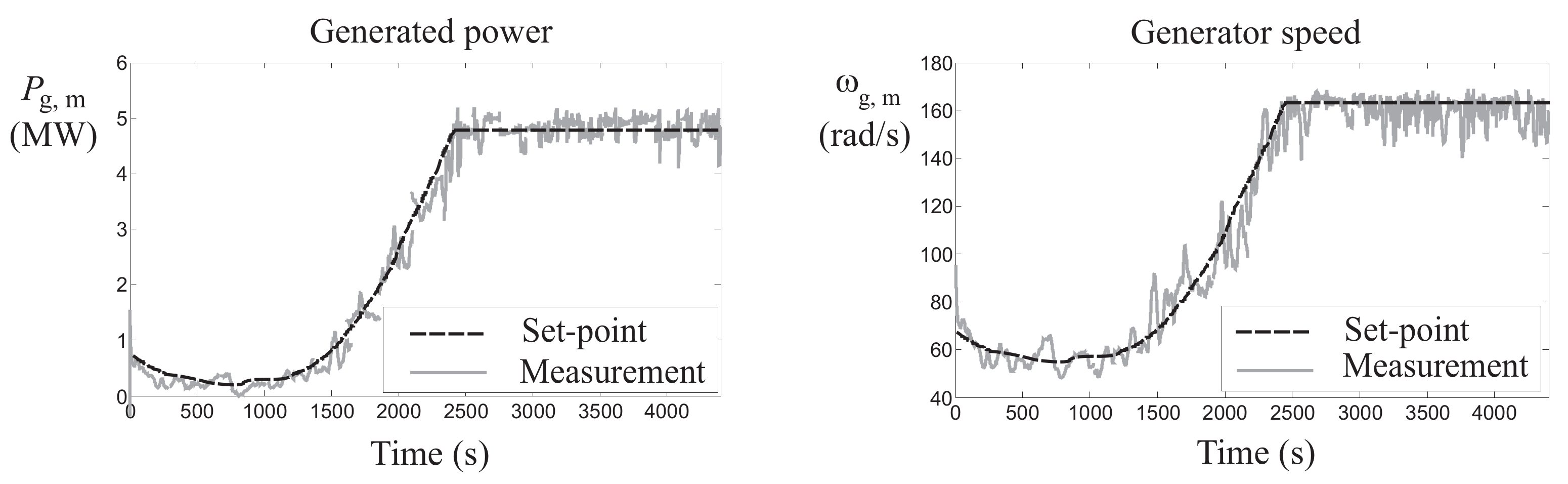
As further example of WT sequences used for the validation of the FDI schemes,
Figure 9 shows the measured outputs
and
with respect to the reference signals, in partial and full load working conditions [
20].
These working conditions represent the operating regions of a WT that motivate the switching blocks used for the torque and the pitch controls sketched in
Figure 1. Therefore, the WT data sequences are generated according to the nominal operating trajectory to satisfy different demands below and above a certain wind speed. A condition monitoring system determines the actual working point of the WT and drives the switches accordingly, as shown in
Figure 1.
When the WT operates in partial load condition, it is driven by the generator torque controller, which should maximise the produced energy, as shown in
Figure 9. On the other hand, when the WT operates in full load condition, both the speed and the power controller are active. These controllers should track the rated generator speed and limit the output power, as depicted in
Figure 9. This behaviour is obtained by properly setting the two switches in
Figure 1. In this way, the data sequences exploited for the validation of the designed FDI schemes are generated.
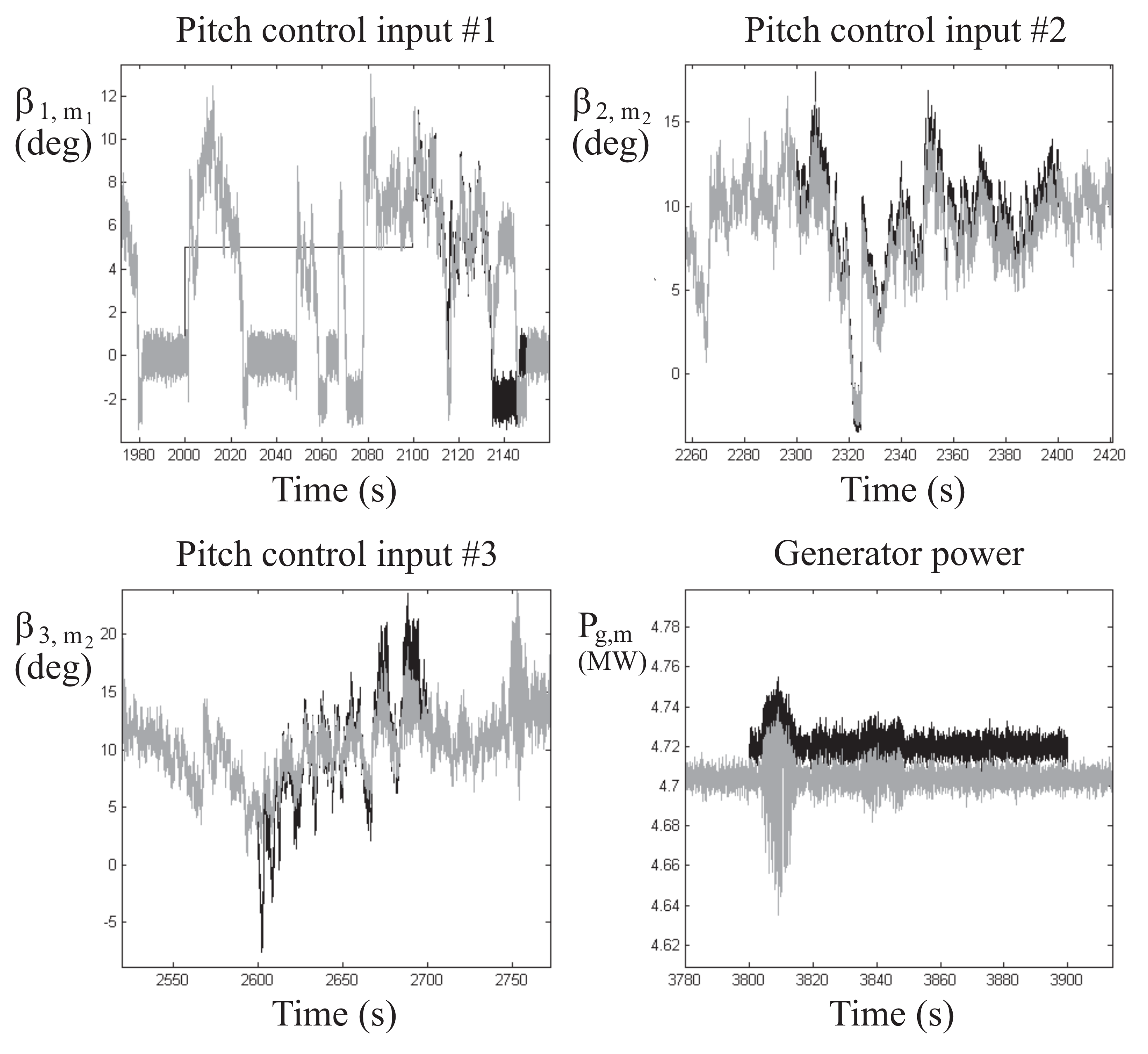
As final example of data sequences used for the identification of the FS and NN prototypes, the measured control inputs of the WT blades
and the generated power
are depicted in
Figure 10 in full load conditions.
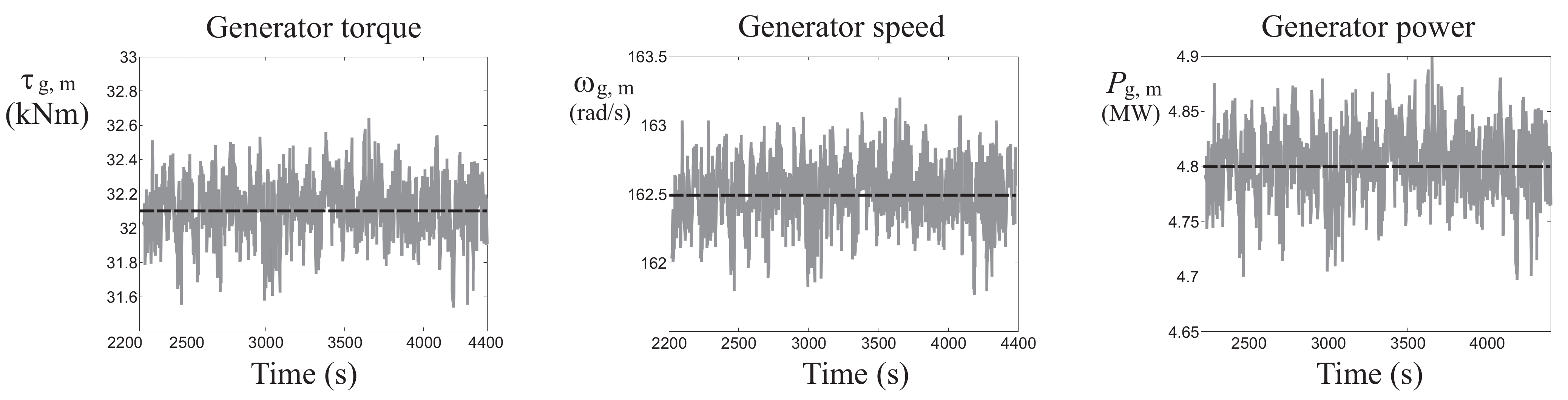
On the other hand,
Figure 11 depicts the WT main variables in full load working conditions.
Therefore, for the generated driving wind sequence
,
Figure 11 depicts the generator speed
and power
, and the control input
.
The results achieved via this HIL tool are reported in
Table 6 that summarises the capabilities of the FDI strategies by means of the RMSE performance index.
Note that the tests summarised in
Table 6 are consistent with the results reported in
Table 4 and
Table 5. Although the accuracy of the simulations seems better than the performance achieved via the HIL tool, some remarks have to be drawn. First, the AWC 500 system uses calculations that are more restrictive than the PC simulator. Moreover, A/D and D/A devices are also exploited, which can introduce further deviations. On the other hand, the testing of real scenarios does not involve the data transfer from a PC to on-board electronics, thus reducing possible errors. Therefore, it can be finally remarked that the achieved results are quite accurate and motivate the application of the developed FDI strategies to real WT installations.
4.2. Comparative Analysis
To analyse the performance of the proposed solutions, this section compares the developed FDI schemes with different methodologies already proposed by the same authors. They rely on a model-based nonlinear approach, i.e., the so-called NonLinear Geometric Approach Adaptive Filter (NLGA-AF) [
31] and a Recursive identification of FSs (RFSs) [
32]. Moreover, the Sliding Mode Observer (SMO) method is also considered [
33].
These comparisons are performed on the basis of the estimation accuracy, as shown in
Table 7.
According to the results summarised in
Table 7, the performance of the NARX NN solution is better than the ones obtained with the other schemes. In more detail, the values of the RMSE index highlights that when the mathematical description of the dynamic process under investigation may be included in the design phase, the NLGA-AF technique with disturbance decoupling still yields to good performances, even if an optimisation procedure is required. However, when modelling errors are present, the offline learning feature of the data-driven fuzzy estimators TS FSs allows to achieve interesting results. For example, this consideration is valid also for the SMO estimators derived via a linearisation procedure. On the other hand, the TS FSs led to more interesting capabilities. With reference to the adaptive scheme, such as the RFS, it takes advantage of its recursive features, since it is able to track possible variations of the WT system, due to operation or model changes. However, it requires quite complicated and not straightforward design procedures relying on data-driven recursive algorithms. Therefore, fuzzy-based schemes use the learning accumulated from data-driven offline simulations, but the training stage can be computationally heavy. Finally, concerning the NARX NN strategy, which represents the solution with the best results, it is rather simple and straightforward. Obviously, the achievable performances of linearised or adaptive methods can be quite limited when applied to nonlinear dynamic processes. It can thus be concluded that the proposed data-driven approaches (NARX NN and TS FS) seem to represent powerful techniques able to cope with uncertainty, disturbance and variable working conditions.
4.3. Discussion and Final Remarks
This section discusses the results shown in
Section 4.2 relying on model-based and data-driven methods. In particular, the FS and NN models were compared to the SMO, the RFS and the NLGA-AF, already proposed for WTs, and applied to the considered benchmark.
SMO was designed on the basis of a linearised model of the WT process. In this case, the design procedure is based on the selection of an appropriate switching manifold, and then on the determination of an input, including a discontinuous term, that ensures the sliding motion in this manifold. This strategy can manage disturbance and modelling errors, which represent the effect of both the linearisation and measurement errors.
The RFS approach used a recursive identification method for synthesising the residual generators for FDI, under the assumption of LPV modes. In fact, the considered WT system has varying parameters caused by the nonlinearity of the aerodynamic relation along the nominal operating trajectory and due to the model uncertainty. In particular, the instantaneous partial derivatives of the aerodynamic torque are part of the linearised model and change along the nominal operating trajectory. These changes were approximated using an affine description in the wind speed.
The NLGA-AF is obtained using differential geometry and nonlinear system analysis tools. In particular, the NLGA-AF methodology, which was developed for the more general problem of FDI, relies on adaptive filters designed with a nonlinear geometric approach to obtain the disturbance de-coupling property.
In order to provide a brief but clear insight into the above mentioned techniques, the comparisons were performed in the same previous working conditions, and based on the RMSE index, when the realistic WT simulator is considered. It is worth noting that the FDI schemes implemented via SMO, FS and NN do not exploit any adaptation mechanism. In fact, the SMO strategy is able to decouple the uncertainty via the sliding motion, whilst NNs and FSs were designed to passively tolerate disturbance and modelling errors via the acquired off-line learning.
The comparisons among the different FDI solutions summarised in
Table 7 highlighted that schemes using adaptive strategies, such as RFS and NLGA-AF, allowed to achieve acceptable performances in terms of estimation errors. The SMO solution can require considerable computational time with respect to the other solutions, without any parameter change, whilst the RFS strategy can lead to larger computational effort at the design stage.
On the other hand, when the mathematical description of the monitored system can be perfectly obtained, in general model-based strategies such as NLGA-AF are preferred. However, when modelling errors and uncertainty are present, alternative schemes relying on adaptation mechanisms, or passive robust methods, showed interesting robustness properties in the presence of unmodelled disturbance, modelling mismatch, and measurement errors. With reference to data-driven methodologies, and in particular to FS and NN, in the case of a monitored system with modelling errors, the off-line learning can lead to very good results. Other explicit disturbance decoupling techniques can take advantage of their robustness capabilities, e.g., the NLGA-AF, but with quite complicated and not straightforward design procedures. The FS and NN-based schemes rely on the learning accumulated from off-line simulations, but the training stage can be computationally heavy. Regarding the considered methods using RFS, or FS, they seem rather simple and straightforward, even if optimisation stages can be required.
It is worth noting how the achieved results have highlighted that data-driven approaches, such as fuzzy structures are able to provide good performances. However, they can be easily outperformed by self-learning schemes, representing data-driven solutions that did not require optimisation stages, adaptation procedures or disturbance compensation methods. Further investigations will be oriented to apply the developed methodologies to real WT installations, in the presence of more realistic disturbance and uncertainty effects. In fact, the methodologies designed in this paper were proposed with the perspective to implement effective FDI solutions that could be included in real installations to improve their reliability and availability, thus increasing the effectiveness of the health monitoring, while improving the energy production, and reducing O&M costs.
Note also that the solutions proposed in this paper rely on data-driven schemes. In fact, model-based methods are designed to detect any discrepancy between real system and model behaviours, and it is assumed that a discrepancy signal is related to (has a response from) a fault. However, the same difference signal can respond to model mismatch or noise in real measurements, which can be (erroneously) detected as a fault, giving rise to a ‘false alarm’ in detection.
These considerations have led to investigate ‘robust’ methods, in which particular attention is paid to the discrimination between actual faults and errors due to model mismatch. Moreover, this work focused on the determination of ‘good’ solutions suitable for robust diagnosis. Moreover, the paper also highlighted how ‘accurate models’ can be obtained from real data. The paper considered the case in which noise and disturbance affects the acquired data. The FDI strategies can be obtained by means of both model-based and data-driven approaches. Comparisons between these strategies were thus addressed.
Therefore, the purpose of the study is to provide guidelines for the data-driven design of robust and reliable FDI schemes. Moreover, attention was paid to the practical application of the methods to realistic WT installations, as reported in this last section. On the other hand, this study can aim also to encourage technology transfer in different engineering fields. In fact, the development of FDI procedures has impacts on all areas of the control discipline. For example, the proposed solutions can be applied to different processes, see e.g., the case of image and speech recognition [
34,
35].
Finally, the key features of this study include viable approaches relying on data-driven methodologies for robust and reliable fault diagnosis, as well as extended application studies using different WT measurement data.