Regular Two-Dimensional Packing of Congruent Objects: Cognitive Analysis of Honeycomb Constructions

Featured Application

Theory of packing and covering, geometry of numbers, combinatorial geometry.

Abstract

A new approach to investigate the two-dimensional, regular packing of arbitrary geometric objects (GOs), using cognitive visualization, is presented. GOs correspond to congruent non-convex polygons with their associated coordinate system. The origins of these coordinate systems are accepted by object poles. The approach considered is based on cognitive processes that are forms of heuristic judgments. According to the first heuristic judgment, regular packing of congruent GOs on the plane have a honeycomb structure, that is, each GO contacts six neighboring GO, the poles of which are vertices of the pole hexagon in the honeycomb construction of packing. Based on the visualization of the honeycomb constructions a second heuristic judgment is obtained, according to which inside the hexagon of the poles, there are fragments of three GOs. The consequence is a third heuristic judgment on the plane covering density with regular packings of congruent GOs. With the help of cognitive visualization, it is established that inside the hexagon of poles there are fragments of exactly three objects. The fourth heuristic judgment is related to the proposal of a triple lattice packing for regular packing of congruent GOs.

1. Introduction

The problem with the regular placing of geometric objects on a plane according to classification [1,2] belongs to the class 2/V/I/C common problem of “Cutting and Packing” (C & P). Russian research in the field of C & P dates back to the work of V.L. Kantorovich. Later, theoretical and practical studies were carried out by such scientists as V.F. Zalgaller, V.L. Rvachev, Yu.G. Stoyan, E.A. Moukhacheva and their followers [2,3,4].

The problem of 2/V/I/C gained practical fame as a problem of optimizing cutting in sheet-stamping production. However, some generalizations of this problem are of purely theoretical interest, providing access to other fields of science, such as theory of packing and covering [5], geometry of numbers [6], combinatorial geometry [7], computational mathematics, etc.

Let there be an object—an arbitrary figure—which is a flat, non-convex polygon having an arbitrary point inside its contour, hereinafter called the pole (Figure 1). The object shown in Figure 1 will be used later.

Figure 2 shows congruent representations of an arbitrary GO (Figure 1) with local poles. Congruent relations between GOs are associated either with the transformation of mutual rotation by a certain angle (type_1), or with the transformation of mutual mirror symmetry (type_2). The combination of these transformations also generates congruent representations (type_3). For a congruent relation, type_0 is entered like oriented GOs. Selecting 180° for the rotation angle ensures the proportionality of congruent GOs in one direction, which is necessary to form regular arrangements. The types of congruent relations introduced for the convenience of subsequent designations are conventional.

Placing a GO on a plane without intersections and overlays is called packing. The packing of GO is called regular if GO lands in the form of a fragment of some single-lattice packing [5,8]. Under tight touch conditions, similar GOs, while maintaining their orientation on the plane, form regular packing (Figure 3). GO poles determine dense, lattice packing. The textured GOs in Figure 3 show the honeycomb construction of packing.

One of the main features of regular packing is its honeycomb structure, that is, any GO of regular packing touches six surrounding GOs. This hexagonal characteristic of regular packing of the same objects is indirectly evidenced by Figures 90 and 95 in [7] and Figure 5 in [9]. The touching of a GO with its six neighbors is presented [10,11]. The honeycomb structure of regular packing produces three GO packing directions (Figure 3), with their translation vectors combining the poles of the two touching GOs in that direction. The position of the pole of any GO in regular packing is determined by the following vector:

$$\overline{E_{j,m}}=\overline{a_j}\times m,\hspace{1em}where m=\pm 1,\pm 2,\dots ,\pm \infty , j=1,2,3$$

(1)

By selecting one of the directions of regular packing (Figure 3), we indicate different rows of objects of the selected direction in color (Figure 4a). Congruent GOs of different types (Figure 1) can be placed in alternating rows. Figure 4b–d shows regular packing of the three introduced congruent relationship types. Two-row packing of congruent GOs is described as double-lattice packing that combines two single-lattice packings, translated one into the other [9,12]. The concept of dense double-lattice packing is introduced [13]. Honeycomb constructions (Figure 4b–d) determine regular packing of congruent GOs and have three parallel packing directions with identical translation vectors in each direction. The last fact determines the necessity of introducing the concept of triple-lattice packing. The analysis of Figure 4 leads us to the following heuristic judgement: “Regular packings of congruent GOs have a honeycomb structure”.

The main objective of this research is to investigate the properties of regular packing of congruent objects on the plane. The main objects of the research were honeycomb constructions of regular packing of congruent GOs. Before proceeding to the analysis of honeycomb constructions of the regular packing of congruent objects, we will consider the methods of their construction.

For accurate construction of regular packing of congruent GOs (Figure 3), the apparatus of functions of tight arrangements (FTA) and algorithms of formation of the FTA hodograph are used [7]. The FTA hodograph for packing two objects on the plane is the pole path of the movable object (Figure 5) with its plane-parallel movement around the fixed object in conditions of constant contact with each other.

According to the Science Citation Index Expanded (Sci-EXPANDED), the number of annual publications on ‘honeycomb’ is constantly growing, now at several hundreds. Honeycomb structures have found widespread applications in various fields, including architecture, transportation, mechanical engineering, and chemical engineering. The geometry of a honeycomb minimizes the amount of material used for minimal weight and minimal cost.

The mathematical structure of honeycomb was first formulated long before B.C. and later was called the honeycomb conjecture, which states “any partition of the plane into regions of equal area has perimeter at least that of the regular hexagonal honeycomb tiling”. The conjecture was finally proven by Thomas C. Hales [14]. No studies of the honeycomb conjecture in regular packings of congruent objects were found.

Approximate generation of FTA hodographs is possible using a suitable graphic editor. Depending on the type of congruent relation, we will distinguish the hodograph of type_0 (Figure 5a), hodograph of type_1 (Figure 5b), hodograph of type_2 (Figure 5c), and hodograph of type_3 (Figure 5d). The centers of all hodographs coincide with the pole of a fixed object.

Development of a honeycomb construction (type_0) involves sequentially performing the following actions:

• The points of intersection of an arbitrary straight line passing through the pole of the object (Figure 6a) with the hodograph (type_0) are fixed as two poles of future objects and centers of future hodographs (type_0);
• The points of intersection of the two new hodographs (type_0) with the already existing hodograph (type_0) are fixed as the four poles of future objects (Figure 6b);
• The obtained six poles make it possible to form a honeycomb construction (Figure 6c).

Let us consider the development of honeycomb constructions of other types of congruent relations using the example of type_1:

• The points of intersection of an arbitrary straight line passing through the pole of the object (Figure 7a) with the hodograph (type_0) are fixed as two poles of future objects and centers of future hodographs (type_1);
• The points of intersection of the two new hodographs (type_1) and the hodograph (type_1) centered at the pole of the object are fixed as four poles of future objects (Figure 7b);
• The obtained six poles make it possible to form a honeycomb construction (Figure 7c).

Replacing the hodograph (type_1) with other types of hodographs will allow obtaining honeycomb constructions of the appropriate types.

2. Methodology

The proposed approach to the analysis of honeycomb constructions of regular packings is based on cognitive processes. Cognitive theory encompasses mental activities, such as the observation of various phenomena in an environment; pattern recognition and problem representation; and analytic reasoning. Beliefs, images, and roles may be the products of cognitive processes that are forms of heuristic judgments.

One method of finding heuristic judgments is related to the use of cognitive visualization—non-trivial graphical representations [15,16]. The analysis of these representations is based on the mechanisms of image-like thinking. The study considers images of honeycomb constructions. Color visual information facilitates the perception of features of regular packing of congruent objects.

The current state of cognitive theory is characterized by the awareness of the search for models close to the mental model [17]. The proposal of motion maps is interesting for this study [17]. Geometric representations are practically absent in publications on the cognitive approach in mathematics [18]. Representative geometry is close to this study and can be used in processing stages between model and brain representations [19].

Studies of double packing lattices [8,9,10,12] contain a graphical interpretation of the content under discussion. The illustrative nature of this interpretation is convenient for mathematical justification but does not lead to cognitive models. In our approach, non-trivial partitioning and the use of color visualization to form representative geometric models is suggested.

The following sequence of activities must be performed to generate representative geometric models.

• Select an arbitrary point within an object (an arbitrary polygon). This point will be the pole of the object;
• Select the type of congruent relationship you want;
• Convert the original object by the type of congruent relationship you want;
• Create a hodograph for congruently oriented initial objects;
• Create a hodograph for objects of the selected congruent relationship;
• Form a honeycomb construction of regular packing of objects of the selected type of congruent relationship using the created hodographs;
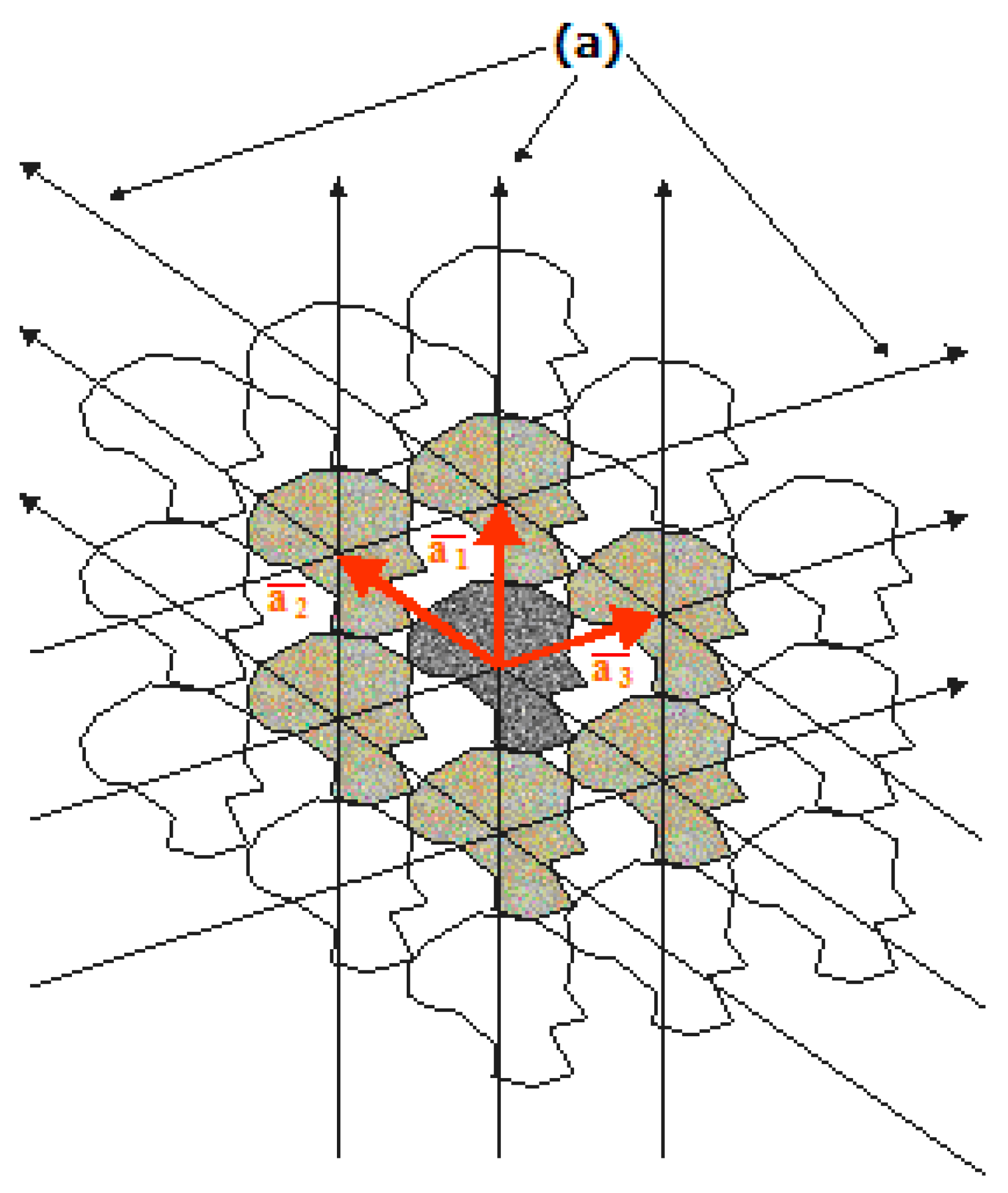
• Connect the poles of seven objects of the formed honeycomb constructionwith straight lines, thereby creating a hexagon of poles;
• Combining the poles of seven objects of a honeycomb construction by straight lines divides the central object into six fragments, each of which is duplicated twice by fragments cut off from six external objects;
• Fill fragments of each of the six groups of identical fragments with their own color.

3. The Analysis of Honeycomb Constructions of Regular Packings of Congruent Objects

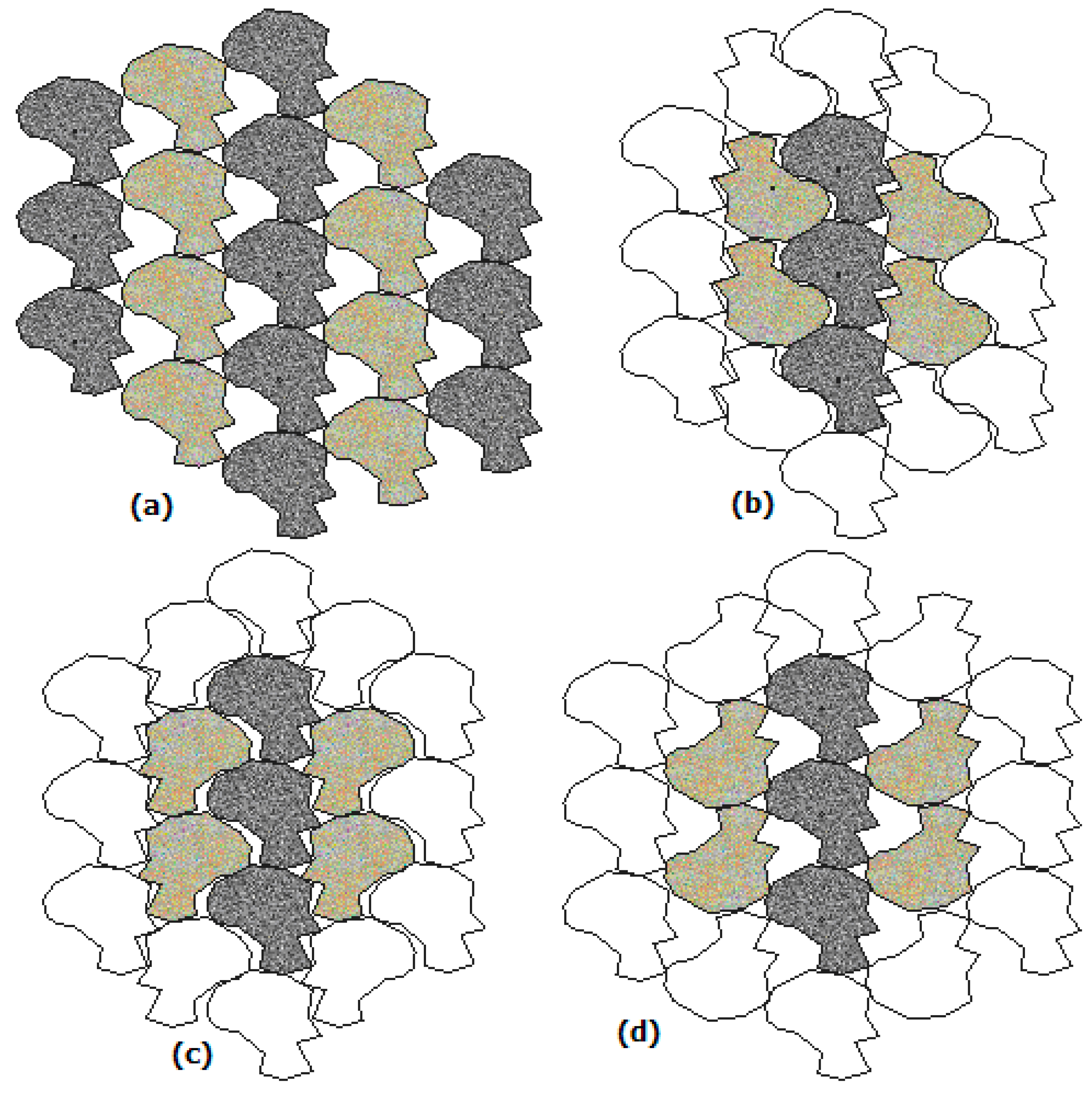
3.1. Regular Packing of Congruent Oriented Objects (Type_0)

Combining the poles of seven GOs of a honeycomb construction by straight lines divides the central GO into six fragments, each of which is duplicated twice by fragments cut off from six external GOs (Figure 8a), that is, three GOs are placed inside the pole hexagon [12].

The pole hexagon (Figure 8b) is centrally symmetric and affine-regular [12], covering the plane tightly (Figure 9a). The six triangles forming the pole hexagon (Figure 8b) are equal to each other. The analysis of GO fragments within triangles I and V and triangles II and IV (Figure 8a) indicates their identity. This allows covering the plane with pole hexagons with overlay (Figure 9b).

As a consequence, the covering density of the plane by regular packing of congruent oriented GOs is determined by the covering density of the pole hexagon.

The analysis of Figure 8a leads us to the following heuristic judgment (our honeycomb conjecture) “any partition of the plane into regions of equal area has perimeter at least that of the affine-regular hexagonal honeycomb tiling”.

Optimization of Regular Packing of Congruent Oriented Objects (Type_0)

The optimal regular packing is the placement of a GO with the maximum possible plane covering density. This makes it possible to develop an intelligent system for optimizing the regular packing of congruent objects.

Figure 10 shows the results of software optimization of regular packing of congruent oriented GOs.

3.2. Regular Packing of Congruent GOs (Type_1, Type_2, Type_3)

Analysis of Figure 11, Figure 12 and Figure 13:

• Leads to the second heuristic judgment: “inside the hexagon of poles three GOs are placed”;
• Shows the identity of triangles I and V, as well as triangles II and IV.

Consequently, the plane can be covered with hexagons of poles that overlap (Figure 11, Figure 12 and Figure 13c) and are similar (Figure 9b). This allows us to formulate the third heuristic judgment: “coverage of the plane by regular packing of congruent GOs is determined by the density of the coating of hexagon poles and equal to the ratio of the three GO squares to the square of hexagon pole of the packing.” Determining the vertices of the hexagons of poles is possible on the basis of algorithms for forming the FTA hodograph [7].

In the packings considered above, one type of congruent relations is represented (Figure 2). It is obvious that it is possible to build regular packings for several types of congruent relations.

3.3. Some Considerations about Lattices Packing of Congruent Objects

To describe the regular packing of congruent GOs (except for type_0), we introduce the concept of triple-lattice packing (Figure 14) that combines two double-lattice packing. In this case, the pole position of any GO in the regular congruent GO packing is determined by the following vector:

$$\overline{E_{m,n,k}}=\overline{a_1}\times m+\overline{b_1}\times n+\overline{b_2}\times k,\hspace{1em}where m=\pm 1,\pm 2\dots ,\pm \infty . n=0,1 k=0,1$$

(2)

4. Discussion

The placement of GO fragments inside the pole hexagon (Figure 8a and Figure 11a, Figure 12a, Figure 13a) for different types of congruent relations showed the following:

• For type_1 and type_2, in the left and right halves of the pole hexagon there are similar sets of fragments;
• For type_0 and type_3 there is no similar placement of fragments.

The regular packing of congruent GOs presented in Figure 4 have the following plane coating densities, confirming the difference in similarity found for various types of congruent ratios (

Table 1. Coverage of the plane by regular packing of congruent GO’s.

Type of Congruent Relation	Square of Hexagon Pole	Dense Factor %
Type_0	88,405.5	75.4
Type_1	65,274.5	94.55
Type_2	66,506.5	92.97
Type_3	82,797	72.2

).

Data for type_1 and type_2 (Table 1) indicate a phenomenon known in the sheet-stamping industry. Both types are widely used in the two-row cutting of parts.

For further discussion, the following provisions are made:

• Formation of cellular structures of regular packages of congruent GOs with the help of FTA hodograph. GOs can be both convex and non-convex polygons;
• Application of the proposed cognitive model for analysis of cellular structures of regular congruent GO packings.

Future research directions will include the mathematical substantiation of honeycomb structures in the regular packing of congruent GOs.

5. Conclusions

As a result of the analysis of regular packings of congruent objects on the plane, the following heuristic judgments are obtained:

• Regular packings of congruent GOs have a honeycomb structure, that is, any GO of a regular packing touches six surrounding GOs;
• Inside the hexagon poles of the cell design there are fragments of three GOs;
• The density of coverage of the plane by regular packing of congruent GOs is determined by the density of the coating hexagon poles of the packing and is equal to the ratio of the three squares of GO to the square of hexagon poles;
• To describe the regular packing of congruent GO’s, triple-lattice packing is suggested;
• Any partition of the plane into regions of equal area has a perimeter at least that of the affine-regular hexagonal honeycomb tiling.