Integrating Predictive Maintenance in Adaptive Process Scheduling for a Safe and Efficient Industrial Process

Abstract

Predictive maintenance (PM) algorithms are widely applied for detecting operational anomalies on industrial processes to schedule for a maintenance intervention before a possible breakdown; however, much less focus has been devoted to the use of such prognostics in process scheduling. The existing solutions mostly integrate preventive approaches to protect the machines, usually causing downtimes. The premise of this study is to develop a process scheduling mechanism that selects an acceptable operating condition for an industrial process to adapt to the predicted anomalies. As PM is largely a data-driven approach (hence, it relies on the setup), we first compare different PM approaches and identify a one-class support vector machine (OCSVM) as the best performing option for the anomaly detection on our setup. Then, we propose a novel pipeline to integrate maintenance predictions into a real-time, adaptive process scheduling mechanism. According to the abnormal readings, it schedules for the most suitable operation, i.e., optimizing for machine health and process efficiency, toward preventing breakdowns while maintaining its availability and operational state, thereby reducing downtimes. To demonstrate the pipeline on the action, we implement our approach on a small-scale conveyor belt, utilizing our Internet of Things (IoT) framework. The results show that our PM-based adaptive process control retains an efficient process under abnormal conditions with less or no downtime. We also conclude that a PM approach does not provide sufficient efficiency without its integration into an autonomous planning process.

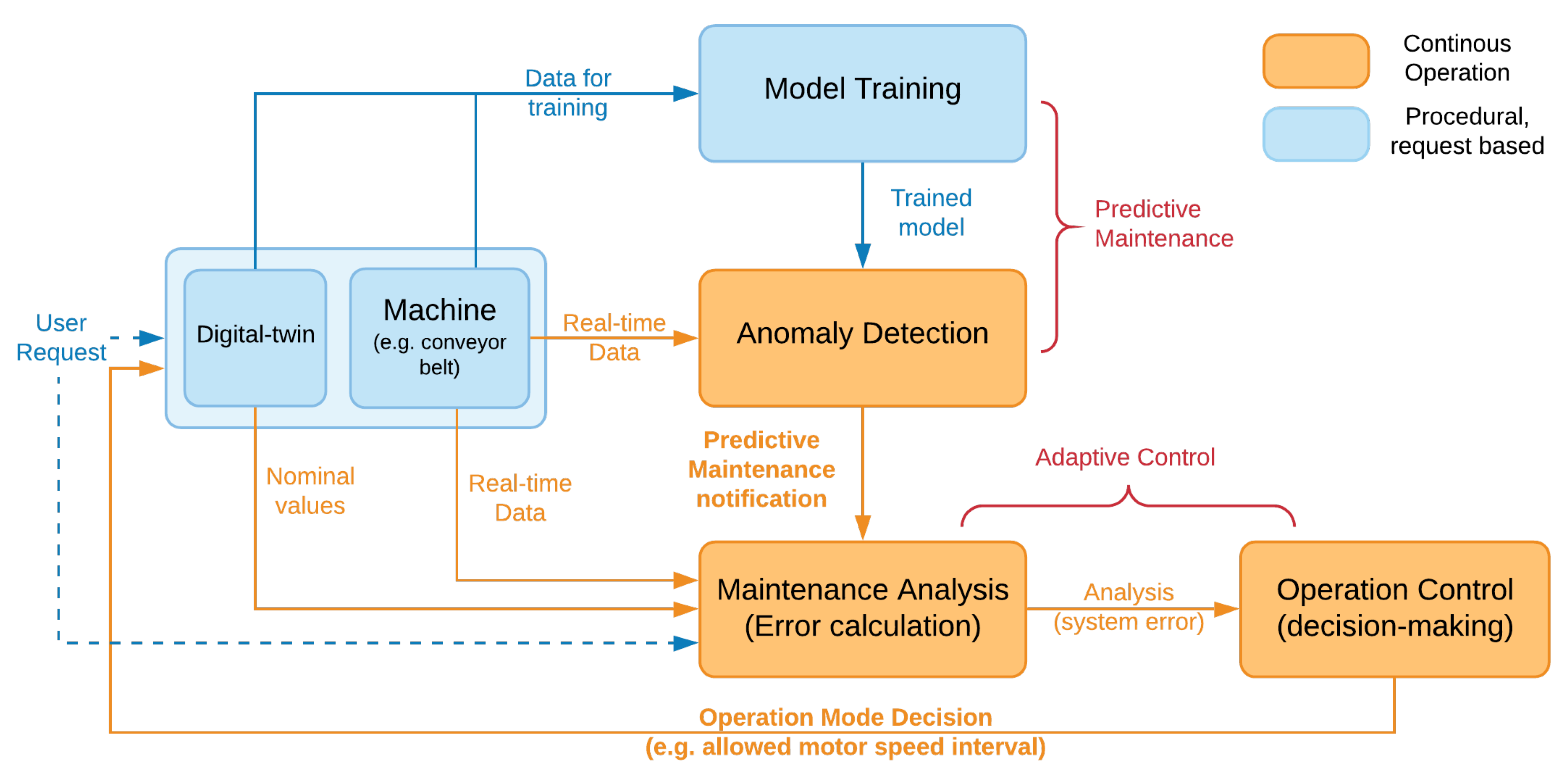
1. Introduction

Industry 4.0 (I4.0) revolutionizes the industry by adopting new paradigms like the Internet of Things (IoT), Cyber-Physical Systems (CPS), cloud computing, and machine learning [1]. Through the CPS concept and an IoT framework, manufacturing processes can be monitored and controlled remotely, even autonomously, at the device-level. Furthermore, the cloud computing and machine learning techniques enable storing, analysing, predicting, and classifying massive data for further optimization of the process in real-time. Predictive maintenance, being one of these optimization processes, is our focus in this study. In modern production lines, small defects can easily cause a chain reaction and paralyze the production line for weeks [2]. Preventive maintenance has been a commonly used approach to avoid such breakdowns, which is performed periodically on the devices to replace or run a regular maintenance check based on mean-time-to-failure (MTTF) or mean-time-between-failures (MTBF) of the devices [3]. However, considering the cases when a device wears out faster or slower than usual and when there is an external disturbance affecting a process, this approach falls short in adapting. For that, predictive maintenance (PM) algorithms have been proposed to predict possible system failures in the future from the sensor readings and the historical data patterns [2].

Since PM is a relatively new application field, how to incorporate predicted machinery states (prognostics) into online decision processes is a rather less discovered area of research. In general, maintenance planning consists of scheduling maintenance intervention based on the state of machinery and carrying out operational decisions to retain or restore a system to an acceptable operating condition [4]. Our research into the online analysis of PM has shown that little to no focus has been given to the latter, that is, the scheduling of operational decisions to adapt better to the changing states of machinery—we refer to this as adaptive process scheduling. Many approaches into prognostics only schedule maintenance through simple control measures like condition-based maintenance (CBM) [5], which may also be categorized as preventive solutions [6]. With the advances in PM, recent studies offer prognostic health management (PHM) applications that run online prognostics to predict the remaining useful life (RUL) of a machine to better schedule maintenance intervention based on fault predictions [6,7,8]. Even though these approaches protect the machines and greatly reduce breakdowns, we believe that they need to be complemented with operational decisions to adapt to the predicted conditions for a more efficient process, until a maintenance intervention is issued.

The advantages of taking PM-based operational decisions can be, for example, delaying a scheduled maintenance intervention by retaining an acceptable operating condition, autonomously recovering when some transient abnormal behavior disappears by itself (e.g., if it is due to a short-lived external disturbance), and finding a new operating condition that may avoid the abnormal behavior and possibly cancel the scheduled intervention. In general, many maintenance interventions and long downtimes could be reduced by such an adaptive process scheduling that optimizes an operation mode. Nevertheless, the conventional process scheduling mechanisms provide dynamic solutions toward maintaining the desired performance, which then usually disregard a machine’s health and maintenance actions. We state that a holistic approach to process scheduling should be developed so that an industrial process jointly optimizes for a more efficient and safe mode of operation until a maintenance intervention is issued.

Our premise in this study is to develop and deploy an adaptive process scheduling that integrates PM analysis as a safety component in scheduling for an operation mode. First of all, we develop a digital twin of an industrial process, in our case a conveyor belt system run by a servo motor (https://github.com/cangorur/servo_motor_simulation, accessed on 30 April 2021), providing massive data to generate a “fingerprint” (i.e., a large collection of nominal operational behavior data) for the system that is used both to train for a more accurate PM and to calculate the expected system behavior for a requested operation during runtime. For our implementation of a PM approach, we conduct a comparative analysis to select the best fitting algorithm to our setup since the performance of an anomaly detection algorithm depends on the pattern of the generated data. We implement commonly-used anomaly detection approaches and compare their performances in terms of training time, classification time, and classification accuracy to finally select and integrate one-class support vector machine (OCSVM) approach as the basis of our real-time PM.

Our main contribution is a novel PM-based adaptive process scheduling pipeline that incorporates obtained PM analysis as feedback to select a new operation mode for an industrial process that prevents machine breakdowns while keeping the operation running with minimum performance degradation. We believe that this pipeline can complement various industrial processes as high-level decision-making to regulate the process toward a safe operation with maximum efficiency. Our mechanism is a closed-loop system that continuously runs PM analysis and each time an abnormal behavior is predicted, a PID error is calculated to analyze the deviation of current system behavior from its nominal behavior, that is, the expected system behavior at a requested operation. An example would be that the expected power drainage at a requested conveyor speed can be calculated by the digital twin during runtime and our system monitors how much the current drainage deviates from it. A process scheduler then schedules an operation that compensates for this deviation in behavior: the new plan reduces the performance (e.g., the running speed of the conveyor) as close to the original request as possible provided that the power readings are within the allowed safe region of a newly scheduled operation. In this way, the risk of causing further damages to the system is reduced while maximum possible performance is still maintained. As for the scheduling, we are agnostic to the algorithm used. We select a state-of-the-art genetic algorithm (GA) as it is one of the most commonly used meta-heuristic adaptive control techniques [9]. Each chromosome in the GA model describes a different operation mode, in our case a range of nominal speed and power values for the conveyor to safely operate, which are obtained from the fingerprint. The scheduler, i.e., the GA, decides on one of these operation modes according to the optimization criteria, that is, system safety and performance. The pipeline also allows a user to adjust the optimization goals by selecting either a performer mode (more weight on maximum speed) or a protective mode (more weight on minimum power), both of which still optimize to protect the machine’s health.

To demonstrate the applicability of our pipeline, we implement it on a small-scale conveyor belt as part of a project called CHARIOT (https://chariot.gt-arc.com/, accessed on 30 April 2021) [10], which aims at the holistic inter-networking of a heterogeneous set of devices and human actors through unified IoT middleware and data models. As a core part of the middleware, a knowledge management system provides services for data storage and access as well as cloud-based machine learning and data analysis services. Our study is an important use-case of CHARIOT, utilizing the framework to obtain data from the connected devices (e.g., servo motors, current sensors, load sensors) and to run PM analysis and our adaptive process scheduler. This enables real-time data analysis and responses, making it possible to demonstrate the applicability of our solution and evaluate it at runtime. We open the access to our knowledge management system that also implements the experimented PM approaches (https://github.com/GT-ARC/chariot-ml-engine, accessed on 30 April 2021). To demonstrate the effectiveness of incorporating PM analysis into automated process control, we compare our system with a reactive, rule-based approach (preventive maintenance) as a baseline and show that such PM-based scheduling provides an efficient operation and can still protect the system. Additionally, we conclude that a PM approach alone does not provide sufficient efficiency if it is not integrated into an automated planning process, which paves the road to industrial automation with maintenance-in-the-loop.

In the rest of this article, after an overview of the related literature (in Section 2), we outline our PM-based adaptive scheduling pipeline (in Section 3.1) and describe the digital twin model (in Section 3.2), followed by the details of our predictive maintenance implementation (in Section 3.3) and the adaptive process control mechanism that describes how PM results are integrated into a process scheduling algorithm (in Section 3.4). In Section 4, we first present our CHARIOT framework used in evaluations (in Section 4.1) and then the experiment setup (in Section 4.2 and Section 4.3). For the results, we start with a comparative analysis for predictive maintenance implementation (in Section 4.4), analyze the performance of our adaptive control system (in Section 4.5), and finally present its comparison with a rule-based approach (in Section 4.6). Section 5 concludes the article with a summary and future work.

2. Related Work

In recent years, thanks to the advances in machine learning and computational technologies, anomaly detection algorithms have been widely applied in fraud detection, intrusion detection and fault detection in many different domains, including predictive maintenance in industrial processes [11,12,13,14]. Predictive maintenance methods can be classified into three main categories: model-based approaches, case-(rule-)based approaches and data-driven approaches [15]. Over the years, data-driven predictive maintenance approaches have progressed and become crucial towards Industry 4.0 [16]. Recently, it has been shown that machine learning techniques increase the feasibility and availability of predictive maintenance, allowing its broad application including the fields that are previously considered hard to conduct maintenance [14,17,18].

Various machine learning approaches for clustering, classification and regression are widely applied for PM and proven to be effective [14,18,19,20]. This includes different PM applications, such as the calculation of the Remaining Useful Life (RUL) [7,21] or condition monitoring to prevent premature failures [3]. In this work, in order to exploit real-time information from massive data obtained from our conveyor belt and its peripheral devices, we apply an online condition monitoring that falls into the domain of anomaly detection. It refers to the problem of finding data points that do not follow the expected behavior. Such data points are usually named as anomalies, exceptions, outliers or novelties in different applications [22]. When a training dataset only involves “normal conditions,” the trained model should be capable of detecting whether a new observation belongs to the model. In that case, it is called a novel pattern that is then incorporated into the normal model after its detection. Any other previously unseen observation that is not categorized as novelty is then considered as an anomaly [23]. In our setup, since we have access mostly to the normal behavior data, we need a novelty detection algorithm that is also considered as a semi-supervised learning anomaly detection as it is a one-class classification problem [22]. Our goal is to classify new data as a novelty (part of normal behavior data) or as an anomaly (abnormal behavior data) if the test data does not relate to the training set [24].

There are various novelty detection techniques, which can be mainly categorized as distance-based, reconstruction-based, domain-based, and probabilistic methods. A widely used distance-based approach is k-nearest neighbor (k-NN) and is based on the assumption that normal data points all have close neighbors. Then, if a data point is far away from its neighbors, it is regarded as an anomaly [25]. An example of a domain-based novelty detection is one-class support vector machine (OCSVM). It is an unsupervised learning method that clusters only one class, which makes it suitable for a PM application detecting rare events with very small amount of abnormal behavior samples [26]. A decision boundary is calculated to indicate the area where most of data points are located. The area outside of this boundary is regarded as a novelty region. Kernel principle component analysis (PCA), on the other hand, is a reconstruction-based approach. It calculates a reconstruction error between the original and the reconstructed dataset, compares with a predefined threshold and decides the novelty of a new observation. Even though there are many other available approaches, they mostly suffer from problems such as excessive computational power requirements during the training stage if the dataset is large or not being sensitive to nonlinear data. Since a PM application is specific to data formats and patterns of different devices, we develop and compare most commonly applied methodologies that are suitable for our conveyor belt setup. For the purpose, we compare a k-NN, an OCSVM and a kernel PCA; and select the best performer to be adopted in our system.

Application of PM is a necessary step, but the utilization of its analysis in an industrial operation to autonomously adapt to an estimated abnormal condition is a rather undiscovered area of research. PM analysis (prognostics) are usually used by prognostic health management applications to calculate RUL of machines and schedule more efficient maintenance interventions [8]. Regarding the process scheduling of a machinery system, the focus has been mostly towards estimating and improving the efficiency of a machine operation. The “adaptive scheduling” concept is proposed to solve the parametric uncertainty problems, such as when there is an extra noise or an operation environment is dynamic [9]. In other words, the goal is to estimate or learn machine parameters online that lead to control signals for a desired performance [27]. There are only a handful of studies implementing data-driven adaptive control using machine learning. In [28], a neural network is constructed to acquire the motor controller gains for a parallel robot manipulator. In [29], the PID controller parameters are constantly modified by an Artificial Neural Network to obtain an optimal performance. Machine learning-based control has been proven to be effective; however, it requires training a model beforehand. This limits its adaptation when the environment is drastically changing. Another approach to data-driven adaptive control is through meta-heuristic methods. In [30,31], the authors compare various meta-heuristic methods to tune PID parameters offline. As an example to online methods, Lin et al. [32] propose a genetic algorithm for PID tuning on a linear induction motor to achieve a minimal position control error. Despite their good performance and wide use, one drawback of meta-heuristic methods [9] is their long convergence time. This may introduce delays in updating a system control signal in real-time.

In general, existing process scheduling approaches are towards satisfying an efficient operation, yet they mostly discard the safety factor. Whereas, there are preventive approaches like condition-based maintenance that prevent machines from harm but they are not efficient due to long downtimes. Our goal, for the first time to our knowledge, is to integrate these approaches using PM analysis as a safety component coupled to an adaptive industrial process scheduling mechanism to optimize for operating condition. Then, the system adapts towards a more efficient and a safer operation mode using PM analysis to protect a machine with less or no downtimes. In particular, we believe that a PM implementation without its analysis integrated into a closed-loop system would not show its full potential, whereas a sole performance-driven adaptive control would discard the machine health. A holistic adaptive control and maintenance ecosystem taking PM analysis as feedback to optimize an operation is necessary for the future of PM applications in autonomous systems.

3. Methodology and Overall Framework

3.1. System Architecture

Our PM-based adaptive process scheduling pipeline is depicted in Figure 1. The architecture consists of a machinery system (in our case, a conveyor belt run by a servo motor), its digital twin, predictive maintenance mechanism, and adaptive control mechanism.

A digital twin model of the conveyor system is developed using the specifications of the servo motor and the conveyor belt, which is then further approximated with the actual values collected from the real system (covered in Section 3.2). In order to reach better classification accuracy for the predictive maintenance, the twin generates normal operation data as well as data under abnormal conditions that are hard to observe and may be harmful for the real machine. The generated (synthetic) data, along with the real motor data, are used in PM classification model training. The data in our case includes speed, power and torque readings from the servo motor driving a conveyor belt. We refer to the collection of data generated under nominal operating conditions as the “fingerprint” of the system. The training step for PM generates a nonlinear decision boundary over the fingerprint data, which is done initially offline and can be updated frequently. That is, with the newly collected data during run-time, our pipeline allows for continuously updating the fingerprint of the system in case the nominal operating conditions for the process changes. This then triggers the training to generate a new decision boundary model. This is a supervised and procedural step since our pipeline cannot automatically detect drastic changes in the nominal (boundary) conditions that may arise from various factors including manual updates in the process, for example, replaced components, changing requirements, carrying heavier loads on the conveyor.

The real-time PM takes place in the Anomaly Detection stage in Figure 1. It takes speed and power readings from the motor as input and uses the trained decision boundary to perform anomaly predictions on the new data in real-time (covered in Section 3.3). Our adaptive control contains two components. First, after an anomaly is detected, the Maintenance Analysis (error calculation) block further analyzes the abnormal readings by calculating the error, that is, the deviation from an expected value under a requested operation (covered in Section 3.4). We call these expected values “nominal values”. During run-time, we use the twin model to calculate the nominal values for the requested operation. After that, the Operation Control block makes a decision by scheduling a new operation mode. We use a state-of-the-art genetic algorithm for this purpose. An operation mode is, in our case, an allowed speed interval to run the conveyor belt motor and it is selected with the optimization criteria of achieving maximum possible performance (speed) while ensuring a safe operation on the system. A user may adjust the optimization goal by giving more weight on more performance or on less power, that is, more protection (covered in Section 3.4.1).

3.2. The Digital Twin Model

We need twin models of the machinery system to be able to simulate and obtain nominal conditions of the system during an operation, as well as abnormal conditions for training and testing purposes. A commonly used approach in modeling the operation of servo motors under changing load is to model the relationship between speed, torque and input power readings. Therefore, our goal is to obtain a mathematical approximation of the real system that is able to generate a power reading given a speed and a torque (load) value. For this purpose, we start from an existing servo motor simulation configured with the datasheet specifications of our servo motor and the conveyor belt mechanism to generate data under ideal conditions. Since the load on the real system is dynamic and nonlinear, we also collect many data from the conveyor setup under various nominal operating conditions, that is, various expected loads under various operation requests. Both the ideal case data and the real data collected are used to obtain an approximation model. The model is generated using polynomial regression over the obtained final readings of speed, torque and power, using a curve fitting approach. The polynomial approximation that serves as the final twin model generating nominal values is given in (1).

$$P(v,\tau )=a+b·v+c·\tau +d·v^2+e·v·\tau +f·{\tau }^2,$$

(1)

where v is the rotation speed of the conveyor belt, $\tau$ is the torque (load) on the motor and $a,b,c,d,e,f$ stand for the constants derived after curve fitting. During runtime, to calculate a nominal power ($P_{nom}$) approximation given the current operation, we use the function above with the requested speed value ($v_{req}$) and the current load (${\tau }_{cur}$) carried on the conveyor system, that is, $P_{nom}=f(v_{req},{\tau }_{cur})$. However, the actual torque on the motor driving the belt is assumed unknown during the operation due to several abnormal conditions like glitches on the gears of the motor or extra friction on the belt. Therefore, we generate speed-power curves for different allowed loads on the conveyor using the data generated from the digital twin model and the real system under normal conditions (as depicted in Figure 2). The combination of all nominal data is named as the fingerprint of our conveyor system, which is then used in the training of the predictive maintenance algorithm, as explained in the next section.

3.3. Predictive Maintenance on a Conveyor Belt

Finding a suitable machine learning approach for a PM operation depends on the applied system, that is, through the pattern of generated data and machine specifications. For the purpose, we examine three commonly used methods, that is, one class SVM, k-NN and kernel PCA, to generate a classification model (i.e., a decision boundary) over the system fingerprint given in Figure 2. PM operation is then an anomaly detection process, checking if a new data is classified as an abnormal or a normal behavior. In this section, we briefly describe the application of these methods to the problem of predictive maintenance. In Section 4.4 we provide a comparative analysis along with a discussion on our selection for the final use.

3.3.1. Anomaly Detection with One-Class SVM

One-class support vector machine (OCSVM) is a popular domain-based novelty detection algorithm, based on support vector machine (SVM) classification. OCSVM acquires a decision boundary on a labeled data and predicts if a new data point belongs to the class defined by the boundary or not. Instead of maximizing the margin between two groups of data points, the algorithm tries to maximize the margin between the data points and the origin using a hyperplane. In OCSVM, the parameters $\nu$ (hyperparameter of the OCSVM algorithm) and $\gamma$ (hyperparameter of the kernel function, which is radial basis function, i.e., RBF, in our case) largely affect the performance of the OCSVM algorithm. The parameter $\nu$ defines the upper bound of the fraction of outliers and a lower bound of the number of samples that are used as the support vector. It controls the upper bound of the target data that are excluded, which is usually tuned to reject the noise. The parameter $\gamma$, on the other hand, controls the smoothness of the decision boundary; the bigger $\gamma$ is, the more jagged the boundary is [33].

Parameter estimation, in general, is done using grid search with cross validation. It helps figuring out how the algorithm performs when there is new data and also prevents the trained model from over-fitting. However, in anomaly detection, the “abnormal data” is usually not available or lacking in terms of data amount and diversity. A typical way to solve this problem is to generate artificial outlier data [12]. k-NN-based edge pattern detection (EPD) is a method to identify several data points that define the edge pattern of the trained models [34]. Based on the EPD algorithm, the “negative shifting” method is proposed to generate high quality outliers [33]. For this purpose, the identified edge pattern is shifted away from the target data by a short distance. Towards higher qualities, the shifting direction should target data density’s negative gradient, where the density of target data drops at the fastest rate. Similarly, “positive shifting” is proposed this time to generate pseudo target data as a validation set to avoid time-consuming cross validation. The pseudo target data can be generated by shifting every target data point along the direction where target data density grows at its fastest rate, which is exactly the opposite direction of the negative shifting. Moreover, the shifting distance should be the minimum projection distance of the k-nearest neighbors of the data point on the shifting direction.

For the fine tuning of all three unsupervised algorithms (Section 3.3.1, Section 3.3.2 and Section 3.3.3) we apply negative shifting and positive shifting on our training dataset so that we obtain artificial outliers using the former and pseudo target data using the latter (as shown in Figure 3).

The two hyperparameters of OCSVM, $\nu$ and $\gamma$, is tuned with the calculated overall error rate using a grid search over the generated dataset. The best parameters in our case are $\nu =0.02$ and $\gamma =10$, and the corresponding trained model with the parameters is demonstrated in Figure 4a. From the graph, we can see that the decision boundary tightly surrounds the training data, the generated artificial outliers are predicted as abnormal and the pseudo target data are classified as normal. However, with this parameter setting, OCSVM is prone to the accuracy of the training data (real data collected under normal conditions). Due to the fluctuations of this data, some jagged edges already occur on the decision boundary. If the training data are contaminated with abnormal behaviors, the accuracy of the model would decrease. Therefore, we conduct an online update of the system fingerprint occasionally, which will automatically update the decision boundary for OCSVM, assuming that the machinery system behavior may change over time (see the request-based training update we implement on our pipeline in Figure 1).

3.3.2. Anomaly Detection with k-NN

The k-NN approach is a distance-based novelty detection method, a suitable algorithm for our application due to its performance in classification under irregular decision boundaries. It is based on the assumption that all normal data points have close neighbors. Therefore, if a data point is far away from its neighbors, it is regarded as an anomaly [25]. Generally, the k-NN-based anomaly detection first finds the k-nearest neighbors for every data point in the training dataset. The distances to the nearest neighbors are used as a novelty score for each data point. Then, a novelty threshold is decided as the largest novelty score among the entire dataset. Finally, to predict whether a new coming data point is a novelty (normal behavior data) or an anomaly, the algorithm inserts the point into the training dataset, finds its k-nearest-neighbors, calculates its novelty score and compares the score with the threshold.

Key parameters for k-NN include the number of the nearest neighbor, k, and the leaf size, $leaf\_size$, of the calculated BDtree or BallTree. The bigger the k is, the smoother the decision boundary gets; therefore, this can also be used to suppress noise. The selection of k value largely depends on the nature of the problem, whereas the $leaf\_size$ defines the minimum cell size in KDTree or BallTree. A smaller leaf size indicates a more complicated tree, whereas a larger $leaf\_size$ leads to a faster tree construction time and less memory space allocation. Our application of k-NN has shown that the $leaf\_size$ does not affect the classification accuracy significantly under the current settings. On the other hand, k value directly affects the performance. When a very small value is chosen, for example, $k=2$, we notice that there are areas towards lower speed values on the fingerprint that are not encompassed even though the decision boundary surrounds most of the training data. This can be regarded as over-fitting. On the contrary, when k becomes larger, the decision boundary is too far away from the training set; hence, it usually causes prediction of false positives. After running a grid search using the pseudo outliers and targets as shown in Figure 3, a trained model with the best combination is obtained for $k=3$ and $leaf\_size=5$. The final model is shown in Figure 4b.

3.3.3. Anomaly Detection with Kernel PCA

Kernel PCA has previously been proposed as a novelty detection algorithm [35]. The novelty detection is carried out by transforming the data from the original feature space to the infinite-dimensional space and vice versa, after which the reconstruction error generated is considered as a novelty measure. Using the same approach, we train a model, transform the input data to infinite-dimensional space and inverse transform the data back to the original space. The reconstruction error is then calculated. Additionally, the influences of the hyperparameter $\gamma$ in RBF kernel and the hyperparameter $\alpha$ of the ridge regression that learns the inverse transform on the performance of the algorithm are also tested and compared. The parameter $\alpha$ stands for regularization strength in ridge regression; the larger $\alpha$ is, the less variance the estimates have. In other words, decreasing the value of $\alpha$ will lead to higher model complexity whereas $\gamma$ serves the same purpose as explained in OCSVM in Section 3.3.1.

Using the same set shown in Figure 3, we run a grid search and calculate the overall error rates to select the best parameter values as $\alpha =0.005$ and $\gamma =15$. The corresponding trained model is demonstrated in Figure 4c. The grid search algorithm favors bigger $\gamma$ and smaller $\alpha$ to obtain a better performance around the decision boundary. A side effect of this parameter combination is that some jagged edges already appear on the decision boundary.

In summary, the parameter effects and the approaches mentioned above are taken into account to redesign all three algorithms for our PM application. Our goal is then to pick the best performing algorithm with respect to the training speed, prediction time and the prediction accuracy. The experiment results, as discussed in Section 4.4, show that OCSVM outperforms the others in our case; hence, it is selected as our final PM algorithm.

3.4. Adaptive Process Scheduling

Predictive maintenance provides a fast and sensitive method for detecting the potential faults or unexpected behaviors in the system. However, detecting such anomalies is not enough if further actions are not taken to protect the device/machine/process from a possible damage. We provide a methodology that incorporates PM results as feedback in mitigating the anomalies autonomously in order to keep the process running as efficient as possible, while protecting the system from damage. This approach also saves time for further inspection and maintenance planning. In general, our PM-based adaptive scheduling mechanism analyzes a predicted abnormal condition to calculate an error that is defined as the deviation of the current system behavior from an expected behavior. We calculate a PID error for this purpose, which is commonly used in industrial control to calculate the deviation between a desired state and a measured state.

Our adaptive scheduling process is shown in Figure 5. First, we calculate the input power error of the conveyor system, which is a direct indicator of abnormal loads or behaviors, for example, glitches on the motor, extra friction on the conveyor belt or extra load on the conveyor system. The PID error ($Er{r}_{op}$) is calculated between the real-time power reading ($P_{real}$) and the nominal power expected to be drained by the system ($P_{nom}$) under a requested condition. This calculation is done by the digital twin using the requested operational speed ($v_{req}$) and a carried load (${\tau }_{cur}$) as covered in Section 3.2. If $Er{r}_{op}$ is larger than a pre-defined threshold, a new scheduling for the operation mode is initiated. The threshold value can be optimized according to the operational requirements, for example, a cautious operation would require a bigger threshold value to act quick to even small deviations. Hence, we set it proportional to the allowed operational limits defined in the selected operation mode to allow rescheduling as soon as the mode is obsolete for the environmental conditions (see the operational limits and their analysis in Section 4.5.2). Finally, an optimal operation mode is adaptively scheduled (according to the error), which provides allowed speed and power intervals for the conveyor belt to run without damaging the system (detailed in Section 3.4.1).

3.4.1. Process Scheduling using a Genetic Algorithm

We implement an adaptive selection algorithm that decides for a system operation mode, that is, speed interval in our case, according to a changing energy consumption. This selection is towards protecting the system from abnormal conditions as well as keeping a maximum possible operational performance. Given these two optimization conditions, the selection of optimization weights is left to the user to pick a desired balance between power-saving (protective mode) or time-saving (performer mode).

The chromosome space contains four genes, which are lower bound speed ($v_{min}$), upper bound speed ($v_{max}$), lower bound power ($P_{min}$) and upper bound power ($P_{max}$), as indicated in

Table 1. The layout of a chromosome.

Gene	1	2	3	4
Label	$v_{min}$	$v_{max}$	$P_{min}$	$P_{max}$

. During the operation, we consider the actual torque on the motor as an unknown parameter as it also reflects the abnormal and unknown conditions, that is, disturbances, along with the real load on the conveyor system. Therefore, we use intervals of possible power and speed values in a chromosome design, allowing the load torque to change within that interval. Generating a population of such a chromosome model is not easy on the real system setup as there needs to be almost all possible conditions executed for various values of speed, power and torque (load). We use the generated fingerprint for this purpose, which already covers almost all nominal cases, as depicted in Figure 6, thanks to the digital twin. We note that the power values are directly calculated from the speed values for different torques meaning that they are dependent variables, that is, $P=f(v,\tau )$ (as described in Section 3.2). We take intervals from the fingerprint each of which define a chromosome, as shown in Figure 6. In this case, the interval size changes the amount of chromosomes in a population, which then affects the performance of the system. This effect is evaluated in Section 4.5.1.

The goal is to maximize a fitness function, that is, the optimization algorithm, by seeking a chromosome suggesting a speed value closest to a requested one, and a lowest power value. In other words, the speed should follow the initial operational request whereas the power should be lowered as there is a predicted abnormal load on the system. The fitness function is given in (2).

$$F=\alpha ·(v_{chr}-v_{req})+{\beta }^{{}^{\prime }}·(P_{real}-P_{chr})$$

(2)

Subject to:

$$\alpha +{\beta }^{{}^{\prime }}=1,$$

(3)

where $v_{req}$ is the initially requested speed value by the system operator and $v_{chr}$ and $P_{chr}$ values are provided by a chromosome. $v_{chr}$ is the average speed using the gene values of $v_{min}$ and $v_{max}$, and $P_{chr}$ is the average of $P_{min}$ and $P_{max}$. Finally, $P_{real}$ is the current (real-time) power reading coming from the system. We note that $P_{chr}$ values are a function of $v_{chr}$, so they are proportionally dependent (see in Equation (1)). $\alpha$ and ${\beta }^{{}^{\prime }}$ are normalized weights of speed and power, respectively.

The ${\beta }^{{}^{\prime }}$ in Equation (2) is an adaptive parameter:

$${\beta }^{{}^{\prime }}=\beta ·(1+\left|\frac{Er{r}_{op}}{C}\right|),$$

(4)

which changes with the calculated PID error, $Er{r}_{op}$. C is a constant to control the changing magnitude of ${\beta }^{{}^{\prime }}$ and can be tuned by the user. Such an adaptive parameter calculation is devised in order to increase the weight of the power optimization for protection purposes. As the error (i.e., the deviation from a nominal power value) becomes larger, the goal is then to select a lower power value to maximize the fitness value. For instance, if the current requested speed causes much more power consumption than in a nominal case, a chromosome with lower power requirement is selected, which also means a lower speed value. In other words, the system autonomously sacrifices from the operational speed for the sake of protecting the system. As it is clear from Equations (2) and (3), the selection of $\alpha$ and $\beta$ values depends on a user’s choice of an operation with more risks or a less risky behavior with a slower operational speed.

An intermediate crossover is used for the genetic algorithm process. It generates values for an offspring around and between the variable values of its parents. As for the mutation, a random number from a normal distribution is added to the genes using the following formula:

$$Va{r}_o=Va{r}_i+\sigma ·N(0,1),$$

(5)

where $\sigma$ is the standard deviation of a normal distribution, which is defined as $0.2$ in the current settings. We also use a tournament selection that several candidates compete with each other and the best have the right to breed. In our case, four candidates compete with each other during the selection process. This method guarantees that the worst individual never gets a chance to reproduce. Last but not least, an elitism mechanism is implemented in the algorithm to keep the fittest individual in the next generation.

4. Experiments and Evaluation

4.1. IoT Knowledge Management: CHARIOT

Our PM-based adaptive control mechanism running a conveyor system have been developed and integrated as part of the CHARIOT project. The CHARIOT framework allows real-time data-driven control through its four-layer structured, namely, physical layer, middleware layer, agent layer, and knowledge layer, as shown in Figure 7. The physical layer is part of the CHARIOT runtime environment integrating many different runtime environments, such as, Robotic Operating System (ROS) (https://www.ros.org/, accessed on 30 April 2021) and KURA (http://www.eclipse.org/kura/, accessed on 30 April 2021). CHARIOT runtime environment is able to integrate simple and resourceful devices, where the former runs on, for example, a raspberry PI and the latter already has its own computational resources. The physical layer directly runs on the device nodes and it installs libraries and interfaces for the devices. The device drivers of our conveyor system scenario run on ROS. The middleware layer serves as a bridge between the physical layer and the CHARIOT framework, where the device agents interface the ROS agents in the physical layer using a websocket protocol (i.e., a fast enough protocol for real-time control).

The device agents physically run on the distributed devices; however, they are a part of the CHARIOT middleware, that is, the agent framework. They act as an abstraction of the real devices and as an interface to the agent layer. The low-level planning and motor control still run on the physical layer (i.e., on ROS drivers) whereas the application agents on the agent layer make high-level decisions and send command signals for the devices, for example, a speed request, through their device agents. Additionally, as a part of the runtime environment, each device runs a data gateway. To provide a real-time access to device data and satisfy a continuous data analysis, we use publish/subscribe type communication from the device to the CHARIOT database through the data gateway components. The knowledge layer provides machine learning functions as services for generic use. An application agent requests for a certain machine learning training and/or prediction on a certain data. For example, the PM Application Agent requests for an anomaly detection on the conveyor motor data, receives the result from the cloud and notifies the Adaptive Control Application Agent. The services are made available through Chariot Cloud API, and once a machine learning request is created, the results (we call knowledge) are available to any other agents running on the CHARIOT framework. Thanks to this framework, we are able to run our distributed conveyor system with heterogeneous devices and PM-based adaptive control mechanism in real-time.

4.2. Experiment Setup

We develop our solutions on an automated conveyor belt system running in a smart factory testbed, which features a small-scale production line with a 3D printer, a conveyor belt, a robot arm and containers for the products, as shown in Figure 8. The products printed are conveyed through one conveyor belt, where a robot arm sorts and places them onto the container area (colored pads). In regular operation, an IR sensor detects the objects, the conveyor belt stops, the robot picks the object and scans it through the color sensor and finally places the object onto a container according to the colors defined by a task. The predictive maintenance application constantly checks for any abnormal behavior on the conveyor, for example, due to excessive load, a glitch or any disturbance on the motor, from the motor readings and notifies the adaptive control application for a new operation mode.

4.3. Abnormal Behavior Data Generation

Abnormal behavior occurs mostly due to an unexpected load on the motor running the conveyor system. The behavior of this unexpected load could be periodic (e.g., a gear in the motor is causing extra friction when it is on a certain angular position), constant (e.g., something rubbing the belt) or random. On the real setup, it is hard to create such unexpected torque requests on the motor; however, we use a friction pad placed under the belt to emulate an abnormal behavior. Whereas on the digital twin, such torque behaviors are simulated through five different functions including step, ramp, linear, logarithm, exponential and sinusoidal. In our experiments, we mainly use a sinusoidal disturbance (in Equation (6)) as it emulates a periodic behavior and it allows to test the system’s adaptation capability, flexibility and smoothness of its responses when a disturbance is introduced and removed.

$${\tau }_{dist}=\frac{a}{2}·sin(\frac{2\pi }{b}·t+\frac{3\pi }{2})+\frac{a}{2},$$

(6)

where a and b are two parameters defining the magnitude (i.e., the wavelength) and ${\tau }_{dist}$ is the sinusoidal torque disturbance that is added to the system load torque at time t.

4.4. Predictive Maintenance: Comparative Analysis for Anomaly Detection

In this section, we compare the performance of three anomaly detection candidates. Since we are using the same artificial outliers and pseudo target datasets for all of the algorithms, we can directly compare their performance through the calculated error rates and the training/prediction times. We use the most optimal parameter sets decided for each algorithm in Section 3.3. The results are shown in

Table 2. The performance comparison of OCSVM, k-NN and kernel PCA.

Items	Error Rate (%)	Training Time (s)	Predicting Time for Pseudo Target Data (s)
OCSVM	2.919	2.232	0.735
k-NN	5.932	4.514	4.349
kernel PCA	4.722	74.616	1.513

.

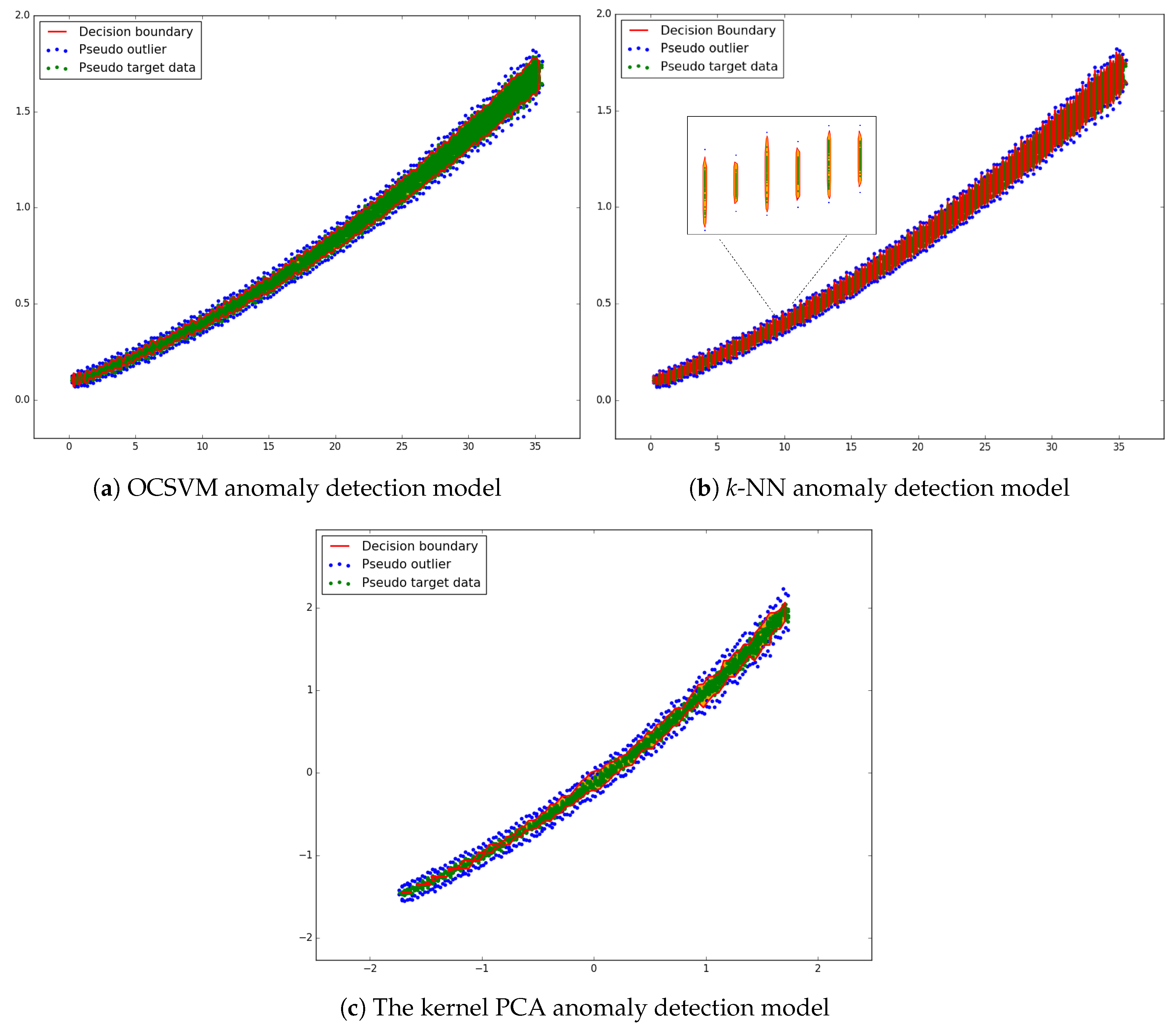
Although the kernel PCA achieves a relatively low error rate, it consumes considerable amount of time even when trained with only 1/8 of the full dataset as opposed to the full size used in training the other two algorithms. Therefore, it is not suitable for real-time applications. As for k-NN, despite its reasonable error rate, it suffers from over-fitting under the current parameter combination. As it can also be seen from Figure 4 that OCSVM provides a more reliable decision boundary for our application. It not only has the lowest error rate, but also spans the shortest training and prediction time.

4.5. Adaptive Scheduling: Performance Analysis

This section details our evaluations and analysis to optimize the scheduling process, specifically, how the chromosome design and the weights of power and speed in the fitness function of our GA algorithm influence the performance of the scheduling process. First of all, in this experiment, we use the digital twin (the simulated model) in order to remove the effect of random and unknown factors that could be introduced on the real conveyor system, such as, unbalanced frictions or inaccurate sensor readings. The simulation also allows us to simulate a wide range of abnormal conditions, which is hard and dangerous to realize on the real system. A speed range of 6 to 32 r/min is used during this experiment as this is the recommended speed range of the real conveyor system according to its motor specifications.

To effectively evaluate the performance of the algorithm under different conditions, we propose a customized efficiency calculation having both power (energy) and speed (distance) as the evaluation metrics with the selected weights of importance (i.e., $\alpha$ and $\beta$). The evaluation metrics are selected to reflect our optimization goals of safety (minimum power) and performance (maximum speed). It is defined as follows:

$$\eta =(1-\frac{E_{\Delta }}{E_{nom}})·\alpha +\frac{S_{real}}{S_{nom}}·\beta ,$$

(7)

where $\alpha$ and $\beta$ are the same weights of the fitness function in Equation (2), that is, the weights of speed and power components. $E_{\Delta }$ is the absolute deviance between the energy consumption under a constant requested speed (i.e., the nominal energy consumed, $E_{nom}$) and the real energy consumption during an operation. $S_{real}$ is the actual amount of travelling distance of the conveyor belt during an operation. $E_{nom}$ is calculated using the total expected traveling distance under a requested speed, $S_{nom}$. Since the real-time power consumption is changing all the time, $E_{\Delta }$ can be calculated by the integral of absolute power difference over time:

$$E_{\Delta }={\int }_{t_0}^{t_0+\Delta t}\int \left|P_{real}-P_{nom}\right|dt,$$

(8)

where $P_{real}$ is the real power value measured during an operation and $P_{nom}$ is the nominal power value expected under the given conditions. $S_{real}$ can be calculated by the integral of real-time speed over time:

$$S_{real}={\int }_{t_0}^{t_0+\Delta t}{v}_{real}dt,$$

(9)

where $v_{real}$ is the measured speed values. $E_{nom}$ and $S_{nom}$ can be calculated as:

$$E_{nom}=P_{nom}·\Delta t$$

(10)

$$S_{nom}=v_{req}·\Delta t.$$

(11)

In our case, a good adaptive control algorithm should provide a reliable response to a load torque increase and decrease. In other words, when a disturbance is introduced and/or withdrawn, the goal is to keep the speed as close as possible to the originally requested one while keeping the motor in a safe operation (lesser power consumption when there is an abnormal behavior predicted). The control mechanism should also satisfy a smooth behavior during the operation by not allowing sudden increase or decrease on the speed when the load drastically changes.

4.5.1. The Effect of Fitness Function Weights on the Performance

In this part, we evaluate the effect of normalized fitness function weights, $\alpha$ (for speed) and $\beta$ (for power), on the performance of the system. How to optimally respond to a predicted maintenance need (i.e., an abnormal condition) depends on the user preferences, which is depicted as a balance between the operational speed and the power drained. However, since the chromosomes are formed from the fingerprint (nominal operation) of the system, each selection ensures a safe operation. Based on the fitness function in Equation (2), to get a fitness as large as possible, the algorithm tends to select an individual with a closer speed value to the requested one as well as a lower allowed power interval to save the motor from the abnormal conditions (details are in Section 3.4.1). Therefore, different combinations of $\alpha$ and $\beta$ can largely affect the performance of the system. The comparison results of different $\alpha$ and $\beta$ are shown in Figure 9. The black sinusoidal signal with a period of $T=50$ s indicates the torque disturbance introduced on the system. Our intention is to simulate a periodic friction that can happen on the angular motion of the motor, for example, a glitch on a part of the gear. The cyan color shows the requested speed, power or efficiency in different graphs. The other colored curves are the actual behavior of our PM-based adaptive control mechanism running with different parameter values.

The speed behaviours in Figure 9a show that most of the speed curves inversely follow the disturbance torque curve, which indicates that the algorithm controls the motor speed to compensate the changes on the torque. A smaller $\alpha$ means more importance is given to reduce the power consumption; hence, the speed values are selected to be lower when the applied load torque increases. In addition, smaller $\alpha$ also means the algorithm gives less importance to match the requested speed when there is a disturbance applied and when it is withdrawn. This can be verified for the case of $\alpha =0.25$ and $\beta =0.75$, where the system is not able to restore the requested behavior when the disturbance drops (see in Figure 9a). For the maximum $\alpha$, the system always satisfies the initially requested speed; however, this time it leads to an excessive power consumption as shown in Figure 9b.

As for the power consumption, results in Figure 9b indicate that our algorithm responds towards neutralizing the power increase caused by the abnormal torque. Bigger values of $\beta$ favors for a safe operation as the power is kept very low during the abnormal conditions. However, we also want to maintain the operation so we are not pursuing a minimum power (i.e., a minimum speed) but a proximity to the requested operation. On the other hand, smaller values of $\beta$ causes the power to dangerously increase and fluctuate a lot to keep the speed as requested. As the balance between preserving speed or power is very sensitive, we use the efficiency algorithm in Equation (7). The calculated efficiency values are shown in Figure 9c. From the graphs, we deduce that the pairs of $\alpha =0.55,\beta =0.45$ and $\alpha =0.6,\beta =0.4$ have the highest efficiencies. The selection of the final values is subject to the user preferences. In our case, a safer option would be to pick the pair of $\alpha =0.55,\beta =0.45$ as it kept the power consumption below the expected one during the abnormal condition, whereas the pair of $\alpha =0.6,\beta =0.4$ may lead to a better preservation of the operational speed. With that, we ensure that the fitness function is well formulated and provides the user with the option of optimizing for the operational needs.

4.5.2. The Effect of Different Operational Limits on the Performance

This experiment is intended to evaluate the performance of different chromosome designs, that is, different operational limits that are defined as the allowed speed interval to operate between $v_{min}$ and $v_{max}$ values. We create populations with the speed intervals of sizes $0.25,0.5,1,2$ and 8 r/min, that is, each operation mode (chromosome) selected only allows for a speed change defined by the interval value and it is the same for all chromosomes. For the experiments, initially requested speed is 25 r/min and the same sinusoidal disturbance in the parameter tests is applied on the system. For this experiment, we pick the parameters of $\alpha =0.55$ and $\beta =0.45$ as discussed in Section 4.5.1. The experiment results (speed, power, and efficiency) of different sizes of intervals are shown in Figure 10.

In Figure 10a we show that systems with bigger interval sizes (allowed speed intervals) react slower than the ones with smaller sizes. This is mainly due to their larger allowed speed and power changes, causing longer reaction times to changing environmental conditions. Since the threshold to trigger for a new scheduling is also set proportional to the allowed interval, a larger interval makes the system more resistive to mode changes (see in Figure 5). Another finding is that the decreased rate of speed is almost the same for different cases. This is because when the speed is decreasing, the calculated PID error is usually much larger than the threshold causing faster genetic algorithm calls. Finally, the cases with smaller intervals exhibit better system recoveries, that is, when the torque is completely withdrawn they show better approximation to the original speed request. As a comparison, when $interval=8$ the speed is not able to increase after the disturbance becomes zero. This is also reflected in power consumption (in Figure 10b) and in the efficiency analysis (in Figure 10c).

The average efficiencies calculated by Equation (7) are shown in

Table 3. The efficiency values under different chromosome designs, i.e., different speed intervals.

Interval size	0.25	0.5	1	2	8
Efficiency (%)	74.5	74.6	72.8	68.7	57.2

. From the table, we conclude that the smaller the interval size, the higher the efficiency. This is expected, as a small interval size indicates a more fine-grained control. The system schedules for another chromosome faster and more frequently since suggested interval sizes are smaller and so exceeded faster. For a better comparison, we run ANOVA (anaylsis of variance) on each two neighboring intervals. The results suggest that, starting from the interval of $0.5$, there are significant differences between the efficiencies ($F(1,3671)=26.99,p=2.16E-7$). However, the significance disappears between 0.25 and 0.5 intervals ($F(1,3671)=0.5084,p=0.4759$).

The similarity on the efficiency of interval groups $0.25$ and $0.5$ can be explained by the computational bottleneck. Normally, with the interval of $0.25$ and smaller we should see a more fine-grained control as discussed. However, in practice, since the scheduling by the genetic algorithm takes time, that is, in this case it is particularly not fast enough to respond to such frequent calls, the advantage of smaller interval size disappears due to the slower response times. This also causes fluctuations on the curves. Since the torque is very dynamic, it constantly changes causing the system to regularly trigger for a new mode selection. In an allowed interval, the system increases the speed and the power consumption; however, a continuous change in the torque triggers the adaptive control switching to a different operation mode (different limitations on the speed). These fluctuations should be theoretically compensated by smaller interval sizes but the computation time of the genetic algorithm is a limiting factor. In our case, the selection of interval $0.5$ would be the best option (also computationally lightweight); however, a better computational resource would allow for smaller interval sizes and so less fluctuations.

4.6. PM-Based Adaptive Scheduling vs. A Rule-Based Preventive System

In conventional systems, rule-based and preventive approaches are used to detect and recover from abnormal behaviors. In general, our system adds more fine-grained control over such conventional approaches thanks to the predicted operational deviations calculated in real-time. Hence, to demonstrate the effectiveness of incorporating PM analysis into such automated control systems, we compare our approach (with the selected settings of $speedinterval=0.5$ r/min, $\alpha =0.55,\beta =0.45$, see in Section 4.5.1 and Section 4.5.2) with a rule-based mechanism as a baseline. We run the two mechanisms on the digital twin motor to be able to simulate harsh abnormal conditions. The experimented rule-based mechanism, as its name suggests, slows down the motor speed based also on PM analysis and on certain rules. In our experiment settings, we set the rule as follows: when the power exceeds 1.5 times of the expected power, the speed drops to $50\%$ of the originally requested speed. If it is more severe, then the system stops. The rule is set as the base performance of our adaptive control mechanism, that is, with a very high speed interval size in chromosomes (13 r/min) that in theory should resemble a rule-based approach. As discussed in Section 4.5.2, when the interval size becomes relatively large, the system is expected to respond to predicted anomalies with a poor sensitivity. The selection of the interval of 13 r/min is due to the available speed range (from 6 to 30 r/min), where there are only two chromosomes generated, one recommending a center speed of $12.5$ r/min. This is exactly $50\%$ of the initially requested speed of 25 r/min; hence, we obtain a similar behavior to the rule-based mechanism.

The results of the speed performance in Figure 11a indicate that our adaptive control with the interval of $0.5$ has a very a sensitive adaptation that it can react fast to torque increase, starting at $5.414$ s (seconds). Rule-based mechanism reacts first at $15.786$ s after the predefined power threshold is reached. We note that the rule-based mechanism’s reaction speed purely depends on the power threshold, a smaller threshold would lead to a shorter reaction time; however, it would show less tolerance to the power increase by directly dropping the speed. On the other hand, our PM-based adaptive control mechanism at the interval of 13 r/min reacts the slowest, at $19.275$ s, since the error calculation has a very large threshold. Even though the PM algorithm throws a notification, as the same PM algorithm runs in the case of $interval=0.5$, a large interval indicates a large threshold, and so a longer waiting time. This shows that although a PM algorithm detects problems earlier, the system behaves just like a rule-based preventive mechanism with the lack of a fine-grained adaptive control, leading to a slow response and a poor protection.

In addition, the rule-based exhibits bad flexibility in terms of speed, that is, the operational speed is not restored back when the disturbance is withdrawn. This is because a rule-based mechanism is usually designed fail-safe to protect a machine. The same effect is also observable with $interval=13$ due to its large error threshold (in Figure 11a). This indicates that such preventive and/or coarsely designed adaptation mechanisms causes longer downtimes on a system even though the disturbance is withdrawn and despite they run a PM. Whereas, our fine-grained PM-based adaptive control mechanism recovers well after the abnormal torque is withdrawn even for a short time (between 40 s and 60 s). The performance of our mechanism is also shown in Figure 11b through the power consumption. The power level is kept almost at the expected level, even slightly below, by changing the speed relatively. The poor reaction times of the other two systems cause a steep increase in the power after the disturbance is introduced. Finally, the efficiency results are shown in Figure 11c and in

Table 4. The average efficiency values of our PM-based adaptive control with interval = $0.5$ r/min, 13 r/min and the rule-based system.

System	PM-Based Adaptive Control ($\mathit{interval}\mathbf{=}\mathbf{0.5}$)	PM-Based Adaptive Control ($\mathit{interval}\mathbf{=}\mathbf{13}$)	Rule-Based Preventive Control
Efficiency(%)	74.657	67.008	66.566

. Our mechanism has the best efficiency performance on average. All the systems exhibit a significant efficiency drop caused by an increase in power consumption or a decrease in speed at the beginning of the operation. The significance of our system is visible through restoring the operation relatively well when the disturbance starts dropping, which is directly related to the adaptation skills of our solution.

One drawback of our system is the fluctuations in the speed during the speed control, as shown in Figure 11. This is a result of our chromosome design, which takes intervals of allowed speed and power as an operation mode (further analysis are in Section 4.5.2). The smaller the interval is the more the system response approaches to a continuous control. Our mechanism lies at the task-level operational decisions; therefore, a decision is selected only when the system predicts an abnormal condition. Our test conditions are the hardest due to a continuous, large and dynamic disturbance; therefore, a new decision needs to be taken in a real-time frequency for the most efficient operation. Our PM-based adaptive control system is able to provide this behavior; however, the response time of the genetic algorithm introduces a computational limitation. A smaller interval size (more chromosomes) with a more computational resource would compensate the fluctuations as mentioned in Section 4.5.2.

In general, we show that incorporating PM as a feedback into automated control mechanisms has significant advantages in terms of increased efficiency while still ensuring the safety of the operation, and that our approach successfully achieves it. By comparing our fine-grained PM-based control with a coarse version of it, that is, a PM-based adaptive control with an allowed operational speed interval of 13 r/min (an approximation to a rule-based system), we demonstrate that a predictive maintenance strategy alone will not be as effective unless it is incorporated into a more sophisticated decision-making algorithm that takes the prognostics, further analyzes the system deviation, and adaptively schedules a new safe and efficient operational decision. Otherwise, a preventive system that schedules for a maintenance intervention still performs similarly with or without a PM analysis at hand.

5. Conclusions

In this work, we aim to design and showcase an adaptive process scheduling mechanism that incorporates predictive maintenance results as an input to take autonomous decisions that regulate an industrial process to minimize downtimes while keeping its operation safe and efficient. Our goal is to show that such a coupled autonomous planning mechanism is needed to complement a PM mechanism, which alone would not provide a significant improvement in the efficiency of the operation when there are no relevant decisions taken accordingly. For this purpose, we propose a pipeline to incorporate PM analysis into conventional industrial process scheduling, complementing maintenance planning approaches based on prognostics (e.g., prognostic health management, i.e., PHM, solutions). In our closed-loop system, each PM notification triggers an error analysis based on a PID error calculation, to find the system deviation from the nominal operation calculated by a twin model in real-time. The rest incorporates this deviation in scheduling an optimal operation mode. We state that our pipeline is agnostic to the scheduling algorithm selected. In our application, we select GA as it is one of the mostly used scheduling algorithm in industrial operations. The fitness function takes into account the calculated error and jointly optimizes on the operation speed (i.e., less or no downtime towards keeping the requested operation) and on the power consumed by the system (i.e., to compensate extra disturbances on the system for protection). We leave the optimization criteria optional to system users, that is, a user can select a protective mode (more weight on preserving power and the machine) or a performer mode (more weight on keeping an initially requested operation). In general, the larger the deviation from an expected operation, the more protective the system gets.

In order to show the impact and the necessity of incorporating PM analysis into an automated adaptive process scheduling, we compared our final system with a rule/condition-based decision mechanism also relying on the same PM analysis as a baseline. That is, after every PM notification a rule-based decision system is triggered, replacing our GA-based adaptive scheduling, that schedules for a maintenance intervention and induces drastic changes on the system for protection. This experiment showed that without such integration, a PM algorithm with a fail-safe, rule-based mechanism would almost perform with the same efficiency of a complete preventive approach. This supports the necessity of complementing PM algorithms with such autonomous adaptive scheduling mechanisms and shows that our approach is capable of doing it. Finally, we compared the performance of our PM-based adaptive scheduling with a conventional rule-based preventive mechanism and showed that it significantly improves the efficiency (by 12.15%) and decreases downtime through adaptive recovery from transient abnormal conditions.

During run-time, we use the twin model to calculate the nominal values for the requested operation. If developing a twin model is not applicable, which might be the case for more complex industrial processes, the nominal conditions can also be obtained from the fingerprint of the system. In that case, the fingerprint can only provide expected lower and upper bounds for the requested operation (see Figure 6). This, however, leads to less accurate error calculations, compared to the case with a twin model that provides precise nominal values. That said, we recommend obtaining a twin model of the process in order to have a more sensitive control. Nevertheless, our proposed pipeline is still functional with a more coarse system model, for example, a fingerprint model only defining input-output relation of the system. Even though the digital twins are deemed part of the future of industrial automation, we acknowledge that the need for such a complex model is a bottleneck of our solution.

One drawback of our system is the computational limitation introduced by the response time of the genetic algorithm. If the algorithm runs a scheduling with the update frequency of the anomaly detection then we encounter a latency. To compensate for it, we triggered a scheduling action with lower frequencies of updates or with higher error thresholds, that is, after larger deviations from the nominal operation. This provided sufficient performance to demonstrate the effectiveness of our pipeline. However, for a real industrial application, responding to every PM result is needed as it provides a much smoother control (i.e., fewer fluctuations in the control signals). As future work, we plan to improve the performance of GA and experiment with another scheduling algorithm having low computational requirements for comparison. Additionally, we only consider the operational speed as the performance component and the power drained as the safety component for the optimization criteria. We are aware that more complex systems may introduce more optimization factors; yet, our goal was to show the effectiveness of introducing PM analysis as one of them. We believe that this pipeline can be integrated into various industrial processes, even if they are very complex, as a complementary solution running on top of the process to ensure their safe and efficient operations toward less or no downtimes. In the future, we will deploy the pipeline on different industrial processes to examine how it scales. For a broader impact, we plan to customize and implement our approach based on the suggestions and findings on another system setup and show its wider applicability and effectiveness.