1. Introduction
Network embedding and link prediction: Network embedding methods [
1], also known as graph representation learning methods, map nodes in a graph onto low-dimensional real vectors, which can then be used for downstream tasks such as graph visualization, link prediction, node classification, and more. Our focus in this paper was on the important downstream task of link prediction.
The purpose of link prediction in networks is to predict future interactions in a temporal network (e.g., social links among members in a social network) or to infer missing links in static networks [
2]. Applications of link prediction in networks range from predicting social network friendships, consumer-product recommendations, citations in citation networks, to protein–protein interactions. While classical approaches for link prediction [
3] remain competitive for now, link prediction methods based on the state-of-the-art network embedding methods already match and regularly exceed them in performance [
4].
Active learning for link prediction: An often-ignored problem affecting all methods for link prediction, and those based on network embedding in particular, is the fact that obtaining information on the connectivity of a network can be challenging, slow, or expensive. As a result, in practice, networks are often only partially observed [
5], while for many node pairs, the link status remains unknown. For example, an online consumer-product network is far from complete as the consumption offline or on other websites is hard to track; some crucial relationships in crime networks can be hidden intentionally; in biological networks (e.g., protein interaction networks), wet lab experiments may have established or ruled out the existence of links between certain pairs of biological entities (e.g., interactions between proteins), while due to limited resources, for most pairs of entities, the link status remains unknown. Moreover, in many real-world networks, new nodes continuously stream in with very limited information on their connectivity to the rest of the network.
In many of these cases, a budget is available to query an “oracle” (e.g., human or expert system) for a limited number of as-yet unobserved link statuses. For instance, wet lab experiments can reveal missing protein–protein interactions, and questionnaires can ask consumers to indicate whether they have seen particular movies before or have a friendship relation with a particular person. Of course, the link statuses of some node pairs are more informative than those of the others. Given the typically high cost of such queries, it is thus of interest to identify those node pairs for which the link status is unobserved, but for which knowing it would add the most value. Obviously, this must be performed before the query is made and thus before the link status is known.
This kind of machine learning setting, where the algorithm can decide for which data points (here: node pairs) it wishes to obtain a training label (here: link status), is known as
active learning. While active learning for the particular problem of link prediction is not new [
6,
7,
8,
9], it has received far less attention than active learning for standard classification or regression problems, and the use of active learning for link prediction based on network embedding methods has to the best of our knowledge remained entirely unexplored. Studying this is the main aim of this paper:
Can we design active learning strategies that identify the node pairs with unobserved link status, of which knowing the link status would be maximally informative for the network embedding-based link prediction? To determine the utility of a candidate node pair, we focused on the link prediction task: querying a node pair’s link status is deemed more useful if the embedding found with this newly obtained link status information is better
for the important purpose of link prediction.
Partially observed networks: To solve this problem, a distinction should be made between node pairs that are known to be unlinked and node pairs for which the link status is not known. In other words, the network should be represented as a partially observed network, with three node pair statuses: linked, unlinked, and unknown. The node pairs with unknown status are then the candidates for querying, and if the result of a query indicates that they are not linked, actual information is added. This contrasts with much of the state-of-the-art in network embedding research, where unlinked and unknown statuses are not distinguished.
Thus, the active learning strategies proposed will need to build on a network embedding method that naturally handles partially observed networks. Given such a method, we then need an active learning query strategy for identifying the unknown candidate link statuses with the highest utility. After querying the oracle for the label of the selected link status, we can use it as additional information to retrain the network embedding model. In this way, more and more informative links and non-links become available for training the model, maximally improving the model’s link prediction ability with a limited number of queries.
The ALPINE framework: We proposed the ALPINE (Active Link Prediction usIng Network Embedding) framework, the first method using active learning for link prediction based on network embedding, and developed different query strategies for ALPINE to quantify the utilities of the candidates. Our proposed query strategies included simple heuristics, as well as principled approaches inspired by the active learning and experimental design literature. ALPINE was based on a network embedding model called Conditional Network Embedding (CNE) [
10], whose objective function is expressed analytically. There are two reasons why we chose to build our work on CNE. The first is that, as we will show, CNE can be easily adapted to work for partially observed networks, as opposed to other popular network embedding methods (including those based on random walks). The second reason is that CNE is an analytical approach (not relying on random walks or sampling strategies), and thus allowed us to derive mathematically principled active learning query strategies. Yet, we note that ALPINE can be applied also to other existing or future network embedding methods with these properties.
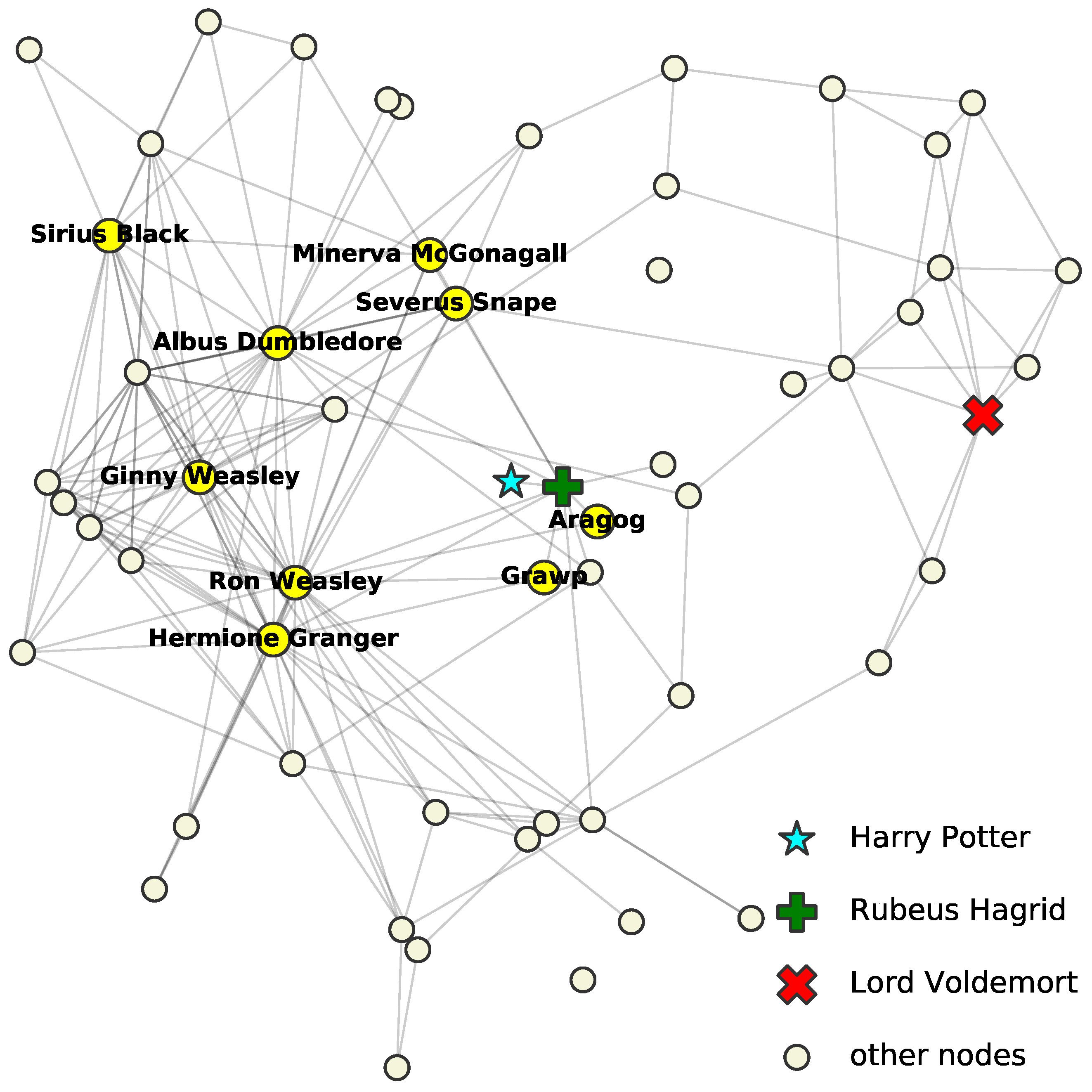
Illustrative example: To illustrate the idea of ALPINE, we give an example on the Harry Potter network [
11]. The network originally had 65 nodes and 223
ally links, but we only took its largest connected component of 59 characters and 218 connections. Note that enemy relation was not considered. We assumed that the network was partially observed: the links and non-links for all characters except “Harry Potter” (the cyan star) were assumed to be fully known, and for Harry Potter, only his relationship with “Rubeus Hagrid” (the green plus) was observed as linked and with “Lord Voldemort” (the red x) as unlinked. The goal was to predict the status of the unobserved node pairs, i.e., whether the other nodes (the circles) were allies of “Harry Potter”. Suppose we have a budget to query five unobserved relationships. We thus want to select the five most informative ones.
ALPINE can quantify the informativeness of the unknown link statuses, using different query strategies. Shown in
Table 1 are the top five queries selected by strategies
max-deg.,
max-prob., and
max-ent., which are defined in
Section 4. Nodes mentioned in the table are highlighted with character names in
Figure 1. Strategy
max-deg. suggests to query the relationships among Harry and the high-degree nodes—those who are known to have many allies. Strategy
max-prob. selects nodes that are highly likely to be Harry’s friends based on the observed part of the network. Finally,
max-ent. proposes to query the most uncertain relationships. A more detailed discussion of these results and a thorough formal evaluation of ALPINE are left for
Section 5, but the reader may agree that the proposed queries are indeed intuitively informative for understanding Harry’s social connections.
Contributions. The main contributions of this paper are:
We proposed the ALPINE framework for actively learning to embed partially observed networks by identifying the node pairs with an as-yet unobserved link status of which the link status is estimated to be maximally informative for the embedding algorithm (
Section 3).
To identify the most informative candidate link statuses, we developed several active learning query strategies for ALPINE, including simple heuristics, uncertainty sampling, and principled variance reduction methods based on D-optimality and V-optimality from experimental design (
Section 4).
Through extensive experiments (the source code of this work is available at
https://github.com/aida-ugent/alpine_public, accessed on 17 October 2020), (1) we showed that CNE adapted for partially observed networks was more accurate for link prediction and more time efficient than when considering unobserved link statuses as unlinked (as most state-of-the-art embedding methods do), and (2) we studied the behaviors of different query strategies under the ALPINE framework both qualitatively and quantitatively (
Section 5).
3. The ALPINE Framework
In this section, we first show how CNE can be modified to use only the observed information, after formally defining the concept of a partially observed network. Then, we introduce the problem of active link prediction using network embedding and propose ALPINE, which tackles the problem.
3.1. Network Embedding for Partially Observed Networks
Network embedding for partially observed networks differs from general network embedding in the way it treats the unknown link statuses. It uses only the observed links and non-links to train the model, where the unobserved part does not participate. We defined an (undirected) Partially Observed Network (PON) as follows:
Definition 1. A Partially Observed Network (PON) is a tuple where V is a set of nodes and and the sets of node pairs with observed linked and observed unlinked status, respectively, where . Thus, represents the observed (known) part, and is the set of node pairs for which the link status is unobserved.
For convenience, we may also represent a PON by means of its adjacency matrix , with and at row i and column j equal to null if , to one if , and to zero if .
Most network embedding methods (and methods for link prediction more generally) do not treat the known unlinked status differently from the unknown status, such that the networks are embedded with possibly wrong link labels. This appears almost inevitable in methods based on random walks (indeed, it is unclear how one could, in a principled manner, distinguish unlinked from unknown statuses in random walks), but also many other methods, such as those based on matrix decompositions, suffer from this shortcoming. We now proceed to show how CNE, on the other hand, can be quite straightforwardly modified to elegantly distinguish unlinked from unknown status, by maximizing the probability only for the observed part
K of the node pairs:
In this way, we do not have to assume that the unobserved links are absent, as state-of-the-art methods do. Furthermore, the link probability in CNE is formed analytically because the embedding is found by solving a Maximum Likelihood Estimation (MLE) problem:
. Based on this, later in
Section 4, we will show how it also allows us to quantify the utility of an unknown link status for active learning.
3.2. Active Link Prediction Using Network Embedding—The Problem
After embedding the PON, we can use the model to predict the unknown link statuses. Often, however, an “oracle” can be queried to obtain the unknown link status of node pairs from U at a certain cost (e.g., through an expensive wet lab experiment). If this is the case, the query result can be added to the known part of the network, after which the link predictions can be improved with this new information taken into account. By carefully querying the most informative nodes, active learning aims to maximally benefit from such a possibility at a minimum cost. More formally, this problem can be formalized as follows.
Problem 1 (ALPINE). Given a partially observed network , a network embedding model, a budget k, a query-pool , and a target set containing all node pairs for which the link statuses are of primary interest, how can we select k node pairs from the pool P such that, after querying the link status of these node pairs, adding them to the respective set E or D depending on the status, and retraining the model, the link predictions made by the network embedding model for the target set T are as accurate as possible?
The pool P defines the candidate link statuses, which are unobserved but accessible (i.e., unknown but can be queried with a cost), while the target set T is the set of link statuses that are directly relevant to the problem at hand. Of course, in solving this problem, both the link prediction task and the active learning query strategy should be based only on the observed information .
The problem is formalized in its general form and can become specific depending on the data accessibility (represented by
P) and the link prediction task (represented by
T). The pool
P may contain all the unobserved information or only a small subset of it. Sets
T and
P may coincide, overlap non-trivially, or be disjoint, depending on the application. We experiment with various options in our quantitative evaluation in
Section 5.3.
3.3. The ALPINE Framework
To tackle the problem of active network embedding for link prediction, we proposed ALPINE, a pool-based [
14] active link prediction approach using network embedding and, to the best of our knowledge, the first method for this task. Our implementation and evaluation of ALPINE was based on CNE, but we stress that our arguments can be applied in principle to any other network embedding method of which the objective function can be expressed analytically. The framework works by finding an optimal network embedding for a given PON
, selecting one or a few candidate node pairs from the pool
with
to query the connectivity according to a query strategy, updating the PON with the new knowledge provided by querying the oracle, and re-embedding the updated PON. The process iterates until a stopping criterion is met, e.g., the budget is exhausted or the predictions are sufficiently accurate.
The PON can be embedded by the modified CNE, and the active learning query strategy, which evaluates the informativeness of the unlabeled node pairs, is the key to our pool-based active link prediction with network embedding. Defined by a
utility function , the query strategy ranks the unobserved link statuses and selects the top ones for querying. The utility quantifies how useful knowing that link status is estimated to be for the purpose of increasing the link prediction accuracy for node pairs in
T. Specifically, each query strategy will select the next query for an appropriate
as:
In practice, not just the single best node pair (i.e., argmax) is selected at each iteration, but the s best ones, with s referred to as the step size.
In summary, given a PON , a network embedding model, a query strategy defined by its utility function , a pool , a target set , a step size s, and a budget k (number of link statuses in P that can be queried), ALPINE iteratively queries an oracle for the link status of s node pairs, selected as follows:
At iteration , initialize the pool as , and the set of node pairs with known link status as , and initialize and ;
Then, repeat:
Compute the optimal embedding for ;
Find the set of queries of size with the largest utilities according to (and T);
Query the oracle for the link statuses of node pairs in , set , and set equal to with node pairs added to the set of known linked or unlinked node pairs (depending on the query result), then set accordingly;
Set , and break if k is zero.
In this formulation, ALPINE stops when the budget is used up. An optional criterion is surpassing a pre-defined accuracy threshold on T.
5. Experiments and Discussion
To evaluate our work, we first studied empirically how partial network embedding with the modified CNE benefited the link prediction task. Then, we investigated the performance of ALPINE with the different query strategies qualitatively and quantitatively. Specifically, we focused on the following research questions in this section:
- Q1
What is the impact of distinguishing an “observed unlinked” from an “unobserved” status of a node pair for partial network embedding?
- Q2
Do the proposed active learning query strategies for ALPINE make sense qualitatively?
- Q3
How do the different active learning query strategies for ALPINE perform quantitatively?
- Q4
How can the query strategies be applied best according to the results?
Data: We used eight real-world networks of varying sizes in the experiments:
The
Harry Potter network (used also in
Section 1) is from the corresponding novel. We used only the ally relationships as edges and its largest connected component, which yielded a network with 59 nodes for the most important characters and 218 ally links among them [
11];
Polbooks is a network of 105 books about U.S. politics among which 441 connections indicate the co-purchasing relations [
40];
C. elegans is a neural network of C. elegans with 297 neurons and 2148 synapses as the links [
41];
USAir is a network of 332 airports connected through 2126 airlines [
42];
MP_cc is a Twitter network we gathered in April 2019 for the Members of Parliament (MP) in the U.K., which originally contained 650 nodes. We only used its largest connected component of 567 nodes and 49,631 friendship (i.e., mutual follow) connections;
Polblogs_cc is the largest connected component of the U.S. Political Blogs Network [
40], containing 1222 nodes and 16,714 undirected hyperlink edges;
PPI is a protein–protein interaction network with 3890 proteins and 76,584 interactions [
43], and we used its largest connected component
PPI_cc of 3852 nodes and 37,841 edges after deleting the self-loops;
Blog is a friendship network of 10,312 bloggers from BlogCatalog, containing 333,983 links [
44].
5.1. The Benefit of Partial Network Embedding
An important hypothesis underlying this work is that distinguishing an “observed unlinked” status of a node pair from an “unknown/unobserved” status, as opposed to treating both as absent, which is commonly performed, will enhance the performance of network embedding. We now empirically investigated this hypothesis by comparing CNE with its variant that performs partial network embedding: (1) the original CNE defined by its objective function in Equation (
1), which does not make this distinction, and (2) the modified version that optimizes Equation (
3), which we called CNE_K (i.e., CNE for the Knowns), which does make the distinction. Specifically, we compared the model fitting time and the link prediction accuracy for both:
Setup: To construct a PON, we first initialized the observed information by randomly sampling a node pair set that contained a proportion of the complete information. The complete information means the total number of links in the complete graph for a given number of nodes. For example, means that of the network link statuses are observed as either linked or unlinked: if the network has n nodes, . The observed is guaranteed connected as this is a common assumption for network embedding methods. Then, we embedded the same PON using both CNE and CNE_K on a machine with an Intel Core i7 CPU 4.20 GHz and 32 GB RAM.
Results: From the results shown in
Figure 2, we see that CNE_K was not only more time efficient, but also provided more accurate link predictions. The ratio
of observed information varied for datasets because the larger the network, the more time consuming the computations are. The time differences for a small observed part were enough to highlight the time efficiency of CNE_K. The two measures examined were: AUC_U—the prediction AUC score for all unobserved node pairs
containing
network information; and t(s)—the model fitting time in seconds. Both values are averaged—for each
averaged over 10 different PONs and each PON with 10 different embeddings (i.e., CNE has local optima) for the first four datasets—while it is
for the fifth and sixth and
for the last dataset.
It is not surprising that the fitting time of CNE_K was almost always shorter than the original CNE as CNE_K only fits the observed information. One exception was the Polbooks network, on which both methods used similar amounts of time, because the network size was not large. However, as the network size increased, CNE_K showed increasing time efficiency. Especially for the Blog network: with , CNE_K was 76 times faster than CNE. CNE_K thus enabled network embedding to scale more easily to large networks.
In addition to time efficiency, CNE_K always achieved a higher AUC than CNE, since CNE will try to model the absence of an edge even where there might actually be an (unobserved) edge. In other words, CNE was trained on data with a substantial amount of label noise: 0 labels (absent edge) that actually must be a 1 (present edge), while CNE_K only used those labels that were known to be correct. Partial network embedding for the knowns is especially useful in settings where only a small part of a large network is observed and the goal is to predict the unobserved links.
5.2. Qualitative Evaluation of ALPINE
In
Section 1, we used the Harry Potter network to illustrate the idea of ALPINE with three of our query strategies, which focused on predicting the unknown links for a target node—“Harry Potter”—who has very limited observed information to the rest of the network. Now, we complete this qualitative evaluation with the same setting for other strategies:
page-rank.,
d-opt., and
v-opt.;
min-dis. was omitted as it approximates
max-prob.Table 3 shows the top five suggestions, and the relevant characters are highlighted in
Figure 3 with their names. Since CNE achieved different local optima, here, we used a different two-dimensional visualization to better display the names. All the suggestions were reasonable and could be explained from different perspectives, proving that ALPINE with those query strategies made sense qualitatively. Similar to
max-deg. and
max-prob.,
page-rank. and
d-opt. had the same top three suggestions: Hermione, Ron, and Albus, which are essential allies of Harry. Knowing whether Harry is linked to them will give a clear big picture of his social relations. The results can further be analyzed according to the strategy definitions.
Strategy page-rank., as max-deg., aims to find out Harry’s relationships with the influencers—nodes that are observed to have many links. With this type of strategy, we learned which influencers Harry is close to, as well as his potential allies connecting to them; and conversely for his unlinked influencers.
The d-opt. strategy selects queries based on the parameter variance reduction. It implies that by knowing whether Harry is linked to the suggested nodes, the node embeddings will have a smaller variance, such that the entire embedding space is more stable, and thus, the link predictions are more reliable. For example, Severus, who ranks the fourth here (also the fourth with max-ent.), was not an obvious ally of Harry, but he helps secretly and is essential in shaping the network structure. The suggestions were considered uncertain and contributed to the reduction of the parameter variance.
The v-opt. strategy quantifies the informativeness of the unobserved link statuses by the amount of estimated prediction variance reduction they cause. It suggests that Harry’s relationships to the Weasley family are informative for minimizing the prediction variance for him. It makes sense as this family is well connected with Rubeus, who is Harry’s known ally, and also connects well with other nodes. As for Fluffy, it was observed to be connected only to Rubeus and unlinked to all other nodes except Harry. Knowing whether Fluffy and Harry are linked greatly reduced the variance on the prediction for the unobserved, because there was no other information for it.
We concluded that, intuitively, the query strategies resulted in expected behavior, although we caution against overinterpretation of this subjective qualitative evaluation. The next, quantitative, evaluation, provided an objective assessment of the merits of the query strategies, relative to passive learning, to each other, and to the single pre-existing method of which we we are aware.
5.3. Quantitative Evaluation of ALPINE
In the quantitative evaluation, we mainly wanted to compare the performance of different query strategies from
Section 4 with passive learning, as well as with the state-of-the-art baseline method HALLP [
9]. Passive learning is represented by the random strategy that uniformly selects node pairs from the pool. As for HALLP, we implemented its query strategy shown in Equation (
2) (since the source code is not publicly available), and set
and
both to one. Note that, as we wanted to compare query strategies in the fairest possible way, the link prediction was performed using CNE_K also for HALLP.
Setup: As before, we constructed a PON by randomly initializing the observed node pair set with a given ratio , while making sure was connected. Then, we applied ALPINE with different query strategies for a budget k and a step size s. More specifically, we investigated three representative different cases depending on the pool P and the target set T:
and : all the unobserved information was accessible, and we were interested in knowing all link statuses in U;
and : only part of U was accessible, and we still wanted to predict the entire U as accurately as possible;
, , and : only part of U was accessible, and we were interested in predicting a different set of unobserved link status that was inaccessible.
For all datasets, we investigated four values of : , to see how the percentage of the observed information affected the strategy performance. All quantitative experiments used a step size depending on the network size: of the network information. For a network with n nodes, it means that unobserved candidate link statuses will be selected for querying in each iteration. Then, the budget k, pool size , and target set size were multiples of s for different cases. The random strategy was a baseline for all three cases, while the HALLP strategy was only used in the first case because it was designed only for this setup.
Below, we first discuss our findings for each of the three cases on the five smallest datasets. After that, we discuss some results on the two larger networks for the most scalable query strategies only.
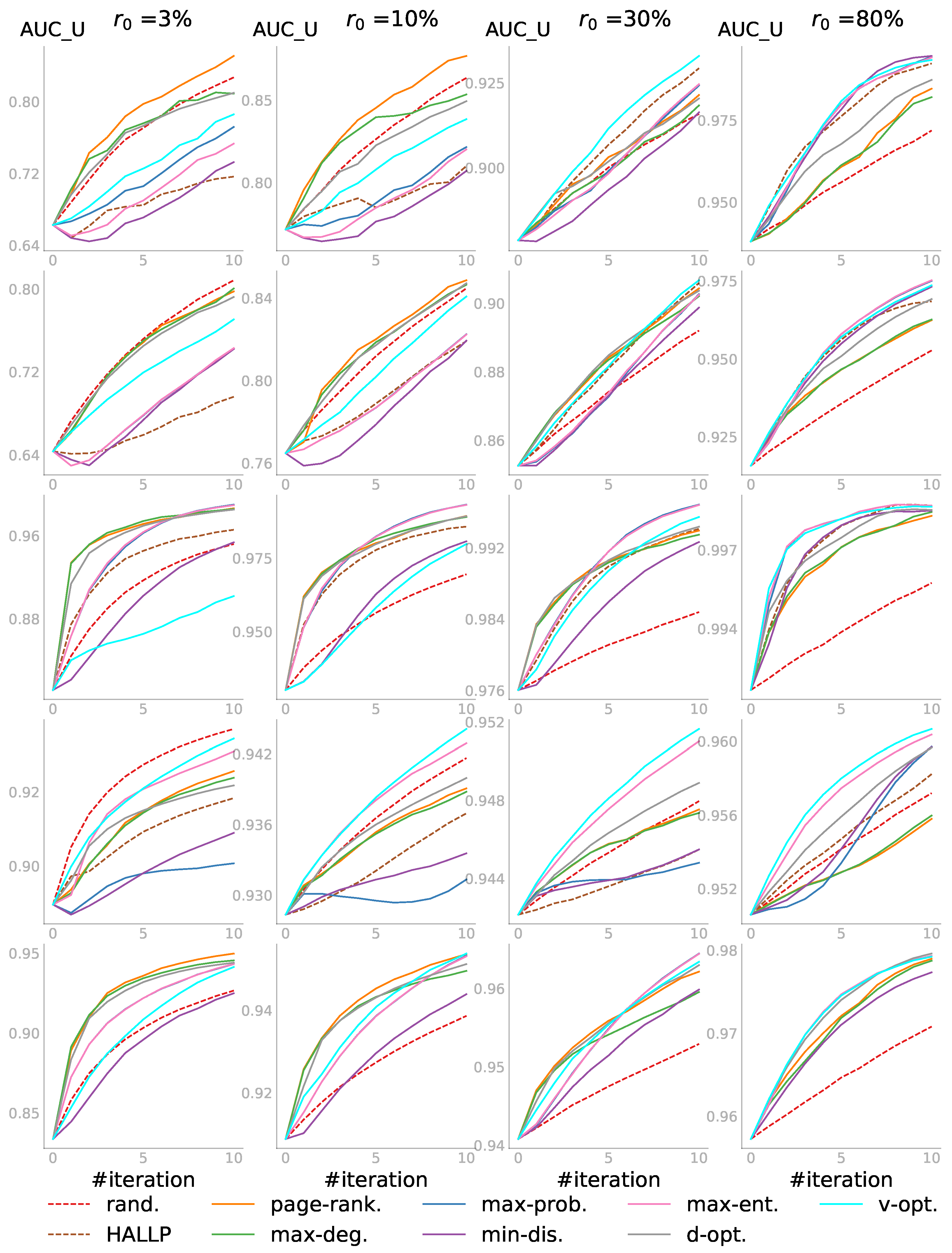
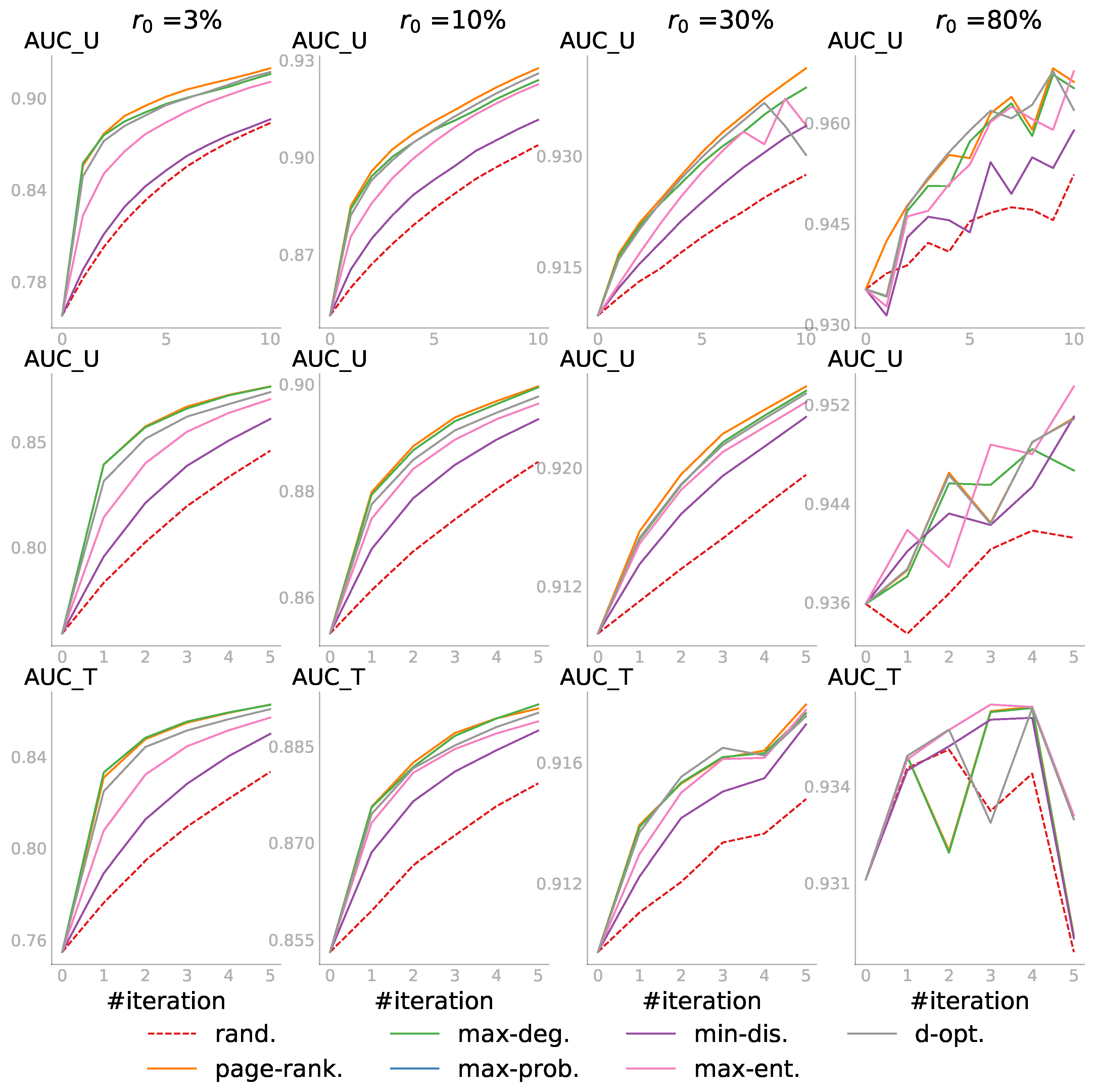
5.3.1. Case 1: and
In the first case, we had the pool of all unobserved link statuses and wanted to predict all the unknowns. Shown in
Figure 4 are the results, in which each row represents a dataset with its step size and each column corresponds to one
value. For every individual subplot, the
is the AUC score for all the initially unobserved link statuses—those not included in
. The budget
k was set to 10 steps, i.e.,
, resulting in 10 iterations. Iteration 0 was the initial performance before the active learning, so there were always
scores. In other words, given the budget
, even for
, we did not query the entire pool and reached only
of the network information. The AUC scores were averaged over several different random PONs, and each PON defined by a
was initialized with different random embeddings (
for the first four networks and
for the last and largest one). Each random strategy score was further averaged over three runs.
In general, the active learning strategies outperformed the
rand. strategy. We saw that when the observed part was relatively small—
or
— the degree-related strategies that did not depend on the embedding usually performed very well, and the random strategy was not always the worst. As more information was observed when
increased (see the plots from the left to the right in each row), we did not only see that the active learning strategies, such as
v-opt. and
max-ent., began to dominate and passive learning became the worst, but also the increase of the starting
. Zooming in to individual subplots, we saw that ALPINE boosted link prediction accuracy with far fewer queries for the active learning strategies, compared to passive learning. Overall, when the observed information was very limited, the embedding-independent strategies
page-rank. and
max-deg. outperformed the others; while for sufficiently enough information,
v-opt. and
max-ent. were the better choices. We speculated that this was the case as the embedding must be of sufficient quality for the embedding-dependent strategies to work, which requires a certain minimum amount of data. Worth noticing is that
d-opt. showed similar performance across different values of
, which will be discussed further in
Section 5.4.
As for the HALLP strategy, which aimed to query the most uncertain node-pairs and thus was similar in spirit to
max-ent., the performance was very variable. In some cases, it performed quite well, as shown in the top right subplot, beating
v-opt. in the first few iterations, while on the MP_cc network, it was one of the worst strategies. In addition to that, the runtime of HALLP was much longer than that of the other strategies; thus, some of the subplots do not have the HALLP result. The runtime analysis for one iteration of the query process on a server with an Intel Xeon Gold CPU 3.00 GHz and 256 GB RAM is shown in
Table 4 below. The results were averaged in the same way as in
Figure 4 for the four values of
and then further averaged over the
values. Across different datasets, HALLP was by far the most computationally expensive strategy as it had to run two link predictors.
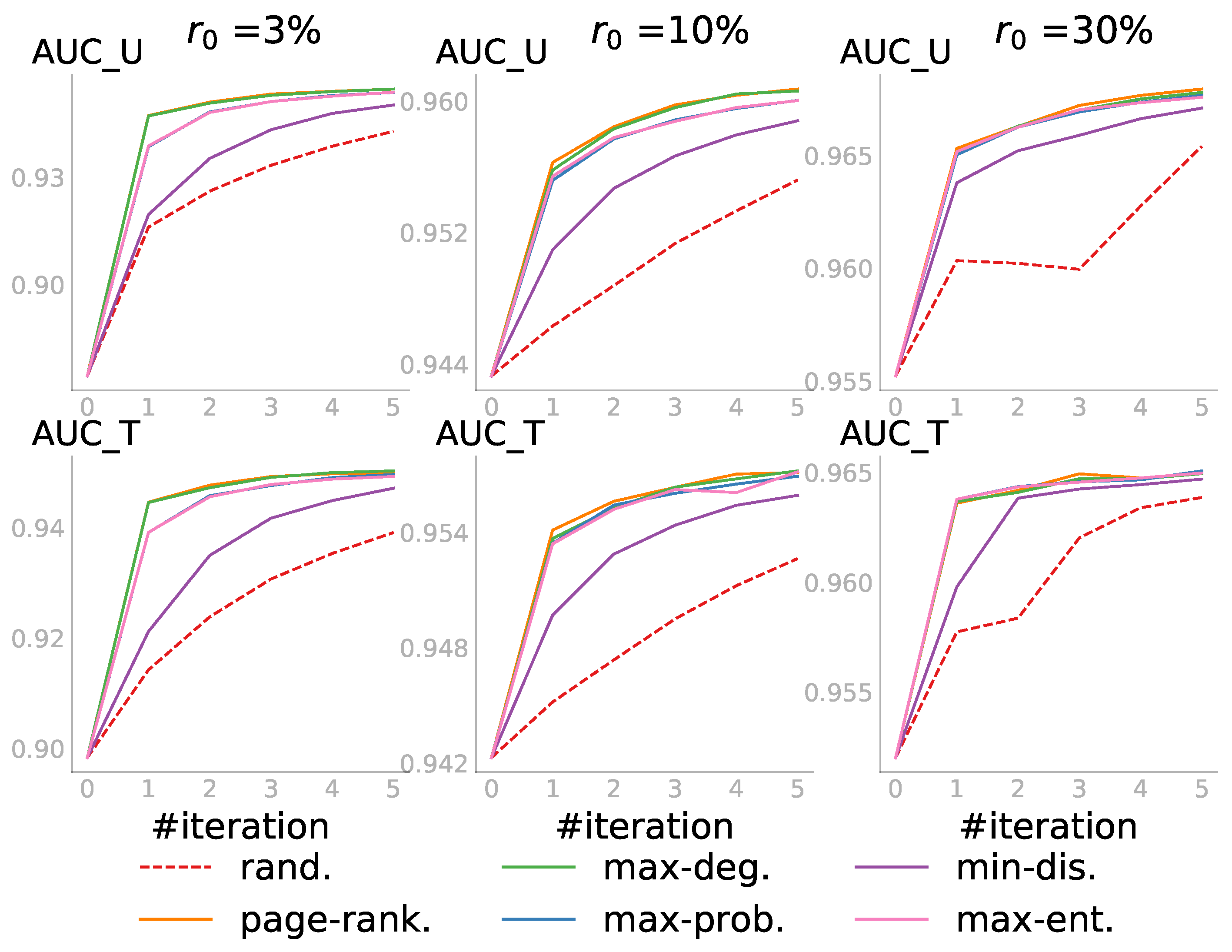
5.3.2. Case 2: and
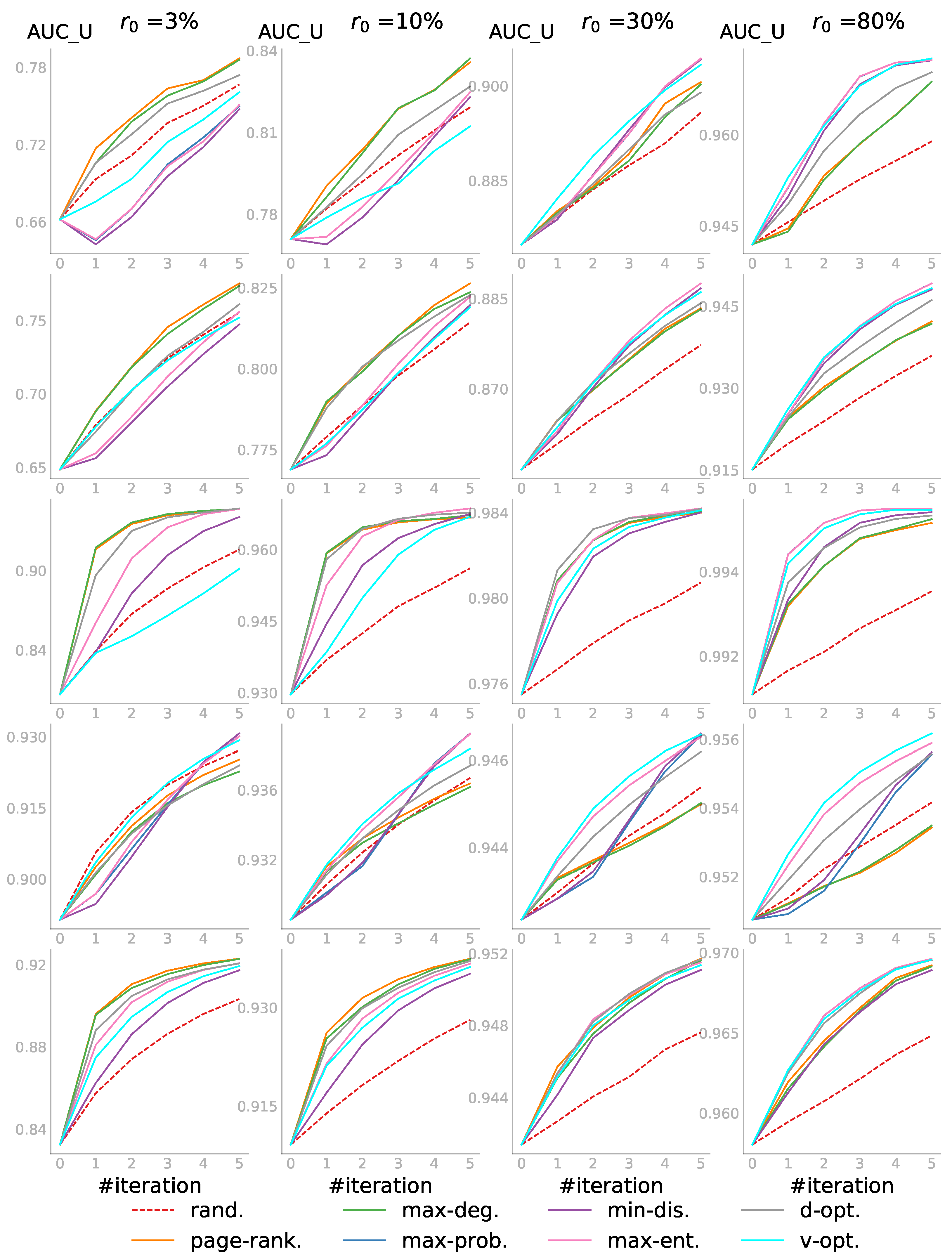
In the second case, we applied ALPINE with a smaller pool, while we were still interested in predicting all the unknown link statuses. The experiment setting was similar to the previous case, but the pool size was set to 10 times the step size——and the budget , i.e., only five iterations were performed. The candidates in the pool were randomly sampled from the unobserved part for each PON in our experiments.
Figure 5 shows the results for this case. Compared to the first case, the
was lower for each individual subplot as the accessible information in the pool was more limited. The results confirmed again that all active learning strategies were better than passive learning, Shown more clearly in the last row in
Figure 5 on the Polblogs_cc network is that the three strategies
page-rank.,
max-deg., and
d-opt. were the winning group for the first two
values. However, in the third and fourth subplot in the same row,
v-opt.,
max-ent., and
d-opt. performed best. The
d-opt. strategy stayed as one of the top strategies across different percentages of the observed information.
5.3.3. Case 3: , , and
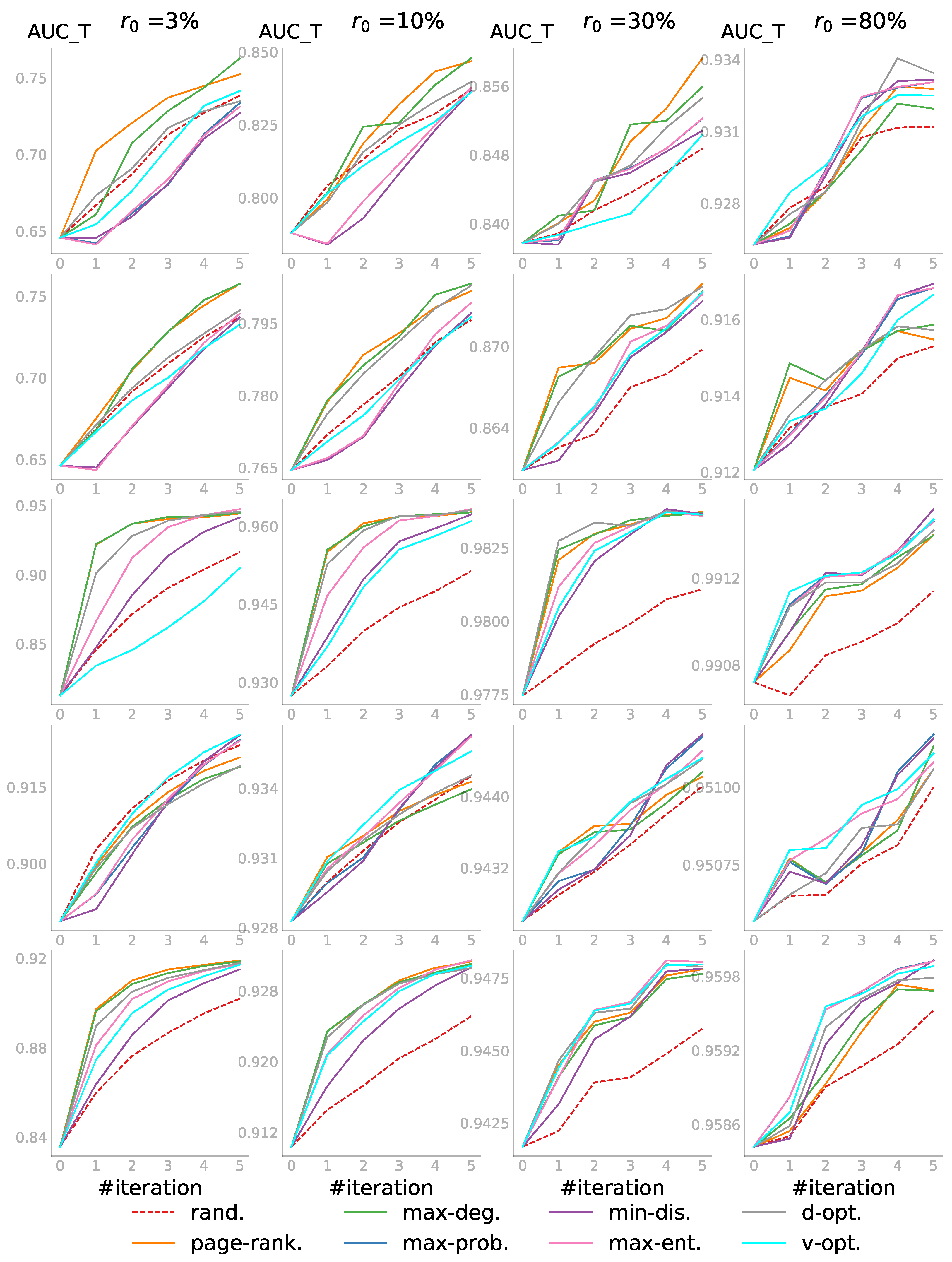
We imposed further constraints in the third case: not only the pool P of node pairs that could be queried was limited, but also the set T of target node-pairs for which we wanted to predict the status was limited. Moreover, both sets were not intersecting. As in the second case, the budget was set to and . The target set size was now taken to be . Both P and T were sampled randomly from U before the querying started.
The results in
Figure 6 confirmed again that active learning outperformed passive learning. One might expect
v-opt. to perform the best in this case because it was the only strategy that explicitly considered
T. Although it was shown to perform quite well in some subplots especially for the first iteration, the quality of the embedding affected its performance. Indeed, as we observed before, the reliability of all embedding-based strategies depended largely on how well the network was embedded, which became much better as
increased.
Compared to the previous two cases, the results here were not as smooth even after averaging. The reason was that the score depended not only on P, but also largely on T, which were both randomly sampled. Whether P contained candidate node pairs that were informative for T affected the score. Overall, the embedding-independent strategies—page-rank. and max-deg.—had the top performance when was small; and the embedding-based strategies became increasingly competitive if more information was observed.
5.3.4. Evaluations on Two Larger Networks
Finally, we conducted a quantitative evaluation on two larger networks: PPI_cc and Blog. The results are shown in
Figure 7 and
Figure 8 and confirmed the observations we made on the five smaller networks.
Figure 7 shows the PPI_cc results for the three cases with seven query strategies, excluding
v-opt. and HALLP, as they were computationally too expensive. The AUC scores were averaged over five sets of random initial
,
P, and
T, and each set with five initial embeddings. The last column looks bumpy since the score was already very high and small randomness in the embedding could cause a slight difference.
Figure 8 shows the results for the second and third case with three values of
. Case 1 was omitted because embedding the Blog network with a large observed part was already quite expensive, and evaluating all the unobserved candidates when
was small made it computationally too demanding.
5.4. Discussion
Our experiments showed that ALPINE in its general form can be adapted for various problem settings, and active learning performed consistently and substantially better than passive learning regardless of which of the investigated query strategies was applied. Now, we discuss how the strategies can be optimally applied based on our observations, with advice and insights that may help a practitioner select the best query strategy given the properties of the data and available computational resources.
Among the seven active learning query strategies we developed, page-rank. and max-deg. did not depend on the network embedding while the other five were embedding based. Thus, as with limited observed information, the network embedding might be of poor quality, in such cases, page-rank. and max-deg. were seen to outperform the others.
The embedding-based strategies began to dominate when more information was observed and the embedding quality improved. The max-ent. and v-opt. had the top performance, but d-opt. had a more stable high performance across different values of . Based on those observations, we recommend a mixed strategy that starts from the degree-related and then switches to other embedding-based strategies.
The complexity of the utility computation depended on the sizes of
P and
T, as well as the network. Normally, the larger the pool, the more expensive the computations were, as we had to consider more candidate node pairs. All query strategies, including
rand., required a similar computing time when given the same size of
P. A notable exception is
v-opt., which was computationally more expensive. Yet, if we had a sufficiently accurate network embedding model, e.g., see the last columns in
Figure 4,
Figure 5 and
Figure 6,
v-opt. was almost always the most accurate, especially for the first few iterations. Thus, when the cost of querying was high as compared to the cost of computations,
v-opt. was preferable as soon as enough data were available such that the embedding was sufficiently accurate. If computational cost was a bottleneck though,
max-ent. and
d-opt. were computationally less expensive substitutes for
v-opt., with comparable accuracies.
The experiments aimed to show how active learning, compared to passive learning, benefited the network embedding based link prediction, namely CNE. Therefore, following the line of research in active learning, we restricted our baselines to only the random and the state-of-the-art active learning strategies for link prediction [
7,
9,
14,
25]. However, it would also be interesting to compare ALPINE with CNE against other types of link prediction methods to gain more insights. For example, a comparison of our work with a state-of-the-art link prediction approach (e.g., SEAL [
45] according to [
46,
47]) could be used to show whether the differentiation between the unknown and the unlinked status together with active learning would improve the link prediction accuracy in general. Note that this type of comparison can be biased as we had three types of link statuses, while other link prediction methods usually have only two. There are also other network embedding methods that can be used in combination with the ALPINE framework; thus the comparison among CNE and other base models can be considered. That leaves many possible opportunities for research to be built on this work.
6. Conclusions
Link prediction is an important task in network analysis, tackled increasingly using network embeddings. It is particularly important in partially observed networks, where finding out whether a node pair is linked is time consuming or costly, such that for a large number of node pairs, it is not known if they are linked. We proposed to make use of active learning in this setting and studied the problem of active learning for link prediction using network embedding in this paper.
More specifically, we proposed the ALPINE framework, a method that actively learns to embed partially observed networks to achieve better link predictions, by querying the labels of the most informative unobserved link statuses. We developed several utility functions for ALPINE to quantify the utility of a node pair: some heuristically motivated and some derived as variance reduction methods based on D-optimality and V-optimality from optimal experimental design.
We implemented ALPINE in combination with Conditional Network Embedding (CNE). To accomplish this, we first adapted CNE to work for partially observed networks. Through experimental investigation, we found that this modified version of CNE was not only more time efficient, but also more accurate for link prediction—an important side-result of the present paper.
We then empirically evaluated the performance of the utility functions we developed for ALPINE, both qualitatively and quantitatively, providing insights into the merits of ALPINE and advice for practitioners on how to optimally apply this method to different problem settings.
More broadly, the application of active learning to the link prediction problem in general, which is usually for partially observed networks, could help us to build more realistic and practical methods. Taking this work as a starting point, we see interesting future directions, including the investigation of a mixed strategy, batch mode active learning for ALPINE, and the application of ALPINE to the cold-start problem in recommender systems. Meanwhile, a thorough comparison of ALPINE with CNE against general link prediction methods, as well as the choice of the base network embedding model to be used with the ALPINE framework remain to be further investigated.