A Metric and Visualization of Completeness in Multi-Dimensional Data Sets of Sensor and Actuator Data Applied to a Condition Monitoring Use Case
Abstract
:Featured Application
Abstract
1. Introduction
2. Definitions and Background
2.1. Data Quality
2.2. Condition-Based Maintenance
3. Related Work in the Area of the Data Quality Dimension Completeness
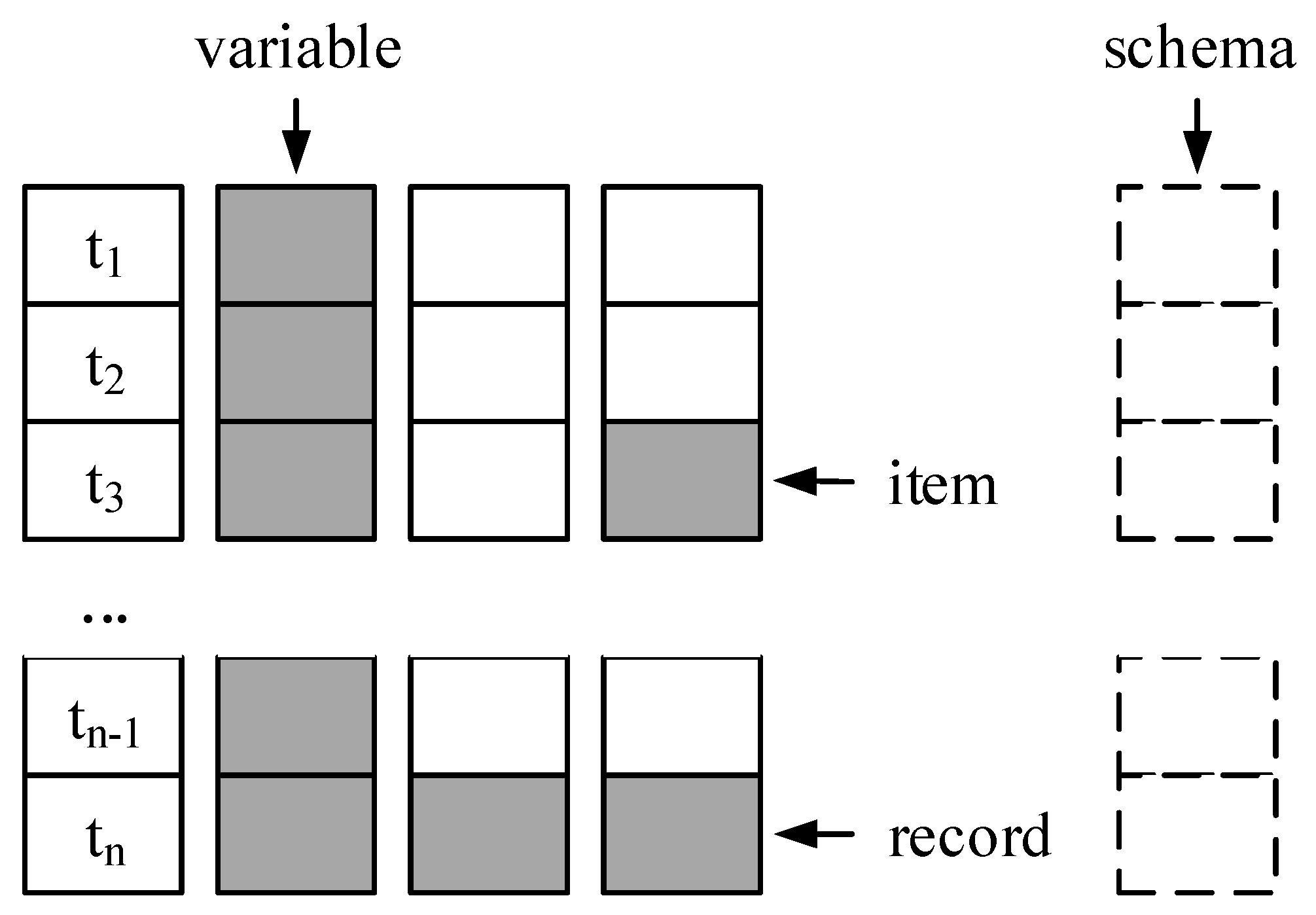
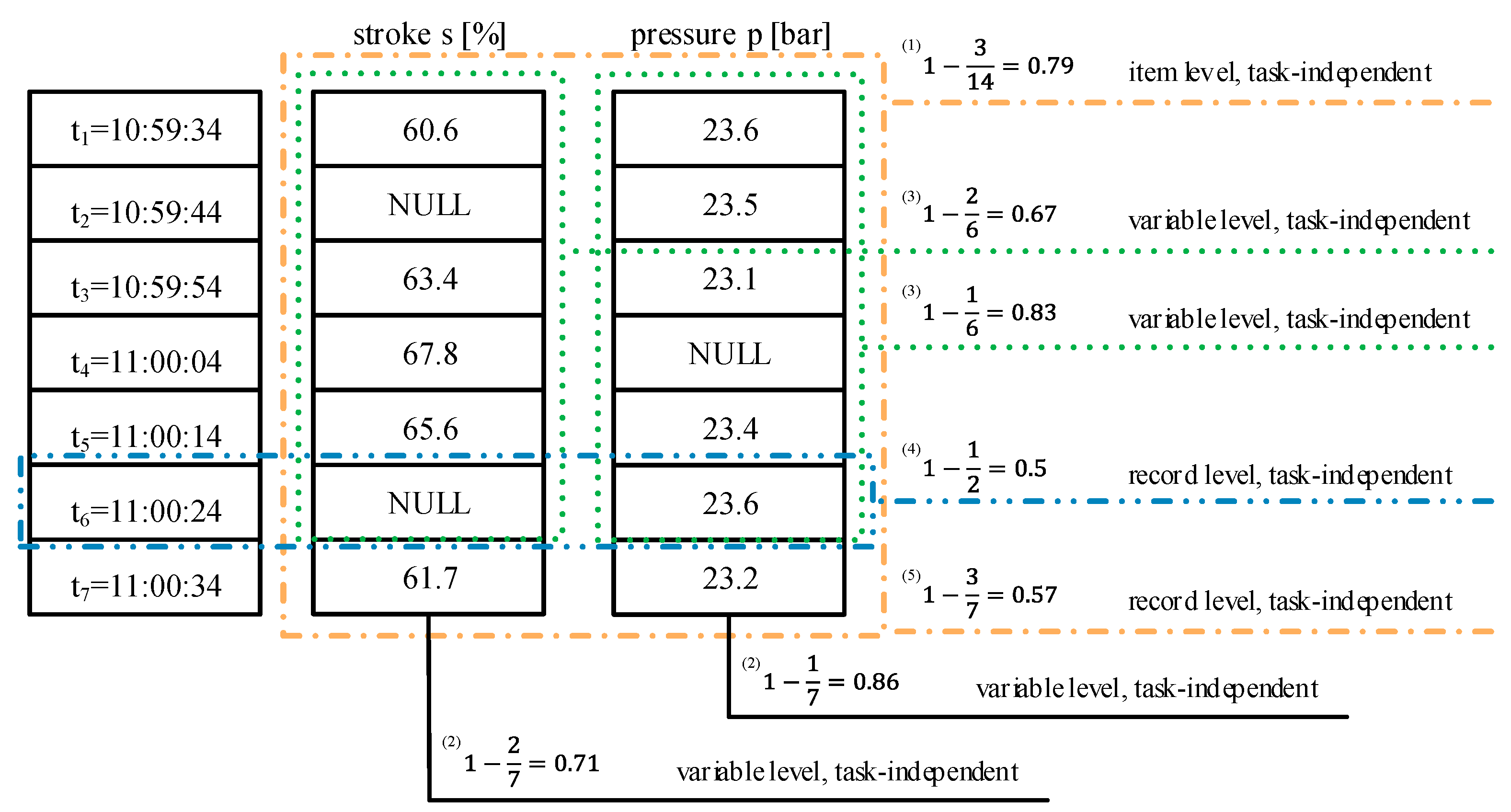
- Task-independent: Several authors introduced an attribute concerning the task-independent completeness on item level, e.g., Value Completeness [34] or Data Item Completeness [30]. Besides their different names, the calculation of the metric is the same. The number of empty items (null values) in a data set is divided by the whole sum of items in the data set [28,30,33,34,35]. Sporadic missing values of sensors caused by, e.g., unstable wireless connection or sensor device outages such as limited battery life or environmental interferences [40], impact this completeness. The example (1) in Figure 5 shows task-independent completeness on item level of (3 items out of 14 are NULL).
- Task-dependent: No attribute is introduced. One specific item is either existing or not. It is not reasonable to evaluate task-dependent completeness on single items.
- Task-independent: The task-independent attribute on variable level considers the empty items of one variable in relation to the number of available records [16,28,33,34,36,37]. The example (2) in Figure 5 illustrate this attribute which is called, among others, Column Completeness [16], Structural Completeness [36] or Attribute Completeness [37]. Even though several different names are introduced over time, the basic concept and the calculation is similar. However, Scannapieco and Batini 2004 further differentiate in a weak and a strong metric [34]. In contrast to the weak completeness (example (2) in Figure 5), the strong completeness is either 0 or 1 (0 for missing values in a variable and 1 for a complete variable). In Figure 5, the Strong Attribute Completeness is 0 for each variable. For sensor data, a window is defined, calculating the completeness value subsequently [38,39]. Based on a window of one minute, example (3) in Figure 5 reveals task-independent completeness on variable level of for stroke and for pressure in the first minute.
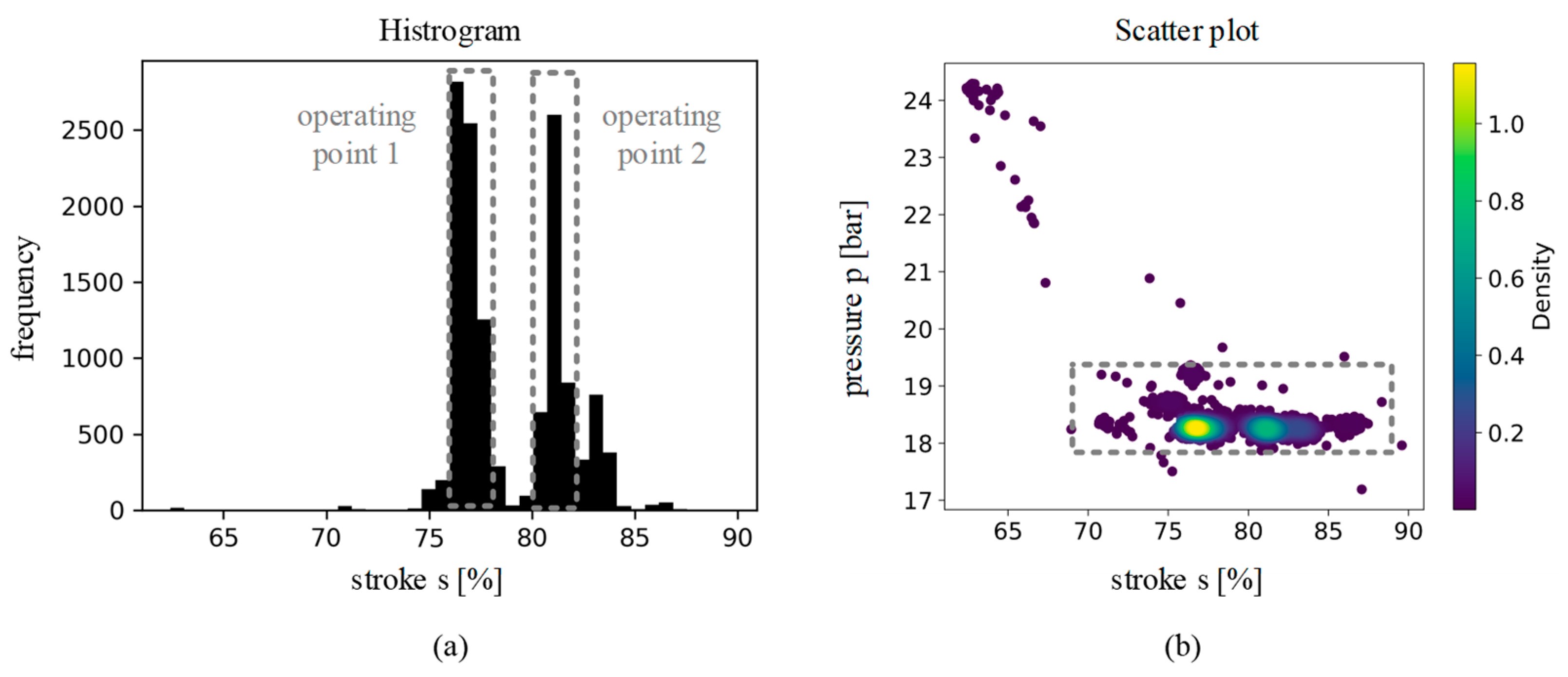
- Task-dependent: For this attribute, the expectations concerning the values or the amount of data are considered, respectively [16,28,34,36,37]. Most metrics observe whether all expected values of a variable are included in the data or not. If the valve’s stroke, which can vary from fully closed (stroke = 0%) to fully opened (stroke = 100%), only contains values between 60% and 90%, task-dependent completeness on variable level, e.g., Population Completeness [16] or Weak Relation Completeness [34], is reduced. The strong relation completeness [34] is 0 in this case. In contrast, the Content Completeness [36] refers to the precision of the data. If data does not contain as much information as required, e.g., only one decimal digit instead of the required three decimal digits, the completeness is reduced. Beside the metrics concerning the values of the variables, also metrics evaluating the amount of data of each variable is reasonable. The completeness concerning the amount of data is reduced if the valve’s stroke is gathered for 2 h even though the use case requires 3 h.
- Task-independent: Two different viewpoints are introduced for the record level. The first viewpoint considers and assess each record individually. This completeness is calculated based on the empty items in one record in relation to the number of variables. The record (example (4) in Figure 5) has a Weak Tuple Completeness [34] and Record Completeness [37] of since one of the two sensor signals is missing. The strong tuple completeness [34] evaluates the completeness of the record as , since it is not complete. The second viewpoint observes how many records with missing values are contained in the data set [37]. In Figure 5, the Empty Records in a Data File [37] is (5).
- Task-dependent: On record level, only one task-dependent attribute is introduced [37] concerning the amount of data rather than the content. The quotient of number of records within a data set and expected number of records describes the Data File Completeness [37]. Like the variable level, this completeness is reduced if the entire data set contains data of 2 h even though 3 h are required. A consideration regarding a metric to assess task-dependent completeness on record level concerning the content is not introduced yet. It is not evaluated if the records show all the combinations of values that are expected.
- Task-independent: No attribute is introduced since it is not reasonable. If the schema is complete and contains all the relevant variables, can only be evaluated based on the expectations of the use case.
- Task-dependent: This attribute is evaluated based on the comparison of available and expected variables. If the condition monitoring of control valves requires a sensor for vibration, a data set containing only stroke, pressure and pressure difference is not complete. Consequently, the Schema completeness [16] and Conceptual Data Model Completeness [37] is reduced. Furthermore, the Conceptual Data Model Attribute Completeness [37] considers the format of the variables. If vibration is measured with a vibration velocity transducer providing values in ; however, the values of an accelerometer in is required and the completeness is reduced.
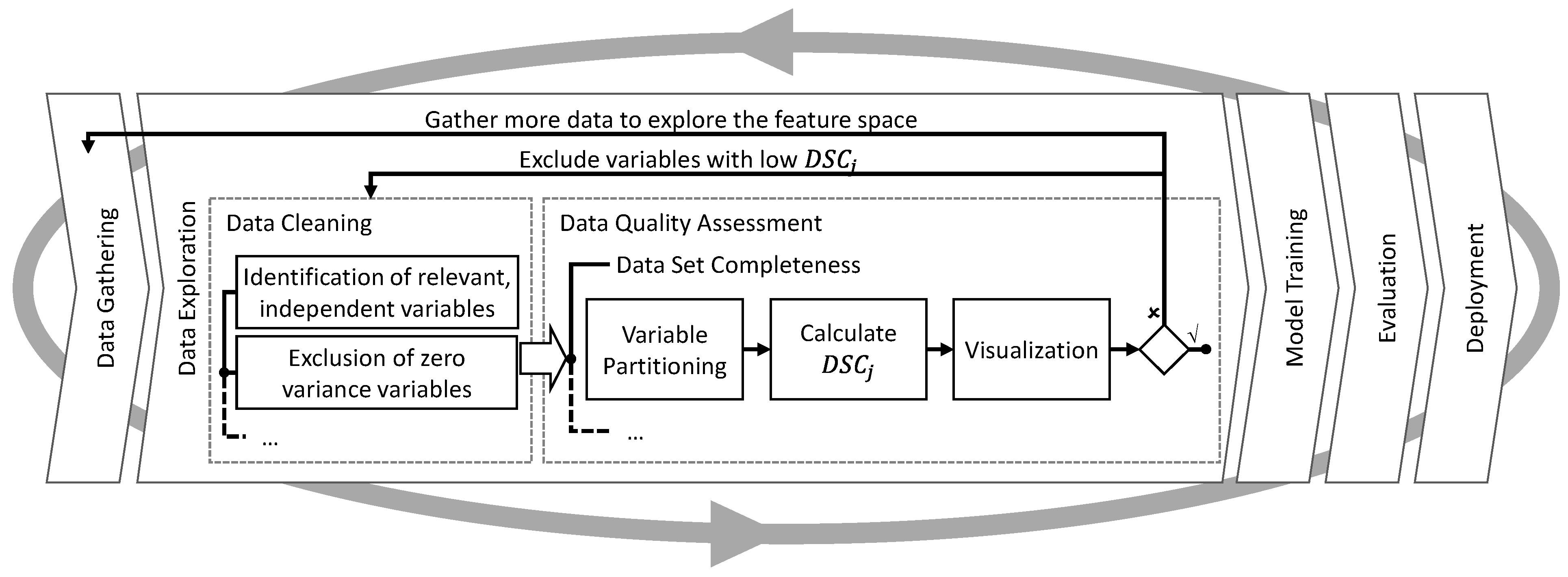
4. The Concept for the Assessment of Data Set Completeness
4.1. Assumptions and Prerequisites
4.2. Metric for Data Set Completeness
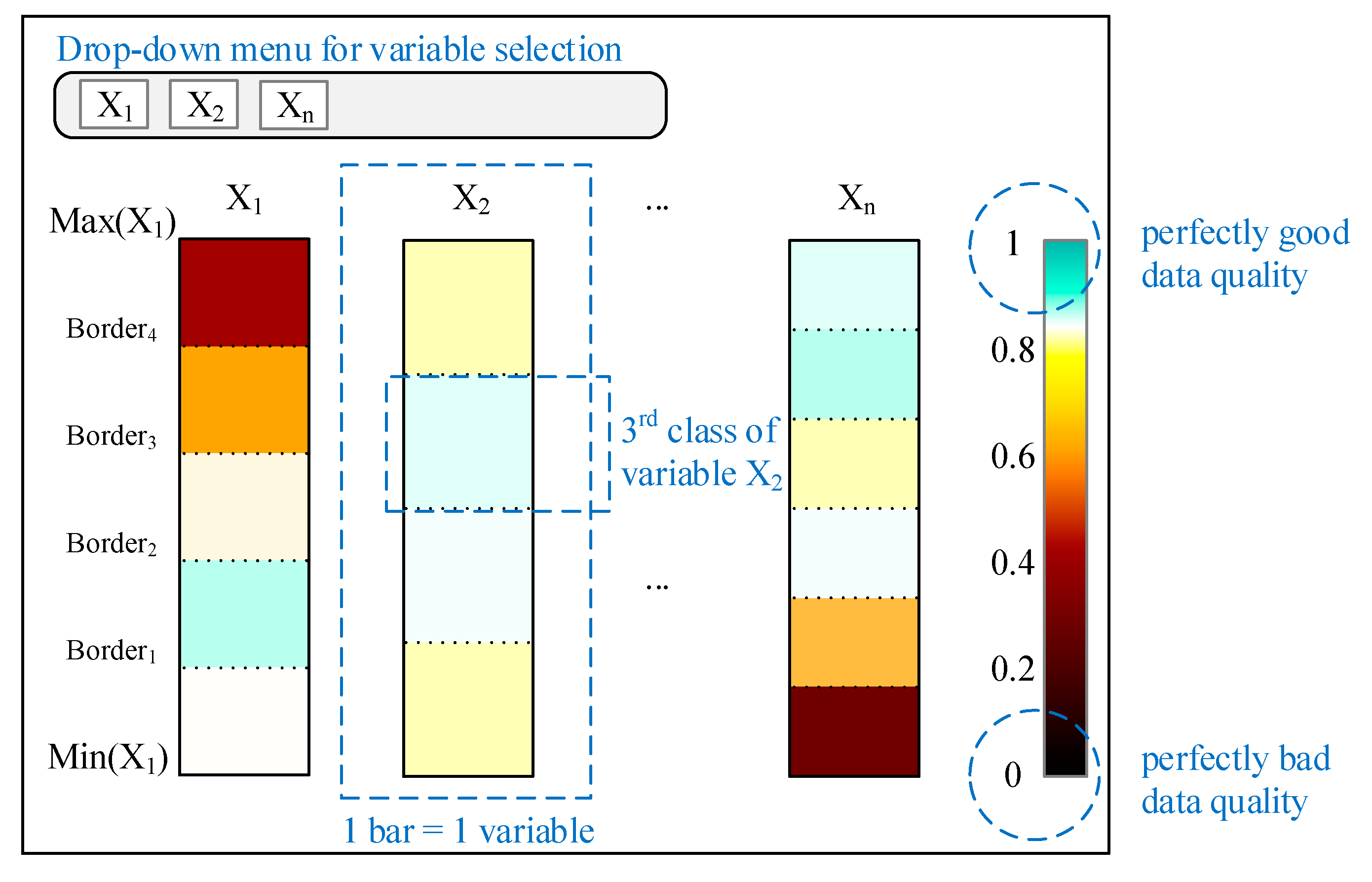
4.3. Visualization of the Data Set Completeness
5. Application and Discussion of the Proposed Metric and Visualization
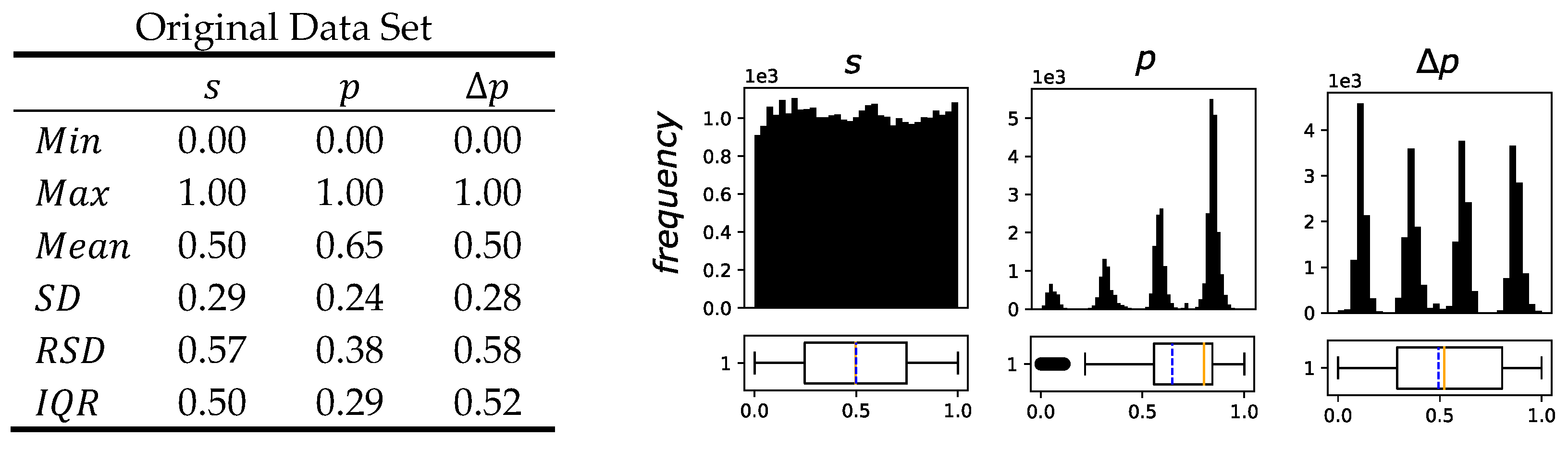
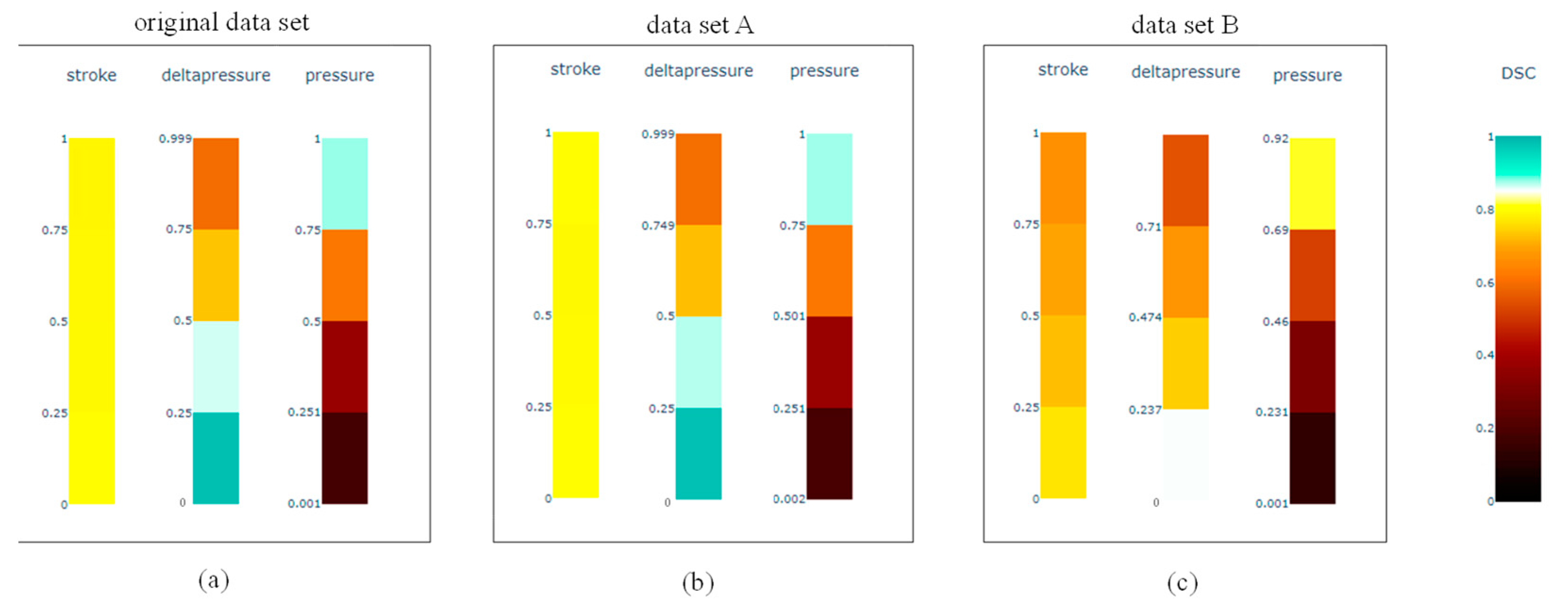
5.1. Comparison of the Different Data Sets
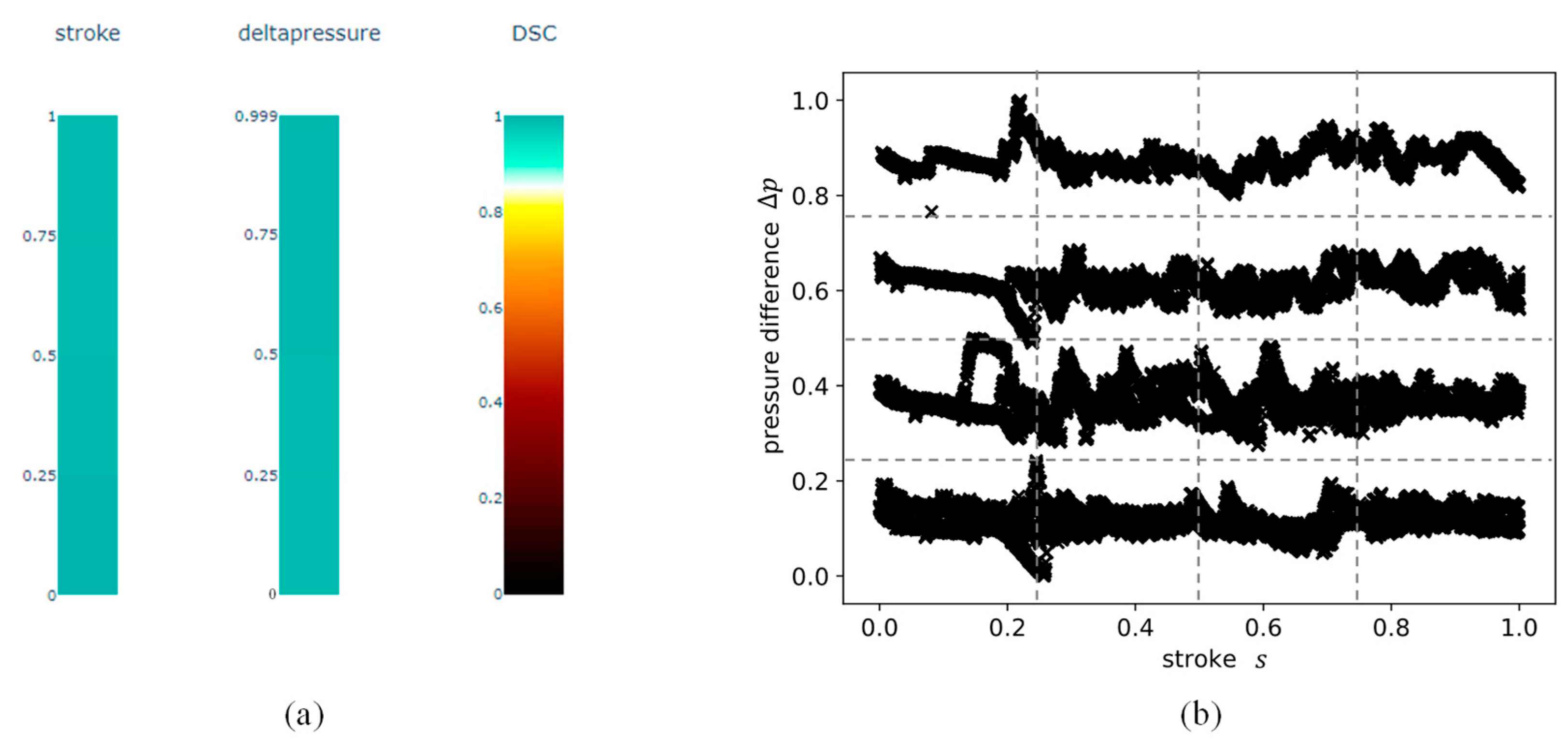
5.2. Application and Comparison of the Data Set Completeness Metric and Visualization of the Different Data Sets
5.3. Results of the Random forest Regression of the Different Data Sets
6. Evaluation of the Metric
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Steckenreiter, T.; Frosch, H.-G. Instandhaltung im Wandel: Neue Strategien erhöhen die Anlagenverfügbarkeit. Chemie Technik [Online]. 3 September 2013. Available online: https://www.chemietechnik.de/energie-utilities/instandhaltung-im-wandel-neue-strategien-erhoehen-die-anlagenverfuegbarkeit.html (accessed on 29 December 2020).
- Weis, I.; Hanel, A.; Trunzer, E.; Pirehgalin, M.F.; Unland, S.; Vogel-Heuser, B. Data-Driven Condition Monitoring of Control Valves in Laboratory Test Runs. In Proceedings of the 17th International Conference on Industrial Informatics (INDIN), Aalto University, Helsinki-Espoo, Finland, 22–25 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1291–1296, ISBN 978-1-7281-2927-3. [Google Scholar]
- Gao, Z.; Cecati, C.; Ding, S. A Survey of Fault Diagnosis and Fault-Tolerant Techniques Part II: Fault Diagnosis with Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef] [Green Version]
- Ahlborn, K.; Bachmann, G.; Biegel, F.; Bienert, J.; Falk, S. Technologieszenario, Künstliche Intelligenz in Der Industrie 4.0; Bundesministerium für Wirtschaft und Energie (BMWi): Berlin, Germany, 2019. [Google Scholar]
- Juran, J.M. Handbuch Der Qualitätsplanung; Verlag Moderne Industrie: Landsberg/Lech, Germany, 1989; ISBN 3478414407. [Google Scholar]
- International Organization for Standardization. ISO 9000:2015 Quality Management Systems—Fundamentals and Vocabulary; International Organization for Standardization: Geneva, Switzerland, 2015; ISBN 978-3-319-24104-3. [Google Scholar]
- Branco, P.; Torgo, L.; Ribeiro, R.P. A Survey of Predictive Modeling on Imbalanced Domains. ACM Comput. Surv. 2016, 49, 1–50. [Google Scholar] [CrossRef]
- Blake, R.; Mangiameli, P. The Effects and Interactions of Data Quality and Problem Complexity on Classification. J. Data Inf. Qual. 2011, 2, 1–28. [Google Scholar] [CrossRef]
- Parssian, A. Managerial decision support with knowledge of accuracy and completeness of the relational aggregate functions. Decis. Support Syst. 2006, 42, 1494–1502. [Google Scholar] [CrossRef]
- Kandel, S.; Heer, J.; Plaisant, C.; Kennedy, J.; van Ham, F.; Riche, N.H.; Weaver, C.; Lee, B.; Brodbeck, D.; Buono, P. Research directions in data wrangling: Visualizations and transformations for usable and credible data. Inf. Vis. 2011, 10, 271–288. [Google Scholar] [CrossRef] [Green Version]
- Wand, Y.; Wang, R.Y. Anchoring data quality dimensions in ontological foundations. Commun. ACM 1996, 39, 86–95. [Google Scholar] [CrossRef]
- Cai, L.; Zhu, Y. The Challenges of Data Quality and Data Quality Assessment in the Big Data Era. CODATA 2015, 14, 2. [Google Scholar] [CrossRef]
- Batini, C.; Scannapieco, M. Data and Information Quality: Dimensions, Principles and Techniques; Springer: Charm, Switzerland, 2016; ISBN 978-3-319-24104-3. [Google Scholar]
- Bovee, M.; Srivastava, R.P.; Mak, B. A conceptual framework and belief-function approach to assessing overall information quality. Int. J. Intell. Syst. 2003, 18, 51–74. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.Y.; Strong, D.M. Beyond Accuracy: What Data Quality Means to Data Consumers. J. Manag. Inf. Syst. 1996, 12, 5–33. [Google Scholar] [CrossRef]
- Pipino, L.L.; Lee, Y.W.; Wang, R.Y. Data quality assessment. Commun. ACM 2002, 45, 211. [Google Scholar] [CrossRef]
- Batini, C.; Cappiello, C.; Francalanci, C.; Maurino, A. Methodologies for data quality assessment and improvement. ACM Comput. Surv. 2009, 41, 1–52. [Google Scholar] [CrossRef] [Green Version]
- Madnick, S.E.; Wang, R.Y.; Lee, Y.W.; Zhu, H. Overview and Framework for Data and Information Quality Research. J. Data Inf. Qual. 2009, 1, 1–22. [Google Scholar] [CrossRef]
- Daniel, F.; Kucherbaev, P.; Cappiello, C.; Benatallah, B.; Allahbakhsh, M. Quality Control in Crowdsourcing. ACM Comput. Surv. 2018, 51, 1–40. [Google Scholar] [CrossRef] [Green Version]
- Epple, M.J.; Münzenmayer, P. Measuring Information Quality in the Web Context: A Survey of State-of-the-Art Instruments and An Application Methodology. In Proceedings of the Seventh International Conference on Information Quality (ICIQ-02), Cambridge, MA, USA, 8–10 November 2002; Fisher, C., Davidson, B.N., Eds.; MIT: Cambridge, MA, USA, 2002; pp. 187–196. [Google Scholar]
- Bicevskis, J.; Nikiforova, A.; Bicevska, Z.; Oditis, I.; Karnitis, G. A Step towards a Data Quality Theory. In Proceedings of the Sixth International Conference on Social Networks Analysis, Management and Security (SNAMS), Granada, Spain, 22–25 October 2019; Alsmirat, M., Jararweh, Y., Eds.; IEEE: Piscataway, NJ, USA, 2019; pp. 303–308, ISBN 978-1-7281-2946-4. [Google Scholar]
- Bamgboye, O.; Liu, X.; Cruickshank, P. Towards Modelling and Reasoning About Uncertain Data of Sensor Measurements for Decision Support in Smart Spaces. In Proceedings of the 42nd Annual Computer Software and Applications Conference, Tokyo, Japan, 23–27 July 2018; Reisman, S., Ed.; IEEE: Piscataway, NJ, USA, 2018; pp. 744–749, ISBN 978-1-5386-2667-2. [Google Scholar]
- European Committee for Standardization. EN 13306:2017 Maintenance—Maintenance Terminology; European Committee for Standardization: Brussels, Belgium, 2017. [Google Scholar]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- He, Q.P.; Wang, J.; Pottmann, M.; Qin, S.J. A Curve Fitting Method for Detecting Valve Stiction in Oscillating Control Loops. Ind. Eng. Chem. Res. 2007, 46, 4549–4560. [Google Scholar] [CrossRef]
- Zulkiffle, P.N.I.N.; Akhir, E.A.P.; Aziz, N.; Cox, K. The Development of Data Quality Metrics using Thematic Analysis. Int. J. Innov. Technol. Explor. Eng. IJITEE 2019, 8, 304–310. [Google Scholar]
- Shankaranarayanan, G.; Cai, Y. Supporting data quality management in decision-making. Decis. Support Syst. 2006, 42, 302–317. [Google Scholar] [CrossRef]
- Redman, T.C. Data Quality for the Information Age; Artech House: Boston, MA, USA, 1996; ISBN 0-89006-883-6. [Google Scholar]
- Even, A.; Shankaranarayanan, G. Utility-driven assessment of data quality. SIGMIS Database 2007, 38, 75. [Google Scholar] [CrossRef]
- Shankaranarayanan, G.; Blake, R. From Content to Context. J. Data Inf. Qual. 2017, 8, 1–28. [Google Scholar] [CrossRef]
- Ballou, D.P.; Pazer, H.L. Modeling Data and Process Quality in Multi-Input, Multi-Output Information Systems. Manag. Sci. 1985, 31, 150–162. [Google Scholar] [CrossRef]
- Naumann, F.; Freytag, J.-C.; Leser, U. Completeness of integrated information sources. Inf. Syst. 2004, 29, 583–615. [Google Scholar] [CrossRef] [Green Version]
- Scannapieco, M.; Batini, C. Completeness in the Relational Model: A Comprehensive Framework. In Proceedings of the Ninth International Conference on Information Quality (ICIQ-04), Cambridge, MA, USA, 24 July 2015; Ponzio, F.J., Ed.; MIT: Cambridge, MA, USA, 2004; pp. 333–345. [Google Scholar]
- Sicari, S.; Cappiello, C.; de Pellegrini, F.; Miorandi, D.; Coen-Porisini, A. A security-and quality-aware system architecture for Internet of Things. Inf. Syst. Front 2016, 18, 665–677. [Google Scholar] [CrossRef] [Green Version]
- Ballou, D.P.; Pazer, H.L. Modeling completeness versus consistency tradeoffs in information decision contexts. IEEE Trans. Knowl. Data Eng. 2003, 15, 241–244. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO/IEC 25024:2015 Systems and Software Engineering—Systems and Software Quality Requirements and Evaluation (SQuaRE)—Measurement of Data Quality; International Organization for Standardization: Geneva, Switzerland, 2015; (ISO/IEC 25024:2015). [Google Scholar]
- Karkouch, A.; Mousannif, H.; Al Moatassime, H.; Noel, T. Data quality in internet of things: A state-of-the-art survey. J. Netw. Comput. Appl. 2016, 73, 57–81. [Google Scholar] [CrossRef]
- Klein, A.; Lehner, W. Representing Data Quality in Sensor Data Streaming Environments. J. Data Inf. Qual. 2009, 1, 1–28. [Google Scholar] [CrossRef]
- Teh, H.Y.; Kempa-Liehr, A.W.; Wang, K.I.-K. Sensor data quality: A systematic review. J. Big Data 2020, 7, 1645. [Google Scholar] [CrossRef] [Green Version]
- Otalvora, W.C.; AlKhudiri, M.; Alsanie, F.; Mathew, B. A Comprehensive Approach to Measure the RealTime Data Quality Using Key Performance Indicators. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 26–28 September 2016; Society of Petroleum Engineers, Ed.; Society of Petroleum Engineers: Richardson, TX, USA, 2016. [Google Scholar]
- Heinrich, B.; Hristova, D.; Klier, M.; Schiller, A.; Szubartowicz, M. Requirements for Data Quality Metrics. J. Data Inf. Qual. 2018, 9, 1–32. [Google Scholar] [CrossRef]
- Sturges, H.A. The Choice of a Class Interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator: L 2 theory. Z. Wahrscheinlichkeitstheorie Verw. Geb. 1981, 57, 453–476. [Google Scholar] [CrossRef] [Green Version]
- Jenks, G.F.; Caspal, F.C. Error on Choroplethic Maps: Definition, Measurements, Reduction. Ann. Assoc. Am. Geogr. 1971, 61, 217–244. [Google Scholar] [CrossRef]
- Ortigosa-Hernández, J.; Inza, I.; Lozano, J.A. Measuring the class-imbalance extent of multi-class problems. Pattern Recognit. Lett. 2017, 98, 32–38. [Google Scholar] [CrossRef]
- Zimek, A.; Schubert, E.; Kriegel, H.-P. A survey on unsupervised outlier detection in high-dimensional numerical data. Stat. Analy Data Min. 2012, 5, 363–387. [Google Scholar] [CrossRef]
- Shukri, I.N.B.M.; Mun, G.Y.; Ibrahim, R.B. A Study on Control Valve Fault Incipient Detection Monitoring System Using Acoustic Emission Technique. In Proceedings of the 3rd International Conference on Computer Research and Development (ICCRD), Shanghai, China, 11–13 March 2011; Zhang, T., Ed.; IEEE: Piscataway, NJ, USA, 2011; pp. 365–370, ISBN 978-1-61284-837-2. [Google Scholar]
- Zhu, L.; Zou, B.; Gao, S.; Wang, Q.; Jia, Z. Research on Gate Valve Gas Internal Leakage AE Characteristics under Variety Operating Conditions. In Proceedings of the Mechatronics and Automation (ICMA), 2015 IEEE International Conference on, Beijing, China, 2–5 August 2015; pp. 409–414, ISBN 978-1-4799-7098-8. [Google Scholar]
- Wang, Y.; Gao, A.; Zheng, S.; Peng, X. Experimental investigation of the fault diagnosis of typical faults in reciprocating compressor valves. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2285–2299. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N. Internal Leakage Detection in Hydraulic Actuators Using Empirical Mode Decomposition and Hilbert Spectrum. IEEE Trans. Instrum. Meas. 2012, 61, 368–378. [Google Scholar] [CrossRef]
- Ayodeji, A.; Liu, Y.-k.; Zhou, W.; Zhou, X.-q. Acoustic Signal-Based Leak Size Estimation for Electric Valves Using Deep Belief Network. In Proceedings of the 5th International Conference on Computer and Communications (ICCC), Chengdu, China, 6–9 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 948–954, ISBN 978-1-7281-4743-7. [Google Scholar]
- Verma, N.K.; Sevakula, R.K.; Thirukovalluru, R. Pattern Analysis Framework with Graphical Indices for Condition-Based Monitoring. IEEE Trans. Rel. 2017, 66, 1085–1100. [Google Scholar] [CrossRef]
- Pichler, K.; Lughofer, E.; Pichler, M.; Buchegger, T.; Klement, E.P.; Huschenbett, M. Fault detection in reciprocating compressor valves under varying load conditions. Mech. Syst. Signal Process. 2016, 70–71, 104–119. [Google Scholar] [CrossRef]
- Jose, S.A.; Samuel, B.G.; Aristides, R.B.; Guillermo, R.V. Improvements in Failure Detection of DAMADICS Control Valve Using Neural Networks. In Proceedings of the Second Ecuador Technical Chapters Meeting (ETCM), Salinas, Ecuador, 16–20 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5, ISBN 978-1-5386-3894-1. [Google Scholar]
- Korablev, Y.A.; Logutova, N.A.; Shestopalov, M.Y. Neural Network Application to Diagnostics of Pneumatic Servo-Motor Actuated Control Valve. In Proceesings of International Conference on Soft Computing and Measurements—SCM’2015, St. Petersburg, Russia, 19–21 May 2015; Shaposhnikov, S.O., Ed.; IEEE: Piscataway, NJ, USA, 2015; pp. 42–46. ISBN 978-1-4673-6961-9. [Google Scholar]
- Sowgath, M.T.; Ahmed, S. Fault detection of Brahmanbaria Gas Plant using Neural Network. In Proceedings of the Electrical and Computer Engineering (ICECE), 2014 International Conference on, Dhaka, Bangladesh, 20–22 December 2014; pp. 733–736, ISBN 978-1-4799-4166-7. [Google Scholar]
- Li, Z.; Li, X. Fault Detection in the Closed-Loop System Using One-Class Support Vector Machine. In Proceedings of the DDCLS, 7th Data Driven Control and Learning Systems Conference, Enshi, China, 25–27 May 2018; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2018; pp. 251–255, ISBN 978-1-5386-2618-4. [Google Scholar]
- Ghorbani, R.; Ghousi, R. Comparing Different Resampling Methods in Predicting Students’ Performance Using Machine Learning Techniques. IEEE Access 2020, 8, 67899–67911. [Google Scholar] [CrossRef]
- Webb, G.I.; Zheng, Z. Multistrategy ensemble learning: Reducing error by combining ensemble learning techniques. IEEE Trans. Knowl. Data Eng. 2004, 16, 980–991. [Google Scholar] [CrossRef] [Green Version]
- Brooke, J. SUS: A “Quick and Dirty” Usability Scale. In Usability Evaluation in Industry; Jordan, P.W., Thomas, B., McClelland, I.L., Weerdmeester, B., Eds.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014; ISBN 978-0748404605. [Google Scholar]








| Literature, Which Introduces Completeness Qualitatively | ||||||||
| Author | Name of the Attribute | Level | Cat. | S | F.5 | |||
| I | V | R | S | |||||
| Redman 1996 [29] | Attribute Compl. | X | Indep. | ○ | ||||
| Entity Compl. | X | Dep. | ○ | |||||
| Ballou & Pazer 1985 [32] | Compl. | X | Indep. | - | ||||
| Wand & Wang 1996 [11] | Compl. | X | X | X | Dep. | ○ | ||
| Wang & Strong 1996 [15] | Compl. | X | X | X | Dep. | - | ||
| Literature, Which Introduces Metrics for Completeness | ||||||||
| Author | Name Attribute | Level | Cat. | S | F.5 | |||
| I | V | R | S | |||||
| Naumann et al. 2004 [33] | Coverage | X | Indep. | - | (1) | |||
| Scannapieco & Batini 2004 [34] | Value Compl. | X | Indep. | ○ | (1) | |||
| Shankaranarayanan & Cai 2006 [28] | Compl. of Raw Data Element | X | Indep. | - | (1) | |||
| Even & Shankaranarayanan 2007 [30] | Data Item Compl. | X | Indep. | - | (1) | |||
| Sicari et al. 2014 [35] | Compl. | X | Indep. | X | (1) | |||
| Pipino et al. 2002 [16] | Column Compl. | X | Indep. | - | (2) | |||
| Population Compl. | X | Dep. | - | |||||
| Ballou & Pazer 2003 [36] | Structural Compl. | X | Indep. | ○ | (2) | |||
| Content Compl. | X | Dep. | ○ | |||||
| Naumann et al. 2004 [33] | Density | X | Indep. | - | ||||
| Compl. | X | Indep. | - | |||||
| Scannapieco & Batini 2004 [34] | Weak Attribute Compl. | X | Indep. | ○ | (2) | |||
| Strong Attribute Compl. | X | Indep. | ○ | |||||
| Weak Relation Compl. | X | Dep. | ○ | |||||
| Strong Relation Compl. | X | Dep. | ○ | |||||
| Shankaranarayanan & Cai 2006 [28] | Compl. of Info. Product Component | X | Indep. | - | (2) | |||
| Perceived Compl. | X | Dep. | - | |||||
| ISO/IEC 25,024:2015 [37] | Attribute Compl. | X | Indep. | - | (2) | |||
| Data Value Compl. | X | Dep. | - | |||||
| Karkouch et al. 2016 [38] | Compl. | X | Indep. | X | (3) | |||
| Klein & Lehner 2009 [39] | Compl. | X | Indep. | X | (3) | |||
| Scannapieco & Batini 2004 [34] | Weak Tuple Compl. | X | Indep. | ○ | (4) | |||
| Strong Tuple Compl. | X | Indep. | ○ | |||||
| ISO/IEC 25,024:2015 [37] | Record Compl. | X | Indep. | - | (4) | |||
| Data File Compl. | X | Dep. | - | |||||
| Empty Records in a Data File | X | Indep. | - | (5) | ||||
| Pipino et al. 2002 [16] | Schema Compl. | X | Dep. | - | ||||
| ISO/IEC 25,024:2015 [37] | Conceptual Data Model Compl. | X | Dep. | - | ||||
| Conceptual Data Model Attribute Compl. | X | Dep. | - | |||||
| Weiß & Vogel-Heuser | Data Set Compl. | X | Dep. | X | ||||
| Parameters | |||
| variables | |||
| Number of variables | |||
| observations | |||
| Number of observations | |||
| Distance of two vectors | |||
| Number of observations in one section | Minimum value | ||
| Maximum value | |||
| Variable vector | Mean value | ||
| Standard deviation | |||
| Relative standard deviation (SD/Mean) | |||
| Number of sections | Interquartile range (3rd quartile–1st quartile) | ||
| Variables | Indices | ||
| Flow | Variable | ||
| Stroke | Class | ||
| Pressure upstream (before the valve) | |||
| Pressure difference before and after the valve | |||
| Signal pressure | |||
| Terms | |||
| variable | A variable represents one sensor or actuator of an aPS. The values of a variable are numerical, either continuous or discrete. | ||
| class | A class describes a specific value interval of a variable. Classes do not overlap but border to each other and cover the whole value range of a variable. | ||
| section | A section represents an area of the n-dimensional feature space described by the respective classes of the n variables. A section is an n-dimensional bin of the feature space. | ||
| feature space | The feature space is the n-dimensional space, which is created between the variables. | ||
| Original | Data Set A | Data Set B | |
|---|---|---|---|
| 0.999 | 0.999 | 0.970 | |
| 0.00268 | 0.00283 | 0.04520 |
| Existence of Minimum and Maximum Metric Values (R1) | Fulfilled |
| The proposed indicator for data set completeness consists of two factors: section balance quantifies the unbalance of the observation in one class compared to the worst possible distribution of this class for the given data set. In this way, the factor ranges from 0 to 1, representing the worst possible distribution and the best possible distribution, respectively. The class volume quantifies the balance of the observations in one variable. This factor also ranges from 0 to 1, representing a maximal unbalanced distribution and an equal distribution of the observations in one variable. Consequently, the data set completeness has a minimum value of 0, indicating perfectly poor data quality in terms of the utilization of the future space. The maximum value of 1, indicating perfectly good data quality, is reached by equally distributed data in the whole feature space. The existence of a minimum and a maximum metric value is given and the requirement is rated as fulfilled. | |
| Interval-scaled metric values (R2) | fulfilled |
| of 0.8. Therefore, the requirement for an interval-scaled metric value is rated as fulfilled. | |
| Quality of the configuration parameters (R3) | not yet fulfilled |
| The calculation of the data set completeness only requires the experts’ input regarding the partitioning of the variables. The experts need to identify the operating points of the considered machine to define the classes that the proposed metric should evaluate. No further input or parameter tuning is required. is required. | |
| Sound aggregation of the metric values (R4) | fulfilled |
| The proposed metric for data set completeness is calculated for each class individually, representing the utilization of the feature space in multi-dimensional data sets. To further aggregate the data set completeness, the mean value for each variable is proposed. Furthermore, the standard deviation should be considered providing information about the homogeneity of the classes of one specific variable. A further aggregation is possible by taking the mean value for the whole data set. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weiß, I.; Vogel-Heuser, B. A Metric and Visualization of Completeness in Multi-Dimensional Data Sets of Sensor and Actuator Data Applied to a Condition Monitoring Use Case. Appl. Sci. 2021, 11, 5022. https://doi.org/10.3390/app11115022
Weiß I, Vogel-Heuser B. A Metric and Visualization of Completeness in Multi-Dimensional Data Sets of Sensor and Actuator Data Applied to a Condition Monitoring Use Case. Applied Sciences. 2021; 11(11):5022. https://doi.org/10.3390/app11115022
Chicago/Turabian StyleWeiß, Iris, and Birgit Vogel-Heuser. 2021. "A Metric and Visualization of Completeness in Multi-Dimensional Data Sets of Sensor and Actuator Data Applied to a Condition Monitoring Use Case" Applied Sciences 11, no. 11: 5022. https://doi.org/10.3390/app11115022
APA StyleWeiß, I., & Vogel-Heuser, B. (2021). A Metric and Visualization of Completeness in Multi-Dimensional Data Sets of Sensor and Actuator Data Applied to a Condition Monitoring Use Case. Applied Sciences, 11(11), 5022. https://doi.org/10.3390/app11115022







