Abstract
Composite materials are becoming more popular in technological applications due to the significant weight savings and strength offered by these materials compared to metallic materials. In many of these practical situations, the structures suffer from drop-impact loads. Materials and structures significantly change their behavior when submitted to impact loading conditions compared to quasi-static loading. The present work is devoted to investigating the thermal process in carbon-fiber-reinforced polymers (CFRP) subjected to a drop test. A novel drop-weight impact test experiment is performed to evaluate parameters specific to 3D composite materials. A strain gauge rosette and infrared thermography are employed to record the kinematic and thermal fields on the composites’ surfaces. This technique is nondestructive and offers an extensive full-field investigation of a material’s response. The combination of strain and infrared thermography data allows a comprehensive analysis of thermoelastic effects in CFRP when subjected to impacts. The experimental results are validated using numerical analysis by developing a MATLAB® code to analyze whether the coupled heat and wave equation phenomenon exists in a two-dimensional polar coordinate system by discretizing through a forward-time central-space (FTCS) finite-difference method (FDM). The results show the coupling has no significant impact as the waves generated due to impact disappears in 0.015 s. In contrast, heat diffusion happens for over a one-second period. This study demonstrates that the heat equation alone governs the CFRP heat flow process, and the thermoelastic effect is negligible for the specific drop-weight impact load.
Keywords:
CFRP; drop test; strain; infrared thermography; NDT; thermoelastic effects; impacts; numerical analysis; FDM 1. Introduction
Materials are the fundamental elements of all natural and human-made structures. New materials usually emerge due to the need to improve structural efficiency and performance. One of the best examples of this interrelated process is a composite material. Composites consist of two or more different materials in various combinations that form a structural unit. Composites are generally used because they have required properties that cannot be achieved through the use of the constituent materials alone. The most common example is a fibrous composite of reinforcing fibers embedded in a binder or matrix material. In general, fibers are the principal load-bearing members, while the surrounding matrix keeps them in their allocated position, and their orientation acts as a load-transfer medium between them and protects them from environmental damage due to chemical corrosion and humidity. Carbon-fiber-reinforced polymers (CFRP) offer a combination of strength and modulus comparable to or better than many traditional metallic materials. Despite the many superior properties of composites over metals, composites are susceptible to damage caused by low-velocity impact that reduce their performance to a large extent [1].
Composites have become the leading structural material in many industries due to their superior properties, including their high strength-to-weight ratio [2]. However, some aspects of switching the traditional structural material from metal to composite have not been well-investigated. A significant amount of research has been conducted to study the mechanical behavior of composites prior to their elastic threshold in relation to their thermal response. However, researchers have made few attempts to analyze this phenomenon with the help of IR thermography.
1.1. Non-Destructive Testing (NDT) of Composites—Thermographic Evaluation Method
IR thermography offers ideal, cost-effective NDT solutions for a wide range of composites applications, including detection of impact damage, delamination, water entrapment, inclusions, density variations, and evaluation of the adhesive bonds [3,4,5]. This technique, which is fast and contact-free, offers wide-area coverage of flat or curved parts. The principle of infrared thermographic NDT systems is based on the detection of infrared energy emitted from an object, and detection devices range from a simple heat gun/IR camera combination to advanced systems capable of defect measurement and advanced materials characterization [6,7].
The IR thermographic method measures temperature changes on the surface of materials resulting from stress-generated or externally applied thermal fields. Thermography can be used to study thermal variations. Excitation sources can be applied externally using thermal or mechanical sources to generate coupled stress and thermal fields. These excitation sources can be in the form of mechanical loads, direct heat, and ultrasonic stress waves. [8,9,10,11].
1.2. Drop-Weight Impact Testing (DWIT)
A drop-weight impact test was designed to examine a material’s behavior under the action of a falling impact weight (Figure 1). It is used to assess the impact properties of composites [12]. The impact weight falls from a predefined height under the action of gravity and hits the material being studied. The specimen used for the test is often a flat plate cut from larger material. The test piece is supported at its edges and impacted centrally by a vertically falling weight. The impact performance of composites is concerned with absorbing energy in the system when the component is struck, either through deformation or damage development. A strain–time curve is obtained from the impact event by attaching a strain gauge rosette. The test results enable the investigation of the behavior of specimens during and after the impact test.
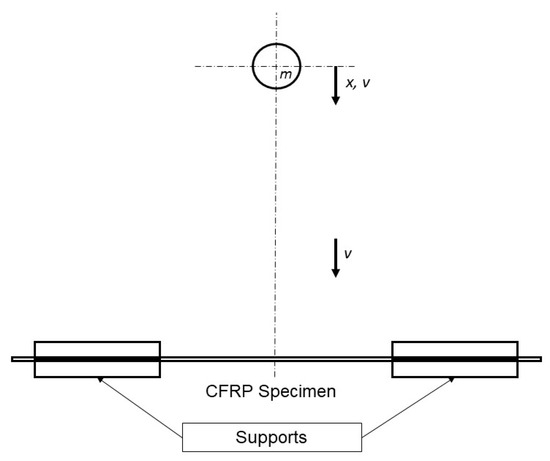
Figure 1.
The drop-weight impact test method.
1.3. Thermoelastic and Thermoplastic Effects
The thermoelastic effect is a small reversible change in the temperature of an object when it undergoes elastic deformation. The thermoelastic effect depends upon the type of strain, which can be elastic or non-elastic. As described by Lord Kelvin in 1853 [13], a purely elastic tensile strain in an adiabatic configuration generates a thermoelastic effect that results in the cooling of isotropic specimens with positive thermal expansion coefficients. However, if inelastic deformation is also present, then the thermoplastic phenomenon occurs, resulting in heating due to the dissipation of the applied mechanical energy; this will normally overcome the thermoelastic contribution and result in a net specimen temperature increase. Mechanical deformation causes temperature changes, but they go unnoticed if the loading is slow, resulting in an isothermal process [14]. At the other extreme, under high-speed loading conditions, considerable viscous heating can occur, possibly leading to localized melting [15].
The thermoelastic response is produced by dilational strain. Tensile stress produces a drop in temperature, whereas compressive stress results in a temperature increase. Nowacki [16] developed the theory of thermoelastic diffusion. In this theory, the coupled thermoelastic model that is used implies infinite speeds for the propagation of thermoelastic waves. The overall effects arising from the coupling of fields of temperature, mass diffusion, and strain in an elastic cylinder have been discussed by Olesiak and Pyryev [17]. Sherief et al. [18,19,20,21] introduced the theory of generalized thermoelastic diffusion, which predicts finite speeds of propagation for thermoelastic and diffusive waves. The present study was motivated by the importance of studying the thermoelastic effect in CFRP.
When composites are subjected to dynamic loading under impact events, the zero or near-zero plasticity of these structures past their yielding points results in a susceptibility to delamination, matrix cracking, and fiber breakage [22].
1.4. Numerical Analysis
Different modeling techniques are used to model the impact dynamics of composite structures. In general, there are four categories considered: energy-balance models, which assume a quasi-static condition; spring-mass models, which simplify the dynamics of the structure; complete models, in which the full behavior of the structure is modeled; and infinite/finite plate models. The infinite plate model can be considered if the deformation wavefront does not reach the boundary of the plate. If the wave propagation reflects on the plate boundaries back to the point of impact, then the finite size of the test sample must be considered [23].
2. Methodology
In this study, the thermoelastic response of carbon-fiber-reinforced polymers (CFRP) subjected to high strain rates was investigated using a novel DWIT experimental setup. Fiber-reinforced composites are usually manufactured by stacking laminae of fiber sheets pre-impregnated with resin. The structure is therefore heterogeneous, and so the stress discontinuities between the fibers and matrix should be considered for the purpose of calculating the overall temperature field [24,25]. It would be expected that the fibers and matrix would experience different temperature fluctuations due to their dissimilar thermoelastic constants [14]. After the drop impact, viscous (frictional) energy is converted into thermal energy. This energy propagates from the point of impact toward the boundaries due to the temperature gradient. The goal of this study was to investigate the thermoelastic phenomenon in the CFRP material that produces spatial variations in the surface temperatures and allows correlation between measured time-averaged IR images, heat flow due to pure diffusion, and the strain waves on the surface.
The study was divided into two phases. The first phase was the experimental study, which involved performing the DWIT with a specialized rosette strain gauge, amplifiers, a high-speed oscilloscope, and an IR thermographic camera. This study yielded useful insight into the oscillatory elastic deformation (Video S1: Drop-Weight Impact Testing (DWIT) video) and internal friction phenomenon captured via IR thermography within the CFRP (Video S2: IR thermographic recording) when subjected to drop-weight impacts.
The second phase was the development of numerical models to describe the physical problem that was predicted from the experimental findings. The heat and wave equations in polar coordinate systems were coupled and solved using the forward-time central-space (FTCS) method and finite-difference method (FDM) using MATLAB® software. The derived numerical analysis solutions were validated using experimental findings to optimize the models.
2.1. CFRP Sample
The CFRP test samples used in this study were sheets of DragonPlate® (Allred and Associates Inc., Elbridge, NY, USA) [26]. Each sample was a solid quasi-isotropic carbon-fiber sheet 1 mm thick (Figure 2) [27]. The CFRP sheets comprised five plies at 0°/+45°/90°/−45°/0° orientation laminates (Figure 2). The samples were composed of a tough and rigid carbon-reinforced epoxy matrix, with a textured finish on both sides. The properties of the samples are given in Table 1.
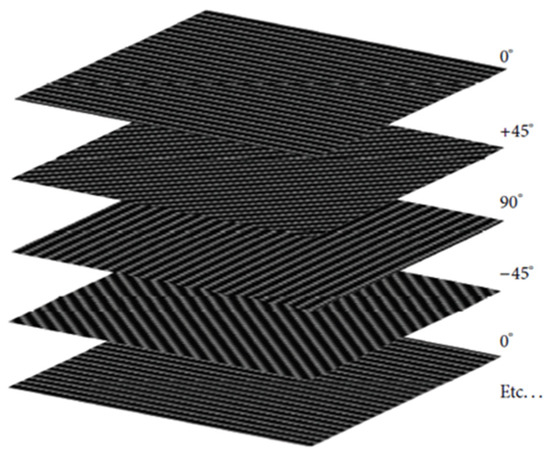
Figure 2.
The carbon fiber quasi-isotropic sheets [28].

Table 1.
Properties of the CFRP samples [27].
2.2. Experimental Setup to Perform a Drop Test
The drop-weight impact test was performed using a spherical steel ball 20 mm in diameter (Figure 3a). The ball was wrapped with black tape to decrease steel reflectance for better thermal images(Figure 3b) [29,30]. A rosette strain gauge in a stacked configuration (at 0°, 45°, and 90° angles) was attached to the back of the CFRP plate (Figure 4). The acquisition of the differential strain vector from the baseline was achieved using an op-amp circuit and a high-speed oscilloscope at a 100 MHz sampling frequency rate. The CFRP plate was clamped in a circular flange to prevent the plate from moving during the DWIT (Figure 5a,b).

Figure 3.
(a) The spherical steel ball, which measured 20 mm in diameter and weighed 33 g. (b) The steel ball wrapped in black tape.

Figure 4.
The rosette strain gauge attached to the back of the CFRP sample.

Figure 5.
(a) The CFRP sample clamped in a circular flange with an inner diameter of 173 mm (top view). (b) The CFRP sample clamped in a circular flange (side view).
The test specimens were monitored using high-speed IR thermography throughout the course of the experiment using an FLIR® T1030sc thermal camera [31], and were analyzed using Researcher IR Max software [32] to investigate the heat generation due to friction and diffusion associated with the thermoelastic effects. The physical process to collect IR thermographic images when excitation occurs through a mechanical impact can be explained in three steps (diagrammatic representation of the experiment is shown in Figure 6):
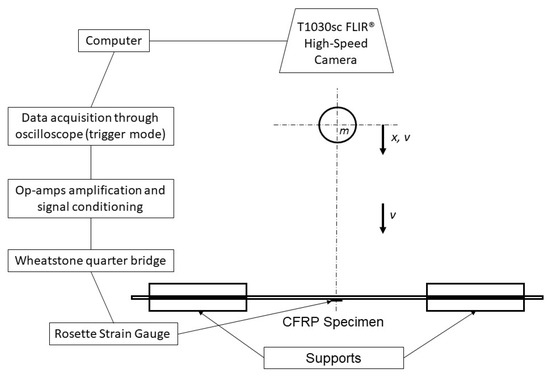
Figure 6.
Diagrammatic representation of the experiment.
(1) The surface of the component was initially at a uniform ambient temperature. The excitation was accomplished using a lightweight indenter; in this study, a 33 g weight steel ball was used.
(2) The frictional energy was converted into thermal energy at the point of impact; heat diffused toward the cooler edges. The CFRP steel friction coefficient was 0.33 [33].
(3) An image of the CFRP plate’s surface temperature was monitored using an IR camera, which collected time-averaged IR radiations emitted from the surface of the sample. The frame rate of the IR camera was approximately 125 Hz.
3. Finite Difference Method (MATLAB®)
The FDM is a numerical method for solving differential equations such as the two-dimensional wave [34,35] and heat equation [36,37,38], as given in Equations (1) and (4). This method approximates the differentials by discretizing the dependent variables (strain and temperature) in the independent variable domains (space and time) [39,40,41]. Each discretized value of the dependent variable is referred to as a nodal value. In this case, 2D wave and heat equations in the cylindrical coordinate system are discretized using FTCS FDM. The discretized equations are given in Equations (3) and (5).
The two-dimensional wave equation in the cylindrical coordinate system is shown in Equation (1):
where is the strain, is the radius, is the angle in degrees, and is the speed of a sound in a medium as shown in Equation (2) [42].
The two-dimensional discretized wave equation in the cylindrical coordinate system is given in Equation (3).
The two-dimensional heat conduction equation in a cylindrical coordinate system with no energy-generation term is given in Equation (4).
The two-dimensional discretized heat equation in a cylindrical coordinate system is shown in Equation (5):
where T is the temperature; t, r, and θ refer to time and positions; Δt is the timestep size in (s); and Δr and Δθ are the differences in the spatial positions of the temperature nodes. α = 0.12 in-plane thermal conductivity of CFRPs [43,44].
Overall temperature changes in the CFRP plate can be obtained by solving the coupled heat and wave equation [45,46,47] as given in Equation (6):
where , which can be obtained from the heat equation in a cylindrical coordinate system as given in Equation (5). = , ε is the thermoelastic strain obtained from wave equation in a cylindrical coordinate system as given in Equation (3), and CTE = [33,42] is the coefficient of thermal expansion of the CFRP.
3.1. Mathematical Model
The mathematical model of the experiment is given by governing Equations (7) and (8) and the initial-boundary values as given in Equations (9) and (10):
where is the temperature and is the trace of the stress tensor. The parameters are the wave speed, thermal conductivity, and thermal expansion factor, respectively. To reach an analytical solution, we introduce and linearize . Then we solve Equation (11) with the boundary conditions given in Equations (12) and (13):
To solve the linearized version of the problem with axisymmetric initial and boundary data, we introduce the eigenvalues and eigenfunctions of the axisymmetric Laplace operator on the circular CFRP sheet with radius , . The eigenfunctions for are given in Equation (14):
where is the th Bessel function of the first kind, and is the th zero of . To simplify the notation, we introduce , the eigenvalue corresponding to the eigenfunctions is . The solution is given in Equations (15) and (16):
The coefficients are then computed as follows in Equation (17) through (19):
where is the first Bessel function of the first kind.
3.2. Numerical Analysis
The two-dimensional discretized wave equation in cylindrical coordinates was initially solved using the FTCS FDM, a numerical method in MATLAB®. The results were compared with the experiments, as discussed in Section 4.2.1. Afterward, the coupled heat and wave equation in the two-dimensional polar coordinate system was solved. As an initial condition, a constant temperature of 21.9 C was specified throughout the domain, except at the source. It is vital for the stability and accuracy of the FDM to choose the correct timestep value. In this work, the Courant–Friedrichs–Lewy (CFL) condition [48] was used to decide the timestep size. The CFL condition is given in Equation (20):
where α is the velocity magnitude, is the timestep, and and are the radius and angle between mesh elements.
For solving the wave equation for a total of 3000 timesteps, the following were taken: dt = 5; % microseconds; dr = 1; % mm; dtheta = 1; % degrees.
For solving the heat equation for a total of 300 timesteps, the following were taken: dt = 5000; % microseconds; dr = 1; % mm; dtheta = 1; % degrees.
4. Results and Discussion
The experiment’s strain data for a fully clamped CFRP plate (with 21,000 times amplification using an op-amp circuit and a high-speed oscilloscope) at a sampling frequency of 100 MHz after signal processing showed a strain-wave frequency of 205 Hz. At the time of impact, the highest value of strain recorded was 2.5 microstrain, but was due to the ball’s momentum and was not representative of the natural response of the CFRP plate. After the ball was removed, the plate vibrated naturally, and a value of 0.5 microstrain was recorded (Figure 7). This value was used to compute the thermoelastic effect while solving the coupled wave and heat equation by the FDM method in MATLAB®. The strain waves experienced significant damping, and the amplitude dropped to 0.15 in 0.012 s. The dynamic strain reflected the behavior of the CFRP under drop impact for in-plane measurement.
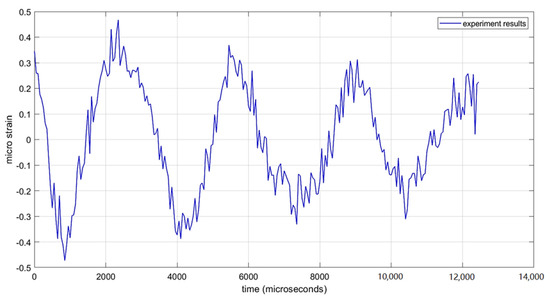
Figure 7.
Experimental strain vs. time data plotted in MATLAB® (natural response after the ball is removed).
4.1. Thermographic Experimental Results
When the steel ball hit the CFRP plate in DWIT, the kinetic energy of the ball was converted into frictional energy that caused localized heating of the specimen at the point of impact. The heat generated due to friction was recorded with an IR thermal camera. Upon impact, some of the energy was also consumed in generating sinusoidal vibrations in the plate, which was being recorded with the help of a rosette strain gauge attached at the center on the backside of the plate. The strain gauge data allowed the interpretation of the thermoelastic effect in the CFRP when it was subjected to impacts.
During the impact event, the infrared camera viewed the CFRP plate from the top, and recorded the thermal signatures that resulted from both the thermoelastic and heat-diffusion phenomenon. The recorded sequences of images were post-processed using FLIR Research IR software. As a primary step, a sequence of ΔT images was created by subtracting the temperature from the ambient temperature recorded before the impact for every image of the sequence recorded during the impact event. More specifically, ΔT was obtained from the relationship given in Equation (21):
where and t is the time instant at which each image is recorded starting from impact. Some ∆T images, at different time instants, are shown in Figure 8. The CFRP plate was impacted from t = 0.216 to 0.258 s. Heat was visible (bright region) at the point of impact due to the friction; a maximum temperature increase of 2.6 C was observed. As the ball moved away from the plate, the point of impact (hotspot) is visible on the CFRP plate. This point of impact slowly dissipates the thermal energy due to the thermal gradient between the center point and plate’s edges. The hotspot can be seen disappearing in the frame at t = 0.649 s.
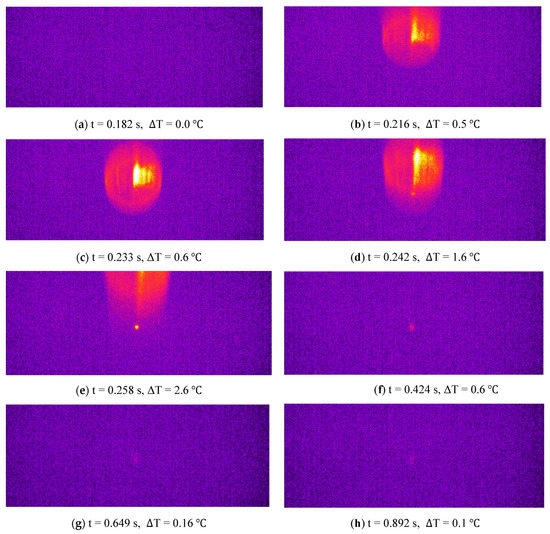
Figure 8.
The ∆T images of the CFRP specimen, impacted with a steel ball.
Figure 9 shows the temperature versus time plot of the DWIT as captured through a thermographic imaging technique. The plot indicates a sharp rise in temperature as the ball strikes the CFRP plate; the temperature increased from 21.9 to 24.5 C. After the impact, the plate began dissipating energy through diffusion and thermoelastic vibrations, and the plate returned to a constant temperature after t = 0.875 s.
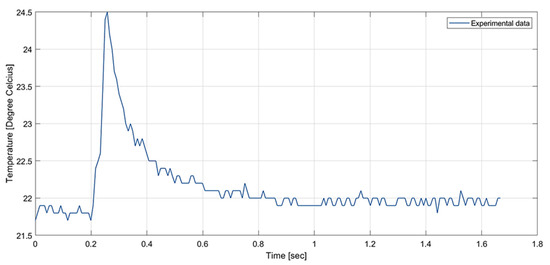
Figure 9.
The temperature vs. time plot of the DWIT captured using thermography.
4.2. Numerical Simulations Results
4.2.1. Wave Equation Results
The discretized wave equation was solved using MATLAB® (time = 3000 timesteps, radius = 87 mm). The initial conditions given in the code were the quadratic profile and a maximum deformation of 0.5 V (recorded by high-frequency oscilloscope from experiments; this value is directly proportional to the strain). The damping term was also added, with a coefficient of damping = 0.006. After plotting the experimental and MATLAB® simulation results together (Figure 10), the wave equation predicted a profile and frequency of 205 Hz, as obtained from the experiments (code is attached in the Appendix).
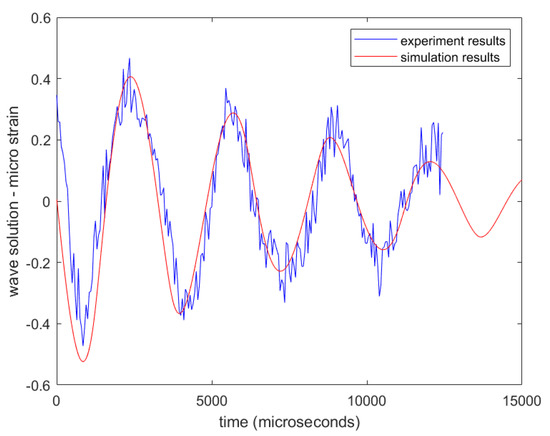
Figure 10.
Strain vs. time plotted plot of experimental and numerical simulations.
4.2.2. Coupled Heat and Wave Equation Results
The discretized coupled-wave and heat equation was solved using the FTCS FDM, a numerical method in a two-dimensional cylindrical coordinate system. The results showed the coupling had no significant impact, as the waves generated due to impact disappeared in 0.015 s. In contrast, heat diffusion occurred for nearly 1.2 s. This proves the heat equation alone is governing the heat-flow process in the CFRP, and the thermoelastic effect is negligible. The coupled wave and heat equations produced the same results as the heat equation alone. The heat equation was solved for a total of 300 timesteps, and one timestep of 25 microseconds was chosen, and space steps of 1 mm and 1° were defined in the code. The IR thermographic frames captured during the experiment at specific time instants were compared to numerical simulations shown as two-dimensional plots (Figure 11). The experimental and simulation frames show heat dissipation from t = 0.258 to 0.892 s. For a better comparison, the experiment and simulation results were plotted on the same grid (Figure 12). The experiment and simulation results were similar, as both showed a similar temperature drop, from 24.5 to 22 C in 1.6 s. Afterward, the CFRP plate was in equilibrium with the surroundings, as the room temperature was 21.9 C.
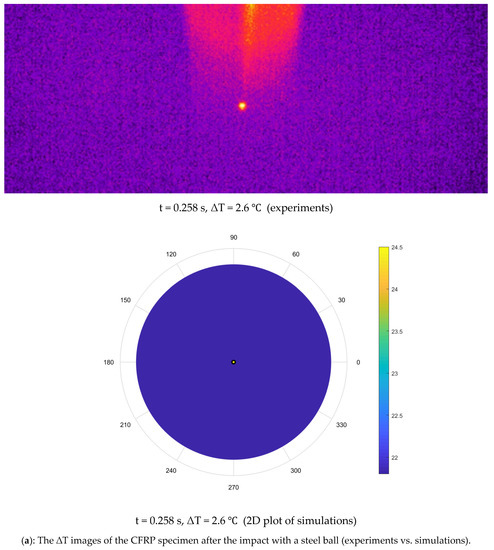
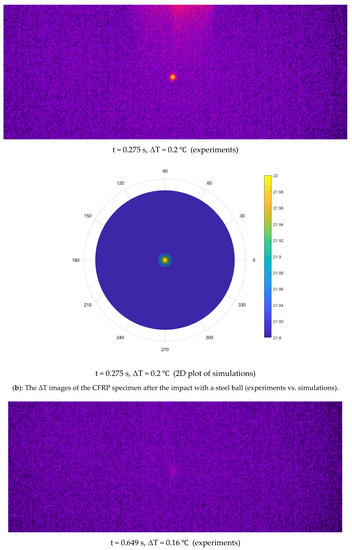
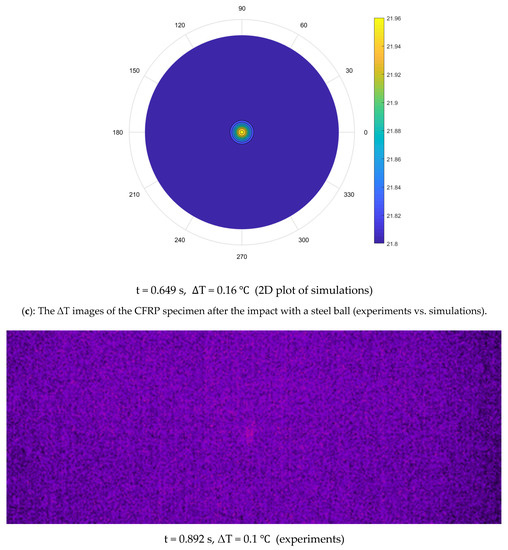
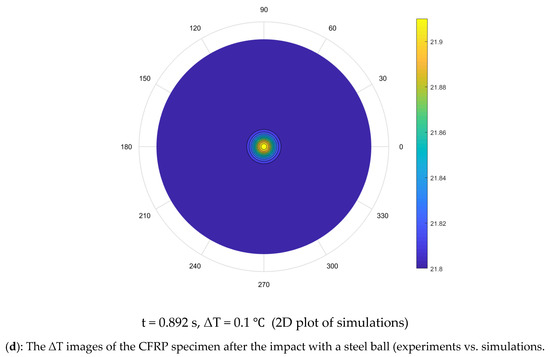
Figure 11.
The ΔT images of the CFRP specimen after the impact with a steel ball (experiments vs. simulations).
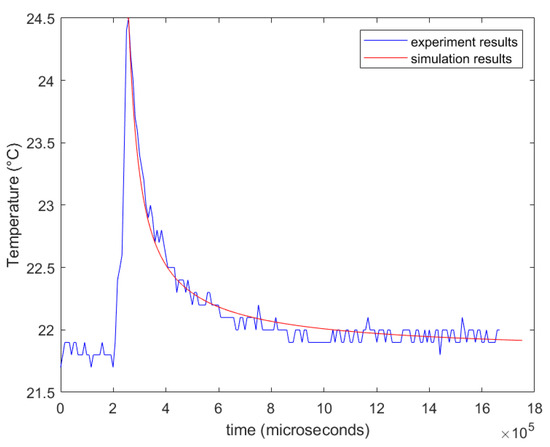
Figure 12.
The temperature drop after impact during the DWIT (experiments vs. numerical simulations).
4.3. Summary
The DWIT and nondestructive thermographic study results illustrate the convenience of using IR thermography to monitor impact tests. Useful information about a material’s behavior can be derived quickly, at almost the same time as the test, without the cumbersome need for post-impact processing.
The temperature versus time images and plots obtained in our study showed that heat is generated in the CFRP upon impact, and then dissipates over time. The coupled wave and heat equation was solved using a numerical method to understand the mechanism for heat generation. The results showed that the thermoelastic phenomenon is high-speed, dissipating in approximately 0.015 s, while heat diffusion occurred for nearly 1.2 s. The results for the heat-diffusion equation, which matched the experimental results captured using IR thermography, validated the findings. Our study found that the thermoelasticity (elastic waves) has a negligible effect, and that heat diffusion is responsible for heat dissipation in the CFRP. This indicates that the heat-diffusion equation entirely governed the heat-conduction mechanism of the CFRP upon impact.
Overall, temperature changes in the CFRP plate upon impact began with a rise in temperature due to friction, followed by the appearance of a hotspot and heat flow towards the edges. The flow of heat obeyed the heat-diffusion equation and mathematical model in a two-dimensional cylindrical coordinate system, as the results agreed with the experimental findings.
5. Conclusions
- The thermoelastic phenomenon generated upon impact in a quasi-isotropic CFRP sheet is high-speed and completes in almost 0.015 s.
- Heat diffusion from the hotspot, which developed due to friction between the steel ball and the CFRP surface, occurs for nearly 1.2 s.
- No significant effect of the coupling heat and wave equation was observed, as temperature change due to thermoelasticity (elastic waves) was minimal compared to temperature change due to heat conduction.
- We found that thermoelasticity has a negligible effect, and heat diffusion alone is responsible for the heat dissipation in the CFRP.
Supplementary Materials
The following are available online at https://www.mdpi.com/2076-3417/11/1/207/s1. Video S1: Drop-Weight Impact Testing (DWIT) video. Video S2: IR thermographic recording.
Author Contributions
Conceptualization: Z.A., S.M., H.A.K., S.A., A.S.N., G.H., and M.M.; Methodology: Z.A., S.M., S.A., H.A.K., and M.M.; Data curation: H.A.K., S.A.; Formal analysis: Z.A., A.S.N.; Investigation: Z.A., A.S.N., S.M., and G.H.; Software: Z.A., A.S.N., H.A.K.; Validation: Z.A., A.S.N., H.A.K.; Project administration: S.M., G.H., H.A.K., and M.M.; Resources: H.A.K., S.A.; Funding acquisition: H.A.K.; Supervision: H.A.K., S.M., G.H., and M.M.; Writing—original draft: Z.A.; Writing—review and editing: Z.A., H.A.K., and A.S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request from the authors.
Acknowledgments
Thanks to Young Kwon of the Naval Postgraduate School, Monterey, CA, USA for providing the CFRP test samples. The publication charges for this article were funded by a grant from the publication fund of UiT-The Arctic University of Norway.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mouti, Z.; Westwood, K.; Kayvantash, K.; Njuguna, J. Low Velocity Impact Behavior of Glass Filled Fiber-Reinforced Thermoplastic Engine Components. Materials 2010, 3, 2463–2473. [Google Scholar] [CrossRef]
- Troncossi, M.; Taddia, S.; Rivola, A.; Martini, A. Experimental Characterization of a High-Damping Viscoelastic Material Enclosed in Carbon Fiber Reinforced Polymer Components. Appl. Sci. 2020, 10, 6193. [Google Scholar] [CrossRef]
- Boccardi, S.; Boffa, N.D.; Carlomagno, G.M.; Meola, C.; Ricci, F.; Russo, P.; Simeoli, G. Infrared thermography to impact damaging of composite materials. Health Monit. Struct. Biol. Syst. 2017, 10170, 1017004. [Google Scholar] [CrossRef]
- Ciminello, M.; Boffa, N.D.; Concilio, A.; Galasso, B.; Romano, F.P.; Monaco, E. Damage Detection of CFRP Stiffened Panels by Using Cross-Correlated Spatially Shifted Distributed Strain Sensors. Appl. Sci. 2020, 10, 2662. [Google Scholar] [CrossRef]
- Sellitto, A.; Saputo, S.; Di Caprio, F.; Riccio, A.; Russo, A.; Acanfora, V. Numerical–Experimental Correlation of Impact-Induced Damages in CFRP Laminates. Appl. Sci. 2019, 9, 2372. [Google Scholar] [CrossRef]
- Rashid, T.; Khawaja, H.; Edvardsen, K. Determination of Thermal Properties of Fresh Water and Sea Water Ice using Multiphysics Analysis. Int. J. Multiphys. 2016, 10, 277–290. [Google Scholar] [CrossRef]
- Nondestructive Testing of Composites (Polymer- and Metal-Matrix Composites)[1]. Nondestruct. Eval. Mater. 2018, 21, 631–658. [CrossRef]
- Wang, X.; Liu, L.; Shen, W.; Zhou, H. CFRP Reinforced Foam Concrete Subjected to Dynamic Compression at Medium Strain Rate. Materials 2019, 13, 10. [Google Scholar] [CrossRef]
- Cao, H.; Ma, M.; Jiang, M.; Sun, L.; Zhang, L.; Jia, L.; Tian, A.; Liang, J. Experimental Investigation of Impactor Diameter Effect on Low-Velocity Impact Response of CFRP Laminates in a Drop-Weight Impact Event. Materials 2020, 13, 4131. [Google Scholar] [CrossRef]
- Maier, A.; Schmidt, R.; Oswald-Tranta, B.; Schledjewski, R. Non-Destructive Thermography Analysis of Impact Damage on Large-Scale CFRP Automotive Parts. Materials 2014, 7, 413–429. [Google Scholar] [CrossRef]
- Andleeb, Z.; Malik, S.; Hussain, G.; Khawaja, H.; Roemer, J.; Boiger, G.; Moatamedi, M. Multiphysics Study of Infrared Thermography (IRT) Applications. Int. J. Multiphys. 2020, 14, 249–271. [Google Scholar] [CrossRef]
- Warnet, L.L.; Reed, P.E. Falling Weight Impact Testing Principles; Springer: Dordrecht, The Netherlands, 1999; pp. 66–70. [Google Scholar]
- Stanley, P.; Chan, W.K. Quantitative stress analysis by means of the thermoelastic effect. J. Strain Anal. Eng. Des. 1985, 20, 129–137. [Google Scholar] [CrossRef]
- Melvin, A.; Lucia, A.; Solomos, G. The thermal response to deformation to fracture of a carbon/epoxy composite laminate. Compos. Sci. Technol. 1993, 46, 345–351. [Google Scholar] [CrossRef]
- Vaidya, R.U.; Chawla, K. Thermal expansion of metal-matrix composites. Compos. Sci. Technol. 1994, 50, 13–22. [Google Scholar] [CrossRef]
- Nowacki, W. Dynamic problems of diffusion in solids. Eng. Fract. Mech. 1976, 8, 261–266. [Google Scholar] [CrossRef]
- Olesiak, Z.; Pyryev, Y. A coupled quasi-stationary problem of thermodiffusion for an elastic cylinder. Int. J. Eng. Sci. 1995, 33, 773–780. [Google Scholar] [CrossRef]
- Sherief, H.H.; Anwar, M.N. State-space approach to two-dimensional generalized thermoelasticity problems. J. Therm. Stress. 1994, 17, 567–590. [Google Scholar] [CrossRef]
- Sherief, H.H.; Anwar, M.N. Problem in Generalized Thermoelasticity. J. Therm. Stress. 1986, 9, 165–181. [Google Scholar] [CrossRef]
- Sherief, H.H.; Ezzat, M.A. Solution of the generalized problem of thermoelasticity in the form of series of functions. J. Therm. Stress. 1994, 17, 75–95. [Google Scholar] [CrossRef]
- Sherief, H.H. Fundamental solution of the generalized thermoelastic problem for short times. J. Therm. Stress. 1986, 9, 151–164. [Google Scholar] [CrossRef]
- Bayandor, J.; Thomson, R.S.; Scott, M.L.; Nguyen, M.Q.; Elder, D.J. Investigation of impact and damage tolerance in advanced aerospace composite structures. Int. J. Crashworthiness 2003, 8, 297–306. [Google Scholar] [CrossRef]
- Hampson, P.R.; Moatamedi, M. A review of composite structures subjected to dynamic loading. Int. J. Crashworthiness 2007, 12, 411–428. [Google Scholar] [CrossRef]
- Andleeb, Z.; Strand, C.; Malik, S.; Hussain, G.; Khawaja, H.; Boiger, G.; Moatamedi, M. Multiphysics Analysis of CFRP Charpy Tests by varying Temperatures. Int. J. Multiphys. 2020, 14, 143–160. [Google Scholar] [CrossRef]
- Khawaja, H.A.; Moatamedi, M.; Andleeb, Z.; Strand, C.; Chen, P.; Guo, B. Multiphysics Impact Analysis of Carbon Fiber Reinforced Polymer (CFRP) Shell. Explos. Shock Waves High Strain Rate Phenom. 2019, 13, 115–120. [Google Scholar] [CrossRef]
- Solid Carbon Fiber Sheets & Plates (DragonPlate). Available online: https://dragonplate.com/solid-carbon-fiber-sheets-plates (accessed on 5 October 2020).
- Quasi-Isotropic Carbon Fiber Uni Sheet ~2 mm × 6″ × 6″, DragonPlate. Available online: https://dragonplate.com/quasi-isotropic-carbon-fiber-uni-sheet-2mm-x-6-x-6 (accessed on 15 October 2020).
- Khawaja, H.A.; Bertelsen, T.A.; Andreassen, R.; Moatamedi, M. Study of CRFP Shell Structures under Dynamic Loading in Shock Tube Setup. J. Struct. 2014, 2014, 1–6. [Google Scholar] [CrossRef]
- Stange, E.; Andleeb, Z.; Khawaja, H.A. Qualitative visualization of the development of stresses through infrared thermography. Vestnik MGTU 2019, 22, 503–507. [Google Scholar] [CrossRef]
- Stange, E.; Andleeb, Z.; Khawaja, H.A.; Moatamedi, M. Multiphysics Study of Tensile Testing using Infrared thermography. Int. J. Multiphys. 2019, 13, 191–202. [Google Scholar] [CrossRef]
- FLIR T1030sc FLIR Systems. Available online: https://www.flir.asia/support/products/t1030sc/#Overview (accessed on 5 October 2020).
- ResearchIR Measurement, Recording, and Analysis Software FLIR Systems. Available online: https://www.flir.asia/products/researchir/ (accessed on 5 October 2020).
- Zhou, F.; Zhang, J.; Song, S.; Yang, D.; Wang, C. Effect of Temperature on Material Properties of Carbon Fiber Reinforced Polymer (CFRP) Tendons: Experiments and Model Assessment. Materials 2019, 12, 1025. [Google Scholar] [CrossRef]
- Münch, A. Optimal design of the support of the control for the 2-D wave equation: A numerical method. Int. J. Numer. Anal. Model. 2008, 5, 331–351. [Google Scholar]
- Zuazua, E. Boundary observability for the finite-difference space semi-discretizations of the 2-d wave equation in the square. J. Math. Pures Appl. 1999, 78, 523–563. [Google Scholar] [CrossRef]
- Liu, J. Numerical solution of forward and backward problem for 2-D heat conduction equation. J. Comput. Appl. Math. 2002, 145, 459–482. [Google Scholar] [CrossRef]
- Widder, D.V. The Heat Equation; Academic Press Institute: London, UK, 1975. [Google Scholar]
- Dawson, C.N.; Du, Q.; Dupont, T.F. A finite difference domain decomposition algorithm for numerical solution of the heat equation. Math. Comput. 1991, 57, 63. [Google Scholar] [CrossRef]
- Moatamedi, M.; Khawaja, H. Finite Element Analysis; CRC Press (Taylor & Francis): Boca Raton, FL, USA, 2018. [Google Scholar]
- Khawaja, H. Application of a 2-D approximation technique for solving stress analyses problem in FEM. Int. J. Multiphys. 2015, 9, 317–324. [Google Scholar] [CrossRef]
- Khawaja, H.A. Applicability extent of 2-D heat equation for numerical analysis of a multiphysics problem. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2017; Volume 1798, p. 20075. [Google Scholar] [CrossRef]
- Kashtalyan, M. Principles of Composite Material Mechanics; Taylor & Francis: Abingdon, UK, 2012. [Google Scholar]
- Joven, R.; Das, R.; Ahmed, A.; Roozbehjavan, P.; Minaie, B. Thermal properties of carbon fiber-epoxy composites with different fabric weaves. In Proceedings of the 44th ISTC International SAMPE Technical Conference, Charleston, SC, USA, 22–25 October 2012. [Google Scholar]
- Martins, M.S.S.; Gomes, R.; Pina, L.; Pereira, C.; Reichmann, O.; Teti, D.; Correia, N.; Rocha, N. Highly Conductive Carbon Fiber-Reinforced Polymer Composite Electronic Box: Out-of-Autoclave Manufacturing for Space Applications. Fibers 2018, 6, 92. [Google Scholar] [CrossRef]
- Zhang, X.; Zuazua, E. Control, observation and polynomial decay for a coupled heat-wave system. Comptes Rendus Math. 2003, 336, 823–828. [Google Scholar] [CrossRef]
- Batty, C.; Paunonen, L.; Seifert, D. Optimal energy decay in a one-dimensional coupled wave–heat system. J. Evol. Equ. 2016, 16, 649–664. [Google Scholar] [CrossRef]
- Zhang, X.; Zuazua, E. Long-Time Behavior of a Coupled Heat-Wave System Arising in Fluid-Structure Interaction. Arch. Ration. Mech. Anal. 2007, 184, 49–120. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).