2. Extra High-Voltage Double-Circuit Electric Power Transmission Line
As the strongest magnetic field in the electrical power system can be generated by the double-circuit 400 kV power transmission line, it is necessary to determine how the magnetic field is distributed in the surroundings of this overhead power transmission line.
This paper determines a three-bundled, double-circuit 400 kV AC power transmission line.
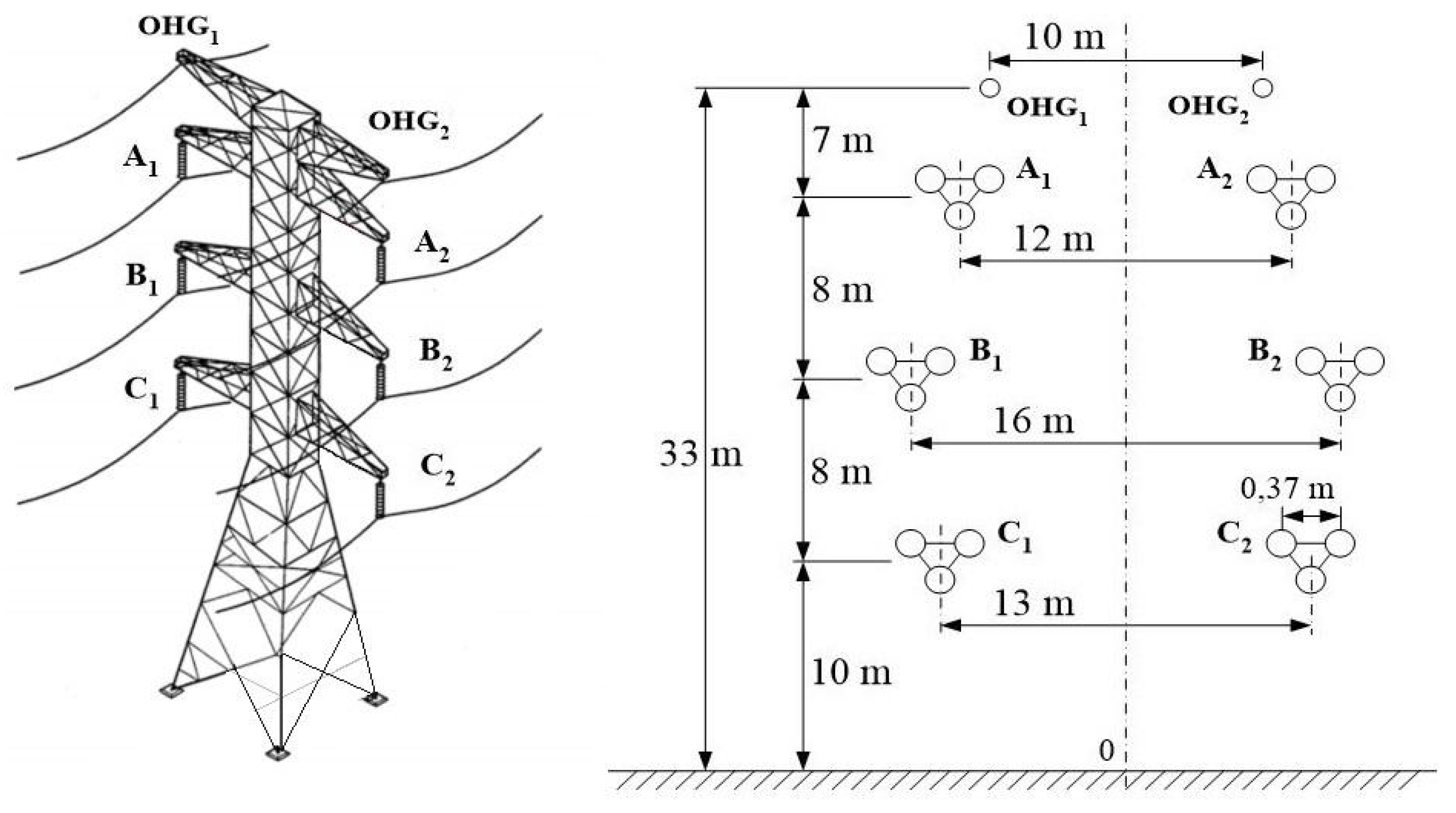
Figure 1 shows a power transmission line of the low-reactance orientation type. The height of conductors shown in the figure is the maximum sag position. The lowest conductors are C
and C
at the height of 10 m above the ground surface level [
1]. Each phase conductor is 0.04 m in diameter. The overhead ground wire has a diameter of 0.015 m.
The height of the 400 kV transmission line supports is 54 m. In this particular case, the lower-phase wires (C
and C
) (see
Figure 1), including their insulators, should be arranged at a height of at least 26 m to the ground surface. The sag of the transmission line amounts for 16 m. Adjacent support-bars are spaced by 350 to 550 m [
2].
The magnetic field generated by the 400 kV overhead transmission line can be approached as the superposition of the magnetic fields of six long, thin current leads. It is also possible to calculate this magnetic field analytically. As the current leads of the 400 kV overhead transmission line are very long and thin wires, difficult mathematical equations are derived for the purpose of calculating the magnetic field they generate.
Moreover, as regards the effect on humans and the environment, the distribution of these current leads is of utmost importance. However, typical analytical mathematical equations for the calculation of this magnetic field are also missing. Thus, digital modeling should be selected as the main method for the investigation of the magnetic field generated by the 400 kV overhead transmission line [
3,
4,
5,
6]. Besides the multitudes of advantages it possesses, modeling also enables the simple assessment of the change in the magnetic field when varying the structure and dimensions of the installation. It also allows the different irregularities and variations of the surroundings to be taken into account. Analytical mathematical equations for the calculation of the magnetic field generated by the double-circuit 400 kV overhead transmission line were derived with the aim of verifying the results of modeling [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16].
3. Magnetic Field Generated by the Single Thin Current Lead
As the double-circuit 400 kV transmission line is comprised of six long, thin current leads, the magnetic field generated by it can be calculated using the method of superposition. We therefore analyze how the magnetic field generated by a single current lead can be calculated. When the magnetic permeability of all points in the space is the same and equal to the permeability of free space
, the calculation of the magnetic field of the given symmetric current system uses the LaPlace–Poisson equations. When current is passed through the current lead with the element
id
l, the length is
if
r represents a radius-vector pointing from the current element
id
l to the point of observation, and the electrical current is distributed within the volume of the current lead
Vj, the vectors of the magnetic field strength
H and of the magnetic field density
B at the point of observation M are calculated as follows [
17,
18,
19,
20,
21,
22]:
The magnetic field generated by the current lead can be calculated using a vector potential. When the electric current flows through the lead, making a circuit
, and the element d
l and electric current density
J within the volume of the current lead
Vj are known, the vector potential
A is expressed as follows:
The density of the magnetic field generated by all the current elements
id
l of the current lead is expressed based on the superposition principle by summing up the constituents of the flux generated by individual current elements [
7,
8,
9,
10,
11,
12,
13,
14,
15,
23].
Due to axial symmetry, the magnetic field strength line of a long and thin current lead with an electric current passing through it have a circular shape, with their centers on the geometrical axis of the current lead, and they are located in planes that are perpendicular to this axis. At any point of such a circle, the directions of the magnetic field strength vector H and distance element dl match.
4. Analysis of Magnetic Field from 400 kV AC Power Transmission Line
In this challenging task regarding magnetic fields, the vectors of magnetic flux density
B or magnetic field strength
H are found to be functions of coordinates when the dependency of the current density vector
J on coordinates is known. As the magnetic field strength or magnetic flux density is to be found in areas in which there are no currents, LaPlace’s equation is solved for the scalar magnetic potential. Such a magnetic field will also be of a potential nature [
7,
8,
9,
10,
11,
12,
13,
14,
15,
23].
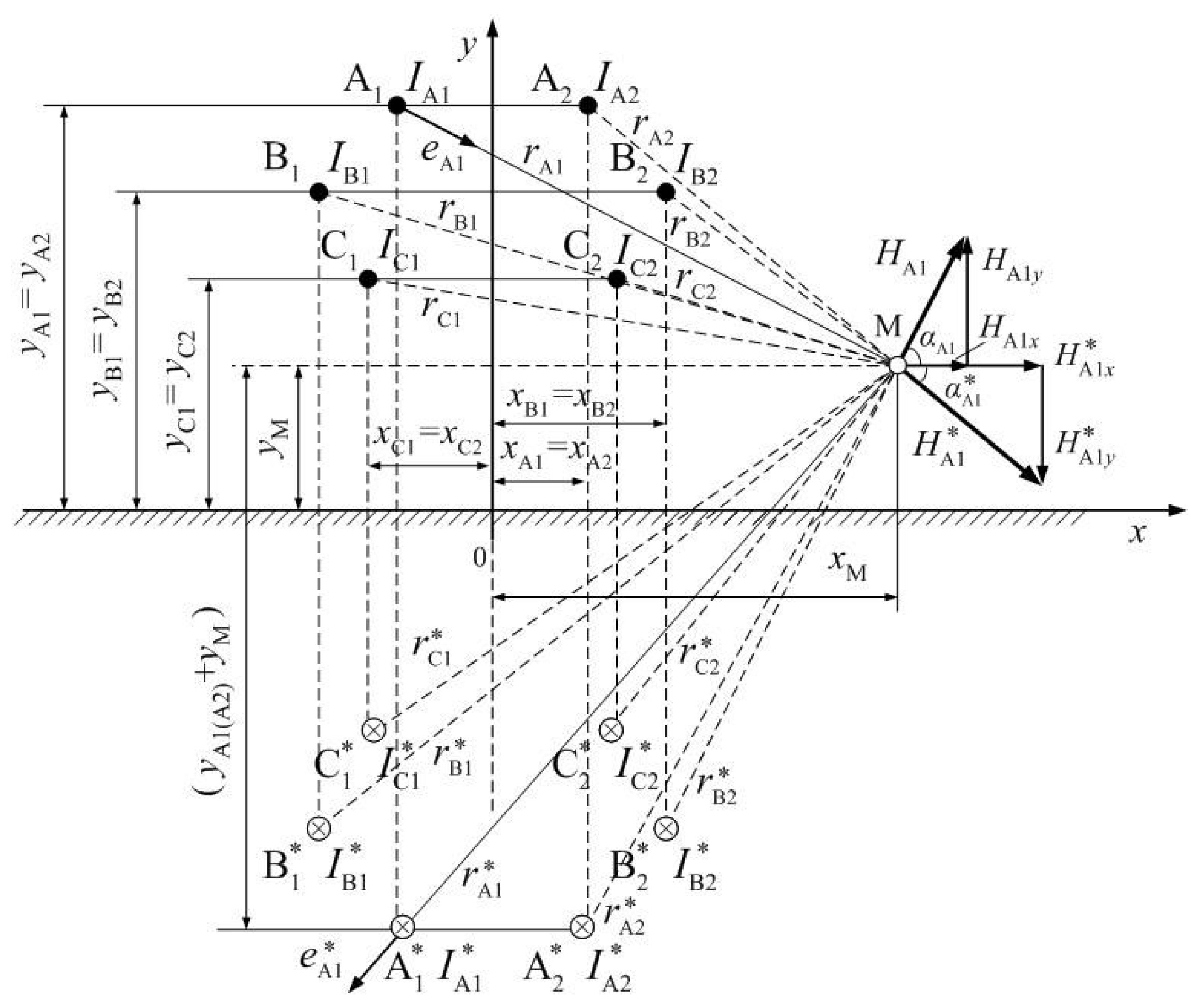
For the purpose of solving this task, the method of reflections is used. The magnetic field of the conductor system in the double-circuit 400 kV overhead transmission line is examined when the conductor system is comprised of long, thin, round cylindrical conductors running in parallel and with flat conductive surfaces with the symmetrical current systems
(
= A
, B
, C
) and
(
= A
, B
, C
) (see
Figure 2). The radii of current leads
≪
are significantly lower than the distance from the ground surface to the current leads. The sag of the double-circuit overhead power line is not taken into consideration.
Following the method of reflections, the magnetic field in which the distribution of currents over the flat surface of the conductor is known is replaced with the magnetic field of currents and that of their reflections-. It is assumed that the distances from the conductors to their respective reflections- are equal; i.e., (i = A, B, C) (n = 1, 2).
With the values of the currents , , , , , being known, the values of reflections of these loads-, -, -, -, -, - are assumed to have the opposite signs.
In order to determine how the values of currents change in a single period of sinusoidal quantity, calculations are made by varying the angle of the phase current at steps of 10; i.e., △wt = 10.
Instantaneous phase current values of a symmetrical current system are interconnected, as follows:
where
is the maximum amplitude value of the phase current, in A.
The 400 kV double-circuit power transmission line has a maximum effective linear current A; thus, the value of the amplitude phase current is as follows: A.
Using Equation (
3), instantaneous current values are calculated at steps of △
wt = 10
.
where
(
i = A, B, C) (
n = 1, 2) shows the phase current flowing through the conductor, which is calculated with Equation (
3), A,
(
i = A, B, C) (
n = 1, 2) are the lengths of distances from phases and their reflections to the reference point M, in m., which are calculated from
Figure 2, and
is the magnetic field strength, in A/m.
The magnetic field strength generated by the double-circuit three-phase 400 kV overhead transmission line in the plane in
Figure 2 is calculated as follows:
where
and
are the constituents of the magnetic field strength vectors with respect to
x and
y axes.
Next, we must examine how the values of
H vary with the measurement point M moving between the phase conductors of the power line. The location of point M with respect to the ground is
. The vectors of the magnetic field strength generated at point M are
and
(
i = A, B, C) (
n = 1, 2). After distributing the directions of
x and
y axes, the following is obtained:
Assuming that constituents of the magnetic field strength vectors at the observation point M are as follows,
the effective value of magnetic field strength at observation point M
is calculated using Equation (
5). One millionth of a Tesla (1 μT) corresponds to 0.8 A/m.
As initial phases of conductors in the double-circuit symmetric 400 kV overhead power line are different by , the total magnetic field will be a rotating one, and for the magnetic field vector, at any observation point M, the time course will define an ellipse in a general way. The normal value of the rotating magnetic field strength is assumed to be the effective value of the sinusoid, the amplitude of which is equal to the semi-major axis of the ellipse orbited by the strength vector at the given point.
To express respective constituents of the magnetic field strength (see
Figure 2), the following markings are introduced: coordinate
of point M,
; height of the conductors above the ground surface,
,
,
. The phase reflections
,
,
,
,
,
are situated at the same distances above the ground surface in the direction of the
axis. The distances from the conductors to the point M in the direction of the
axis are as follows:
is the distance from phase to point M;
is the distance from phase to point M;
is the distance from phase to point M;
is the distance from phase to point M;
is the distance from phase to point M;
is the distance from phase to point M.
The conductors’ phase reflections , , , , , are situated at the same distances in the direction of the axis.
Figure 2 shows that magnetic field strength vector
is distributed into two vectors as follows: vector
, which varies following the law of sines; and vector
, which varies following the law of cosines. The magnetic field strength reflection vector
is distributed analogically. The numerical values of the constituents
,
,
, and
(
i = A, B, C) (
n = 1, 2) are found as follows:
The values of the angles
and
(
i = A, B, C) (
n = 1, 2) are used to consider the positions of the conductor phases and their reflections of the double-circuit 400 kV overhead power line as well as the position of the reference point M with respect to the ground surface and their distances. The values of these trigonometric functions are found from
Figure 2. In the general case, these angles
,
are calculated in the following sequence:
1. The angle or is deducted from the conductor phase under investigation or its reflection’s magnetic field vector and measurement point M’s position with respect to the ground surface.
2. The arctan function of the angle
or
(
i = A, B, C) (
n = 1, 2) is calculated as follows:
3. The functions cos and sin of angles or are calculated with the sign “±” depending on the trigonometric function cos and sin quarter in which the phase load electric field vector is calculated.
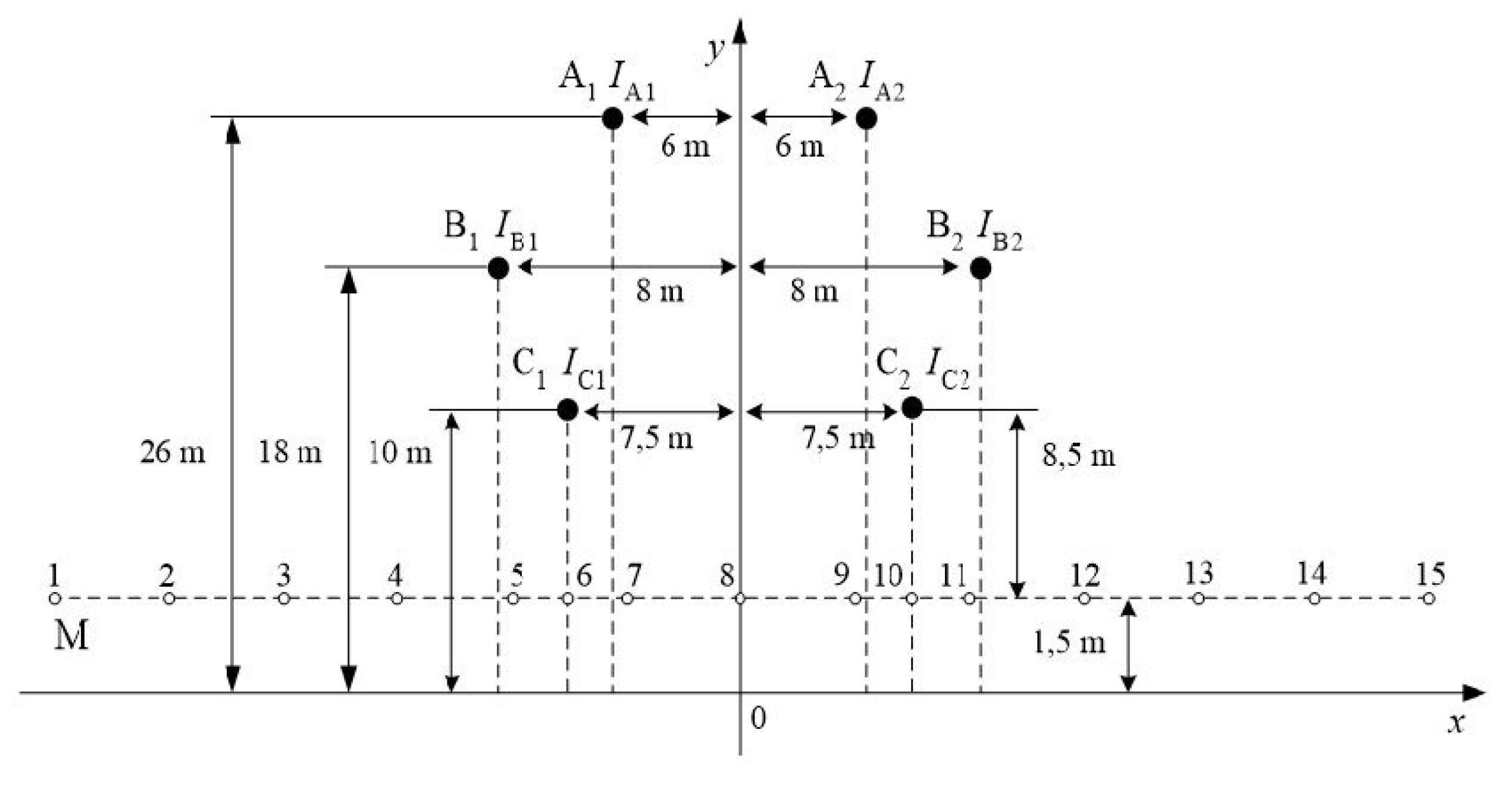
For the purpose of the mathematical calculation of the magnetic field strength, a 400 kV double-circuit three-phase AC conductor system was selected, which was laid out vertically starting from the ground surface as follows: 1. is at a height of 10 m; 2. and are at a height of 18 m; 3. and are at a height of 26 m.
The following are the horizontal distances between the different link phases of the conductor: 1. 12 m between and ; 2. 16 m between and ; 3. 13 m between and .
Measurement point M is located 1.5 m vertically from the ground surface. In order for the obtained results of the mathematical calculations to be as precise as possible, 15 total positions of the measurement point M were selected, which were spaced by 5 m and located at 1.5 m vertically from the ground surface (see
Figure 3).
In this paper, extra high-voltage, double-circuit power transmission lines are studied; all six groups with six types of conductor transmission line transpositions are included in the case of long-distance distribution. For 400 kV AC lines, there are six types of first group transposition. There are 36 different transposition layouts possible of the phases in 400 kV double-circuit overhead power lines. For these six different groups of phase conductor transpositions, changes in their transposition sequences influence the results of mathematical calculations [
1,
24]. The six groups of transposition are as follows (see
Figure 1):
Group 1 (, , );
Group 2 (, , );
Group 3 (, , );
Group 4 (, , );
Group 5 (, , );
Group 6 (, , ).
5. Discussion
The results obtained from mathematical calculations of the magnetic field in the selected locations of point M
i are presented mathematically in
Table 1. The mathematical calculation results in
Table 1 suggest that the magnetic field strength achieves its maximum values at points M
6 and M
11, and these values are grouped into six categories with six types of conductor transposition.
These points of observation are situated near phases B
1 and B
2 and between phases C
1 and C
2 of the double-circuit 400 kV overhead power line conductor system. The observation point M
8 is at the very centre of the 400 kV overhead power line (see
Figure 3). At this particular point, the magnetic field strength values are lower.
These points of observation are situated near phases B
1 and B
2 and between phases C
1 and C
2 of the double-circuit 400 kV overhead power line conductor system. The observation point M
8 is at the very centre of the 400 kV overhead power line (see
Figure 3). At this particular point, the magnetic field strength values are also lower.
The obtained analytical results were also verified through a simulation using the software package COMSOL Multiphysics 3.5. The model simulation additionally assessed the marginal and ambient conditions [
6]. Results obtained from a finite element method (FEM) simulation of the magnetic field in the selected locations of point M
i are presented mathematically in
Table 2. The FEM simulation results in
Table 2 suggest that the magnetic field strength reaches its maximum values at points M
6 and M
11, and these values are also grouped into six categories with six types of conductor transposition.
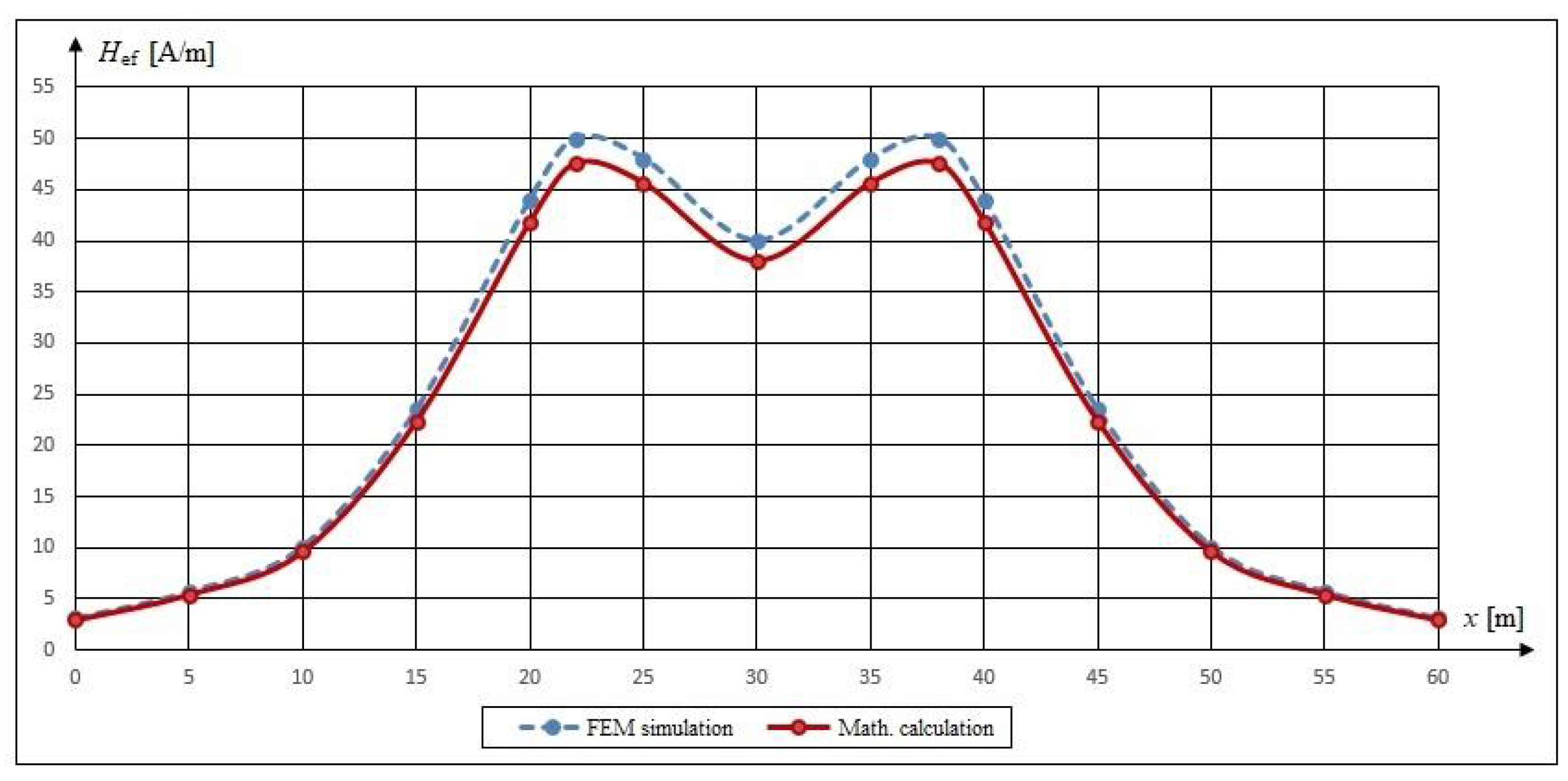
The results of the simulation (see the upper curve of
Figure 4) were found to be close to the analytical results; consequently, the proposed methodology can be used to investigate the relevant magnetic field. The assessment of our findings and the obtained results lead us to the following suggestions: The mean error between the analytical findings and simulation results is below 4%. The methodology described here allows the calculation of the magnetic field strength at any point under the three-phase double-circle power transmission line.
The graph in
Figure 4 shows that as the measurement point M
i gets farther from the outside phases of the double-circuit 400 kV overhead power line conductor system, the magnetic field strength decreases proportionally. However, at the distance of 12 m from phases B
1 and B
2, the magnetic field strength still exceeds 16 A/m (i.e.,
B is more than 20 μT).
The assessment of the calculation results revealed that values of the magnetic field strength exceed the numerical values established in the EU Hygiene Standard HN 104:2011. The regulation on the hygienic norms of the European Union and of the Republic of Lithuania states that the numerical values of the electromagnetic field parameters of electric power transmission lines in residential and public buildings—as well as in residential areas—should never exceed the permissible values provided for in EU HN 104:2011.
When locations are identified in which the magnetic field strength values are exceeded, the regulation on the hygienic norms of the European Union and of the Republic of Lithuania obliges operators of the power transmission system, who are responsible for the power transmission lines in operation, to ensure that the permissible values of the electromagnetic field parameters provided for in EU Hygiene Standard HN 104:2011 are adhered to. If the electromagnetic field parameters are found to exceed permissible values, it is compulsory to undertake appropriate actions and to reduce the values of the electromagnetic field parameters to the levels allowed.
With the aim of reducing the potential hazards to human health and to ensure safe living conditions in residential areas, it is suggested that experimental measurements of electromagnetic fields should be undertaken in locations or areas with the maximum exposure to electrical or magnetic fields. To mitigate the values of such magnetic fields, it is also recommended that the height of support bars should be increased or that any individual or commercial activities in their surroundings should be restricted.