Harmony Search Algorithm Based Management of Distributed Energy Resources and Storage Systems in Microgrids
Abstract
1. Introduction
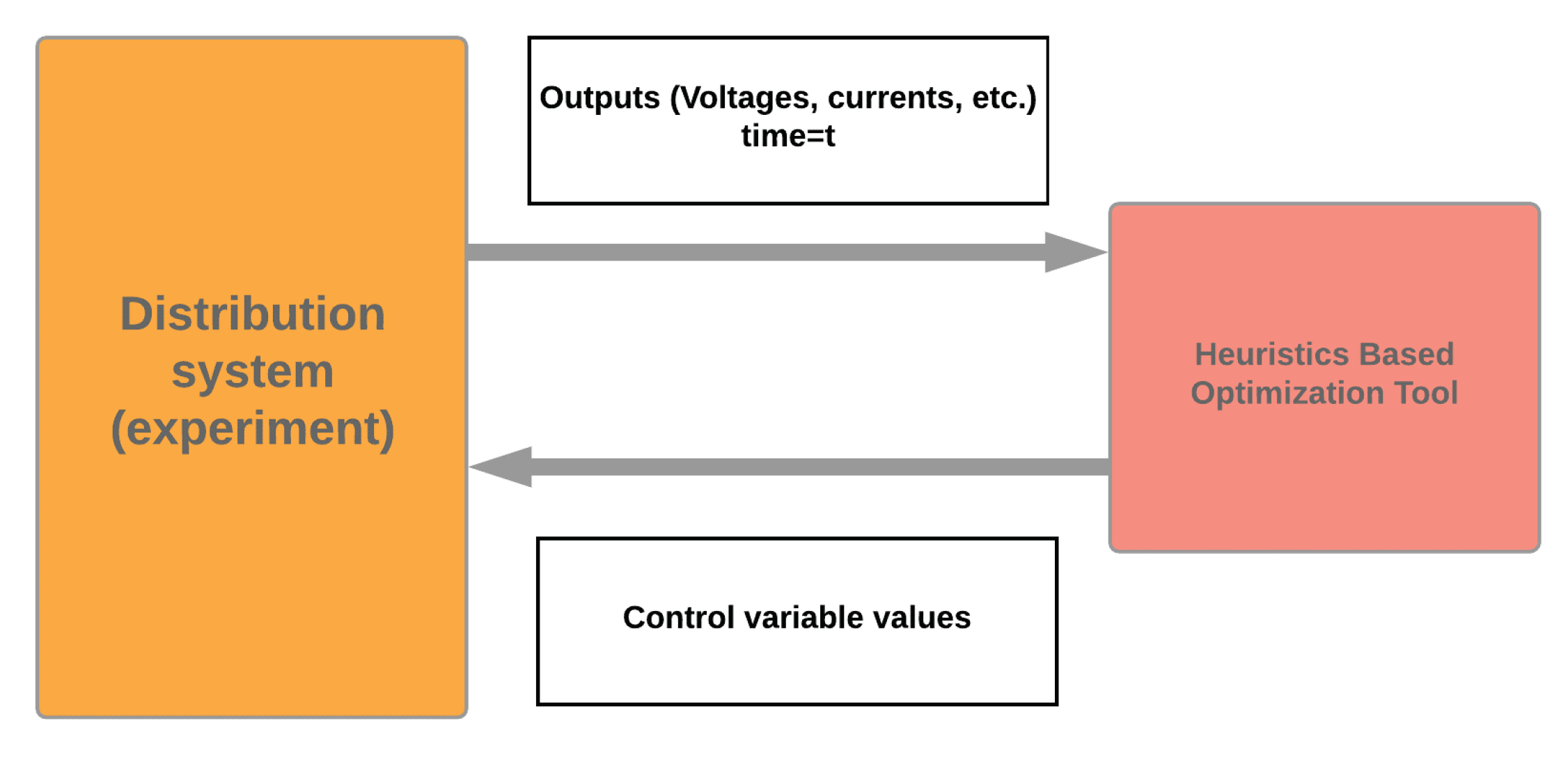
2. Model and Simulation Structure
2.1. Simulation Model
2.2. Optimization Model
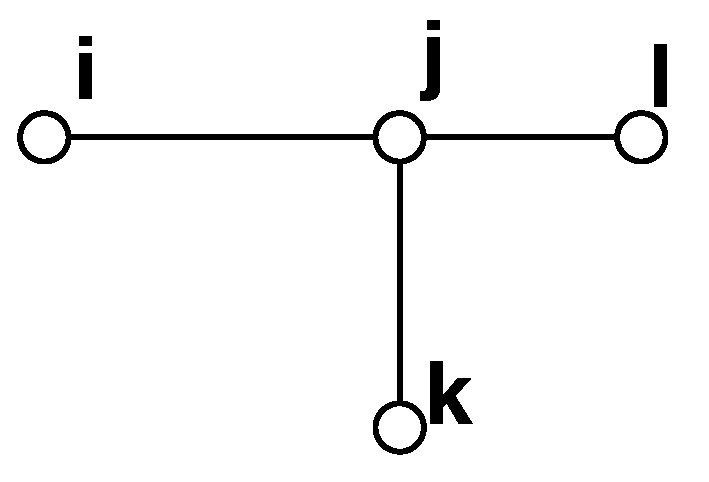
2.3. Ladder Iterative Technique
- The voltage magnitudes at the end nodes are assumed to be same as the first node (see nodes k and l in Figure 2).
- Then the load currents at the end node(s) are calculated by using .
- The current flows on the lines are calculated (, ). Normally, these values are equal to the negative values of the currents on end nodes. However, for the junction nodes (see node j in Figure 2) this will be different: i.e., will be the arithmetic sum of , and the node current using Kirchoff Current Law.
- By using Kirchoff’s Voltage Law, the voltage on the next nodes are calculated (node i).
- This computation procedure continues until the initial node. Then the actual voltage magnitude of the initial node is compared to that of the calculated one. If this value is smaller than a predefined tolerance, the algorithm stops otherwise the algorithm continues.
- Perform the backward sweep calculations to compute the voltage magnitudes on the end nodes.
3. Implementation of the Harmony Search Based Optimization Algorithm
- The first step includes selection of the parameters of the harmony search algorithm: harmony memory size (HMS), harmony memory consideration rate (HMCR), pitch adjusting rate (PAR). Note that, HMS represents the solution candidates in each iteration. HMCR and PAR are equivalent to crossover rate and mutation rate in genetic algorithms.
- Randomly create initial solution candidates in the allowed ranges of the variables (active and reactive power limits). A sample HM structure is shown as given in Equation (2). Note that the HMS is m, and the number of variables to be optimized is n for this specific example.
- Input each row of this matrix to ladder iterative technique based power flow module. Use the voltage magnitude outputs to calculate the objective function values one by one. Save those values.
- Perform improvisation and create a new solution candidate by applying the following procedure for all variables.
- Compare HMCR with a randomly generated number in [0,1] interval.
- -
- If this number is smaller than HMCR, construct a new member of the solution candidate vector by randomly picking an element from the candidate solution matrix. For example, for the first variable, one can randomly select the 5th solution candidate however for the next variable another solution candidate, say the 7th solution candidate may be selected. Moreover, a mutation like operation may be performed. For this aim, another random number in between 0 and 1 is created and compared to the value of PAR. If it is bigger than PAR nothing needs to be done, for the opposite case then the value of the variable is perturbed either in positive or negative direction randomly.
- -
- If this number is not smaller than HMCR, then a random number in the range of the corresponding variable is created. Note that all the variables considered for this specific problem are either the active or reactive power outputs of DERs. These limits are defined according to the condition of the test system.
- Find the numerical value of the objective function of the new solution candidate vector and compare it to the worst one in HM. If it is bigger nothing needs to be done otherwise replace the row related to the worst one with the new solution candidate vector.
- If a predefined maximum number of iterations are run, or other predefined stopping criteria are reached stop, otherwise continue from step 3.
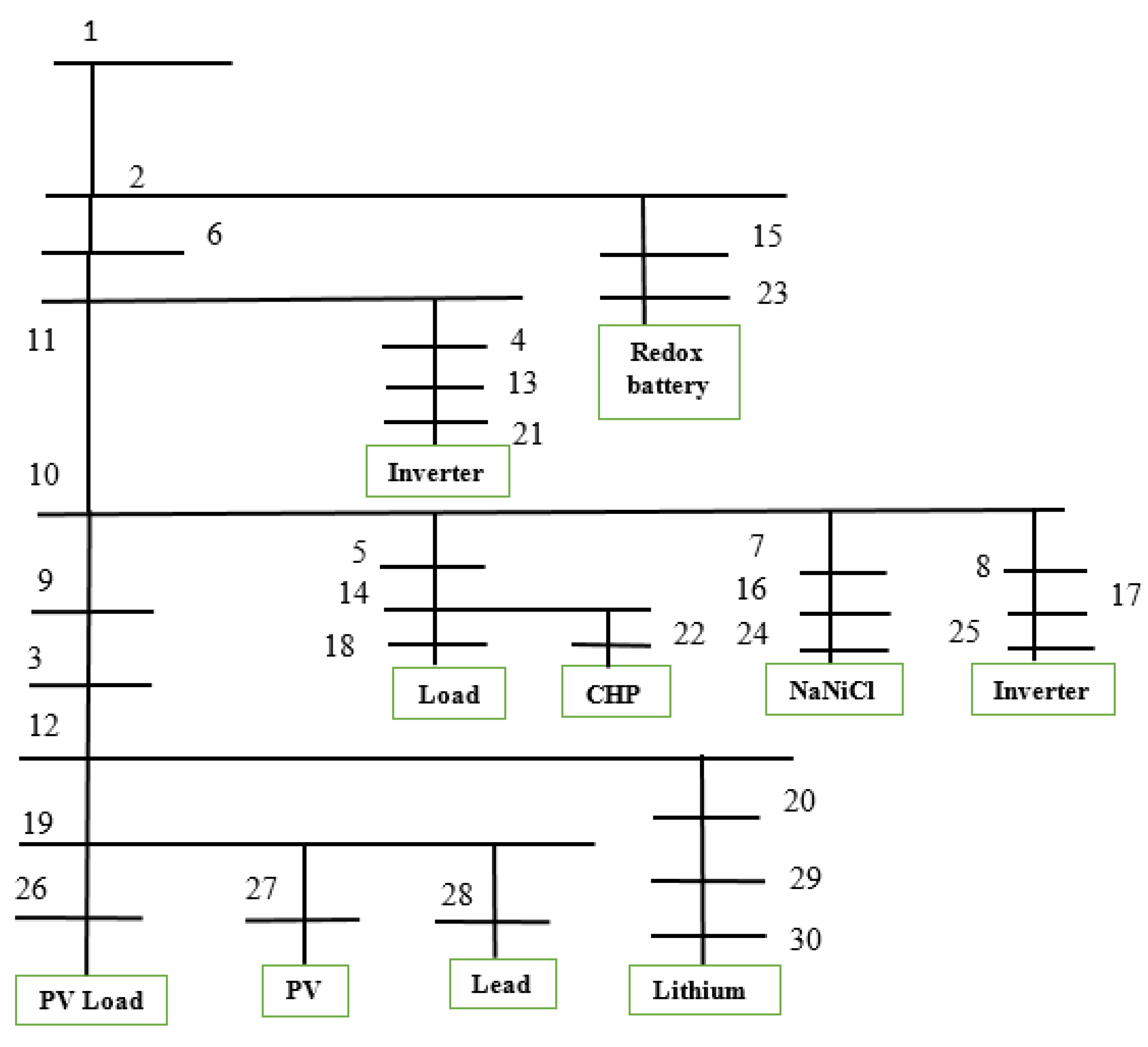
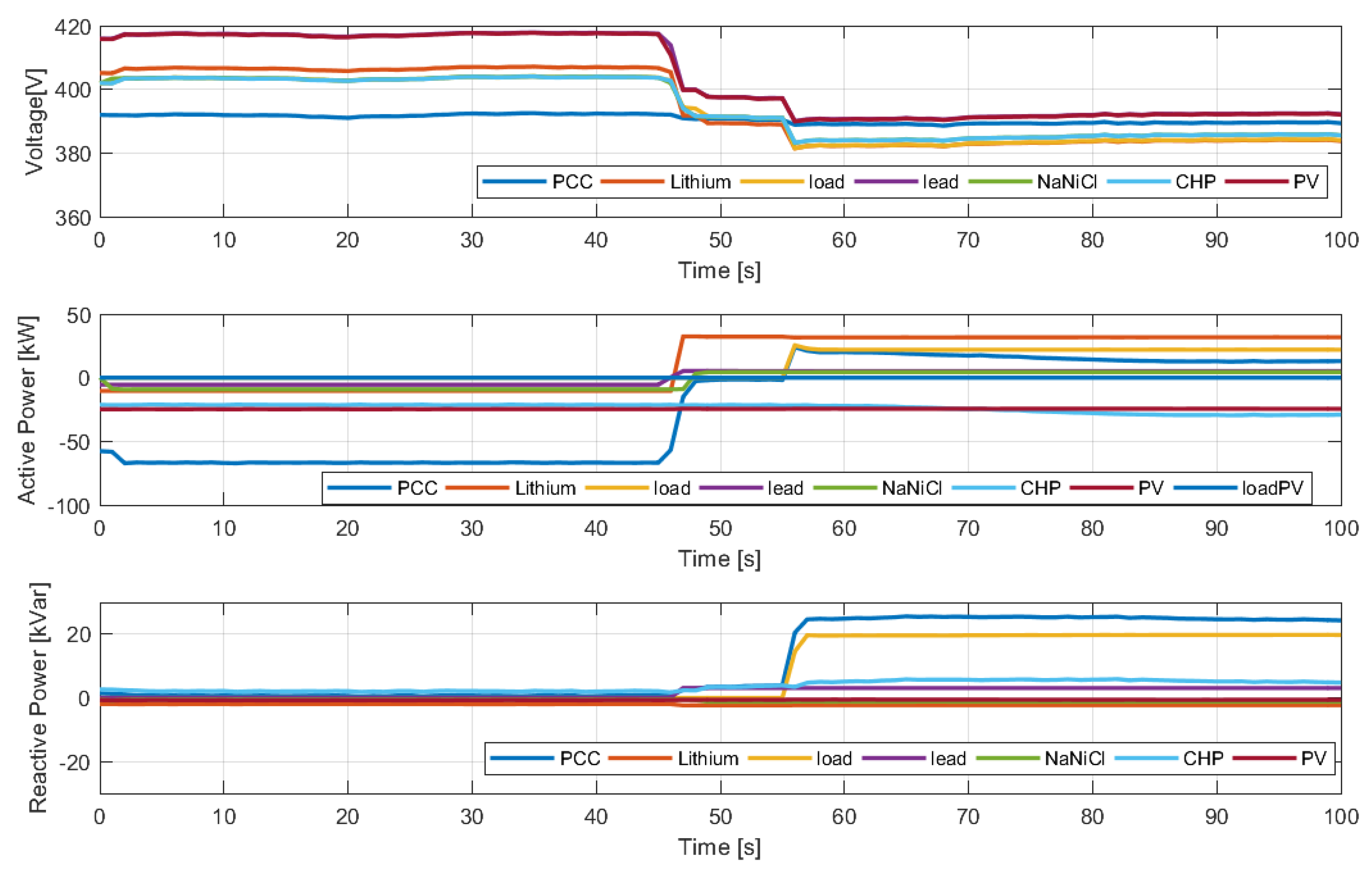
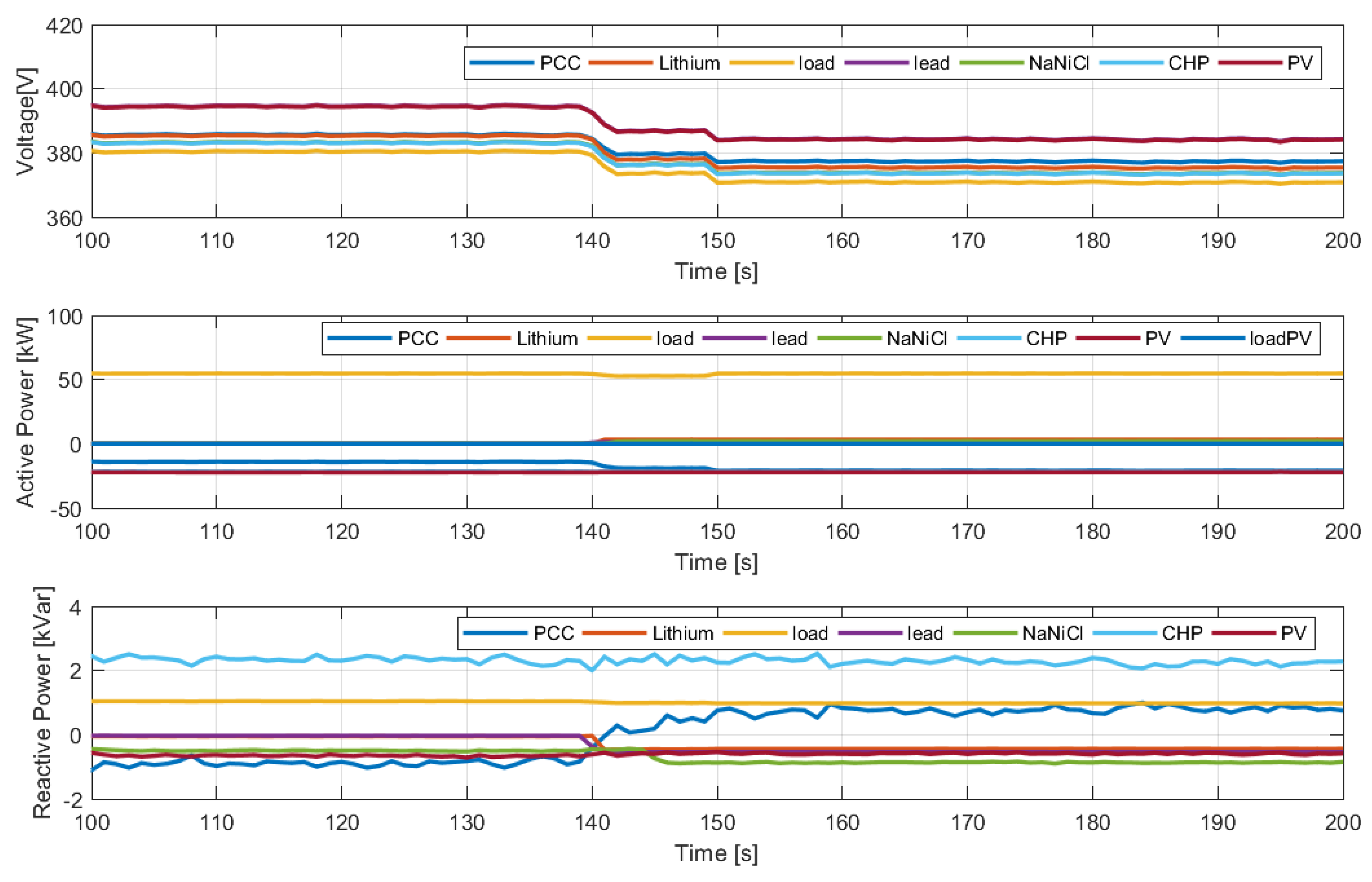
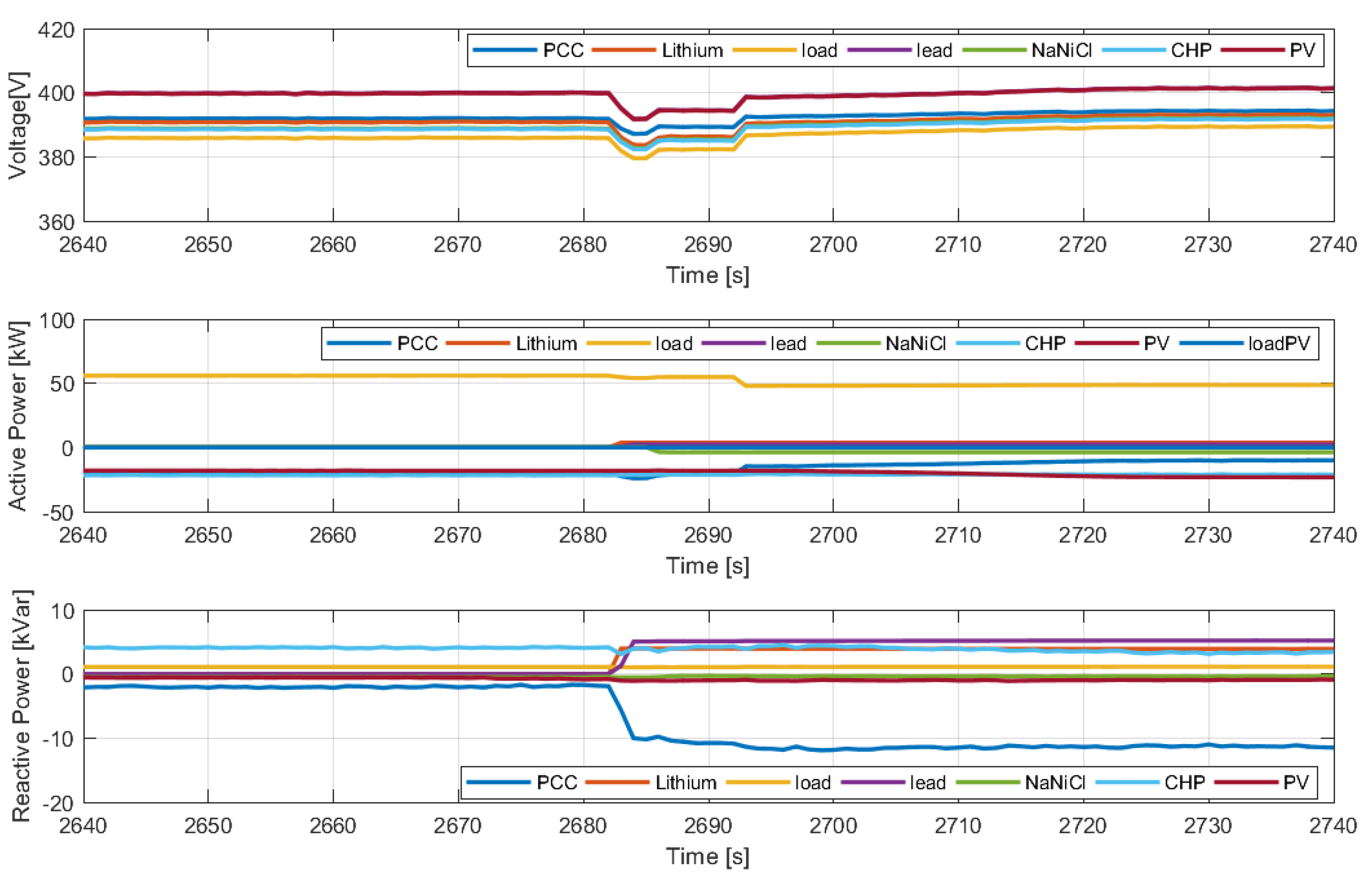
4. Tests and Numerical Results
4.1. Grid Connected Tests
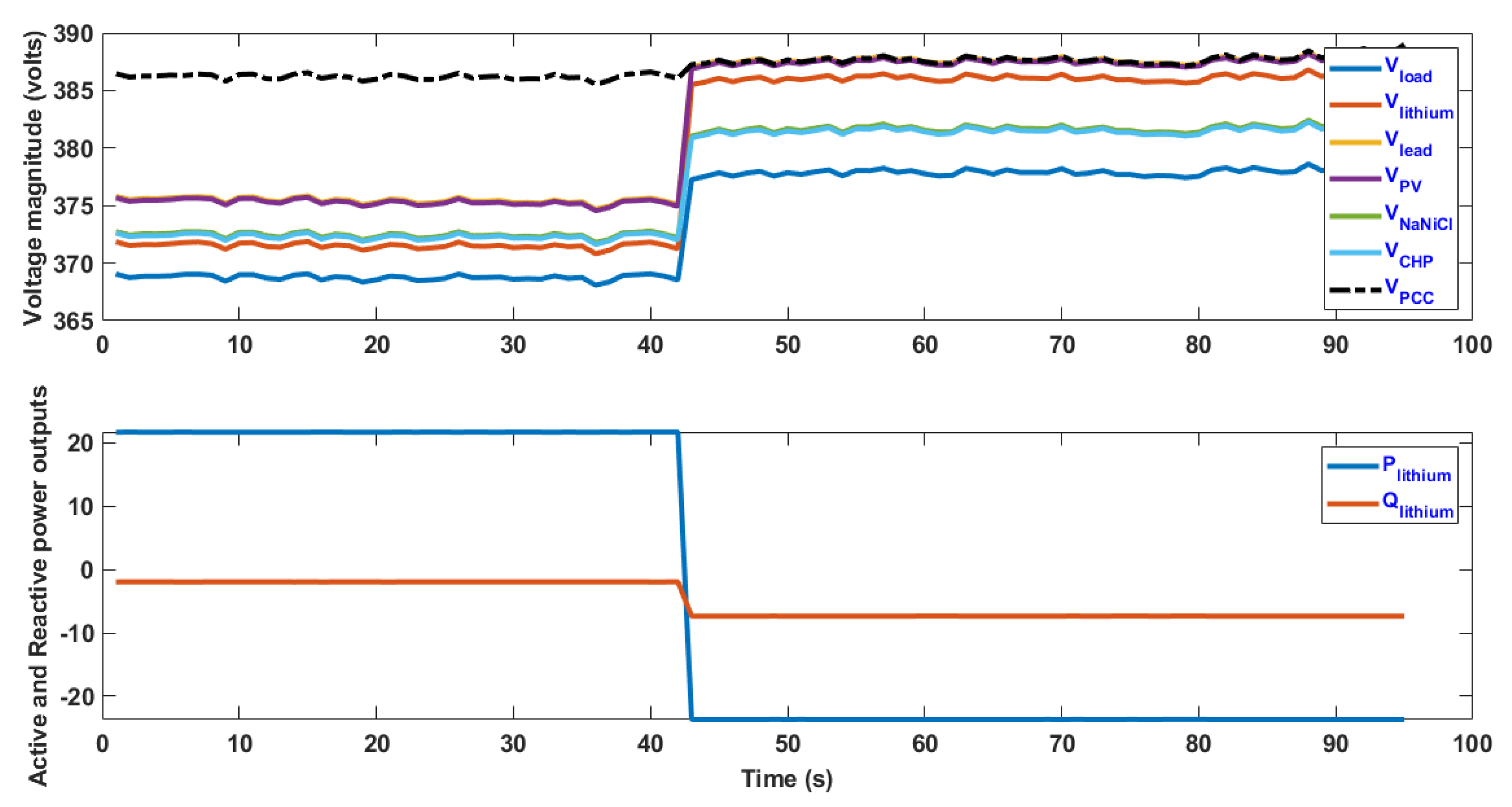
4.2. Islanded Operating Mode Tests
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Line Parameters for grid Connected and Island Operating Mode Configurations
| Node 1 | Node 2 | R () | jX () |
|---|---|---|---|
| 1 | 2 | 0.00702 | 0.00675 |
| 2 | 6 | 0 | 0.00001 |
| 6 | 11 | 0 | 0.00001 |
| 11 | 10 | 0.05157 | 0.02025 |
| 10 | 9 | 0.01910 | 0.00750 |
| 9 | 3 | 0 | 0.00001 |
| 3 | 12 | 0 | 0.00000 |
| 12 | 19 | 0.18112 | 0.02925 |
| 19 | 26 | 0 | 0.00001 |
| 19 | 27 | 0 | 0.00001 |
| 19 | 28 | 0.00907 | 0.00813 |
| 10 | 5 | 0 | 0.00001 |
| 5 | 14 | 0 | 0.00001 |
| 14 | 18 | 0 | 0.00001 |
| 14 | 22 | 0.00955 | 0.00375 |
| 12 | 20 | 0.00819 | 0.00735 |
| 20 | 29 | 0.01814 | 0.01626 |
| 20 | 30 | 0.01814 | 0.01626 |
| 10 | 7 | 0 | 0.00001 |
| 7 | 16 | 0 | 0.00001 |
| 16 | 24 | 0.01021 | 0.00481 |
| 10 | 8 | 0 | 0.00001 |
| 8 | 17 | 0 | 0.00001 |
| 17 | 25 | 0.01177 | 0.00555 |
| 11 | 4 | 0 | 0.00001 |
| 4 | 13 | 0 | 0.00001 |
| 13 | 21 | 0.01242 | 0.00487 |
| 6 | 15 | 0 | 0.00001 |
| 15 | 23 | 0.00785 | 0.00370 |
| Node 1 | Node 2 | R () | jX () |
|---|---|---|---|
| 1 | 2 | 0.01242 | 0.00487 |
| 2 | 3 | 0.00785 | 0.00370 |
| 2 | 4 | 0.05157 | 0.02025 |
| 4 | 5 | 0.01625 | 0.00455 |
| 4 | 6 | 0.00955 | 0.00375 |
| 4 | 7 | 0.01021 | 0.00481 |
| 4 | 8 | 0.01910 | 0.00750 |
| 8 | 9 | 0.18112 | 0.02925 |
| 9 | 10 | 0 | 0.00001 |
| 9 | 11 | 0 | 0.00001 |
| 9 | 12 | 0.00907 | 0.00813 |
| 8 | 13 | 0.00819 | 0.00735 |
| 13 | 14 | 0.01814 | 0.01626 |
References
- Farhangi, H. The path of the smart grid. IEEE Power Energy Mag. 2010, 8, 18–28. [Google Scholar] [CrossRef]
- Sulzberger, C. Pearl Street in Miniature: Models of the Electric Generating Station [History]. IEEE Power Energy Mag. 2013, 11, 76–85. [Google Scholar] [CrossRef]
- IEEE Guide for Identifying and Improving Voltage Quality in Power Systems. IEEE Std 1250-2018 (Revision IEEE Std 1250-2011) 2018. [CrossRef]
- Gonen, T. Electric Power Distribution System Engineering; Taylor and Francis: Abingdon, UK, 2008. [Google Scholar]
- Ceylan, O.; Liu, G.; Xu, Y.; Tomsovic, K. Distribution system voltage regulation by distributed energy resources. In Proceedings of the 2014 North American Power Symposium (NAPS), Pullman, WA, USA, 7–9 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Ceylan, O.; Liu, G.; Tomsovic, K. Coordinated distribution network control of tap changer transformers, capacitors and PV inverters. Electr. Eng. 2017, 100, 1133–1146. [Google Scholar] [CrossRef]
- Ceylan, O.; Paudyal, S.; Bhattarai, B.P.; Myers, K.S. Photovoltaic hosting capacity of feeders with reactive power control and tap changers. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Ferreira, P.D.; Carvalho, P.M.; Ferreira, L.A.; Ilic, M.D. Distributed energy resources integration challenges in low-voltage networks: Voltage control limitations and risk of cascading. IEEE Trans. Sustain. Energy 2013, 4, 82–88. [Google Scholar] [CrossRef]
- Carvalho, P.M.; Correia, P.F.; Ferreira, L.A. Distributed reactive power generation control for voltage rise mitigation in distribution networks. IEEE Trans. Power Syst. 2008, 23, 766–772. [Google Scholar] [CrossRef]
- Coster, E.J.; Myrzik, J.M.; Kruimer, B.; Kling, W.L. Integration issues of distributed generation in distribution grids. Proc. IEEE 2011, 99, 28–39. [Google Scholar] [CrossRef]
- Kulmala, A.; Repo, S.; Jarventausta, P. Coordinated voltage control in distribution networks including several distributed energy resources. IEEE Trans. Smart Grid 2014, 5, 2010–2020. [Google Scholar] [CrossRef]
- Yu, L.; Czarkowski, D.; De León, F. Optimal distributed voltage regulation for secondary networks with DGs. IEEE Trans. Smart Grid 2012, 3, 959–967. [Google Scholar] [CrossRef]
- Antoniadou-Plytaria, K.E.; Kouveliotis-Lysikatos, I.N.; Georgilakis, P.S.; Hatziargyriou, N.D. Distributed and Decentralized Voltage Control of Smart Distribution Networks: Models, Methods, and Future Research. IEEE Trans. Smart Grid 2017, 8, 2999–3008. [Google Scholar] [CrossRef]
- Schiffer, J.; Seel, T.; Raisch, J.; Sezi, T. Voltage Stability and Reactive Power Sharing in Inverter-Based Microgrids with Consensus-Based Distributed Voltage Control. IEEE Trans. Control Syst. Technol. 2016, 24, 96–109. [Google Scholar] [CrossRef]
- Calderaro, V.; Conio, G.; Galdi, V.; Massa, G.; Piccolo, A. Optimal decentralized voltage control for distribution systems with inverter-based distributed generators. IEEE Trans. Power Systems 2014, 29, 230–241. [Google Scholar] [CrossRef]
- Paridari, K.; Hamzeh, M.; Emamian, S.; Karimi, H.; Bakhshai, A. A new decentralized voltage control scheme of an autonomous microgrid under unbalanced and nonlinear load conditions. In Proceedings of the IEEE International Conference on Industrial Technology, Cape Town, South Africa, 25–28 February 2013; pp. 1812–1817. [Google Scholar] [CrossRef]
- Vovos, P.N.; Kiprakis, A.E.; Wallace, A.R.; Harrison, G.P. Centralized and distributed voltage control: Impact on distributed generation penetration. IEEE Trans. Power Syst. 2007, 22, 476–483. [Google Scholar] [CrossRef]
- Madureira, A.G.; Pecas Lopes, J.A. Coordinated voltage support in distribution networks with distributed generation and microgrids. IET Renew. Power Gener. 2009, 3, 439–454. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization: Theory and Practice; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, Y.; Guo, Y.; Wang, B.; Wang, H.; Liu, H. A hybrid harmony search algorithm with differential evolution for day-ahead scheduling problem of a microgrid with consideration of power flow constraints. Appl. Energy 2016, 183, 791–804. [Google Scholar] [CrossRef]
- Li, P.; Xu, D.; Zhou, Z.; Lee, W.; Zhao, B. Stochastic Optimal Operation of Microgrid Based on Chaotic Binary Particle Swarm Optimization. IEEE Trans. Smart Grid 2016, 7, 66–73. [Google Scholar] [CrossRef]
- Hemmati, M.; Amjady, N.; Ehsan, M. System modeling and optimization for islanded micro-grid using multi-cross learning-based chaotic differential evolution algorithm. Int. J. Electr. Power Energy Syst. 2014, 56, 349–360. [Google Scholar] [CrossRef]
- Sandroni, C.; Verga, M.; Lazzari, R.; Fantini, M.; Sacchi, M.; Prandoni, V. RSE’s microgrid: A facility for research, development and testing of future distributed generation and microgrid technologies. In Proceedings of the 2016 AEIT International Annual Conference (AEIT), Capri, Italy, 5–7 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- De Brabandere, K.; Bolsens, B.; Van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A Voltage and Frequency Droop Control Method for Parallel Inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]


| −30 kW, 30 kW | −10 kVar, 10kVar | −5 kW, 15 kW | −3 kVar, 3kVar | −10 kW, 10 kW |
| −5 kVar, 5 kVar | 25 kW, 50 kW | −5 kVar, 5 kVar | 0 kW, 90 kW | 0 kVar,60 kVar |
| Load | Lithium | Lead | NaNiCl | CHP | |||||
|---|---|---|---|---|---|---|---|---|---|
| P (kW) | P (kW) | P (kW) | Q (kVar) | P (kW) | Q (kVar) | P (kW) | Q (kVar) | P (kVar) | PF |
| 75 | 0 | 20 | −2 | 0 | 0 | 0 | 0 | 25 | 1 |
| Load | Lithium | Lead | NaNiCl | CHP | |||||
|---|---|---|---|---|---|---|---|---|---|
| P(kW) | P(kW) | P(kW) | Q(kVar) | P(kW) | Q(kVar) | P(kW) | Q(kVar) | P(kVar) | PF |
| 0 | 0 | −10 | −2 | −5 | 0 | 10 | 0 | 25 | 1 |
| Load | Lithium | Lead | NaNiCl | CHP | |||||
|---|---|---|---|---|---|---|---|---|---|
| P (kW) | P (kW) | P (kW) | Q (kVar) | P (kW) | Q (kVar) | P (kW) | Q (kVar) | P (kVar) | PF |
| 60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceylan, O.; Sezgin, M.E.; Göl, M.; Verga, M.; Lazzari, R.; Kwaye, M.P.; Sandroni, C. Harmony Search Algorithm Based Management of Distributed Energy Resources and Storage Systems in Microgrids. Appl. Sci. 2020, 10, 3252. https://doi.org/10.3390/app10093252
Ceylan O, Sezgin ME, Göl M, Verga M, Lazzari R, Kwaye MP, Sandroni C. Harmony Search Algorithm Based Management of Distributed Energy Resources and Storage Systems in Microgrids. Applied Sciences. 2020; 10(9):3252. https://doi.org/10.3390/app10093252
Chicago/Turabian StyleCeylan, Oğuzhan, Mustafa Erdem Sezgin, Murat Göl, Maurizio Verga, Riccardo Lazzari, Marcel Pendieu Kwaye, and Carlo Sandroni. 2020. "Harmony Search Algorithm Based Management of Distributed Energy Resources and Storage Systems in Microgrids" Applied Sciences 10, no. 9: 3252. https://doi.org/10.3390/app10093252
APA StyleCeylan, O., Sezgin, M. E., Göl, M., Verga, M., Lazzari, R., Kwaye, M. P., & Sandroni, C. (2020). Harmony Search Algorithm Based Management of Distributed Energy Resources and Storage Systems in Microgrids. Applied Sciences, 10(9), 3252. https://doi.org/10.3390/app10093252






