Performance Analysis of Interferometer Direction of Arrival Estimation under Frequency Mismatch of Array Manifold: DOA of Frequency Hopping Signal
Abstract
1. Introduction
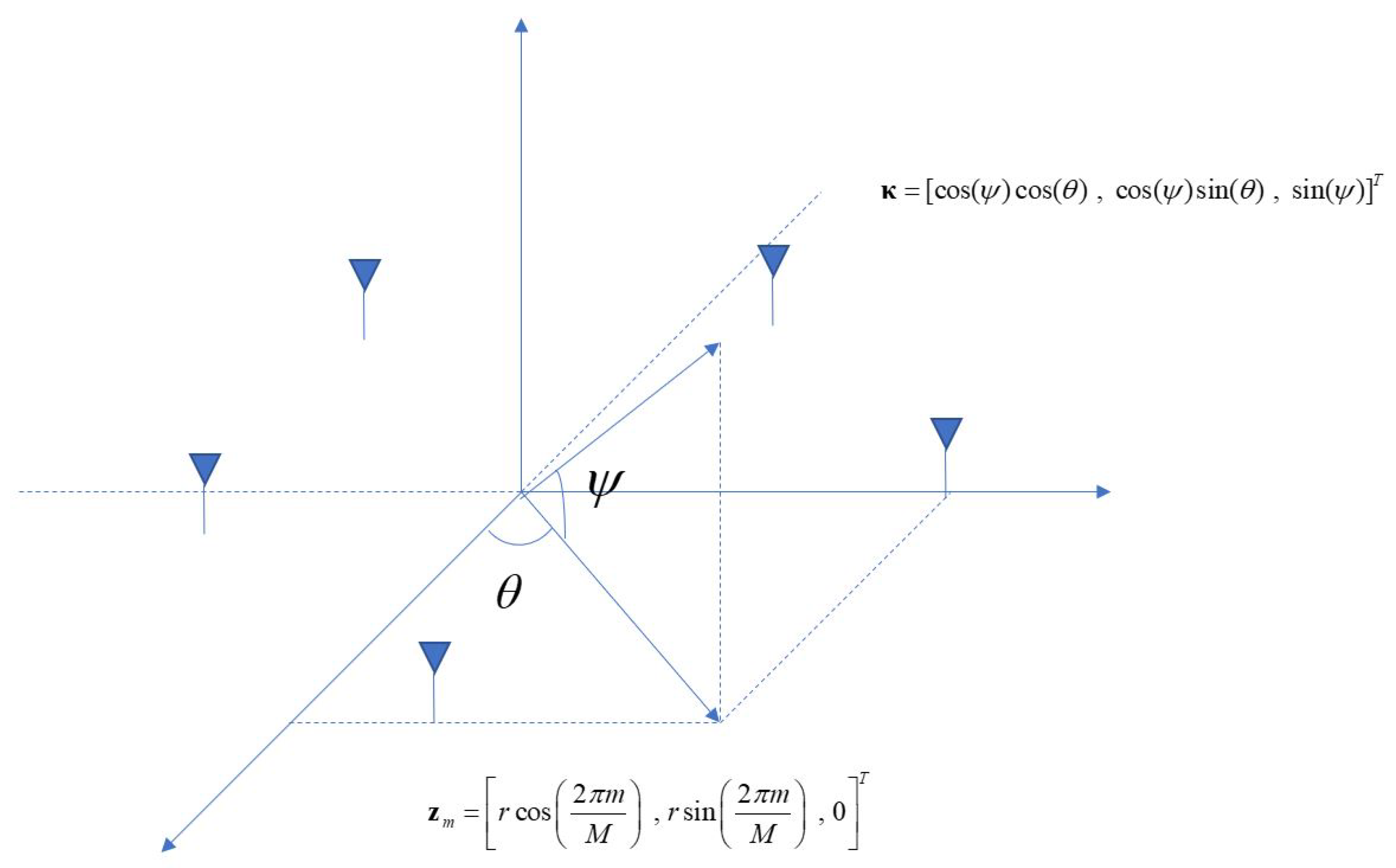
2. Derivation of the Azimuth and the Elevation Error under Frequency Mismatch
2.1. Partial Derivative of the Cost Function with Respect to the Azimuth
2.2. Partial Derivative of the Cost Function with Respect to Elevation
2.2.1. First Condition for the Partial Derivative with Respect to the Azimuth at to be Zero:
2.2.2. Second Condition for the Partial Derivative with Respect to the Azimuth at to be Zero: Cos
3. Summary of the Analytic Derivation of the Azimuth Estimation Error and the Elevation Estimation Error
3.1. First Condition:
- Second order equation in
- Fourth order equation in
3.2. Second Condition:
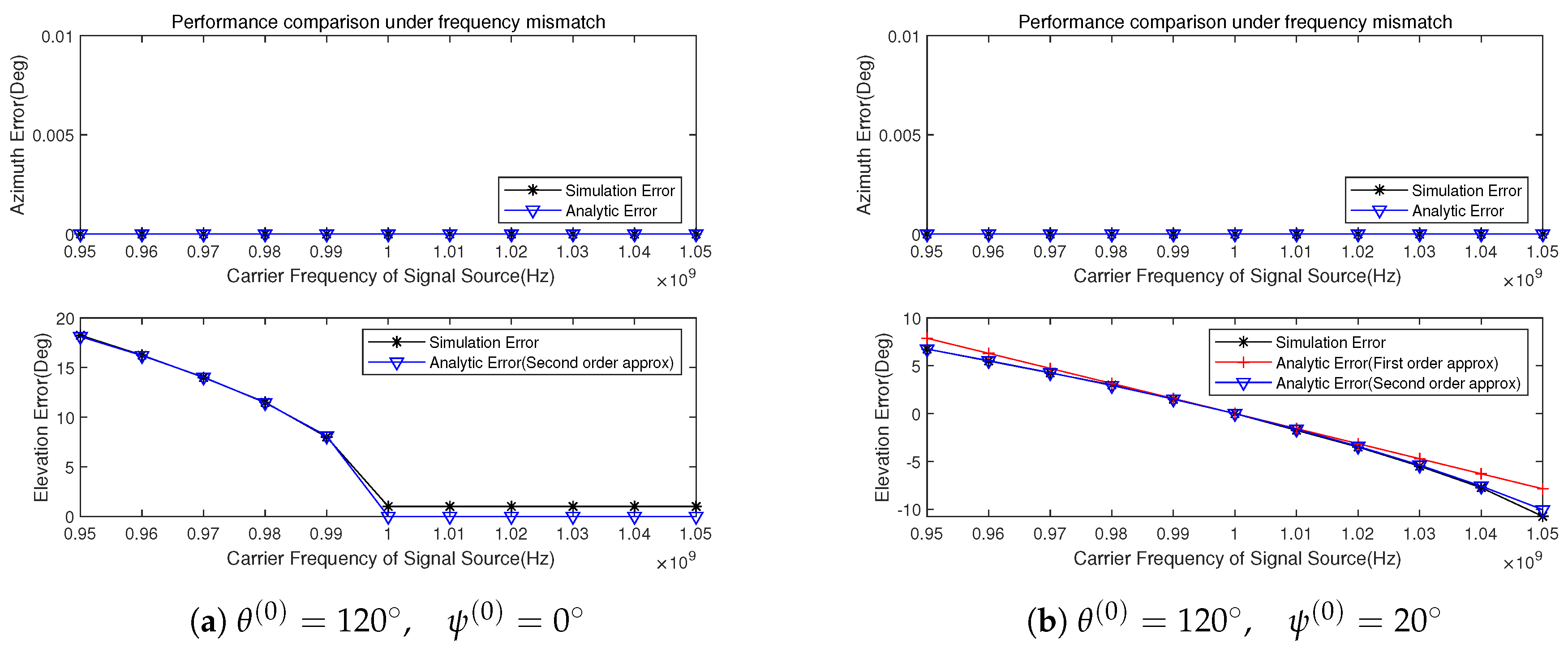
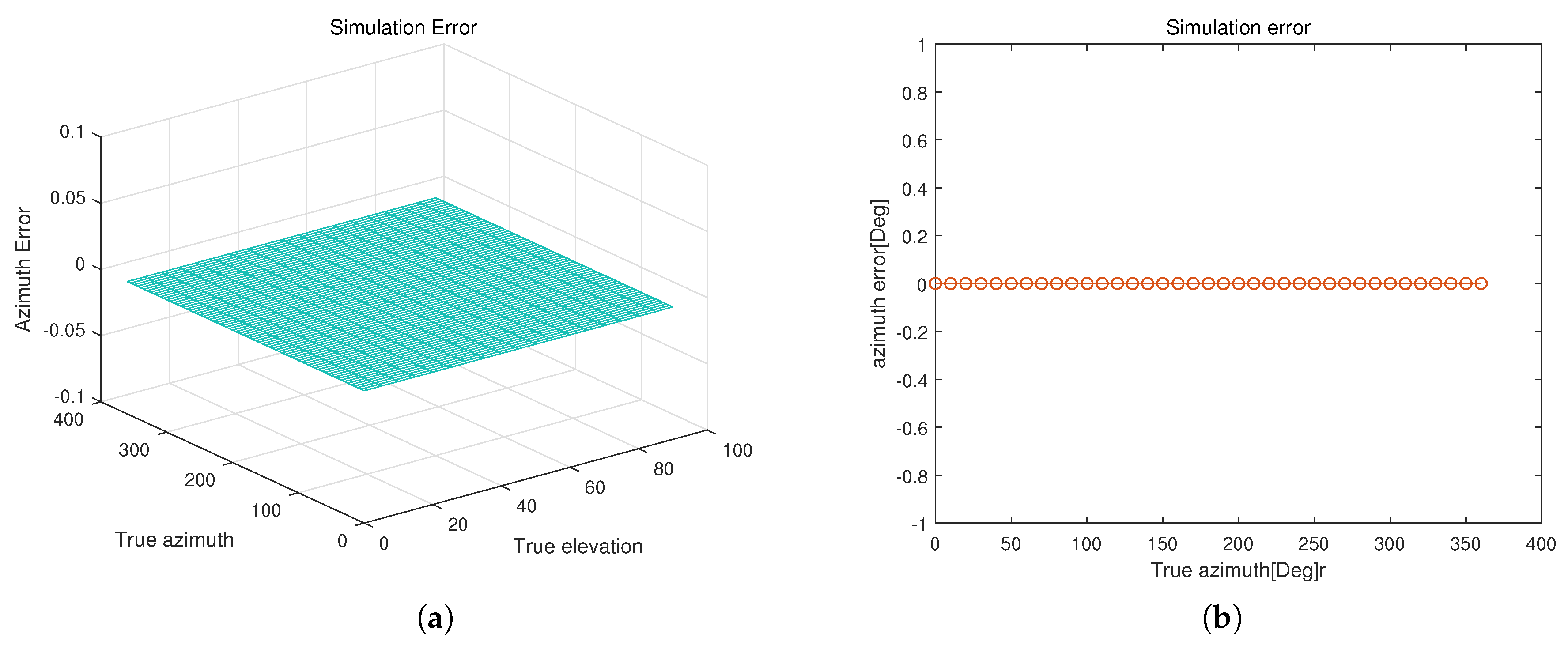
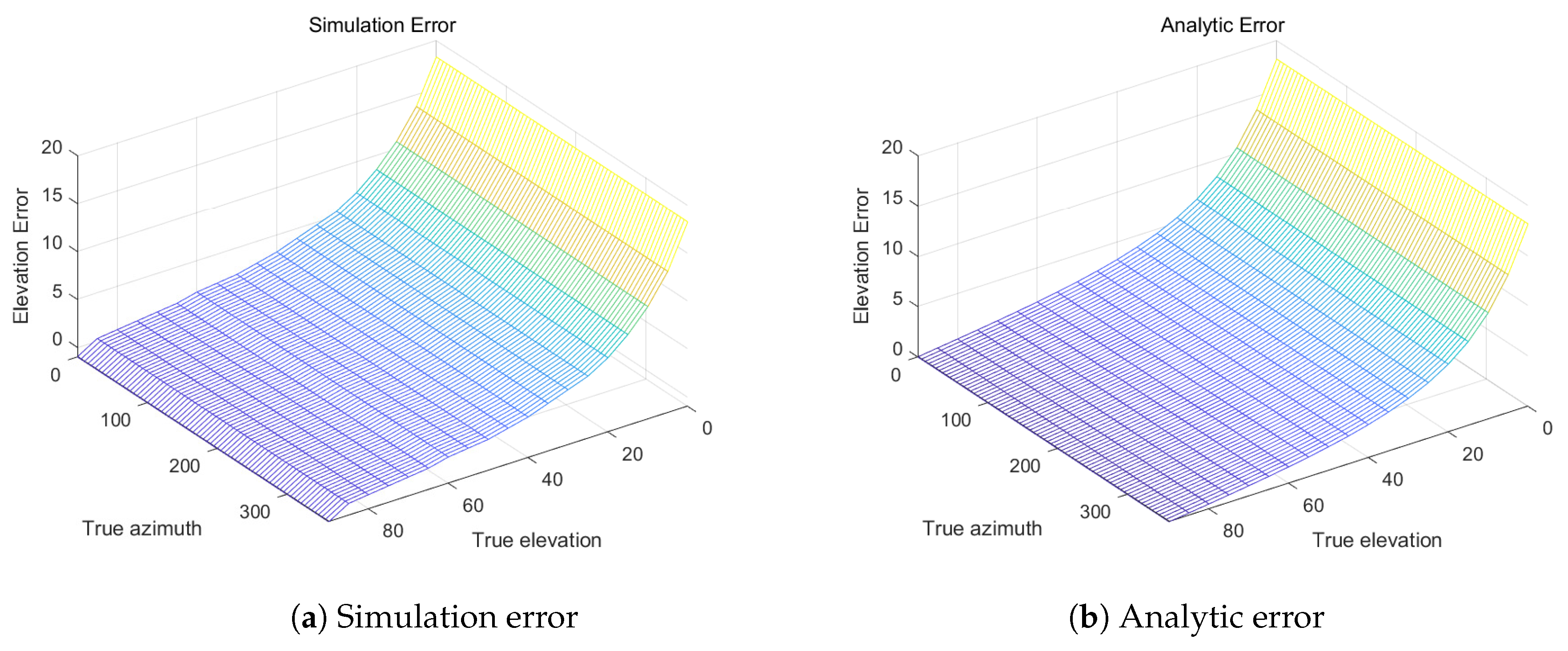
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Phase Difference between the Phase at the Sensor Location and the Phase at the Origin for an Incident Wave from and with a Wavelength of
Appendix B. Proof of
References
- Abeywickrama, S.; Jayasinghe, L.; Fu, H.; Yuen, C. RF-based direction finding of UAVs using DNN. ArXiv 2017, arXiv:1712.01154. [Google Scholar]
- Chang, X.; Yang, C.; Shi, X.; Li, P.; Shi, Z.; Chen, J. Feature extracted DOA estimation algorithm using acoustic array for drone surveillance. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar]
- Blair, W.D.; Watson, G.A.; Kirubarajan, T.; Bar-Shalom, Y. Benchmark for radar allocation and tracking in ECM. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 1097–1114. [Google Scholar] [CrossRef]
- Zheng, Y.; Tseng, S.; Yu, K. Closed-form four-channel monopulse two-target resolution. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1083–1089. [Google Scholar] [CrossRef]
- Sharenson, S. Angle estimation accuracy with a monopulse radar in the search mode. IEEE Trans. Aerosp. Navig. Electron. 1962, 9, 175–179. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Zheng, J.; Kaveh, M. Sparse spatial spectral estimation: A covariance fitting algorithm, performacne and regularization. IEEE Trans. Signal Process. 2013, 61, 2767–2777. [Google Scholar] [CrossRef]
- Das, A.; Sejnowski, T.J. Narrowband and wideband off-grid direction of arrival estimation via sparse bayesian learning. IEEE J. Ocean. Eng. 2018, 43, 108–118. [Google Scholar] [CrossRef]
- Kim, S.; Oh, D.; Lee, A.J. Joint DFT-ESPRIT estimation for TOA and DOA in vehicle FMCW Radars. IEEE Antennas Wirel. Propag. Lett. 2018, 43, 108–118. [Google Scholar] [CrossRef]
- Stallings, W. Wireless Communications and Networks; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Kamel, A.; Abdelfettah, C.; Moussa, Y. Application of the technical Frequency-Hopped to the localization of sources by array of sensors and application to the algorithm Music. In Proceedings of the IEEE Sixth International Symposium on Spread Spectrum Techniques and Applications, Parsippany, NJ, USA, 6–8 September 2000; Volume 1, pp. 78–82. [Google Scholar]
- Eric, M.; Dukic, M.L.; Obradovic, M. Frequency hopping signal separation by spatio-frequency analysis based on the MUSIC method. In Proceedings of the 2000 IEEE Sixth International Symposium on Spread Spectrum Techniques and Applications, ISSTA 2000, Parsippany, NJ, USA, 6–8 September 2000; Volume 1, pp. 78–82. [Google Scholar]
- Aydin, L.; Polydoros, A. Joint hop-timing estimation for FH signals using a coarsely channelized receiver. Mil. Commun. Conf. 1995, 1, 769–773. [Google Scholar]
- Wong, K.T. Blind beamforming/geolocation for wideband-FFH”s with unknown hop-sequences. IEEE Trans. Aerosp. Electron. Syst. 2001, 1, 65–76. [Google Scholar] [CrossRef]
- Younger, J.P.; Reid, I.M. Interferometer AOA determination using precalculated phases. IEEE Radio Sci. 2017, 52, 1058–1066. [Google Scholar] [CrossRef]
- Burtnyk, N.; McLeish, C.W.; Wolfe, J. Performance of an interferometer direction finder for the H.F. band. Proc. Inst. Electr. Eng. 1965, 112, 2055–2059. [Google Scholar] [CrossRef]
- Li, C.; Xian-Ci, X. Performance study of 2-D DOA estimation using UCA with five sensors. In Proceedings of the IEEE 2002 International Conference on Communications, Circuits and Systems and West Sino Expositions, Chengdu, China, 29 June–1 July 2002; Volume 2, pp. 1012–1026. [Google Scholar]
- Jiang, K.; Wu, Y.; Wu, X.; Cai, Y.; Zhou, J.; Du, L. A novel ambiguity resolution method of rolling Interferometer based on differential reduction. Radio Sci. 2007, 52, 1058–1066. [Google Scholar]
- Liu, Z.; Guo, F. Azimuth and elevation estimation with rotating long-baseline interferometers. IEEE Trans. Signal Process. 2015, 63, 2405–2419. [Google Scholar] [CrossRef]
- Moghaddasi, J.; Djerafi, T.; Wu, K. Multiport interferometer-enabled 2-D angle of arrival (AOA) estimation system. IEEE Trans. Microw. Theory Tech. 2017, 65, 1767–1779. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Balogh, L.; Kollar, I. Angle of arrival estimation based on interferometer principle. Proc. IEEE Int. Symp. Intell. Signal Process. 2003, 52, 1058–1066. [Google Scholar]
- Wei, H.; Wang, J.; Ye, S. An algorithm of estimation direction of arrival for phase interferometer array using cosine function. J. Electron. Inf. Technol. (Chin.) 2007, 29, 2665–2668. [Google Scholar]
- An, X.; Feng, Z.; Wang, W.; Li, T. A single channel correlative interferometer direction finder using VXI receiver. In Proceedings of the International Conference on Microwave and Milimeter Wave Technology, Beijing, China, 17–19 August 2002; pp. 1158–1161. [Google Scholar]
- Qin, L.; Jia, K.; He, Z. Performance analysis of correlative interferometer direction finder using cosine function. In Proceedings of the 2010 the 10th IEEE International Conference on Signal Processing ICSP2010, Beijing, China, 24–28 October 2010. [Google Scholar]
- Wei, H.W.; Shi, Y.G. Performance analysis and comparison of correlative interferometers for direction finding. In Proceedings of the 2010 the 10th IEEE International Conference on Signal Processing ICSP2010, Beijing, China, 24–28 October 2010. [Google Scholar]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wideband sources. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Hung, H.; Kaveh, M. Focusing matrices for coherent signal-subspace processing. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1272–1281. [Google Scholar] [CrossRef]
- Di Claudio, E.D.; Parisi, R. WAVES: Weighted average of signal subspaces for robust wideband direction finding. IEEE Trans. Signal Process. 2001, 49, 2179–2191. [Google Scholar] [CrossRef]
- Lee, T.-S. Efficient wide-band source localization using beamforming invariance technique. IEEE Trans. Signal Process. 1994, 42, 1376–1387. [Google Scholar]
- Yoon, Y.-S.; Kaplan, L.M.; McClellan, J.J. TOPS: New DOA estimator for wideband signals. IEEE Trans. Signal Process. 2006, 54, 1977–1989. [Google Scholar] [CrossRef]

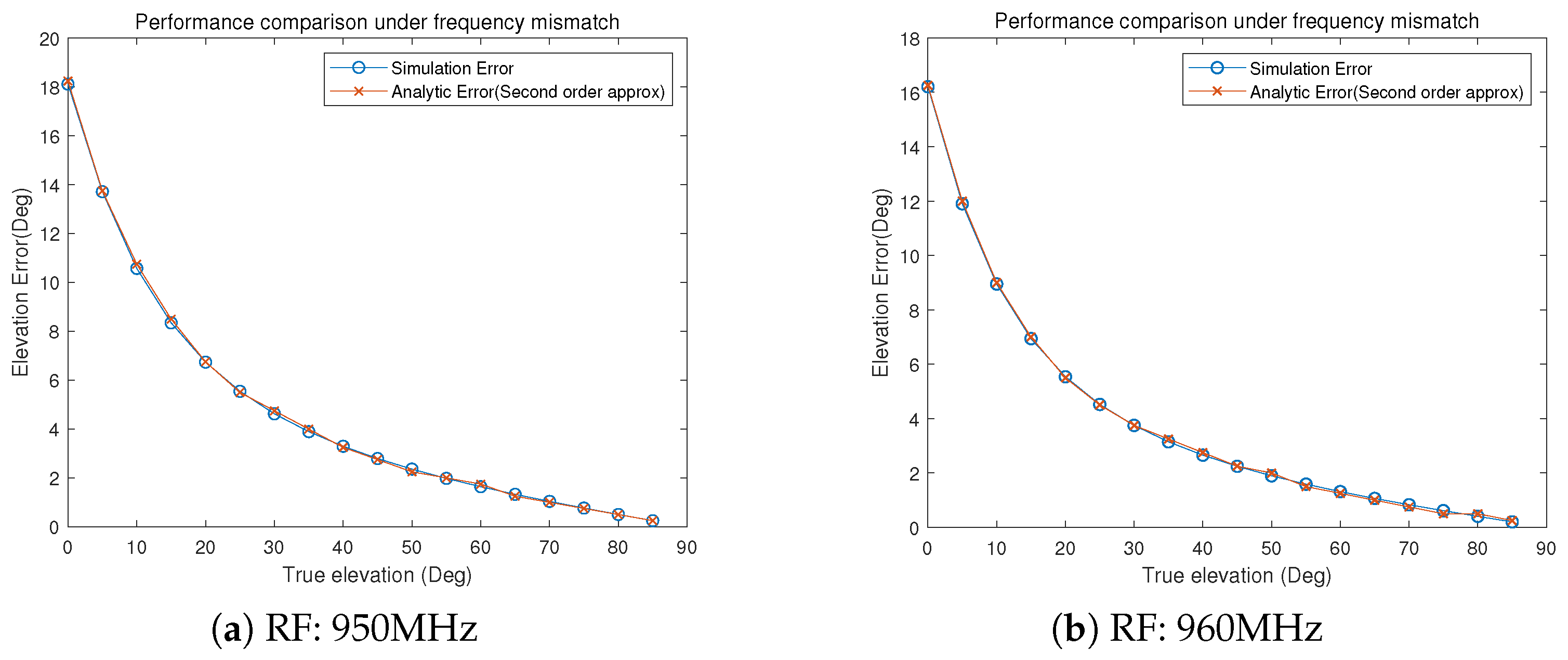

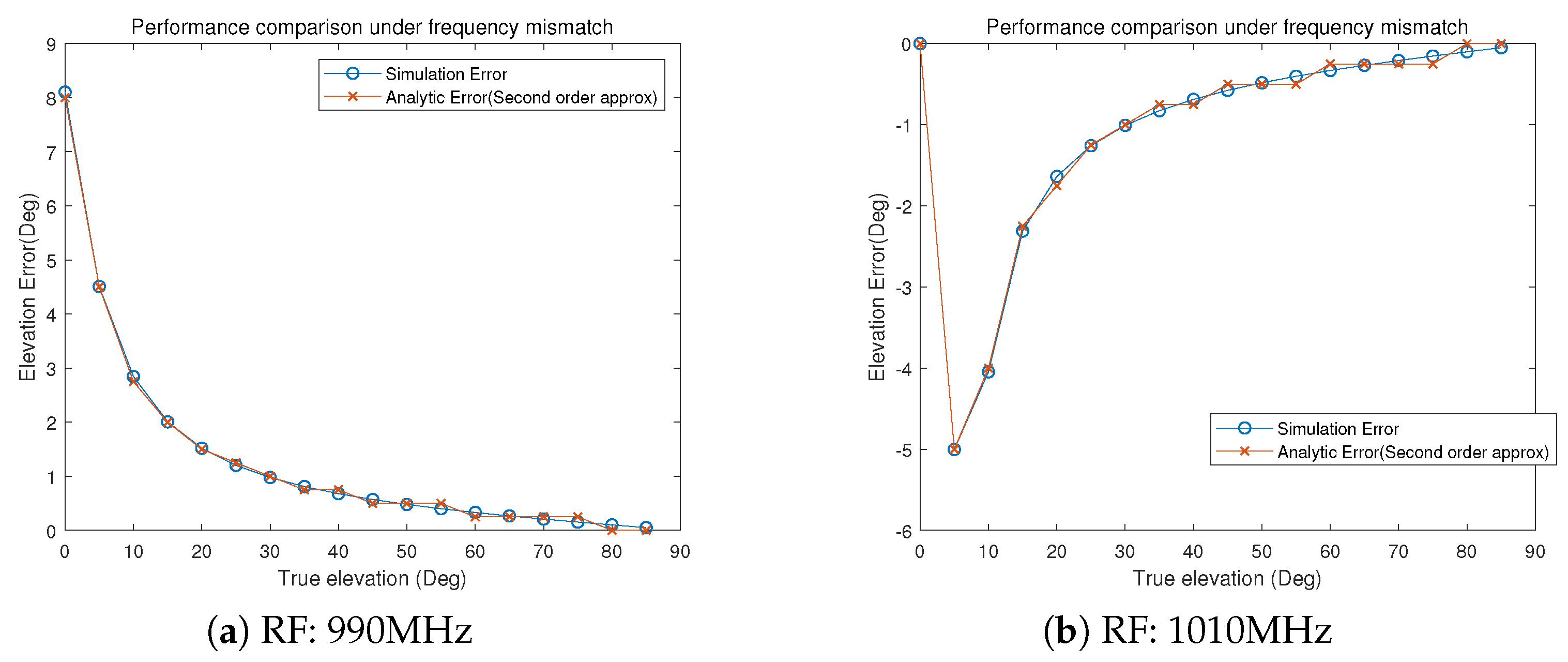
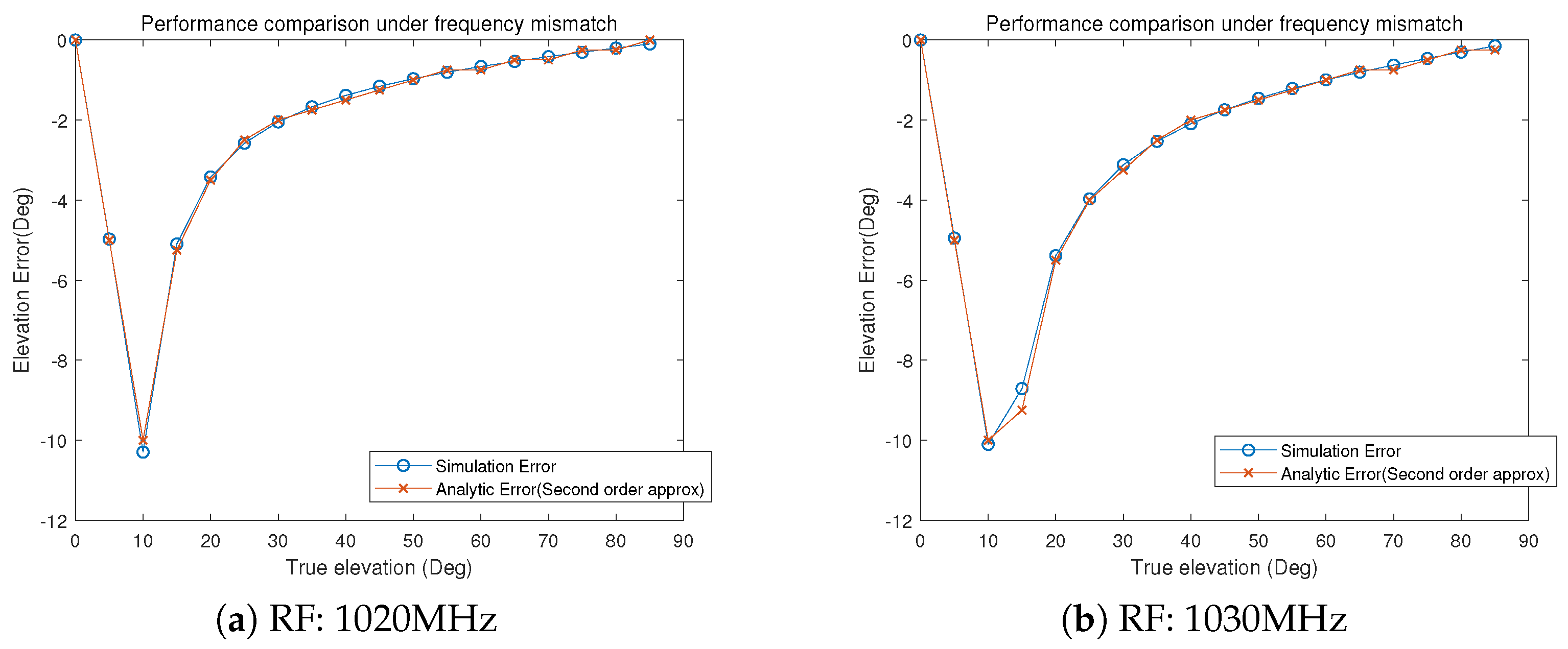

| Parameter | Value |
|---|---|
| Number of sensors | 5 |
| Array architecture | UCA |
| Azimuth and elevation search step | 0.25° |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, C.-B.; Lee, J.-H. Performance Analysis of Interferometer Direction of Arrival Estimation under Frequency Mismatch of Array Manifold: DOA of Frequency Hopping Signal. Appl. Sci. 2020, 10, 2331. https://doi.org/10.3390/app10072331
Ko C-B, Lee J-H. Performance Analysis of Interferometer Direction of Arrival Estimation under Frequency Mismatch of Array Manifold: DOA of Frequency Hopping Signal. Applied Sciences. 2020; 10(7):2331. https://doi.org/10.3390/app10072331
Chicago/Turabian StyleKo, Chan-Bin, and Joon-Ho Lee. 2020. "Performance Analysis of Interferometer Direction of Arrival Estimation under Frequency Mismatch of Array Manifold: DOA of Frequency Hopping Signal" Applied Sciences 10, no. 7: 2331. https://doi.org/10.3390/app10072331
APA StyleKo, C.-B., & Lee, J.-H. (2020). Performance Analysis of Interferometer Direction of Arrival Estimation under Frequency Mismatch of Array Manifold: DOA of Frequency Hopping Signal. Applied Sciences, 10(7), 2331. https://doi.org/10.3390/app10072331




