Asymptotic Performance Analysis of the MUSIC Algorithm for Direction-of-Arrival Estimation
Abstract
1. Introduction
- Statistical description of perturbations
- How various perturbations can be statistically described in terms of probability density function, moments to get a closed-form expression of the MSE of the estimate.
- Taylor series
- How Taylor series can be adopted to obtain explicit expression of the MSE of the estimate
- Eigenvector perturbation and eigenvalue perturbation
- How the eigenvectors and the eigenvalues of a matrix are perturbed due to the perturbations in the entries of the matrix.
2. Notation
| L | The number of snapshots |
| M | The number of antennas |
| n | The index of incident signal () |
| Transpose of a matrix | |
| Hermitian of a matrix | |
| Inverse matrix | |
| Statistical expectation | |
| The n-th true azimuth of d incident signals () | |
| The n-th azimuth estimate in (47) | |
| The difference between and | |
| The n-th azimuth estimate in (38) | |
| The difference between and | |
| The n-th azimuth estimate in (39) | |
| The difference between and | |
| zero-mean Gaussian random vector representing the noise on the antenna | |
| The wavelength of a incident signal | |
| The unit vector indicating the DOA of the incident signal | |
| The coordinate of the m-th antenna | |
| The distance between the adjacent antenna elements | |
| r | Radius of antenna array |
| The true covariance matrix | |
| The sample covariance matrix | |
| The difference between the sample covariance and the true covariance matrix | |
| The signal eigenvector matrix of matrix whose columns are the signal eigenvectors of | |
| The signal eigenvector matrix of matrix whose columns are the signal eigenvectors of | |
| The difference between and | |
| The projection matrix onto the column space of | |
| The projection matrix onto the column space of | |
| The difference between and | |
| MUSIC spectrum as a function of azimuth associated with covariance matrix | |
| MUSIC spectrum as a function of azimuth associated with covariance matrix | |
| Approximate MUSIC spectrum due to the g-th order approximation of the signal eigenvectors, Approximation of | |
| The h-th Taylor expansion-based approximation of |
3. MUSIC Algorithm
4. Difference between the True Covariance Matrix and the Sample Covariance Matrix: R
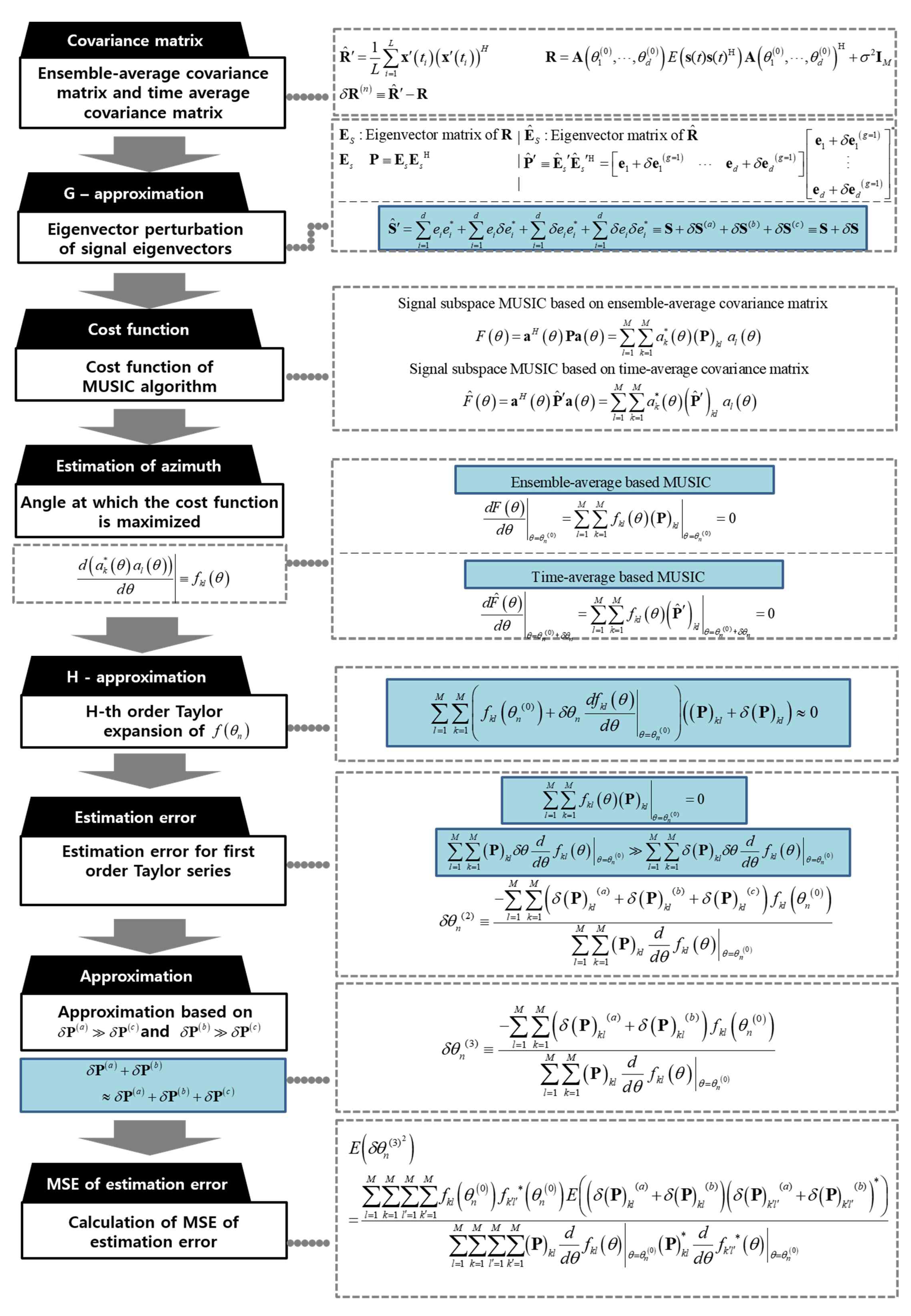
5. Eigenvector Perturbation
6. Closed-Form Expression of Estimation Error
7. Closed-Form Expression of Mean Square Error
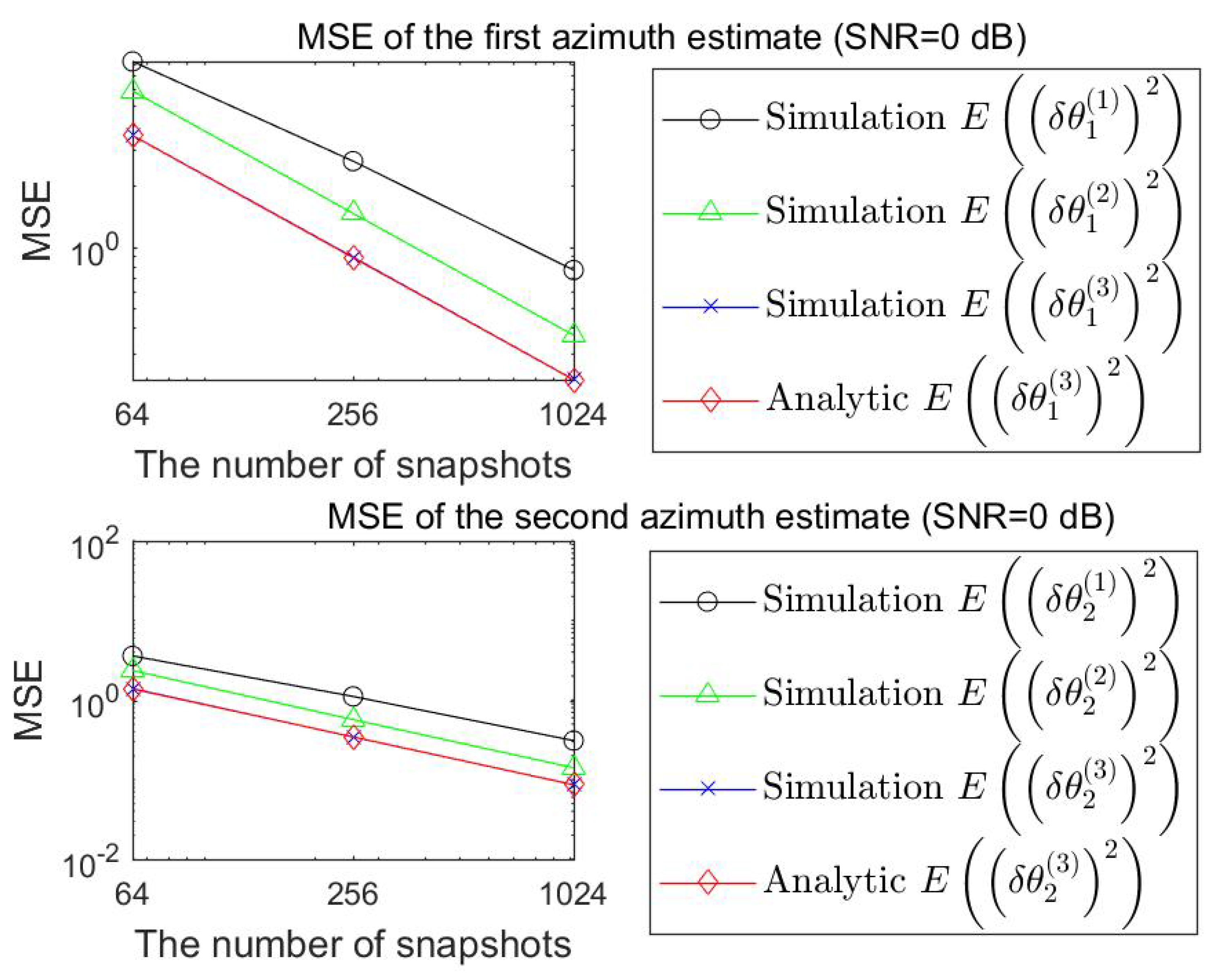
8. Numerical Results
9. Applications of Derived Analytic Expression of MSE of the MUSIC Algorithm
9.1. Evaluation of cOvariance Matrix of AOA-Based Localization in Underwater Acoustics
9.2. Evaluating the Performance of Ultrasonic Imaging
9.3. Evaluation of Ranging Accuracy in the MUSIC-Based Laser Ranging Algorithm in Terms of the Mean Square Error
9.4. Localization Accuracy in the MUSIC Algorithm for Use With Super Resolution Fluorescence Microscopy
9.5. Accuracy in the MUSIC-Based Scattering Center Estimation
10. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Calculation of
Appendix B. Calculation of
Appendix C. Calculation of
References
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Kaveh, M.; Barabell, A. The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves in noise. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 331–341. [Google Scholar] [CrossRef]
- Jeffries, D.; Farrier, D. Asymptotic results for eigenvector methods. IEE Proc. F-Commun. Radar Signal Process. 1985, 132, 589–594. [Google Scholar] [CrossRef]
- Ferreol, A.; Larzabal, P.; Viberg, M. On the asymptotic performance analysis of subspace DOA estimation in the presence of modeling errors: Case of MUSIC. IEEE Trans. Signal Process. 2006, 54, 907–920. [Google Scholar] [CrossRef]
- Zhang, Q. Probability of resolution of the MUSIC algorithm. IEEE Trans. Signal Process. 1995, 43, 978–987. [Google Scholar] [CrossRef]
- Swindlehurst, A.L.; Kailath, T. A performance analysis of subspace-based methods in the presence of model errors, Part I: The MUSIC algorithm. IEEE Trans. Signal Process. 1992, 40, 1758–1774. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound: Further results and comparisons. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 2140–2150. [Google Scholar] [CrossRef]
- Pillai, S.U.; Kwon, B.H. Performance analysis of MUSIC-type high resolution estimators for direction finding in correlated and coherent scenes. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1176–1189. [Google Scholar] [CrossRef]
- Cho, Y.S.; Seo, J.M.; Lee, J.H. Performance analysis of two-dimensional maximum likelihood direction-of-arrival estimation algorithm using the UCA. Int. J. Antennas Propag. 2017, 2017, 6926825. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Z.; Nehorai, A. Performance analysis of coarray-based MUSIC in the presence of sensor location errors. IEEE Trans. Signal Process. 2018, 66, 3074–3085. [Google Scholar] [CrossRef]
- Wang, B.; Gu, Y.; Wang, W. Off-grid direction-of-arrival estimation based on steering vector approximation. Circuits Syst. Signal Process. 2019, 38, 1287–1300. [Google Scholar] [CrossRef]
- Vincent, F.; Pascal, F.; Besson, O. A bias-compensated MUSIC for small number of samples. Signal Process. 2017, 138, 117–120. [Google Scholar] [CrossRef][Green Version]
- Liu, B.; Gui, G.; Matsushita, S.; Xu, L. Dimension-reduced direction-of-arrival estimation based on ℓ2,1-norm penalty. IEEE Access 2018, 6, 44433–44444. [Google Scholar] [CrossRef]
- Vallet, P.; Mestre, X.; Loubaton, P. Performance analysis of an improved MUSIC DoA estimator. IEEE Trans. Signal Process. 2015, 63, 6407–6422. [Google Scholar] [CrossRef]
- An, D.J.; Lee, J.H. Performance analysis of amplitude comparison monopulse direction-of-arrival estimation. Appl. Sci. 2020, 10, 1246. [Google Scholar] [CrossRef]
- Lin, Y.; Guo, T.; Guo, M.; Fu, Y. Motion compensation for SAA FMCW radar based on specific switching scheme. Appl. Sci. 2019, 9, 3441. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y.; Wan, J. In-depth exploration of signal self-cancellation phenomenon to achieve DOA estimation of underwater acoustic sources. Appl. Sci. 2019, 9, 570. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Yan, Y. Target speaker localization based on the complex watson mixture model and time-frequency selection neural network. Appl. Sci. 2018, 8, 2326. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, Z.; Ritz, C.H. Enhancing target speech based on nonlinear soft masking using a single acoustic vector sensor. Appl. Sci. 2018, 8, 1436. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Camarinha-Matos, L.M.; Oliveira, L.B. Distributed localization with complemented RSS and AOA measurements: Theory and Methods. Appl. Sci. 2020, 10, 272. [Google Scholar] [CrossRef]
- Yagüe-Jiménez, V.; Ibáñez Rodríguez, A.; Parrilla Romero, M.; Martínez-Graullera, O. Rician beamforming: Despeckle method via coarray projection stochastic analysis. Appl. Sci. 2020, 10, 847. [Google Scholar] [CrossRef]
- Mohamed, K.S.; Alias, M.Y.; Roslee, M. Interference avoidance using TDMA-beamforming in location aware small cell systems. Appl. Sci. 2019, 9, 4979. [Google Scholar] [CrossRef]
- Gadiel, G.M.; Lee, K. Energy-efficient hybrid beamforming with variable and constant phase shifters. Appl. Sci. 2019, 9, 4476. [Google Scholar] [CrossRef]
- Xie, J.; Li, X.; Xing, Z.; Zhang, B.; Bao, W.; Zhang, J. Improved distributed minimum variance distortionless response (MVDR) beamforming method based on a local average consensus algorithm for bird audio enhancement in wireless acoustic sensor networks. Appl. Sci. 2019, 9, 3153. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; Johns Hopkins University Press: Baltimore, MD, USA, 2012; Volume 3. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis; Cengage Learning Press: Boston, MA, USA, 2010; Volume 9. [Google Scholar]
- Pages-Zamora, A.; Vidal, J.; Brooks, D.H. Closed-form solution for positioning based on angle of arrival measurements. In Proceedings of the 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Pavilhao Altantico, Lisboa, Portugal, 18 September 2002; Volume 4, pp. 1522–1526. [Google Scholar]
- Fan, C.; Caleap, M.; Pan, M.; Drinkwater, B.W. A comparison between ultrasonic array beamforming and super resolution imaging algorithms for non-destructive evaluation. Ultrasonics 2014, 54, 1842–1850. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, F.; Shi, C.; Qu, X. High-precision frequency estimation for frequency modulated continuous wave laser ranging using the multiple signal classification method. Appl. Opt. 2017, 56, 6956–6961. [Google Scholar] [CrossRef]
- Agarwal, K.; Macháň, R. Multiple signal classification algorithm for super-resolution fluorescence microscopy. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef]
- Kim, K.T.; Seo, D.K.; Kim, H.T. Efficient radar target recognition using the MUSIC algorithm and invariant features. IEEE Trans. Antennas Propag. 2002, 50, 325–337. [Google Scholar]






| Ref. | Algorithm | Application | Main Idea | Contribution |
|---|---|---|---|---|
| [17] | Amplitude comparison monopulse DOA estimation | Radar tracking | Analytic performance analysis | Computationally inexpensive performance analysis |
| [18] | Conventional beamforming (Bartlett beamforming) algorithm | FMCW automotive radar | Motion compensated Bartlett beamforming | Estimation error reduction by explicitly taking the motion induced phase into account |
| [19] | MVDR beamforming-based DOA algorithm | DOA of underwater acoustic sources | Signal self-cancellation MVDR | Performance improvement of MVDR algorithm for underwater acoustic source localization |
| [20] | New DOA estimation algorithm based on Complex Watson mixture model and time-frequency selection | Acoustic source localization | Isolation of target speaker by time-frequency selection | Performance improvement of DOA estimation of target speaker |
| [21] | DOA estimation with acoustic vector sensor (AVS): Preprocessing for target speech enhancement | Enhancement of target speech | Estimated DOA-based isolation of target speech in time-frequency distribution for enhancement | Superiority of AVS-SMASK over AVS-FMV |
| [22] | Array signal processing-based DOA estimation algorithms using array antennas and DOA estimation using single directional antenna | AOA-based localization | Not applicable [Review paper] | Not applicable [Review paper] |
| [23] | Rician beamforming for array design [Not beamforming-based DOA estimation algorithm] | Ultrasonic imaging | Rician beamforming-based array design for ultrasonic imaging using convex optimization | Improved despeckle in ultrasonic imaging via beamforming-based array design |
| [24] | TDMA-beamforming for array design [Not beamforming-based DOA estimation algorithm] | Interference suppression in communication system | Interference suppression via spatial filtering | Improved interference avoidance |
| [25] | Hybrid beamforming for array design [Not beamforming-based DOA estimation algorithm] | Massive MIMO system | Optimal combination of variable phase shifters and constant phase shifters | Improvement in beamforming performance |
| [26] | MVDR beamforming for array design [Not beamforming-based DOA estimation algorithm] | Bird audio enhancement | Beamforming method based on a local average consensus algorithm | Efficient implementation of acoustic wireless sensor network for surveillance |
| Ref. | How to Validate the Schemes Presented in [17,18,19,20,21,22,23,24,25,26] | How to Apply the Derivations of This Paper to the Problems in [17,18,19,20,21,22,23,24,25,26] |
|---|---|---|
| [17] | Agreement between analytic MSE and simulation-based MSE | [17]: Performance analysis of amplitude comparison monopulse algorithm. This paper: Performance analysis of the MUSIC algorithm |
| [18] | Reduction in estimation error of the motion compensated conventional beamforming algorithm in comparison with the estimation error of original conventional beamforming algorithm without motion compensation in the DOA spectrum | The analytic expression of the MSE of motion-compensated Bartlett beamforming algorithm can be obtained by modifying the derivation in this paper |
| [19] | Superiority of performance of SCC-MVDR algorithm over MVDR algorithm in the view point of RMSE | The analytic expression of the MSE of SCC-MVDR algorithm can be obtained by modifying the derivation in this paper |
| [20] | Superiority of the proposed scheme over the previously existing algorithms in terms of gross error rate (GER) and mean square error (MSE) | Performance of the proposed algorithm in terms of the MSE can be analytically obtained by modifying the derivation in this paper |
| [21] | Performance comparison in terms of signal-to-noise ratio, signal-to-interference ratio, signal-to-interference ratio, signal-to-interference plus noise ratio, log spectral density, and perceptual evaluation of speech quality | Performance of preprocessing DOA estimation with AVS algorithm, given by estimation error, can be obtained by modifying the derivation leading to (38) and (39), since the derivation of the MUSIC estimate should be modified to the derivation of the AVS-based DOA estimate |
| [22] | Not applicable [Review paper] | Performance of AOA-based localization algorithm depends on performance of DOA estimation: The MSE of the MUSIC algorithm can be obtained from (40) of this paper. The MSE of other DOA estimation algorithm can be obtained by modifying the derivation leading to (40). |
| [23] | Comparison of images in terms of quality and localized estimations on image noise | Rician beamforming-based array design is formulated as a convex optimization problem, and the MSEs of the array design parameters can be analytically obtained by modifying the derivation leading to (40) since array design can be formulated as parameter estimation problem |
| [24] | Superiority of the proposed scheme in terms of throughput, Jain’s fairness model, and SINR. | The MSEs of the estimated array parameters in array design problem can be analytically derived by modifying the approach leading to (40). |
| [25] | Superiority of the proposed algorithm in terms of average sum-rate and energy efficiency | The MSEs of the estimates in hybrid beamforming based array design can be evaluated by modification of the derivation leading to (40). |
| [26] | Improvement in MSE, SegSNR and PESQ | The MSE of the estimated array design parameters can be evaluated by modification of the derivation leading to (40). |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, S.-H.; Son, B.-k.; Lee, J.-H. Asymptotic Performance Analysis of the MUSIC Algorithm for Direction-of-Arrival Estimation. Appl. Sci. 2020, 10, 2063. https://doi.org/10.3390/app10062063
Jeong S-H, Son B-k, Lee J-H. Asymptotic Performance Analysis of the MUSIC Algorithm for Direction-of-Arrival Estimation. Applied Sciences. 2020; 10(6):2063. https://doi.org/10.3390/app10062063
Chicago/Turabian StyleJeong, So-Hee, Byung-kwon Son, and Joon-Ho Lee. 2020. "Asymptotic Performance Analysis of the MUSIC Algorithm for Direction-of-Arrival Estimation" Applied Sciences 10, no. 6: 2063. https://doi.org/10.3390/app10062063
APA StyleJeong, S.-H., Son, B.-k., & Lee, J.-H. (2020). Asymptotic Performance Analysis of the MUSIC Algorithm for Direction-of-Arrival Estimation. Applied Sciences, 10(6), 2063. https://doi.org/10.3390/app10062063




