Quantum Approximation for Wireless Scheduling

Abstract

This paper proposes an application algorithm based on a quantum approximate optimization algorithm (QAOA) for wireless scheduling problems. QAOA is one of the promising hybrid quantum-classical algorithms to solve combinatorial optimization problems and it provides great approximate solutions to non-deterministic polynomial-time (NP) hard problems. QAOA maps the given problem into Hilbert space, and then it generates the Hamiltonian for the given objective and constraint. Then, QAOA finds proper parameters from the classical optimization loop in order to optimize the expectation value of the generated Hamiltonian. Based on the parameters, the optimal solution to the given problem can be obtained from the optimum of the expectation value of the Hamiltonian. Inspired by QAOA, a quantum approximate optimization for scheduling (QAOS) algorithm is proposed. The proposed QAOS designs the Hamiltonian of the wireless scheduling problem which is formulated by the maximum weight independent set (MWIS). The designed Hamiltonian is converted into a unitary operator and implemented as a quantum gate operation. After that, the iterative QAOS sequence solves the wireless scheduling problem. The novelty of QAOS is verified with simulation results implemented via Cirq and TensorFlow-Quantum.

1. Introduction

Nowadays, quantum computing and communications have received a lot of attention from academia and industry research communities. In particular, quantum computing-based non-deterministic polynomial-time (NP) hard problem solving is of great interest [1,2,3,4]. Among the available methods, the quantum approximate optimization algorithm (QAOA) is one of the well-known quantum computing-based optimization solvers, and it has been verified that the QAOA outperforms others in many combinatorial problems that are closely related to wireless scheduling problems [5,6,7,8,9]. Therefore, it is obvious that quantum computing can be used for various communications applications [10,11,12,13].

In this paper, a wireless scheduling problem is formulated with maximum weight independent set (MWIS) formulation, where the weight is defined as the queue backlog to be transmitted over wireless channels [14,15,16,17]. Due to the fact that the MWIS problem is an NP-hard problem, heuristic algorithms are desired; thus, a QAOA application algorithm, quantum approximate optimization for scheduling (QAOS), is designed to solve MWIS-based wireless scheduling problems.

The proposed QAOS works as follows. First of all, the objective function and constraint functions are formulated for MWIS. Next, the corresponding objective Hamiltonian and constraint Hamiltonian are designed, which map the objective function and the constraint function, respectively; then, the problem Hamiltonian, which should be optimized, is formulated as the form of linear combinations of the objective Hamiltonian and constraint Hamiltonian. In addition, the mixing Hamiltonian is formulated using the Pauli-X operator, which provides the number of different cases via bit flip. Based on the definitions of the problem Hamiltonian and the mixing Hamiltonian, two corresponding unitary operators, i.e., the problem operator and mixing operator, can be defined, respectively; then, the parameterized state can be generated by alternately applying the two unitary operators. The sample solutions can be obtained by the measurement of the expectation value of the problem Hamiltonian on the parameterized state, and the parameters can be optimized in a classical optimization loop, using—for example—stochastic gradient methods. Here, the measurement is used to project a quantum state into one of the eigenstates (=eigenkets) of the problem operator, according to the Copenhagen interpretation [18]. Finally, the optimal solution of the MWIS problem can be obtained by the measurement of the expectation value of the problem Hamiltonian on the state generated by optimal parameters. As verified in performance evaluation, the QAOS outperforms the random search and greedy search.

QAOS is a novel attempt to carry out application research on wireless communication via QAOA. In the noisy intermediate-scale quantum (NISQ) era, research on hybrid quantum-classical algorithms such as QAOS is essential [6]. However, the research on QAOA-based applications such as QAOS is still in its infancy. Therefore, it is reasonable to increase the utilization of QAOA through convergence and transformation in various fields. From this point of view, QAOS, the novel attempt via QAOA, is very encouraging.

The rest of this paper is organized as follows. Section 2 presents the preliminary knowledge. Section 3 introduces MWIS-based wireless scheduling modeling. Section 4 presents the details of the proposed QAOS algorithm, and the performance is evaluated in Section 5. Finally, Section 6 concludes the paper.

2. Preliminaries

Prior to problem modeling, this section briefly explains bra–ket notation, basic quantum gates, and QAOA [5].

2.1. Bra–Ket Notation

In quantum computing, the bra–ket notation is generally used to represent qubit states (or quantum states). It is also called the Dirac notation, as well as the notation for observable vectors in Hilbert spaces. A ket and a bra can represent the column and row vectors, respectively. Thus, single qubit states, i.e., |0〉 and |1〉, are represented as follows:

$$|0\rangle =\left[\begin{array}{c}1\\ 0\end{array}\right],\mathrm{and}|1\rangle =\left[\begin{array}{c}0\\ 1\end{array}\right],$$

(1)

$$\begin{array}{ccc}\hfill \mathrm{and}\mathrm{also}|0\rangle ={\langle 0|}^{†}& =& {\left[\begin{array}{cc}1& 0\end{array}\right]}^{†},\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill |1\rangle ={\langle 1|}^{†}& =& {\left[\begin{array}{cc}0& 1\end{array}\right]}^{†}.\hfill \end{array}$$

(3)

Note that † means Hermitian transpose. Accordingly, the superposition state of a single qubit can be represented as follows:

$$c_1|0\rangle +c_2|1\rangle =\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right],$$

(4)

where $c_1$ and $c_2$ are probability amplitudes that are complex numbers [19].

2.2. Basic Quantum Gates

This section introduces several commonly used basic quantum gates (or operators) that represent the single-qubit or 2-qubit operations [19]. The Hadamard gate H, Pauli-X gate X, Pauli-Y gate Y, and Pauli-Z gate Z are represented as follows:

$$H=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right],X=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],Y=\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right],\mathrm{and}Z=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right].$$

(5)

The rotation-X gate $RX\left(\theta \right)$, rotation-Y gate $RY\left(\theta \right)$, and rotation-Z gate $RZ\left(\theta \right)$ are represented as follows:

$$RX\left(\theta \right)=\left[\begin{array}{cc}cos\frac{\theta }{2}& -isin\frac{\theta }{2}\\ -isin\frac{\theta }{2}& cos\frac{\theta }{2}\end{array}\right],RY\left(\theta \right)=\left[\begin{array}{cc}cos\frac{\theta }{2}& -sin\frac{\theta }{2}\\ sin\frac{\theta }{2}& cos\frac{\theta }{2}\end{array}\right],\mathrm{and}RZ\left(\theta \right)=\left[\begin{array}{cc}{e}^{-i\frac{\theta }{2}}& 0\\ 0& e^{i\frac{\theta }{2}}\end{array}\right],$$

(6)

where $\theta$ is the angle. The controlled-NOT gate $CNOT$ and swap gate $SWAP$ are represented as follows:

$$CNOT=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right],\mathrm{and}SWAP=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right].$$

(7)

In this paper, H, X, Z, $RX\left(\theta \right)$, $RZ\left(\theta \right)$, and $CNOT$ are used.

2.3. Quantum Approximate Optimization Algorithm (QAOA)

QAOA is one of the well-known NISQ optimization algorithms to combat combinatorial problems [5,6,7,8]. QAOA formulates $H_P$ (i.e., problem Hamiltonian) and $H_M$ (i.e., mixing Hamiltonian) from the objective function $f\left(y\right)$; and then generates the parameterized states $|\gamma ,\beta \rangle$ by alternately applying the $H_P$ and $H_M$ on initial state |s〉. Here, $f\left(y\right)$, $H_P|y\rangle$, $H_M$, and $|\gamma ,\beta \rangle$ are defined as follows:

$$\begin{array}{ccc}\hfill f\left(y\right)& \triangleq & f(y_1,y_2,\dots ,y_n),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill H_P|y\rangle & \triangleq & f\left(y\right)|y\rangle ,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill H_M& \triangleq & \sum _{k=1}^n{X}_k,\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill |\gamma ,\beta \rangle & \triangleq & e^{-i{\beta }_p{H}_M}{e}^{-i{\gamma }_p{H}_P}\cdots e^{-i{\beta }_2{H}_M}{e}^{-i{\gamma }_2{H}_P}{e}^{-i{\beta }_1{H}_M}{e}^{-i{\gamma }_1{H}_P}|s\rangle ,\hfill \end{array}$$

(11)

where $n\in {\mathbb{Z}}^{+}$, $p\in {\mathbb{Z}}^{+}$, and $X_k$ is the Pauli-X operator applying on the kth qubit; $\gamma$ and $\beta$ are learnable parameters that tune the result. Note that $H_P$ encodes $f\left(y\right)$ in Equation (9), operating diagonally in the n-qubit quantum computational basis states [20].

In QAOA, through iterative measurement of $|\gamma ,\beta \rangle$, the expectation value of $H_P$ should be taken; then, eventually, the samples of $f\left(y\right)$ should be computed as follows [5]:

$${\langle f\left(y\right)\rangle }_{\gamma ,\beta }=\langle \gamma ,\beta |H_P|\gamma ,\beta \rangle .$$

(12)

The optimal values of the parameters $\gamma$ and $\beta$ can be obtained via classical numerical optimization methods such as gradient descent [21,22]. Therefore, the solution can be computed from Equation (12) via the parameters obtained. Thus, QAOA is a hybrid quantum-classical optimization algorithm in which proper Hamiltonian design and the discovery of good parameters in a classical optimization loop are key [20,23,24].

3. Wireless Scheduling Modeling Using Maximum Weight Independent Set (MWIS)

Suppose a wireless network consists of a set of one-hop links under very high transmission power using millimeter wave [14]. Due to the high data transmission rate, the queue backlog should always be cleared; otherwise, the signal decoding always fails because of extremely high interference. For the scheduling, a conflict graph is organized where the set of vertices is (the links) and two vertices are connected by an edge if the corresponding links suffer from interference. The conflict graph can be formulated by its adjacency matrix, whose ${\mathcal{E}}_{(i,j)}$ are defined as follows:

$${\mathcal{E}}_{(i,j)}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{l}_i\mathrm{interferes}\mathrm{with}{l}_j\mathrm{where}\hfill \\ \hfill & l_i\in \mathcal{L},l_j\in \mathcal{L},\mathrm{and}i\ne j,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(13)

For wireless network scheduling, the objective is for finding the set of links (i.e., nodes of the conflict graph) where two adjacent links connected via edges cannot be simultaneously selected because the two adjacent connected links are interfering with each other. This is equivalent to the case which maximizes the summation of weights of all possible independent sets in a given conflict graph. Thus, it is obvious that wireless network scheduling can be formulated with MWIS as follows:

$$\begin{array}{ccc}\hfill max:& & \sum _{\forall l_k\in \mathcal{L}}{w}_k{\mathcal{I}}_k,\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill \mathrm{s}.\mathrm{t}.& & {\mathcal{I}}_i+{\mathcal{I}}_j+{\mathcal{E}}_{(i,j)}\le 2,\forall l_i\in \mathcal{L},\forall l_j\in \mathcal{L},\hfill \end{array}$$

(15)

$$\begin{array}{ccc}& & {\mathcal{I}}_i\in \{0,1\},\forall l_i\in \mathcal{L},\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \mathrm{where}& & {\mathcal{I}}_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{l}_i\mathrm{is}\mathrm{scheduled}\mathrm{where}{l}_i\in \mathcal{L},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(17)

Here, $w_k$ is a positive integer weight at $\forall l_k\in \mathcal{L}$. The above formulation ensures that conflicting links are not scheduled simultaneously: if ${\mathcal{E}}_{(i,j)}=0$ (no edge between $l_i$ and $l_j$), then ${\mathcal{I}}_i+{\mathcal{I}}_j\le 2$, i.e., both indicator functions can be 1. In contrast, if ${\mathcal{E}}_{(i,j)}=1$, ${\mathcal{I}}_i+{\mathcal{I}}_j\le 1$, i.e., at most, one of the two indicators can be 1. In wireless communication research, the $w_k$ where $\forall l_k\in \mathcal{L}$ is usually considered as the transmission queue backlog which should be processed when the link is scheduled. More details are can be found in [14].

4. Quantum Approximate Optimization for Scheduling (QAOS)

In this section, Hamiltonians of QAOA are designed based on the scheduling model in Section 3; then, the quantum approximate optimization for scheduling (QAOS) algorithm is proposed by applying the designed Hamiltonian to QAOA.

4.1. Design of the Problem Hamiltonian

The problem Hamiltonian $H_P$ is designed by a linear combination of the objective Hamiltonian $H_O$ and the constraint Hamiltonian $H_C$. The objectives and constraints of the problem are contained by $H_O$ and $H_C$, respectively.

4.1.1. Design of the Objective Hamiltonian

Suppose that a basic Boolean function $B_1\left(x\right)$ exists as follows:

$$B_1\left(x\right)=x\mathrm{where}x\in \{0,1\}.$$

(18)

Due to quantum Fourier expansion, Equation (18) can be mapped to Boolean Hamiltonian $H_{B_1}$ where I and Z are an identity operator and the Pauli-Z operator, respectively [25]:

$$H_{B_1}=\frac{1}{2}(I-Z).$$

(19)

According to Equations (18) and (19), the objective function Equation (14) can be mapped to the following Hamiltonian:

$$H_{O^{\prime }}=\sum _{\forall l_k\in \mathcal{L}}\frac{1}{2}{w}_k(I-Z_k),$$

(20)

where $Z_k$ is the Pauli-Z operator applied to ${\mathcal{I}}_k$. Since $H_{O^{\prime }}$ is mapped from the objective function Equation (14), which should be maximized, $H_{O^{\prime }}$ should also be maximized. Therefore, the objective Hamiltonian $H_O$ should be minimized is as follows:

$$H_O=\sum _{\forall l_k\in \mathcal{L}}\frac{1}{2}{w}_k{Z}_k.$$

(21)

4.1.2. Design of the Constraint Hamiltonian

In the MWIS-based wireless scheduling problem, a banned event is a case where both adjacent nodes of the conflict graph are scheduled, as shown in Case C of Figure 1. If the weights of $N_i$ and $N_j$ in Case C are defined as $W_{N_i}$ and $W_{N_j}$ respectively; then the constraint function $C^{\prime }(i,j)$, which counts the banned events, can be represented as follows:

$$C^{\prime }(i,j)=\sum _{i=1}^n\sum _{j=1}^n(W_{N_i}+W_{N_j})\left|E_C(N_i,N_j)\right|\mathrm{where}i>j.$$

(22)

Here, n is the number of nodes and $|E_C(N_i,N_j)|$ is the number of $E_C(N_i,N_j)$; $i>j$ is a condition to avoid the duplication of the same edge.

According to Equations (13)–(17), $C^{\prime }(i,j)$ can be redefined as $C(i,j)$ with symbols in Section 3 as follows:

$$\begin{array}{ccc}\hfill C(i,j)& =& \sum _{\forall l_i\in \mathcal{L}}\sum _{\forall l_j\in \mathcal{L}}(w_i+w_j){\mathcal{E}}_{(i,j)}\mathrm{where}i>j\hfill \\ & =& \sum _{\forall l_i\in \mathcal{L}}\sum _{\forall l_j\in \mathcal{L}}(w_i+w_j)({\mathcal{I}}_i\wedge {\mathcal{I}}_j)\mathrm{where}i>j.\hfill \end{array}$$

(23)

Here, ∧ is a Boolean AND operator and $C(i,j)$, which counts the banned events, must be 0 or the minimum value. Due to quantum Fourier expansion, the AND Boolean function $B_2(x_1,x_2)$ can be mapped to the following Boolean Hamiltonian $H_{B_2}$ [25]:

$$\begin{array}{ccc}\hfill B_2(x_1,x_2)& =& x_1\wedge x_2\mathrm{where}\hfill \end{array}$$

$$\begin{array}{ccc}& & x_1\in \{0,1\}\mathrm{and}{x}_2\in \{0,1\},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill H_{B_2}& =& \frac{1}{4}(I-Z_1-Z_2+Z_1{Z}_2),\hfill \end{array}$$

(25)

where $Z_1$ and $Z_2$ are the Pauli-Z operators applying on $x_1$ and $x_2$, respectively.

According to Equations (24) and (25), the constraint function Equation (23) can be represented as following Hamiltonian:

$$H_{C^{\prime }}=\sum _{\forall l_i\in \mathcal{L}}\sum _{\forall l_j\in \mathcal{L}}\frac{1}{4}(w_i+w_j)(I-Z_i-Z_j+Z_i{Z}_j)\mathrm{where}i>j.$$

(26)

Here, $Z_i$ and $Z_j$ are the Pauli-Z operators applied to ${\mathcal{I}}_i$ and ${\mathcal{I}}_j$, respectively. Since $C(i,j)$ must be 0 or the minimum value, $H_{C^{\prime }}$, mapped from $C(i,j)$, should be minimized. Therefore, the constraint Hamiltonian $H_C$, which is a simplified form of $H_{C^{\prime }}$, is as follows:

$$H_C=\sum _{\forall l_i\in \mathcal{L}}\sum _{\forall l_j\in \mathcal{L}}-\frac{1}{4}(w_i+w_j)(Z_i+Z_j-Z_i{Z}_j)\mathrm{where}i>j.$$

(27)

Based on the definitions of $H_O$ and $H_C$, the problem Hamiltonian $H_P$ can be defined as follows:

$$H_P=H_O+\rho H_C,$$

(28)

where $\rho \ge 1$ is the penalty rate, which indicates the rate at which $H_C$ affects $H_P$ compared to $H_O$ in the implementation.

4.2. Design of the Mixing Hamiltonian

The mixing Hamiltonian, denoted by $H_M$, generates a variety of cases that can appear in the problem. MWIS can be formulated by a binary bit string that represents a set of nodes (e.g., |1010101〉); thus, various cases can be created by flipping the state of each node, represented by |0〉 or |1〉. The bit-flip can be handled by the Pauli-X operator, thus $H_M$ is as follows:

$$H_M=\sum _{\forall l_k\in \mathcal{L}}{X}_k.$$

(29)

4.3. Apply to QAOA Sequence

The application of the designed Hamiltonian to the QAOA sequence starts to occur when the design of Hamiltonians, i.e., $H_P$ and $H_M$, are completed. First, the parameterized state $|\gamma ,\beta \rangle$ can be generated by applying $H_P$ and $H_M$, defined in Equations (21), (27), (28) and (29), to (11). Here, the initial state |s〉 is set to the equivalent superposition state using the Hadamard gates. The expectation value of $H_P$ can be measured on the generated parameterized state $|\gamma ,\beta \rangle$. The parameters $\gamma$ and $\beta$ are iteratively updated in a classical optimization loop. When the QAOA sequence terminates, the optimal parameters ${\gamma }_{opt}$ and ${\beta }_{opt}$ are obtained. Thus, the scheduling solution can be obtained by the measurement of the expectation value of $H_P$ on the optimal state $|{\gamma }_{opt},{\beta }_{opt}\rangle$ as follows:

$$\langle F\rangle =\langle {\gamma }_{opt},{\beta }_{opt}|H_P|{\gamma }_{opt},{\beta }_{opt}\rangle ,$$

(30)

where 〈F〉 is the expectation value of the objective function Equation (14) over the returned solution samples.

5. Performance Evaluation

The proposed QAOS algorithm is implemented using Cirq and TensorFlow-Quantum, which were developed for the NISQ algorithm and quantum machine learning computation [26].

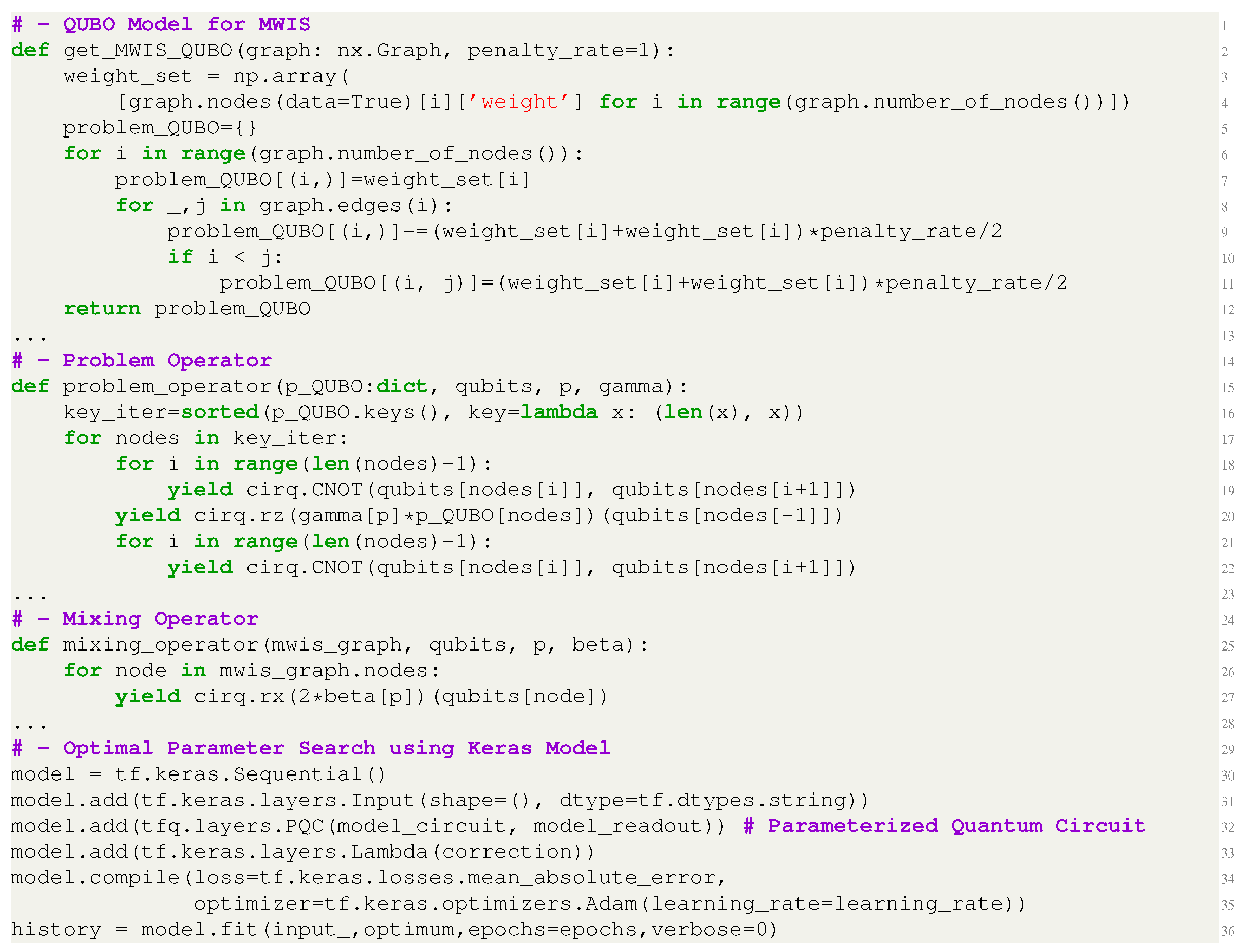
5.1. Software Implementation

The application of the quantum gates, the basic units of the quantum circuit, is expressed by unitary operators. Based on the definitions of Hamiltonians in Section 4, the objective operator $U_O\left({\gamma }_{\zeta }\right)$, constraint operator $U_C\left({\gamma }_{\zeta }\right)$, problem operator $U_P\left({\gamma }_{\zeta }\right)$, and mixing operator $U_M\left({\beta }_{\zeta }\right)$, which are unitary operators, can be defined as follows:

$$\begin{array}{ccc}\hfill U_O\left({\gamma }_{\zeta }\right)& =& e^{-i{\gamma }_{\zeta }{H}_O},\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill U_C\left({\gamma }_{\zeta }\right)& =& e^{-i{\gamma }_{\zeta }\rho H_C},\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill U_P\left({\gamma }_{\zeta }\right)& =& U_O\left({\gamma }_{\zeta }\right)U_C\left({\gamma }_{\zeta }\right)=e^{-i{\gamma }_{\zeta }(H_O+\rho H_C)},\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill U_M\left({\beta }_{\zeta }\right)& =& e^{-i{\beta }_{\zeta }{H}_M},\hfill \end{array}$$

(34)

where ${\gamma }_{\zeta }$ and ${\beta }_{\zeta }$ are in $\gamma \equiv {\gamma }_1\cdots {\gamma }_p$ and $\beta \equiv {\beta }_1\cdots {\beta }_p$, respectively: $\zeta \in {\mathbb{Z}}^{+}$ and $1\le \zeta \le p$. Note that the implementation of $U_P\left({\gamma }_{\zeta }\right)$ and $U_M\left({\beta }_{\zeta }\right)$ is the core of QAOS implementation.

In Figure 2, cirq.rz() and cirq.CNOT() are used for the implementation of $U_P\left({\gamma }_{\zeta }\right)$. Note that, cirq.rz() and cirq.CNOT() represent the rotation-Z gate and the controlled-NOT gate, respectively. In addition, $U_M\left({\beta }_{\zeta }\right)$ is implemented using cirq.rx(), which represents the rotation-X gate.

The part that finds the optimal parameters using Keras (one of the well-known open-source deep learning computation libraries) is shown in Figure 2, from line 29 to line 36. Here, the parametrized quantum circuit (PQC) layer provides the auto-management of variables in the parameterized circuit. In this model, Adam is used as a gradient-based optimizer [27,28].

5.2. Experiments

This experiment demonstrates the possibility of a novel quantum approach via QAOS by focusing on simple and light methods to wireless scheduling problems. In the classical approaches, a message-passing algorithm consisting of linear programming relaxation, maximum product method, and maximum a posteriori estimation is mainly used to solve the MWIS-based wireless scheduling problem [14,16,17]. However, if the network requires a more simple and lighter algorithm, the random and greedy-based algorithms are also used for wireless scheduling [29,30]. Thus, the performance of the proposed QAOS, based on QAOA, one of the simple and light quantum algorithms that intuitively express the state with qubit rotation, is compared with the random search and greedy search, which are simple and light classical algorithms [31,32]. In addition, the QAOS algorithm is executed with different p value settings, where the p value means the number of alternations of $U_P\left({\gamma }_{\zeta }\right)$ and $U_M\left({\beta }_{\zeta }\right)$ in Equations (33) and (34), i.e., $\zeta \in {\mathbb{Z}}^{+}$ and $1\le \zeta \le p$.

For the performance evaluation, random conflict graphs with 10 nodes are generated; then, random search, greedy search, and QAOS algorithms are performed for the given random conflict graphs. The measurement of each QAOS is performed 1000 times in each simulation (i.e., in each randomly generated conflict graph). The performance of each algorithm is quantitatively measured with $\eta$ as follows:

$$\eta \triangleq \frac{a}{b},$$

(35)

where a and b are the summations of weights of the scheduled nodes by the used algorithms and the summations of weights of the scheduled nodes by brute-force search (i.e., exhaustive search), respectively, for the given randomly generated graphs. As shown in Figure 3, the cumulative distribution functions (CDF) of $\eta$ for each algorithm are computed.

As presented in Figure 3, QAOS algorithms with $p\ge 8$ present a better performance than random search and greedy search, in any kind of randomly generated conflict graph. In these repeated simulations, the performances of QAOS algorithms are improved as the p value increases. In particular, the performance of the QAOS algorithm with $p=10$ is much better than the QAOS algorithms with $p=8$ and $p=9$. As shown in

Table 1. Percentage of optimal solution computation.

QAOS, $\mathit{p}=10$	QAOS, $\mathit{p}=9$	QAOS, $\mathit{p}=8$	Greedy	Random
69.50%	49.67%	42.83%	33.83%	15.17%

, the QAOS algorithm with $p=10$ returns optimal solutions (i.e., equivalent to the solutions obtained by brute-force search) with a ratio of 69.50%. Through these results, we have verified that the proposed QAOS algorithm presents beautiful results in terms of the accuracy of the solutions.

6. Concluding Remarks and Future Work

Wireless scheduling was modeled with the MWIS problem, which is one of the well-known NP-hard problems. In order to solve the MWIS problem, a QAOA-based scheduling algorithm, so-called quantum approximate optimization for scheduling (QAOS), was proposed. The proposed QAOS was implemented using Cirq and TensorFlow-Quantum. QAOS outperformed greedy search and random search in the performance evaluation on the random conflict graphs. Therefore, our novel quantum approach to the wireless scheduling problem via QAOS was meaningful.

Future research will focus on improving the performance of QAOS. In one method, introducing an error correction code to QAOS is considered. This method is expected to improve the sampling quality. Another method is to develop a new optimizer that can more accurately find the optimal parameters of QAOS. A novel optimizer is needed that is more suitable for quantum models than the mainly used optimizers such as Adam, Nelder–Mead (NM), and Broyden–Fletcher–Goldfarb–Shanno (BFGS). From the perspective of quantum machine learning, developing a novel optimizer for the parameterized quantum circuit like the QAOS circuit will be a meaningful challenge.