Experimental Study on the Torsional Behaviour of Prestressed HSC Hollow Beams
Abstract
1. Introduction
2. Experimental Program
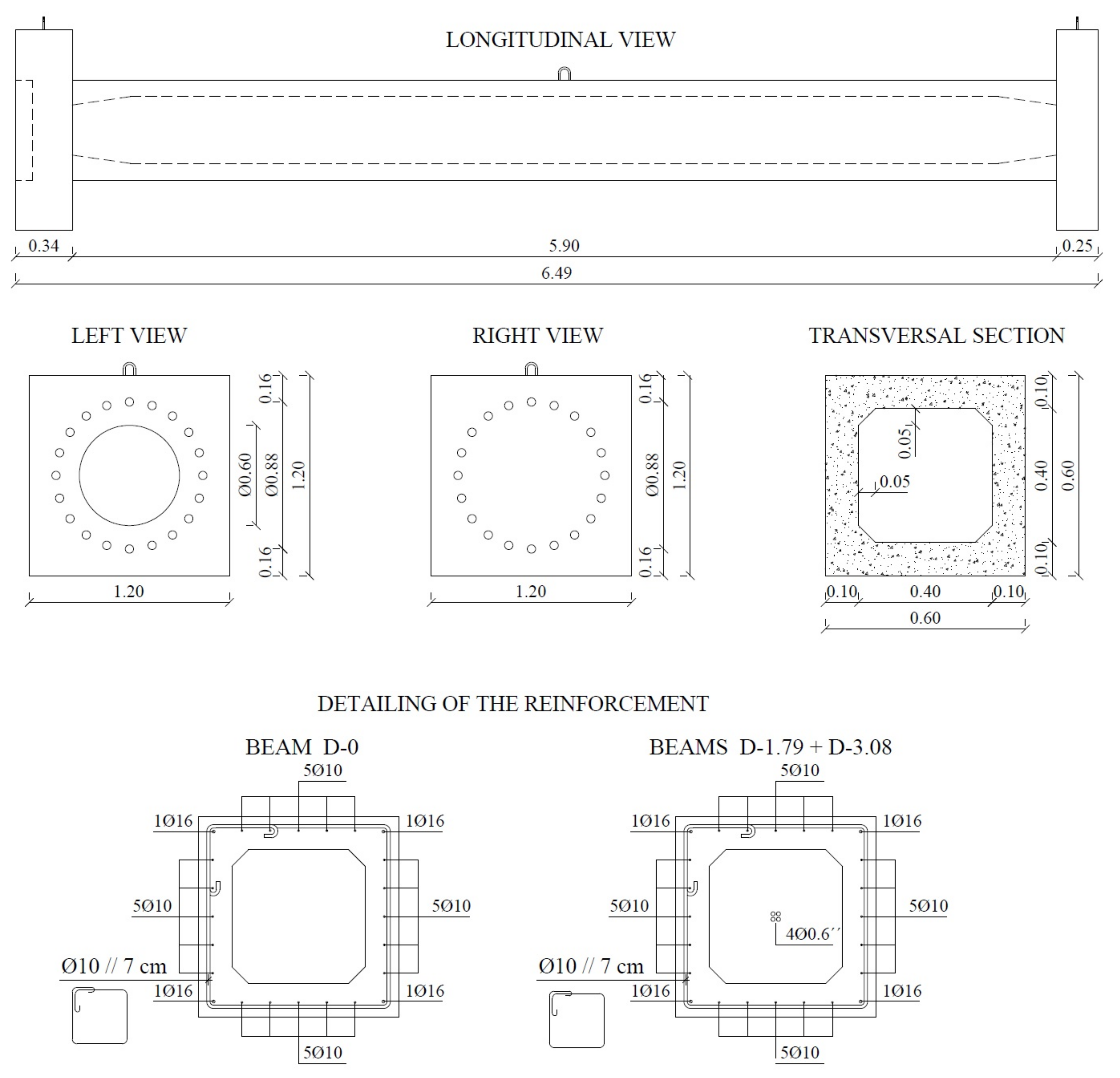
2.1. Test Specimens
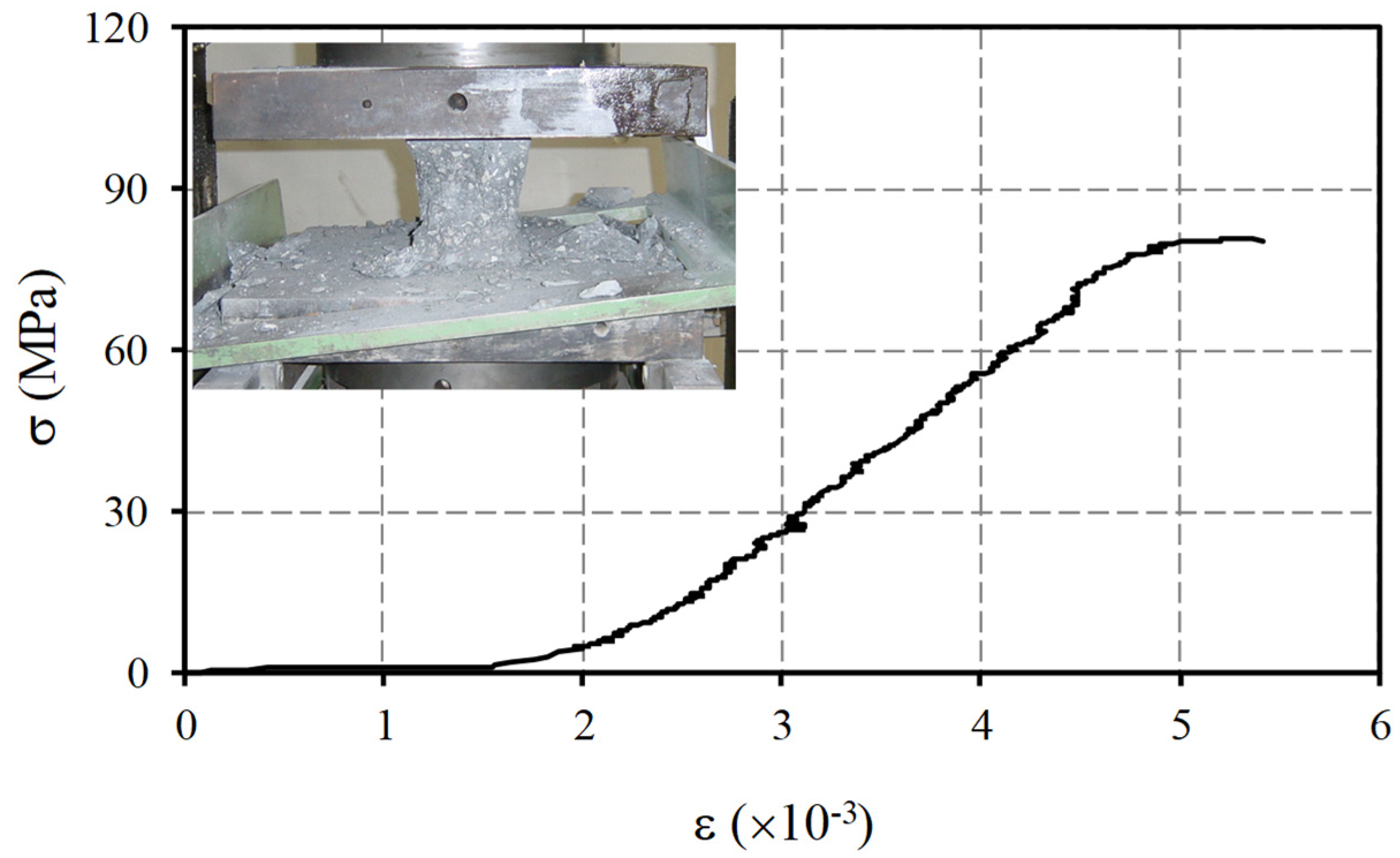
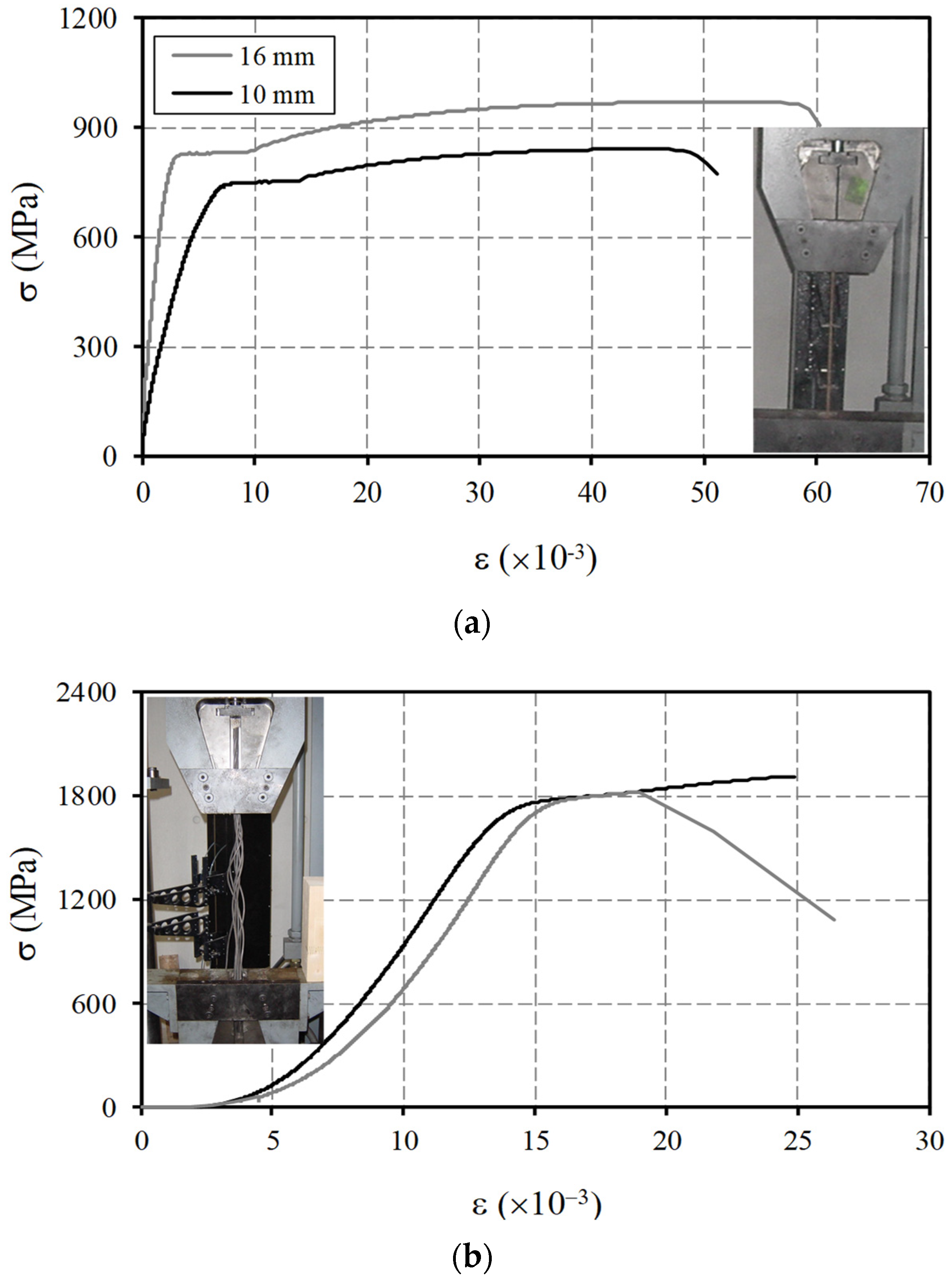
2.2. Materials Properties
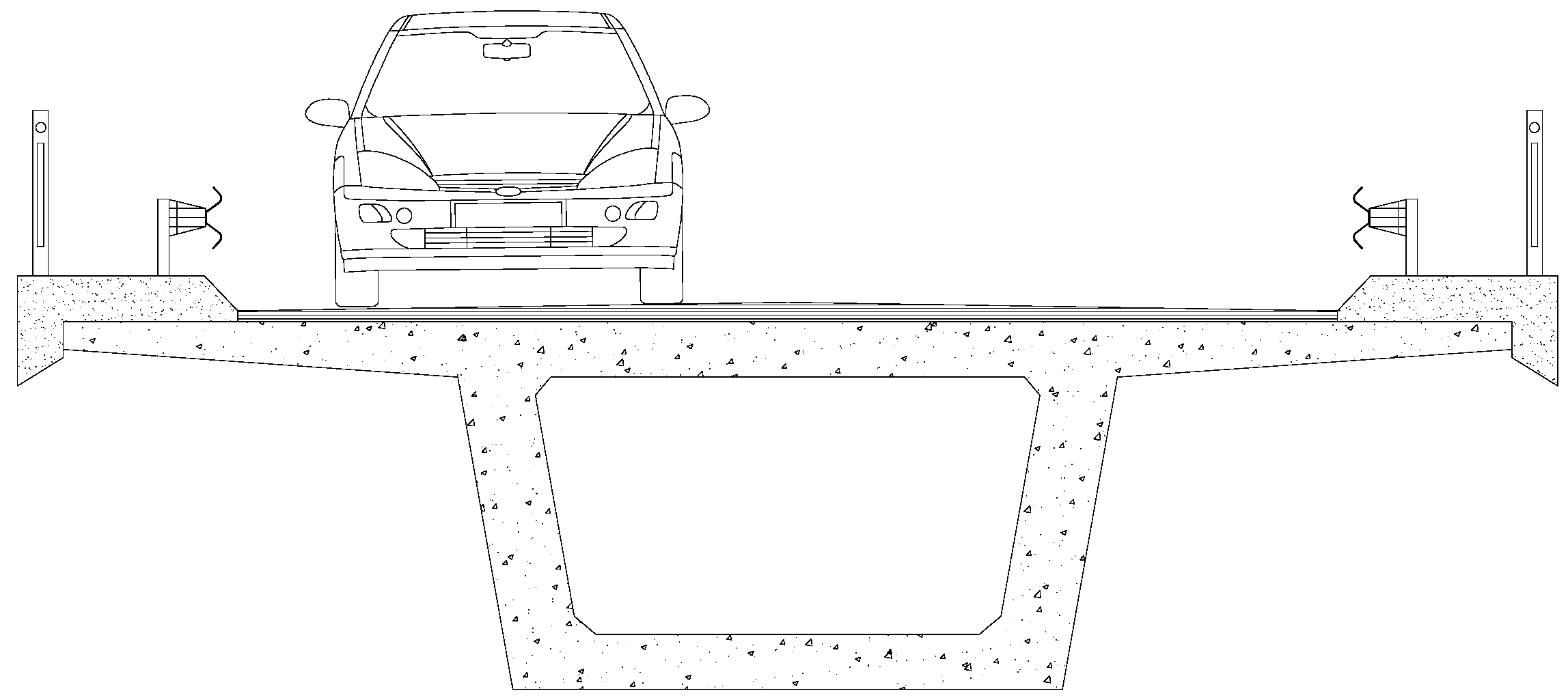
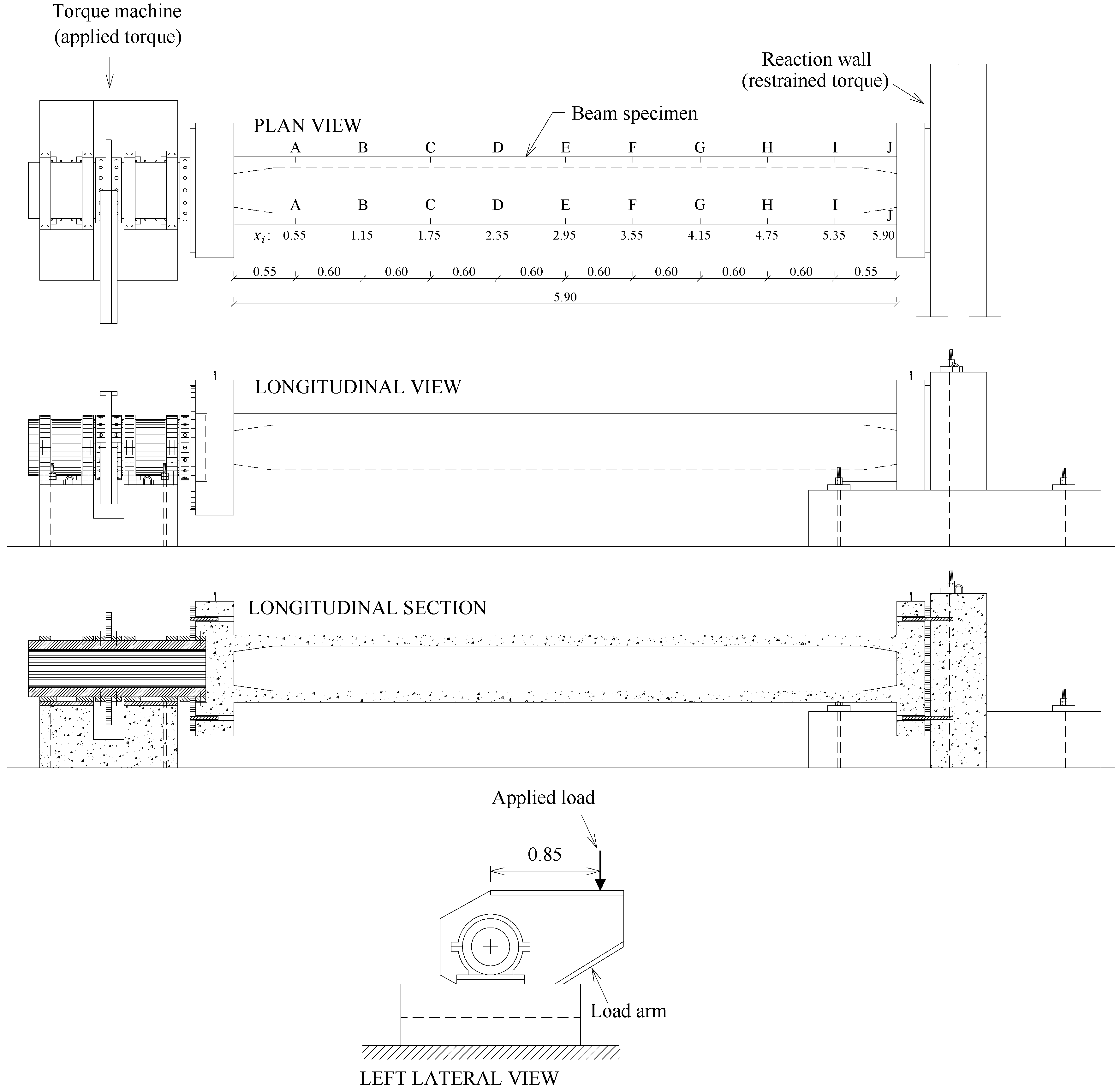
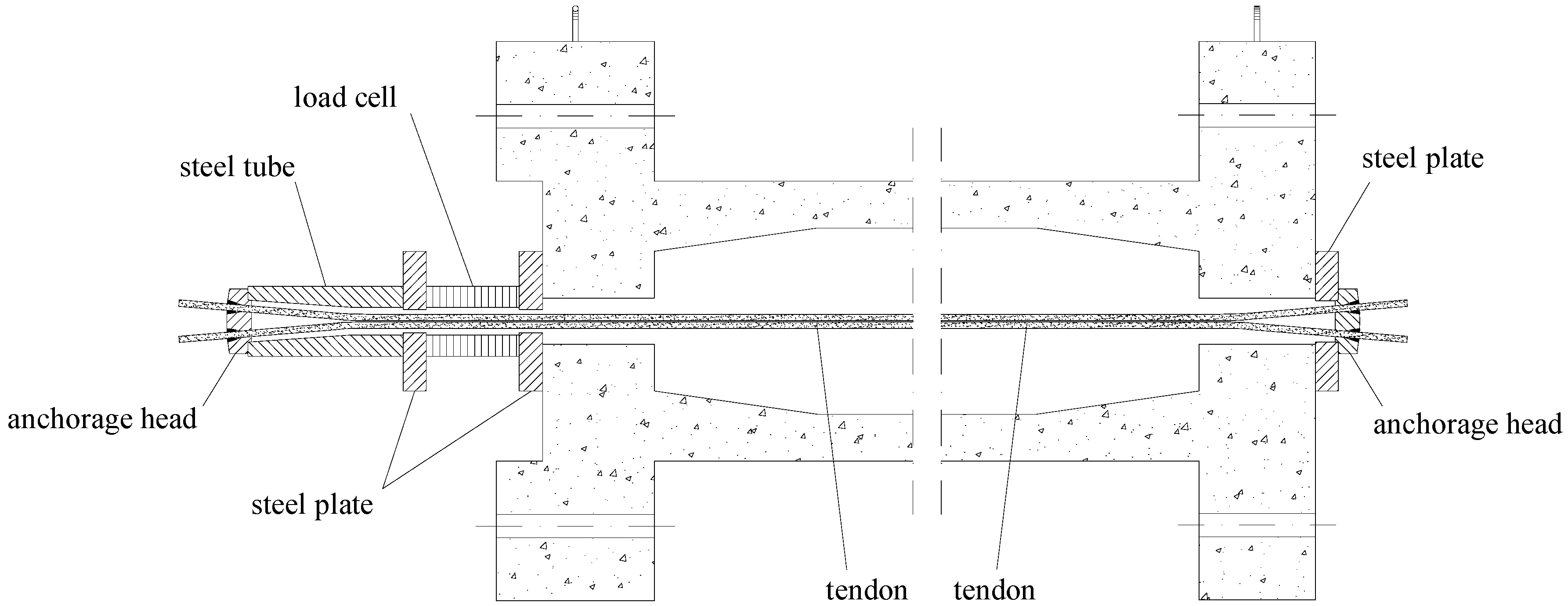
2.3. Testing Procedure
- a test frame where the mechanical actuator is fixed;
- a device that receives the load from the mechanical actuator and applies a torsional moment in one end of the test beams;
- a device that fixes the test beam at the other end, restricting its transversal rotation (twist) and allowing its longitudinal deformation (elongation).
3. Global Analysis of the Experimental Results
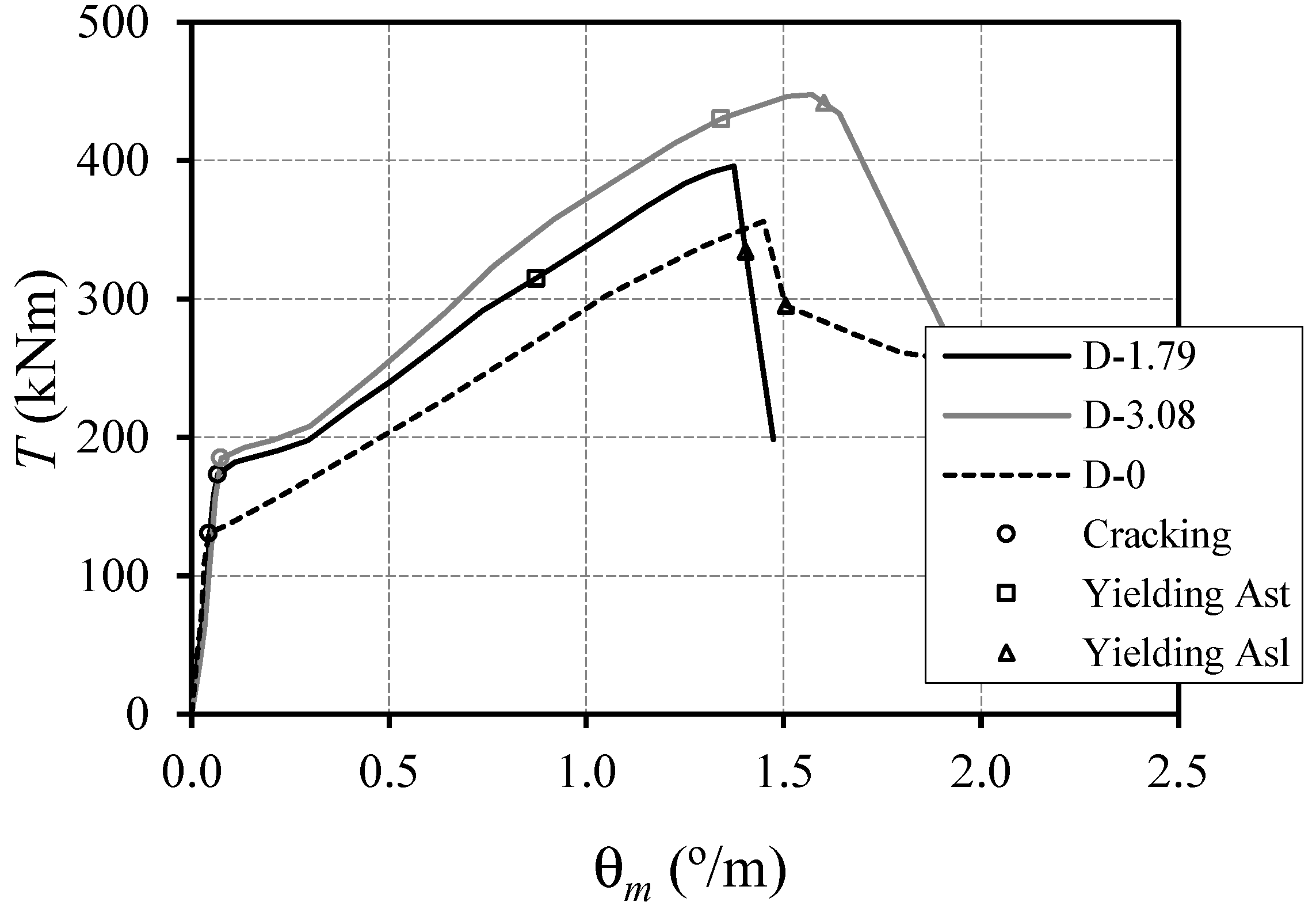
3.1. Torsional Moments vs. Twists
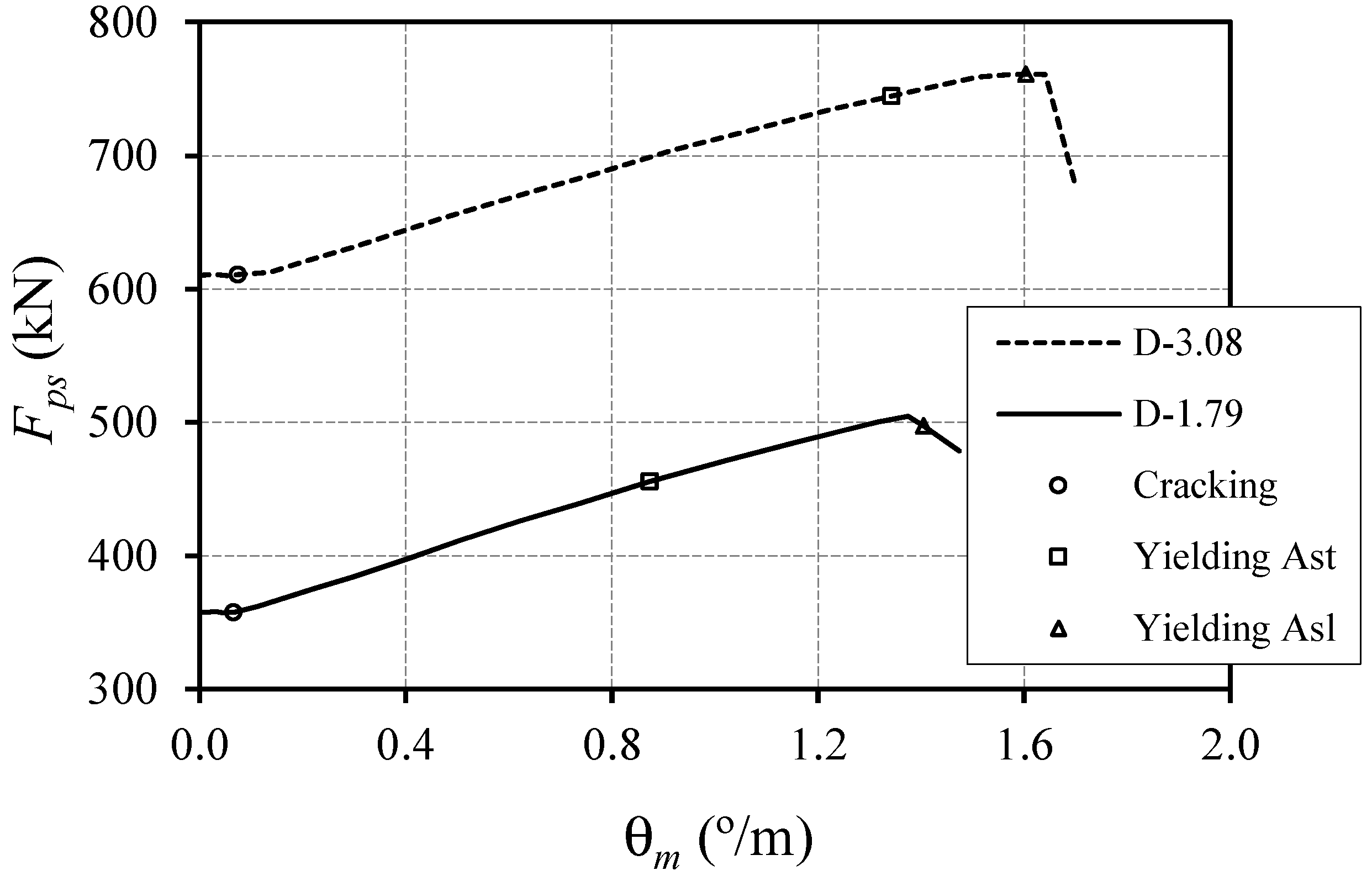
3.2. Force in the Prestress Reinforcement vs. Twists
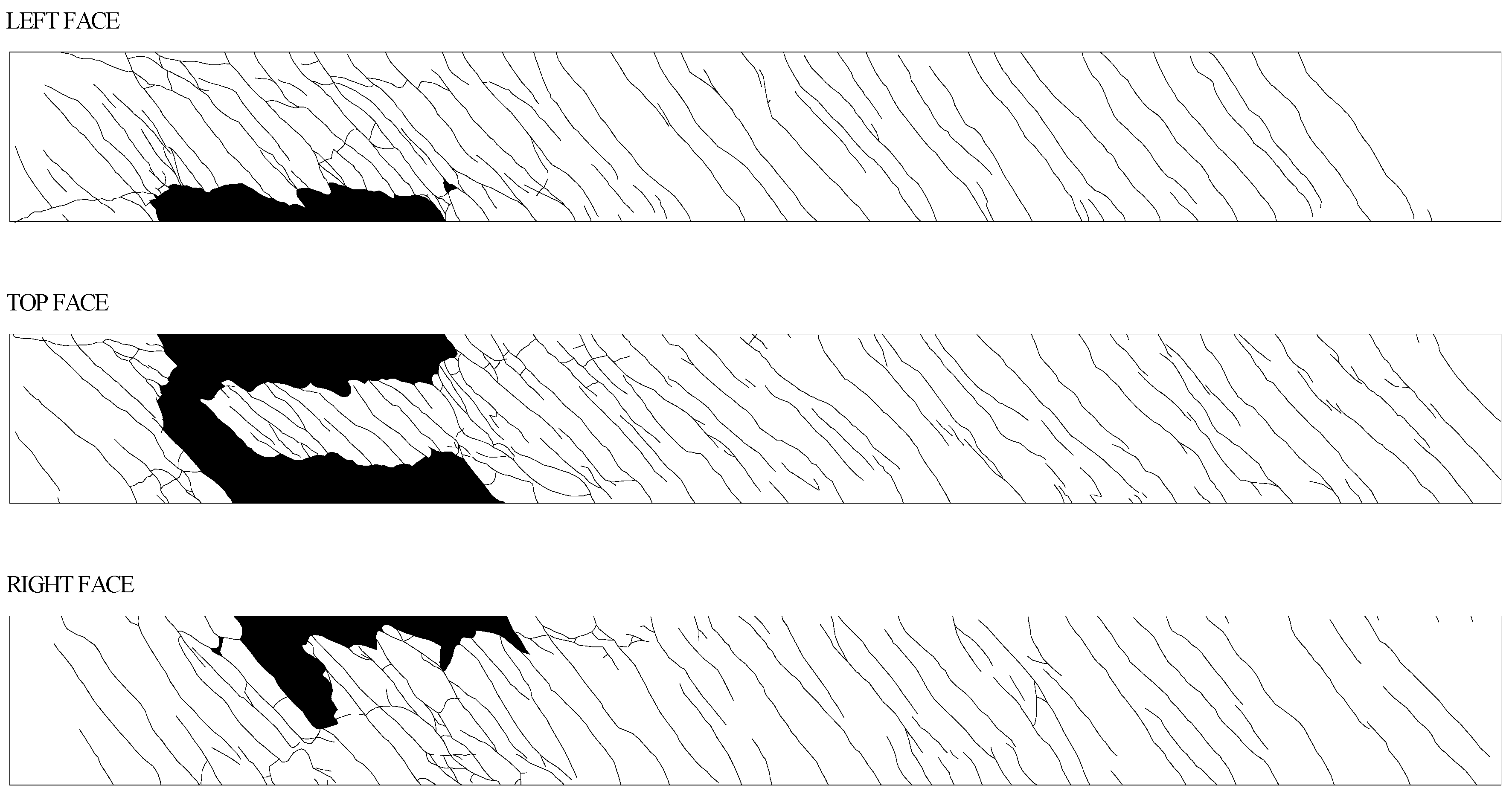
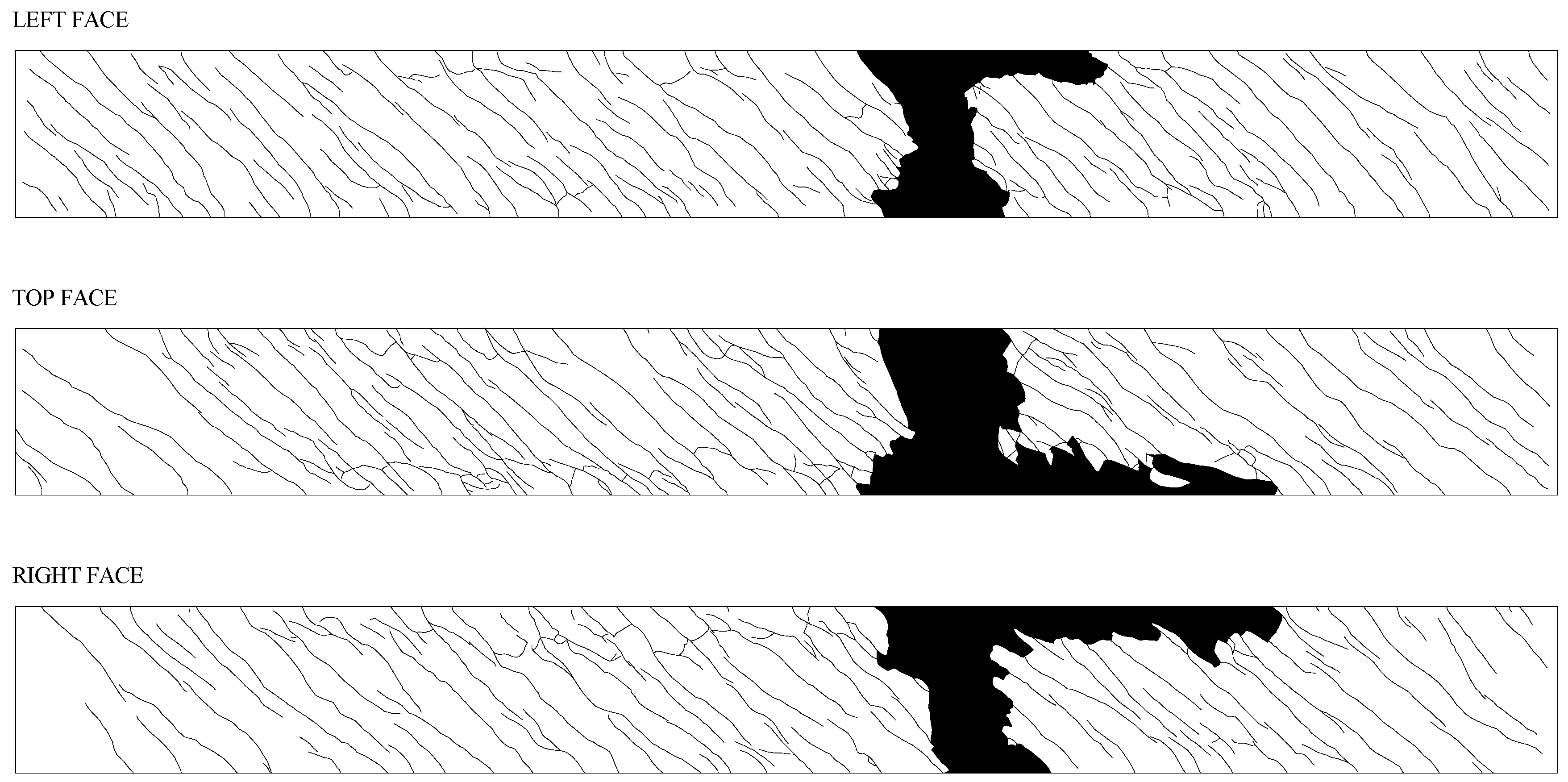
4. Failure Modes and Cracking Patterns
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dahl, K.K.B. Uniaxial Stress-Strain Curve for Normal and High Strength Concrete; Report No. 182; Department of Structural Engineering, Technical University of Denmark: Kgs. Lyngby, Denmark, 1992; p. 58. [Google Scholar]
- Hsu, T.T.C. Torsion of Structural Concrete—Behavior of Reinforced Concrete Rectangular Members; Torsion of Structural Concrete, SP-18; American Concrete Institute: Detroit, MI, USA, 1968; pp. 261–306. [Google Scholar]
- Lampert, P.; Thürlimann, B. Essais de Poutre en Béton Armé Sous Torsion Simple et Flexion Combinées (Tests on Reinforced Concrete Beams under Pure Torsion and Combined Bending); Torsion, Bulletin d´Information Nº 71, Comitée Européen du Béton: Brussels, Belgium, 1969; pp. 177–207. [Google Scholar]
- Mitchell, D.; Collins, M.P. Behavior of Structural Concrete Beams in Pure Torsion; Civil Engineering Publication No.74-06; Department of civil Engineering, University of Toronto: Toronto, ON, Canada, 1974; p. 88. [Google Scholar]
- Leonhardt, F.; Schelling, G. Torsionsversuche na Stahlbetonbalken (Torsion Tests on Reinforced Concrete Beams); Bulletin No. 239; Deutscher Ausschuss für Stahlbeton: Berlin, Germany, 1974; p. 122. [Google Scholar]
- Bernardo, L.F.A.; Lopes, S.M.R. Torsion in HSC Hollow Beams: Strength and Ductility Analysis. ACI Struct. J. 2009, 106, 39–48. [Google Scholar]
- Jeng, C.H. Unified Softened Membrane Model for Torsion in Hollow and Solid Reinforced Concrete Members: Modeling Precracking and Postcracking Behavior. J. Struct. Eng. 2015, 141, 04014243. [Google Scholar] [CrossRef]
- Bernardo, L.F.A.; Lopes, S.M.R. Behaviour of Concrete Beams under Torsion—NSC Plain and Hollow Beams. Mater. Struct. 2008, 41, 1143–1167. [Google Scholar] [CrossRef]
- Bernardo, L.F.A.; Lopes, S.M.R. Theoretical Behaviour of HSC Sections under Torsion. Eng. Struct. 2011, 33, 3702–3714. [Google Scholar] [CrossRef]
- Lopes, S.M.R.; Bernardo, L.F.A. Twist Behaviour of High-Strength Concrete Hollow Beams—Formation of Plastic Hinges along the Length. Eng. Struct. 2009, 31, 138–149. [Google Scholar] [CrossRef]
- Lopes, S.M.R.; Bernardo, L.F.A. Plastic Rotation Capacity of High-Strength Concrete Beams. Mater. Struct. 2003, 36, 22–31. [Google Scholar] [CrossRef][Green Version]
- Bernardo, L.F.A.; Lopes, S.M.R. Plastic Analysis of HSC Beams in Flexure. Mater. Struct. 2009, 42, 51–69. [Google Scholar] [CrossRef][Green Version]
- El-Degwy, W.M.; McMullen, A.E. Prestressed Concrete Tests Compared with torsion Theories. PCI J. 1985, 30, 96–127. [Google Scholar]
- Hsu, T.T.C.; Mo, Y.L. Softening of Concrete in Torsional Members—Prestressed Concrete. J. Am. Concr. Inst. 1985, 82, 603–615. [Google Scholar]
- Wafa, F.F.; Shihata, S.A.; Ashour, S.A.; Akhtaruzzaman, A.A. Prestressed High-Strength Concrete Beams Under Torsion. J. Struct. Eng. 1995, 121, 1280–1286. [Google Scholar] [CrossRef]
- NP EN 1992–1-1. Eurocode 2: Design of Concrete Structures—Part 1: General Rules and Rules for Buildings; European Committee for Standardization—CEN: Brussels, Belgium, 2010.
- Hsu, T.T.C. Torsion of Reinforced Concrete; Van Nostrand Reinhold Company: New York, NY, USA, 1984; p. 516. [Google Scholar]




| Beam. | cm | cm | cm | cm2 | cm2 | cm2 | cm | % | % | % | MPa | MPa | GPa | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D-0 | 10.9 | 53.5 | 53.7 | 23.75 | 0.79 | 0 | 7.0 | 0.66 | 0.67 | 1.33 | 0.99 | 77.8 | 4.33 | 40.7 |
| D-1.79 | 11.4 | 54.3 | 54.2 | 23.75 | 0.79 | 5.60 | 7.0 | 0.66 | 0.68 | 1.34 | 0.97 | 80.8 | 4.43 | 41.1 |
| D-3.08 | 11.5 | 55.0 | 54.6 | 23.75 | 0.79 | 5.60 | 7.0 | 0.66 | 0.68 | 1.34 | 0.96 | 78.8 | 3.66 | 37.4 |
| Components | Dosage |
|---|---|
| Thin sand | 164 kg |
| Thick sand | 908 kg |
| Crushed Granit 5–11 mm | 734 kg |
| Normal Portland Cement (C): Type I/42.5R | 375 kg |
| Admixture—Rheobuild 1000 | |
| Silica Fume (Sikacrete HD) | 41 kg |
| Water (A) | |
| A/(C + Additions) | 0.35 |
| Beam | kNm | °/m | kNm2 | kNm2 | kNm | °/m | kNm | °/m | |
|---|---|---|---|---|---|---|---|---|---|
| D-0 | 130.5 | 0.04 | 172,940 | a = 170.87; b = 119.43 | 9790 | - | - | 355.9 | 1.45 |
| D-1.79 | 172.9 | 0.07 | 152,188 | a = 194.73; b = 142.95 | 11,157 | 314.9 | 0.87 | 396.0 | 1.38 |
| D-3.08 | 184.7 | 0.08 | 141,823 | a = 148.05; b = 132.34 | 14,212 | 430.0 | 1.34 | 447.7 | 1.57 |
| Beam | cm | ° |
|---|---|---|
| D-0 | 13.0 | 46.3 |
| D-1.79 | 12.9 | 44.8 |
| D-3.08 | 13.6 | 44.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernardo, L.; Lopes, S.; Teixeira, M. Experimental Study on the Torsional Behaviour of Prestressed HSC Hollow Beams. Appl. Sci. 2020, 10, 642. https://doi.org/10.3390/app10020642
Bernardo L, Lopes S, Teixeira M. Experimental Study on the Torsional Behaviour of Prestressed HSC Hollow Beams. Applied Sciences. 2020; 10(2):642. https://doi.org/10.3390/app10020642
Chicago/Turabian StyleBernardo, Luís, Sérgio Lopes, and Mafalda Teixeira. 2020. "Experimental Study on the Torsional Behaviour of Prestressed HSC Hollow Beams" Applied Sciences 10, no. 2: 642. https://doi.org/10.3390/app10020642
APA StyleBernardo, L., Lopes, S., & Teixeira, M. (2020). Experimental Study on the Torsional Behaviour of Prestressed HSC Hollow Beams. Applied Sciences, 10(2), 642. https://doi.org/10.3390/app10020642







