3.1. 3D Printing Orientation
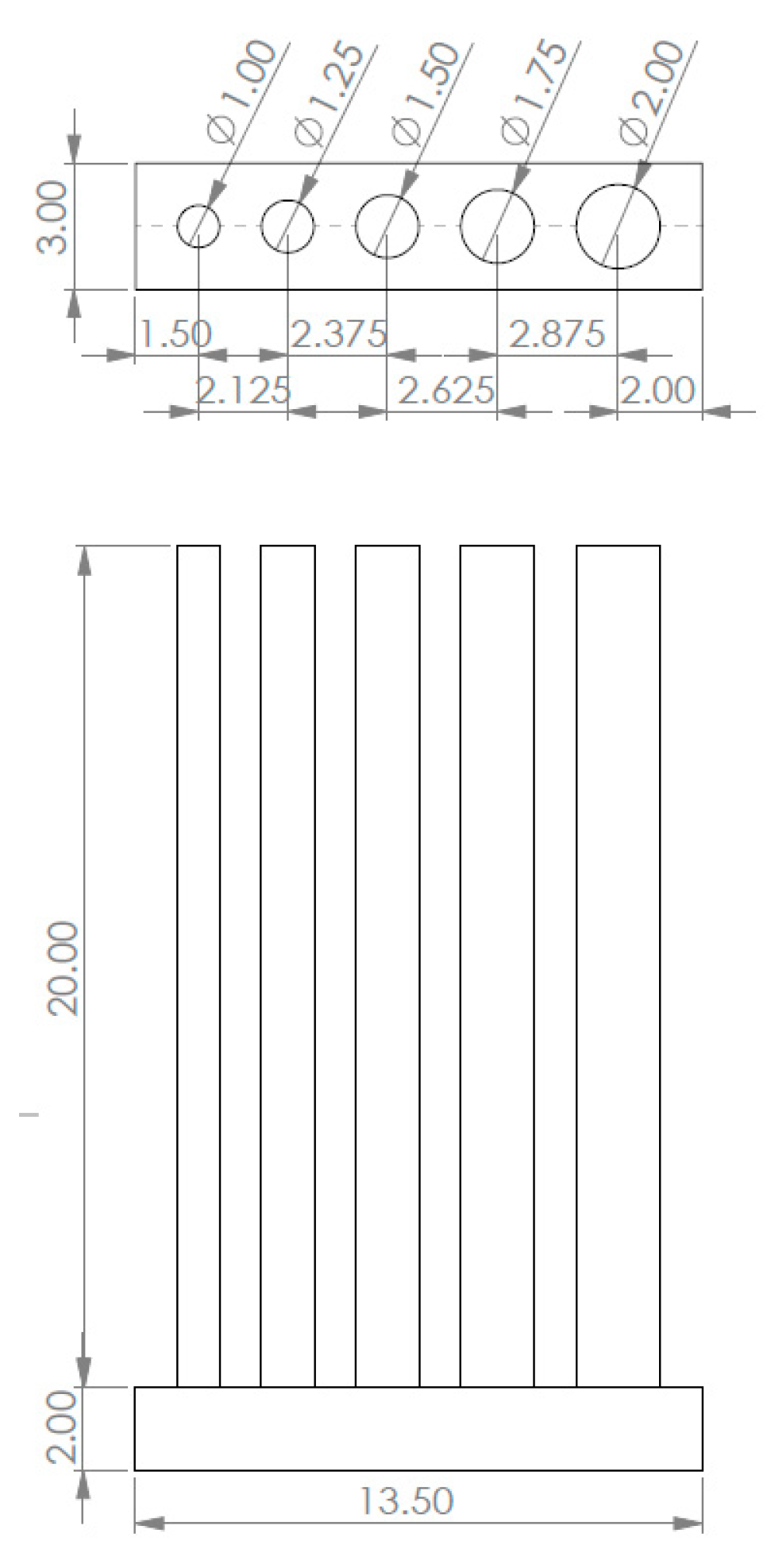
The variation in the number of support structures showed that they have a great influence on the shape accuracy, which was expected–the higher the number, the better the shape accuracy (see B1 to B3 in
Figure 7). Thus, all test prints without support structures show forming inaccuracies with a bar diameter <2 mm (see B1, B4 to B6 in
Figure 7). In order to develop a printing regime for structures that are as filigree as possible with as few supporting structures as possible, the printing orientation was also varied. It was found that nonangled specimens (without support structures) are more accurate in shape than angled ones at very small diameters (see B1 in comparison to B4, B5 and B6: the 1 mm bar (smallest) is incompletely printed at B1). However, the orientation (rotation in z-axis) of the specimens on the building platform has no influence on the shape accuracy (see B4 and B6 in
Figure 7).
As a result, for the selected material (Flexible Resin V2), the 3D printing unit (Formlabs V2) and the printing parameters used (0.05 mm layer height, no support structure), with a free length of the individual bar of 20 mm, a bar diameter of 1.75 mm (corresponds to the target diameter created in CAD) should not be undercut in order to achieve a high probability of forming accuracy (B2 and B3 have subtle forming inaccuracies). Of all the samples, the target diameter of 2 mm created in CAD showed the smallest form deviations and was therefore selected for all further tests and simulations. There was a difference between the nominal diameter created in CAD and the actual diameter obtained after 3D printing (pl. see
Section 3.4).
The following diameter specifications in the simulation therefore refer to the real diameter of 1.7 mm.
3.2. Material Characterization and Young’s Modulus
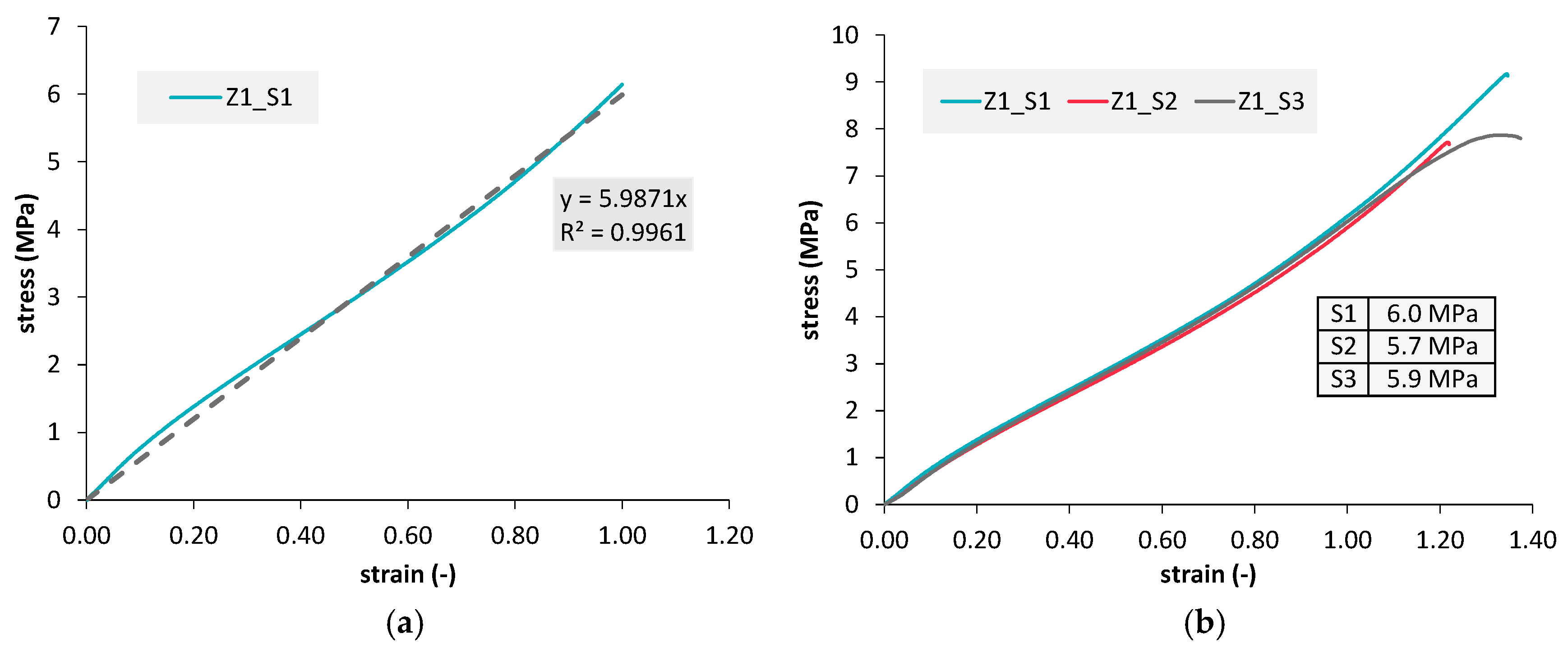
Using the findings of the minimal printable diameter, round tension bars were defined, additively manufactured and mechanically tested. All three measured samples show a similar curve progression as shown in
Figure 8. Since the curves, in this case, show an almost linear-elastic shape and all three curves are almost identical, it is therefore warranted to determine the mechanical parameters (Young’s modulus) required for the simulation by means of a quasi-static tension test.
Figure 8b shows an exemplary regression line for one sample. All regression lines were created in the uniform range up to the engineering strain of ε = 100%. The values of Youngs’ modulus thus determined are given in the table in
Figure 8b and show similar values. This allows the calculation of the Young’s modulus required for simulation as an average of the values obtained. As a result of those parameter combinations (material and printing parameter), the modulus of 5.9 MPa (5.9 N/mm
2) was determined, which was rounded to 6 MPa (6 N/mm
2) and then used in later simulations. A potential unloading behavior may occur that is different from the loading stage. In the following numerical investigation, only the loading of the structure is analyzed. A more complex material characterization will be part of further studies.
3.3. Preliminary Study of Net Parameters
In the first design step, the parameters of the net structure were investigated concerning the prospects for everting behavior and possible occurrence of critical loadings. The parameters are strongly linked to each other, due to the discrete nature of the net and amount of crossing points. With a given number of circumferential crossing points, the length of bars scales the angles between them and vice versa. At a given bar length, an increase of circumferential crossing points leads to changed angles between bars. On the other hand, with a given cylinder height, the number of crossing points in the cylinder axis direction changes bar lengths and angles. Hence, some parameters were fixed and the alteration of the main variable defines the remaining dependent parameters.
The number of circumferential crossing points was set to
, which results in a section angle
(
Figure 9). The number of crossing points
in the cylinder axis direction was chosen to give a cylinder height of
near
, which reaches the maximum printable height. The cylinder radius was set to
. The angle
between the bar and horizontal axis was chosen as the main variable. The angle
between the bar and vertical axis and the bar length itself
results from the main variable and fixed parameters. The geometric model was built via Ansys APDL script, so that the crossing points were defined and connected with straight beam elements to structure the tubular geometry. With the script, the model was then transferred into LS-Dyna keywords. At the same time, load coordinate systems were defined to overcome the strict Cartesian restriction in LS-Dyna, which allows no general load definition in a cylindrical coordinate system.
Three variations 30°, 45° and 60° of the main variable
were modeled in LS-Dyna with beam elements (default type 1, Hughes-Liu with cross-section integration). Each bar consists of four beam elements (diameter of 1.7 mm) to account for the bending compliance of bars. The lower tube end nodes were fixed in all degrees of freedom, which models a clamping of the lower end. For the upper end nodes, a prescribed nodal translational in radial tube direction was applied for each node in the beginning of the simulation, using the already defined local Cartesian coordinate systems (
Figure 9a). Additionally, a translational motion in the negative z-direction (toward the lower end nodes) completes the initial everting stage and allows for a further continuous everting progress. The beams use a purely linear–elastic material model (*MAT_002) with Young’s modulus of
(6 N/mm
2) (according to evaluation of tensile test above), density of
and a Poisson’s ratio of
according to hyperelastic characteristics of material. A self-contact of the tube was defined using a single beam element set within the contact-card *CONTACT_AUTOMATIC_GENERAL. Otherwise, excessive self-penetration would occur. The total simulation time was set to 2 s to ensure a nearly quasi-static loading condition. This leads to a negative axial motion with a velocity of the upper-end tube nodes of −
in the z-direction.
The explicit solver with single-precision was used in LS-Dyna R11.0.0 winx64 (SMP type) to perform the computations on an eight-core desktop PC.
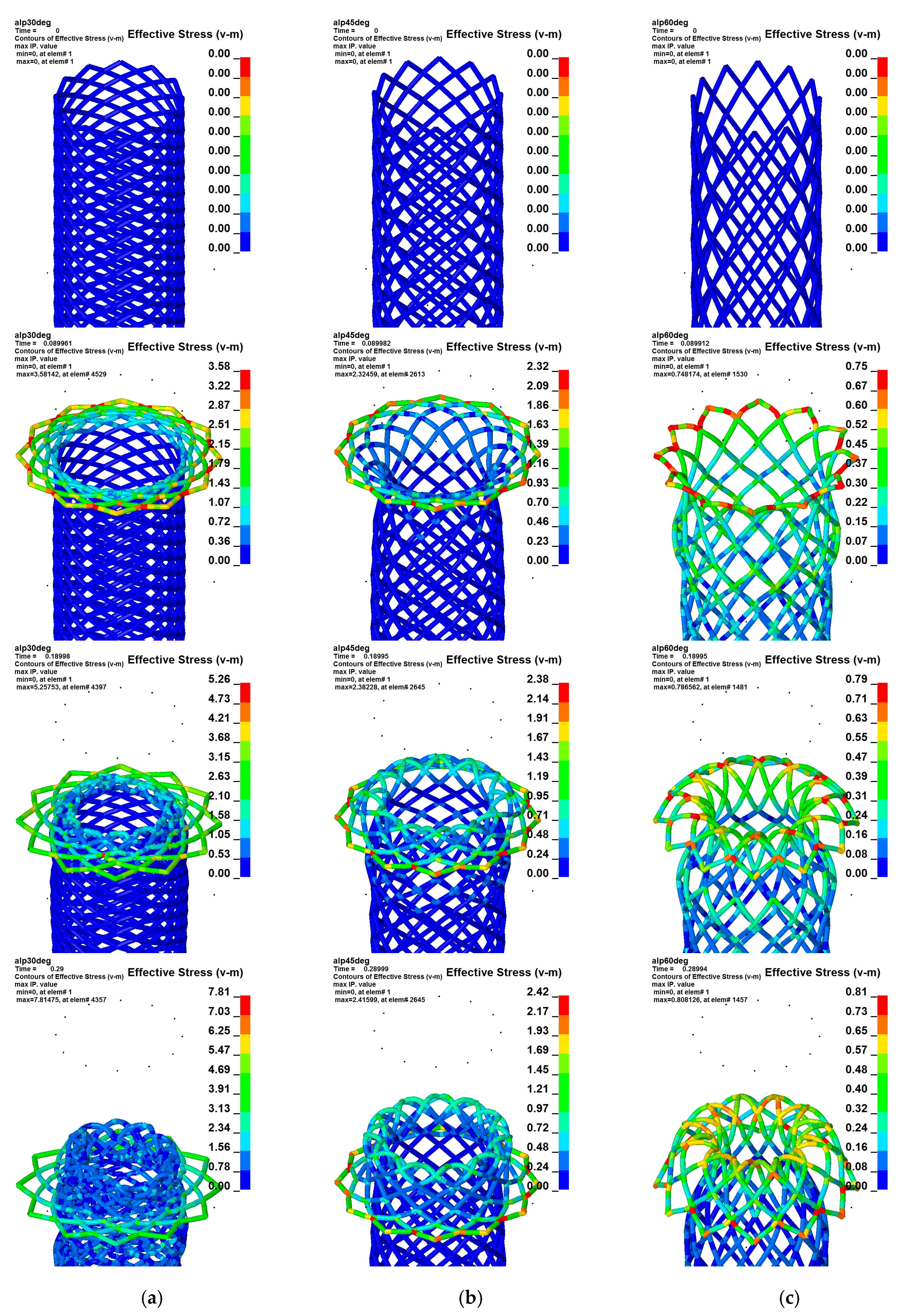
Figure 10 shows the results of the three geometry variation simulations (main variable
) as a comparison of equivalent von Mises stress distribution of the three models along everting simulation time. Each column (
Figure 10a–c) represents a single model with results of four simulation times. The times were recorded at equal simulation points and hence loading stages (rows in
Figure 10).
The model with the main angle of
(
Figure 10a) shows a very unstable evert behavior due to the highest structural stiffness against everting. In the initial everting stage, the structure below the everting zone is equally deformed (angles
and
) until a critical structural stiffness is reached; the whole tube shows an unstable deformation behavior in simulation after evert-buckling in the initial stage. Furthermore, in the initial everting stage, high equivalent von Mises stresses of about 4 MPa (4 N/mm
2) occur in the simulation.
Figure 10b shows the same everting process with an angle of
between the bar and horizontal axis. The initial stage is characterized by more stable everting behavior. Nevertheless, the deformed bar structure below the evert zone possesses a high stiffness. The elastic energy is mainly stored in the uneverted free zone below. The initial everting takes place after the structural stiffness of the tube below the everting zone is higher than the stiffness in the deformed everting zone. The observed average von Mises equivalent stress amounts to 2.5 MPa (2.5 N/mm
2). Further continuous everting takes place under stable conditions. Minor buckling on the free tubular surface below the evert-buckling zone was recorded. The third model with an angle of
shows very easy initial evert-buckling due to reduced structural stiffness against the nodal motion. Higher global instabilities can be seen, but in the initial phase, the everting behavior is the best of the three models. In the later continuous everting stage, some buckling in the region of still uneverted structures occurs. However, a stable continuous everting is possible. The average von Mises stress amounts to 0.8 MPa (0.8 N/mm
2).
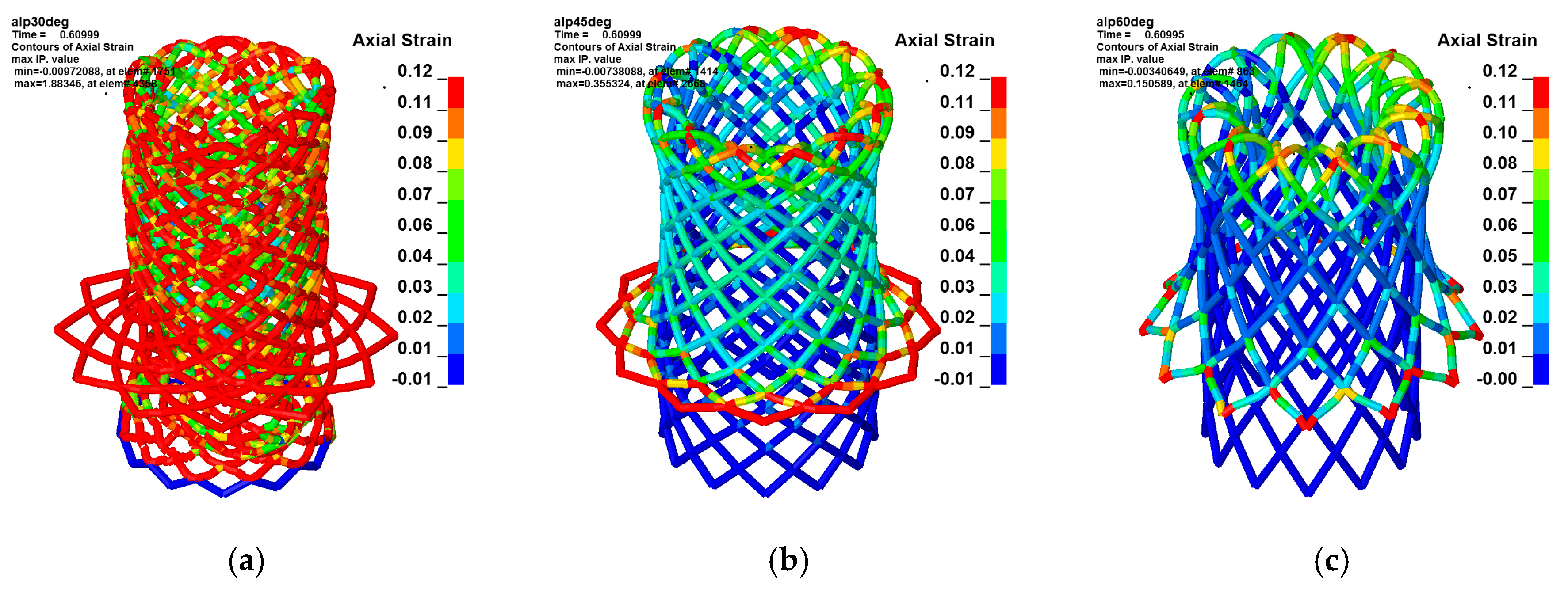
The strain in the everting zone follows directly from the stresses, due to assumed linear–elastic material behavior. Strain peaks of 0.12 for a net angle of 60° up to 0.16 for an angle of 30° arise in the everting zone (
Figure 11). The model with a net angle 30° shows a very unstable everting process (pl. see
Figure 11a).
3.4. Dimensional Stability and Net Quality
The visual characterization of all additively manufactured geometries showed that the printed bar diameter is always smaller than the target diameter, with an average of 12%, a minimum of 10% and a maximum of 16% (exemplary to see in
Table 1 and
Table 2). This deviation has to be considered by defining the construction parameter. The diameter of one single bar exhibits a nearly constant value with a variance of less than 1%. For the simulation, the average value determined was rounded from 1727.58 μm to 1.70 mm.
After performing the functional test on the initial net geometry, fractures appeared on the structure. A detailed visual check identified three failure patterns: most frequently failure was found on geometrical notches at the nodes (
Figure 12a) and sporadic failures were found on printing misalignments along printing layers (
Figure 12b) and on topological notches (
Figure 12c).
A detailed examination of all nodes using qualitative microscopy and the statistical analysis of the results showed that 80% of the fractures were caused by geometrical notches, as shown in
Figure 12a. In
Figure 13, the local distribution of the failure patterns is shown. It can be seen that the errors are mainly located in the upper part of the structure. The reason for this is the process of initialization, which requires an enormous expansion of the net. Likewise, the overturning was only done up to half of the total length of the net tube. However, it can be assumed that the geometric notches in particular will lead to damage along the entire structure if the load continues to be applied. Therefore, an improvement of the net geometry using simulation was implemented to increase the repeatability and endurance strength of the net structure.
3.5. Improvement of Geometry with a Fine Model of a Unit Cell
Because of the local failure at the crossing points, a detailed model was used to investigate and ideally to improve the local geometry loading. Hence, based on the initial printing geometry, a detailed model with solid elements was built in LS-Dyna. The smallest periodically recurring structure (unit cell) was retrieved by radial and axial cutting through the center of crossing points. After meshing, the unit cell model consisted of nearly 200,000 tetrahedral solid elements with an average edge length of 0.15 mm. The two lower ends of a unit cell were clamped with boundary conditions on all nodes of the cutting planes. For the upper two ends, two Cartesian coordinate systems were provided in the same manner as above (global beam model) to reach a strictly radial translation of nodes on the cutting planes. Two external massless nodes were positioned above the two node sets of both bar ends and connected to the respective node sets via keyword *CONSTRAINED_INTERPOLATION. A motion vector was then defined for each massless node, which was directed radial outwards and additionally contained a component downwards toward the clamped end of the unit cell (
Figure 14). The nature of the load leads to a simulative bending test, which was only used to compare different geometry loadings, such as peak stresses and their locations.
A corresponding model with slightly changed geometry was built. After some iterative changes, the bar length was increased and the waist of the crossing point was broadened. Furthermore, the waist was rounded to avoid joined sharp border edges of the bars and thus stress peaks in those regions.
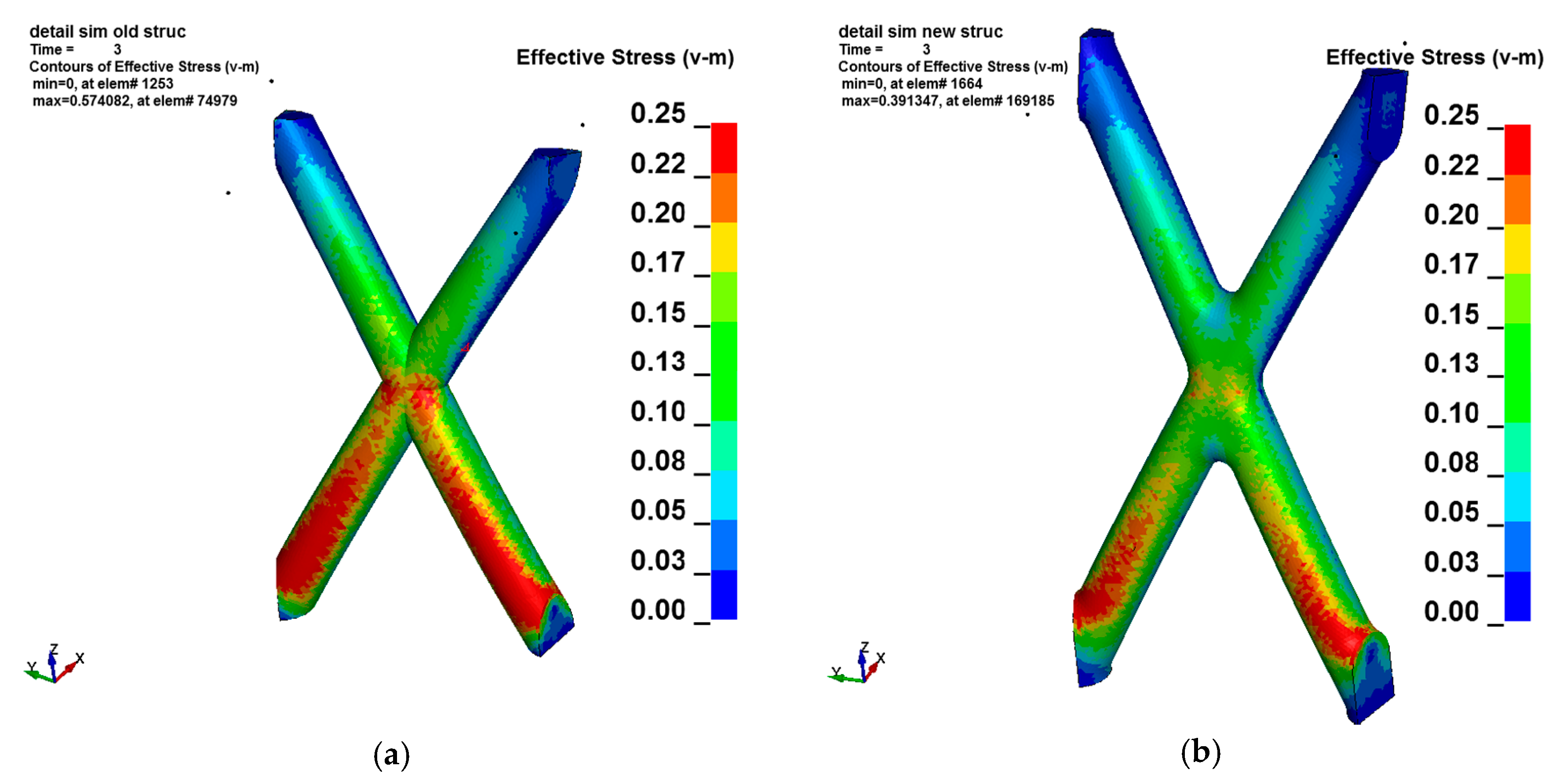
Figure 14 compares the initial geometry with the improved final version with changed waist and bar length. Due to the bending test nature of the load, the regions near the clamping showed the highest stresses. Nevertheless, the sharp border lines in the crossing point in
Figure 15a also tended to carry high loadings. With the improved geometry, pictured in
Figure 15b, the high stresses in the crossing point especially can be avoided. The structural bending stiffness is reduced due to the increased bar length. Therefore, the main angle
had to be changed from 60° to nearly 65° to maintain the crossing point number.
The improved tubular net structure has an inner diameter of 19 mm, a bar diameter of 1.7 mm, a free length of 150 mm and 24 bars which are positioned at an angle of 65° to each other (net angles) (pl. see
Figure 4 and
Figure 16). The surface shows a typical topology caused by the printing process (see
Figure 16).