Quantum Proxy Signature Scheme with Discrete Time Quantum Walks and Quantum One-Time Pad CNOT Operation
Abstract
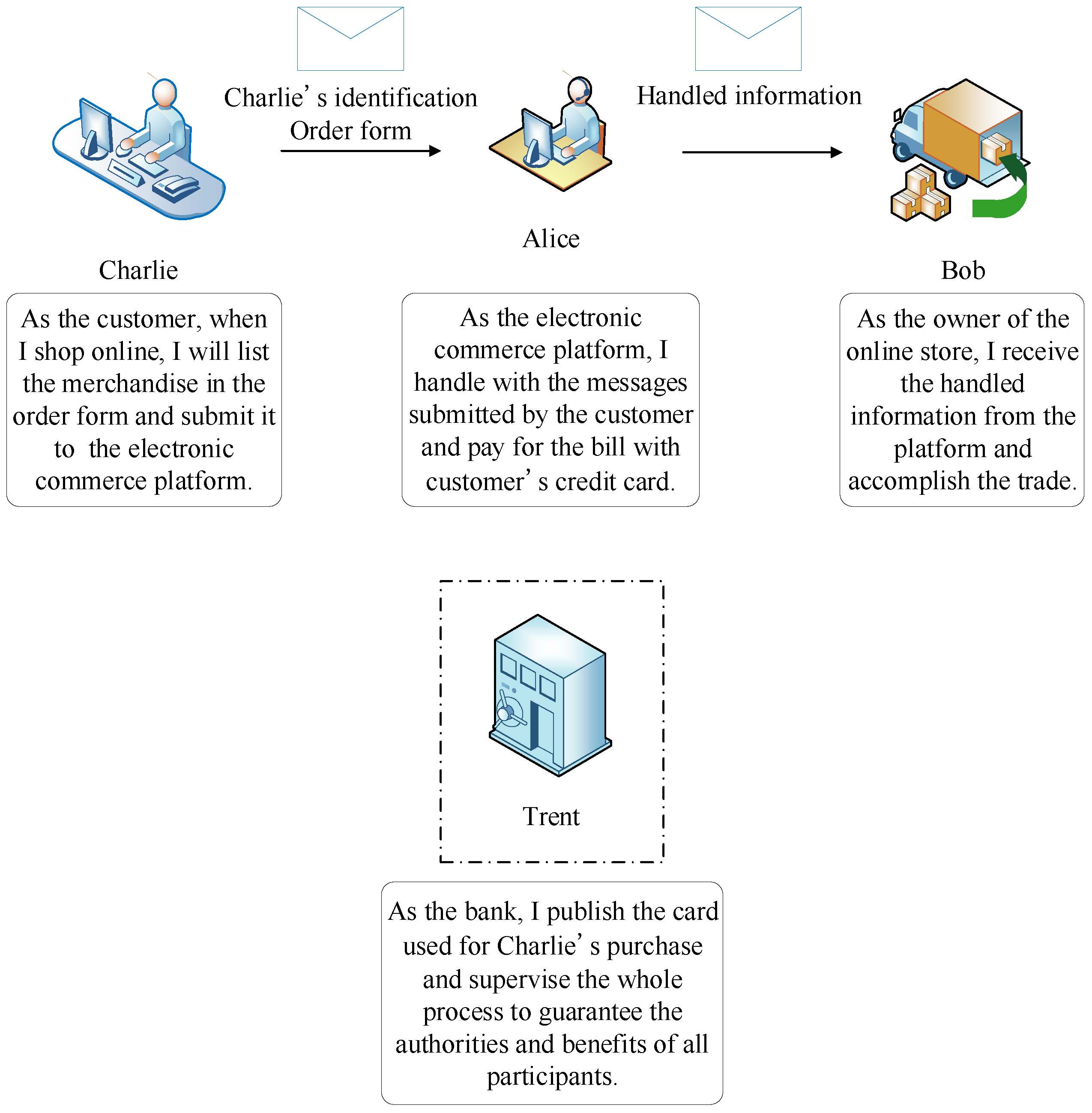
1. Introduction
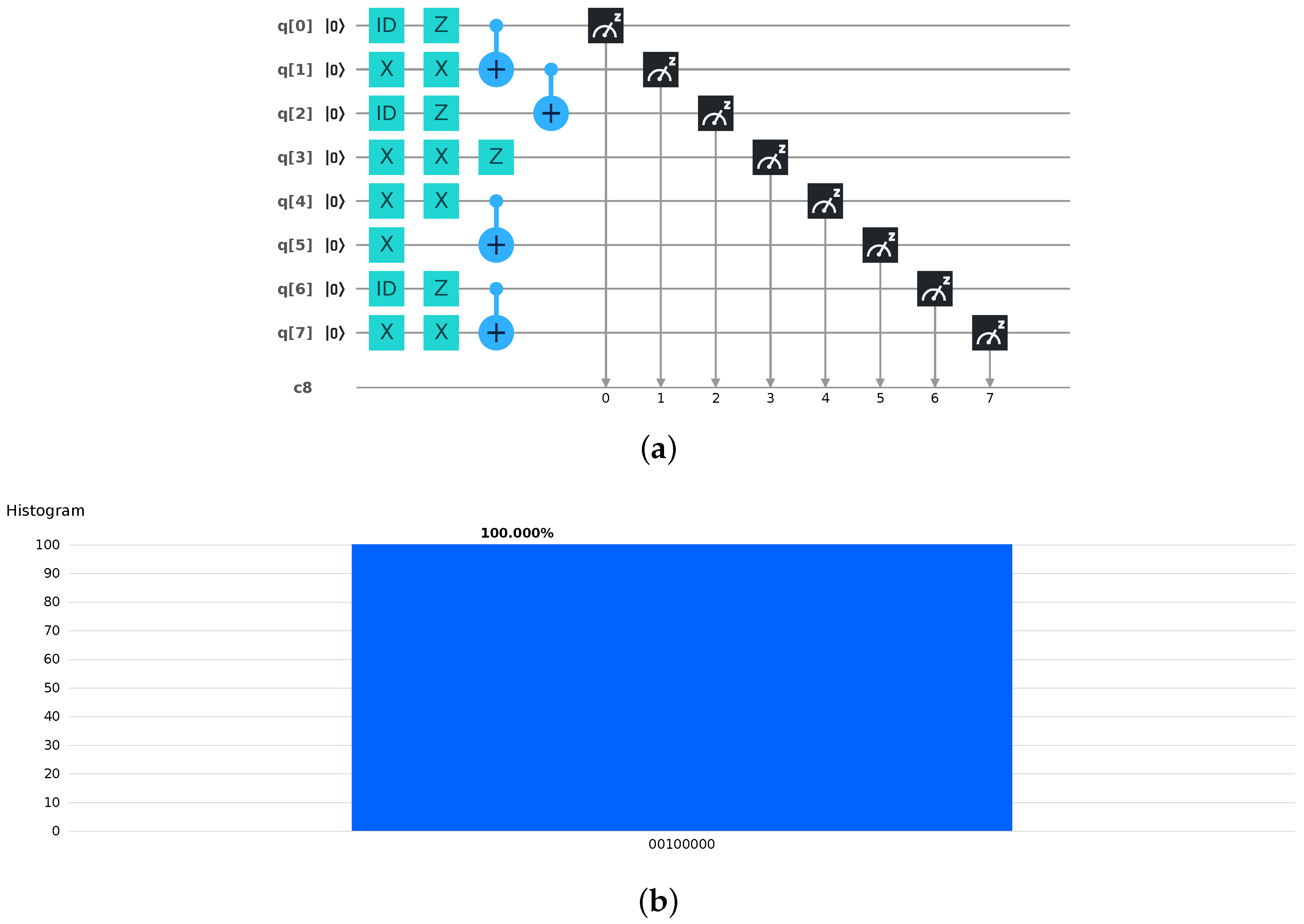
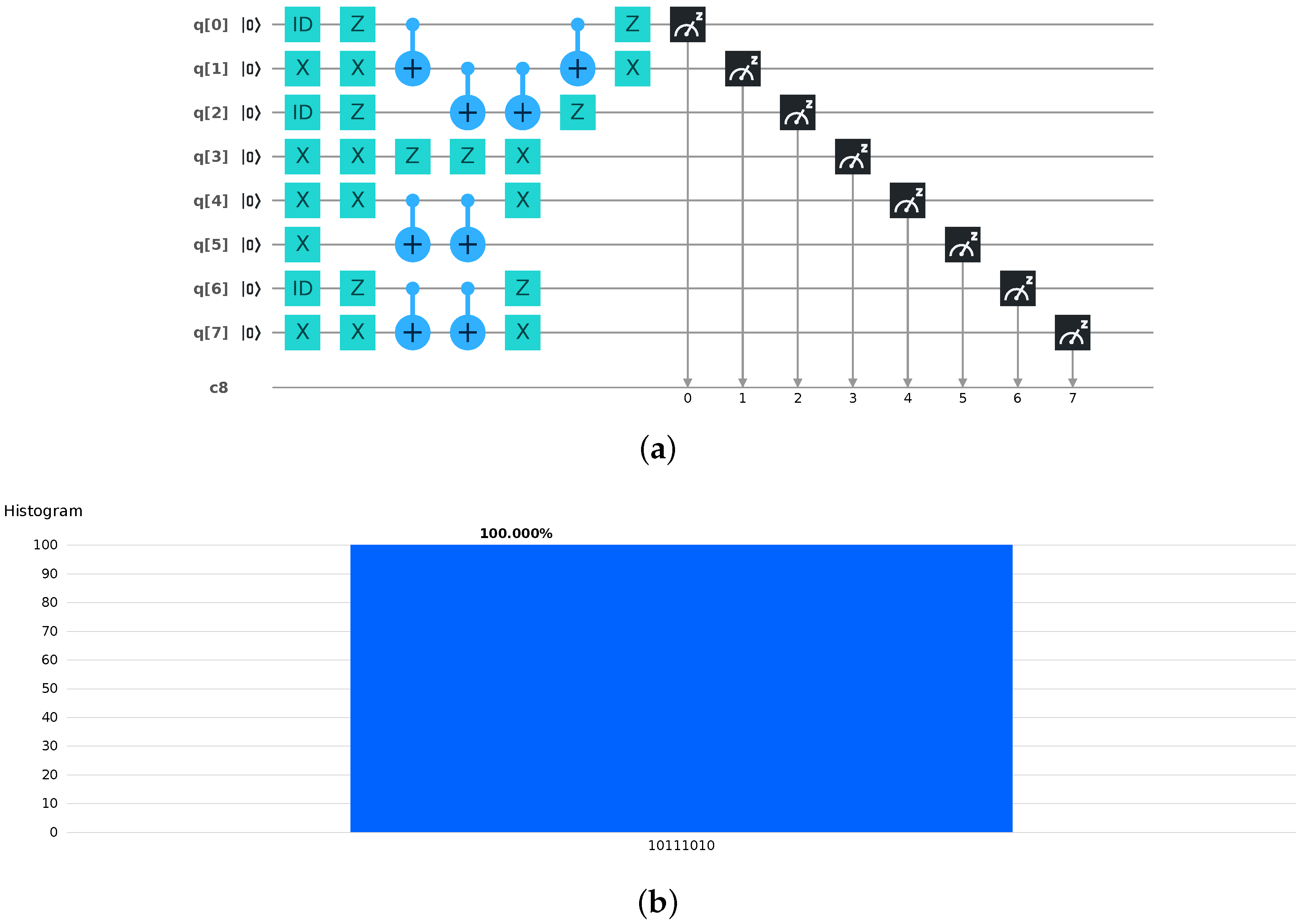
- Before generating the proxy signature, the random binary sequence is circularly used to encrypt the original message. Then the QOTP-CNOT operation is used to generate the proxy signature state with the length of the secret keys being the same as that of the message to be encrypted, which reduces the length of the required keys by three times in terms of efficiency and improves the security of the presented scheme. The introduction of CNOT operation into the QOTP makes the encrypted qubit related to not only the qubit and the key of the current position but also other qubits and keys of other positions, which can resist against the proxy signatory’s disavowal attack and the receiver’s forgery attack on the proxy signature by modifying the qubits of particular positions in it.
- Quantum walks on circles are used to transfer the random sequence to verify the validity of the proxy warranty and the corresponding quantum teleportation protocol is performed to transmit the message copy of ciphertext from the proxy signatory to the verifier, which assists the verifier to complete the verification of the validity of the proxy signature, in which it is unnecessary to generate entangled states in advance as quantum channels and the essential entangled states can be created by quantum walks. We note that this model differs from the formalisms of quantum walks employed in [12,14] and that it is firstly employed in quantum proxy signature.
2. Methods
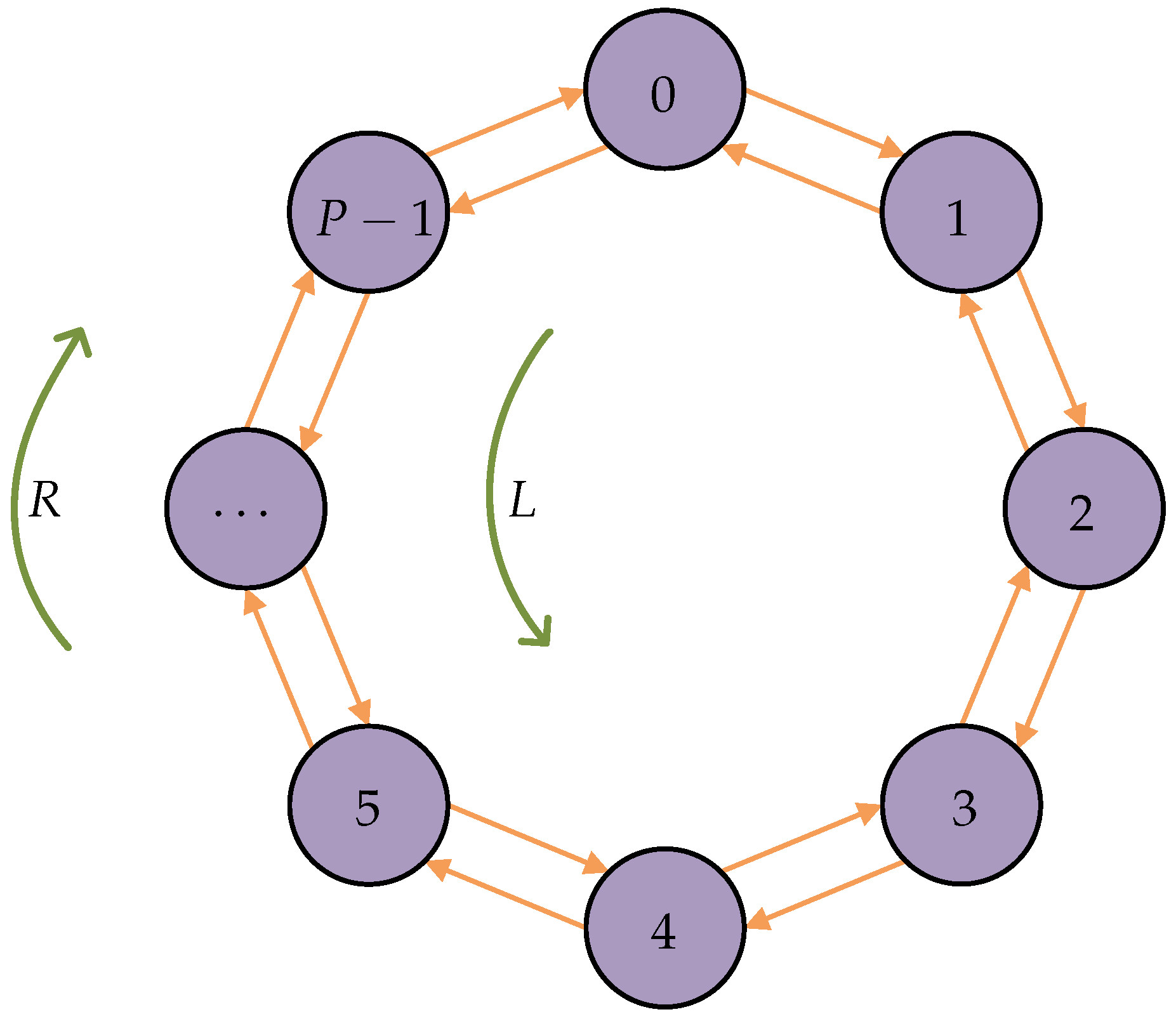
2.1. Quantum Walks on Circles
2.2. Teleportation with Quantum Walks on Circles
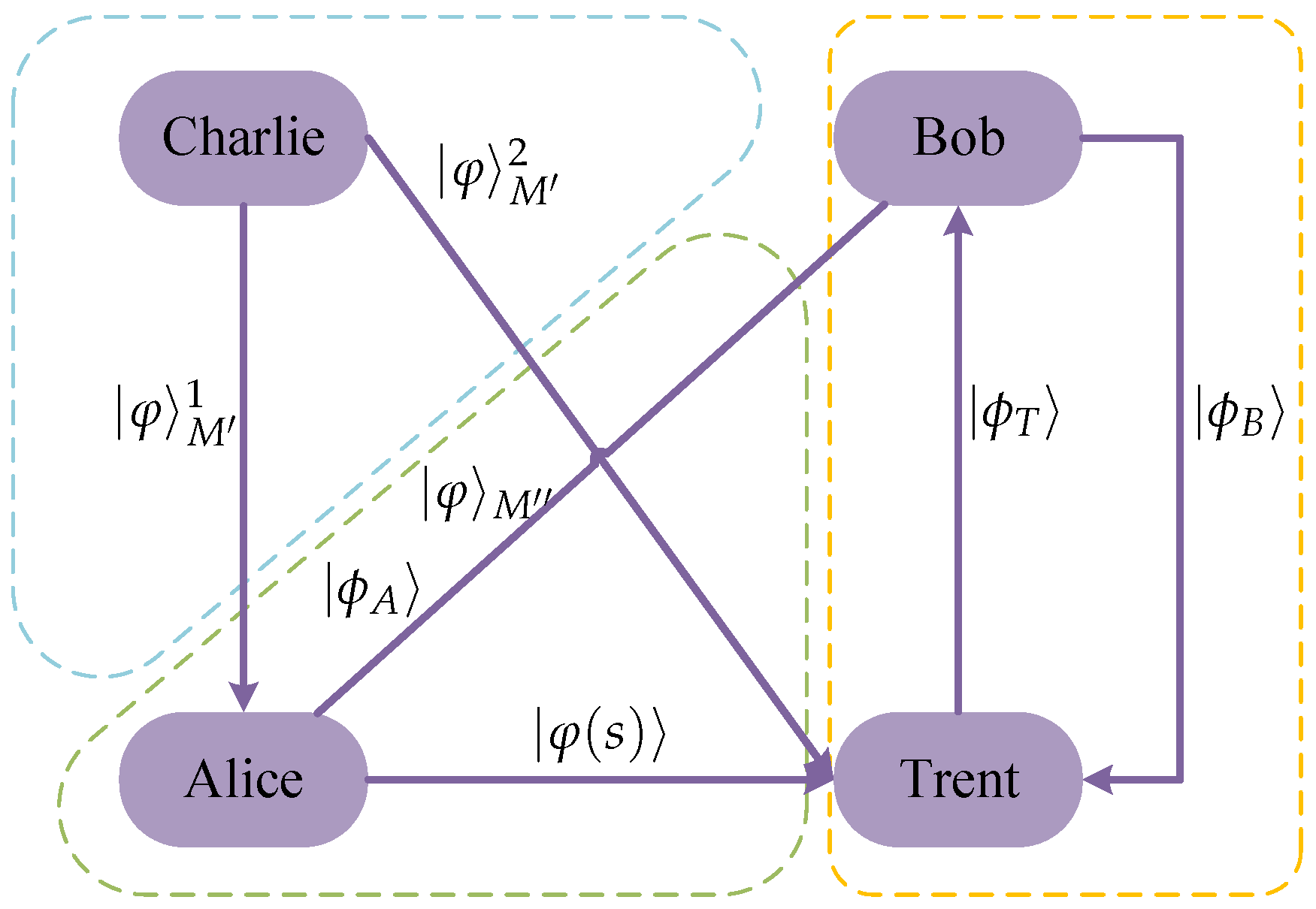
2.3. Quantum Proxy Signature Scheme
2.3.1. Initializing Phase
2.3.2. Authorizing Phase
2.3.3. Signing Phase
2.3.4. Verifying Phase
3. Results
3.1. Impossibility of Denials
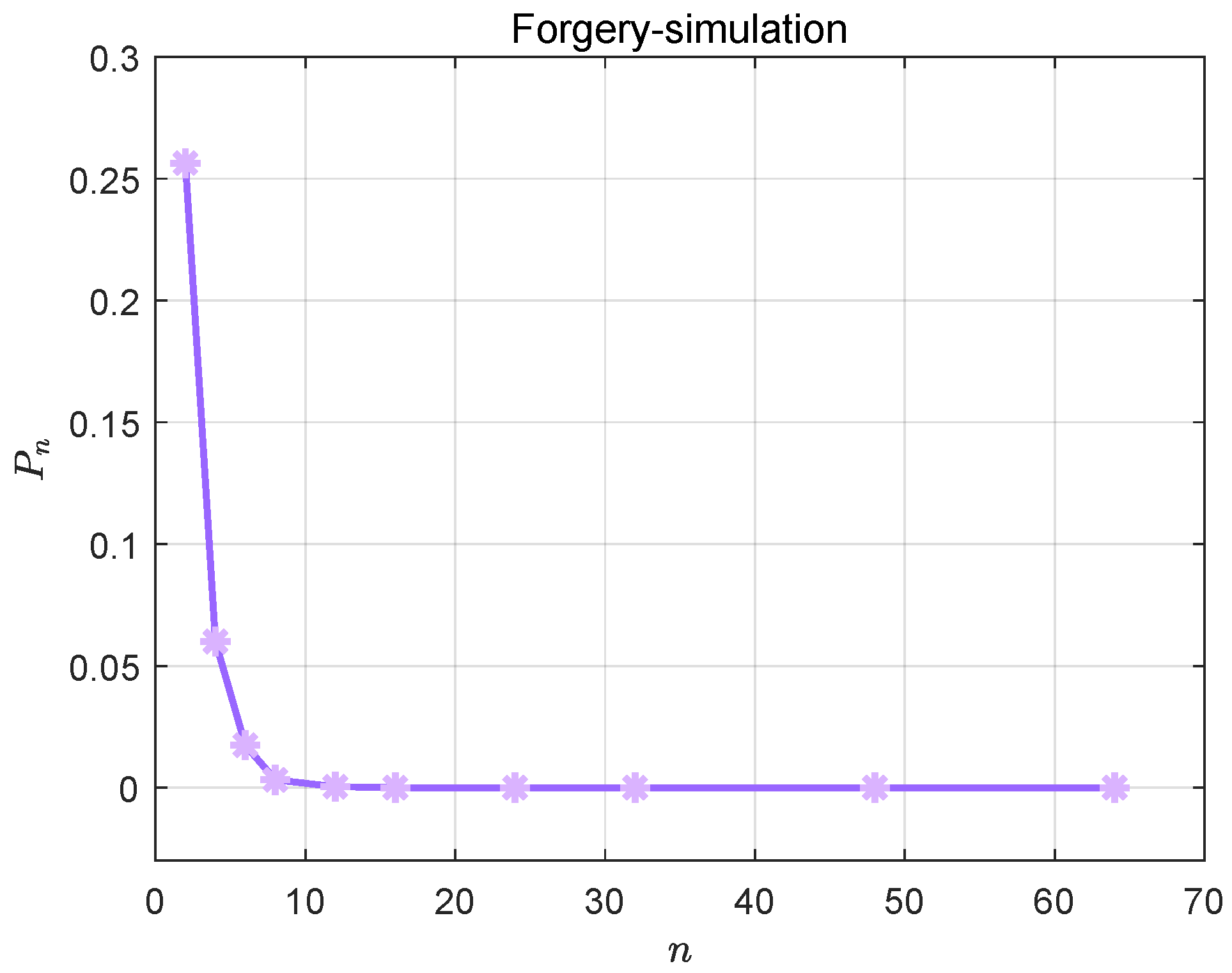
3.2. Impossibility of Forgeries
3.3. Impossibility of Repudiations
4. Discussions
4.1. Discussion of Complexity
4.2. Discussion of Applications
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Phys. Rev. Lett. 1997, 79, 325–328. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Busch, P.; Heinonen, T.; Lahti, P. Heisenberg’s Uncertainty Principle. Phys. Rep. 2007, 452, 155–176. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, Y.; Xue, P. Generalized teleportation by quantum walks. Quantum Inf. Process. 2017, 16, 221. [Google Scholar] [CrossRef]
- Shang, Y.; Wang, Y.; Li, M.; Lu, R.Q. Quantum communication protocols by quantum walks with two coins. Europhys. Lett. 2018, 124, 60009. [Google Scholar] [CrossRef]
- Shang, Y.; Li, M. Experimental realization of state transfer by quantum walks with two coins. Quantum Sci. Technol. 2020, 5, 015005. [Google Scholar] [CrossRef]
- Chatterjee, Y.; Devrari, V.; Behera, B.K.; Panigrahi, P.K. Experimental realization of quantum teleportation using coined quantum walks. Quantum Inf. Process. 2020, 19, 31. [Google Scholar] [CrossRef]
- Li, H.J.; Chen, X.B.; Wang, Y.L.; Hou, Y.Y.; Li, J. A new kind of flexible quantum teleportation of an arbitrary multi-qubit state by multi-walker quantum walks. Quantum Inf. Process. 2019, 18, 266. [Google Scholar] [CrossRef]
- Vlachou, C.; Krawec, W.; Mateus, P.; Paunkovic, N.; Souto, A. Quantum key distribution with quantum walks. Quantum Inf. Process. 2018, 17, 288. [Google Scholar] [CrossRef]
- Shi, J.; Chen, H.; Zhou, F.; Huang, L.; Chen, S.; Shi, R. Quantum Blind Signature Scheme with Cluster States Based on Quantum Walk Cryptosystem. Int. J. Theor. Phys. 2019, 58, 1337–1349. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Shi, J.; Zhou, J.; Guo, Y. Arbitrated quantum signature scheme with quantum walk-based teleportation. Quantum Inf. Process. 2019, 18, 154. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Shi, J.; Guo, Y. Arbitrated quantum signature scheme based on quantum walks. Aata Phys. Sin. 2019, 68, 120302. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Shi, J.; Zhao, W.; Lu, Y.; Tang, Y. Arbitrated quantum signature protocol with boson sampling-based random unitary encryption. J. Phys. A Math. Theor. 2020, 53, 135301. [Google Scholar] [CrossRef]
- Li, X.Y.; Chang, Y.; Zhang, S.B.; Dai, J.Q.; Zheng, T. Quantum Blind Signature Scheme Based on Quantum Walk. Int. J. Theor. Phys. 2020, 59, 2059–2073. [Google Scholar] [CrossRef]
- Di, T.; Hillery, M.; Zubairy, M.S. Cavity QED-based quantum walk. Phys. Rev. A 2004, 70, 032304. [Google Scholar] [CrossRef]
- Eckert, K.; Mompart, J.; Birkl, G.; Lewenstein, M. One-and two-dimensional quantum walks in arrays of optical traps. Phys. Rev. A 2005, 72, 012327. [Google Scholar] [CrossRef]
- Zou, X.; Dong, Y.; Guo, G. Optical implementation of one-dimensional quantum random walks using orbital angular momentum of a single photon. New J. Phys. 2006, 8, 81. [Google Scholar] [CrossRef]
- Du, J.; Li, H.; Xu, X.; Shi, M.; Wu, J.; Zhou, X.; Han, R. Experimental implementation of the quantum random-walk algorithm. Phys. Rev. A 2003, 67, 042316. [Google Scholar] [CrossRef]
- Tang, H.; Lin, X.F.; Feng, Z.; Chen, J.Y.; Gao, J.; Sun, K.; Wang, C.Y.; Lai, P.C.; Xu, X.Y.; Wang, Y.; et al. Experimental two-dimensional quantum walk on a photonic chip. Sci. Adv. 2018, 4, eaat3174. [Google Scholar] [CrossRef]
- Bian, Z.H.; Li, J.; Zhan, X.; Twamley, J.; Xue, P. Experimental implementation of a quantum walk on a circle with single photons. Phys. Rev. A 2017, 95, 052338. [Google Scholar] [CrossRef]
- Mambo, M.; Usuda, K.; Okamoto, E. Proxy signatures: Delegation of the power to sign messages. IEICE Trans. Fund. Electron. 1996, 79, 1338–1354. [Google Scholar]
- Gottesman, D.; Chuang, I. Quantum Digital Signatures. arXiv 2001, arXiv:quant-ph/0105032v2. [Google Scholar]
- Zeng, G.; Keitel, C.H. Arbitrated quantum-signature scheme. Phys. Rev. A 2002, 65, 042312. [Google Scholar] [CrossRef]
- Chang, Z.L.; Zhou, J.X.; Zhang, J.; Wen, Q.Y. Quantum proxy signature scheme based on EPR state. Appl. Res. Comput. 2010, 27, 675–677. [Google Scholar]
- Zhou, J.; Zhou, Y.; Niu, X.; Yang, Y. Quantum proxy signature scheme with public verifiability. Sci. China Phys. Mech. 2011, 54, 1828–1832. [Google Scholar] [CrossRef]
- Cao, H.J.; Zhu, Y.Y.; Li, P.F. A Quantum Proxy Weak Blind Signature Scheme. Int. J. Theor. Phys. 2014, 53, 419–425. [Google Scholar] [CrossRef]
- Zhang, K.J.; Jia, H.Y. Cryptanalysis of a Quantum Proxy Weak Blind Signature Scheme. Int. J. Theor. Phys. 2015, 54, 582–588. [Google Scholar] [CrossRef]
- Cao, H.J.; Yu, Y.F.; Song, Q.; Gao, L.X. A Quantum Proxy Weak Blind Signature Scheme Based on Controlled Quantum Teleportation. Int. J. Theor. Phys. 2015, 54, 1325–1333. [Google Scholar] [CrossRef]
- Xu, G.B. Novel Quantum Proxy Signature without Entanglement. Int. J. Theor. Phys. 2015, 54, 2605–2612. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, J.Z.; Li, Y.P.; An, W. Multi-proxy Strong Blind Quantum Signature Scheme. Int. J. Theor. Phys. 2016, 55, 3524–3536. [Google Scholar] [CrossRef]
- Qin, H.; Tang, W.K.; Tso, R. Batch quantum multi-proxy signature. Opt. Quantum Electron. 2018, 50, 450.1–450.8. [Google Scholar] [CrossRef]
- Niu, X.F.; Ma, W.P.; Chen, B.Q.; Liu, G.; Wang, Q.Z. A Quantum Proxy Blind Signature Scheme Based on Superdense Coding. Int. J. Theor. Phys. 2020, 59, 1121–1128. [Google Scholar] [CrossRef]
- Zou, X.; Qiu, D. Security analysis and improvements of arbitrated quantum signature schemes. Phys. Rev. A 2010, 82, 042325. [Google Scholar] [CrossRef]
- Gao, F.; Qin, S.J.; Guo, F.Z.; Wen, Q.Y. Cryptanalysis of the arbitrated quantum signature protocols. Phys. Rev. A 2011, 84, 022344. [Google Scholar] [CrossRef]
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687–1690. [Google Scholar] [CrossRef]
- Ambainis, A.; Bach, E.; Nayak, A.; Vishwanath, A.; Watrous, J. One-dimensional quantum walks. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing (STOC01), Hersonissos, Crete, Greece, 6–8 July 2001; pp. 37–49. [Google Scholar]
- Aharonov, D.; Ambainis, A.; Kempe, J.; Vazirani, U. Quantum walks on graphs. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing (STOC01), Hersonissos, Crete, Greece, 6–8 July 2001; pp. 50–59. [Google Scholar]
- Meyer, D.A. From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 1996, 85, 551–574. [Google Scholar] [CrossRef]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915. [Google Scholar] [CrossRef]
- Jozef, K. Two models of quantum random walk. Cent. Eur. J. Phys. 2003, 1, 556–573. [Google Scholar]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A. Long-distance continuous-variable quantum key distribution with a Gaussian modulation. Phys. Rev. A 2011, 84, 062317. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Shi, R.H.; Guo, Y. Multipartite continuous variable quantum communication with entanglement in the middle. J. Phys. A Math. Theor. 2018, 51, 295301. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, R.; Zeng, G.; Guo, Y. Coherent attacking continuous-variable quantum key distribution with entanglement in the middle. Quantum Inf. Process. 2018, 17, 133. [Google Scholar] [CrossRef]
- Shor, P.W.; Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Inamori, H.; Lutkenhaus, N.; Mayers, D. Unconditional security of practical quantum key distribution. Eur. Phys. J. D 2007, 41, 599–627. [Google Scholar] [CrossRef]
- Leung, D.W. Quantum Vernam Cipher. Quantum Inf. Comput. 2001, 2, 14. [Google Scholar]
- Boykin, P.O.; Roychowdhury, V. Optimal encryption of quantum bits. Phys. Rev. A 2003, 67, 042317. [Google Scholar] [CrossRef]
- Li, F.G.; Shi, J.H. An arbitrated quantum signature protocol based on the chained CNOT operations encryption. Quantum Inf. Process. 2015, 14, 2171–2181. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, H.W.; Zhang, K.J.; Jia, H.Y. An improved arbitrated quantum signature protocol based on the key-controlled chained CNOT encryption. Quantum Inf. Process. 2017, 16, 70. [Google Scholar] [CrossRef]
- Buhrman, H.; Cleve, R.; Watrous, J.; De Wolf, R. Quantum fingerprinting. Phys. Rev. Lett. 2001, 87, 167902. [Google Scholar] [CrossRef]
- Zhang, K.J.; Zhang, W.W.; Li, D. Improving the security of arbitrated quantum signature against the forgery attack. Quantum Inf. Process. 2013, 12, 2655–2669. [Google Scholar] [CrossRef]
- Wen, X.J.; Nie, Z. An E-payment system based on quantum blind and group signature. Phys. Scr. 2010, 82, 5468–5478. [Google Scholar]
- Wen, X.J.; Chen, Y.Z.; Fang, J.B. An inter-bank E-payment protocol based on quantum proxy blind signature. Quantum. Inf. Process. 2013, 12, 549–558. [Google Scholar] [CrossRef]
- Tian, J.H.; Zhang, J.Z.; Li, Y.P. A voting protocol based on the controlled quantum operation teleportation. Int. J. Theor. Phys. 2016, 55, 2303–2310. [Google Scholar] [CrossRef]
- Cao, H.J.; Ding, L.Y.; Yu, Y.F.; Li, P.F. A Electronic Voting Scheme Achieved by Using Quantum Proxy Signature. Int. J. Theor. Phys. 2016, 55, 4081–4088. [Google Scholar] [CrossRef]
- Shao, A.X.; Zhang, J.Z.; Xie, S.C. An E-payment Protocol Based on Quantum Multi-proxy Blind Signature. Int. J. Theor. Phys. 2017, 56, 1241–1248. [Google Scholar] [CrossRef]
- Damgård, I.B.; Fehr, S.; Salvail, L.; Schaffner, C. Cryptography in the bounded-quantum-storage model. SIAM J. Comput. 2008, 37, 1865–1890. [Google Scholar] [CrossRef]
- Wehner, S.; Schaffner, C.; Terhal, B.M. Cryptography from noisy storage. Phys. Rev. Lett. 2008, 100, 220502. [Google Scholar] [CrossRef]
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum internet: A vision for the road ahead. Science 2018, 362, eaam9288. [Google Scholar] [CrossRef]

| Unitary Operation | ||
|---|---|---|
| 2 | 1 | I |
| 2 | −1 | Z |
| 0 | 1 | X |
| 0 | −1 |
| Unitary Operator | Matrix Representation | |
|---|---|---|
| 00 | I | |
| 01 | ||
| 10 | ||
| 11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Zhang, Q.; Shi, J.; Chen, S.; Shi, R. Quantum Proxy Signature Scheme with Discrete Time Quantum Walks and Quantum One-Time Pad CNOT Operation. Appl. Sci. 2020, 10, 5770. https://doi.org/10.3390/app10175770
Feng Y, Zhang Q, Shi J, Chen S, Shi R. Quantum Proxy Signature Scheme with Discrete Time Quantum Walks and Quantum One-Time Pad CNOT Operation. Applied Sciences. 2020; 10(17):5770. https://doi.org/10.3390/app10175770
Chicago/Turabian StyleFeng, Yanyan, Qian Zhang, Jinjing Shi, Shuhui Chen, and Ronghua Shi. 2020. "Quantum Proxy Signature Scheme with Discrete Time Quantum Walks and Quantum One-Time Pad CNOT Operation" Applied Sciences 10, no. 17: 5770. https://doi.org/10.3390/app10175770
APA StyleFeng, Y., Zhang, Q., Shi, J., Chen, S., & Shi, R. (2020). Quantum Proxy Signature Scheme with Discrete Time Quantum Walks and Quantum One-Time Pad CNOT Operation. Applied Sciences, 10(17), 5770. https://doi.org/10.3390/app10175770





