Lengthening Transmission Distance of Continuous Variable Quantum Key Distribution with Discrete Modulation through Photon Catalyzing

Abstract

Establishing global secure networks is a potential implementation of continuous-variable quantum key distribution (CVQKD) but it is also challenged with respect to long-distance transmission. The discrete modulation (DM) can make up for the shortage of transmission distance in that it has a unique advantage against all side-channel attacks; however, its further performance improvement requires source preparation in the presence of noise and loss. Here, we consider the effects of photon catalysis (PC) on the DM-involved source preparation for improving the transmission distance. We address a zero-photon-catalysis (ZPC)-based source preparation for enhancing the DM–CVQKD system. The statistical fluctuation is taken into account for the practical security analysis. Numerical simulations show that the ZPC-based source preparation can not only achieve the long-distance transmission, but also contributes to the reasonable increase of the secret key rate.

1. Introduction

Quantum key distribution (QKD) [1,2,3,4] allows legal participants to share a secret key and enables theoretically information-secure communications [5,6,7]. Recently, it has spurred much interest, resulting in two approaches, i.e., discrete-variable (DV) QKD [8,9] and continuous-variable (CV) QKD [10,11,12,13,14,15,16,17,18,19,20]. A possible breakthrough may come from the practical implementation of CVQKD, which has an advantage of being practically implemented with modern telecommunications, thus allowing for the exploitation of the heritage of integrability in existing optical communication system.

At present, there are several mainstream modulations in CVQKD, such as Gaussian modulation (GM) [11,12,13,14,15] and discrete modulation (DM) [16,17,18,19,20]. In the former, the transmitter generates the key bits in the quadratures of the Gaussian modulated optical field, while the receiver recovers the secret key using a coherent detector [13]. It is GM–CVQKD that could achieve the potential high secret key rate. Unfortunately, it is still limited to the transmission distance, compared with its DVQKD counterpart. A challenge is that the resulting reconciliation efficiency [14,15] is still low, which is unsuitable for long-distance transmission, whereas in the latter, one can solve this problem by using a DM source for CVQKD [16], where it generates nonorthogonal coherent states, taking advantage of the randomly measured quadrature for information encoding rather than exploiting the fixed quadrature in source preparation [17]. Consequently, it results in a merit of both high reconciliation efficiency and high tolerance against the excess noise [11,12,13,14,15] such that it can extend the transmission distance of the CVQKD system [18]. Actually, GM–CVQKD is simpler for theoretical performance analysis than DM–CVQKD, and the secret key rates can approach the theoretical limits [17], whereas GM–CVQKD itself is alway approximated by the DM sources, which may be taken into account for security analysis [18]. Moreover, as GM–CVQKD usually requires more resources in terms of randomness and classical post-processing resources, DM–CVQKD can offer further simplified implementation in experiments. While theoretics and experiments of DM–CVQKD have suggested that we can achieve the above-mentioned goal, there are still some potential challenges while promoting its performances.

Currently, photon catalysis (PC) [21,22,23,24,25], which is a non-Gaussian operation with n-photon state input/output in essence, has been utilized for security improvement attributed to the photon catalyzing operation, which increases the entanglement degree of the two-participant system by increasing the correlation between the transmitter and the receiver [21]. In a certain low-squeezing parameter, the entanglement of the two-mode squeezed vacuum (TMSV) state can be enhanced by increasing the catalysis photon number [22]. Due to equivalence of the entanglement-based (EB) CVQKD system and the prepare-and-measure (PM) CVQKD system [11,12,13,14,15,16,17,18,19,20], the PC-involved DM–CVQKD system may be implemented with existing optical technologies. Motivated by the above advantages, we propose an improved DM–CVQKD system through photon catalyzing. The DM scheme is employed for the source preparation because it can tolerate a lower signal-to-noise ratio (SNR) well, resulting in the long-distance transmission of the CVQKD system. Meanwhile, a zero-photon catalysis (ZPC) operation with zero-photon state input/output is adopted in the DM-involved source preparation at the transmitter. The ZPC-based CVQKD protocol has been proven to be beneficial for tolerating lower reconciliation efficiency [24,25] and extending the maximal transmission distance, thus promoting its practical implementations with underlying technology.

As for the performance analysis of the proposed DM–CVQKD system, we take into account the asymptotic case [17] where the secure key rate can be obtained via the covariance matrix approach. It is a theoretically calculated value without involving the finite-size effect. Unfortunately, the derived upper bound is difficult to obtain in practical implementations. Therefore, we have to consider the finite-size effects [26,27]. Though the secure key rate is still pessimistic, it approaches to the practical implementation. Its security analysis is based on the finite-size effects; hence, we can achieve the upper bound of the maximal transmission distance.

This paper is structured as follows. In Section 2, we propose the PC-based DM source for CVQKD, and then elaborate on the characteristics of the ZPC-based scheme for improving the DM–CVQKD system. In Section 3, we demonstrate the transmission distance improvement of the DM–CVQKD system via the ZPC-based source preparation scheme. Finally, we draw a conclusion in Section 4.

2. The DM Source Preparation via ZPC Operations

In what follows, we elaborate the ZPC-involved DM source preparation for performance improvement of the CVQKD system. To make the derivation self-contained, we suggest the ZPC-involved CVQKD system with the DM source preparation.

2.1. The CVQKD System with the DM Source Preparation

For the prepare-and-measure (PM) version of CVQKD that can be used for practical implementations, Alice randomly draws n quaternary or octal variables, each corresponding to a coherent state of $\left|{\alpha }_k^N\right.⟩=\left|\alpha e^{ik\pi /N}\right.⟩,\forall k\in \{1,2,\cdots ,N\}$, where $\alpha$ is a real positive number related to the modulation variance of coherent state given by $V_A=2{\alpha }^2$ [16,17,18,19,20]. For $N=4$ and $N=8$, we have the four-state DM source and the eight-state DM source, as shown in Figure 1 [28,29].

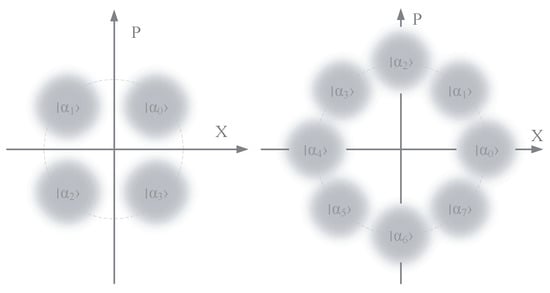
Figure 1. The discrete-modulation (DM)-based sources for four states (left) and eight states (right).

Alice generates n coherent states, which are sent through quantum channel characterized by transmission T and excess noise $\epsilon$. Then, for the received state, Bob measures one of quadratures (i.e., $\widehat{x}$ or $\widehat{p}$) by homodyne detector.

Theoretical analysis of CVQKD is considered through using its equivalent entanglement-based (EB) version. The transmitter Alice starts with a pure bipartite state $\left|\mathsf{\Psi }\right.⟩$ with variance $V=V_A+1$. Subsequently, she performs a projective measurement on the first half of this state, whereas the second half is sent to the receiver Bob. For the DM–CVQKD protocol, to apply the security analysis technique as the GM–CVQKD protocol [11,12,13,14,15], we therefore want to find a purification $\left|\mathsf{\Psi }\right.⟩$ with a covariance matrix $\gamma$. This covariance matrix has the form given by [26,27]

$${\gamma }_N=\left(\begin{array}{cc}(V_A+1)\mathbb{I}& Z_N{\sigma }_z\\ Z_N{\sigma }_z& (V_A+1)\mathbb{I}\end{array}\right),$$

(1)

where $\mathbb{I}=\mathrm{diag}(1,1)$ and ${\sigma }_z=\mathrm{diag}(1,-1)$. For example, taking $N=4$ into account, we have the four-state scheme given by

$$Z_4=V_A\sum _{k=0}^3\frac{{\lambda }_{k-1}^{3/2}}{\sqrt{{\lambda }_k}},$$

(2)

with the parameters ${\lambda }_{0,2}$ and ${\lambda }_{1,3}$ given by ${\lambda }_{0,2}=\frac{1}{2}{e}^{-{\alpha }^2}(cosh\left({\alpha }^2\right)\pm cos\left({\alpha }^2\right))$ and ${\lambda }_{1,3}=\frac{1}{2}{e}^{-{\alpha }^2}(sinh\left({\alpha }^2\right)\pm sin\left({\alpha }^2\right))$ [24].

We note that the DM source has a positive effect on CVQKD. For example, we have $Z_4\le Z_8\le Z_G$ for $N=4$ and $N=8$ in the DM–CVQKD protocol, where $Z_G=\sqrt{V_A^2+2V_A}$ represents the GM–CVQKD protocol. However, it is difficult to distinguish $Z_4$, $Z_8$ and $Z_G$ for $V_A\le 0.5$, as shown in Figure 2. Therefore, we attempt to derive the security bounds of DM–CVQKD referring to that of GM–CVQKD.

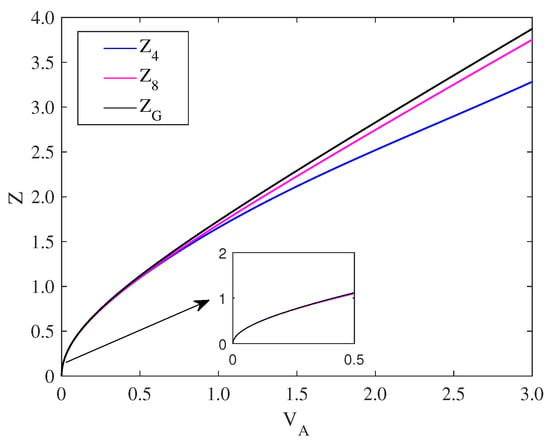
Figure 2. The correlation comparison of $Z_4$, $Z_8$ and $Z_G$.

2.2. The ZPC-Based DM Source Preparation

It is known that ZPC, which is a non-Gaussian operation with zero-photon state input/output [21,22], can enhance the correlation of the two-participant entangled quantum system [25,30]. In what follows, we suggest an improved CVQKD system with ZPC operation for the DM source preparation, as shown in Figure 3. In the auxiliary mode C, the zero-photon Fock state $\left|0\right.⟩$ is injected at one input port of beam splitter (BS) with transmittance $\tau$, and quantum state ${\left|\psi \right.⟩}_{in}$ of the mode B is simultaneously injected at another input port. Subsequently, we detect the zero-photon Fock state $\left|0\right.⟩$ at one of the output ports of the BS using a photon number resolving detector (PNRD), resulting in the ZPC-enhanced quantum state ${\left|\psi \right.⟩}_{out}$ from another output port.

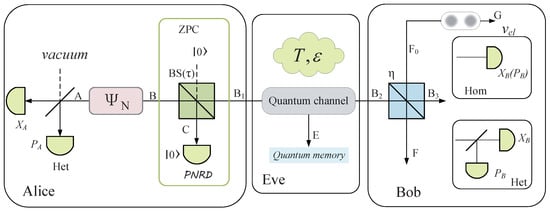
Figure 3. Schematic diagram of continuous-variable quantum key distribution (CVQKD) with zero-photon-catalysis (ZPC)-based DM source preparation.

Similar to the traditional photon subtraction operation [30,31,32,33], the ZPC operation can be used for performance improvement of CVQKD. In order to describe the ZPC-based DM source preparation, the ZPC operation can be described as [22,25]

$${\widehat{\mathrm{O}}}_0={\left(\sqrt{\tau }\right)}^{b^{†}b}.$$

(3)

For an input ${\left|\psi \right.⟩}_{in}$, we have output ${\left|\psi \right.⟩}_{out}$ given by

$${\left|\psi \right.⟩}_{out}=\frac{{\widehat{O}}_0}{\sqrt{P_0}}{\left|\psi \right.⟩}_{in},$$

(4)

where $P_0$ denotes the success probability of the operation given by $P_0=e^{(T-1)|{\alpha }_k{|}^2}$ as function of parameters $V_A$ and $\tau$, as shown in Figure 4. We find that the large $V_A$ and $\tau$ result in the high success probability. Note that we have ${\left|\psi \right.⟩}_{out}={\left|\psi \right.⟩}_{in}$ for $\tau =1$, indicating that there is no ZPC effect.

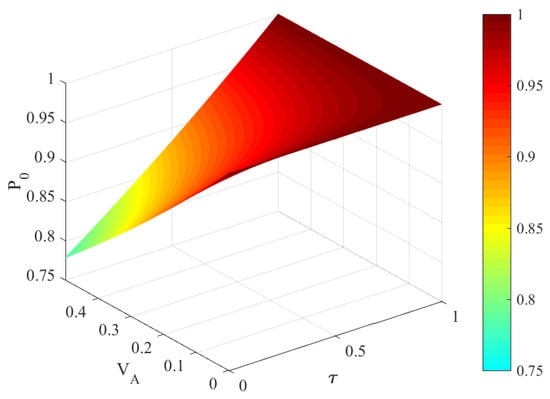
Figure 4. Success probabilities of ZPC with transmittances $\tau$ and modulation variance $V_A$.

In the PM version of CVQKD, Alice randomly draws n quaternary or octal variables, each corresponding to a coherent state of $\left|{\alpha }_k^N\right.⟩$. Subsequently, Alice performs the ZPC operation on these n coherent states, which is modeled (BS) with transmittance $\tau$, resulting in the catalyzed state

$$\left|{\tilde{\alpha }}_k\right.⟩=\frac{e^{{(\tau -1)\left|\alpha \right|}^2}}{\sqrt{P_0}}\left|\sqrt{\tau }{\alpha }_k\right.⟩.$$

(5)

We note that the relationship of the transformed amplitudes can be written as ${\tilde{\alpha }}_k=\sqrt{\tau }{\alpha }_k$. After that, the catalyzed quantum state is sent to Bob through the Eve-controlled channel. Bob may perform either homodyne (Hom) or heterodyne (Het) detection on the resulting quantum state. Finally, Alice and Bob distill the shared secret key after they conduct the classical post-processing procedure. In the EB version of the CVQKD system, as shown in Figure 3, Alice prepares for ${\left|\mathsf{\Psi }\right.⟩}_N$, and performs heterodyne detection (Het) on mode A. Mode B, which is performed with the ZPC operation, is sent to Bob. The role of the ZPC operation is for source-entanglement enhancement while promoting the mode transition between B and $B_1$, resulting in the covariance matrix ${\gamma }_{A{B}_1}$ of the catalyzed state ${\rho }_{A{B}_1}$ given by

$${\gamma }_{A{B}_1}=\left(\begin{array}{cc}(\tau V_A+1)\mathbb{I}& Z_N^{\prime }{\sigma }_z\\ Z_N^{\prime }{\sigma }_z& (\tau V_A+1)\mathbb{I}\end{array}\right),$$

(6)

with the parameters

$$Z_N^{\prime }=\tau V_A\sum _{k=0}^{N-1}\frac{{\tilde{\lambda }}_{N-1}^{3/2}}{\sqrt{{\tilde{\lambda }}_k}},$$

(7)

where the calculation of ${\tilde{\lambda }}_k$ is similar to that of ${\lambda }_k$ in Equation (2), but note that $\alpha$ is replaced by $\sqrt{\tau }\alpha$.

We note that we can obtain the effect of the ZPC operation on the DM source from the derived covariance matrix ${\gamma }_{A{B}_1}$. The parameter $Z_N^{\prime }$, which can be calculated from modulation variances of the initially prepared coherent states, demonstrates the relation of the modes A and $B_1$ for source preparation. In what follows, we will show the effect of $Z_N^{\prime }$ on the performance of the CVQKD system.

In addition, there are the other similar operations, such as local Gaussian operation [34], photon subtraction and addition operations [35], which can be used for improving entanglement of a two-mode state. These operations, whether they are Gaussian or not, may be similarly employed for source preparation while considering performance improvement of the CVQKD system. However, due to the elegant structure of the ZPC operation that can be conventionally integrated with the practical quantum system, in this paper, we consider the ZPC-based DM source preparation for extending the maximal transmission distance of the CVQKD system.

3. Security Analysis

In this section, we demonstrate the effect of the DM source preparation on CVQKD in both asymptotic [32,33] and finite-size cases [33] with numeric simulation results. For the detailed derivation of the secret key rate of the CVQKD system in asymptotic and finite-size cases, please see Appendices Appendix A and Appendix B, respectively.

For the ZPC-based DM source preparation, we show the success probability of ZPC operation in Figure 4. We find that the success probability increases with the increased modulation variance, and simultaneously increases with the increased transmittance. In the security analysis, the transmittance $\tau$ is tunable to satisfy the optimality of the ZPC operation. Taking $V_A\le 0.5$ into account, no matter what the value of $V_A$ is, the success probability can remain more than 0.75. This is a feasible solution to improve the CVQKD system.

As usual, it is necessary to select an optimal modulation variance $V_A$ for the performance improvement of CVQKD involving the ZPC operation. As shown in Figure 5, solid lines denote the secret key rate of the eight state CVQKD system, while dashed lines represent that of the four-state CVQKD system. In addition, we let $\beta =90\%$, $\eta =0.6$ and $v_{el}=0.05$. We find that for $\epsilon =0.01$, the secret key rate decreases as the transmission distance, while the inserted subgraph shows that the secret key rate decreases with the excess noise at the distance of 80km. Moreover, for $V_A=0.5$ the secret key rate can reach the optimal value, and hence we let $V_A=0.5$ in the subsequent simulations.

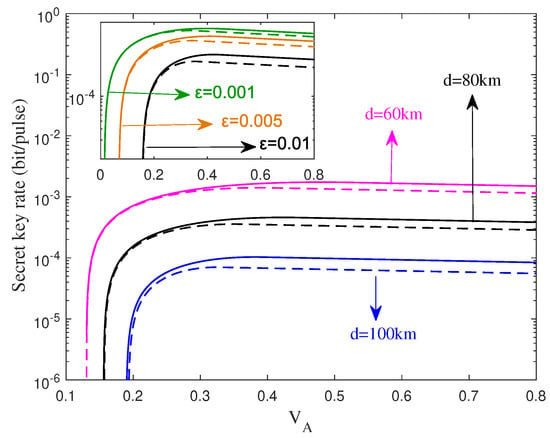
Figure 5. Asymptotic secret key rate of the CVQKD system with the ZPC-based DM source preparation for $\epsilon =0.01$, where solid lines denote the eight-state DM source preparation, while dashed lines represent the four-state DM source preparation. The inserted subgraph shows that asymptotic secret key rate of the CVQKD system for L = 80 km.

In Figure 6a, we show the asymptotic secret key rate of the ZPC-based CVQKD system, where solid lines denote homodyne detection and dashed lines represent heterodyne detection. It seems that performances of homodyne and heterodyne detectors are almost similar, and thus we employ the homodyne detector in security analysis. The performance of the ZPC-based CVQKD is better than that of the traditional CVQKD whether it is four-state modulation or not.

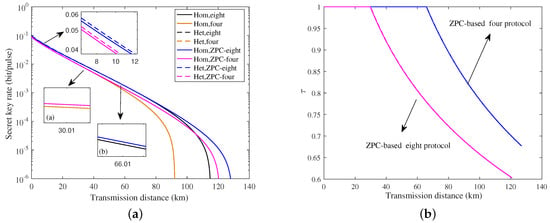
Figure 6. (a) Asymptotic secret key rate of DM–CVQKD involving the ZPC operation for $\epsilon =0.01$, where solid lines denote homodyne detection, while dashed lines heterodyne detection. (b) Corresponding to (a), the transmittance $\tau$ varies with the transmission distance.

The eight-state modulation scheme demonstrates better performance than the four-state modulation scheme in the traditional CVQKD system. However, after performing the ZPC operation, the performance of the ZPC-based four-state modulation scheme exceeds the eight-state modulation scheme. Therefore, the ZPC-based source preparation is an effective way to improve the DM–CVQKD system. We note that the effect of the ZPC operation does not work over the whole transmission distance. In the short distance range, there are few catalytic effects. As shown in Figure 6b, the performance of the ZPC-based system is almost similar to that of the traditional system for $\tau =1$. For the four-state DM source preparation, the ZPC effect occurs at the distance of L = 60 km, whereas for the eight-state DM source preparation, it occurs at L = 30 km.

Usually, one assumes that the quantum channel is given in an asymptotic regime. However, one does not know the quantum channel in advance in the finite-size scenario. Therefore, we take into account effect of the finite-size on the ZPC-based CVQKD. As shown in Figure 7, the proposed CVQKD system in finite-size scenario performs worse than that in the asymptotic limit. As the number N of the exchanged signals is increased, the corresponding curves approach to the asymptotic scenario. The reason is that the large number of the exchanged signals results in the perfect signals parameter estimation. However, it is infeasible to achieve the infinite number of the exchanged signals in practice. Nonetheless, it still has resulted in an improvement, compared with the traditional system in the finite-size regime, as shown in Figure 8.

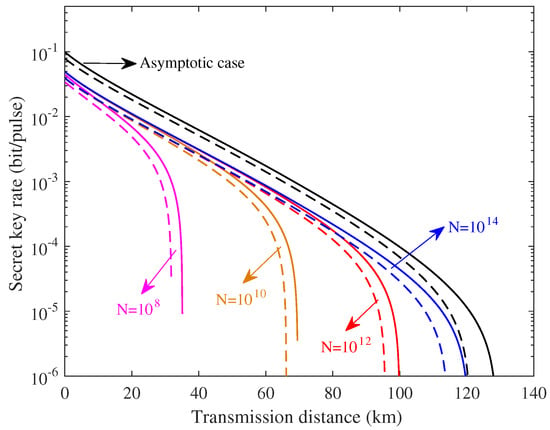
Figure 7. Finite-size key rate of CVQKD involving the ZPC operation for $\epsilon =0.01$, where solid lines represent the eight-state DM source preparation and dotted lines represent the four-state DM source preparation, respectively.

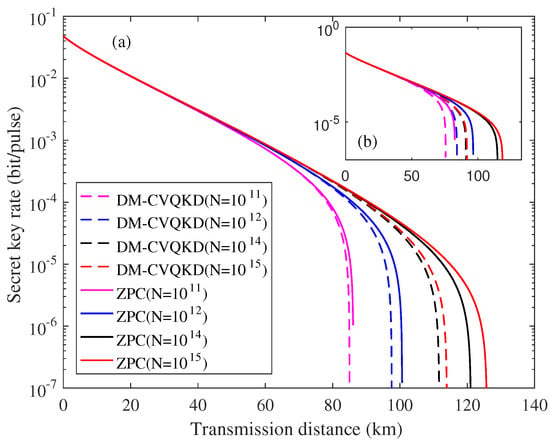
Figure 8. Finite-size key rate of CVQKD involving the ZPC operation for $\epsilon =0.01$, where the (a) represents eight-state DM source preparation, and inset (b) represents four-state DM source preparation.

In addition, we show the effect of the ZPC-involved source on the tolerable excess noise of CVQKD, as shown in Figure 9. We find that CVQKD involving the ZPC-involved source performs better than the traditional system in terms of maximal transmission distance.

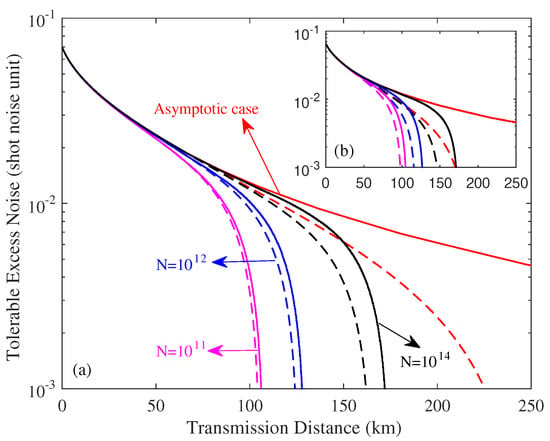
Figure 9. The maximal tolerable excess noise of CVQKD involving the ZPC operation (dotted lines and solid lines) for the traditional CVQKD (dotted lines) and the ZPC-based CVQKD (solid lines), where (a) represents eight-state DM source preparation, and inset (b) represents four-state DM source preparation.

Moreover, reconciliation efficiency is the other important parameter that has an effect on the performance of CVQKD. Figure 10 suggests the effect of the ZPC-based source on the secret key rate of CVQKD related to the reconciliation efficiency. We find that the ZPC-based source can tolerate low reconciliation efficiency. Therefore, the ZPC-based source preparation can reduce the requirements for reconciliation efficiency, thereby reducing costs of practical implementation of the high-rate long-distance quantum communications.

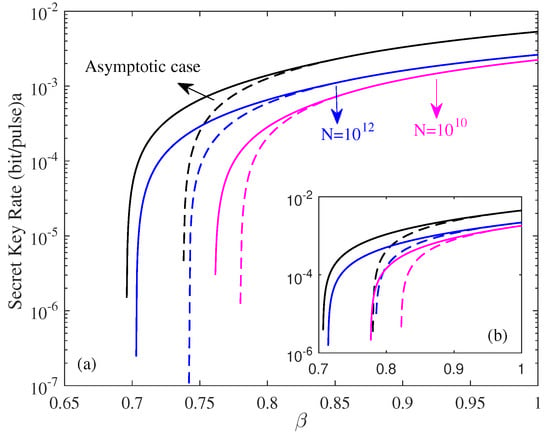
Figure 10. The secret key rate of the CVQKD system involving the ZPC operation with L = 50 km and $\epsilon =0.01$ for the traditional CVQKD system (dotted lines) and the ZPC-based CVQKD system (solid lines), where (a) represents eight-state DM source preparation, and inset (b) represents four-state DM source preparation.

4. Conclusions

We have suggested a ZPC-based source preparation scheme for improving the DM–CVQKD system in metropolitan areas. The PC operation, which is non-Gaussian, has been deployed for the source preparation at the transmitter. We consider the effect of the ZPC-based DM source on the performance of CVQKD. Numerical simulations show that the ZPC-involved DM source can extend the maximal transmission distance of the CVQKD system. Moreover, it can tolerate high excess noise and low reconciliation efficiency, compared with the traditional CVQKD system. Taking the finite-size effect into account, we obtain the tight bound of the maximal transmission distance, which can be experimentally achieved with state-of-the-art technologies.