1. Introduction
Over the past 10 years, different technologies have boosted data-acquisition, communications, and processing capabilities. This strong development has led to the inauguration of a new concept: the Internet of Things (IoT). Although this concept might have direct applications in the daily life of the public, its successful implementation in industrial environments seems to be a more complex issue, as recent reviews have outlined [
1]. This is the case of machining workshops, where many factors limit the range of IoT solutions. First, the integration of new sensors in existing machines is not easy, as durable machine-tools are usually designed for a long life and most existing machines were built before the development of the IoT or the Industry 4.0 paradigms [
2]. Therefore, communication capabilities and integrated sensors built into machine-tools are very limited. In those cases, the only way to extract information from them would be through the machine’s CNC (Computer Numerical Control). However, the CNC is not often available, given that its primary function is to control the machine-tool. Therefore, the most common solution is to access the PLC (Programmable Logic Controller) of the machine. Reading the PLC parameters is one way of extracting many parametric values from the CNC. This solution has been widely used during the last decade; i.e., for developing adaptive remote controllers for milling machines through an internet connection [
3].
The first element for suitable IoT solutions in small workshops should therefore be a Data Acquisition Platform (DAP) connected to the PLC of the machine. The first DAP for manufacturing tasks was demonstrated over 20 years ago [
4] for tool condition monitoring. However, the opportunity of setting up a real implementation was never demonstrated, due mainly to the very limited access to commercial CNCs at that time. To overcome this limitation, open architecture CNCs, once very rare in industrial workshops, were used in most studies over the past twenty years. In very recent years, some studies have described the new communication capabilities incorporated in commercial CNCs.
Having established reliable solutions for data communication, the research focus moved on towards the definition of the best Key Performance Indicators extracted from the IoT platforms for manufacturing optimization.
However, the data-acquisition stage is, however, not the only challenge for machine-workshop IoT solutions. Data processing and analysis are also subject to very restricted conditions and data features. As will be explained, the analysis of workshop machining processes will often have to contend with incomplete and unbalanced datasets. Besides, the data will have too many inputs, lessening its reliability. It will therefore be necessary to reduce the number of inputs and to eliminate repeated instances without losing information.
Machine-learning techniques have many capabilities that are especially suitable to overcome these limitations. First, they generalize models to new conditions, thereby reducing the number of expensive experimental tests to be performed. Second, machine-learning techniques can extract useful information for unbalanced datasets. Third, machine-learning techniques reduce the number of features without losing information. Fourth, machine-learning techniques are able to complete missing attributes, due to sensor malfunctions and data-transmission errors.
Nevertheless, the studies on machine-learning algorithm applications to predict machining-process performance have been demonstrated in laboratory datasets. Datasets generated under laboratory conditions have some extremely different features to those generated in real workshops. Under laboratory conditions, a very small number of inputs are varied from one experiment to the next, there is almost no experimental repetition, the experimental conditions are carefully selected, mainly by factorial or Taguchi experimental design, and all inputs and outputs are carefully measured, and validated before the next experiment is performed, as outlined by the most exemplary reviews [
5,
6]. However, as Bustillo et al. demonstrated [
7], under industrial conditions, most of the experiments refer to the same cutting conditions, a very broad range of parameters are at the same time varied, and the data present many empty values and values of limited confidence.
Most of these features can be joined in one dataset property: artificially balanced datasets. Balance means that there is a similar proportion of all the tested conditions and the values of the outputs in the dataset. This condition is however far from the industrial reality, where most of the instances in the acquired dataset will show a normal behavior and very few will show an abnormal behavior, independent of the considered machining process or output that is to be predicted.
The starting point of this study is completely unlike previous works: the aim is to design a reliable data-acquisition system and to connect it to a machining center in a workshop, acquiring data almost under blind conditions. The machine will be monitored over a sufficient period of time to gain a general overview of its operation, in this case 3 months. The machine has a commercial, non-open architecture CNC that will ensure a suitable IoT solution for all other machine-tools. Then, different machine-learning algorithms will be used to model continuous features, such as motor temperatures, and some discretized features, such as machine state and working mode.
The novelty of this approach is not that it develops a breakthrough approach for data acquisition and IoT implementation, nor is it in the design of new machine-learning algorithms. It refers to both the design and the validation of a reliable IoT solution for its immediate implementation in real workshops. The solution is based on the most suitable machine-learning algorithms for each of the proposed industrial tasks (identification of temperature patterns and machine working states). This suitability will be proven with a real and extensive dataset, where different machining processes are mixed with no clear identification: milling, drilling, etc. Our solution, as previously outlined, is different to the previously presented proposals, because it is not built up from laboratory datasets and specifically designed machining tests (i.e. only face-milling tests at different cutting speeds), but from real datasets with many repetitions, different cutting conditions and processes, etc. Besides, no pre-processing techniques are applied to the dataset, to assure that the selected machine-learning algorithms will be ready to process real information later on without the intervention of a human expert.
The existing bibliography, summarized in
Section 2, proposes solutions for certain industrial problems (e.g., tool breakage or wear monitoring in drilling, milling or turning, surface quality or dimensional accuracy prediction in machined workpieces, etc.). However, in this case, the solution is open to extract any useful information, merely by changing the inputs and outputs of the trained model and without any previous classification of the cutting process that took place. This feature is assured through continuous and discretized outputs of industrial interest. Therefore, the novelty of this research, rather than a solution for a specific manufacturing task, proves a more generic solution and a suitable approach to extract useful information from real manufacturing data.
The paper will be organized as follows. A brief state of the art of IoT platforms for machining workshops and some examples of the most common machine-learning algorithms used on those platforms will be included in
Section 2. In
Section 3, the IoT data-acquisition platform and the machine connected to it will be presented. Then, in
Section 4, the dataset extracted from the data-acquisition platform will be presented with the machine-learning techniques to model the two datasets. Special attention will be paid to the most suitable metrics to evaluate model performance. The results of such modeling and the industrial use of the best model will be presented in
Section 5. Finally, the most relevant results will be summarized in the conclusions (
Section 6) and pointers will be given for future lines of research.
3. Data-Acquisition Set Up
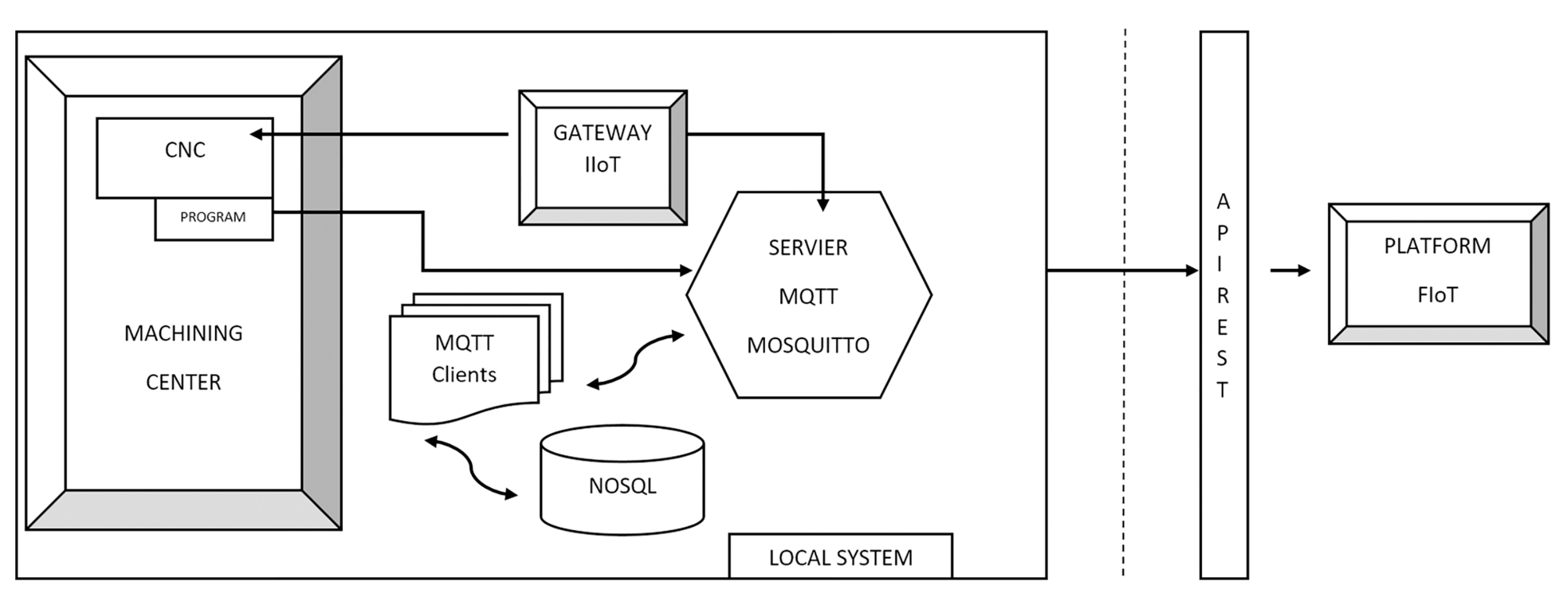
The IoT solution developed in this investigation was, at the machine level, composed of a data-acquisition system connected to the machine control, in this case, a five-axis machining center equipped with Heidenhain 640 CNC. The machining center milling head was equipped with a Pt100 temperature sensor. It had two continuous rotatory axes specially designed for machining aeronautical components. The other three axes were the transversal longitudinal ones X, Y, Z. It can perform multiple operations through a CNC with very little human intervention. These operations use cutting and rotating tools, such as mills and drills. This data-acquisition system transfers the collected data to a database through an accessible Internet connection in the workshop. The database will oversee automatic and periodic analysis of data collected in real-time.
Figure 1 schematically shows the operation of the IoT design solution. Note that only read operations are performed, so the process will never alter the operation of the machine.
Communication between the acquisition system and the machining center is carried out through an automatic CNC variable reading process. Developed in Python 2.7, information may be captured with this process, using the internal variable name (mnemonic) used in the PLC. The Python library “pyjh” [
29] (which is a proprietary software from Heidenhain 640 CNC) was used to read the CNC variables. The equipment can monitor all the parameters of the CNC of the machining center at variable sampling frequencies with which data can be compiled on the general dynamics of the machine, its consumption, its thermal evolution, significant averages of vibrations and shocks and the entire alarm table that occurs.
The output of the reading process of the CNC variables was performed using the “Internet of Things” protocol, MQTT (Message Queue Telemetry Transport), establishing communication between the system and any IoT platform that supports the MQTT protocol. The controller of the machining center must be on the same network as the IIoT Gateway (i.e.; Industrial IoT Gateway). According to [
30] an IoT Gateway “is a connecting link between the sensor network and the traditional communication network”. Nowadays, IIoT Gateways can perform many other tasks, besides their function as a mere protocol converter, such as for example encrypting, buffering, and preprocessing the information. In our case, this device (1) reads the information from the CNC using TCP/IP sockets, and (2) “monitors” it (i.e., builds a JSON (JavaScript Object Notation) object with this information to be published by an MQTT client). There are another two main MQTT clients in this architecture: one to store these JSON objects in a database, and another open to further uses (e.g., plotting graphical information).
The acquired data were recorded in real-time on a private MQTT Mosquitto server in the machining workshop. This server was operated through the publication and subscription system. Each monitoring device has a publication topic within a hierarchical structure that can be used to subscribe to one or more information topics. The MQTT Broker is the server where all requests from MQTT Clients are received. In addition to the three above-mentioned clients that publish information, other clients preprocess and structure the published data.
The preprocessed data is grouped into different categories: consumption, axes, cutters, mandrel, temperature, etc. for future data analysis using data-mining techniques. The MQTT normalization clients republish the information in the MQTT Broker, to which they are subscribed, but already normalized and structured in another topic. Then, the MQTT Client subscribed to those pre-processed data topics will obtain the data and store it persistently in a local non-relational database (NoSQL) (
Figure 1). The use of an NoSQL database is required, because of the large data volumes collected per unit of time. It avoids potential scalability problems and improves the speed of querying and writing to the database. These data volumes are temporarily stored in the control server itself.
Twice a day, the information is sent to the Fiware Internet of Things (FIoT) data-processing platform through a communication interface with REST software architecture. The data volumes included in this work that were collected on the FIoT platform exceeded 1,500,000 datums grouped by category, over 3 months of machining center operations, although the specific study described in the following sections only analyzed a very limited part of this information. In this process, another data filtering operation was performed: eliminating possible captures of erroneous measures and adding extra information for later use. This captured information is tagged with machine identifiers, company, location, date, and origin of the data. JSON annotation was also used for the correct management of this information.
5. Results and Industrial Interpretation
A dataset has been created for each of the six variables to be predicted. All these sets have the same input variables, and have a single output variable, which is different in each of them.
For both classification and regression problems, the methods described in the previous section were applied to each of the datasets using 10 × 10 stratified cross-validation. For each of the metrics, the average values were found in the 10 repetitions × 10 partitions. The corrected re-sampled
t-test was used [
53] at a confidence level of 95%, in order to determine whether there were significant differences in the results for each metric between two methods applied to the same data set.
5.1. Classification: State and Mode Prediction
Table 3 shows the 13 classification methods tested in the experiment. Each method is compared with the other 12 methods for the 2 classification problems State and Mode (i.e.;
comparisons). One method for each one of these 24 comparisons can receive a significantly better result than the other method. So, in this case, we say that the method “wins”. The method can also get a significantly worse result than the other method, and then we say that it “loses”. Finally, the comparison may return no significant differences.
In
Table 3, columns
V and
D respectively represent the number of these significant wins and losses in the two classification problems for the method in that row versus all other methods. Then, the difference “
” is computed by subtracting D from V. This difference is taken as an indicator of what the best method is. In
Table 3, the methods are ordered by
. We can see from the table that the two best positioned methods are tied with
equal to 16. They win 16 times from the 24 matches, and they never lose.
The two rightmost columns of
Table 3 contain the average F-Macro values for each method and predicted variable. These average values are computed from the 100 experiments from the
CV. When these values are followed by “*”, they are significantly worse than the one achieved by the first
ranked method (i.e., Rotation Forest of Random Forest in the table, but we also tested that “*”s keep unchanged, if the best method was considered Random Forest). The best F-Macros for each predicted variable are highlighted in bold (i.e., LogitBoost for State and Bagging of Random Balance of C4.5 for Mode). We also tested that “*”s in the State column keep unchanged, if the methods were compared to LogitBoost, as well as in the Mode column, if the methods were compared to Bagging of Random Balance.
The following conclusions may be identified from
Table 3:
- 1.
Very good results may be found with just one single C4.5 decision tree. It could, on the one hand, mean that the input variables adequately describe the output variables and, on the other hand, that the number of instances is also sufficient.
- 2.
Both problems are not suitable for a linear classification in view of the results of the linear SVM.
- 3.
Classifiers based on the optimization of a complex function, such as Neural Networks or Radial Basis Function SVM, do not obtain competitive results despite the computational cost involved in the parameter optimization process.
- 4.
All the top ranked methods are ensembles, which hardly vary from each other in their performance.
- 5.
kNN is the best of the non-ensemble methods. It is once again due to the low number of characteristics (i.e., there is no curse of dimensionality) and the high number of instances.
Conclusions 2 and 3 point out the complexity of the decision boundaries for both problems.
Table 4 and
Table 5 repeat the same structure as
Table 3, but using F-Micro and MCC. In
Table 4, the best F-Micro for State is achieved by LogitBoost (i.e., not by the best ranked method), although we checked that “*”s remained the same in the State column, if the methods were compared to LogitBoost. However, in
Table 5, the best MCC value for the Mode variable is achieved by the second ranked method (Bagging of Random Balance of C4.5). In this case, when the methods were compared to this Bagging variant, every other method would be tagged with “*”. So, when MCC was chosen as a metric, Bagging of Random Balance of C4.5 was significantly better than all the other methods for the Mode variable.
Some additional conclusions that could be drawn from these two tables are:
- 1.
The C4.5 tree reached very similar values to those of some ensembles. Usually, it is expected that the variance component of the classification error decreases as the training dataset increases [
54]. It is known that Bagging-based ensembles reduced this error component, as Boosting-based ensembles also do in their later iterations [
55]. Hence, these similar results of C4.5 vs. ensembles can be explained, at least in part, by the dataset size and the superiority of decision trees over the other non-ensemble methods.
- 2.
It is also interesting to note that the F-Micro and MCC for State variable prediction almost reaches one (i.e., the maximum possible value) in many of the classifiers that were tested, and in nearly all in the case of F-Micro. This points out again that the State is well characterized by the attributes of this data set.
- 3.
However, the Mode variable figures are worse. For both F-Macro and MCC metrics, Random Balance Bagging, which is a specific method for imbalanced datasets, is the best choice. The “+” sign in this method in
Table 5 indicates that the MCC obtained is significantly better than the first method in the ranking.
These last 2 conclusions can be explained by the fact that the Mode variable has a much clearer majority class (i.e., has 74% of the instances); while the State variable is distributed between states 1 and 2 in a quite balanced way for 90% of the instances.
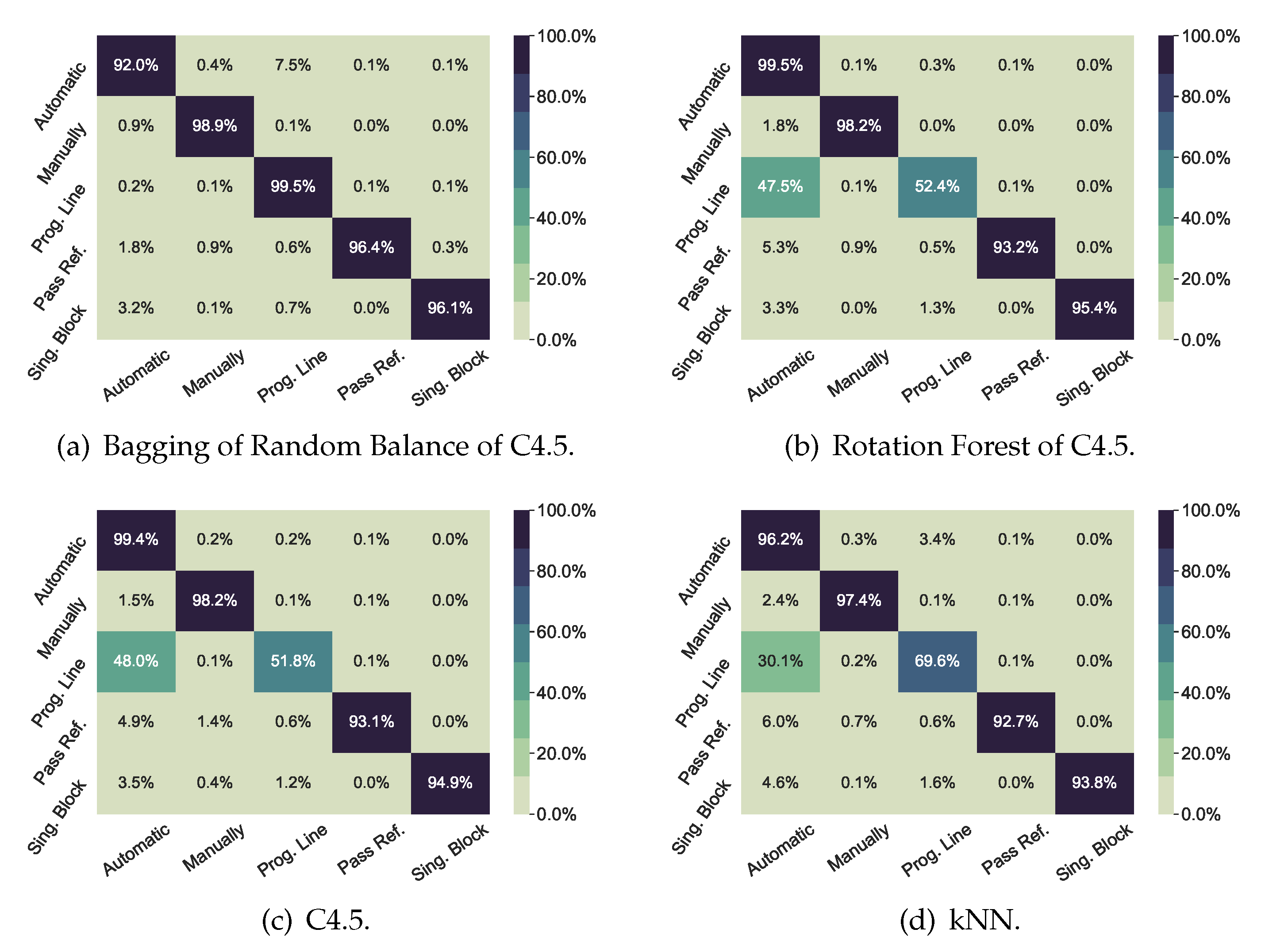
The computation of confusion matrices for some of the methods can provide deeper insight into their accuracy. In a confusion matrix, the element in row i and column j represents the number of times the class in row i is predicted by the method as the class in column j.
In an ideal classifier that is correct of the time, the elements of the diagonal will achieve values (i.e., the elements of class i will always be correctly predicted as belonging to class i). Also, the rest of the cells within that ideal classifier that lie outside the diagonal will have a value of (i.e., the elements of class i would never be predicted as belonging to a different class j).
A CV was performed (i.e., 5 repetitions of 2 folds cross validation), to produce reliable confusion-matrix values. Hence, the data set for a CV was randomly divided into 2 parts at . One part was used to train the classifier and the other, to validate the model by counting which class it rightly or wrongly predicted for each test instance. Then, the partitions were swapped (i.e., The partition that was previously used for training was then used for validation and vice-versa). The random split differed for each of the 5 repetitions. Once that procedure had finished, values for each cell of the matrix were obtained. The figures on the following page represent the average values of those 10 results. The data are shown as percentages instead of absolute values, so that minority classes are not underrepresented.
Figure 2 shows the confusion matrices for the Mode classification problem. The two upper matrices represent the best methods in that problem (i.e., Bagging of Random Balance, because it has the highest values for F-Macro and MCC, and Rotation Forest of C4.5, because it has the highest value for F-Micro). The two lower matrices represent the two best non-ensemble methods (i.e., a C4.5 decision tree and k-NN). All the classifiers show diagonal values above
, except for
Prog Line class, which is confused half the time with
Automatic class. This confusion can be explained, as the first time that a new machining program is executed, the machine operator will usually run it line by line, so that its performance can be closely controlled. In this way, the operator can quickly stop the program execution, if a program error is detected that might damage the workpiece or the cutting tool. Once the program has been validated by machining a first workpiece, automatic mode will be used to run this program in the future. Therefore, the machine-learning algorithm will find no difference between automatic mode and line by line mode in those cases. However, Bagging of Random Balance performs well even for that fuzzy case.
In contrast,
Figure 3 showed high performance in all scenarios with any of the classifiers of the figures.
In short, the high performance that Bagging of Random Balance achieved for Mode prediction, and LogitBoost for State, will guarantee that this model can identify these two process parameters. The combination of both can surely identify the main production activity of the machining center. Some examples of these combinations are: (1) reference fixation of a new workpiece (idle state and manual mode); (2) workpiece milling operation (working state and automatic mode), test of a new milling program (idle state and MDI mode), and load/unload of a workpiece (stopped state and Pass mode). Therefore, the prediction model can extract useful information on how the machining time is distributed, not from an Engineering Department planning report, but from the real workshop reports on the daily situation.
5.2. Regression
As for regression experiments (
Table 6), there is one method that significantly beats all others in all the variables to be predicted, which is Rotation Forest of REP-Trees.
Again, the ensembles are in the lead. Linear regressors (i.e., Linear Regression and Linear SVM) are left in the tail positions, which suggests that these are not linear problems. As with classification problems, a single decision tree is still the best performing non-ensemble method.
WEKA gives the name ZeroR to the naive regressor that always predicts the average. For that reason, it is at the end, since by definition RRS will always take a value of 100%. ZeroR is taken as the baseline.
The average of the absolute error was calculated for the best method (i.e., Rotation Forest of REP-Tree) and for ZeroR (
Table 7), to compute the physical magnitude of the error committed. The absolute error is defined as the absolute value of the difference between the actual value and the predicted value. The table shows average absolute errors ranging from 0.68
C for
, to 1.99
C to
.
For a deeper understanding of temperature behavior,
Figure 4 was plotted.
Figure 4 shows the box-plot diagram for the four motor temperatures. In the box-plot diagrams the data are split into four quartiles depending on their value: the lower, second, third and upper quartiles, each of them with 25% of the data. The box-plot diagrams show: (1) the median of the variable with a green line; (2) the area with 50% of the middle data (data in the second and third quartiles) with a blue box; (3) two black lines or whiskers; and, (4) the data outside the whiskers with black circles. The whiskers are calculated as 1.5 times the interquartile range (distance between the upper and the lower quartile). Whiskers are a fundamental measure because any data outside the whisker should be considered as abnormal data or outliers [
56].
Figure 4 shows that the temperatures do not deviate by more than 2.5
C from the temperature of the median for any motor. The temperature dispersion, evaluated from the whiskers distance, is approximately the same for the linear axes: those that are most stressed during a machining operation). In the case of the milling head, the temperature dispersion is smaller, as expected in a thermalized milling head. However,
Figure 4 also shows:
- 1.
Many outliers at low temperatures for T, T and T, which may be due to the latency in the system’s heating curves at start-up.
- 2.
Some outliers for the Z-axis at high temperatures. These points may indicate that this axis has been over-worked and strained at certain points during machining, and their identification may be important to avoid damage to the spindle motor or to increase the average life of the tool.
- 3.
Some outliers for the milling head temperature T at high temperatures, but not far away from the median temperature. These values may indicate some rotating efforts of the milling head during 5-axis machining, but not too high to overcome the limit of 35 C.
The comparison of the errors for ensemble models are shown in
Table 7 and the 2.5
C deviations around the median, in
Figure 4, point out that these predictors are useful to detect the outliers, which are of greater interest, because they can refer to overly demanding cutting conditions or abnormal programming of the machine. Moreover, those absolute error values may seem a little high for data close to the median. However, these data instances are the ones with the lowest industrial value, as they are corrected by the continuous action of the cooling system.
6. Conclusions
The main contribution of this work may be summarized as follows:
A real data-extraction architecture connected to an IoT platform for small workshops has been described.
The data that are extracted can be useful for solving industrial problems. High performance results can be achieved for industrial problems related to both imbalanced classification and regression.
The best performance was obtained by machine-learning ensemble methods, which require no method optimizations, yielding a straight-forward and simple way for optimal exploitation of the data that were gathered for this study.
The IoT platform with which we have experimented was able to extract many useful inputs from the CNC of the machine without interfering with the production process. In the present work it collected a dataset consisting of measurements of real machining operation during lengthy time periods (3 months, which means 52,592 instances) and the different conditions included in it: milling and drilling processes of many different workpieces, many warm-up cycles, tools with strong wear effects and new tools, etc. Within this period, the machine state and operation mode, the position and speed of its axis and of the cutting tool and the temperature of 4 different components were all measured.
As for the use of the dataset that was obtained with machine-learning models, the present work represents an attempt to see whether these machine-learning techniques will also work properly with real data from machining workshops, to extract useful information on production planning and performance. Two types of industrial problems have been addressed by applying several classification and regression algorithms.
The prediction of two discrete variables: State and Mode (i.e., two classification problems).
The prediction of four continuous variables: T, T, T, T (i.e., four regression problems).
IoT in small workshops will usually have to negotiate with unbalanced and not very reliable data. However, prediction tasks are performed with high accuracy, despite the strongly unbalanced nature of the acquired data. State prediction performed well even with a single decision tree, although, in general, ensembles improved these results. In fact, there are several methods that are close to reach the maximum value of “1” for F-Macro, F-Micro and MCC metrics. On the other hand, Mode prediction is more problematic, and the best results have been obtained with an unbalanced problem-oriented ensemble, such as Random Balance’s Bagging.
In the four regression (i.e., temperature prediction) problems, however, there is a clearly better method, as Rotation Forest always outperforms all other methods significantly. This algorithm is of limited accuracy when predicting the favorable temperature operating conditions of the spindles, but under these conditions its predictions are not useful, as the supervision of operating temperatures is done properly by the machine’s cooling system. In contrast, this method has proved to be sufficiently accurate at identifying atypical temperature behaviors, which can permit early correction and, more interestingly, the programming of new machining conditions to avoid temperature malfunctions, and thereby, ensure a longer average life of the machine tool and its most critical elements that are monitored.
A common feature to all six problems is that competitive results were not produced by the methods that entailed higher computational costs due to the tuning of some of their parameters (i.e., SVMs and neural networks). Therefore, there is an easy and computationally low-cost way to leverage the extracted data.
The results suggest that the ensembles might be more suitable, as they predict from a voting scheme of their base classifiers. These base classifiers differ between each other, as they are trained by resampling the data set, and/or by giving more weight to some instances and input features than others. In this way, they do not work with a single version of the data set, but with as many as there are base predictors (100 in the experiments), which will somehow generalize patterns that might not have been identified.
Finally, three future works are proposed. The first one will be the exploration of multi-label methods [
57] to try to improve the results for the mode classification and the four regression problems. Secondly, the identification of the programmer’s footprint will be on the research focus; that is, the subtle characteristics of each machine programmer that can optimize machining programs. Thirdly, the implementation of these methods will be in a cloud service connected to the IoT FIoT platform, as described in this paper. An innovative development that will integrate the entire process on one system: from data acquisition to the extraction of useful information for the end user.