Abstract
Fingerprint classification is a stage of biometric identification systems that aims to group fingerprints and reduce search times and computational complexity in the databases of fingerprints. The most recent works on this problem propose methods based on deep convolutional neural networks (CNNs) by adopting fingerprint images as inputs. These networks have achieved high classification performances, but with a high computational cost in the network training process, even by using high-performance computing techniques. In this paper, we introduce a novel fingerprint classification approach based on feature extractor models, and basic and modified extreme learning machines (ELMs), being the first time that this approach is adopted. The weighted ELMs naturally address the problem of unbalanced data, such as fingerprint databases. Some of the best and most recent extractors (Capelli02, Hong08, and Liu10), which are based on the most relevant visual characteristics of the fingerprint image, are considered. Considering the unbalanced classes for fingerprint identification schemes, we optimize the ELMs (standard, original weighted, and decay weighted) in terms of the geometric mean by estimating their hyper-parameters (regularization parameter, number of hidden neurons, and decay parameter). At the same time, the classic accuracy and penetration-rate metrics are computed for comparison purposes with the superior CNN-based methods reported in the literature. The experimental results show that weighted ELM with the presence of the golden-ratio in the weighted matrix (W-ELM2) overall outperforms the rest of the ELMs. The combination of the Hong08 extractor and W-ELM2 competes with CNNs in terms of the fingerprint classification efficacy, but the ELMs-based methods have been demonstrated their extremely fast training speeds in any context.
1. Introduction
Fingerprint is one of the widely used biometric techniques for individuals identification purposes because of its bio-invariant and reliability characteristics. Besides, it provides sufficient and necessary details for the differentiation of people [1]. It should be noted that fingerprint is chosen among other biometric techniques (iris, face, voice, hand, and others) due to its high accuracy and low acquisition cost. Fingerprint recognition has several applications for security goals such as forensic and civil registering, as well as an alternative for user authentication [2].
An automatic fingerprint recognition system requires the matching of an input fingerprint sample with a large number of fingerprint templates registered in the biometric database [3]. Taking into account a massive database for a real-world application, an individuals identification system is excessively expensive in terms of search-time and computational cost [4]. For example, the FBI database contains more than 100 million fingerprints, delaying the identification of a person up to 30 min in the best scenario. Of course, high-performance computing methods are employed to get this time.
Fingerprint classification is the most adopted approach to reduce the penetration rate in the database [5]. Fingerprint images have structural characteristics based on the pattern of ridges. Thus, according to the morphology of its ridge structure, fingerprints can be classified into five major categories [6]: arch, tented arch, left loop, right loop, and whorl, which are not evenly distributed. Figure 1 depicts these fingerprint classes and their frequency of occurrence in the overall population. In other words, an unbalanced dataset is naturally experienced in which two classes are under-represented relative to others. The problem of unbalanced data is commonly associated with asymmetric costs of misclassifying elements of the diverse classes [7]. In order to deal with unbalanced data, the following methodologies can be adopted: under-sampling approaches [8], over-sampling techniques [9], and algorithmic methods [10]. The former can lead to loss of majority class information, the second approach may produce distortion of the minority class, and the latter is to set different misclassification costs according to each particular class, which is adopted in our work for simplicity and effectiveness purposes.
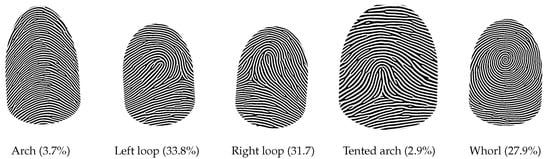
Figure 1.
Fingerprint image samples generated, which represent the five fingerprint categories along with their frequency of occurrence in the total population.
The fingerprint classification task typically consists of three main processes [11,12]: (i) pre-processing, to reduce the noises and interference in images; (ii) feature extraction, to represent the image as a vector of characteristics; and (iii) classification procedure. This methodology allows building extremely precise classifiers with an acceptable computational cost [2,5]. An alternative for classifying fingerprints in a single stage is deep convolutional neural networks (CNNs) [1,3,13,14], which are characterized by millions network parameters involved in the learning phase. These approaches obtain yields close to 100% but with a time-consuming training process, despite using computers with the latest generation parallel software and hardware.
Extreme learning machine (ELM) has been proposed as a promising training algorithm for single hidden layer feedforward neural networks [7]. In the ELM algorithm, the weights and biases of the hidden layer are randomly generated. Then, the weights of the output layer may be analytically computed via solving a linear system thanks to the Moore–Penrose pseudoinverse matrix [15,16]. Previous results, both in regression and classification problems, have shown the low computational complexity of ELM compared to the popular backpropagation-based algorithm and support vector machines, especially for high dimensional and large data applications [7,15,17,18]. Besides, it is highlighted for its fast and stable training process, easy implementation, and accuracy in modeling and prediction.
Nevertheless, the prediction accuracy of the ELM algorithm can be susceptible to outlier interference, which is presented for unbalanced datasets [19], such as a fingerprint database. Namely, the basic ELM algorithm trained with an unbalanced dataset may be biased towards the majority class and obtain a superior accuracy on the majority class by affecting minority class accuracy for classification problems. In a fingerprint recognition system, this issue will conduce to some important persons that cannot be found timely. Aiming to face the unbalanced data issue, weighted ELMs were introduced by Zong et al. [10]. This improved ELM incorporates weights to mitigate interference from outliers in the learning procedure. A weighted ELM may automatically adjust the correlation weight of ELM based on the training errors in the training procedure. The weighted ELM shows the best performance on unbalanced datasets contrasted to standard ELM by maintaining the benefits from it (convenient implementation and easy application on multi-class data classification) [20]. Consequently, a weighted ELM is more suitable for fingerprint classification. In our work, standard and weighted ELMs are developed to demonstrate the advantage of the latter for unbalanced datasets.
In [21], the problem of fingerprint classification using a standard ELM has been briefly addressed. This study introduces a modified descriptor of the histogram of oriented gradients. The authors of [21] arbitrarily use a radial base activation function, discarding the regularization parameter (over-fitting can occur in the modeling process) for the original ELM, and they do not declare the number of neurons in the hidden layer. Moreover, they do not provide any comparison against other classifiers and use a well-known database (the Fingerprint Verification Competition (FVC) of 2004) only divided into four categories (the arch and tended arch classes are joined as a single class), which can increase the penetration rate and computational cost for the fingerprint identification system.
In this paper, we introduce the combination of the better feature extractors and several versions of the ELM for fingerprint classification purposes. The feature extraction step obtains a set of meaningful global features of the fingerprint. On the other hand, the ELM algorithm classifies each fingerprint as one of the five classes of fingerprints. In our study, we consider three feature descriptors (e.g., Capelli02 [22], Hong08 [23], and Liu10 [24]), which will be termed with the name of the first author and the year of publication in the rest of the paper. In addition, three ELM models (e.g., basic ELM [17], original weighted ELM [10] and decay weighted ELM [20]) are developed. The Synthetic Fingerprint Generator (SFINGE) dataset [25,26] is utilized since its images are naturally distributed into five classes. In addition, this dataset contains fingerprints of different qualities (high, normal, and low), by allowing the simulation of several real-world scenarios. The main novelties and contributions of our study can be summarized as follows:
- (i)
- As fingerprint classification system, we propose an ELM model based on feature descriptors with the highest performance for fingerprint identification. The introduction of the ELM algorithm is due to its training stage consumes short time, which allows to increase the identification in large fingerprint databases.
- (ii)
- In the weighted ELM, original and decay weighting schemes are developed to improve the classification capability of the classifier by considering complex data distribution, such as fingerprint classes.
- (iii)
- The hyper-parameters of the ELMs (regularization and decay parameters, and the number of hidden nodes) are numerically optimized in terms of the geometric mean since this metric normalizes the classification accuracy of each class.
- (iv)
- The combination of the Hong08 feature extractor and the weighted ELM with the presence of the golden-ratio in the weighted matrix is superior to the rest of combinations of feature extractors and ELMs, and almost matches the CNN-based methods in terms of accuracy and penetration rate. Nevertheless, our approach has the benefit of a fast learning speed by using any commercial computer.
The rest of the paper has the following organization. Section 2 presents the state-of-the-art regarding the fingerprint classification issue. Section 3 exposes the best feature extractors reported in the literature as well as the ELMs for balance and unbalance datasets. Section 4 presents the methodology, which is comprised of the fingerprint database, a k-fold cross-validation scheme, and performance metrics. Section 5 shows the results and discussion. Finally, Section 6 provides some concluding remarks and future works.
2. Related Works
Fingerprint classification is the most common approach to reduce the database penetration rate of a fingerprint identification system. It is well-known, fingerprints can be classified into five major categories: arch, tented arch, left loop, right loop, and whorl, as shown in Figure 1. On this regard, several approaches have been proposed, and two main tendencies are identified to address the fingerprint classification problem (refer to Table 1):

Table 1.
Summary of the state-of-the-art approaches for the fingerprint classification problem.
- (i)
- Via feature extractors that obtain the most important characteristics of the fingerprint image, by reducing the original size severally. In this context, the feature extractor models with the best-reported results in the literature are [3,5]: Capelli02 [22], Hong08 [23], and Liu10 [24], which are based on global level characteristics of the image such as orientation maps, ridge structure, and singular points, respectively. Afterward, the classification problem is performed trough a supervised learning technique, e.g., support vector machines, or artificial neural networks based on the gradient operation.
- (ii)
- By employing only a CNN directly on the input images, where the feature extractors are discarded. In practice, CNNs are complex networks that combine different types of neuron layers (convolutional, pooling, and fully connected) with diverse activation functions (e.g., Rectified linear unit (RELU), softmax, RELU plus dropout). Besides, it can be accompanied by a Bayesian framework. However, CNN-based approaches require very time-consuming training process with millions of parameters to be optimized.
Table 1 summarizes state-of-the-art approaches on the fingerprint classification problem during the last decade. It contains the following information: author(s), year, feature extractor, classifier, database, classification accuracy, and evaluation time of the artificial neural machine. Whereas the first group (feature extractor along with classifier) allows exceeding 90% as classification performance without increasing the complexity time, the CNN-based approaches are near to 100% accuracy but with large learning time, in the order of hours. It should be noticed that this drawn-back comes from even in the presence of high-performance computing methods [1,3,4,13]. Furthermore, it can be seen than the most of works consider some version of fingerprint databases from the National Institute of Standard and Technologies (NIST) [27] or the FVC [28], which obey to uniform and natural class distribution, respectively. Furthermore, an specific version of both databases is composed by small images of fingerprints (from 1000 to 3000 samples approximately), which limits overall observations (a real fingerprint identification system deals with extremely large databases) due to training/validation/testing results can be optimistic and/or wrong. In other words, the origin (database) of these studies, their solutions (feature extractors and/or classifiers), and conclusions can not directly implement a fingerprint identification scheme.
3. Background
In this Section, we outline the best feature extractors as well as the unweighted and weighed ELMs because they are the fundamentals of this investigation. It should be highlighted that we focus on ELMs because these networks are used for fingerprint classification for the first time.
3.1. Feature Extractors
Based on the classification given by Feng and Jain [43], there are three categories of fingerprint features representation: global, local, and fine-detail. However, only global feature descriptors are used for fingerprint classification because fingerprint classes are intuitively defined from global characteristics [2]. Therefore, feature-based approaches for fingerprint classification are closely related to the ridge orientations and the singular points representations. Ridge orientations are represented in an orientation map (OM), which is a representation of the local flow of the ridges. On the other hand, locations with ridge flow changes are selected as singular points, being two main types known as cores and deltas. Thus, each fingerprint class can be defined based on the distribution of its ridge orientations and singular points [2].
The OM extraction is the first step in any feature-based fingerprint classification system. OM-based representations are obtained as a description of the local ridge flow for every block in the fingerprint. The OM of a fingerprint sample of pixels is a matrix of computed for orientation blocks of . The OM matrix stores the orientation angles expressed in radians in the range of or . Once the OM is obtained, it is used for detecting singular points by analyzing the behavior of the ridges [44].
Galar et al. [2] present a refined taxonomy of the feature extraction methods for fingerprint classification. They classified the feature extractors into four categories: orientation image, singular points, ridge-line flow, and Gabor filter responses. Besides, the authors of [3,5] extensively studied the performance of different feature extraction methods for fingerprint classification. Thus, in order to complement our proposed method based on ELMs, we use three global feature extractors with the best-reported results in the literature [3,5], which have different characteristics and are described as follows:
- (i)
- Capelli02 [22] is based on the orientation map of the fingerprint. The approach registers the core point by using the Poincare method [45]. Then, the fingerprint is represented by a vector of five positions, which is computed by applying a set of dynamic masks directly derived from each class. The feature vector also stores the orientations.
- (ii)
- Hong08 [23] improves the FingerCode feature vector [46] by including ridge-tracing information and singular points. Besides, the representation encodes the position and distance between the endpoints of the pseudo-ridge relative to the primary core point.
- (iii)
- Liu10 [24] represents the fingerprint by building a feature vector based on the relative measures among the singular points. Singular points are detected by computing complex filter responses at multiple scales [47]. Thus, the feature vector consists of the relative position, direction, and certainties of each singular point for each scale.
3.2. Extreme Learning Machines
ELM results in an algorithm for single hidden layer feedforward neural networks (SLFNs), massively popular for its fast learning speed and excellent performance in generalization. Huang et al. [17] have shown that ELM outperforms gradient-based artificial neural networks and support vector machines in terms of prediction performance.
Given a training set with L samples, the basic ELM maps inputs (data samples) and outputs (labels) by employing a single hidden layer composed by N nodes. As mathematical representation [7,48]:
where H is the hidden layer output matrix, denotes the output weights matrix between the hidden layer and output layer, T represents the target output results of the output layer, refers to a non-linear piecewise continuous function, such as the sigmoid function, is the input weight vector between the input node and jth hidden node, refers to the ith input data where n means the dimension of the input layer, represents the bias of the jth hidden node, denotes the output weight vector between the jth hidden neuron and output nodes, and is the m-dimensional target vector originated by . Furthermore, and result from any continuous probability distribution, such as the rectangular distribution; the human intervention consequently decreases. To conclude, the term comes to be the inner product of and . For clarification purposes, the structure of the traditional ELM is shown in Figure 2 where all layers are identified in detail.
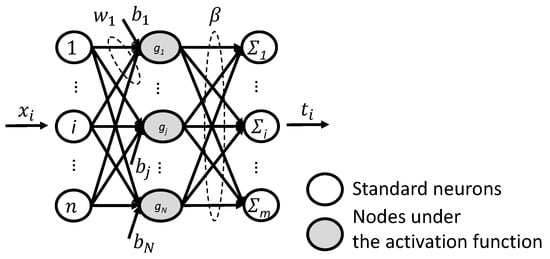
Figure 2.
General architecture of a single hidden layer feedforward neural network (SLFN) with the extreme learning machine (ELM) algorithm.
The least square solution with minimal norm can be analytically calculated through the Moore–Penrose generalized inverse of H as follows [16,17]:
with I and C being a unit matrix and regularization parameter , respectively. The I dimensions depend on the relationship between N and L, and C is added in order to balance the training error and the norm of output weights, by avoiding the over-fitting.
Like the rest of conventional learning algorithms, the learning capability of the original ELM can be affected by the class distribution [19]. It provides superior performance in the case of balanced datasets; however, the unbalanced classification can be difficult. To this end, samples with high training errors must be related to small weights and vice-versa in the ELM algorithm [20]. According to the Karush–Kuhn–Tucker theorem, the solution to acquires the form of [10]:
where W denotes the misclassification cost matrix. It is a diagonal matrix according to the class distribution as follows [19]:
where refers to the number of samples in the class . In the weighted ELM1 (W-ELM1), the unbalanced datasets reach a cardinal balance. To further decrease the weights of the majority class data, the weighted ELM2 (W-ELM2) is more suitable, which considers the golden ratio. The trade-off between the ELM and W-ELM1 is given by the W-ELM2.
Numerous techniques have been developed to properly solve the unbalanced data classification in ELMs such as improved weighted ELM [49], improved neutrosophic weighted ELM [50], dual activation function-based ELM [51], weighted regularized ELM [19], among others. In terms of simplicity and improvement, the decay weighted ELM (DW-ELM) must be highlighted [20]. For balance and optimization learning, an extra degree of freedom is inserted to the weighted ELM, which is known as the decaying parameter d. The weighted matrix may be written as [20]:
As the decaying parameter increases, the minority class is more relevant than the majority class. Namely, by varying this parameter, the classifier would get better boundary positions. If , the DW-ELM converges to the original ELM. Note that any weighted ELM increases the computational cost respect to the standard ELM, comparing Equations (2) and (3). Finally, the training stage of any version of the ELM has the following steps (Algorithm 1):
| Algorithm 1 ELM learning procedure. |
| Given the training set , activation function , regularization parameter C, and hidden neuron number N. |
|
4. Methodology
In this Section, we expose the experimental set-up employed to carry out the experiments and, hence, to develop the results and discussion displayed in Section 5.
4.1. Fingerprint Database
We replicate the experiments carried out in [3] by using the SFINGE software [25,26]. Following the natural class distribution (refer to Figure 1), it can generate synthetic fingerprints with a real appearance of quality levels (translations, rotations, and geometric deformations), and with true class labels. Consequently, the performance of the classifiers can be easily evaluated thanks to this software. To emulate various scenarios, we have taken into account three different quality profiles in the generation of the fingerprints, labeled as HQNoPert, Default, and VQAndPert, see Figure 3. The HQNoPert database is formed by high quality, no perturbations fingerprints. In the Default database, a fingerprint is characterized by middle quality, slight localization, and rotation perturbation. Fingerprint captions of varying qualities are presented in the VQAndPert database, where location, rotation, and geometric perturbations also occur. The scanner and generation parameters employed for the generation of the fingerprints in SFINGE software can be seen in [3,5]. The quality of the generated images is the only difference between the databases. To conclude, we generate 10,000 fingerprints of each quality, being a total of 30,000 fingerprints.

Figure 3.
Fingerprint examples of the different studied databases.
4.2. Results Evaluation by the Five-Fold Cross-Validation Scheme
To assess the quality of the novel technique, we follow a perspective oriented to machine learning known as five-fold cross-validation approach [52]. This scheme results in an unbiased and accurate measurement of the classifier performance due to the training and testing are not developed on fixed parts. To this end, the database is split into five-folds, each one containing 20% of the samples of the database. For each split, the classification model is trained by using the 80% of fingerprints from the rest of the folds, whereas testing is done on the current fold. For each database and classifier, the overall results are reported from averaging five executions. In particular, in order to estimate the optimal hyper-parameters of the ELM (see Section 5.1), we destine the 20% of each training set for validation purposes according to the methodology exposed in [18]. Hence, the validation set is intended to find the ELM hyper-parameters (e.g., the regularization parameter C and the number of hidden nodes N) that will maximize its performance. The previous scheme allows a direct comparison with results obtained by the benchmark proposal [3] since the experiments are performed on the same testing sets. Figure 4 depicts the five-fold cross-validation approach proposed in this section for the experimental evaluation, where the validation set is discarded for a better understanding.
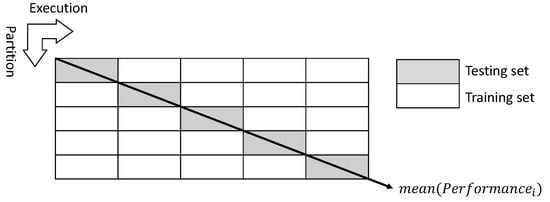
Figure 4.
Representation of the five-fold cross-validation scheme, validation set is discarded.
4.3. Performance Metrics
To assess the fingerprint classification of the new approach (feature extractors along with ELMs) and the comparative CNNs-based methods [3,53], the geometric mean (G-mean), root mean square error (Acc), and the absolute error of the Penetration Rate (PR) metrics are utilized as evaluation criteria. While values of G-mean and Accuracy near to 1 indicate that the corresponding model has better classification performance, it happens for the PR closest to 0. These metrics are defined as follows [1,10,54]:
where , , , and in Equation (7) respectively stand for true positive, true negative, false positive, and false negative in a binary classification problem for example purposes. In other words, it can be interpreted as the square root of majority class accuracy times minority class accuracy. For the multi(M)-classification context, the G-mean becomes the Mth root of the product of the accuracies within each class, which are denoted as in the following. In Equation (8), K denotes the number of fingerprint samples, while and denote the real and the prediction values of the fingerprint classification process, respectively. Finally, M means the number of classes and is the relationship of fingerprint belonging to the ith class in Equation (9). We adopt the absolute error of the penetration rate (termed as PR in the rest of the manuscript) to easily contrast classifiers. The 0.2948 constant results from the ideal penetration rate by following the natural class distribution of the SFINGE fingerprints [3,5].
As mentioned, the accuracy calculates the total deviation between the real and estimated values, being the most preferred criteria for assessing the performance of classifiers in the literature [55,56]. Indeed, the overall accuracy can be considered as de facto metric adopted by fingerprint recognition systems, as can be seen in all works of Table 1 as instances. Nevertheless, the G-mean is more suitable than the accuracy for unbalance data classification due to the possible presence of significant class unbalanced (minority samples is more numerous than majority samples by a large margin) [19], as it happens in fingerprint databases (see Figure 1). Namely, the accuracy can be affected by the class distribution and could give misleading results in certain cases. Instead, it does not occur for the G-mean metric (refer to observations provided in Section 5.2 for demonstration purposes). Consequently, we also consider the G-mean as many studies regarding weighted ELMs oriented to regression and classification problems also do [10,20,49,50]. Finally, in the context of fingerprint classification, the PR metric has been recently adopted [1,3] in order to give propitious information regarding the effectiveness of CNNs along with unbalance datasets.
To summarize, all materials and methods (Section 3 along with Section 4) are depicted in Figure 5 where the fingerprint classification system (the combination of a feature extractor and ELM) is proposed for the first time.
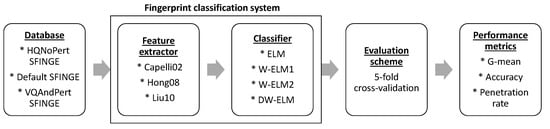
Figure 5.
Outline of the methodology where the proposed fingerprint classification system is highlighted.
5. Results and Discussion
Throughout the manuscript, the sigmoid excitation function: is adopted since it guarantees the universal approximation capability of SLFNs prone to any ELM algorithm [48], and the weights of the input layer and the biases in the hidden layer randomly come from a rectangular distribution defined in the interval [−1,1] [17].
5.1. Estimation of Optimal Hyper-Parameters of the ELMs
In order to maximize the G-means metric, the hyper-parameters of ELMs to be estimated are the regularization parameter (C) and the number of neurons in the hidden layer (N) in the validation set. Remember that the G-means makes sense in unbalanced datasets because it allows the normalization of the accuracies of each class. As mentioned in the Section 4.2, the dataset was divided into three subsets: training, validation, and testing. Figure 6, Figure 7 and Figure 8 show the validation results using G-mean in terms of these hyper-parameters for the standard ELM, W-ELM1, and W-ELM2, respectively. Aiming to establish overall observations, the regularization parameter varied from to (very-small and very-large positive numbers based on its definition, see Equation (2)), and the number of hidden nodes gradually increased. All studied feature extractors (Capelli02, Hong08, and Liu10) and datasets (HQNoPert, Default, and VQAndPert) were taking into account.
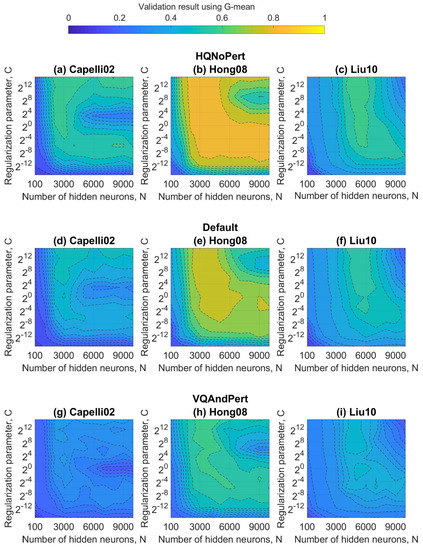
Figure 6.
Validation results obtained by the standard ELM as a function of the regularization parameter and number of hidden neurons. Each subfigure illustrates the database and feature extractor.
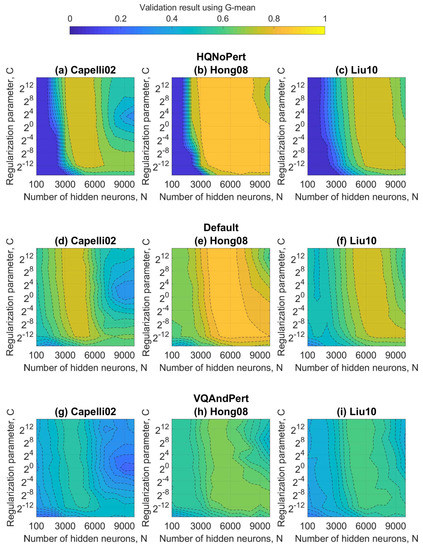
Figure 7.
Validation results obtained by the weighted ELM (W-ELM1) as a function of the regularization parameter and number of hidden neurons. Each subfigure illustrates the database and feature extractor.
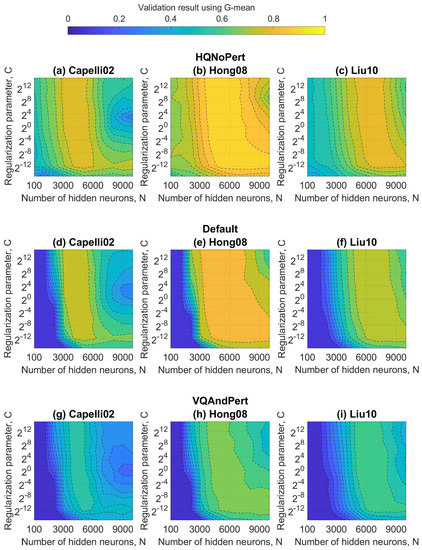
Figure 8.
Validation results obtained by the W-ELM2as a function of the regularization parameter and number of hidden neurons. Each subfigure illustrates the database and feature extractor.
According to each subfigure, an ELM could achieve higher performance for some values of the hyper-parameters that mostly form a continuous and irregular region. For resolution reasons, determining the relationship of C and N that maximizes the G-mean was unfeasible. Fortunately, the ELM performance within the maximization zone could be considered as invariable. Note that this brute-force optimization procedure was only feasible in ELM algorithms since parameters of neurons were arbitrarily generated. Instead, the input weights and biases of other learning algorithms required iterative processes and/or high-performance computing methods [15,17].
Table 2 illustrates the G-means metric with the optimal values of the number of hidden nodes and the regularization parameter for all artificial neural networks. Once again in the study, the results for each dataset and feature extractor were exposed. The best values of N and C were determined through the intersection of the best performing areas on the datasets. This procedure was carried out aiming for the optimization of hyper-parameters that did not depend on the fingerprint quality. For all types of ELMs, the highest performance was obtained on the best quality database, resulting in the best feature extractor corresponds to Hong08. In a general sense, it appears that the W-ELM2 (refer to Table 2c) achieved the best classification performance. This result is explained by the fact that studied databases were comprised of unbalanced data (i.e., they did not follow a uniform distribution), and W-ELM2 could effectively classify this kind of data thanks to considering the golden ratio in its matrix of weights (see Equation (5)). On the other hand, as expected, the basic ELM was the worst classifier because it was prone to outlier interference, which naturally occurred for fingerprint datasets (refer to Table 2a). Finally, it can be seen that the adoption of the Hong08 and W-ELM2 as the feature extractor and classifier, respectively, produced the highest G-mean for any fingerprint quality.

Table 2.
Results of the G-means metric obtained by (a) Standard ELM, (b) W-ELM1, and (c) W-ELM2 on the testing sets for the combination of optimal hyper-parameters (N and C). All datasets and feature extractors are considered.
Figure 9 and Table 3 present the previous study for the DW-ELM. This network has three hyper-parameters, the extra degree of freedom comes to be d (see expression 6), which is related to the weights of the misclassification cost matrix in the ELM algorithm. The rest of the adopted hyper-parameters (i.e., N and C) correspond to those of the W-ELM1 that are displayed in Table 2b since the DW-ELM is an extended version of the W-ELM1. It can be seen that the additional parameter does not affect the classification performance. In general terms, the G-mean metric of the DW-ELM ranges between the values reported by the WELM1 and WELM2. Hence, a modified version of the original weighted ELM, which can augment the computational complexity of the neural network, is not necessary. In the following, the ELMs composed of their optimal hyper-parameters are adopted.
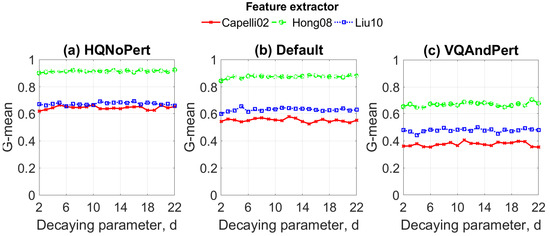
Figure 9.
Graphics of the obtained G-mean against the decaying parameter of the decay weighted ELM (DW-ELM) for each feature extractor and database during the validation stage. The number of hidden neurons and regularization parameter are adopted from the optimal weighted ELMs.

Table 3.
Results of the G-means from the optimal decaying parameters in the testing stage for each studied databases and feature extractors.
5.2. Evaluation and Comparison by Using Classical Metrics: Accuracy and Penetration Rate
Firstly, Table 4 presents the Acc and PR results for the different databases, feature extractors, and ELM variants. While the accuracy is commonly used for regression and classification problems, the PR is recently adopted in the fingerprint classification context [1,3]. Apart from the reasons exposed in Section 4.3, both metrics were considered for comparison purposes with the CNNs proposed by Peralta et al. [3]. It is observed that the Hong08 feature extractor and W-ELM2 must be positively highlighted. In fact, the combination of these produced again the superior metrics, especially for the PR. Instead, the Capelli02 feature extractor and standard ELM hadve the lowest performances. Among the ELM models, the W-ELM2 is able to enhance the recognition rate of minority class to maximize the G-mean and PR values, as well as to guarantee the proper classification of the majority class, keeping a superior Acc (see the outcomes of Section 5.1 and Table 4). Additionally, it is worth to note that the differences among ELMs in terms of Acc and PR metrics were minimum in contrast to the G-mean metric given a feature extractor. Consequently, the relevance of the G-mean as a performance metric for unbalanced datasets is demonstrated.

Table 4.
Accuracy and absolute-error penetration rates in terms of database and feature extractor by adopting the optimal hyper-parameters of the studied ELMs.
For comparison purposes, a benchmark work of the state-of-the-art is considered. Peralta et al. [3] introduce a novel CNN-based model and, also, exploit a modification of the CaffeNet CNN [30] for the fingerprint classification problem. Fingerprint images without computing an explicit feature extractor were processed by both CNNs. The classification performance in terms of the accuracy and penetration rate was only calculated by considering the NIST and SFINGE databases. This paper implements the five-fold cross-validation scheme, and the reported performance was averaged from the five testing sets, which are the same experimental settings used in our work (refer to Section 4.2) by allowing a proper comparison.
Table 5 presents the comparison between the best results obtained in our study (W-ELM2 with Hong08 feature extractor) and the CNN-based models proposed in [3]. The results of [3] were extracted from the last columns of its Table 8. In general, the results of our proposal were slightly lower than those obtained with CNNs, being more competitive in terms of the classification accuracy.

Table 5.
Comparison of the results achieved by the best combination (feature extractor and type of ELM), the modified CaffeNET CNN [3,30], and the CNN model proposed in [3].
5.3. Complexity Analysis
In order to contrast the degree of complexity of CNN-based classification methods [3] with our best performance proposal (Hong08 feature extractor in combination with W-ELM2), we have evaluated the learning speed on each studied database, see Table 6. While the results provided by Peralta et al. [3] were obtained by using one Nvidia GeForce GTX TITAN GPU (2688 cores, 6144 MB GDDR5 RAM), our training times were evaluated without parallel computing in a simple computer with the following characteristics: an Intel Core i5 processor at 2.6 GHz clock speed and 4 GB RAM. Furthermore, the observations of CNNs and our approach were computed by utilizing the Caffe library, which is written in C++ software, and MATLAB R2018a environment, respectively. Due to MATLAB being a high-level programming language, it demands more computational cost than C++ applications. Despite the previous hardware/software disadvantages, our results have been achieved in shorter training times than those required by CNNs. In addition, there are several studies that confirm that ELMs can be trained in very short times for any classification or regression task [7,15,18,20,57,58]. As mentioned in Section 1 and as presented in Section 3.2, it occurs owing to the input weights and hidden layer biases are generated randomly in the ELM and, then, its training process results in a single linear system thanks to the Moore–Penrose generalized inverse matrix, which means a very fast learning process. Instead, the CNN learning comes to be the optimization of the weights of each neuron in order have the desired value for each input [1,3,4,13,14,29], which is based on an improved of the next algorithm: back propagation with gradient descent. Consequently, the dimensionality of the search space is given by very-large number of weights. Finally, in order to properly assess our results, it should be noticed that the studied ELMs had a single hidden layer, while CNNs had numerous fully connected, convolutional, and pooling layers, each of which had diverse number of nodes subject to an activation function to introduce a nonlinearity. Notice that given a classifier method, the training times were almost the same for the diverse databases owing to these sets have the same number of samples.

Table 6.
Comparison in terms of the model learning time expressed in seconds.
6. Conclusions
In this work, we have carried out an extensive study to address fingerprint classification problems by introducing basic and weighted ELMs as classifiers for the first time. Regarding this purpose, we have considered fingerprint databases of high, normal, and low qualities, and three feature extraction methods, which have been reported in the literature as the top performers. The weighted ELMs are able to deal with data with unbalanced class distribution, such as fingerprint databases. Three weighting schemes are tested in terms of the geometric mean, accuracy, and penetration rate, which demonstrate the better performance of weighted ELM contrasted with standard ELM. All the highlights presented in the study open the possibility of using our introduced classifier for large-scale fingerprint identification systems.
Investigations regarding the standard and improved ELMs can be directed towards the introduction of multilayer ELMs for fingerprint recognition systems in order to increase overall effectiveness while maintaining a fast learning speed [59,60]. As CNNs, multilayer ELMs can ignore the feature extraction stage, i.e., the image processing will be included in the training of the classifier. Comparison results with CNNs in terms of the computational cost are still open questions. To this end, the same hardware and software should be used to establish non-questionable conclusions. For the purpose of emulating real and complex identification problems, finally, the analysis with very-large fingerprint databases (in the order of hundreds of thousands) is proposed as a pending task.
Author Contributions
Conceptualization, D.Z.-B. and M.M.; methodology, D.Z.-B. and M.M.; software, D.Z.-B. and M.M.; formal analysis, D.Z.-B. and M.M.; investigation, D.Z.-B. and M.M.; writing—original draft preparation, D.Z.-B., M.M., and R.H.-G.; writing—review and editing, D.Z.-B., M.M., R.H.-G., R.J.B., and J.N.-T.; project administration, D.Z.-B. and M.M.; funding acquisition, D.Z.-B., M.M., and R.J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by FONDECYT REGULAR 2020 Nº 1200810 Very Large Fingerprint Classification based on a Fast and Distributed Extreme Learning Machine, Agencia Nacional de Investigación y Desarrollo, Ministerio de Ciencia, Tecnología, Conocimiento e Innovación, Gobierno de Chile, and Project CONICYT FONDEF/ Cuarto Concurso IDeA en dos Etapas del Fondo de Fomento al Desarrollo Científico y Tecnológico, Programa IDeA, FONDEF/CONICYT 2017 ID17i10254.
Acknowledgments
The authors of the paper thank Daniel Peralta, international collaborator of the FONDECYT REGULAR 2020 Nº 1200810 and FONDEF 2017 ID17i10254 projects. We consider that his contribution allowed to theoretically understand the fingerprint classification and fingerprint recognition problems. Finally, this work was supported by the Vicerrectoría de Investigación y Posgrado (VRIP) of the Universidad Católica del Maule and the Laboratory of Technological Research in Pattern Recognition (LITRP) https://www.litrp.cl (accessed on).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Convolutional neural network |
| ELM | Extreme learning machine |
| SLFN | Single hidden layer feedforward neural network |
| NIST | National institute of standard and technologies |
| FVC | Fingerprint verification competition |
| OM | Orientation map |
| SFINGE | Synthetic fingerprint generator |
| RELU | Rectified linear unit |
| W-ELM1 | Weighted ELM1 |
| W-ELM2 | Weighted ELM2 |
| DW-ELM | Decay weighted |
| G-mean | Geometric mean |
| Acc | Root mean square error |
| PR | Absolute error of the penetration rate |
References
- Tehseen, Z.; Mubeen, G.; Syed, A.T.; Imtiaz, A.T. Robust fingerprint classification with Bayesian convolutional networks. IET Image Process. 2019, 13, 1280–1288. [Google Scholar]
- Galar, M.; Derrac, J.; Peralta, D.; Triguero, I.; Paternain, D.; Lopez-Molina, C.; García, S.; Benítez, J.M.; Pagola, M.; Barrenechea, E.; et al. A survey of fingerprint classification Part I: Taxonomies on feature extraction methods and learning models. Knowl.-Based Syst. 2015, 81, 76–97. [Google Scholar] [CrossRef]
- Peralta, D.; Triguero, I.; Garcia, S.; Saeys, Y.; Benitez, J.M.; Herrera, F. On the use of convolutional neural networks for robust classification of multiple fingerprint captures. Int. J. Intell. Syst. 2018, 33, 213–230. [Google Scholar] [CrossRef]
- Shrein, J.M. Fingerprint classification using convolutional neural networks and ridge orientation images. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–8. [Google Scholar]
- Galar, M.; Derrac, J.; Peralta, D.; Triguero, I.; Paternain, D.; Lopez-Molina, C.; Garcia, S.; Benitez, J.M.; Pagola, M.; Barrenechea, E.; et al. A survey of fingerprint classification Part II: Experimental analysis and ensemble proposal. Knowl.-Based Syst. 2015, 81, 98–116. [Google Scholar] [CrossRef]
- Henry, E.R. Classification and Uses of Finger Prints; HM Stationery Office: London, UK, 1905. [Google Scholar]
- Ding, S.; Zhao, H.; Zhang, Y.; Xu, X.; Nie, R. Extreme learning machine: Algorithm, theory and applications. Artif. Intell. Rev. 2015, 44, 103–115. [Google Scholar] [CrossRef]
- Koziarski, M. Radial-based undersampling for imbalanced data classification. Pattern Recognit. 2020, 102, 107262. [Google Scholar] [CrossRef]
- Han, W.; Huang, Z.; Li, S.L.; Jia, Y. Distribution-sensitive unbalanced data oversampling method for medical diagnosis. J. Med. Syst. 2019, 43, 39. [Google Scholar] [CrossRef]
- Zong, W.; Huang, G.B.; Chen, Y. Weighted extreme learning machine for imbalance learning. Neurocomputing 2013, 101, 229–242. [Google Scholar] [CrossRef]
- Guo, J.M.; Liu, Y.F.; Chang, J.Y.; Lee, J.D. Fingerprint classification based on decision tree from singular points and orientation field. Expert Syst. Appl. 2014, 41, 752–764. [Google Scholar] [CrossRef]
- Peralta, D.; Triguero, I.; GarcÃa, S.; Saeys, Y.; Benitez, J.M.; Herrera, F. Distributed incremental fingerprint identification with reduced database penetration rate using a hierarchical classification based on feature fusion and selection. Knowl.-Based Syst. 2017, 126, 91–103. [Google Scholar] [CrossRef]
- Michelsanti, D.; Ene, A.D.; Guichi, Y.; Stef, R.; Nasrollahi, K.; Moeslund, T.B. Fast fingerprint classification with deep neural networks. In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), Porto, Portugal, 27 February–1 March 2017; pp. 202–209. [Google Scholar]
- Ge, S.; Bai, C.; Liu, Y.; Liu, Y.; Zhao, T. Deep and discriminative feature learning for fingerprint classification. In Proceedings of the 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 1942–1946. [Google Scholar]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Zabala-Blanco, D.; Mora, M.; Azurdia-Meza, C.A.; Dehghan Firoozabadi, A. Extreme learning machines to combat phase noise in RoF-OFDM schemes. Electronics 2019, 8, 921. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.; Song, S.; Gupta, J.N.D.; Wu, C. Semi-supervised and unsupervised extreme learning machines. IEEE Trans. Cybern. 2014, 44, 2405–2417. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, M. Outlier-robust extreme learning machine for regression problems. Neurocomputing 2015, 151, 1519–1527. [Google Scholar] [CrossRef]
- Shen, Q.; Ban, X.; Liu, R.; Wang, Y. Decay-weighted extreme learning machine for balance and optimization learning. Mach. Vis. Appl. 2017, 28, 743753. [Google Scholar] [CrossRef]
- Saeed, F.; Hussain, M.; Aboalsamh, H.A. Classification of live scanned fingerprints using histogram of gradient descriptor. In Proceedings of the 21st Saudi Computer Society National Computer Conference (NCC), Riyadh, Saudi Arabia, 25–26 April 2018; pp. 1–5. [Google Scholar]
- Cappelli, R.; Maio, D.; Maltoni, D. A multi-classifier approach to fingerprint classification. Pattern Anal. Appl. 2002, 5, 136–144. [Google Scholar] [CrossRef]
- Hong, J.H.; Min, J.K.; Cho, U.K.; Cho, S.B. Fingerprint classification using one-vs-all support vector machines dynamically ordered with naive Bayes classifiers. Pattern Recognit. 2008, 41, 662–671. [Google Scholar] [CrossRef]
- Liu, M. Fingerprint classification based on Adaboost learning from singularity features. Pattern Recognit. 2010, 43, 1062–1070. [Google Scholar] [CrossRef]
- Cappelli, R.; Maio, D.; Maltoni, D. Synthetic fingerprint-database generation. In Object Recognition Supported by User Interaction for Service Robots; IEEE: New York, USA, 2002; Volume 3, pp. 744–747. [Google Scholar]
- Maltoni, D.; Maio, D.; Jain, A.K.; Prabhakar, S. Handbook of Fingerprint Recognition; Springer: London, UK, 2009. [Google Scholar]
- Fingerprint Database NIST-4. Available online: https://www.nist.gov/srd/nist-special-database-4 (accessed on 20 May 2020).
- Fingerprint Database FVC-2004. Available online: http://bias.csr.unibo.it/fvc2004/download.asp (accessed on 20 May 2020).
- El-Hamdi, D.; Elouedi, I.; Fathallah, A.; Nguyen, M.K.; Hamouda, A. Fingerprint classification using conic radon transform and convolutional neural networks. In Advanced Concepts for Intelligent Vision Systems; Blanc-Talon, J., Helbert, D., Philips, W., Popescu, D., Scheunders, P., Eds.; Springer International Publishing: New York, NY, USA, 2018; pp. 402–413. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Chatfield, K.; Simonyan, K.; Vedaldi, A.; Zisserman, A. Return of the devil in the details: Delving deep into convolutional nets. Br. Mach. Vis. Conf. 2014, arXiv:cs/1405.3531. [Google Scholar]
- Alias, N.A.; Radzi, N.H.M. Fingerprint classification using support vector machine. In Proceedings of the Fifth ICT International Student Project Conference (ICT-ISPC), Nakhon Pathom, Thailand, 27–28 May 2016; pp. 105–108. [Google Scholar]
- Wang, R.; Han, C.; Guo, T. A novel fingerprint classification method based on deep learning. In Proceedings of the 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 931–936. [Google Scholar]
- Gupta, P.; Gupta, P. A robust singular point detection algorithm. Appl. Soft Comput. 2015, 29, 411–423. [Google Scholar] [CrossRef]
- Dorasamy, K.; Webb, L.; Tapamo, J.; Khanyile, N.P. Fingerprint classification using a simplified rule-set based on directional patterns and singularity features. In Proceedings of the International Conference on Biometrics (ICB), Phuket, Thailand, 19–22 May 2015; pp. 400–407. [Google Scholar]
- Jung, H.W.; Lee, J.H. Noisy and incomplete fingerprint classification using local ridge distribution models. Pattern Recognit. 2015, 48, 473–484. [Google Scholar] [CrossRef]
- Vitello, G.; Sorbello, F.; Migliore, G.I.M.; Conti, V.; Vitabile, S. A novel technique for fingerprint classification based on fuzzy C-means and naive Bayes classifier. In Proceedings of the Eighth International Conference on Complex, Intelligent and Software Intensive Systems, Birmingham, UK, 2–4 July 2014; pp. 155–161. [Google Scholar]
- Galar, M.; Sanz, J.; Pagola, M.; Bustince, H.; Herrera, F. A preliminary study on fingerprint classification using fuzzy rule-based classification systems. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Beijing, China, 6–11 July 2014; pp. 554–560. [Google Scholar]
- Luo, J.; Song, D.; Xiu, C.; Geng, S.; Dong, T. Fingerprint classification combining curvelet transform and gray-level cooccurrence matrix. Math. Probl. Eng. 2014, 2014, 1–15. [Google Scholar] [CrossRef]
- Saini, M.K.; Saini, J.S.; Sharma, S. Moment based wavelet filter design for fingerprint classification. In Proceedings of the International Conference On Signal Processing And Communication (ICSC), Noida, India, 12–14 December 2013; pp. 267–270. [Google Scholar] [CrossRef]
- Cao, K.; Pang, L.; Liang, J.; Tian, J. Fingerprint classification by a hierarchical classifier. Pattern Recognit. 2013, 46, 3186–3197. [Google Scholar] [CrossRef]
- Rajanna, U.; Erol, A.; Bebis, G. A comparative study on feature extraction for fingerprint classification and performance improvements using rank-level fusion. Pattern Anal. Appl. 2010, 13, 263–272. [Google Scholar] [CrossRef]
- Feng, J.; Jain, A.K. Fingerprint reconstruction: From minutiae to phase. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 209–223. [Google Scholar] [CrossRef]
- Bazen, A.M.; Gerez, S.H. Systematic methods for the computation of the directional fields and singular points of fingerprints. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 905–919. [Google Scholar] [CrossRef]
- Kawagoe, M.; Tojo, A. Fingerprint pattern classification. Pattern Recognit. 1984, 17, 295–303. [Google Scholar] [CrossRef]
- Jain, A.K.; Prabhakar, S.; Hong, L. A multichannel approach to fingerprint classification. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 348–359. [Google Scholar] [CrossRef]
- Nilsson, K.; Bigun, J. Localization of corresponding points in fingerprints by complex filtering. Pattern Recognit. Lett. 2003, 24, 2135–2144. [Google Scholar] [CrossRef]
- Zabala-Blanco, D.; Mora, M.; Azurdia-Meza, C.A.; Dehghan Firoozabadi, A.; Palacios Jativa, P.; Soto, I. Relaxation of the radio-frequency linewidth for coherent-optical orthogonal frequency-division multiplexing schemes by employing the improved extreme learning machine. Symmetry 2020, 12, 632. [Google Scholar] [CrossRef]
- Lu, C.; Ke, H.; Zhang, G.; Mei, Y.; Xu, H. An improved weighted extreme learning machine for imbalanced data classification. Memet. Comput. 2019, 11, 27–34. [Google Scholar] [CrossRef]
- Akbulut, Y.; Şengür, A.; Guo, Y.; Smarandache, F. A novel neutrosophic weighted extreme learning machine for imbalanced data set. Symmetry 2017, 9, 142. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Sagan, V.; Sidike, P.; Kwasniewski, M.T. Dual activation function-based extreme learning machine (ELM) for estimating grapevine berry yield and quality. Remote Sens. 2019, 11, 740. [Google Scholar] [CrossRef]
- Moreno-Torres, J.G.; Saez, J.A.; Herrera, F. Study on the impact of partition-induced dataset shift on k-fold cross-validation. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1304–1312. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Kai, L.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Huang, N.; Yuan, C.; Cai, G.; Xing, E. Hybrid short term wind speed forecasting using variational mode decomposition and a weighted regularized extreme learning machine. Energies 2016, 9, 989. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Ferri, C.; Hernández-Orallo, J.; Modroiu, R. An experimental comparison of performance measures for classification. Pattern Recognit. Lett. 2009, 30, 27–38. [Google Scholar] [CrossRef]
- Khellal, A.; Ma, H.; Fei, Q. Convolutional neural network features comparison between back-propagation and extreme learning machine. In Proceedings of the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 9629–9634. [Google Scholar]
- Pang, S.; Yang, X. Deep convolutional extreme learning machine and its application in handwritten digit classification. Comput. Intell. Neurosci. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Lekamalage, C.K.L.; Song, K.; Huang, G.; Cui, D.; Liang, K. Multi layer multi objective extreme learning machine. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 1297–1301. [Google Scholar]
- Tang, J.; Deng, C.; Huang, G. Extreme learning machine for multilayer perceptron. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 809–821. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).