Novel Active Disturbance Rejection Control Based on Nested Linear Extended State Observers
Abstract
Featured Application
Abstract
1. Introduction
- (1)
- For the LESO to increase the estimation accuracy, the bandwidth of the LESO has to be increased, which tolerates noise and leads to hardware difficulties. Additionally, the LESO suffers from a peaking phenomenon due to large gain values.
- (2)
- For the nonlinear ESO, the performance will abruptly deteriorate when the amplitude or derivative of the generalized disturbance goes large to a certain degree [20]. Moreover, stability analysis and performance analysis are very complicated for the nonlinear ESO.
- (3)
- For other classes of observers like the AESO, the parameter tuning process becomes more time-consuming as the observer order goes higher.
2. Problem Description and Contribution
2.1. Problem Description
2.2. Paper Contribution
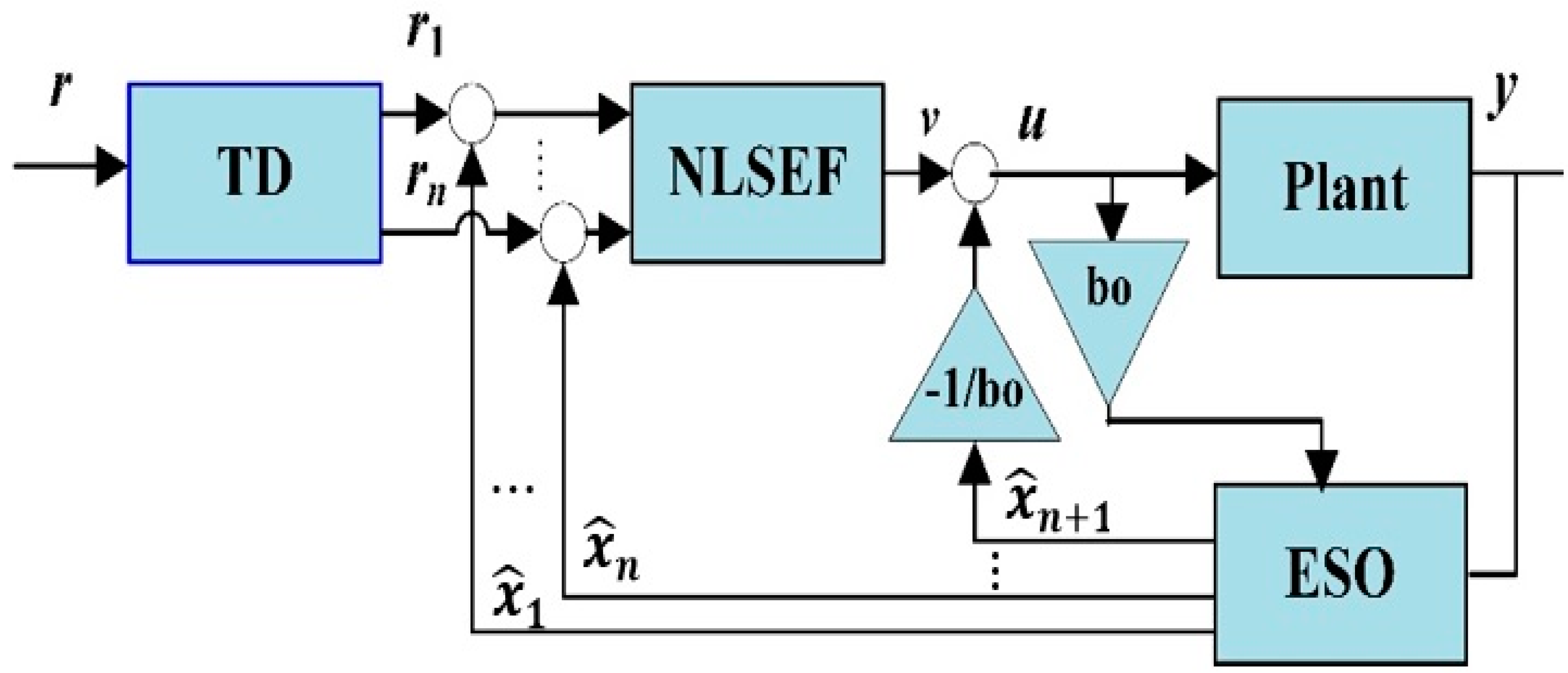
3. Conventional Active Disturbance Rejection Control Problem
3.1. Tracking Differentiator (TD)
3.2. Nonlinear State Error Feedback (NLSEF)
3.3. Extended State Observer
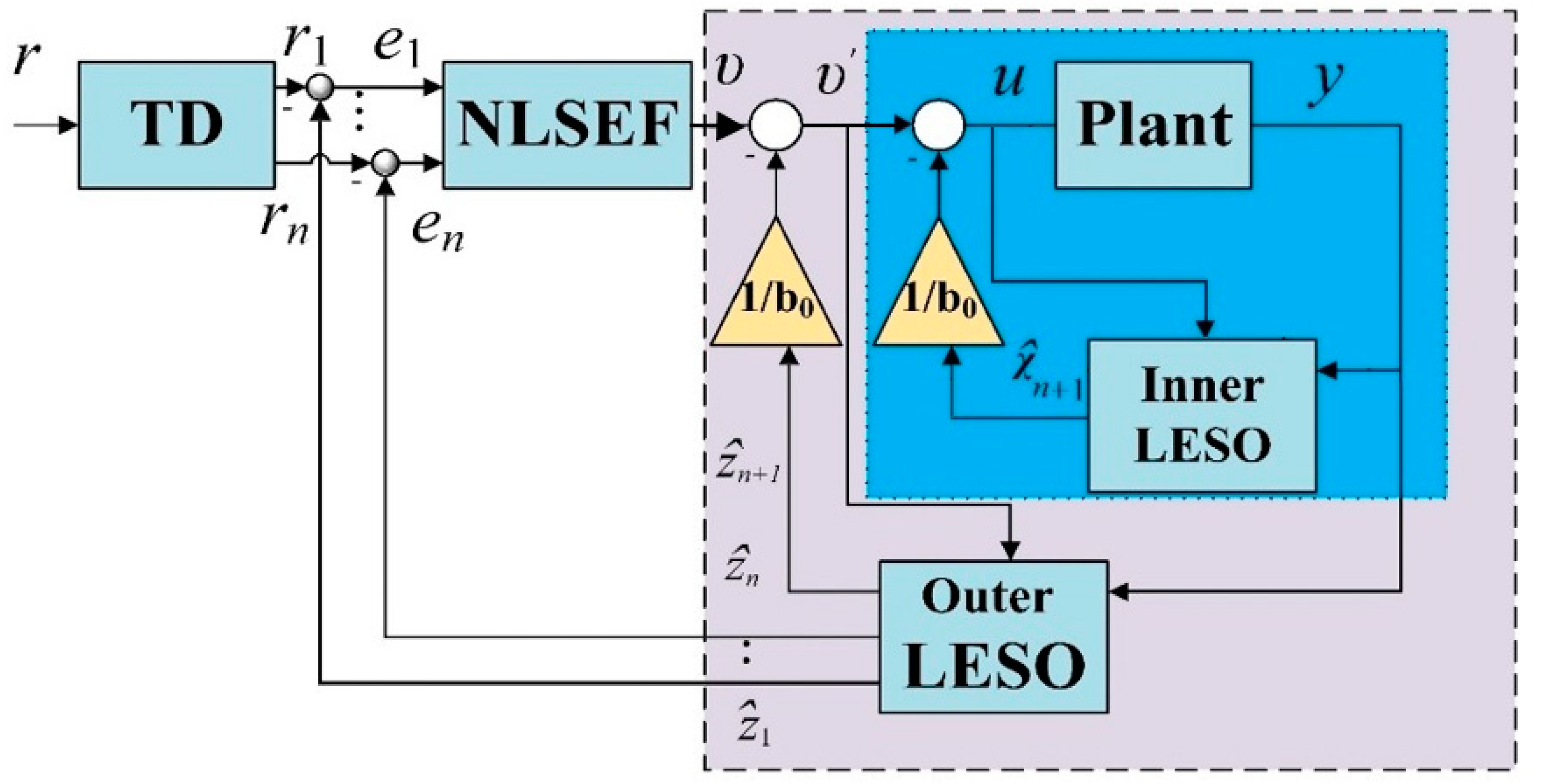
4. Main Results
- where is an even nonlinear gain function.
- where is the tracking error. Assuming that Assumptions A3 and A4 hold true, then, the closed-loop system is asymptotically stable, i.e., .
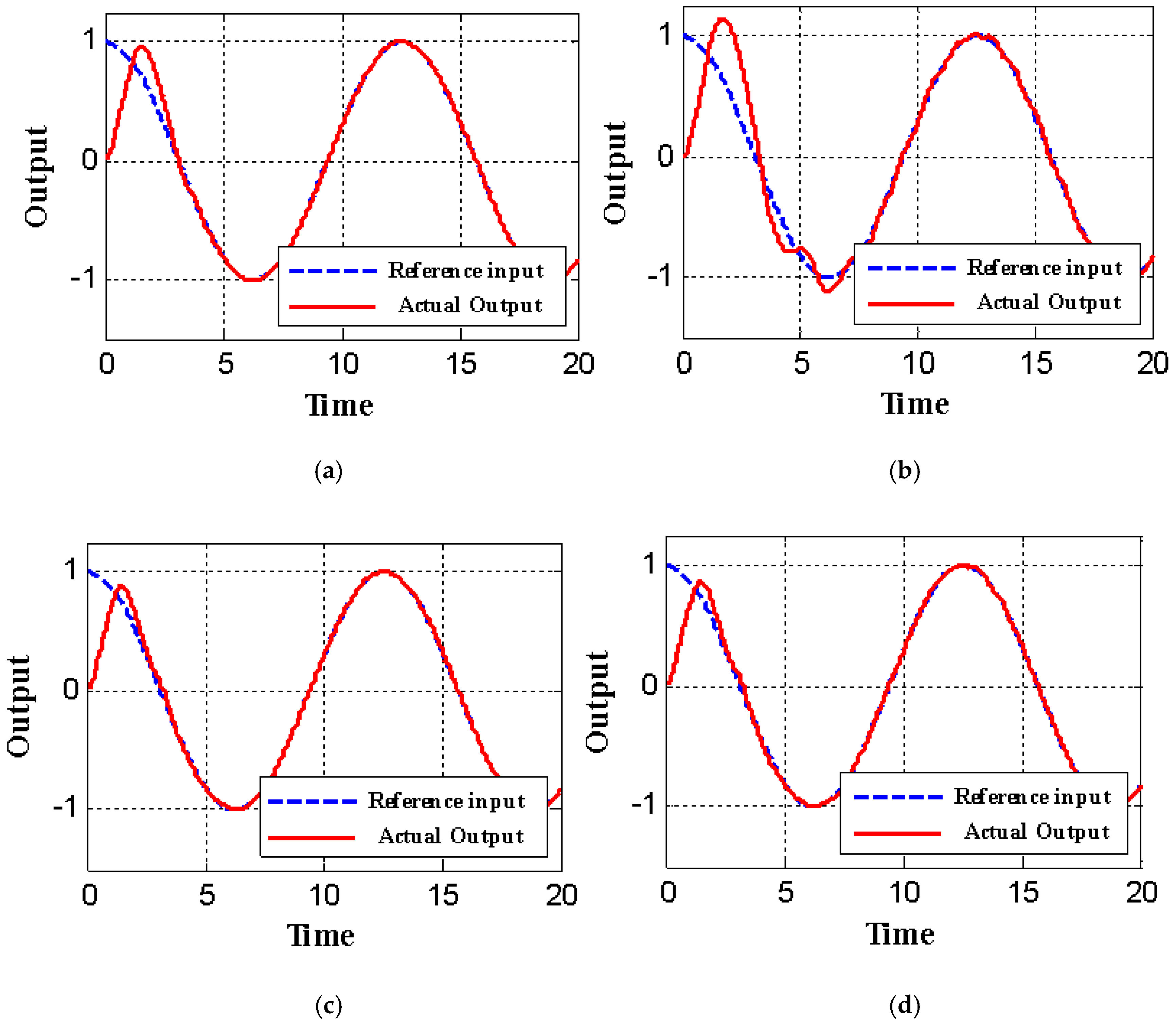
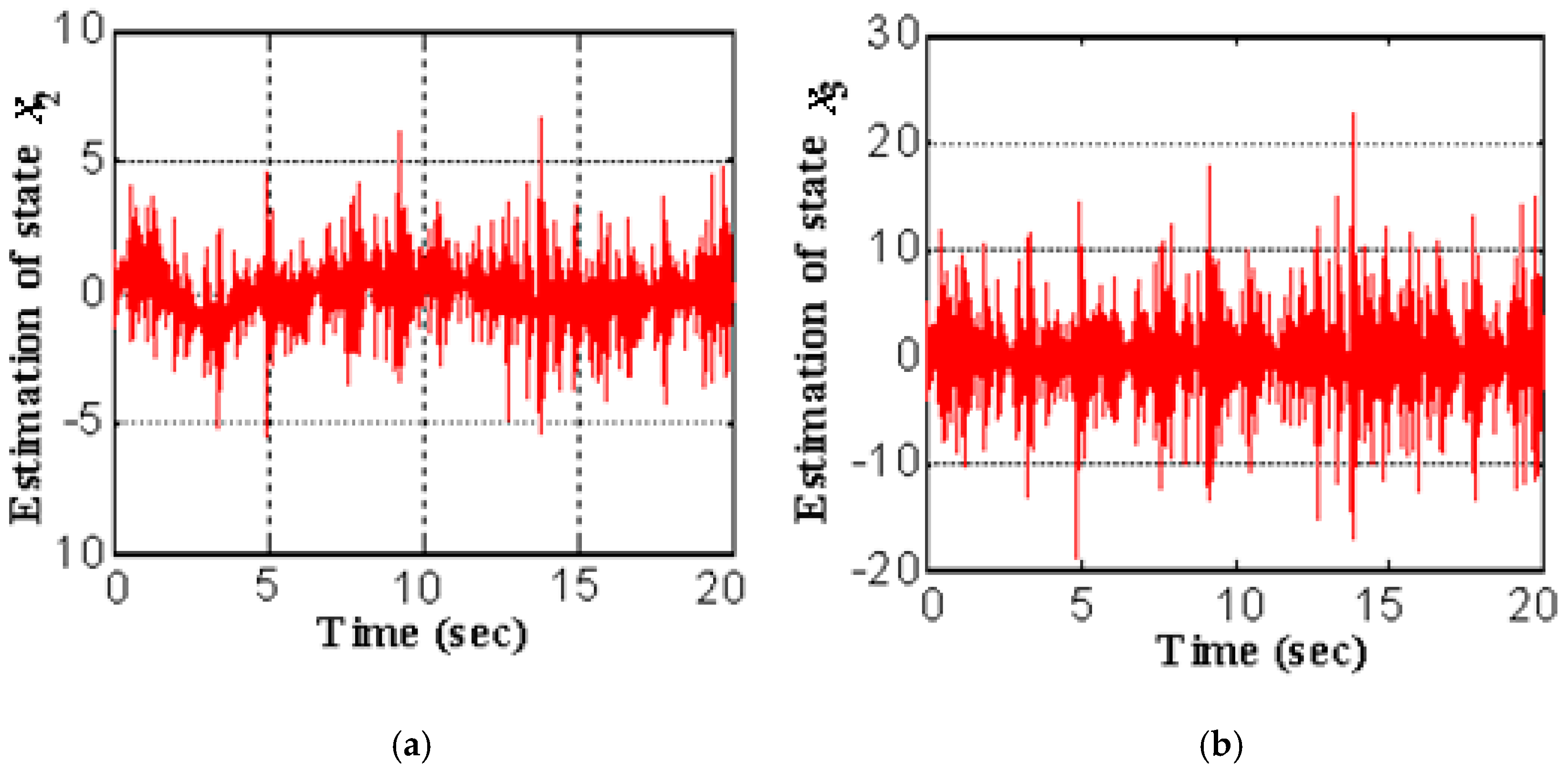
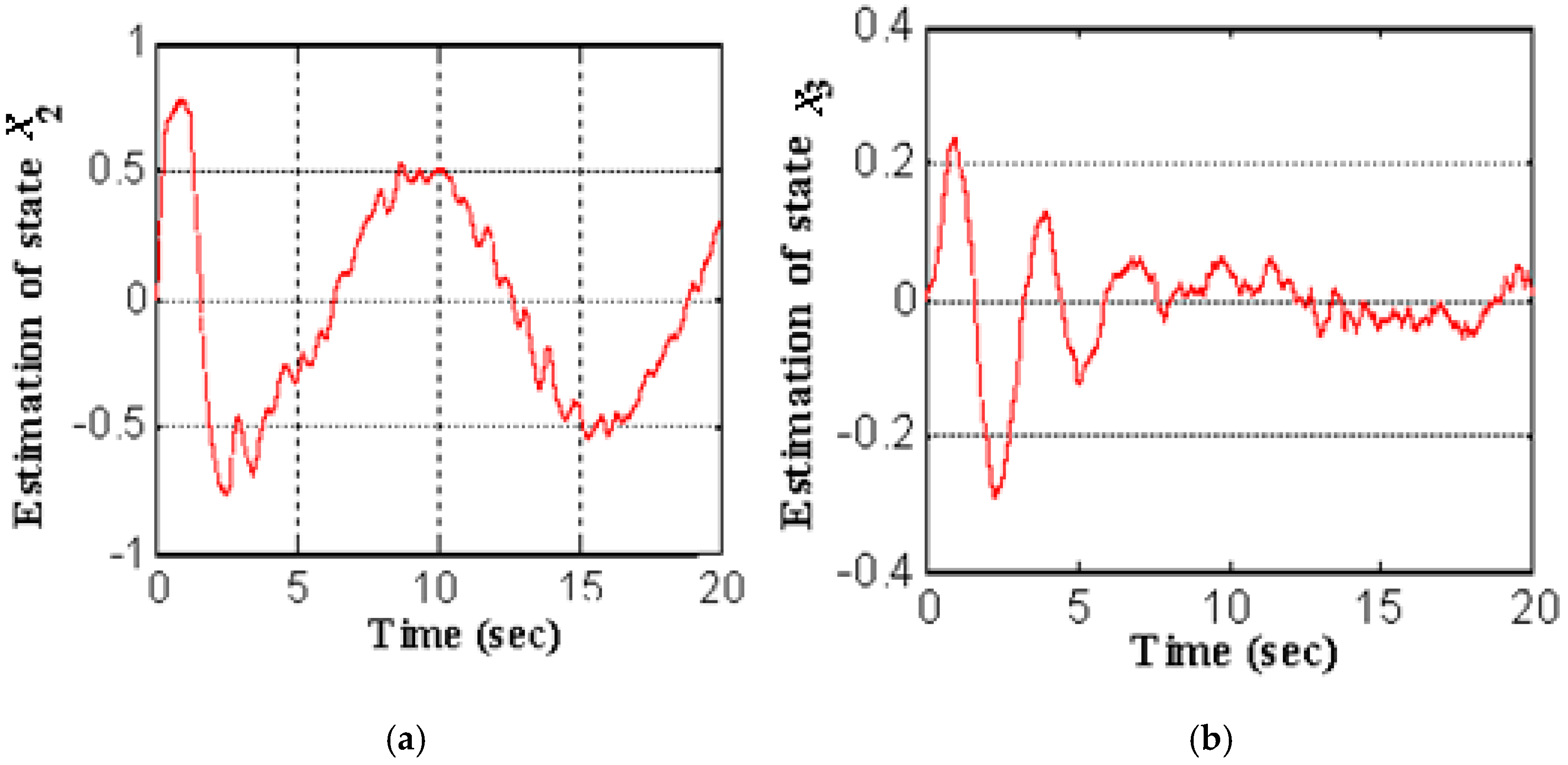
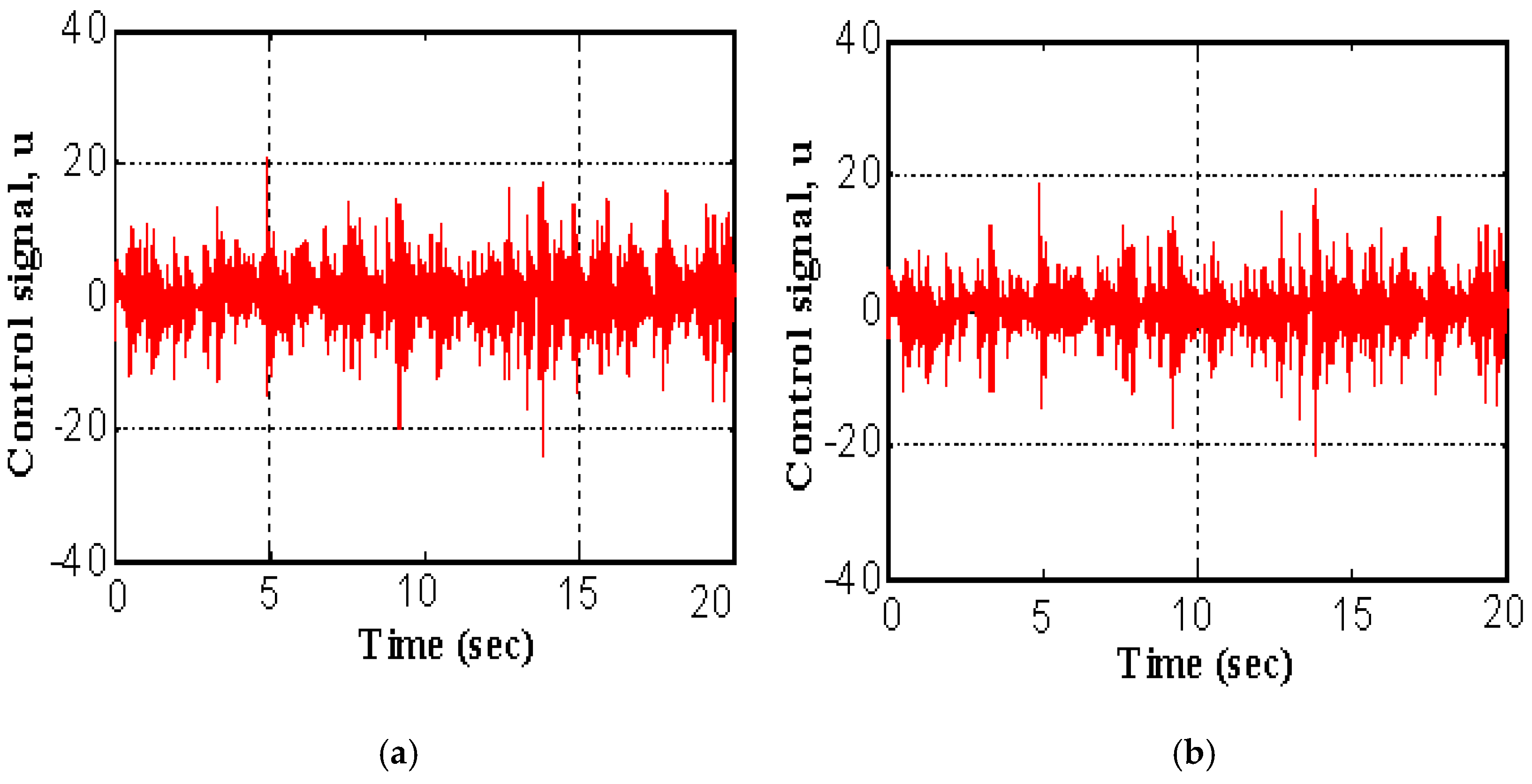
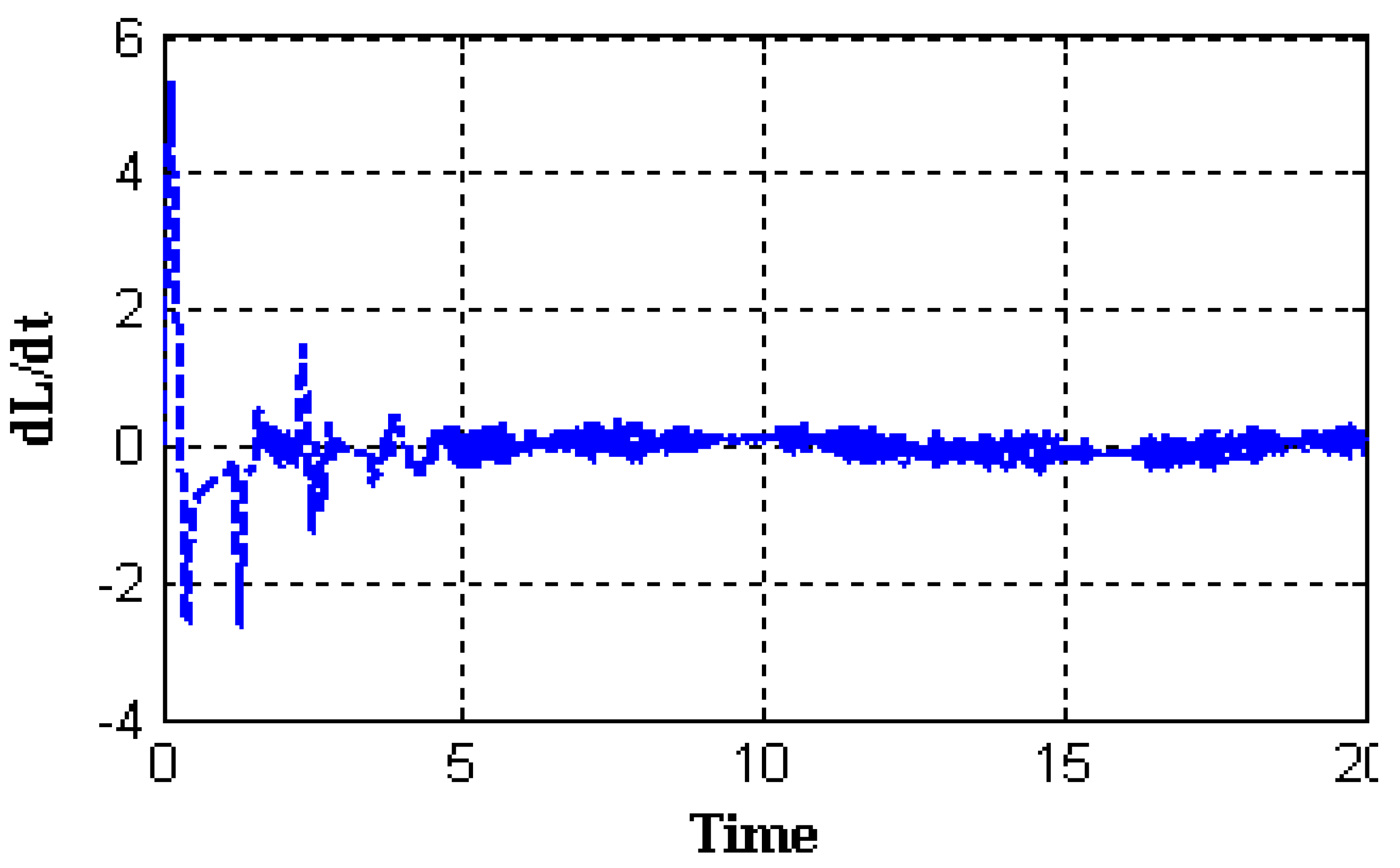
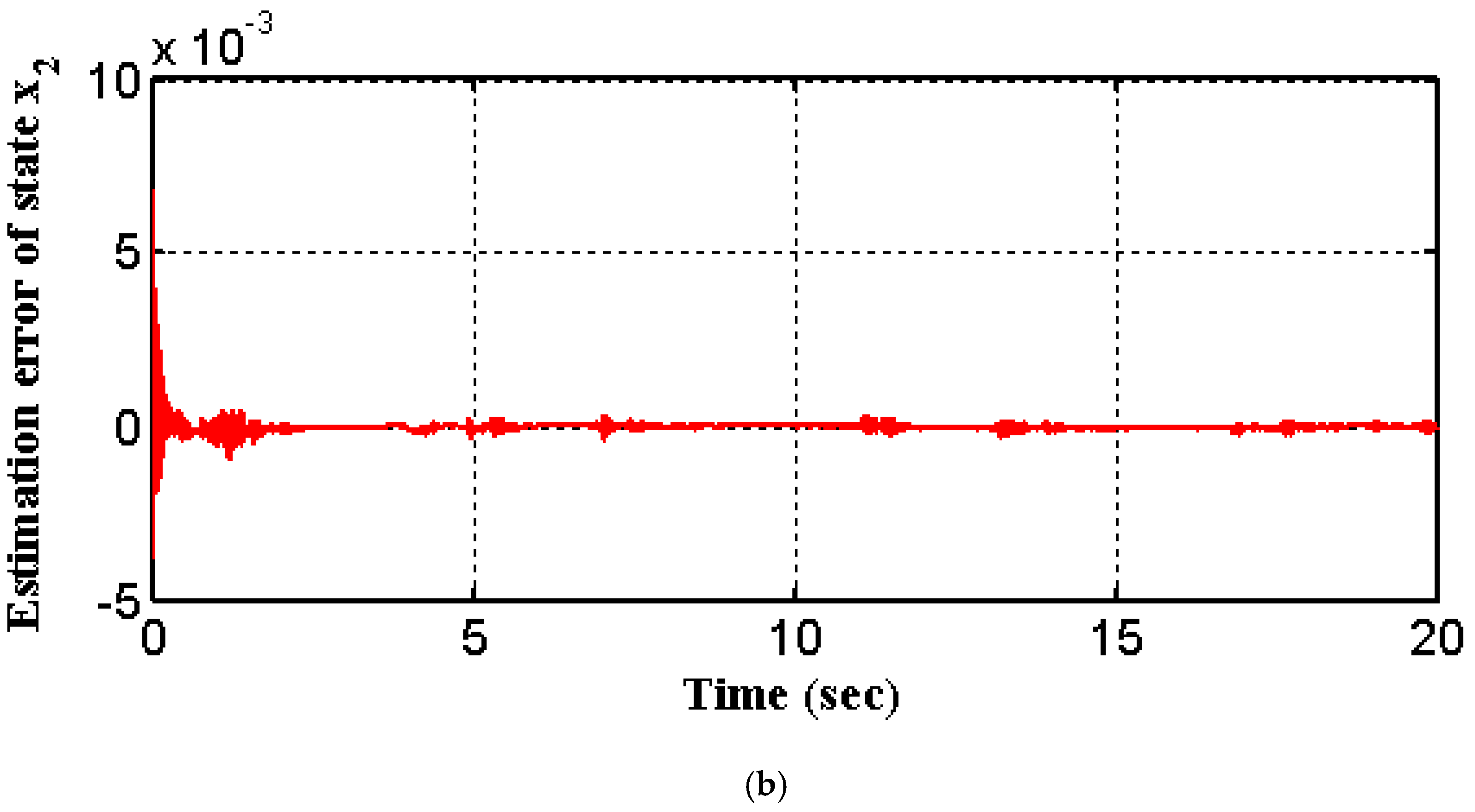
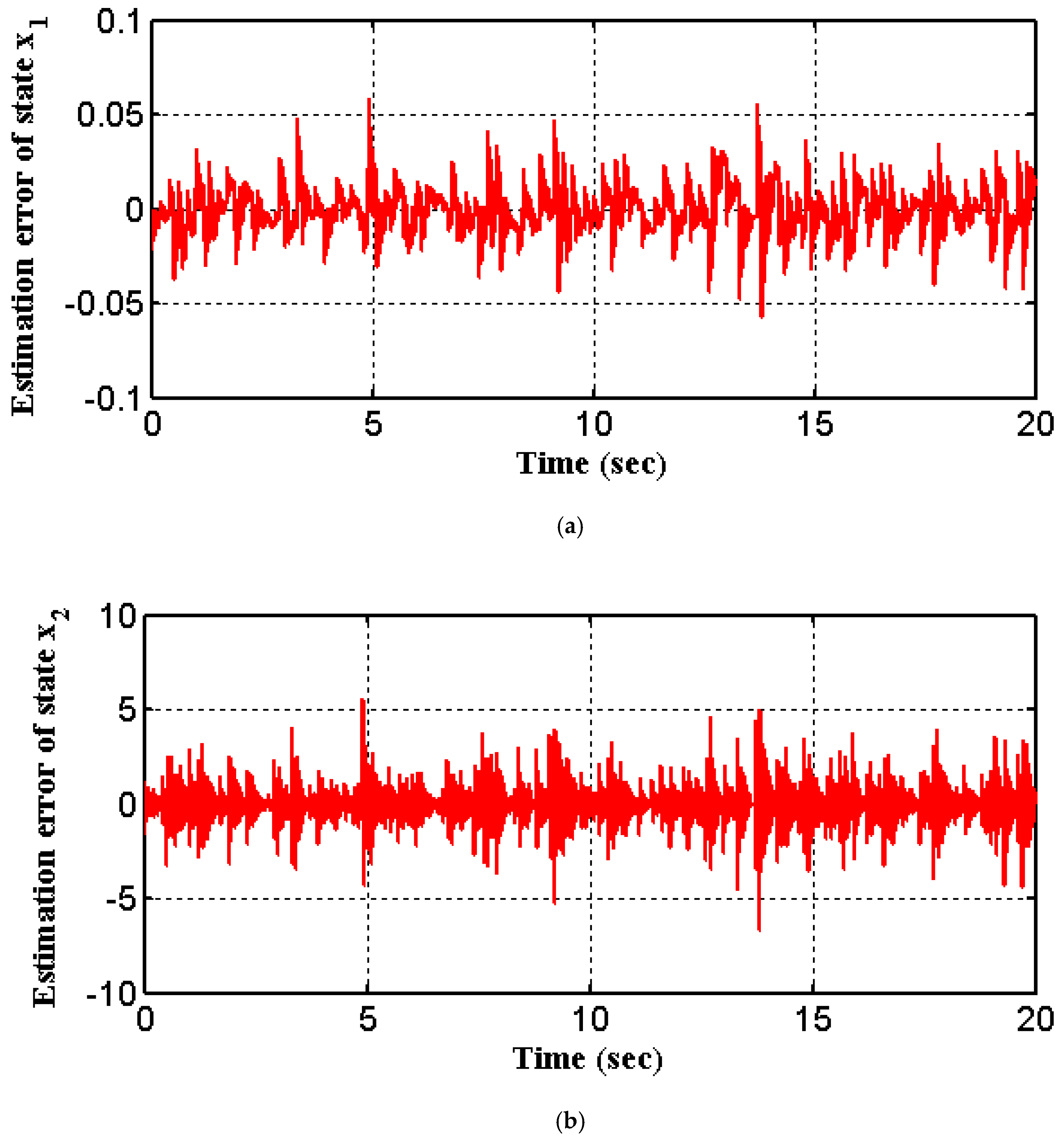
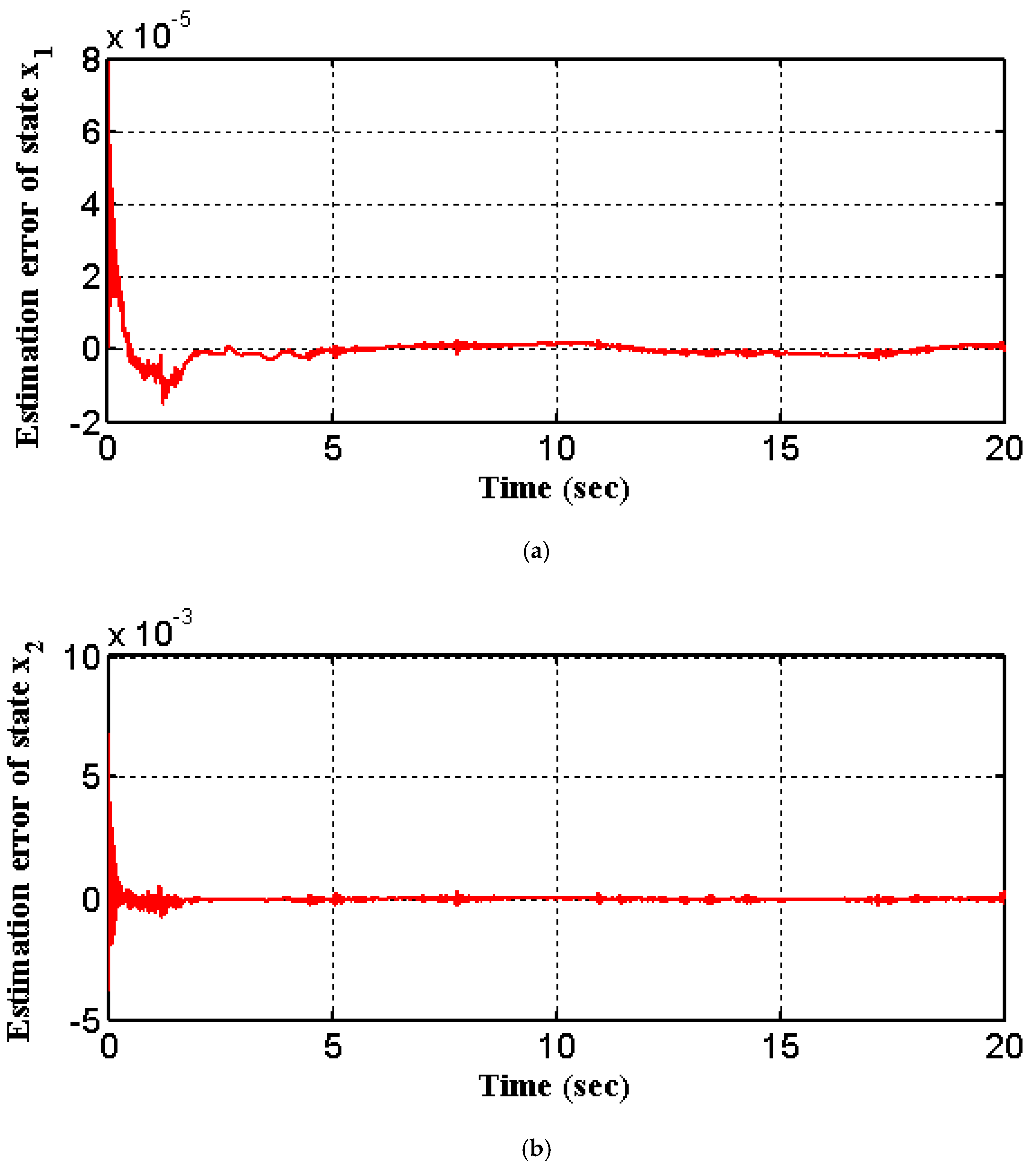
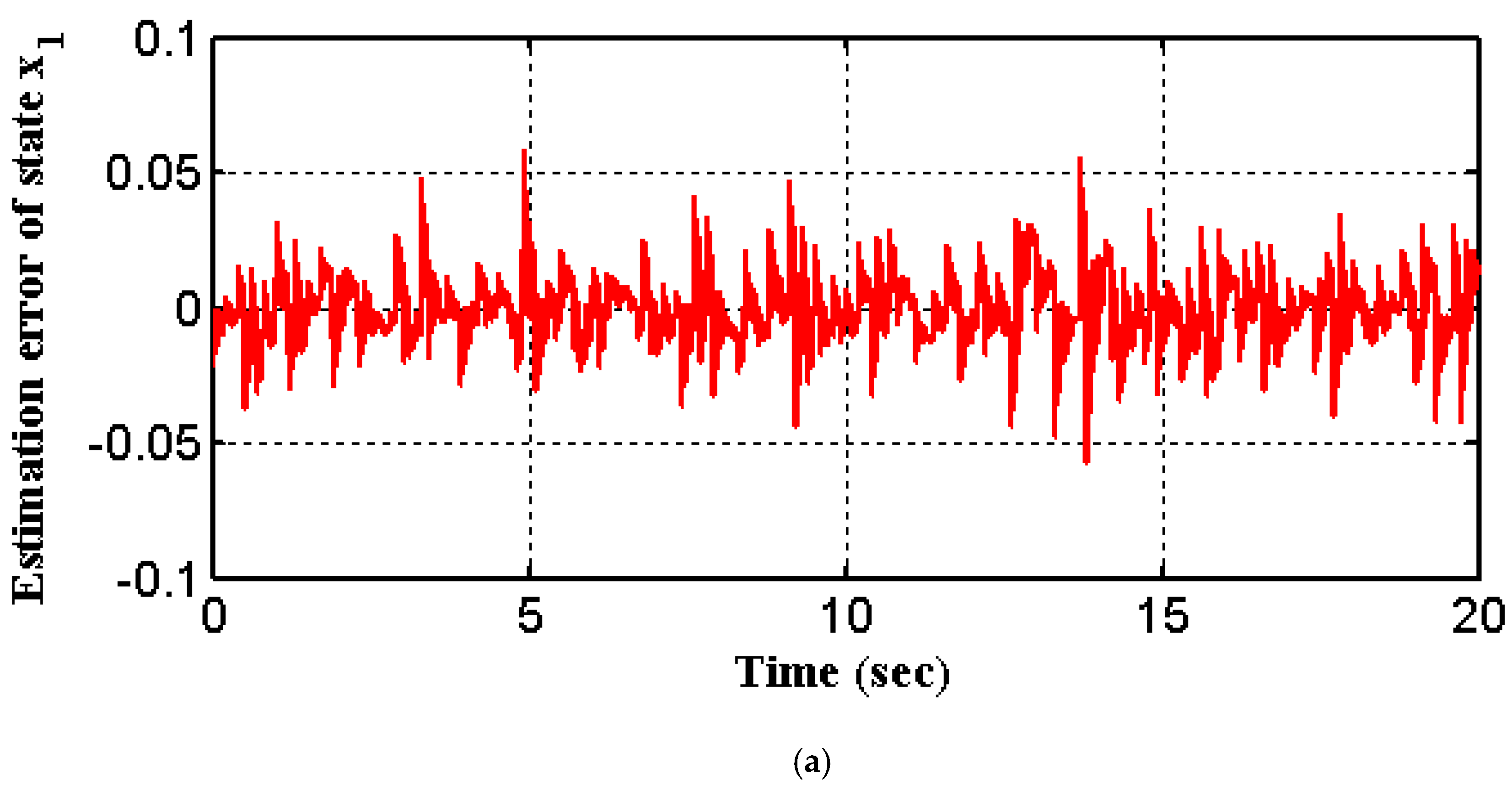
5. Simulations Results
5.1. Hypothetical Model
- (a)
- LESO:where is the observer state vector, and is the observer gain vector. The design parameters of the LESO were set to , , , , and 00.
- (b)
- The NLSEF control law:where is described as in Equation (7), and is the tracking error vector which can be defined as , . The design parameters of the control law were set to , .
- (c)
- The TD is given as [11]:where is tracking signal of the input , and tracking signal of the derivative of the input , and where .
- (a)
- Inner-loop LESO
- (b)
- Outer-loop LESOwhere is the observer state vector, and T is the observer gain vector. The design parameters where selected as , , , and , and
- (c)
- The control law is selected as in Equation (52) with the same parameter values and tracking error vector defined as , as illustrated in Figure 2.
- (d)
- The TD for the N-ADRC is identical to Equation (53) with the same parameter values.
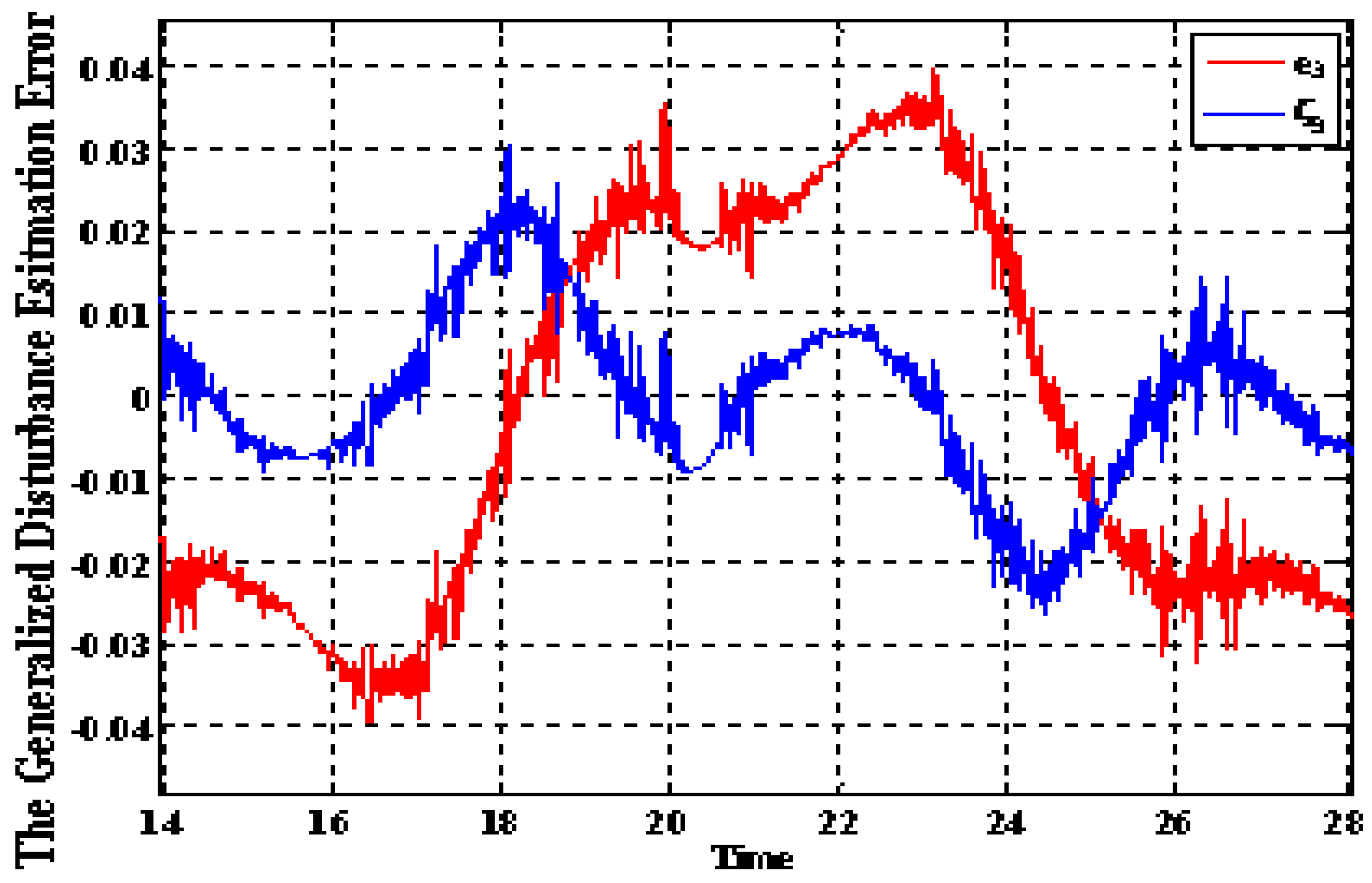
5.2. The Nonlinear Mass–Spring–Damper Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, J.; Chen, W.H.; Li, S. Non-linear disturbance observer-based robust control for systems with mismatched disturbances/uncertainties. IET Control Theory Appl. 2011, 5, 2053–2062. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Wang, H.P.; Zheng, D.; Tian, Y. High pressure common rail injection system modeling and control. ISA Trans. 2016, 63, 265–273. [Google Scholar] [CrossRef]
- Li, S.; Wang, H.; Tian, Y.; Aitouch, A.; Klein, J. Direct power control of DFIG wind turbine systems based on an intelligent proportional-integral sliding mode control. ISA Trans. 2016, 64, 431–439. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, Y.; Han, J. An alternative paradigm for control system design. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 4578–4585. [Google Scholar]
- Sayem, A.H.M.; Cao, Z.; Man, Z. Model Free ESO-based Repetitive Control for Rejecting Periodic and Aperiodic Disturbances. IEEE Trans. Ind. Electron. 2017, 64, 3433–3441. [Google Scholar] [CrossRef]
- Li, G.; Xu, W.; Zhao, J.; Wang, S.; Li, B. Precise robust adaptive dynamic surface control of permanent magnet synchronous motor based on extended state observer. IET Sci. Meas. Technol. 2017, 11, 590–599. [Google Scholar] [CrossRef]
- Abdul-Adheem, W.R.; Ibraheem, I.K. An Improved Active Disturbance Rejection Control for a Differential Drive Mobile Robot with Mismatched Disturbances and Uncertainties. arXiv 2018, arXiv:1805.12170. [Google Scholar]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Generalized extended state observer based control for systems with mismatched uncertainties. IEEE Trans. Ind. Electron. 2012, 59, 4792–4802. [Google Scholar] [CrossRef]
- Liu, H.; Li, S. Speed control for PMSM servo system using predictive functional control and extended state observer. IEEE Trans. Ind. Electron. 2012, 59, 1171–1183. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Adaptive sliding mode control for attitude stabilization with actuator saturation. IEEE Trans. Ind. Electron. 2011, 58, 4898–4907. [Google Scholar] [CrossRef]
- Yang, J.; Su, J.; Li, S.; Yu, X. High-order mismatched disturbance compensation for motion control systems via a continuous dynamic sliding-mode approach. IEEE Trans. Ind. Inform. 2014, 10, 604–614. [Google Scholar] [CrossRef]
- Abdul-adheem, W.R.; Ibraheem, I.K. Improved Sliding Mode Nonlinear Extended State Observer based Active Disturbance Rejection Control for Uncertain Systems with Unknown Total Disturbance. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 80–93. [Google Scholar]
- Pu, Z.; Yuan, R.; Yi, J.; Tan, X. A Class of Adaptive Extended State Observers for Nonlinear Disturbed Systems. IEEE Trans. Ind. Electron. 2015, 62, 5858–5869. [Google Scholar] [CrossRef]
- Zhiqiang, P.; Ruyi, Y.; Xiangmin, T.; Jianqiang, Y. Design and Analysis of Time-varying Extended State Observer. In Proceedings of the 34th Chinese Control Conferrence, Hangzhou, China, 28–30 July 2015; pp. 753–758. [Google Scholar]
- Zhang, X.; Wang, H.; Tian, Y.; Peyrodie, L.; Wang, X. Model-free based neural network control with time-delay estimation for lower extremity exoskeleton. Neurocomputing 2018, 272, 178–188. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control and intelligent PID controllers: Towards a possible trivialization of nonlinear control? IFAC Proc. 2009, 15, 1531–1550. [Google Scholar] [CrossRef]
- Bakhshande, F.; Bach, R.; Söffker, D. Robust control of a hydraulic cylinder using an observer-based sliding mode control: Theoretical development and experimental validation. Control Eng. Pract. 2020, 95, 104272. [Google Scholar] [CrossRef]
- Bakhshande, F.; Söffker, D. Proportional-Integral-Observer-Based Backstepping Approach for Position Control of a Hydraulic Differential Cylinder System with Model Uncertainties and Disturbances. J. Dyn. Syst. Meas. Control Trans. ASME 2018, 140, 121006. [Google Scholar] [CrossRef]
- Li, J.; Xia, Y.; Qi, X.; Gao, Z. On the Necessity, Scheme, and Basis of the Linear-Nonlinear Switching in Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2017, 64, 1425–1435. [Google Scholar] [CrossRef]
- Zheng, Q.; Gaol, L.Q.; Gao, Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the 46th Annual Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3501–3506. [Google Scholar]
- Farza, M.; Hern, O.; Saad, M.M.; Cedex, C. Cascade predictors design for a class of nonlinear uncertain systems with delayed state- Application to bioreactor. In Proceedings of the 17th International Conference on Automatic Control and Computer Engineering, Sousse, Tunisia, 19–21 November 2016; pp. 753–760. [Google Scholar]
- Vasconcelos, J.F.; Silvestre, C.; Oliveira, P. Pose Observers for Unmanned Air Vehicles. In Proceedings of the European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 3989–3994. [Google Scholar]
- Jiang, P.; Hao, J.Y.; Zong, X.P.; Wang, P.G. Modeling and simulation of Active-Disturbance-Rejection Controller with Simulink. In Proceedings of the 2010 International Conference on Machine Learning and Cybernetics ICMLC, Qingdao, China, 11–14 July 2010; pp. 927–931. [Google Scholar]
- Parvathy, R.; Daniel, A.E. A survey on active disturbance rejection control. In Proceedings of the 2013 International Multi Conference on Automation, Computing, Control, Communication and Compressed Sensing, Kottayam, India, 22–23 March 2013; pp. 330–335. [Google Scholar]
- Nowicki, M.; Madoński, R.; Kozłowski, K. First look at conditions on applicability of ADRC. In Proceedings of the 10th International Workshop on Robot Motion and Control (RoMoCo), Poznan, Poland, 6–8 July 2015; pp. 294–299. [Google Scholar]
- Al-Kalbani, F.; Al Hosni, S.M.; Zhang, J. Active Disturbance Rejection Control of a methanol-water separation distillation column. In Proceedings of the 2015 IEEE 8th GCC Conference Exhibition, Muscat, Oman, 1–4 February 2015; pp. 1–6. [Google Scholar]
- Lin, H.; Wang, X. Design and analysis of a continuous hybrid differentiator. IET Control Theory Appl. 2011, 5, 1321–1334. [Google Scholar]
- Wang, X.; Shirinzadeh, B. Rapid-convergent nonlinear differentiator. Mech. Syst. Signal Process. 2012, 28, 414–431. [Google Scholar] [CrossRef][Green Version]
- Angulo, M.T.; Moreno, J.A.; Fridman, L. Robust exact uniformly convergent arbitrary order differentiator. Automatica 2013, 49, 2489–2495. [Google Scholar] [CrossRef]
- Ibraheem, I.K.; Abdul-adheem, W.R. On the Improved Nonlinear Tracking Differentiator based Nonlinear PID Controller Design. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 234–241. [Google Scholar]
- Abdul-adheem, W.R.; Ibraheem, K. From PID to Nonlinear State Error Feedback Controller. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 312–322. [Google Scholar]
- Kang, Y.L.; Shresta, G.B.; Lie, T.T. Application of an NLPID controller on a UPFC to improve transient stability of a power system. IEE Proc. Gener. Transm. Distrib. 2001, 148, 523–529. [Google Scholar] [CrossRef]
- Ma, L.; Lin, F.; You, X.; Zheng, T.Q. Nonlinear PID Control of Three-Phase Pulse Width Modulation Rectifier. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 3417–3422. [Google Scholar]
- Salim, S.N.S.; Ismail, Z.H.; Rahmat, M.F.; Faudzi, A.A.M.; Sunar, N.H.; Samsudin, S.I. Tracking performance and disturbance rejection of pneumatic actuator system. In Proceedings of the 9th Asian Control Conference, Istanbul, Turkey, 23–26 June 2013; pp. 1–6. [Google Scholar]
- Luenberger, D.G. Observing the State of a Linear System. IEEE Trans. Mil. Electron. 1964, 8, 74–80. [Google Scholar] [CrossRef]
- Goel, A.; Swarup, A. Performance Analysis of Active Disturbance Rejection Controlled Robotic Manipulator based on Evolutionary Algorithm. Int. J. Hybrid Inf. Technol. 2016, 9, 65–80. [Google Scholar] [CrossRef]
- Bao, D.; Tang, W. Adaptive sliding mode control of ball screw drive system with extended state observer. In Proceedings of the 2016 2nd International Conference on Control, Automation and Robotics ICCAR, Hong Kong, China, 28–29 April 2016; pp. 133–138. [Google Scholar]
- Godbole, A.A.; Kolhe, J.P.; Talole, S.E. Performance analysis of generalized extended state observer in tackling sinusoidal disturbances. IEEE Trans. Control Syst. Technol. 2013, 21, 2212–2223. [Google Scholar] [CrossRef]
- Pan, H.; Sun, W.; Gao, H.; Hayat, T.; Alsaadi, F. Nonlinear tracking control based on extended state observer for vehicle active suspensions with performance constraints. Mechatronics 2015, 30, 363–370. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.; Zheng, T.; Li, Y.; Cui, M.; Peeta, S. Extended-State-Observer-Based Double-Loop Integral Sliding-Mode Control of Electronic Throttle Valve. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2501–2510. [Google Scholar] [CrossRef]
- Ball, A.A.; Khalil, H.K. High-gain observers in the presence of measurement noise: A nonlinear gain approach. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 Dcember 2008; pp. 2288–2293. [Google Scholar]
- Xiu, Z.; Wang, W. A Novel Nonlinear PID Controller Designed By Takagi-Sugeno Fuzzy Model. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 3724–3728. [Google Scholar]
- Ibraheem, I.K. A Digital-Based Optimal AVR Design of Synchronous Generator Exciter using LQR Technique. Al-Khwarizmi Eng. J. 2011, 7, 82–94. [Google Scholar]
- Mohammed, I.A.; Mahir, R.A.; Ibraheem, I.K. Robust Controller Design for Load Frequency Control in Power Systems using State-Space Approach. J. Eng. Coll. Eng. Baghdad Univ. 2011, 17, 265–278. [Google Scholar]
- Ibraheem, I.K. Design of a two-Degree-of-Freedom Controller for a Magnetic Levitation System Based on LQG Technique. Al-Nahrain Eng. J. College Eng. Al-Nahrain Univ. 2013, 16, 67–77. [Google Scholar]
- Ibraheem, I.K.; Ajeil, F.H. Path Planning of an autonomous Mobile Robot using Swarm based Optimization Techniques. Al-KAwarizmi Eng. J. 2016, 12, 12–25. [Google Scholar] [CrossRef]
- Ibraheem, I.K. Anti-Disturbance Compensator Design for Unmanned Aerial Vehicle. J. Eng. 2020, 26, 86–103. [Google Scholar] [CrossRef][Green Version]
- Abdul-Adheem, W.R.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. Improved Active Disturbance Rejection-Based Decentralized control for MIMO Nonlinear Systems: Comparison with The Decoupled Control Scheme. Appl. Sci. 2020, 10, 2515. [Google Scholar] [CrossRef]
- Ajeil, F.H.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. Grid-Based Mobile Robot Path Planning Using Aging-Based Ant Colony Optimization Algorithm in Static and Dynamic Environments. Sensors 2020, 20, 1880. [Google Scholar] [CrossRef]
- Ibraheem, G.A.R.; Azar, A.T.; Ibraheem, I.K.; Humaidi, A.J. A Novel Design of a Neural Network based Fractional PID Controller for Mobile Robots Using Hybridized Fruit Fly and Particle Swarm Optimization. Complexity 2020. [Google Scholar] [CrossRef]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dyn. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]

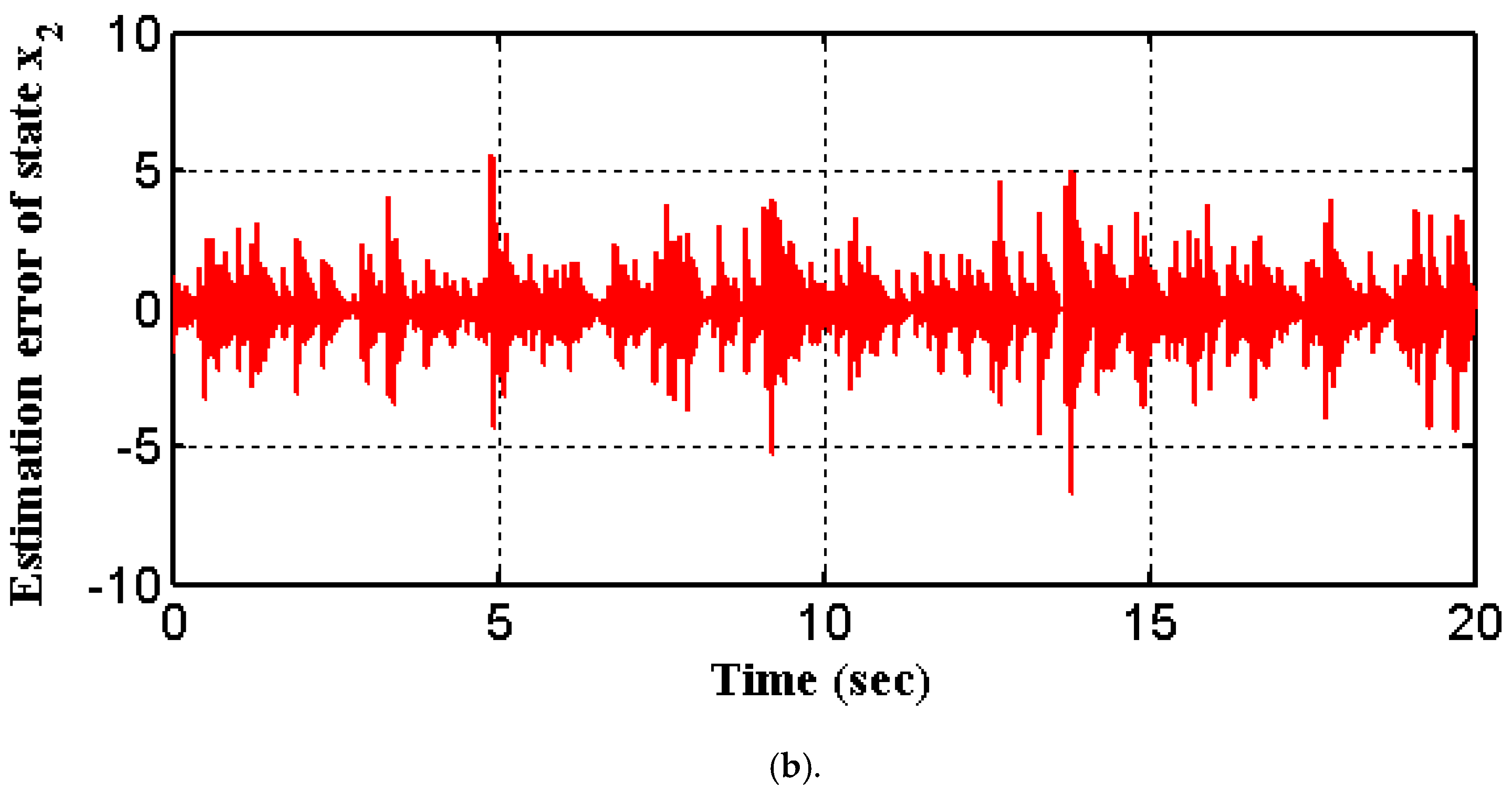
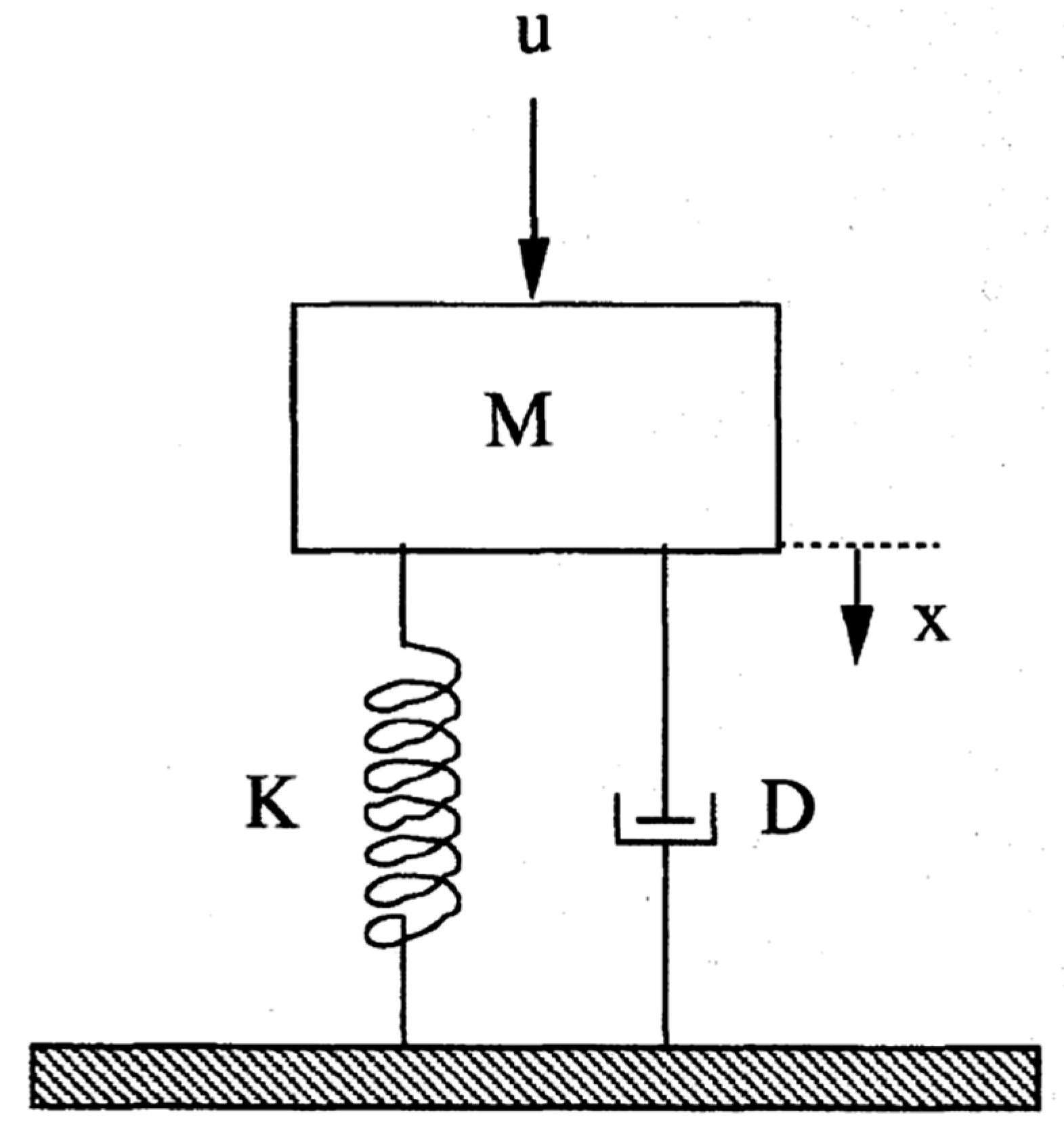
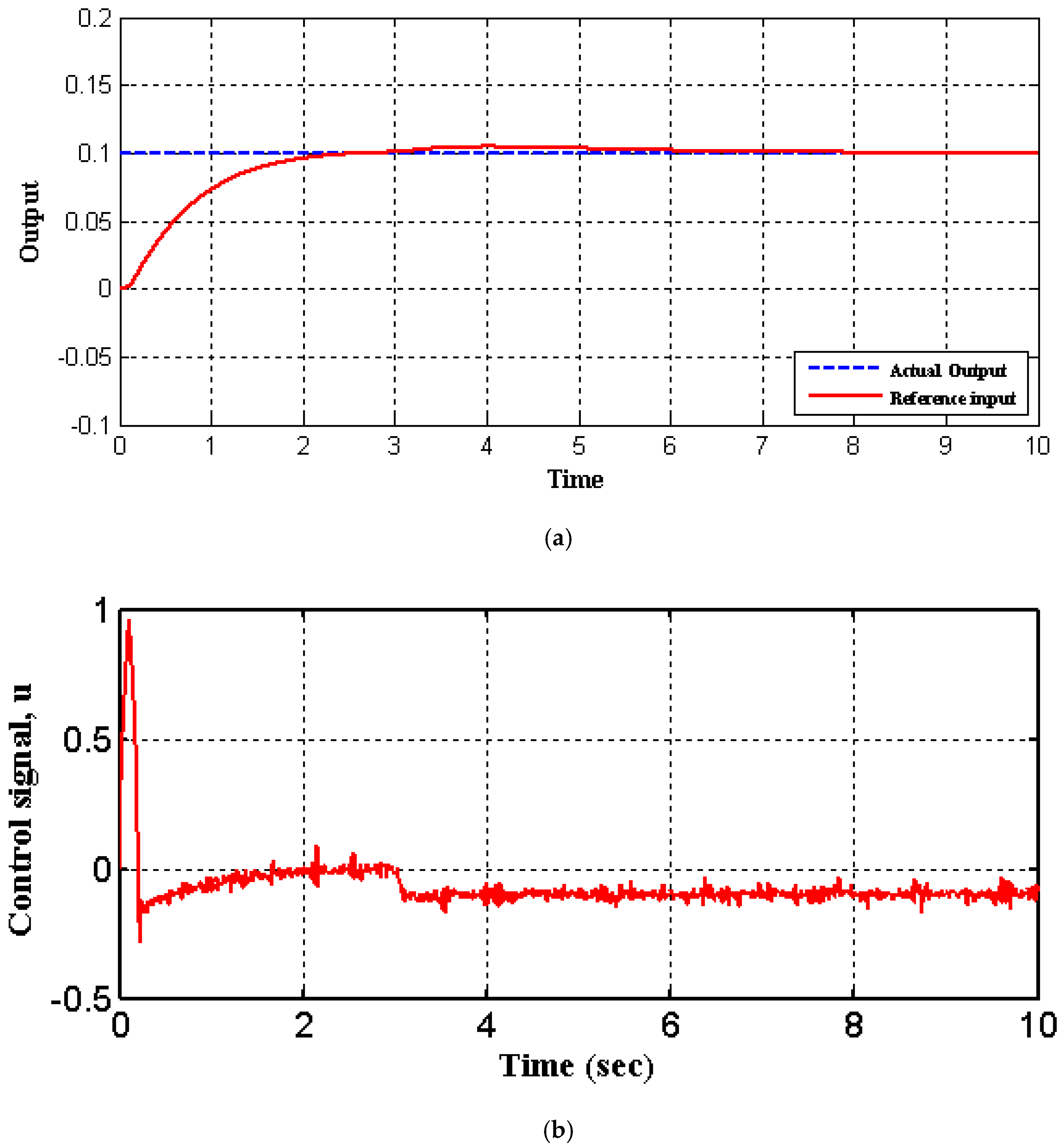
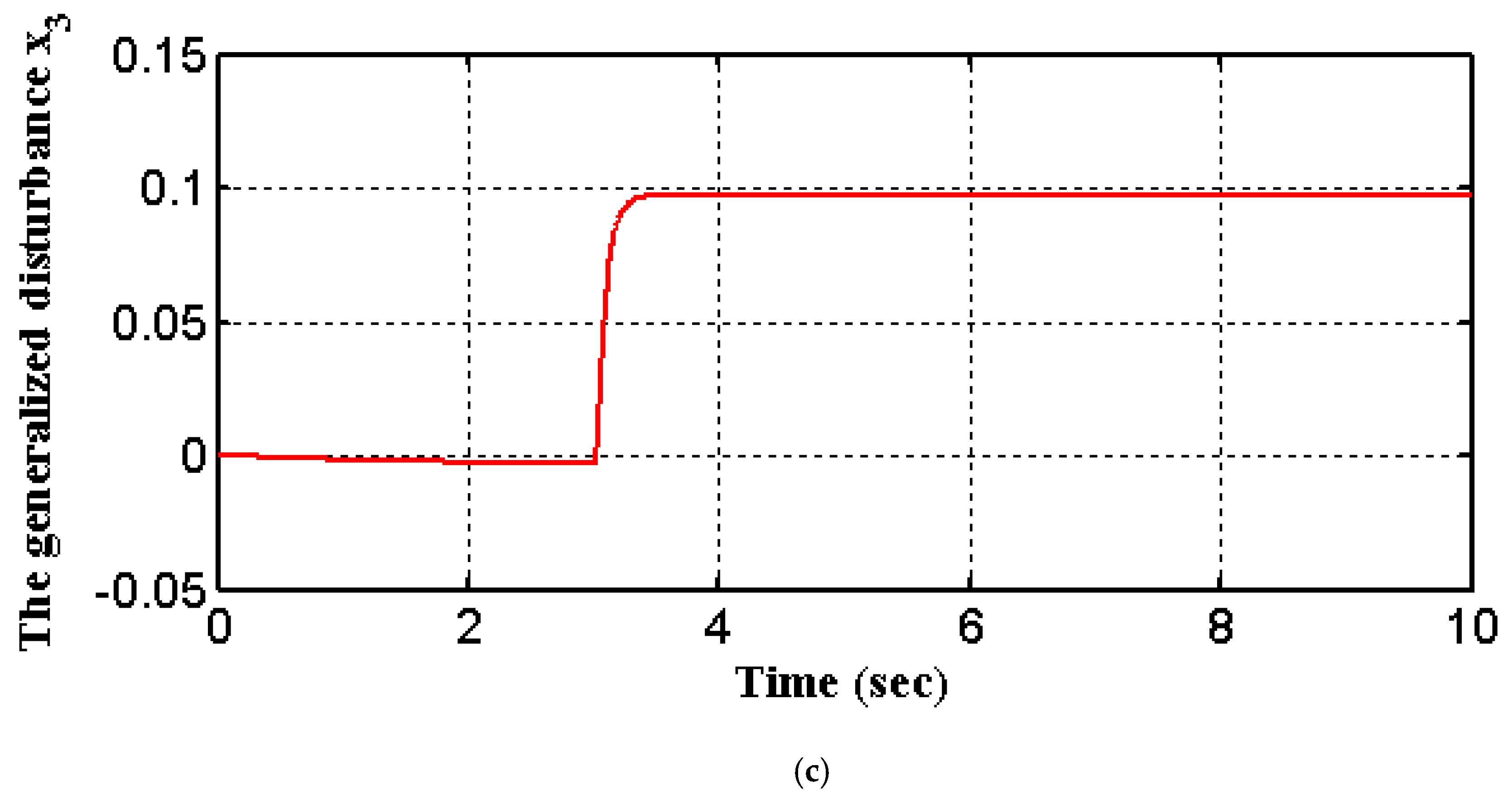
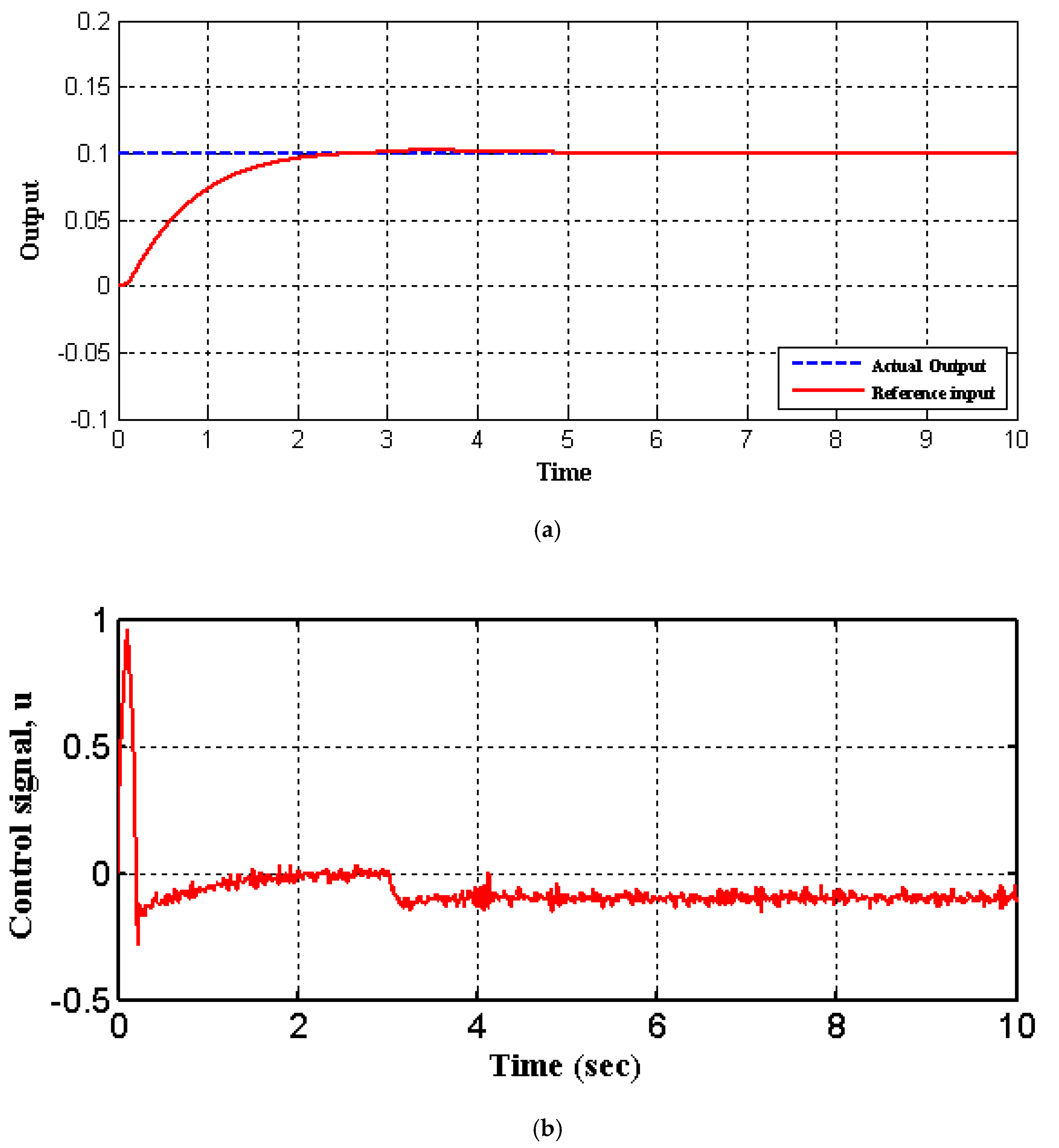
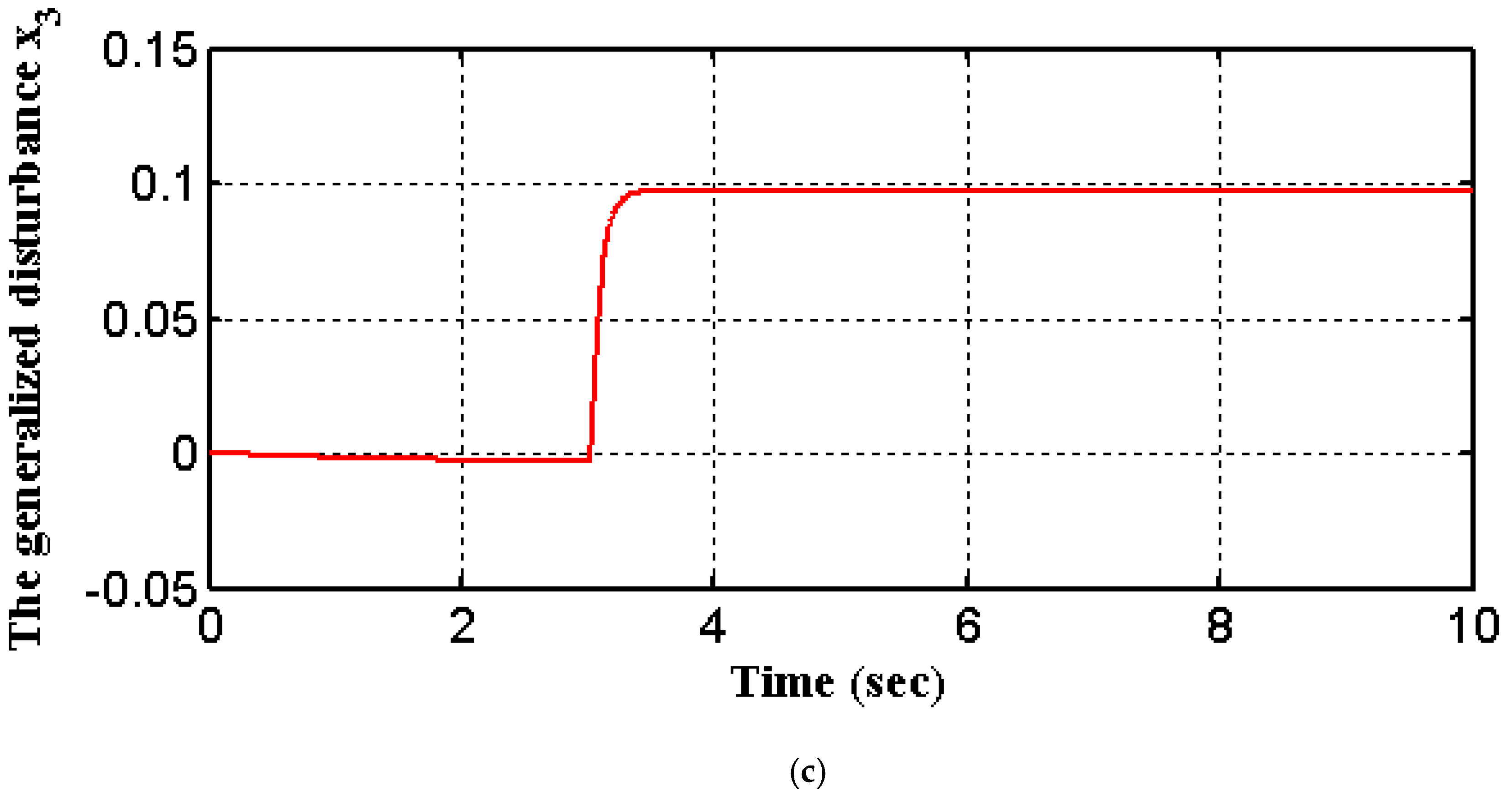
| Symbol | Without Noise | With Noise | ||
|---|---|---|---|---|
| ITAE | ISU | ITAE | ISU | |
| C-ADRC | 1.71 | 7.17 | 7.07 | 457.30 |
| N-ADRC | 1.33 | 6.63 | 2.13 | 310.91 |
| Reduction (%) | 22.32 | 7.51 | 69.87 | 32.01 |
| Parameter | Value |
|---|---|
| Controller | ITAE | ISU |
|---|---|---|
| C-ADRC | 0.10 | 0.17 |
| N-ADRC | 0.05 | 0.16 |
| Reduction (%) | 50 | 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdul-Adheem, W.R.; Azar, A.T.; Ibraheem, I.K.; Humaidi, A.J. Novel Active Disturbance Rejection Control Based on Nested Linear Extended State Observers. Appl. Sci. 2020, 10, 4069. https://doi.org/10.3390/app10124069
Abdul-Adheem WR, Azar AT, Ibraheem IK, Humaidi AJ. Novel Active Disturbance Rejection Control Based on Nested Linear Extended State Observers. Applied Sciences. 2020; 10(12):4069. https://doi.org/10.3390/app10124069
Chicago/Turabian StyleAbdul-Adheem, Wameedh Riyadh, Ahmad Taher Azar, Ibraheem Kasim Ibraheem, and Amjad J. Humaidi. 2020. "Novel Active Disturbance Rejection Control Based on Nested Linear Extended State Observers" Applied Sciences 10, no. 12: 4069. https://doi.org/10.3390/app10124069
APA StyleAbdul-Adheem, W. R., Azar, A. T., Ibraheem, I. K., & Humaidi, A. J. (2020). Novel Active Disturbance Rejection Control Based on Nested Linear Extended State Observers. Applied Sciences, 10(12), 4069. https://doi.org/10.3390/app10124069







