Approximation of the Mechanical Response of Large Lattice Domains Using Homogenization and Design of Experiments
Abstract
1. Introduction
2. Literature Review
2.1. Lattice Structures and Material Homogenization
2.2. Modeling and Simulation of Lattice Structures
2.3. Conclusions of the Literature Review
3. Methodology
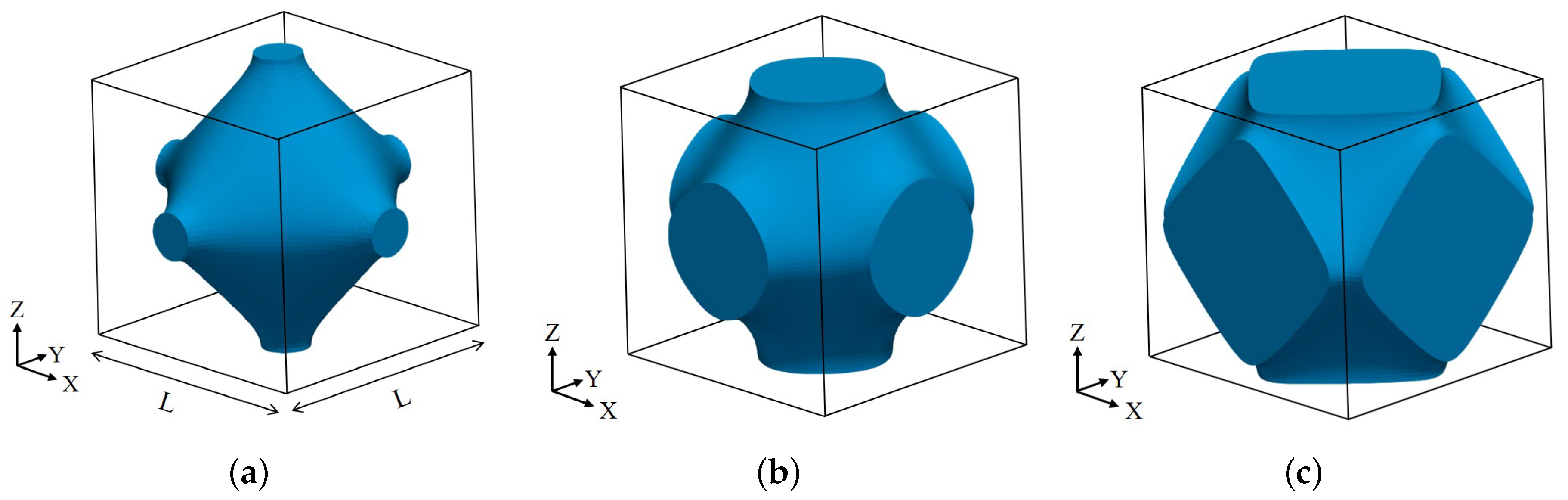
3.1. Schwarz Primitive Lattice Structures
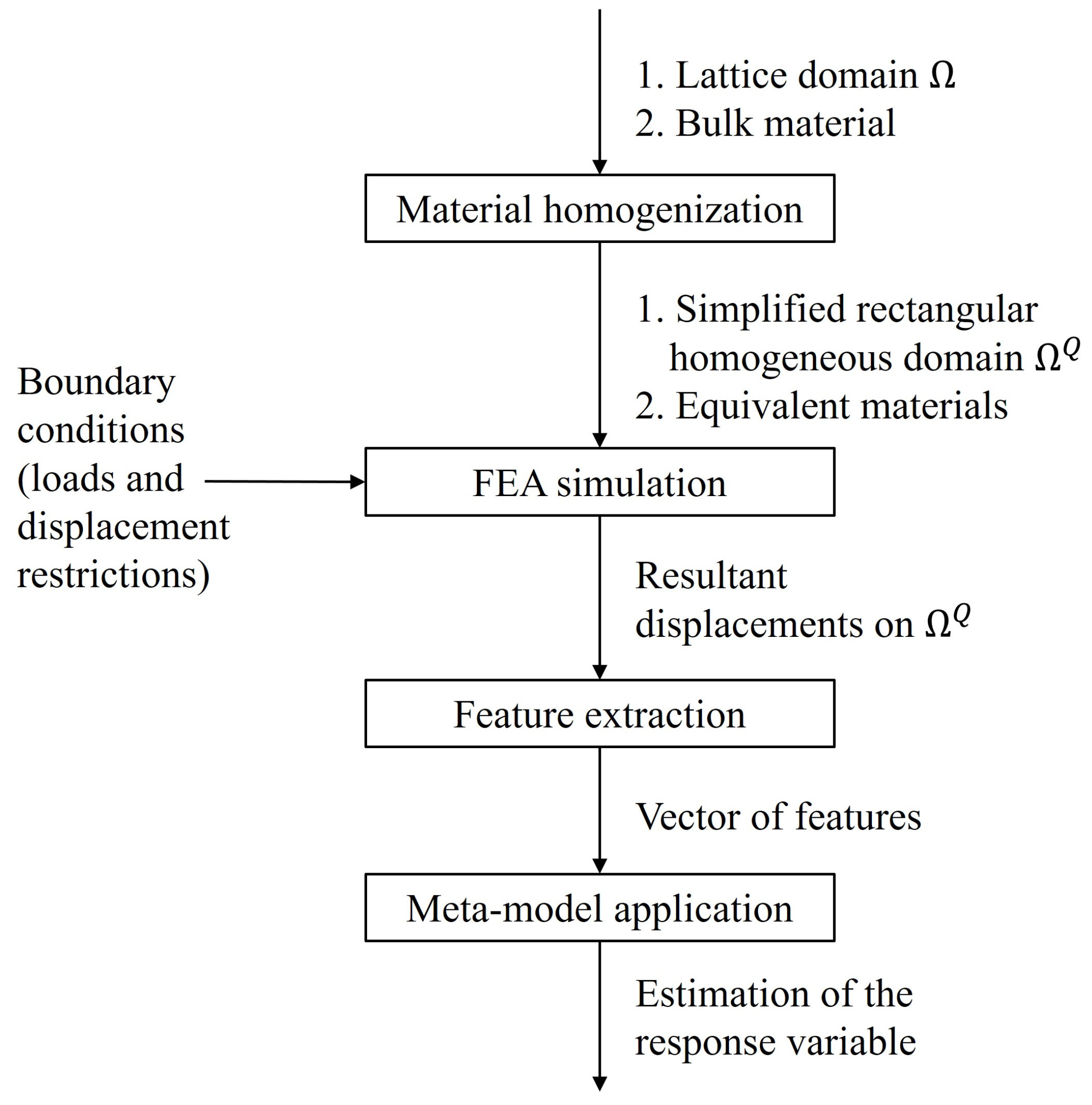
3.2. Methodology to Estimate the Stress–Strain Response of Lattice Structures
3.2.1. Material Homogenization
3.2.2. FEA Simulation of the Homogeneous Domain
3.2.3. Feature Extraction
3.2.4. Meta-Model Execution
3.3. Material Homogenization
3.4. Generation of Meta-Models Using DOE
3.4.1. Factor Identification
3.4.2. Factor Selection
3.4.3. Meta-Model Development
4. Results
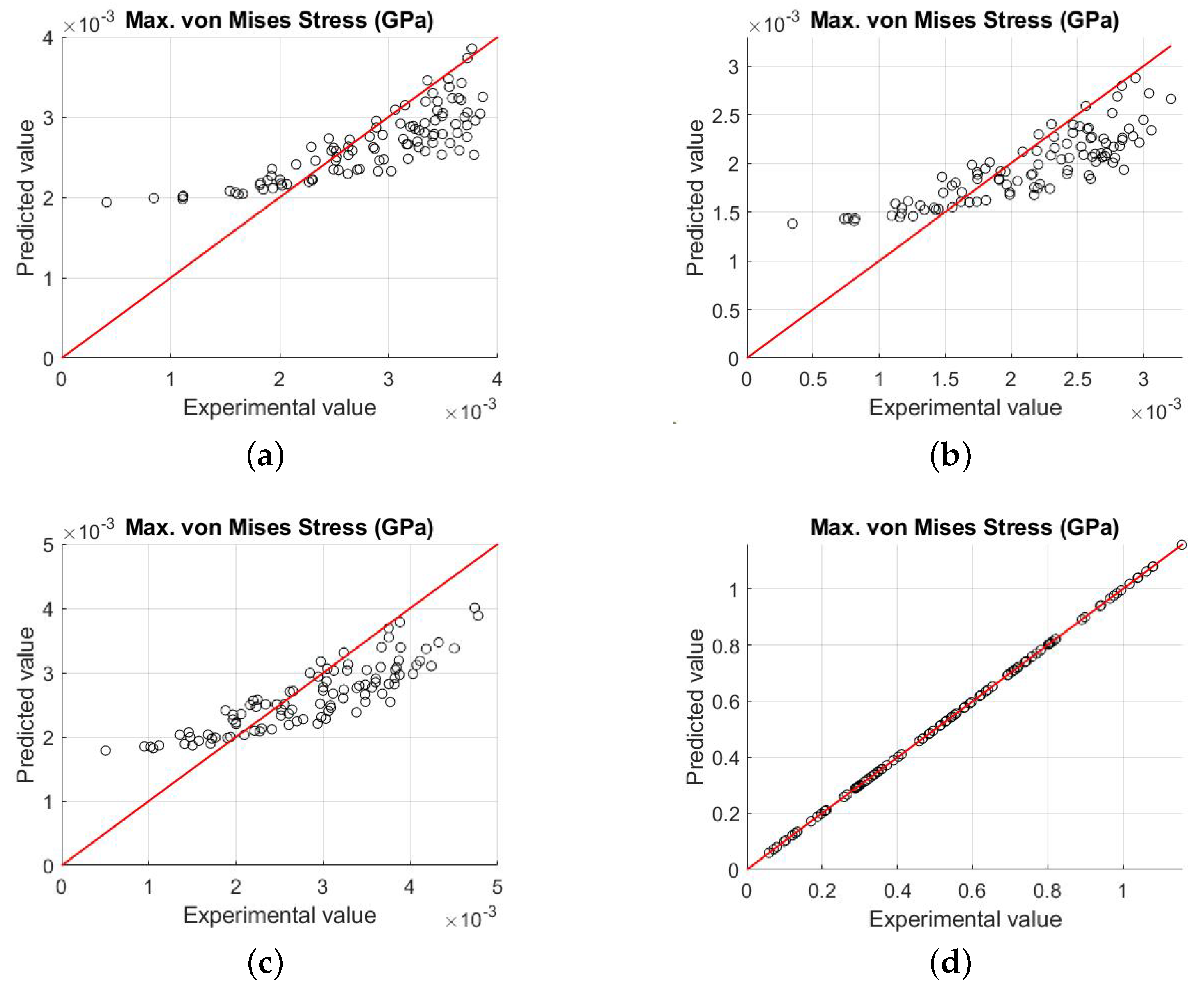
4.1. Validation of the Proposed Methodology
4.1.1. Material Homogenization in Schwarz Primitive Lattice Structures
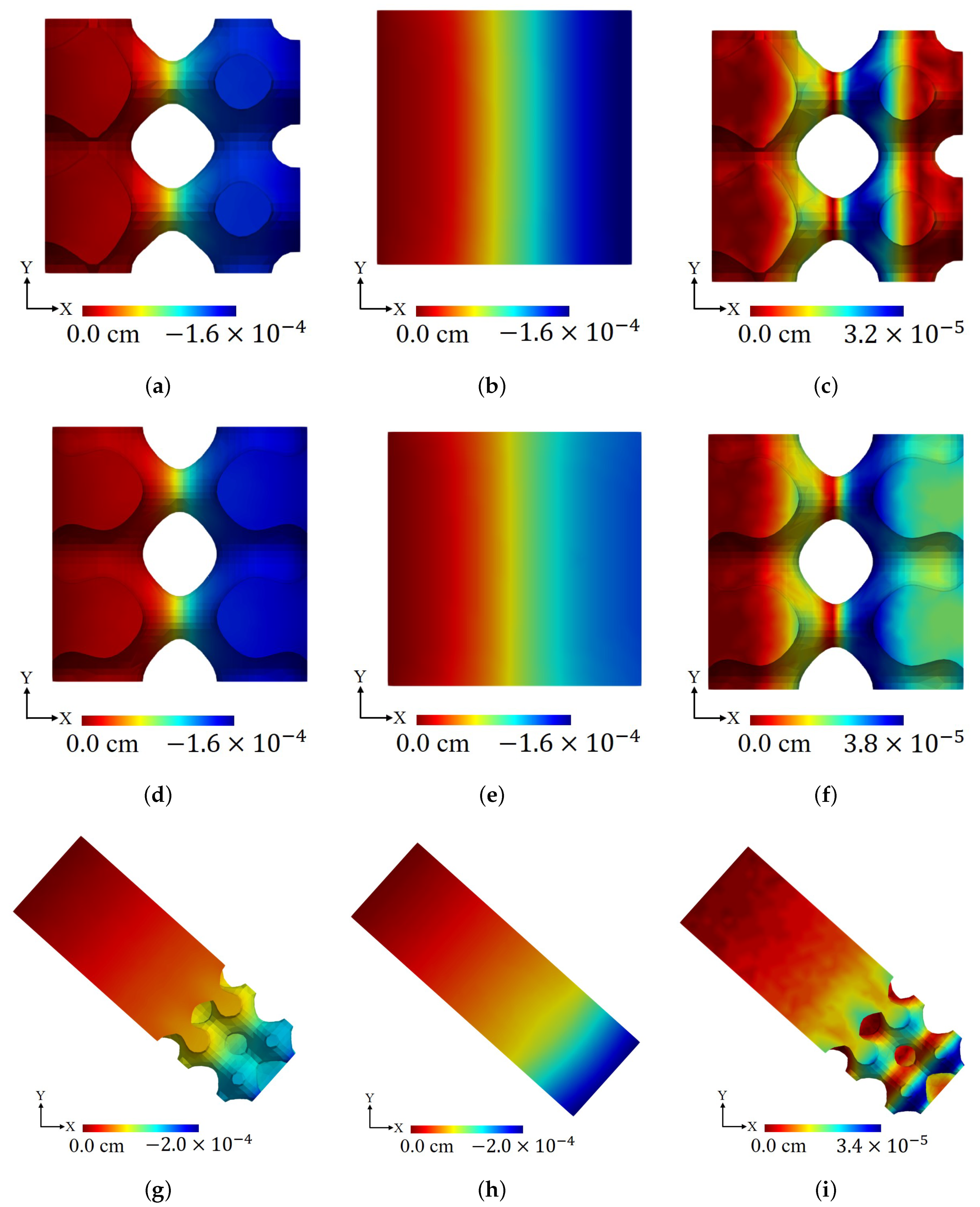
4.1.2. Comparison between FEA and Our Methodology
- To consider more displacement-based features located inside the cell, not only on the boundary of the cell.
- To develop meta-models for more relative densities. Currently, it is limited to meta-models of density .
- To enlarge the range of analysis of the displacement-based features, since in a single load case, the magnitude of the deformation of the lattice domain varies in every zone. Currently, the allowed normal strains are limited to the interval .
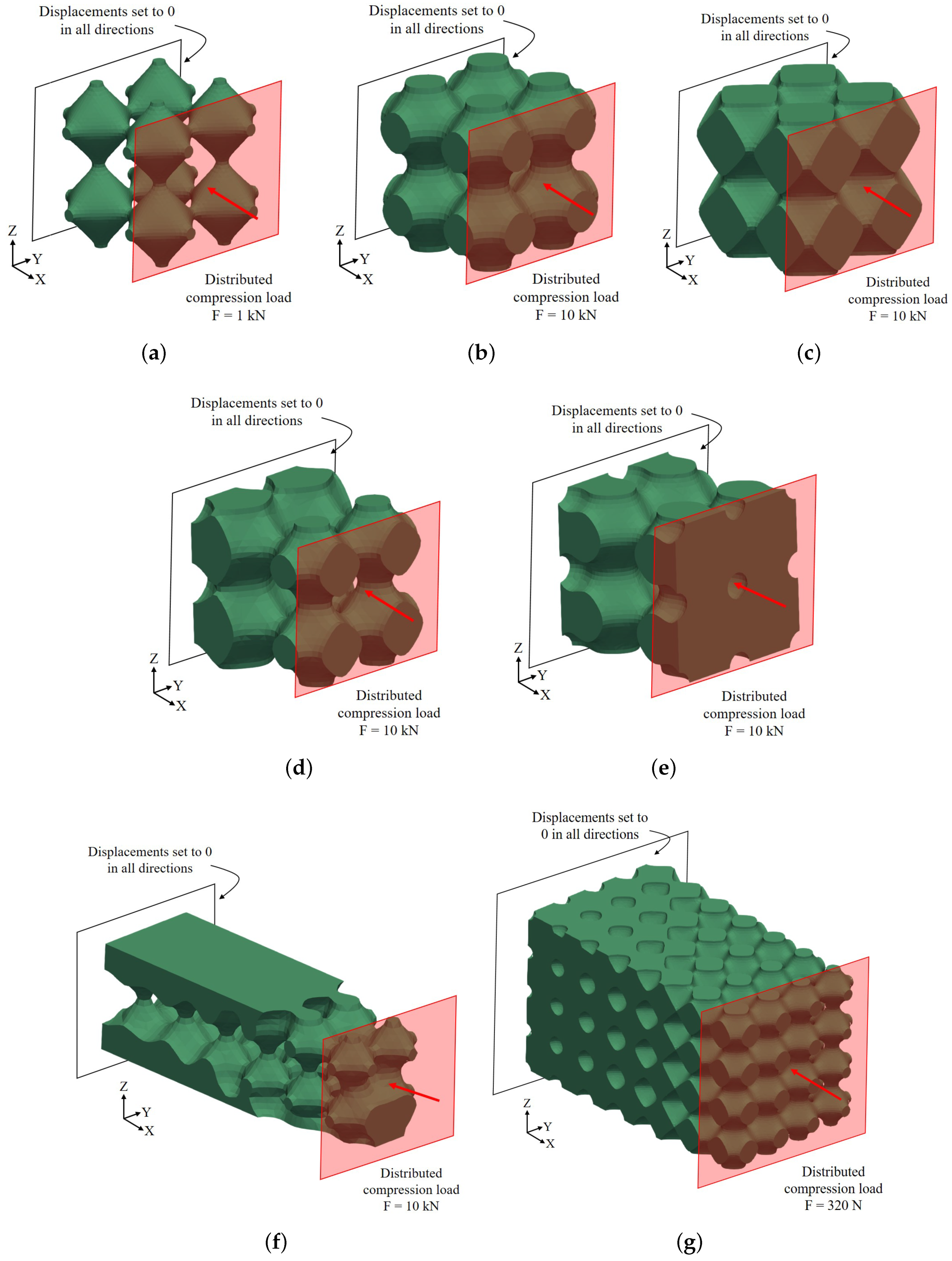
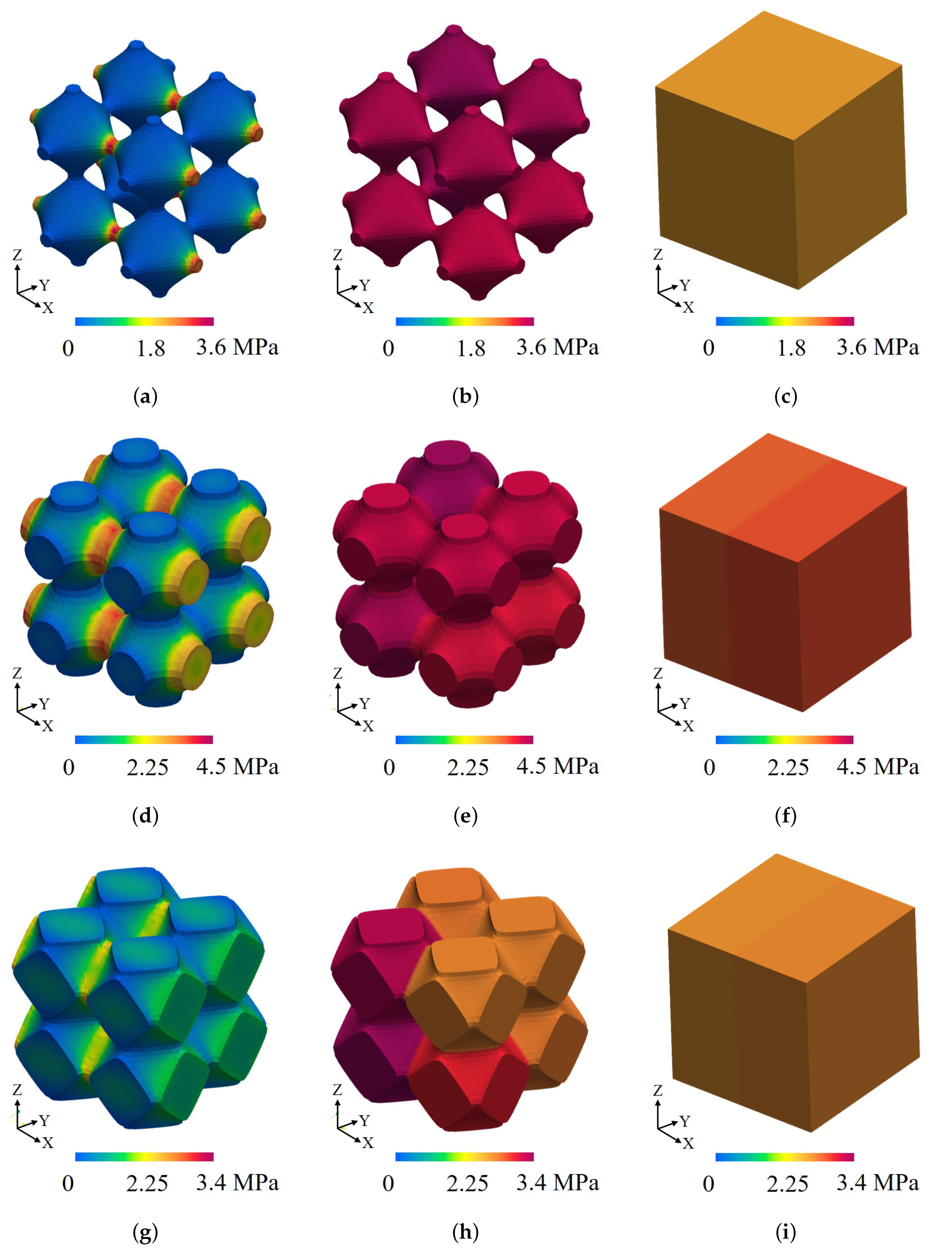
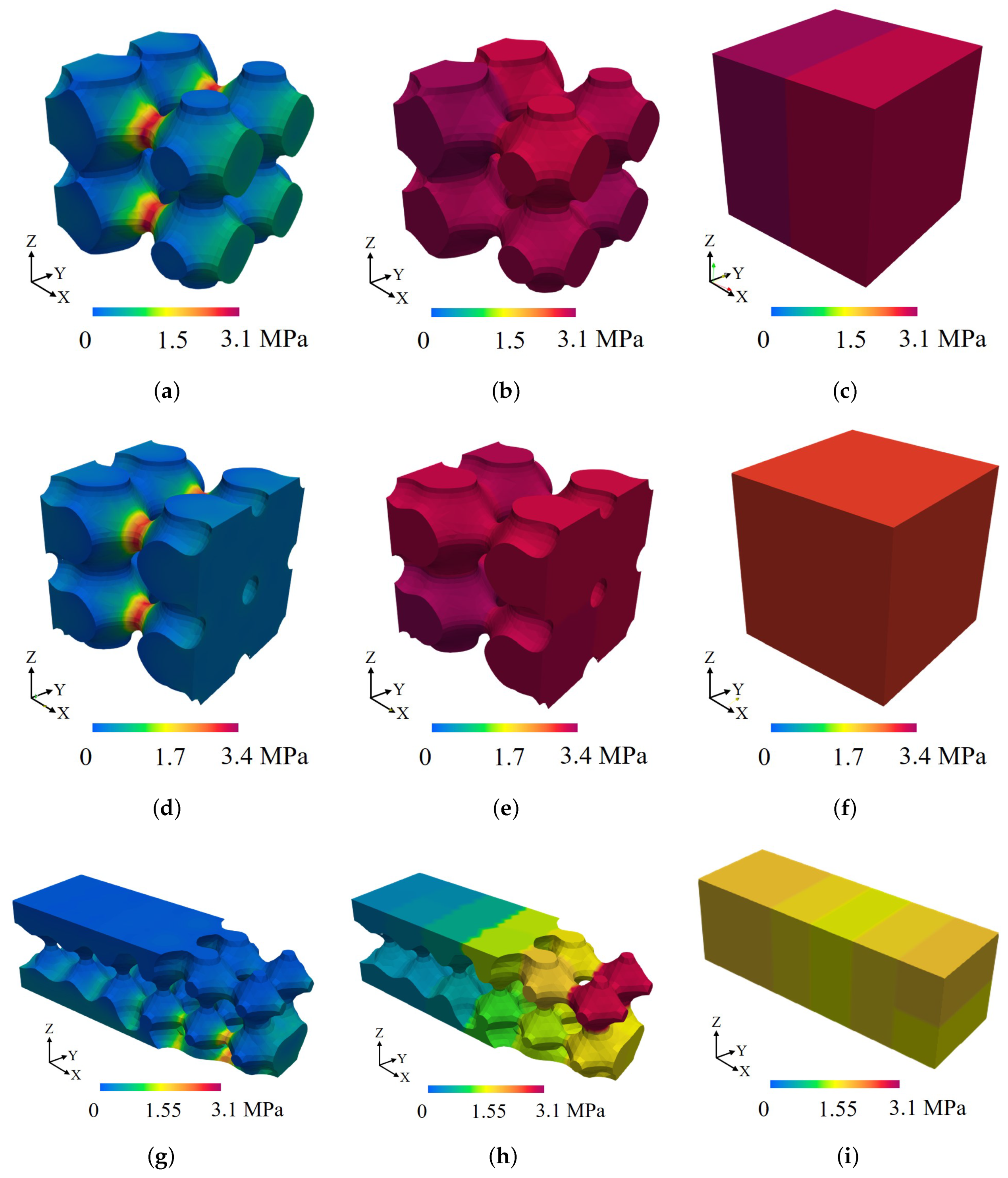
4.2. Application of Our Methodology to Large Lattice Domains
5. Conclusions
Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing. |
| CCF | Central composite face-centered design. |
| DOE | Design of experiments. |
| FEA | Finite element analysis. |
| Subsets of that represents the lattice domain and the equivalent homogeneous domain, respectively . | |
| Young’s moduli of the bulk and equivalent material, respectively (Pa). | |
| Poisson’s ratio of the bulk and equivalent material, respectively. | |
| Von Mises stress (Pa). | |
| L | Length of the Schwarz primitive cell . |
| Relative density or volume fraction of a Schwarz primitive cell . | |
| t | Iso-value used to generate the Schwarz primitive cell . |
References
- Posada, J.; Toro, C.; Barandiaran, I.; Oyarzun, D.; Stricker, D.; de Amicis, R.; Pinto, E.B.; Eisert, P.; Döllner, J.; Vallarino, I. Visual Computing as a Key Enabling Technology for Industrie 4.0 and Industrial Internet. IEEE Comput. Graph. Appl. 2015, 35, 26–40. [Google Scholar] [CrossRef]
- Helou, M.; Kara, S. Design, analysis and manufacturing of lattice structures: An overview. Int. J. Comput. Integr. Manuf. 2018, 31, 243–261. [Google Scholar] [CrossRef]
- Cortés, C.; Osorno, M.; Uribe, D.; Steeb, H.; Ruiz-Salguero, O.; Barandiaran, I.; Flórez, J. Geometry simplification of open-cell porous materials for elastic deformation FEA. Eng. Comput. 2019, 35, 257–276. [Google Scholar] [CrossRef]
- Terriault, P.; Brailovski, V. Modeling and simulation of large, conformal, porosity-graded and lightweight lattice structures made by additive manufacturing. Finite Elem. Anal. Des. 2018, 138, 1–11. [Google Scholar] [CrossRef]
- Montoya-Zapata, D.; Acosta, D.A.; Cortés, C.; Pareja-Corcho, J.; Moreno, A.; Posada, J.; Ruiz-Salguero, O. Meta-modeling of Lattice Mechanical Responses via Design of Experiments. In Proceedings of the 2nd International Conference on Mathematics and Computers in Science and Engineering (MACISE 2020), Madrid, Spain, 18–20 January 2020. [Google Scholar]
- Li, D.; Liao, W.; Dai, N.; Dong, G.; Tang, Y.; Xie, Y.M. Optimal design and modeling of gyroid-based functionally graded cellular structures for additive manufacturing. Comput. Aided Des. 2018, 104, 87–99. [Google Scholar] [CrossRef]
- Montoya-Zapata, D.; Moreno, A.; Pareja-Corcho, J.; Posada, J.; Ruiz-Salguero, O. Density-Sensitive Implicit Functions Using Sub-Voxel Sampling in Additive Manufacturing. Metals 2019, 9. [Google Scholar] [CrossRef]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for Additive Manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Wu, J.; Wang, W.; Gao, X. Design and Optimization of Conforming Lattice Structures. IEEE Trans. Vis. Comput. Graph. 2019, 1. [Google Scholar] [CrossRef]
- Ataee, A.; Li, Y.; Fraser, D.; Song, G.; Wen, C. Anisotropic Ti-6Al-4V gyroid scaffolds manufactured by electron beam melting (EBM) for bone implant applications. Mater. Des. 2018, 137, 345–354. [Google Scholar] [CrossRef]
- Melchels, F.P.; Bertoldi, K.; Gabbrielli, R.; Velders, A.H.; Feijen, J.; Grijpma, D.W. Mathematically defined tissue engineering scaffold architectures prepared by stereolithography. Biomaterials 2010, 31, 6909–6916. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, P.; Biyikli, E.; Bai, J.; Robbins, J.; To, A. Efficient design optimization of variable-density cellular structures for additive manufacturing: Theory and experimental validation. Rapid Prototyp. J. 2017, 23, 660–677. [Google Scholar] [CrossRef]
- Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and failure response of imperfect three-dimensional metallic lattices: The role of geometric defects induced by Selective Laser Melting. J. Mech. Phys. Solids 2017, 107, 160–184. [Google Scholar] [CrossRef]
- Park, S.I.; Rosen, D.W. Homogenization of Mechanical Properties for Material Extrusion Periodic Lattice Structures Considering Joint Stiffening Effects. J. Mech. Des. 2018, 140, 111414. [Google Scholar] [CrossRef]
- Bonatti, C.; Mohr, D. Mechanical performance of additively-manufactured anisotropic and isotropic smooth shell-lattice materials: Simulations & experiments. J. Mech. Phys. Solids 2019, 122, 1–26. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of compressive properties of SLM-fabricated multi-layer lattice structures by experimental test and μ-CT-based finite element analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Montoya-Zapata, D.; Cortés, C.; Ruiz-Salguero, O. FE-simulations with a simplified model for open-cell porous materials: A Kelvin cell approach. J. Comput. Methods Sci. Eng. 2019, 19, 989–1000. [Google Scholar] [CrossRef]
- Tryland, T.; Hopperstad, O.S.; Langseth, M. Design of experiments to identify material properties. Mater. Des. 2000, 21, 477–492. [Google Scholar] [CrossRef]
- Kovalovs, A.; Chate, A.; Gaidukovs, S.; Medvids, A. Finite Element Simulation of Indentation Experiment on Branched Epoxy Novolac Resin. IOP Conf. Ser. Mater. Sci. Eng. 2019, 500, 012006. [Google Scholar] [CrossRef]
- Oliveira, L.Á.; Santos, J.C.; Panzera, T.H.; Freire, R.T.; Vieira, L.M.; Scarpa, F. Evaluation of hybrid-short-coir-fibre-reinforced composites via full factorial design. Compos. Struct. 2018, 202, 313–323. [Google Scholar] [CrossRef]
- Phanphet, S.; Dechjarern, S.; Jomjanyong, S. Above-knee prosthesis design based on fatigue life using finite element method and design of experiment. Med. Eng. Phys. 2017, 43, 86–91. [Google Scholar] [CrossRef]
- Schäfer, C.; Finke, E. Shape optimisation by design of experiments and finite element methods—An application of steel wheels. Struct. Multidiscip. Optim. 2008, 36, 477–491. [Google Scholar] [CrossRef]
- Lozanovski, B.; Downing, D.; Tran, P.; Shidid, D.; Qian, M.; Choong, P.; Brandt, M.; Leary, M. A Monte Carlo simulation-based approach to realistic modelling of additively manufactured lattice structures. Addit. Manuf. 2020, 32, 101092. [Google Scholar] [CrossRef]
- Mendenhall, W.M.; Sincich, T.L. Statistics for Engineering and the Sciences, 6th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Wohlgemuth, M.; Yufa, N.; Hoffman, J.; Thomas, E.L. Triply Periodic Bicontinuous Cubic Microdomain Morphologies by Symmetries. Macromolecules 2001, 34, 6083–6089. [Google Scholar] [CrossRef]
- Maskery, I.; Sturm, L.; Aremu, A.; Panesar, A.; Williams, C.; Tuck, C.; Wildman, R.; Ashcroft, I.; Hague, R. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer 2018, 152, 62. [Google Scholar] [CrossRef]
- Steven, G.P. Homogenization of multicomponent composite orthotropic materials using FEA. Commun. Numer. Methods Eng. 1997, 13, 517–531. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, J.S.; Hunter, W.G. Statistics for Experimenters: Design, Discovery, and Innovation, 2nd ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- NIST/SEMATECH. e-Handbook of Statistical Methods. Available online: http://www.itl.nist.gov/div898/handbook/ (accessed on 4 December 2019).
- Rizzuto, J. Experimental investigation of reciprocally supported element (RSE) lattice honeycomb domes structural behaviour. Eng. Struct. 2018, 166, 496–510. [Google Scholar] [CrossRef]
- Yu, H.; Huang, J.; Zou, B.; Shao, W.; Liu, J. Stress-constrained shell-lattice infill structural optimisation for additive manufacturing. Virtual Phys. Prototyp. 2020, 15, 35–48. [Google Scholar] [CrossRef]
- Ren, X.; Xiao, L.; Hao, Z. Multi-property cellular material design approach based on the mechanical behaviour analysis of the reinforced lattice structure. Mater. Des. 2019, 174, 107785. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]



| Relative Density () | Equivalent Young’s Modulus () | Equivalent Poisson’s Ratio () |
|---|---|---|
| GPa | ||
| GPa | ||
| GPa | ||
| GPa | ||
| GPa | ||
| GPa | ||
| GPa | ||
| GPa | ||
| 114 GPa |
| Relative Density | Average Relative Error | Max. Relative Error | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.25 | 0.0438 | 0.0010 | 0.0013 | 0.0005 | 0.0089 | 0.0075 | 0.0067 | 19% | 370% |
| 0.50 | 0.0369 | 0.0019 | 0.0021 | 0.0019 | 0.0076 | 0.0073 | 0.0074 | 20% | 298% |
| 0.75 | 0.0419 | 0.0041 | 0.0039 | 0.0036 | 0.0089 | 0.0098 | 0.0091 | 21% | 255% |
| 1.0 | 0.4036 | N/A | N/A | N/A | N/A | N/A | N/A | 0% | 0% |
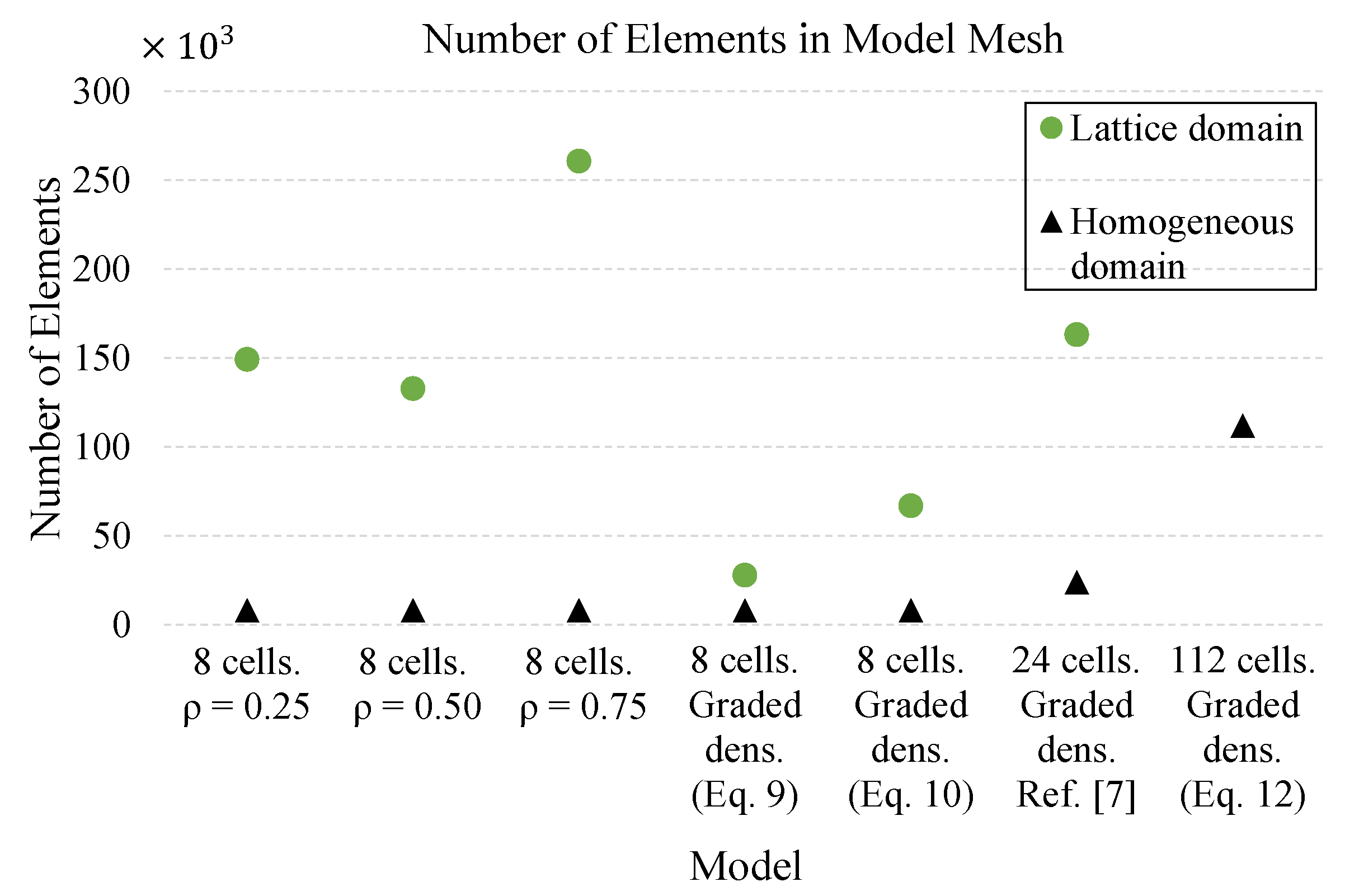
| Domain | Figure Number | No. of Elements in Lattice Domain | No. of Elements in Homogeneous Domain |
|---|---|---|---|
| 8 cells. Uniform density with | Figure 5a | 149,090 | 8000 |
| 8 cells. Uniform density with | Figure 5b | 132,710 | 8000 |
| 8 cells. Uniform density with | Figure 5c | 260,610 | 8000 |
| 8 cells. Graded density per Equation (9) | Figure 5d | 27,863 | 8000 |
| 8 cells. Graded density per Equation (10) | Figure 5e | 66,890 | 8000 |
| 24 cells. Graded density per [7] | Figure 5f | 163,080 | 24,000 |
| 112 cells. Graded density per Equation (12) | Figure 5g | N/A | 112,000 |
| Domain | Figure Number | Max. : FEA (MPa) | Max. : Our Method (MPa) | Rel. Error |
|---|---|---|---|---|
| Eight cells. Uniform density with | Figure 5a | |||
| Eight cells. Uniform density with | Figure 5b | |||
| Eight cells. Uniform density with | Figure 5c | |||
| Eight cells. Graded density per Equation (9) | Figure 5d | |||
| Eight cells. Graded density per Equation (10) | Figure 5e | |||
| 24 cells. Graded density per [7] | Figure 5f |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya-Zapata, D.; Acosta, D.A.; Cortés, C.; Pareja-Corcho, J.; Moreno, A.; Posada, J.; Ruiz-Salguero, O. Approximation of the Mechanical Response of Large Lattice Domains Using Homogenization and Design of Experiments. Appl. Sci. 2020, 10, 3858. https://doi.org/10.3390/app10113858
Montoya-Zapata D, Acosta DA, Cortés C, Pareja-Corcho J, Moreno A, Posada J, Ruiz-Salguero O. Approximation of the Mechanical Response of Large Lattice Domains Using Homogenization and Design of Experiments. Applied Sciences. 2020; 10(11):3858. https://doi.org/10.3390/app10113858
Chicago/Turabian StyleMontoya-Zapata, Diego, Diego A. Acosta, Camilo Cortés, Juan Pareja-Corcho, Aitor Moreno, Jorge Posada, and Oscar Ruiz-Salguero. 2020. "Approximation of the Mechanical Response of Large Lattice Domains Using Homogenization and Design of Experiments" Applied Sciences 10, no. 11: 3858. https://doi.org/10.3390/app10113858
APA StyleMontoya-Zapata, D., Acosta, D. A., Cortés, C., Pareja-Corcho, J., Moreno, A., Posada, J., & Ruiz-Salguero, O. (2020). Approximation of the Mechanical Response of Large Lattice Domains Using Homogenization and Design of Experiments. Applied Sciences, 10(11), 3858. https://doi.org/10.3390/app10113858






