1. Introduction
Among the high-performance concrete (HPC) used in structural engineering, high-strength concrete (HSC) has received the most significant attention. The HSC is used in several structural engineering projects and is mostly considered at a compressive strength of >60 MPa due to the benefits it offers [
1]. Despite the lack of a clear difference between HSC and normal-strength concrete (NSC), several approaches and studies have determined varying ranges of compressive strength (CS) for differentiating NSC from HSC [
2]. This study, however, followed the ACI 363R-10, which described HSC as concrete with CS of >40 MPa [
3]. HSC has significant benefits, which have boosted its implementation in construction activity globally. Such advantages include its improved physicomechanical properties such as CS, long-term durability, and stiffness. HSC attracts great interest due to the economic usefulness associated with it as it helps in reducing geometrical sections and gain in structures. Thus, HSC is preferred over NSC for economic, aesthetic, and technical purposes [
4]. Practically, HSC is known to be brittle [
4] as studies have shown sudden cracking and traversing aggregate particles in HSC, which produces fracture planes that are relatively smooth [
5]. As with NSC, these cracks do not cover whole aggregate particles. Concrete shear strength is significantly reduced by smooth fracture surfaces by reducing the aggregate interlock contribution at the shear fracture planes.
For a reinforced concrete (RC) beam without transverse reinforcement, its failure mechanism can be considered as the generation of three internal forces that contribute to shear resistance. These internal forces include the concretes’ contribution in the compression region (
Vc), the shear contribution due to the dowel action of longitudinal rebars (
Vd), and the shear contribution due to the aggregate interlock (
Va). Consequently, the overall shear resistance is the summation of all these internal forces. Components
Va and
Vd are ineffective if the diagonal crack opening is excessive. As a result, all the shear on the section will be on component
Vc, leading to beam collapse as the concrete is crushed in compression [
6].
The shear capacity of beams is mainly influenced by the aggregate interlocking mechanism; thus, the beams’ ultimate load capacity under shear is influenced by this mechanism [
7,
8]. As per [
9],
Va for beams of CS ranging between 26 and 49 MPa accounts for 33% to 50% of the overall shear resistance of such beams. However,
Va seems not to contribute significantly towards shear at higher concrete strengths as evidenced by the smooth fracture planes and straight cracks, which do not cover the whole aggregates as earlier mentioned. Similarly, [
10] suggested taking
Va as zero for concrete with CS of >62 MPa.
Based on the existing literature on RC shear slender beams without web reinforcement, it is evident that no common rational theory exists to explain the collaboration between the three internal forces that contribute to shear resistance, particularly for HSC [
11]. It appears that the precise estimation of shear capacity of HCS slender RC beam in the absence of shear stirrups is an open topic in research communities of structural engineering [
12,
13]. The relationship between the intricate modeling variable has a remarkable influence on the shear capacity of HSC slender beams without stirrups. As such, the regression-based models are not considered ideal for such an application [
14]. The existing stochasticity or nonlinearity in the experimental database initiates a very complex regression problem that needs a sophisticated modeling approach to mimic its actual internal mechanism. Artificial intelligence (AI) models have found wide application in solving different problems in civil engineering due to their interesting features, such as their auto-search and adaptation capability when finding multi-variable interrelationships [
15,
16,
17,
18,
19,
20]. The shear strength (
Ss) problem related to the structural engineering field has been investigated using the feasibility of AI models that have demonstrated positive progress [
8,
21,
22].
Several versions of AI models have been developed for beam
Ss prediction, such as artificial neural network (ANN) [
15,
23,
24,
25], support vector machine (SVM) [
26,
27,
28,
29], evolutionary computing models (ECM) [
30,
31,
32,
33], and adaptive neuro-fuzzy inference system (ANFIS) [
34,
35,
36,
37,
38]. Among all the aforementioned AI models, ANFIS confirmed its potential in modeling beam
Ss mechanisms over the other models. The ANFIS model is characterized by the capability to mimic and capture the associated non-linearity and stochasticity of data time series [
39]. However, the ANFIS model is associated with a major drawback, which is the membership function tuning parameters. Thus, combining the optimization algorithms, which are inspired by the behavior of animals and plants in nature, with a standalone ANFIS model appears as a new alternative model for improving its performances in solving difficult problems [
40,
41]. The hybrid ANFIS model exhibited a noticeable implementation for diverse civil engineering applications [
42,
43,
44]. In the current research, some parameters of the optimization algorithms (e.g., mutation probability) were assigned based on the reported literature review studies, while the appropriate values of those parameters can be obtained using the Taguchi approach [
45]. This study assumes that the prediction modeling is associated with only input variables and model structures uncertainties, while the other uncertainty sources such as measurement errors, data handling, and inadequate sampling were ignored. The modeled dataset was hypothesized to be associated with redundant observations, and thus the dataset was constructed based on two scenarios of non-processed and pre-processed.
The main motivation of this study is to investigate the feasibility of the novel hybrid ANFIS models for modeling high-strength concrete beam Ss. The modeling procedure is involved in several experiments of HSC slender beams. Being that deep beams behave differently compared to the slender beams (owing to size effect), only slender beams were used in this research. The data analysis focused on ascertaining the model validity and establishing its limitations. Before the prediction process, several input combinations were constructed using the related physical properties including the effective depth of beam (d), shear span (a), maximum size of aggregate (ag), compressive strength of concrete (fc), and percentage of tension reinforcement (ρ). The Ss of the HSC slender beams is predicted using two different modeling scenarios based on (i) non-processed (initial) dataset (NP) and (ii) pre-processed dataset (PP) to investigate the impact of the non-homogeneity of the dataset on prediction result accuracy.
3. Results and Discussion
The main focus of this paper is to establish a reliable and robust model based on the ability of different types of hybrid ANFIS approaches to predict the Ss prediction of HSC. The challenges of the mathematical and empirical relations establishing the appropriate relationship between the Ss and HSC properties highlight the intervention of soft computing aids. However, establishing the internal mechanism between the related predictors towards the Ss of HSC has a substantial motive for investigation and examination. Furthermore, robust and reliable models can always construct a precise intelligence-optimizing technology in the field of structural engineering. Thus, the proposal of a new hybrid intelligence model can enhance the reliable contribution to the structure design along with various reinforcement concrete engineering perspectives.
The proposed hybrid intelligence models and the standalone ANFIS models were evaluated based on various performance metrics and graphical presentations, including heat map, scatterplot, boxplot, and Taylor diagrams over the training and testing phase for modeling Ss of HSC. Besides, the new ANFIS models were assessed based on the hybridization algorithms, variables, and data uncertainty.
The performance of classical ANFIS is assessed in both training and testing period for different input combination models (Model 1–18) using RMSE, MAE, LMI, CC, WI, and SRMSE (
Table 2). The input combination of Model 8 (Incorporated:
a,
ag,
fc, and
ρ) appeared to be the most appropriate choice for generating good prediction results over the training and testing stages. The acquired magnitudes of assessing metrics in training and testing are: ANFIS (
RMSE = 0.263, 0.314;
MAE = 0.198, 0.224;
LMI = 0.675, 0.640;
CC = 0.936, 0.920;
WI = 0.966, 0.957;
SRMSE = 15.011, 19.584).
The hybrid ANFIS-ACO model produced the lowest magnitudes of
RMSE,
MAE, SRMSE, and highest
LMI, CC, and
WI values (
RMSE ≈ 0.377, 0.399,
MAE ≈ 0.282,
0.289, SRMSE ≈ 21.563, 24.912) and (
LMI ≈ 0.537, 0.536,
CC ≈ 0.863, 0.870,
WI ≈ 0.921, 0.918) for both training and testing stages, respectively. The best prediction was achieved for the input combination of Model-16 (incorporated:
d,
ρ, a/d, fc). These metrics for other input combination models using ANFIS-ACO can be seen in
Table 3. Likewise, the preciseness of ANFIS-ACO with input combination in Model-16 is considerably good for predicting
Ss (
Table 3).
Table 4 and
Table 5 present the statistical performance accuracy of ANFIS-DE and ANFIS-GA models. The ANFIS-DE with input combination in Model-13 (incorporated:
d,
ρ, a/d, ag/d, fc) performed the reasonable prediction for the
Ss by obtaining (
RMSE = 0.375, 0.398;
MAE = 0.281, 0.291;
LMI = 0.538, 0.533;
CC = 0.865, 0.870;
WI = 0.922, 0.919;
SRMSE = 21.417, 24.838) for both training and testing phases. However, ANFIS-GA with Model-16 (incorporated:
d,
ρ, a/d, fc) achieved highest level of accuracy in accordance the statistical metrics (
RMSE = 0.286, 0.296;
MAE = 0.224, 0.243;
LMI = 0.632, 0.610;
CC = 0.924, 0.930;
WI = 0.959, 0.962;
SRMSE = 16.358, 18.477) (
Table 5).
The best performing hybrid model (i.e., ANFIS-PSO) used input combination Model-7 configured with pre-processed variables (
d, a, ag, fc, and
ρ) (
Table 6). The best inputs combination (i.e., Model-7) was generated good prediction results over both modeling phases with statistical results (
RMSE = 0.206, 0.283;
MAE = 0.157, 0.213;
LMI = 0.742, 0.659;
CC = 0.961, 0.935;
WI = 0.980, 0.965;
SRMSE = 11.791, 17.671).
The uncertainties arise in model, variables, and data are reported in
Table 7 based on the interquartile range (IQR) indices. The assessment metrics attained in investigating model and variable uncertainties are
RMSE = 0.691, 0.403;
MAE = 0.649, 0.424;
LMI = 0.649, 0.424;
CC = 0.687, 0.482;
WI = 0.806, 0.702, and
SRMSE = 0.806, 0.403, respectively. Based on the minimal absolute error metrics (i.e., RMSE, MAE, and SRMSE), the model uncertainty was higher as compared to variable and data uncertainty.
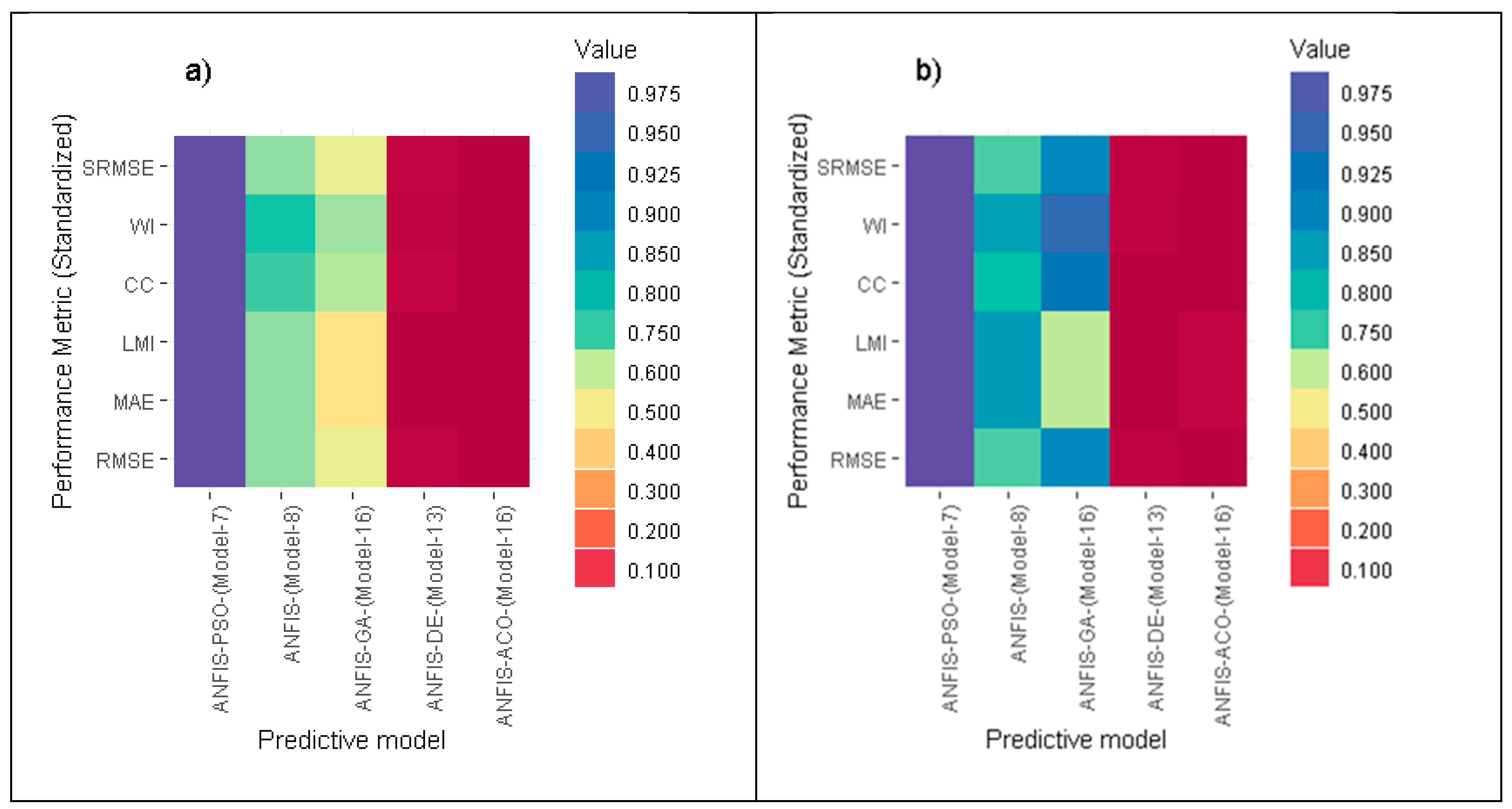
To finalize the best relation between proposed models and the performance metrics, a heat map was created, where this diagram depicts the graphical comparison between models in term of standardized performance indices. It can be seen in
Figure 3 that all the standardized performance indices of ANFIS-PSO (Model-7) have a dark blue color (best performance) in both training and testing phases, while ANFIS-ACO (Model-16) appeared to be the lowest in terms of these performance metrics (dark red color).
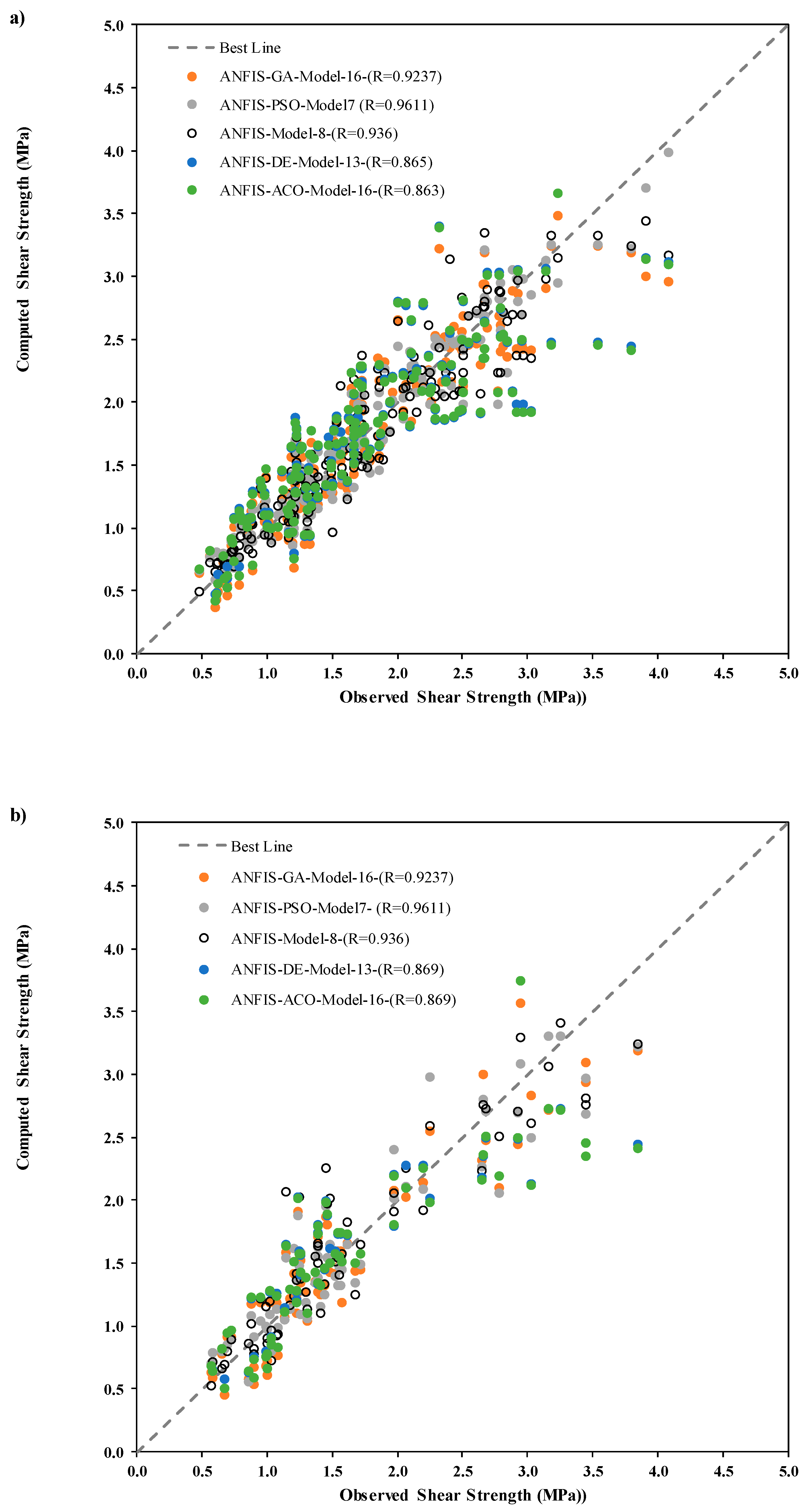
The scatter plots were generated between observed and predicted
Ss for the cases of training and testing phases to strengthen the visualization of the applied model’s performance accuracy with the correlation coefficient (
R) magnitude (
Figure 4). The ANFIS-PSO model was revealed to have better correlation in comparison with the other applied models by achieving higher
R value as follows: (ANFIS-PSO ≈ 0.9611, ANFIS ≈ 0.936, ANFIS-GA ≈ 0.9237, ANFIS-DE ≈ 0.865, ANFIS-ACO ≈ 0.863) in training phase and (ANFIS-PSO ≈ 0.9611, ANFIS ≈ 0.936, ANFIS-GA ≈ 0.9237, ANFIS-DE ≈ 0.869, ANFIS-ACO ≈ 0.869) in the testing phase.
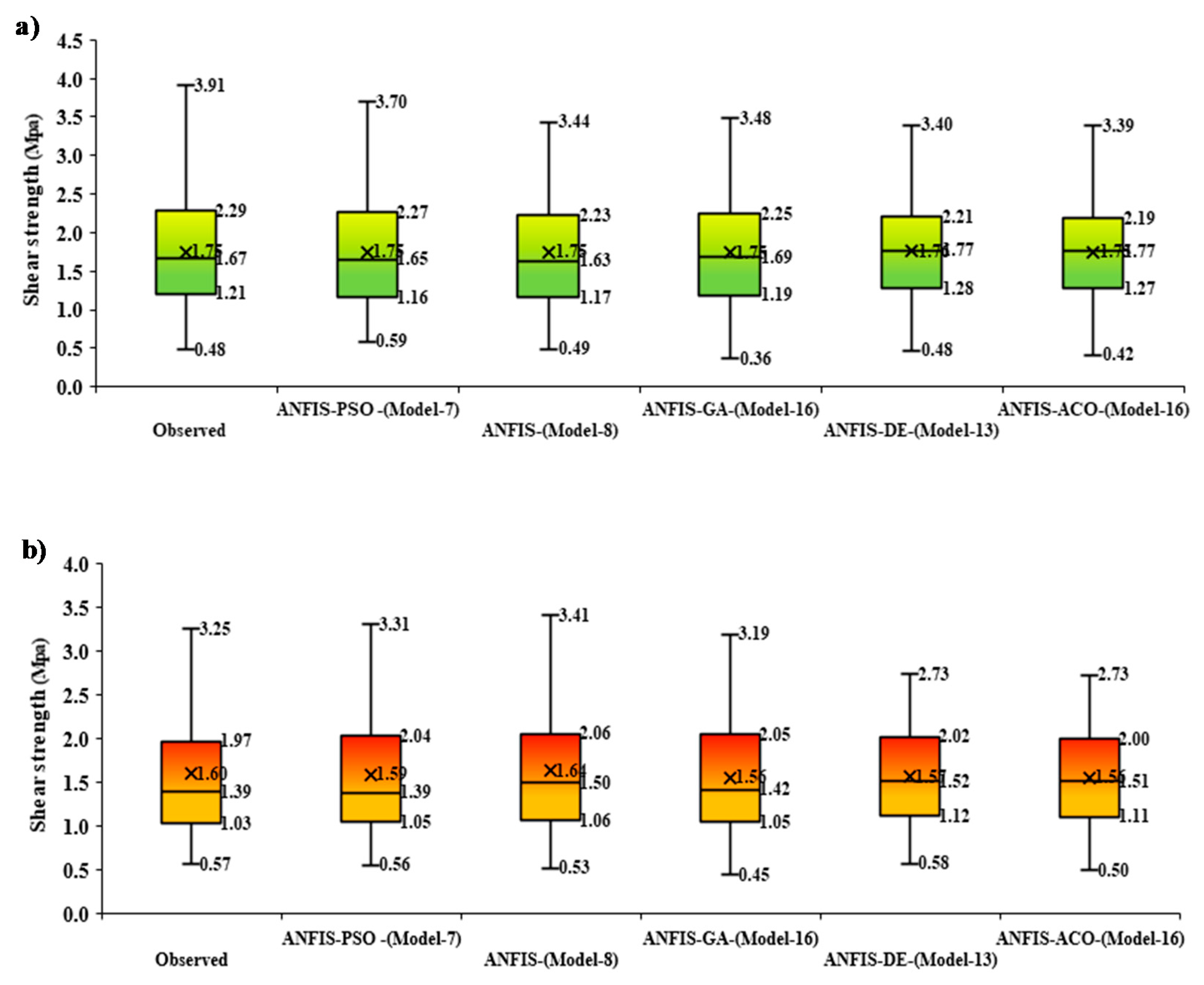
To establish the relationship of the interquartile range (IQR) between observed and predicted
Ss by various proposed models, the boxplots of both training (yellow) and testing (green) phases were displayed in
Figure 5. The distinction of performances is visible since the prediction was generated via ANFIS-PSO (Model-7) against observed (experimental)
Ss, which were significantly accurate in comparison with ANFIS (Model-8), ANFIS-GA (Model-16), ANFIS-DE (Model-13), and ANFIS-ACO (Model-16). Hence, the boxplots, together with the benchmark models against observed
Ss, ascertain the better accuracy of ANFIS-PSO model.
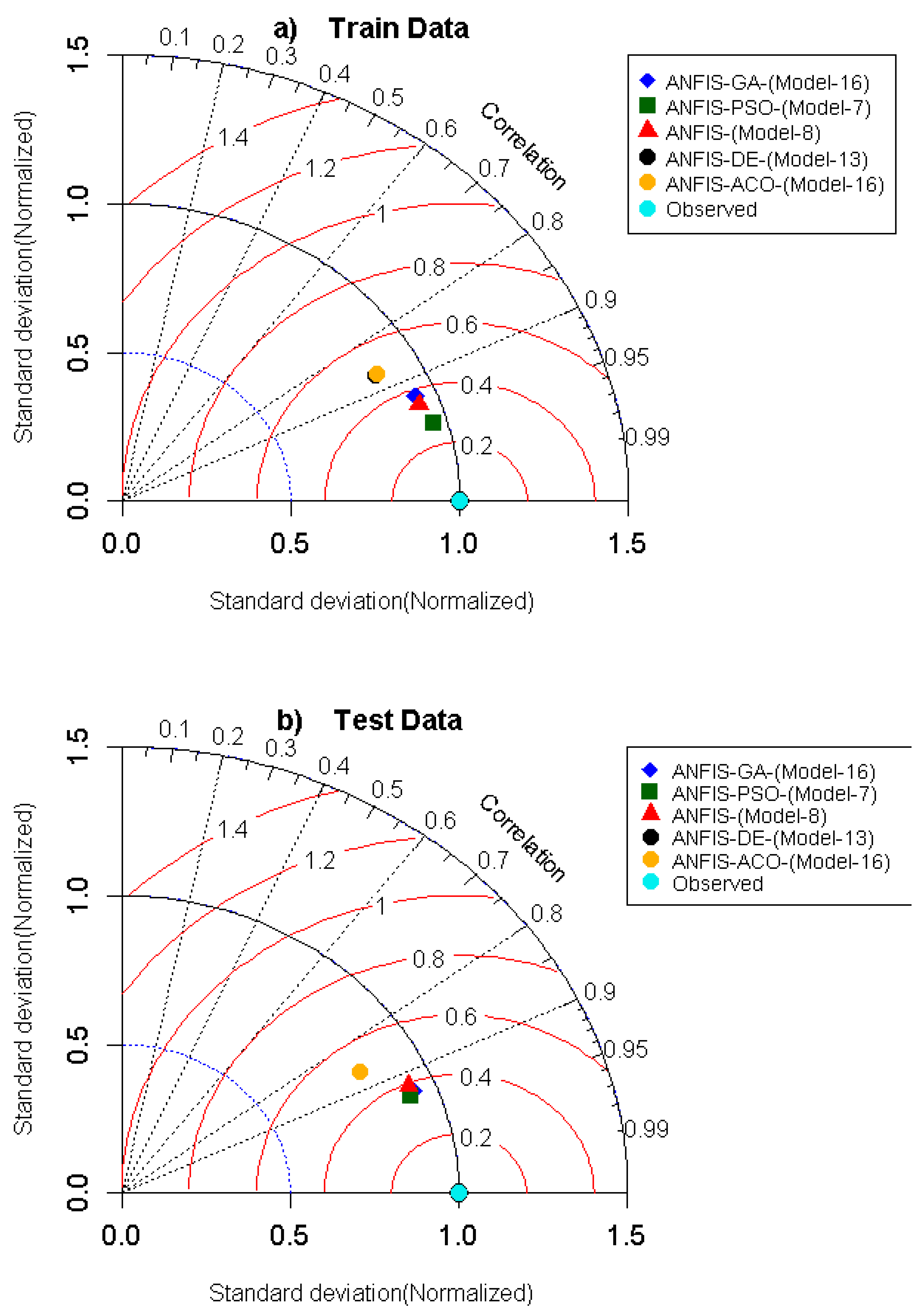
To scale the degree between predicted and experimental
Ss of HSC for all proposed hybrid and standalone ANFIS models, a Taylor diagram was drawn (
Figure 6). The magnitudes of correlation are shown in the form of the Taylor diagram that generates a more detailed appraisal of the model performances [
101] for training and testing phases. The Taylor diagram illustrates a more tangible and convincing statistical relationship between the predicted and observed
Ss depending on correlation with respect to standard deviations. It is seen that the benchmark models ANFIS-DE and ANFIS-ACO are not appropriate in the training session, as the correlation to standard deviation points was highly parted from the ideal observed point as compared to ANFIS-PSO, ANFIS, and ANFIS-GA. The hybrid ANFIS-PSO model lay close to the perfect observed point in the testing phase more closely, followed by ANFIS-GA, ANFIS, ANFI-DE, and ANFIS-ACO models, which confirms that the prediction accuracy of ANFS-PSO was reasonably higher than the benchmark models.
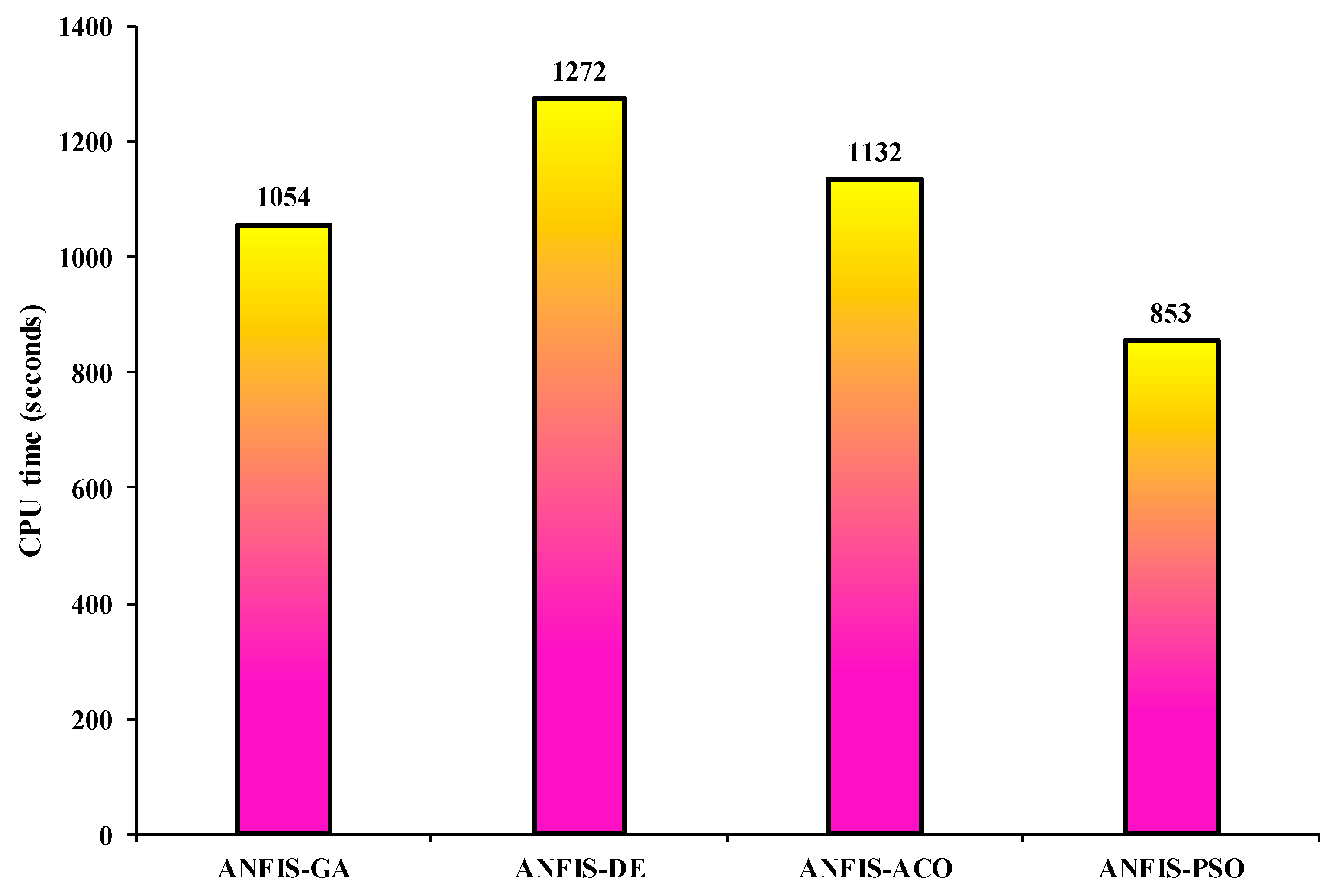
To evaluate the trade-off between the accuracy and efficiency of the newly developed models, their computational time (CPU time) is presented in
Figure 7.
From
Figure 7, it is evident that the lowest CPU time (853.23 s) is observed in ANFIS-PSO, while the ANFIS-DE offers the highest value (1272.06 s). The results confirm that the ANFIS-PSO model provides the highest performance prediction with most top convergence speed in comparison with other hybrid techniques.
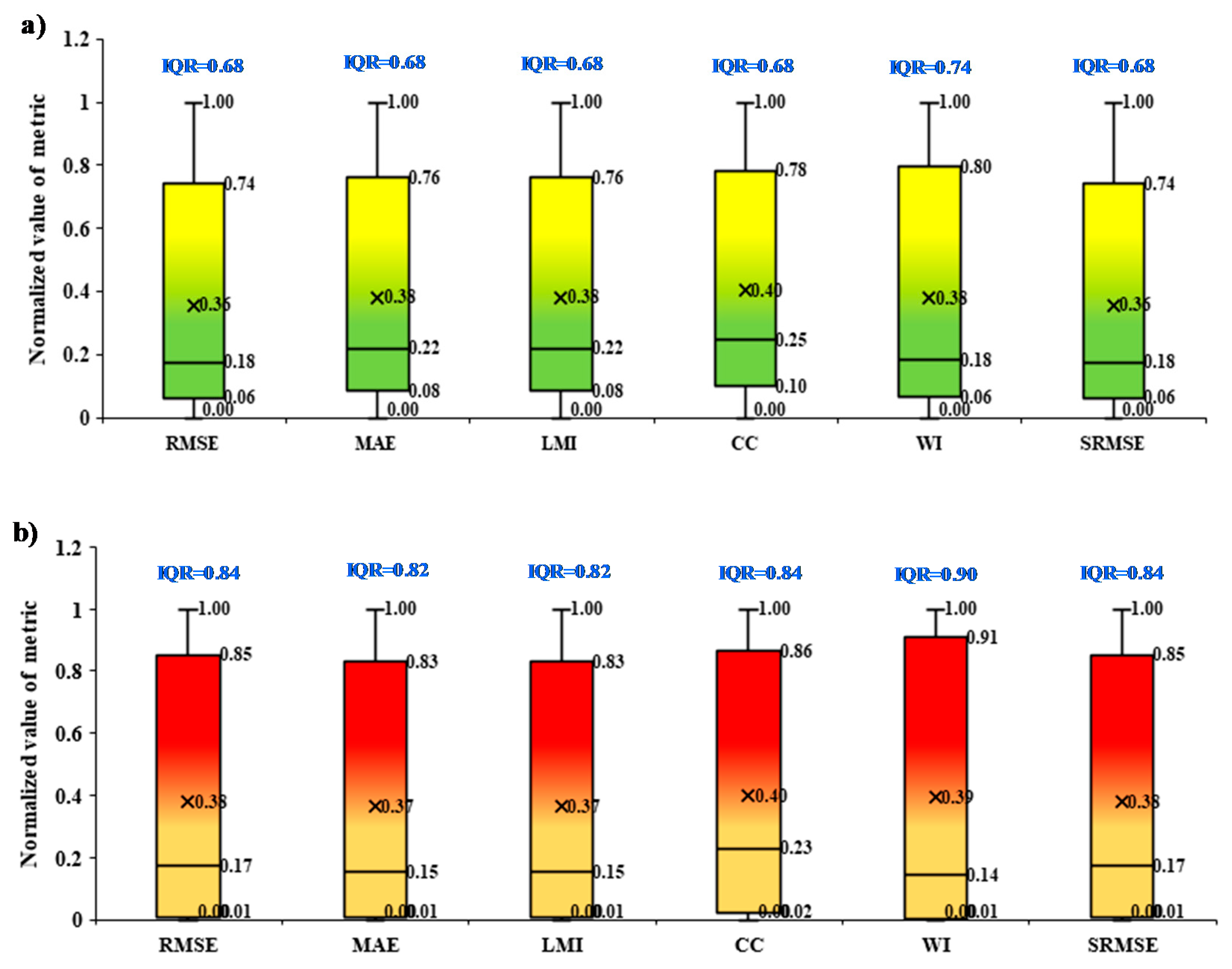
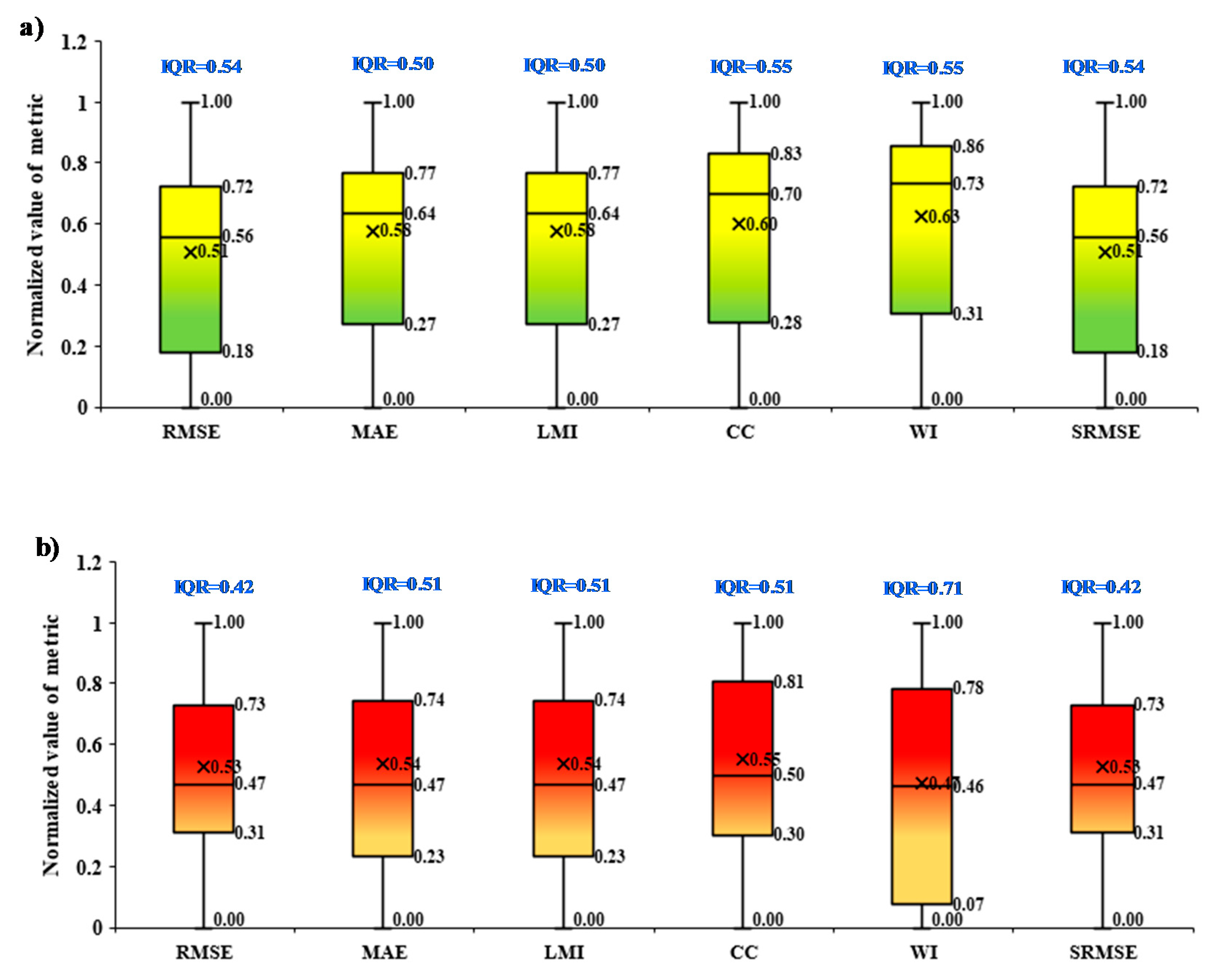
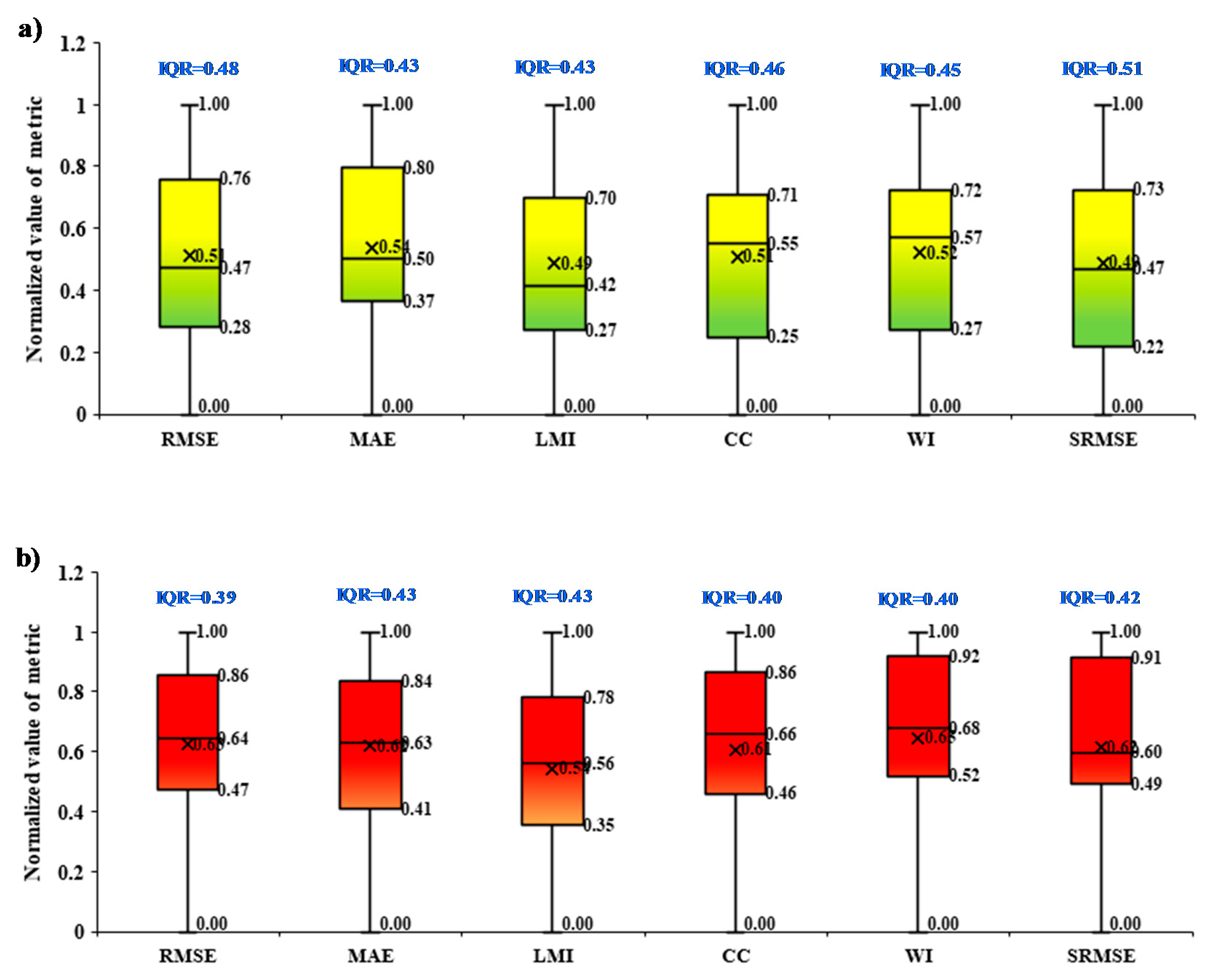
The uncertainties of model, variables, and data were evaluated on the basis of boxplots presentation based on the performance metrics over the training and testing phases at 25%, 50%, and 75% quantile together with IQR (Figured 8, 9, and 10). In the cases of the model’s uncertainty based on performance metrics over the training and testing phases, the majority of the cases revealed a median value towards the 1
st quartile for both training and testing phases (
Figure 8). However, in the case of the training set, all performance metrics exhibited marginal higher redundant than testing phase with the average values of IQR lies at 0.68 and 0.84, respectively. In cases of variable’s uncertainty based on performance metrics over the training and testing phases were exhibited the distinguished characters (
Figure 9); during the training phase, the median value tends towards the 3rd quartile in most of the performance metrics. In contrast, it was mixed, tending towards the 1st quartile (for
RMSE,
CC, and
SRMSE), 2nd quartile (for
MAE and
LMI), and 3rd quartile (for
WI) in the testing phase. In the cases of the data’s uncertainty based on performance metrics over the training and testing phases were presented mixed characteristics such as the median line of boxplot tends towards 1st quartile for
RMSE,
MAE and
LMI, whereas
CC and
WI were opposite towards the 3rd quartile but remained almost in the middle position in case of
SRMSE (
Figure 10). However, the testing phase has demonstrated the stability, which is near the middle for all performance metrics except
WI and
SRMSE, which were towards the 1st quartile.
The aptness of the hybrid and standalone ANFIS models using different input combinations (Model-1, Model-2… Model-18) to predict
Ss was explored in this paper. The accuracy of the hybrid ANFIS-PSO with input combination (Model-7) was reasonably superior to the other models (i.e., ANFIS-ACO, ANFIS-GA, ANFIS-DE, and ANFIS) with different combinations of inputs (
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6), demonstrating that the ANFIS-PSO was a well-designed algorithm to extract pertinent features for
Ss prediction. The precision of ANFIS-PSO with other algorithms revealed that the different input combinations were also advantageous in indicating the pertinent features making the model parsimonious.
Since the fundamental operations of the AI models of machine learning are significantly contingent upon the patterns in historical datasets that can substantially disturb the learning strategy, the results here assured the suitability of input combinations to sort out the best combination capturing minimum pertinent features and characteristics. Prior to the prediction process, several input combinations are constructed using related physical properties. The Ss of the HSC slender beams was predicted using two different modeling scenarios based on (i) non-processed (initial) dataset (NP) (i.e., Model-1, Model-2, …, Model-6) and (ii) pre-processed dataset (PP) (i.e., Model-7, Model-8, …, Model-18). This was to examine the influence of the non-homogeneity of the dataset on model prediction accuracy. Apparently, the PP data were excellent data cleaning prior to the model’s construction. This is due to the fact that some redundant measures associated with some error can influence the learning process, which leads to poor predictability capacity.
Based on the attained modeling results, a couple limitations are observed, which are worth to be highlighted for future research. The investigated computer aid model’s performance can be inspected based on the changes in the type of aggregated consideration and evaluating the weight of the interlock strength of the total shear strength. Besides, this is clear, noting that the impact of high strength beam was reported successfully. However, the impact of normal beam shear strength could be a prospective objective. Further, the lateral stability of the slender beam can be investigated, which is totally dependent upon the data availability of the experiments.