Optical Birefringence Growth Driven by Magnetic Field in Liquids: The Case of Dibutyl Phosphate/Propylamine System

Abstract

Magnetically-induced birefringence is usually low in molecular liquids owing to the low magnetic energy of molecules with respect to the thermal one. Despite this, it has been found that a mixture of dibutyl phosphate and propylamine at propylamine molar ratio (X) around 0.33 surprisingly gives an intense effect (∆n/λ ≈ −0.1 at 1 Tesla). In this paper the time- and intensity- response to the magnetic field of such mixture have been studied. It was found that the reaction to the magnetic field is unusually slow (from several minutes to hours) depending of the magnetic field intensity. On the basis of the data, the model of orientable dipoles dispersed in a matrix enables to interpret the magnetic field-induced self-assembly in terms of soft molecules-based nanostructures. The analogy with systems made of magnetically polarizable (solid or soft) particles dispersed in liquid carrier allows understanding, at the microscopic scale, the molecular origin and the supra-molecular dynamics involved in the observed behavior. The data present a novel phenomenon in liquid phase where the progressive building up/change of ordered and strongly interacting amphiphiles is driven by the magnetic field.

1. Introduction

Simple liquids usually respond to external magnetic fields quite quickly thanks to the fast molecular orientational dynamics taking place in timescales of the order of nanoseconds. Despite the fast molecular dynamics occurring in simple liquids, the orientational order generated by the magnetic field is usually low at room temperature since the thermal energy surpasses the magnetic energy of individual molecule. For these reasons fast response and relatively low value of magnetically induced optical birefringence are usually observed in simple molecular liquids.

From the technological point of view, only highly optically anisotropic molecules/particles (e.g., liquid crystals) can be exploited in order to induce a significant birefringence. This puts very restricting limitations on system behavior and the possible applications.

This work follows recent investigations in surfactant-based complex systems [1] highlighting that a lot of unexpected and intriguing emerging properties arise when two neat liquid amphiphiles are mixed. The resulting surfactant-based liquid mixtures can exhibit local intermolecular self-assembly [2,3], enhanced proton conductivity [4,5], one-dimensional (1D) anomalous proton diffusion [6], peculiar solubilizing properties towards inorganic salts [7,8,9] or functional molecules [10] and anti-Arrhenian behavior of conductivity [11]. In some cases, even ionic liquids are produced [12]. In this ambit, not only these diversified properties promote their use in several research fields, for example as amphiphile self-assembly reaction media [13,14] or reaction catalyst in organic synthesis [15,16], as a solvent phase in microemulsions and emulsions or in the emerging field of nanostructured inorganic materials synthesis [17], but a peculiarly intriguing property deserving attention is the optical birefringence arising as a response to an external magnetic field [18].

It has been shown that mixing specific amounts of dibutyl phosphate and propylamine, which themselves are diamagnetic molecules and have very low intrinsic anisotropy, results in a system with an unusual response to external magnetic fields [19]. Unlike the generally fast response and low induced birefringence expected for molecular liquids and their mixtures, an extremely slow response has been observed, with an induced birefringence significantly higher than that observed for mixtures of simple molecular liquids of anisotropic molecules [20]. Significant birefringence is, in fact, more often observed in dispersions of highly magnetic minerals [21].

The origin of this feature yields on the opportune choice of amphiphiles: if one is basic (for example a short alkyl chain alkylamine) and the other is acidic (for example protic alkyl phosphate), then the direct acid-base interaction can give a strong H bond or a neat proton transfer, resulting anyway in a molecular pair which is inherently anisotropic. These pairs, although dynamical in nature, can further self-assemble into larger super-molecular aggregates whose net magnetic energy exceeds the thermal energy making them magnetically susceptible. For amphiphile binary systems, this process involves all the molecules present in the systems, which are all interacting with each other making the system dense, viscous and structurally and dynamically complex. Here, the system cannot be imagined as a dispersion of individual and spatially separated anisotropic entities in a uniform and magnetically neutral liquid matrix, but rather a somehow percolated structure of molecules subjected to steric hindrance, polar-polar, polar-apolar, van der Waals and magnetic interactions.

The present work aims at shedding light in this phenomenon by studying the response of dibutyl phosphate (DBP)/propylamine (PA) binary mixture against an applied magnetic field as a function of time and of magnetic field intensity. The intriguing data will be modeled and interpreted from the molecular basis.

2. Experimental Part

2.1. Materials

Dibutyl phosphate (DBP, Aldrich > 99.5%) and n-propylamine (PA, Aldrich 99%) were used as received.

2.2. Method

2.2.1. Sample Preparation

DBP/PA mixtures were prepared by weight at compositions expressed as amine molar fraction (X).

Mixing PA and DBP causes release of a considerable amount of heat, which can be taken as a first clue of the occurrence of the exothermic acid-base reaction. Please note that, given the low boiling point of PA (about 49 °C), opportune precautions must be taken (slow addition, gentle mixing, cooling steps, closed vials). Please also note that although the acid-base reaction can be considered complete in a short time (stirring + diffusion), due to the viscosity of the resulting mixture the precaution of storing overnight the mixture in sealed vial prior to the measurements was adopted. The mixtures are optically clear and colorless. If checked under polarizing microscope they do not show sign of any Schliren patterns. In the light of these observations, the samples do not show any (observable) sign of liquid-crystallinity.

The structure and dynamics of such mixtures were reported in a recent paper [12].

In order to check if any large structures exist in studied mixture the sample was tested with Dynamic Light Scattering (DLS) technique (see Figure S1 in Supplementary Material). The analysis is reported in supplementary material and shows that the scattering signal is compatible with the presence of 1.4 μm sized particles. However, it should be remembered that our system is not a dilute dispersion of rigid particles in some carrier liquid of known viscosity for which Stokes-Einstein relation was derived. In our systems any structure is, instead, soft with a dynamical nature of size and shape. The diffusion found concerns rather the dynamics of local phase-separation/self-segregation process and relates to movements of the boundaries (walls) of the aggregates.

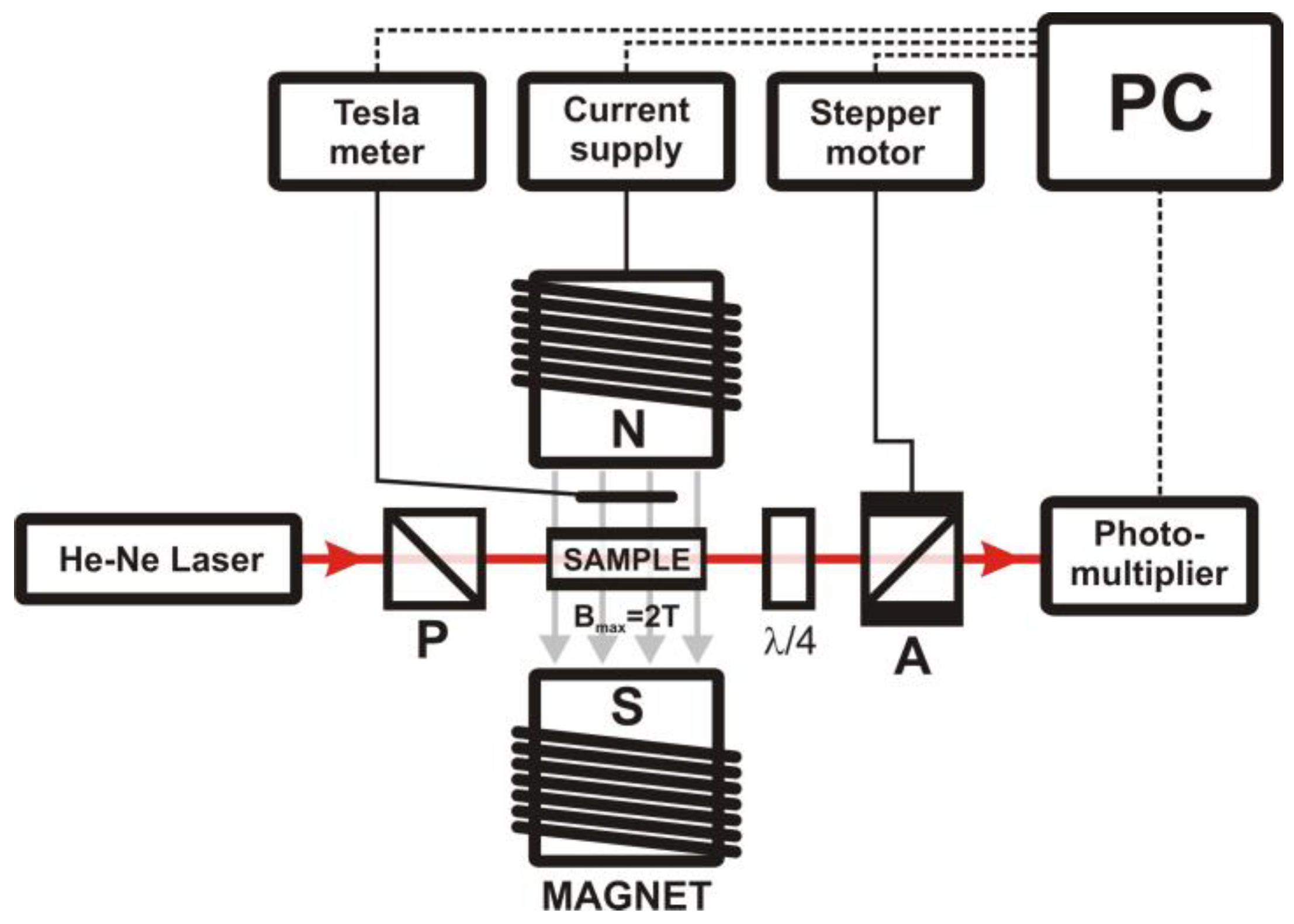
2.2.2. Measurement of Magnetically-Induced Optical Birefringence

Optical linear birefringence was measured using a laboratory made polarimeter set-up depicted schematically in Scheme 1. The details are reported in ref [22]. Briefly, the sample was held in a glass cell between poles of iron-core electromagnet (B ≤ 2 T, length of the cell 130 mm). Magnetic field induction was measured by a teslameter placed in the middle of the optical path. The magnetic field intensity distribution along the optical path was uniform (within 1.5%) except for the very ends of the poles (5 mm from each side). The probe light from He–Ne laser (λ = 632.8 nm) was firstly linearly polarized by high quality Glan–Thompson polariser (P) whose transmission axis was oriented at 45° azimuth angle with respect to the magnetic field direction. After turning the magnetic field on, the sample becomes axially anisotropic and thus birefringent. Consequently, light beam passing through the sample changes its polarization state from linear into the elliptical one. The role of the quarter-wave plate (λ/4) is to restore the linear polarization state. For this purpose, its optical axis is oriented along the azimuth angle of polarizer P. In such an arrangement, any polarization ellipticity (being the signature of birefringence) is converted into the rotation of the plane of polarization. To find the angle of rotation, α, the light is passed through another linear polarizer, working as an analyzer (A). The angle α is found from the position of the analyzer for which light intensity reaching the photomultiplier is at its minimum. The value of induced birefringence can be easily calculated from the measured value of α:

$$\Delta n=\alpha \frac{\lambda }{\pi L}$$

(1)

For a given laser wavelength, the uncertainty of ∆n measurement depends on the optical path L and precision of estimation of angle α. For our system where L = 0.13 m and ∆α = ±2 × 10⁻⁵ rad, uncertainty of ∆n is estimated to be about ±10⁻¹⁰.

All measurements were performed at a constant temperature of 25 °C.

It must be noted that, during the experiments, the liquid was kept in a sealed cuvette and the whole of its volume was exposed to uniform magnetic field. No liquid could flow in or out of the cell. For this reason, any anisotropy generated by directional flow or liquid shearing can be disregarded.

3. Theoretical Background

This paragraph will be devoted to furnish the basic (and naïve) description of the arising of birefringence after the application of a magnetic field (magnetically-induced birefringence). This information will be of help in better understanding the results of this work and their final modelling.

3.1. Magnetically Induced Birefringence in Liquids

Optical birefringence appears when the optical property (refractive index) of the system is different along different spatial directions. Unlike in solids, where this property is often inherent and given by stable atomic structure, in liquid systems induction of preferred orientation of molecules is required. Such preferential orientation is usually achieved by application of external physical fields (electric, magnetic, shear, etc.) [23,24]. In addition, the molecules need to be optically anisotropic, meaning that their high-frequency electronic properties depend on the molecule coordinate system (optical polarizability tensor is not symmetric). In the case of magnetically induced birefringence, the preferential orientation of molecules is triggered by the imposition of an external magnetic field. In this case, the energy of the magnetic dipole in the external magnetic field will be minimized when the direction of the dipole and the field coincide. This results in a torque acting on a dipole trying to orient it along the external field direction. Perfect orientation is always impeded by thermal motions and the degree of equilibrium orientational order is given by the ratio of magnetic to thermal energy of the system. If such an orientational process is applied to all dipolar and optically anisotropic molecules of the liquid system, it will translate to its macroscopic optical anisotropy, and thus make it birefringent.

3.2. Magnetically Induced Birefringence in Absence of Permanent Magnetic Dipoles

Many molecular liquids are diamagnetic and do not possess a permanent dipole moment. In such a case, the dipole moment can always be induced by the field itself through interaction of the field with the tensor magnetic susceptibility (magnetic polarizability) of the particle.

In this case, the magnetic susceptibility must be anisotropic. Otherwise, the direction of the induced dipole will always coincide with the direction of the field and no torque will be acting on such molecule. As a result, no induced orientation will be observed. On the contrary, if the magnetic susceptibility is anisotropic, the direction of induced dipole will depend on the orientation of the molecule and the molecules will be forced to orient its direction of highest magnetic susceptibility along the magnetic field. Although the mathematical description of the interaction between induced dipole with its parent magnetic field is more complex, the phenomenological description of the orientational mechanism is the same as this given in a section above.

3.3. Sign of Induced Birefringence

The sign of the induced birefringence (negative or positive) depends on which direction refractive index of the sample is higher (along or perpendicular to magnetic field direction). From the molecular description, this is given by the relative orientations of magnetic and electric susceptibility (polarizability) ellipsoids. By convention, if the direction of the highest magnetic polarizability coincides with direction of highest electric polarizability, the induced birefringence is positive [25].

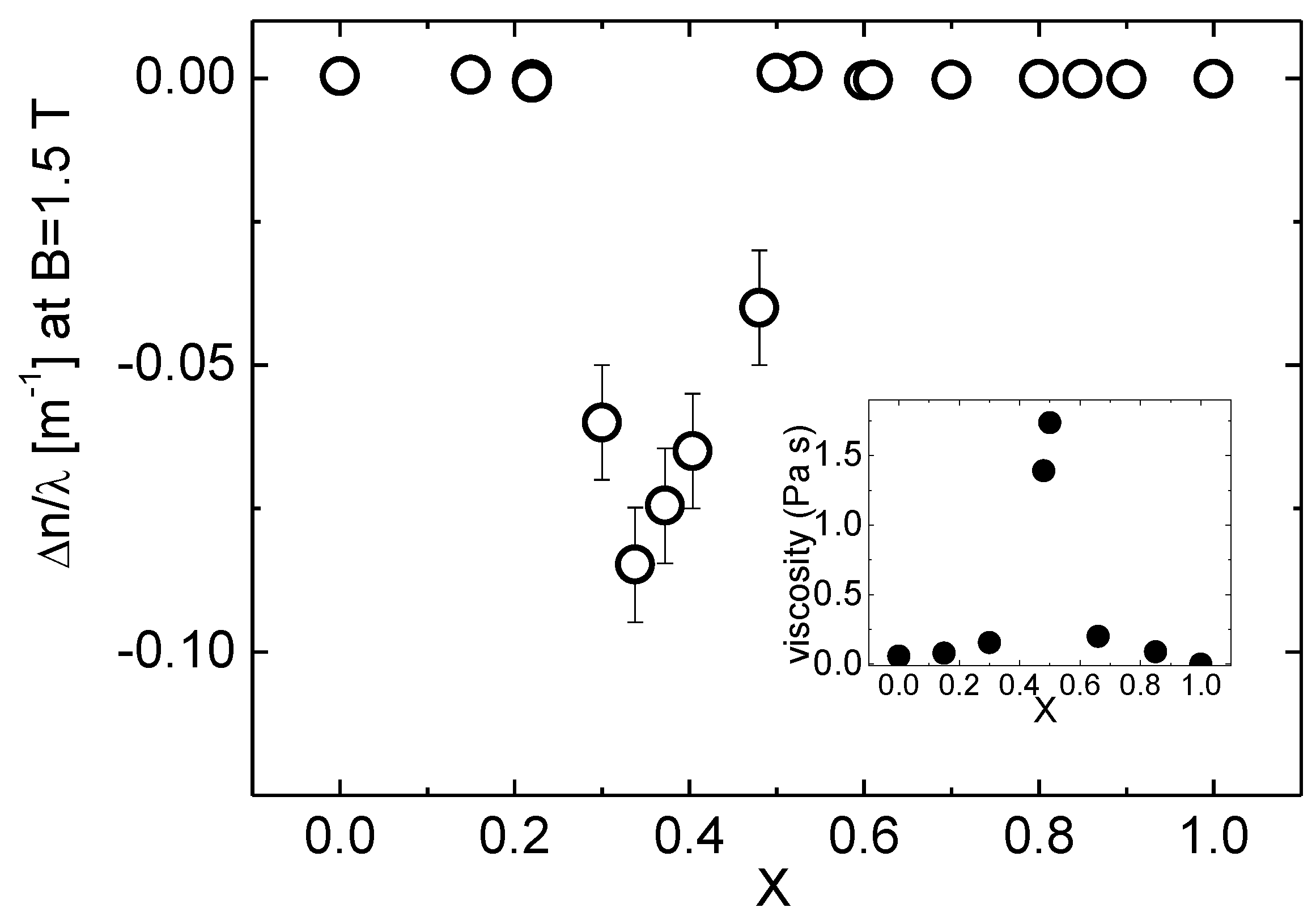
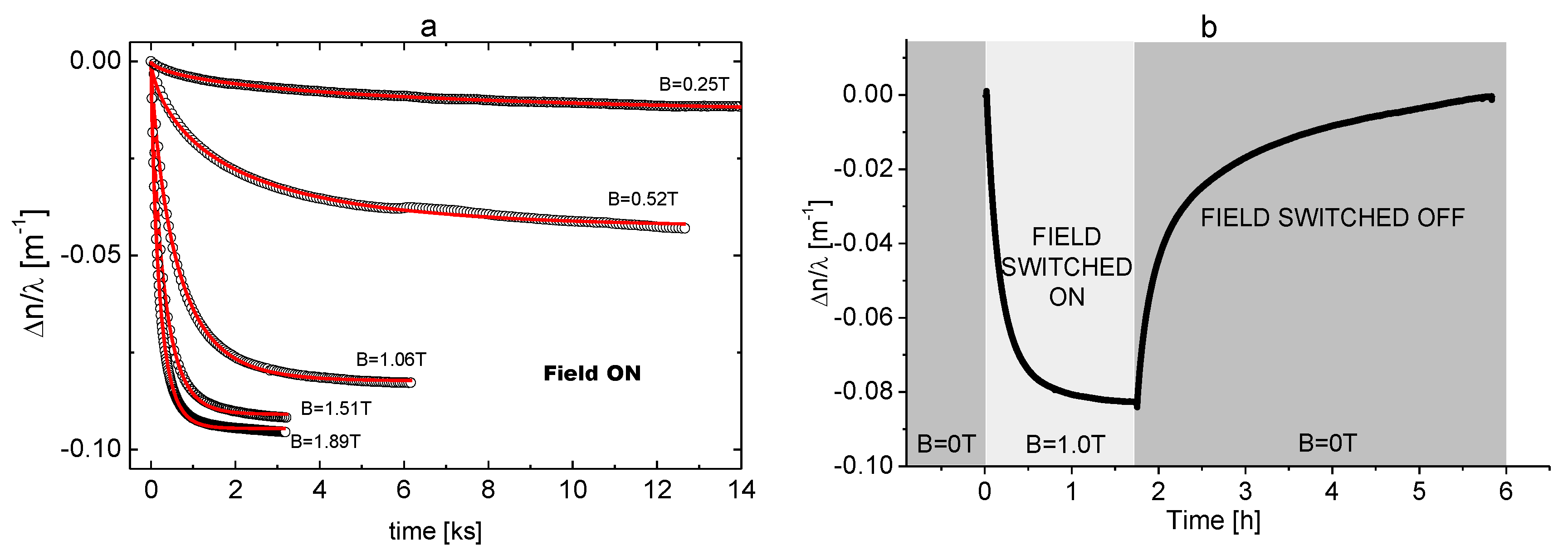
4. Results

Figure 1 shows the maximum of the magnetically induced birefringence recorded at equilibrium conditions (long times) at a magnetic induction of 1.5 T as a function of the PA molar ratio (X). It can be seen that only a restricted region of composition i.e., in the range 0.3 < X < 0.5 a significant effect is present. It must be noted that the composition at which the birefringence shows its maximum is different to that at which the viscosity has its maximum. The birefringence taking place at X = 0.33 has been then measured as a function of time and as a function of magnetic field strength. This has been reported in Figure 2a. It can be noticed that the saturation value of induced birefringence, as well as the time necessary to reach the saturation condition, depend on the magnetic field induction.

Additionally, the trend of induced birefringence has been tailored after the field has been switched off, as schematically shown in Figure 2b, which shows the behavior after steeply switching the field at 1 T on and off. Interestingly, when the field is switched on and off, the system response takes different times, and this happens for all the magnetic field explored. It was found that this phenomenon is reversible, independently of the history of the sample.

In order to quantify these observations, we described the time dependence of induced birefringence by a stretched exponential function:

$$\left(\frac{\Delta n}{\lambda }\right)={\left(\frac{\Delta n}{\lambda }\right)}_{MAX}\cdot \left(1-e^{-{\left(\frac{t}{\tau }\right)}^{\beta }}\right)\mathrm{for}\mathrm{field}\mathrm{ON}$$

(2)

$$\left(\frac{\Delta n}{\lambda }\right)={\left(\frac{\Delta n}{\lambda }\right)}_{MAX}{e}^{-{\left(\frac{t}{\tau }\right)}^{\beta }}\mathrm{for}\mathrm{field}\mathrm{OFF}$$

(3)

where (∆n/λ)_MAX is the amplitude of induced birefringence normalized to wavelength of probing light λ, τ is the characteristic equilibration/relaxation time and β describes stretching of the relaxation time distribution. Stretched exponential functions have been chosen since simple exponential functions did not give adequate description of the experimental data. The fitting was satisfactory, as can be seen by comparing the red lines (fitting curves) and the experimental points (black open circles) in Figure 2a.

The fitting parameters, i.e., the time constant τ, the stretching of the relaxation time distribution β and the amplitude of induced birefringence normalized to wavelength (∆n/λ)_MAX, have been derived and reported in Figure 3 as a function of magnetic induction, both for switching the magnetic field on (full symbols) and off (open symbols).

As can be seen from Figure 3a, after the liquid mixture is exposed to the external magnetic field, the time needed to reach the stationary birefringence conditions decreases with increasing the magnetic induction value. On the other hand, the return to the equilibrium (after the magnetic field has been turned off) is almost independent of the magnetic field value. In other words, return to equilibrium takes the same amount of time (within the limit of accuracy) independently of the history of the sample.

As can be seen from Figure 3b, similarly to the characteristic relaxation times, their distributions also depend on whether the magnetic field was turned on or tuned off. After turning the external field on, the organization process is characterized by narrower distribution and the β value approaches 1 when the magnetic induction increases. On the other hand, return to equilibrium after turning the magnetic field off is always characterized by broad distribution with no particular dependence on the initial magnetic induction value.

Finally, as can be seen from Figure 3c, the amplitude of the induced birefringence (the value expected to be reached after infinite time of waiting after the field has been turned on or off) increases rapidly for moderate magnetic inductions and tends to saturate at higher value of B (close to 2 T in the present case).

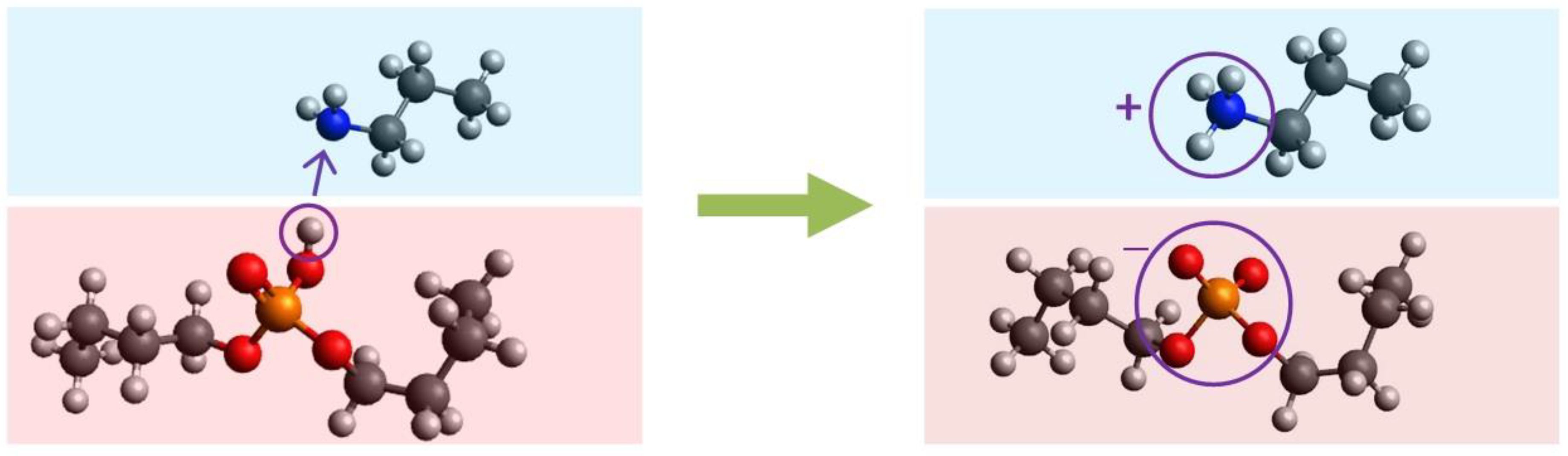
5. Discussion

5.1. Data

The very first comment must focus on the composition dependence of the induced birefringence (Figure 1).

An influence of binary mixture composition on the dependence of induced birefringence composition is expected. It was shown before [20], that already in weakly interacting liquid mixtures, measured birefringence slightly deviates from simplest additive behavior (maximum deviation in ∆n/λ at 1.5 T is about −4 × 10⁻⁴ m⁻¹ for equimolar composition). This can be rationalized by formation of statistical binary molecular pairs. In this respect, the induced birefringence observed for currently studied amphiphile mixture behaves much differently. Instead of smooth composition dependence of ∆n/λ, a distinct increase in a relatively small composition range is observed. More importantly, the magnitude of the birefringence in this range reaches the value of 0.1 m⁻¹, being about three orders of magnitude higher than for simple mixtures. As the effect is observed in mixture of molecules characterized with small optical anisotropy, this proves that the effect does not come from orientation of individual molecules. In this limited composition range, molecules have to be organized in supra-molecular structures. The negative sign of induced birefringence indicates that the direction of the highest magnetic polarizability is perpendicular with the direction of the highest electric polarizability.

The fact that induced birefringence takes place only in a restricted interval of composition suggests a specific DBP/PA ratio at which the effect is maximized. The strongest effect takes place around X = 0.33, which means that the DBP-to-PA ratio is 2:1. It must be noted that this composition is different to that at which the viscosity has its maximum (see inset of Figure 1, with the viscosity data taken from Reference [12]). This observation is important, since it suggests that the birefringence and viscosity increase are related to different phenomena. Whereas viscosity increase is due to the generation of charged species as a result of the DBP-to-PA proton migration and formation of ionic liquid (see Scheme 2), the birefringence must be ascribed to something else. At X = 0.33, in fact, (i) the system can be described as DBP-PA ionic liquids dissolved in the excess of DBP [12]. It can be argued that at this composition, the excess DBP, which is, however, capable of forming H-bonds, can establish strong and directional H-bonds with the charged species of protonated PA and deprotonated DBP. This would further increase the local anisotropy helping the building up of bigger aggregates (see later). A comparison with the magnetically induced birefringence shown by dibutylphosphate/bis (2-ethylhexyl) amine [18], i.e., where the amine molecular architecture is bigger having two branched alkyl tails (instead of a single and short one as in the case of PA), can be useful. In that mixture, the magnitude of the induced birefringence is even higher (|∆n/λ| > 0.8) and occurs at a different composition (amine molar ratio of 0.7). This means that the alkyl chain size/length can play a pivotal role in determining this effect, highlighting the complexity of the scenario of all the interactions involved in the magnetically-induced intermolecular assembly in surfactant-based liquid mixtures.

Another interesting observation regards the time evolution of the system after the field is switched on (see Figure 3a): the process is very slow (hours), strikingly slower than expected from typical molecular rotational diffusion. This is itself worth of note, since the response to a magnetic field is typically fast even in solutions of big molecules such as peptides [26]. However, in some applications where magnetic birefringence was used for in situ monitoring of the morphological changes in diamagnetic polymersomes during shape-transformation by dialysis [27], the process was also found to proceed over long time, suggesting that the response is the overall results of complex interplay between molecular size and the inter-molecular interactions involved.

Therefore, molecular reorientation is expected to be coupled to a self-assembly process triggered by the magnetic field. It is worth noticing that it can be assisted, in turn, by the peculiar orientation itself that the molecules adopt in presence of magnetic field. The slow increase of magnetic birefringence with time must result therefore from the building up of bigger and bigger structures together with, in principle, change in their shape and orientation along the magnetic field. Therefore, the system can be described in terms of orientable magnetic dipoles dispersed in a matrix where magnetic properties appear from the interaction with magnetic field as a consequence of the magnetically-induced formation/deformation of soft molecules-based nanoparticles. In this process, the local viscosity, the slowing down the molecular diffusion, the strength of the interactions and the accessibility of the molecular domains involved influence the kinetics of the process. Taking into account the very short timescale in diffusion limited phenomena, the observed timescale can be the consequence of a complex mechanism where statistically improbable molecular moves are needed at each step for the structure to be built.

On the other hand, the destruction of the assembled structures by thermal agitation when the field is switched off turns out to be even less probable as shown by the higher τ value. This can be the consequence of the fact that (i) inter-molecular interactions within the supramolecular aggregate built up by the external magnetic field are quite strong and that (ii) significant long range correlation exists between the orientations of all the supramolecular aggregates. It can be argued the even the local viscosity cannot be the same as the bulk one. The data suggest that it is particularly high due to the presence of the structures themselves. Earlier translational diffusion measurement taken on the similar system [18] indicated that local molecular motions are somehow influenced by the structural complexity of the system. However, measured values of diffusivities cannot explain the drastically slow kinetics observed after external magnetic field was turned off. Therefore, it is more probable that the molecules forming an aggregate can easily exchange (with its usual fast rate). During this process, however, the shape and size of the super-aggregate is barely influenced.

As can be seen from Figure 3b, the behavior of β is in accordance with that of τ, with a different trend if the field is switched on or off. β is related to the distribution in relaxation times (higher β equals narrower distribution of τ), which, in turn, can be connected with distribution in aggregate size/shape/composition. When the external field is switched on, the observed β is higher (narrower distribution of τ) than that observed when the field is switched off. This shows that the field is an ordering external stimulus also towards the polydispersity of relaxors. This is also confirmed by the trend of β value as a function of field intensity, since it is increasing with the field and approaches a value of 1 when describing single exponential dynamics. On the other hand, return to equilibrium after turning the magnetic field off is always characterized by broad distribution with no particular dependence on the initial magnetic induction value, as a consequence of the system inherent polydispersity and lack of magnetic field ordering.

As follows from Figure 3a–c, (∆n/λ)_max and τ are all correlated: the higher the field, the higher the induced birefringence, the short is the time needed to reach the final equilibrium as a consequence of the stronger magnetic driving force. The facts that (i) in Figure 2b the signal returns to zero values when the field is switched off and (ii) in Figure 3c the points collected after the switching on (solid symbols) and off (open symbols) almost coincide within the experimental error, are indications of absence of signal drift and constancy of baseline.

The trend of (∆n/λ)_max as a function of magnetic field is even more interesting. In addition to a reasonable monotonic increase as a function of B, the trend shows saturation for high B values. This suggests that there is a limit of induced directional ordering that can be achieved with a relatively weak magnetic field. The obtained sigmoidal shape is qualitatively similar to that often observed in liquid dispersions where induced birefringence results from particles being oriented with their magnetic dipole along the field direction [21,22,23,24,28].

Below, we will model the dependence presented in Figure 3c, assuming that our system behaves like a liquid dispersion of dipolar particles.

5.2. Modeling

The behavior of observed birefringence in Figure 3c resembles what is observed in dispersions of magnetic particles [21,25,29]. The usual explanation assumes that the system under investigation consists of individual optically anisotropic particles (both solid [22,30,31] or soft [25,27,28,32,33]) dispersed in a liquid carrier.

Assuming that particles are diamagnetic (no permanent dipole moment), when the system is exposed to external magnetic field, the magnetic dipole is induced in the particles. Since particles are magnetically anisotropic, each dipole direction does not coincide with the direction of external field. Consequently, a torque (resulting from the interaction between induced magnetic dipole and the external magnetic field) on the particles arises and the particles are induced to orient along the magnetic field. Since each particle is optically anisotropic, the dispersion as a whole becomes optically anisotropic and so birefringent.

It must be noticed that some similarities between the model and the system object of this work are present: acid-base adducts are inherently anisotropic due to the directional H-bond or the direction of DBP-to-PA proton transfer in the case of ion pairs. In addition, these structures are in liquid phase. The principle is schematically depicted in Scheme 2.

As a result of this similarity the theory from dispersion of magnetic particles can be borrowed to be applied to the present data. Here, the dimensionless magnetic energy, U, for a system composed of magnetically anisotropic objects (described by anisotropy in magnetic susceptibility (∆χ)) placed in the external magnetic field of induction B, can be defined:

$$U=\frac{\Delta \chi }{2k_{B}T}{B}^2$$

(4)

where k_B is Boltzmann constant and T is the temperature. The knowledge of the magnetic energy U allows calculating the average orientation of the anisotropic particles with respect to the external magnetic field. This is formally given by the value of the orientational order parameter S:

$$S=\frac{1}{2}\left(3\langle {\cos }^2(\theta )\rangle -1\right)$$

(5)

The average square of cosine of the orientation angle θ, < cos² (θ) >, can be calculated from:

$$\langle {\cos }^2(\theta )\rangle =-\frac{1}{2U}+\frac{e^U}{\sqrt{\pi U}merf(\sqrt{U})}$$

(6)

where merf stands for modified error function.

Finally, birefringence dependence of magnetic field can be calculated from:

$$\Delta n/\lambda ={(\Delta n/\lambda )}_{MAX}S$$

(7)

where (∆n/λ)_MAX is saturation birefringence observed for high magnetic energies and is proportional to the anisotropy in optical polarizability, ∆α, of the individual objects.

The fit with Equation 7 to experimental data is shown on Figure 3c as a continuous line. The data are satisfactorily reproduced. There are obvious differences between our system and the ordinary dispersion for which the model was developed; specifically, (i) in our system, no individual particle exists and (ii) separate micellar objects are not expected but, rather, only loosely connected self-aggregated aggregates can be imagined. Despite of these differences, the model seems to also possess some descriptive ability for such systems. It is surprising how well the model derived for simple liquid dispersion describes the behavior of our DPB/PA system even if it obviously does not fulfill the assumptions. This, in conclusion, suggests that the fact that acid-base adducts can be considered inherently anisotropic (due to the directional H-bond or the direction of DBP-to-PA proton transfer in the case of ion pairs) and dispersed in liquid phase, allows the magnetically-induced formation of structures, which can be, therefore, described as magnetically-deformable soft nanoparticles.

6. Perspectives

To the best of our knowledge, there is no theoretical description of magnetically induced birefringence in soft, dynamical, self-aggregated inter-penetrable (high concentration) structures. The fact that the behavior of complex system resembles that of the simple one may be of help during the development of the proper description. The present data have shown the need of clarifying whether the structures are intrinsically anisotropic or the anisotropy appears as a result of the change of structure shape as a result, in turn, of the action of magnetic field. It would be interesting to understand whether a magnetic field could induce a liquid crystalline state. To answer this question, deeper and ad hoc investigations are needed, such as specific microscopies. In this ambit, scattering experiments, both X-ray and neutron, have proven to be unique in acquiring detailed structural information not only of local intermolecular assemblies [34] but also in complex systems [35,36], which can be the starting point to mimic biological systems [37,38] where the interactions between amphiphilic molecules/aggregates and bio-structures can produce bioactivity effects [39,40,41,42]. In our systems, the existence of stable supra-molecular aggregates formed through H-bonds and stabilized by steric constrains resembles, in fact, many biological systems, where molecules forming an aggregate, even if constantly exchanging, do not affect the loss of stability of the whole structure. Scattering measurements in presence and in absence of magnetic field would shed light on the induced formation and destruction of the supramolecular aggregates networks, kinetics included. For the future, we are strongly convinced that efforts are to be directed to link the behavior of such kind of systems with the bio-mimetic ones. The first attempts can be made by taking into account for the physics involved in References [37,38,39,40,41,42].

A big, and challenging, question is why the response to the external stimulus is so slow in our liquids in comparison with the typical dynamics in fluids far from glass transition. Evidently, the evolution of the systems needs molecular moves that are highly improbable. In this respect, one can suspect that such kind of an effect can be possessed also by other systems, and probably even by other kinds of systems, which has probably not been unveiled just for the simple fact that the studies have been focused to shorter times. This might have been happened for practical reasons, or because eventual changes with long times are somehow unexpected. In a broader sense, we wish that our work can tickle researchers’ imagination by following the responses of systems also to unexpectedly long times, although (we are conscious of this) this can be resources-consuming. On the other hand, we feel obliged to point out that imagination in complex materials science and visionary studies in this field can play a pivotal role for cutting-edge discoveries [43].

Another big deal would be the behavior of such structured fluids on solids, since fluids self-assembly on a solid surface involves an adaptive change of the molecular structure especially at droplets edges, which is intriguing and challenging to study [44].

Finally, we need to consider that: (i) tuning the amphiphilicity of the building blocks allows the chemical control of self-assembly and disassembly [45], (ii) modifying the structure and topology of amphiphilic systems can induce novel structural and dynamic transitions [46,47,48] and (iii) a wide range of component materials are being monitored for their self-assembly processes as key players in the novel field of nanoarchitectonics [49]. It is clear that all these potentialities can be greatly enhanced if the systems can also structurally and dynamically respond to an external magnetic field, a fact that would strikingly widen the scenario of possible applications in all fields. Therefore, the molecular parameters (size, structure, topology, polarity, amphiphilicity) need to be changed in future experiments, in order to better understand the reason, at the molecule base, of the new effect shown in this paper, as well as to better define its fine details. We believe that this work can be a starting point for new research in this sense, and we hope to have opened a new door in material science research.

7. Conclusions

We showed that a magnetic field can induce significant birefringence in mixtures of dibutyl phosphate (DBP) and propylamine liquids (PA), which are themselves weakly optically anisotropic. In addition, another striking discovery is that this effect arises in a matter of hours, despite that the typical molecular reorientations usually occur in timescales of nanoseconds. This effect does not arise from the orientation of individual molecules but from their organization in supra-molecular structures driven by the action of the external magnetic field. Therefore, the system can be described as containing magnetically deformable soft molecules-based nanostructures. The effects of composition, time and field intensity have been investigated. All the data consistently indicate that the structures built by the ordering action of the applied magnetic field are very stable as hold by electrostatic interactions (protonated PA and deprotonated DBP), H-bonds and steric constrains. However, the process is reversible and reproducible and the systems returns to isotropy once the field is switched off, as a result of the thermal agitation randomizing molecular orientations/positions. The magnitude of induced birefringence as a function of applied field intensity has been modelled in terms of individual particles free-to-move in a liquid medium. Despite the obvious differences between the model and the true physical-chemistry of the systems under investigation, the model describes the data well, indicating a starting point for the interpretation of the process. To the best of our knowledge, there has not yet been a theoretical description of magnetically induced birefringence in self-aggregated molecular structures; thus, our findings open new ways for the comprehension of the dynamics in these liquids. In addition to the theoretical interest, this discovery is worth to be tailored for biological applications, where the interactions between large molecules/aggregates and bio-structures can give bioactivity effects, and in the novel field of nanoarchitectonics, where the potentialities can be greatly enhanced if the systems can also react to an external magnetic field, a fact that would strikingly widen the scenario of possible applications in all fields.