Bentonite Extrusion into Near-Borehole Fracture
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Numerical Modeling
2.2.1. Governing Equations
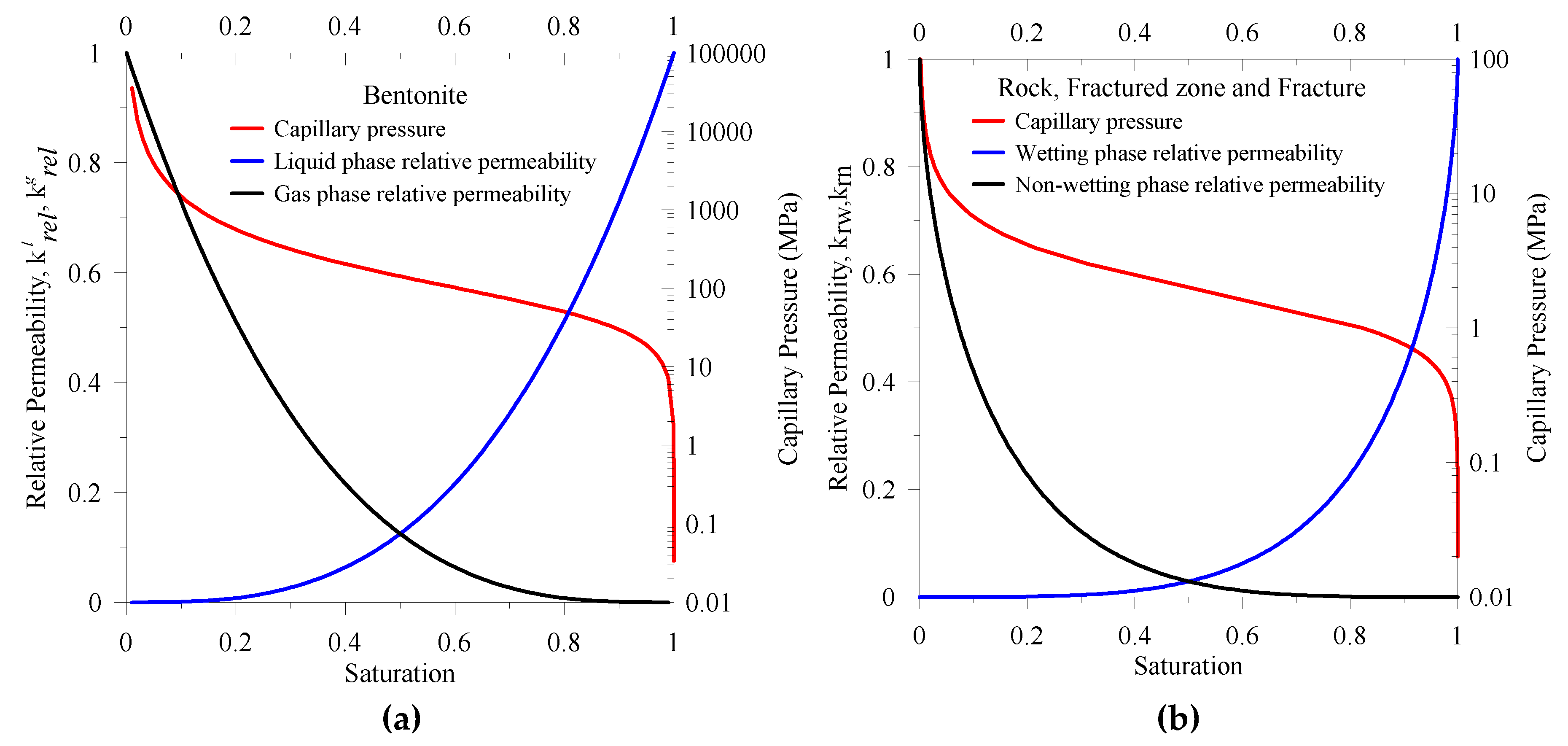
2.2.2. Capillary Pressure and Saturation Relations
2.2.3. Constitutive Relations for Solid
2.2.4. Constitutive Relations for Fluid Flow in the Fracture
2.2.5. Initial and Boundary Conditions
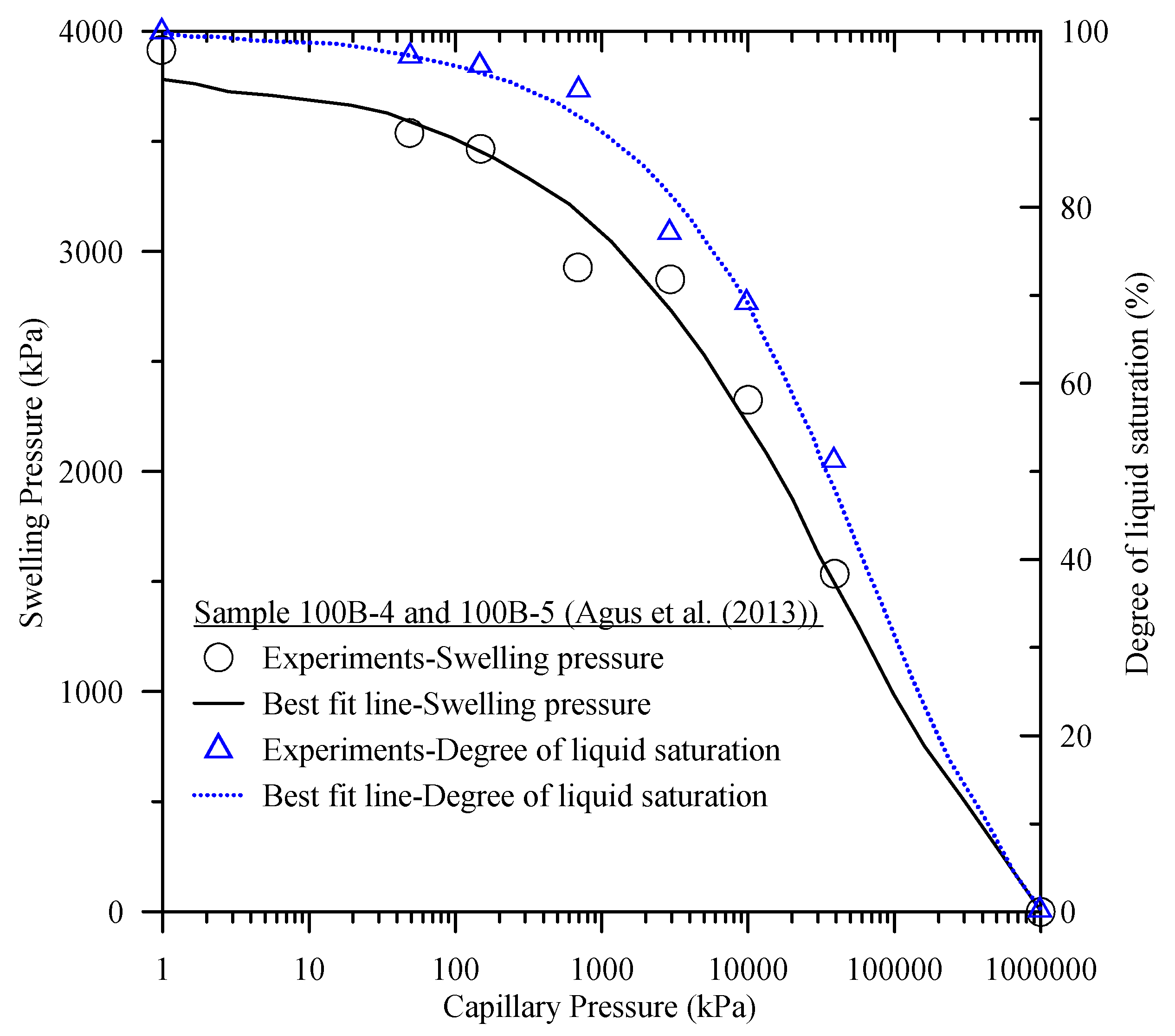
2.3. Material and Fluid Properties
3. Results and Discussions
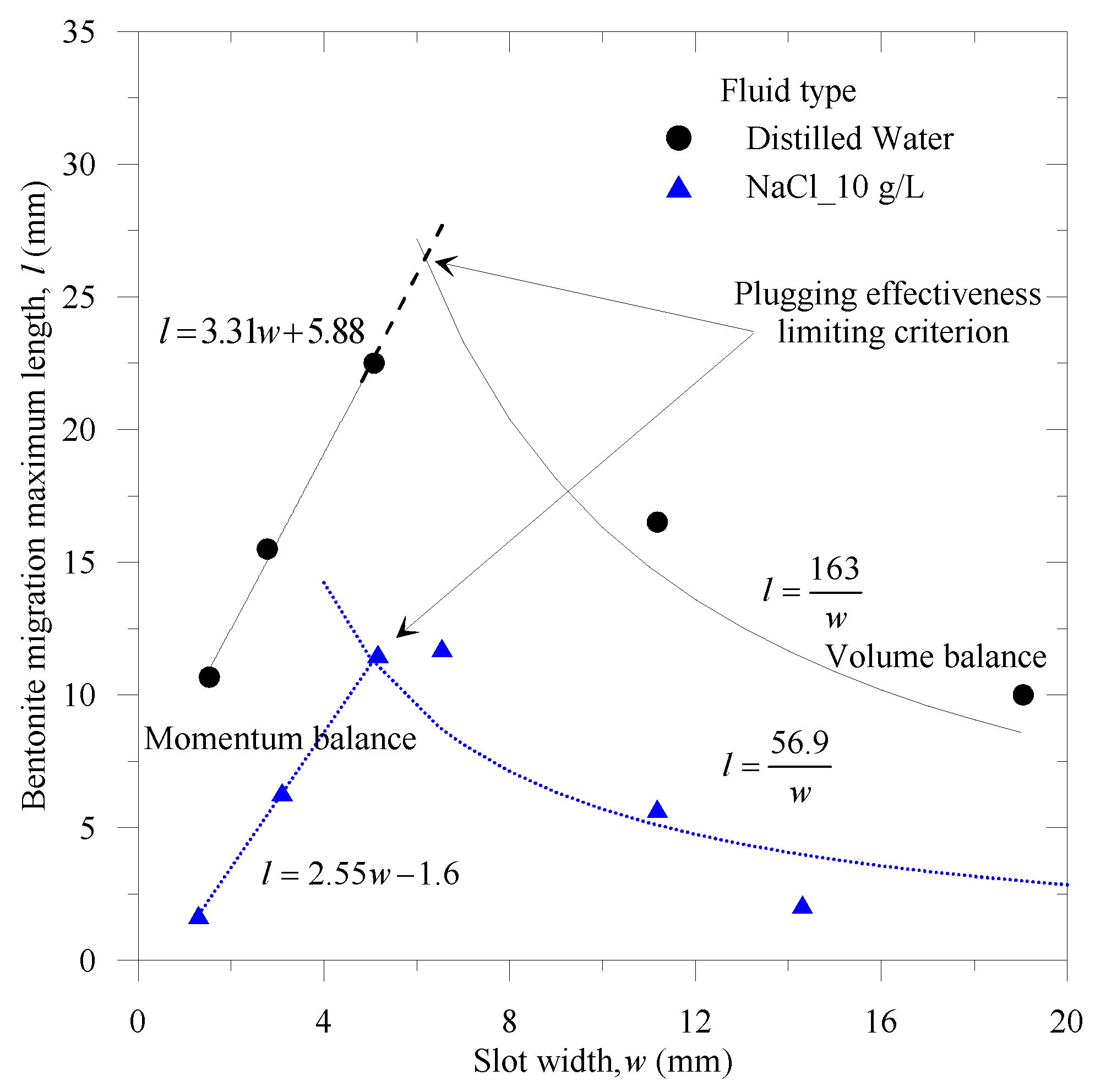
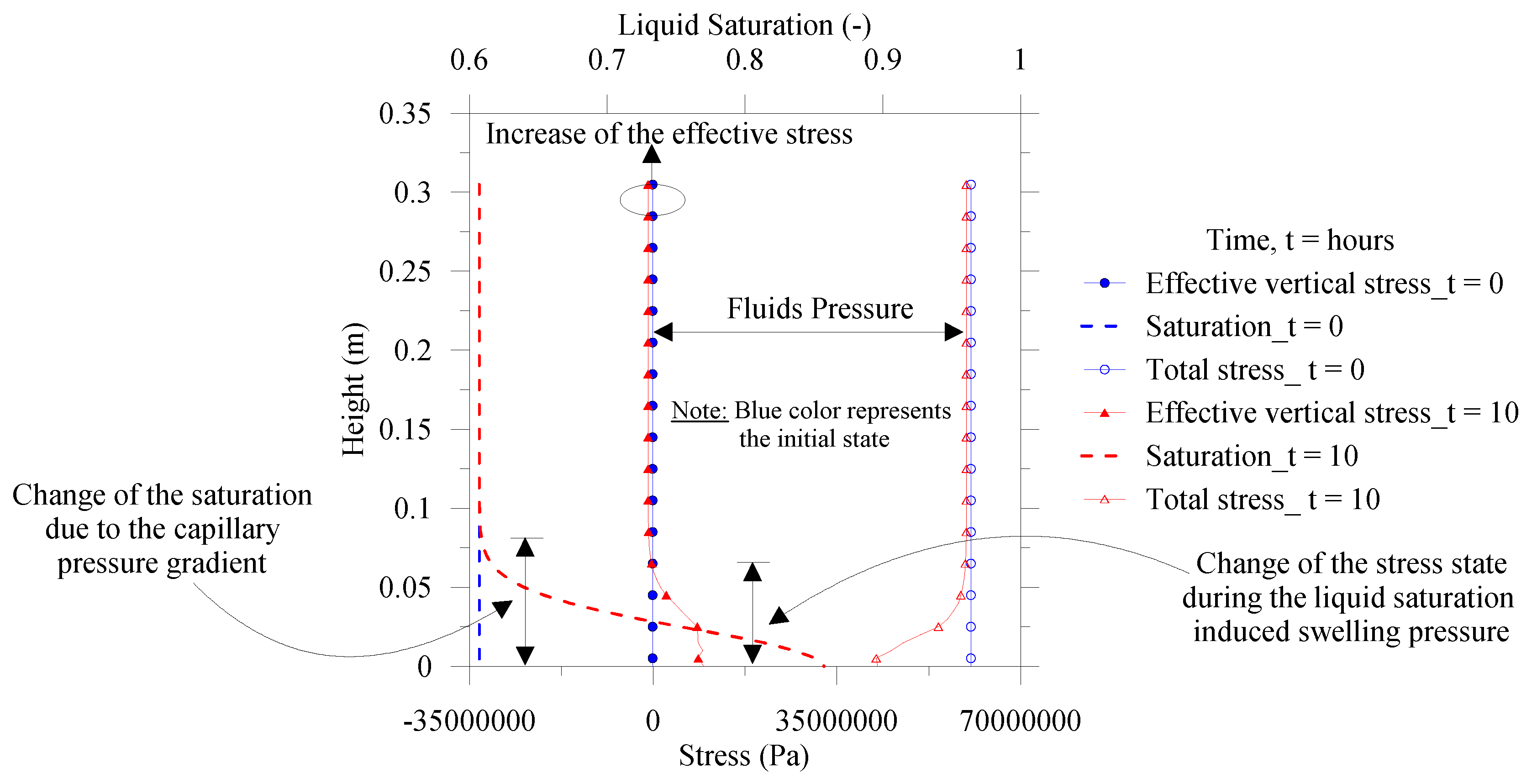
3.1. Experimental Results
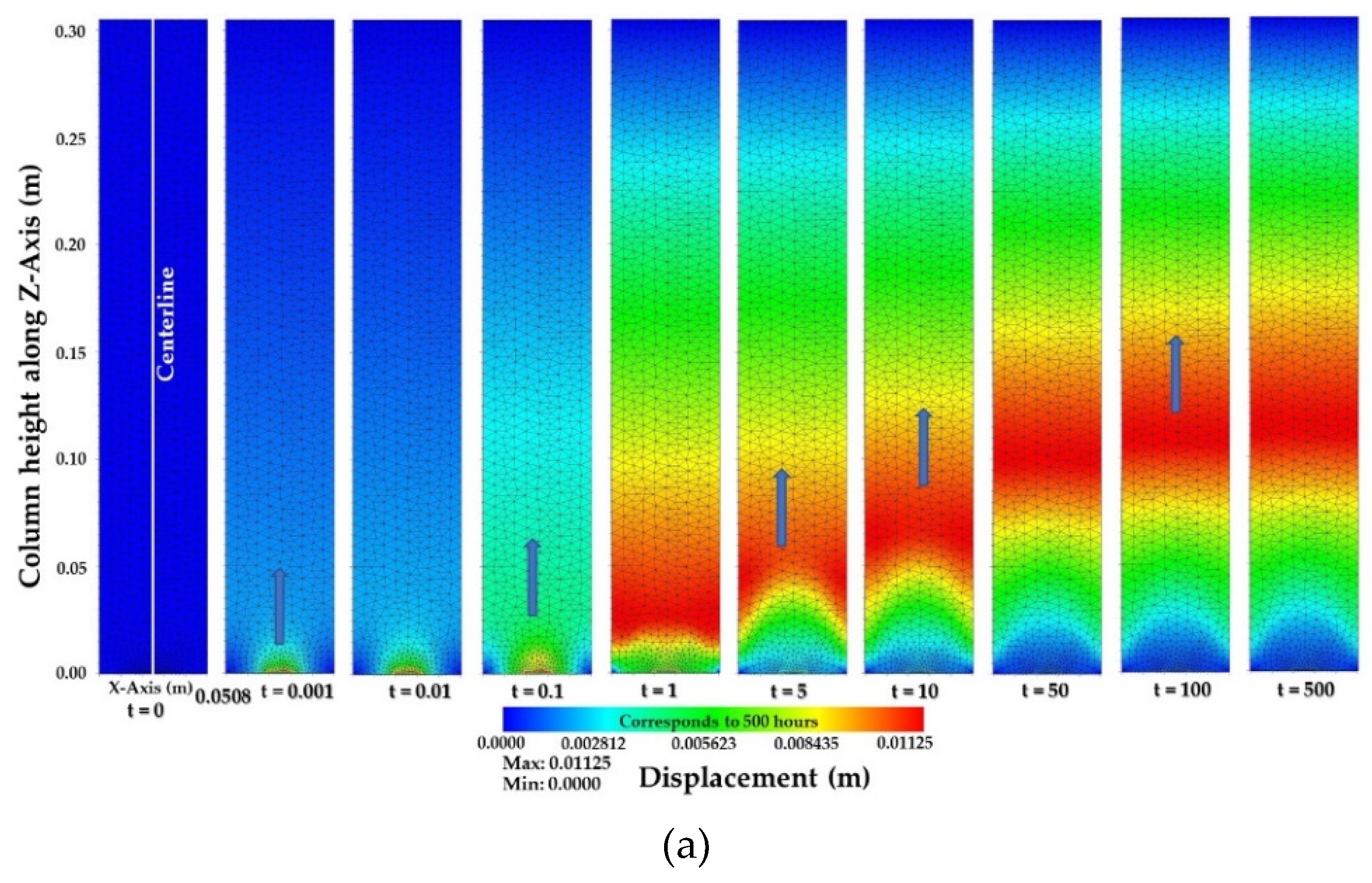
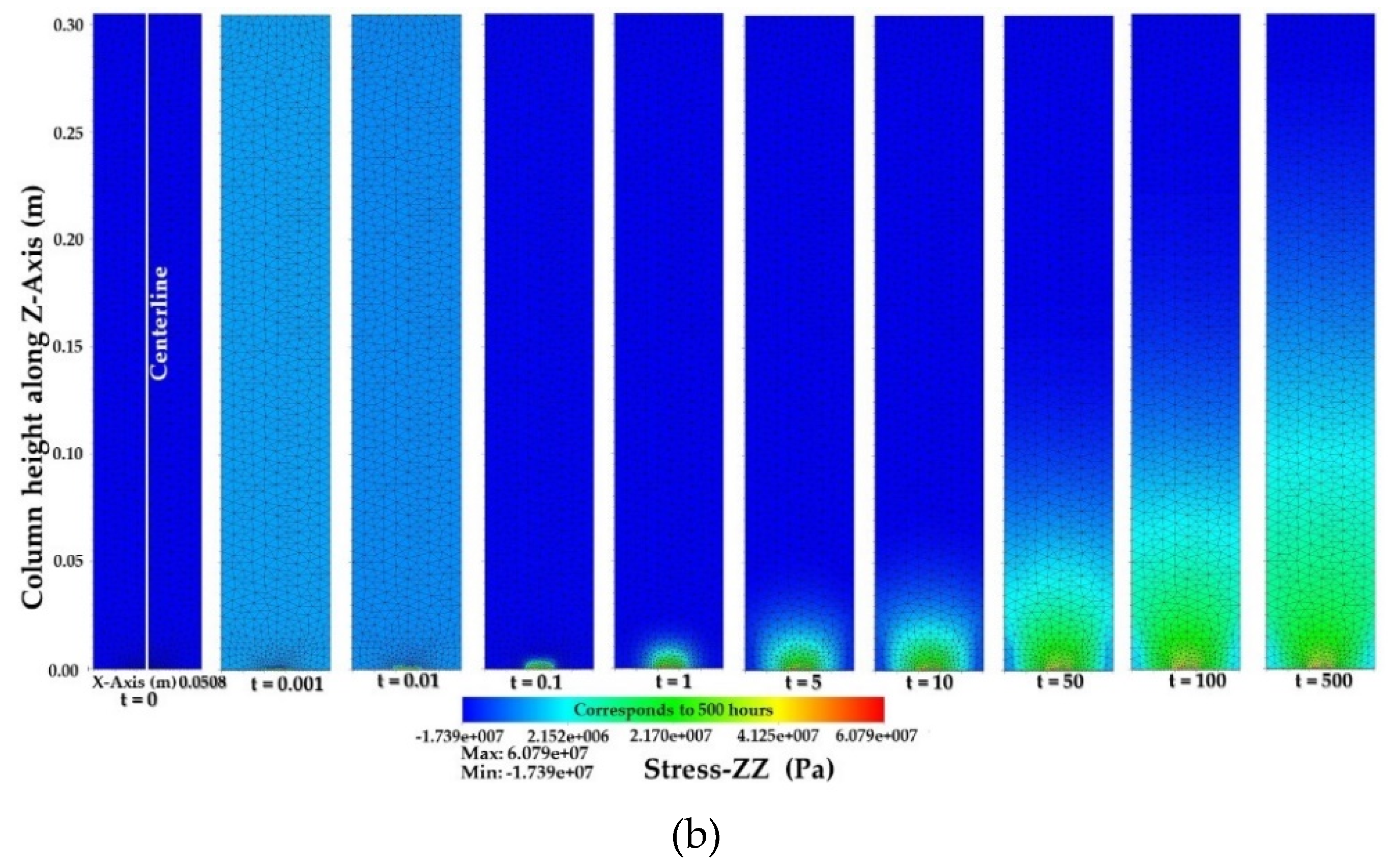
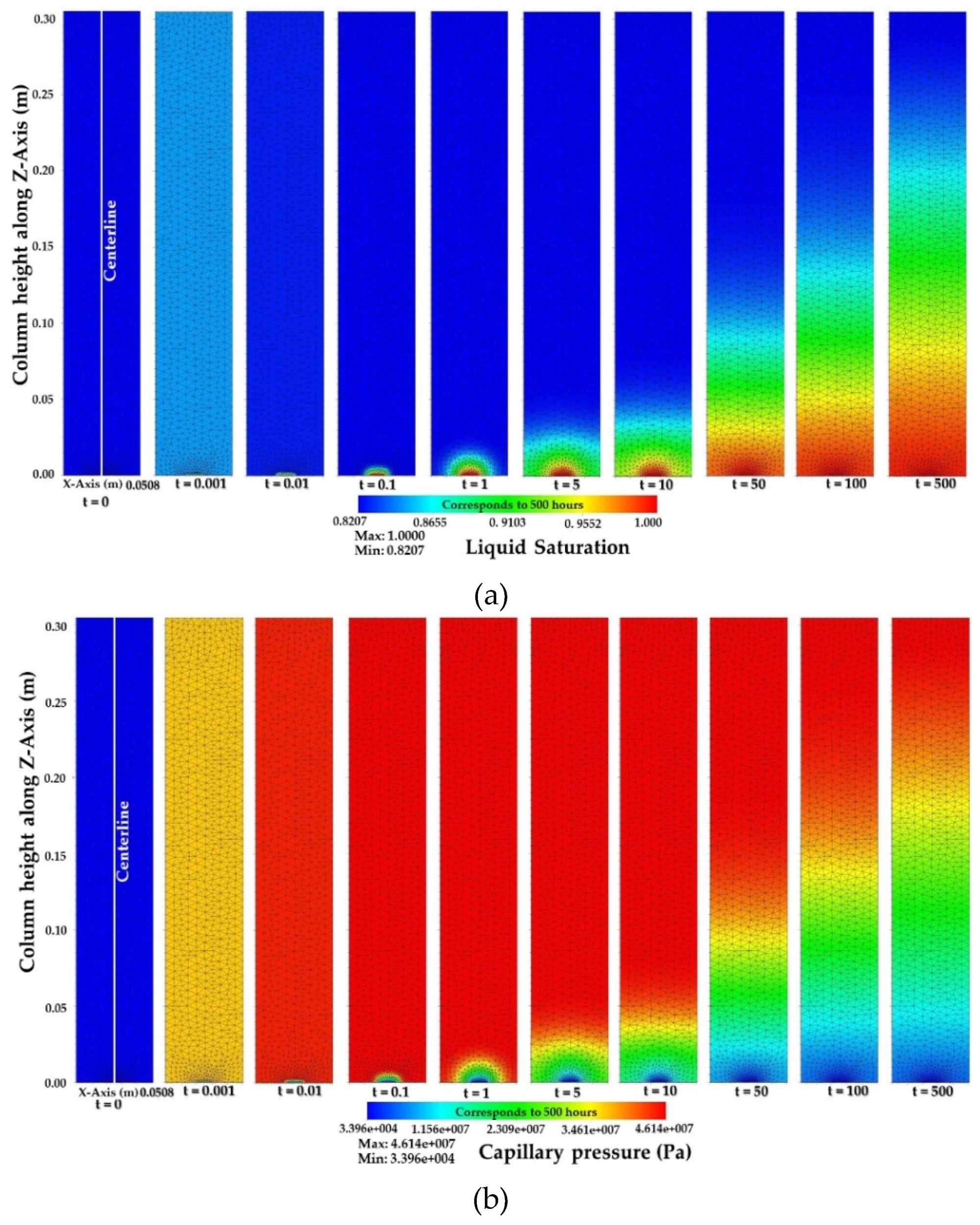
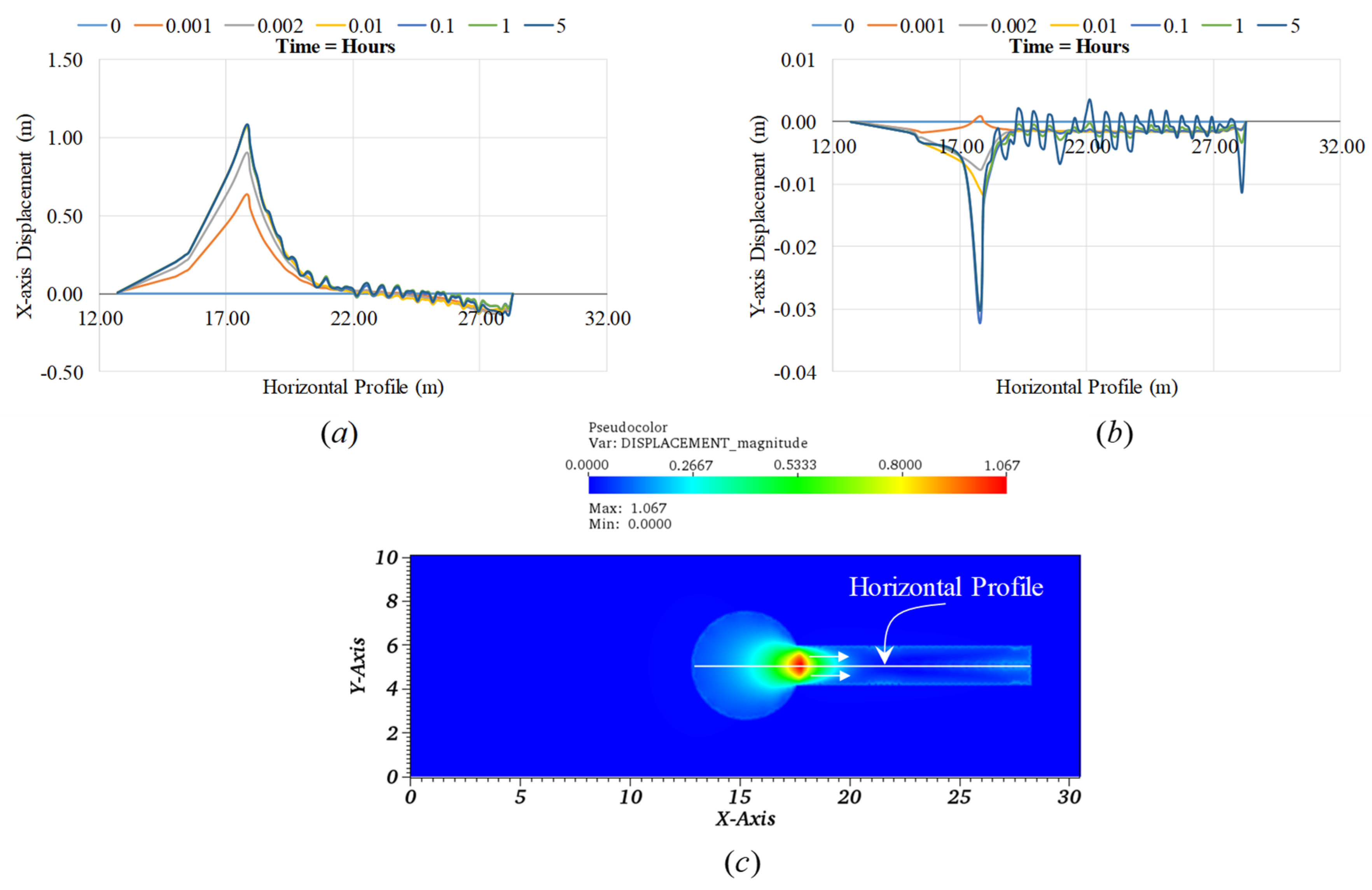
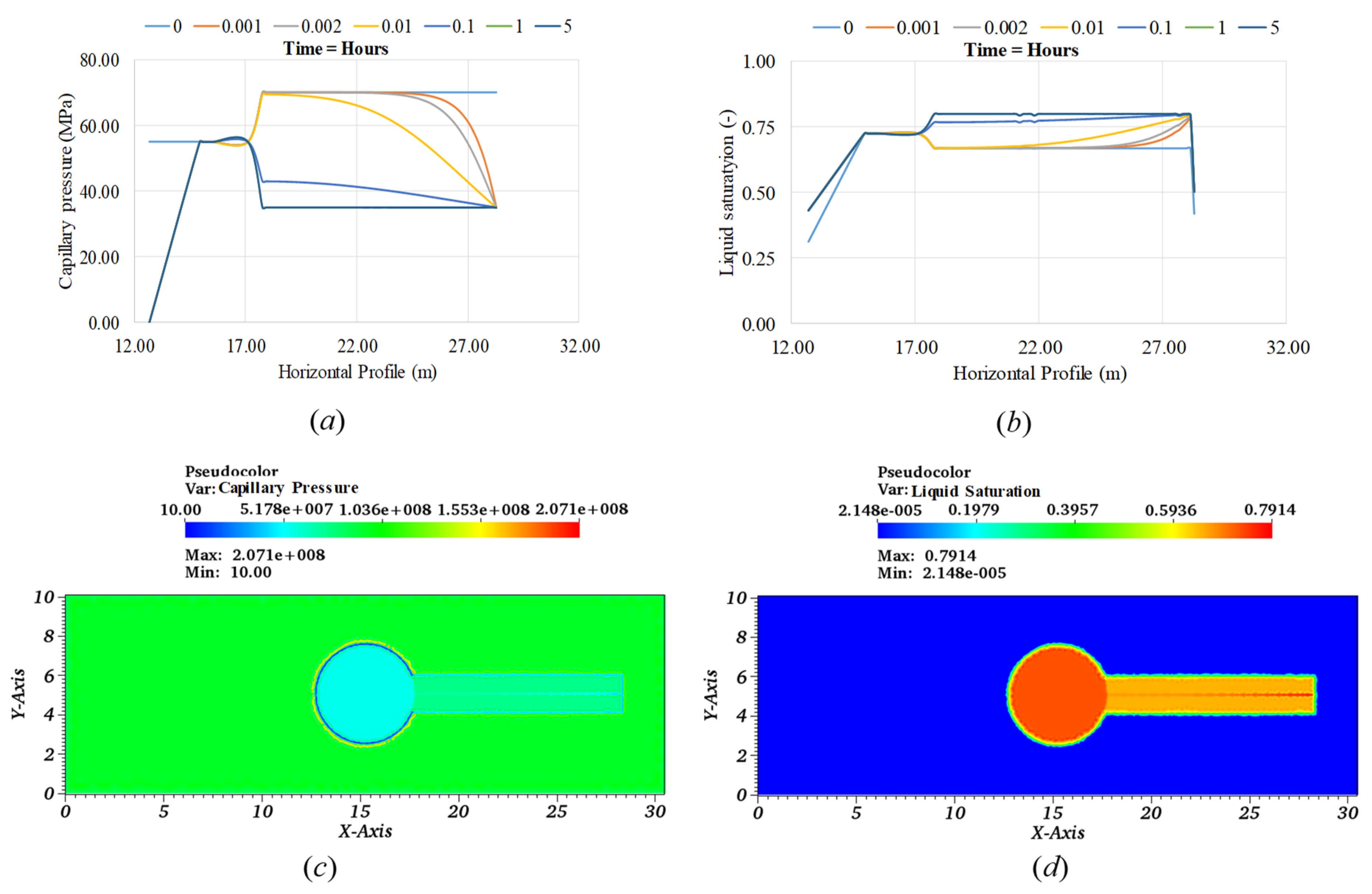
3.2. Numerical Simulation Results
4. Conclusions and Discussions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FE | Finite Element |
| MCC | Modified Cam Clay |
| PADEP | The Pennsylvania Department of Environmental Protection |
| PMMA | Poly (methyl methacrylate) |
Appendix A. Constitutive Relations in Governing Equations
Appendix B. Derivation of Plastic Strain,

Appendix C. Coupled Finite Element Solutions
Appendix D. Validation of Bentonite Model

Appendix E. Analytical Model
References
- Ide, S.T.; Friedmann, S.J.; Herzog, H.J. CO2 leakage through existing wells: Current technology and regulations. In Proceedings of the 8th Greenhouse Gas Technology Conference, Trondjhei, Norway, 19–22 June 2006; pp. 19–22. [Google Scholar]
- Towler, B.F.; Firouzi, M.; Mortezapour, A.; Hywel-Evans, P.D. Plugging CSG wells with bentonite: Review and preliminary lab results. In Proceedings of the SPE Asia Pacific Unconventional Resources Conference and Exhibition, Brisbane, Australia, 9–11 November 2015; p. 10. [Google Scholar]
- Yong, R.N.; Boonsinsuk, P.; Wong, G. Formulation of backfill material for a nuclear fuel waste disposal vault. Can. Geotech. J. 1986, 23, 216–228. [Google Scholar] [CrossRef]
- Beswick, J. Status of technology for deep borehole disposal. Contract No. NP 01185 2008, 1185, 16–18. [Google Scholar]
- Brady, P.V.; Freeze, G.A.; Kuhlman, K.L.; Hardin, E.L.; Sassani, D.C.; MacKinnon, R.J. Deep borehole disposal of nuclear waste: US perspective. In Geological Repository Systems for Safe Disposal of Spent Nuclear Fuels and Radioactive Waste, 2nd ed.; Woodhead Publishing: Cambridge, UK, 2017; pp. 89–112. [Google Scholar] [CrossRef]
- Townsend-Small, A.; Ferrara, T.W.; Lyon, D.R.; Fries, A.E.; Lamb, B.K. Emissions of coalbed and natural gas methane from abandoned oil and gas wells in the United States. Geophys. Res. Lett. 2016, 43, 2283–2290. [Google Scholar] [CrossRef]
- Dilmore, R.M.; Sams, J.I.; Glosser, D.; Carter, K.M.; Bain, D.J. Spatial and temporal characteristics of historical oil and gas wells in pennsylvania: Implications for new shale gas resources. Environ. Sci. Technol. 2015, 49, 12015–12023. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, A.L.; Casman, E.A. Economic incentives and regulatory framework for shale gas well site reclamation in Pennsylvania. Environ. Sci. Technol. 2011, 45, 9506–9514. [Google Scholar] [CrossRef] [PubMed]
- Kanno, T.; Wakamatsu, H. Experimental Study on Bentonite Gel Migration from a Deposition Hole. In Proceedings of the third international conference on nuclear fuel reprocessing and waste management, RECOD′91, Sendai, Japan, 14–18 April 1991; pp. 1005–1010. [Google Scholar]
- Tanai, K.; Matsumoto, K. A study of extrusion behavior of buffer material into fractures. Sci. Technol. Ser. 2008, 334, 57–64. [Google Scholar]
- Bolchover, P.; Myers, T.G.; Peletier, M.A.; Ahmer, W.M. Behaviour of Bentonite Clay in Toxic Waste Barriers. In Proceedings of the European Study Group with Industry 1998 Final Reports, Southampton, UK, 22–27 March 1998; pp. 1–13. [Google Scholar]
- Svoboda, J. The experimental study of bentonite swelling into fissures. Clay Miner. 2013, 48, 383–389. [Google Scholar] [CrossRef]
- Kanno, T.; Iwata, Y.; Sugino, H. Modelling of bentonite swelling as solid particle diffusion. In Clay Science for Engineering; Adachi, K., Fukue, M., Eds.; CRC Press: Boca Raton, FL, USA, 2001; pp. 561–570. [Google Scholar]
- Borrelli, R.A.; Ahn, J. Numerical modeling of bentonite extrusion and radionuclide migration in a saturated planar fracture. Phys. Chem. Earth. 2008, 33, S131–S141. [Google Scholar] [CrossRef]
- Sanchez, M.; Gens, A.; do Nascimento Guimarães, L.; Olivella, S. A double structure generalized plasticity model for expansive materials. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 751–787. [Google Scholar] [CrossRef]
- Helmig, R. Multiphase Flow and Transport Processes in the Subsurface: A Contribution to the Modeling of Hydrosystems; Springer: New York, NY, USA, 1997. [Google Scholar]
- Kueper, B.H.; Frind, E.O. Two-phase flow in heterogeneous porous media: 1. Model development. Water Resour. Res. 1991, 27, 1049–1057. [Google Scholar] [CrossRef]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation; Applied Science Publishers Ltd.: London, UK, 1979. [Google Scholar]
- Park, C.H.; Böttcher, N.; Wang, W.; Kolditz, O. Are upwind techniques in multi-phase flow models necessary? J. Comput. Phys. 2011, 230. [Google Scholar] [CrossRef]
- Shad, S.; Maini, B.B.; Gates, I.D. Effect of gap and flow orientation on two-phase flow in an oil-wet gap: Relative permeability curves and flow structures. Int. J. Multiphase Flow 2013, 57, 78–87. [Google Scholar] [CrossRef]
- Snow, D.T. Anisotropie permeability of fractured media. Water Resour. Res. 1969, 5, 1273–1289. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.S.Y.; Iwai, K.; Gale, J.E. Validity of Cubic Law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, A.M.; Cui, Y.-J.; Delage, P.; Gatmiri, B. Experimental study on the swelling behaviour of bentonite/claystone mixture. Eng. Geol. 2012, 124, 59–66. [Google Scholar] [CrossRef]
- Islam, M.N.; Upadhyay, R.; Wehner, C.; Bunger, A.P. Experimental demonstration of mechanisms for effective near-borehole crack plugging with bentonite (ID: 19636). In Proceedings of the American Nuclear Society (ANS-2017), International High-Level Radioactive Waste Management (IHLRWM 2017), Charlotte, NC, USA, 9–13 April 2017; pp. 1–5. [Google Scholar]
- Kolditz, O.; Bauer, S.; Bilke, L.; Böttcher, N.; Delfs, J.O.; Fischer, T.; Görke, U.J.; Kalbacher, T.; Kosakowski, G.; McDermott, C.I.; et al. OpenGeoSys: An open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 2012, 67, 589–599. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Bethel, E.W.; Childs, H.; Hansen, C. High Performance Visualization: Enabling Extreme-Scale Scientific Insight; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Roscoe, K.H.; Burland, J.B. On the generalized stress-strain behavior of wet clay. In Engineering Plasticity; Heyman, J., Leckie, F.A., Eds.; Cambridge University Press: Cambridge, UK, 1968; pp. 535–609. [Google Scholar]
- Rutqvist, J. Coupled Thermal-Hydrological-Mechanical Analysis with the Framework of DECOVALEX-THMC in ‘DECOVALEX-THMC Task D: Long-Term Permeability/Porosity Changes in the EDZ and Near Field Due to THM and THC Processes in Volcanic and Crystaline-Bentonite Systems’ by Birkholzer, J. et al. (2005); Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2005; pp. 204–249. [Google Scholar]
- Coussy, O. Poromechanics; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Lewis, R.W.; Schrefler, B.A. The Finite Element Method in the Static and Dynamic Deformation and Consolidation of Porous Media, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Ehlers, W.; Bluhm, J. Porous Media: Theory, Experiments and Numerical Applications; Springer: New York, NY, USA, 2002. [Google Scholar]
- Potts, D.M.; Zdravkovic, L. Finite Element Analysis in Geotechnical Engineering: Theory; Thomas Telford: Heron Quay, London, UK, 1999. [Google Scholar]
- Kolditz, O.; Gorke, U.-J.; Shao, H.; Wang, W. Thermo-Hydro-Mechanical-Chemical Processes in Fractured Porous Media: Benchmarks and Examples; Springer: Heidelberg, Germany, 2012. [Google Scholar]
- Chen, Z.; Huan, G.; Ma, Y. Computational Methods for Multiphase Flows in Porous Media; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006. [Google Scholar]
- Paniconi, C.; Putti, M. A comparison of Picard and Newton iteration in the numerical solution of multidimensional variably saturated flow problems. Water Resour. Res. 1994, 30, 3357–3374. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Paris: Dalmont, 1856. Available online: https://gallica.bnf.fr/ark:/12148/bpt6k624312.image (accessed on 24 November 2019).
- Bear, J.; Bachmat, Y. Introduction to Modeling of Transport Phenomena in Porous Media; Kluwer Academic Publishers: London, UK, 1990; Volume 4. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media, Hydrology Papers 3; Colorado State University: Fort Collins, CO, USA, 1964; p. 27. [Google Scholar]
- Burdine, N.T. Relative Permeability Calculations from Pore Size Distribution Data. Pet. Trans. AIME 1953, 198, 71–78. [Google Scholar] [CrossRef]
- Schofield, A.N.; Wroth, P. Critical State Soil Mechanics; McGrawHill: London, UK, 1968. [Google Scholar]
- Desai, C.; Siriwardane, H.J. Constitutive Laws For Engineering Materials; Prentice-Hall: Upper Saddle River, NJ, USA, 1984. [Google Scholar]
- Yi, H.; Wang, W.; Kolditz, O.; Shao, H.; Zhou, H. Hydromechanical modelling of the SEALEX experiments. Environ. Earth Sci. 2017, 76, 737. [Google Scholar] [CrossRef]
- Agus, S.S.; Arifin, Y.F.; Tripathy, S.; Schanz, T. Swelling pressure–suction relationship of heavily compacted bentonite–sand mixtures. Acta Geotech. 2013, 8, 155–165. [Google Scholar] [CrossRef]
- Islam, M.N.; Gnanendran, C.T.; Massoudi, M. Finite element simulations of an elasto-viscoplastic model for clay. Geosciences 2019, 9, 145. [Google Scholar] [CrossRef]
- Islam, M.N.; Gnanendran, C.T. Elastic-viscoplastic model for clays: Development, validation, and application. J. Eng. Mech. 2017, 143. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Birkholzer, J.; Rutqvist, J.; Sonnenthal, E.; Barr, D. DECOVALEX-THMC Task D: Long-Term Permeability/Porosity Changes in the EDZ and Near Field due to THM and THC Processes in Volcanic and Crystaline-Bentonite Systems, Status Report October 2005; Ernest Orlando Lawrence Berkeley NationalLaboratory: Berkeley, CA, USA, 2005. [Google Scholar]
- Wang, W.; Rutqvist, J.; Görke, U.-J.; Birkholzer, J.T.; Kolditz, O. Non-isothermal flow in low permeable porous media: A comparison of Richards’ and two-phase flow approaches. Environ. Earth Sci. 2011, 62, 1197–1207. [Google Scholar] [CrossRef]
- Yih, C.-S. Fluid Mechanics: A Concise Introduction to The Theory [see Equation 341]; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Bear, J.; Berkowitz, B. Groundwater flow and pollution in fractured rock aquifers. Developments in Hydraulic Engineering; Novak, P., Ed.; Elsevier: New York, NY, USA, 1987; Volume 4, pp. 175–238. [Google Scholar]
- Fourar, M.; Bories, S. Experimental study of air-water two-phase flow through a fracture (narrow channel). Int. J. Multiphase Flow 1995, 21, 621–637. [Google Scholar] [CrossRef]
- Oron, A.P.; Berkowitz, B. Flow in rock fractures: The local cubic law assumption reexamined. Water Resour. Res. 1998, 34, 2811–2825. [Google Scholar] [CrossRef]
- Crandall, D.; Moore, J.; Gill, M.; Stadelman, M. CT scanning and flow measurements of shale fractures after multiple shearing events. Int. J. Rock Mech. Min. Sci. 2017, 100, 177–187. [Google Scholar] [CrossRef]
- Anandarajah, A. Computational Methods in Elasticity and Plasticity Solids and Porous Media; Springer: Berlin, Germany, 2010. [Google Scholar]
- Karnland, O. Bentonite swelling pressure in strong NaCl Solutions: Correlation of model calculations to experimentally determined data. (No. POSIVA-98-01); Posiva Oy: Eurajjoki, Finland, 1998. [Google Scholar]
- Baik, M.-H.; Cho, W.-J.; Hahn, P.-S. Erosion of bentonite particles at the interface of a compacted bentonite and a fractured granite. Eng. Geol. 2007, 91, 229–239. [Google Scholar] [CrossRef]
- Chen, Y.-G.; Jia, L.-Y.; Ye, W.-M.; Chen, B.; Cui, Y.-J. Advances in experimental investigation on hydraulic fracturing behavior of bentonite-based materials used for HLW disposal. Environ. Earth Sci. 2016, 75, 787. [Google Scholar] [CrossRef]
- Rutqvist, J.; Börgesson, L.; Chijimatsu, M.; Nguyen, T.S.; Jing, L.; Noorishad, J.; Tsang, C.F. Coupled thermo-hydro-mechanical analysis of a heater test in fractured rock and bentonite at Kamaishi Mine—comparison of field results to predictions of four finite element codes. Int. J. Rock Mech. Min. Sci. 2001, 38, 129–142. [Google Scholar] [CrossRef]
- Xie, M.; Wang, W.; De Jonge, J.; Kolditz, O. Numerical modelling of swelling pressure in unsaturated expansive elasto-plastic porous media. Transp. Porous Media 2007, 66, 311–339. [Google Scholar] [CrossRef]
- Mielenz, R.C.; King, M.E. Physical-Chemical properties and engineering performance of clays. Clays Clay Miner. 1952, 1, 196–254. [Google Scholar] [CrossRef]
- Sun, D.A.; Sun, W.; Fang, L. Swelling characteristics of Gaomiaozi bentonite and its prediction. J. Rock Mech. Geotech. Eng. 2014, 6, 113–118. [Google Scholar] [CrossRef] [Green Version]
- Borst, R. Computational Methods for Fracture in Porous Media: Isogeometric and Extended Finite Element Methods; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Allen III, M.B.; Behie, G.A.; Trangenstein, J.A. Multiphase Flow in Porous Media: Mechanics, Mathematics and Numerics; Springer: Berlin, Germany, 1988. [Google Scholar]
- Kwasniewski, M.; Li, X.; Takahashi, M. True triaxial Testing of Rocks; Taylor and Francis Group, CRC Press: London, UK, 2013. [Google Scholar]
- Sheng, D.; Sloan, W.S.; Yu, S.H. Aspects of finite element implementation of critical state models. Comput. Mech. 2000, 26, 185–196. [Google Scholar] [CrossRef]
- Habib, P. Influence of the variation of the average principal stress upon the shearing strength of soils. Proceedings of 3rd International Conference on Soil Mechanics and Foundation Engineering, Zurich, Switzerland, 16–27 August 1953; Volume 1, pp. 131–136. [Google Scholar]
- Prashant, A.; Penumadu, D. A laboratory study of normally consolidated kaolin clay. Can. Geotech. J. 2005, 42, 27–37. [Google Scholar] [CrossRef]
- Wood, W.L. Practical time-stepping schemes; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Wang, Q.; Cui, Y.-J.; Tang, A.M.; Barnichon, J.-D.; Saba, S.; Ye, W.-M. Hydraulic conductivity and microstructure changes of compacted bentonite/sand mixture during hydration. Eng. Geol. 2013, 164, 67–76. [Google Scholar] [CrossRef]
- Vogel, P.; Mabmann, J.; Ziefle, G.; Yi, H.; Wang, W.; Zhou, H. Chapter 7: Hydro-Mechanical (Consolidation) Proceses. In Thermo-Hydro-Mechanical-Chemical Processes in Fractured Porous Media: Modelling and Benchmarking; Kolditz, O., Gorke, U.-J., Shao, H., Wang, W., Bauer, S., Eds.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Helwany, S. Applied Soil Mechanics with Abaqus Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]








| Properties | Symbol | Unit | Value | |||
|---|---|---|---|---|---|---|
| Rock ** | Bentonite * | Fractured Zone ** | Fracture ** | |||
| Density | Kg·m3 | 2700 | 1970 | 2000 | 1700 | |
| Porosity | --- | 0.01 | 0.279 | 0.3 | 1.0 | |
| Permeability | m2 | 1.0 × 10−17 | 4.3 × 10−21 | 1.0 × 10−15 | ||
| Young’s Modulus | Pa | 3.5 × 1010 | 8.6 × 106 | 3.5 × 107 | 3.5 × 106 | |
| Poisson’s ratio | -- | 0.40 | 0.30 | 0.30 | 0.30 | |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Slope of the critical state line | - | 1.84 | |
| Virgin compression index | - | 0.12 | |
| Swelling/recompression index | - | 0.024 | |
| Initial preconsolidation pressure | MPa | 2.43 | |
| Initial void ratio | - | 0.6376 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.N.; Bunger, A.P.; Huerta, N.; Dilmore, R. Bentonite Extrusion into Near-Borehole Fracture. Geosciences 2019, 9, 495. https://doi.org/10.3390/geosciences9120495
Islam MN, Bunger AP, Huerta N, Dilmore R. Bentonite Extrusion into Near-Borehole Fracture. Geosciences. 2019; 9(12):495. https://doi.org/10.3390/geosciences9120495
Chicago/Turabian StyleIslam, Mohammad N., Andrew P. Bunger, Nicolas Huerta, and Robert Dilmore. 2019. "Bentonite Extrusion into Near-Borehole Fracture" Geosciences 9, no. 12: 495. https://doi.org/10.3390/geosciences9120495
APA StyleIslam, M. N., Bunger, A. P., Huerta, N., & Dilmore, R. (2019). Bentonite Extrusion into Near-Borehole Fracture. Geosciences, 9(12), 495. https://doi.org/10.3390/geosciences9120495





