Next Article in Journal
Structure and Composition of Basement and Sedimentary Cover in the Southwestern Part of the Siljan Ring, Central Sweden: New Data from the C-C-1 Drill Core
Next Article in Special Issue
Fluid-Rock Interactions in a Paleo-Geothermal Reservoir (Noble Hills Granite, California, USA). Part 1: Granite Pervasive Alteration Processes away from Fracture Zones
Previous Article in Journal
Geochemistry of Pyritic Mudstones from the Singa Formation, Malaysia: Insights into Gold Potential, Source of Sulfur and Organic Matter
Previous Article in Special Issue
Scaling in a Geothermal Heat Exchanger at Soultz-Sous-Forêts (Upper Rhine Graben, France): A XRD and SEM-EDS Characterization of Sulfide Precipitates
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 11
Issue 7
10.3390/geosciences11070280
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), Application to Geothermal Reservoirs

by
Arezki Chabani
1,*,
Ghislain Trullenque
1,
Béatrice A. Ledésert
2 and
Johanne Klee
1
1
UniLaSalle, UPJV, B2R UMR 2018.C100, U2R 7511, 19 rue Pierre Waguet, F-60026 Beauvais, France
2
Geosciences and Environnent Cergy, CY Cergy Paris Université, 1 rue Descartes, F-95000 Neuville sur Oise, France
*
Author to whom correspondence should be addressed.
Geosciences 2021, 11(7), 280; https://doi.org/10.3390/geosciences11070280
Submission received: 10 June 2021 / Revised: 25 June 2021 / Accepted: 30 June 2021 / Published: 3 July 2021
(This article belongs to the Special Issue Enhanced Geothermal Systems and other Deep Geothermal Applications throughout Europe: The MEET Project)
Browse Figures
Versions Notes

Abstract

:
In the basement fractured reservoirs, geometric parameters of fractures constitute the main properties for modeling and prediction of reservoir behavior and then fluid flow. This study aims to propose geometric description and quantify the multiscale network organization and its effect on connectivity using a wide-ranging scale analysis and orders scale classification. This work takes place in the Noble Hills (NH) range, located in the Death Valley (DV, USA). The statistical analyses were performed from regional maps to thin sections. The combination of the length datasets has led to compute a power law exponent around −2, meaning that the connectivity is ruled by the small and the large fractures. Three domains have been highlighted in the NH: (1) domain A is characterized by a dominance of the NW/SE direction at the fourth order scale; (2) domain B is characterized by a dominance of the E/W and the NW/SE directions at respectively the fourth and third order scales; (3) domain C is also marked by the E/W direction dominance followed by the NW/SE direction respectively at the fourth and third order scale. The numerical simulations should consider that the orientation depends on scale observation, while the length is independent of scale observation.

1. Introduction

Fluid flow in fractured rocks of very low matrix permeability is localized mainly in few fractures [1]. The complex geometry of fracture and fault patterns is the main cause of the complexity of fluid flow. In that case, numerous studies have been undertaken worldwide to show the control of the fracture network on the fluid circulations especially in hydrocarbon and aquifers reservoirs [2,3,4,5], in heat transfer [6], and thus also in geothermal reservoirs [7,8,9].
A fracture system is characterized by geometrical parameters as fracture lengths, spacings, orientations, and relations between them [1,10,11,12]. In order to access hierarchical and mechanical relationships between fracture systems, many authors undertook a multiscale approach, in sedimentary [2,12,13,14,15], and in Crystalline [16,17,18,19,20] rocks. This approach allows to model and predict hydraulic reservoir properties, by studying several geometric attributes, such as the distribution of orientations, lengths, widths, spacings and densities classically considered in spatial arrangement analysis [21,22,23,24].
The geometric parameters are commonly collected for (1) explicitly constructing deterministic models (Discrete Fracture Network: DFNs, [2]) or (2) ensuring inputs of stochastic simulations by determining fracture distribution functions from sampled fracture networks [23,25,26,27]. The main goal is to better understand the fracture network connectivity and then the fluid flow patterns [3,22,28]. Subsequently, the main question is whether data correspond to scale-limited lognormal or exponential distributions, or scale-invariant power laws, corresponding to fractal patterns? Several orders of magnitude based on length and spacing characteristics are thus mandatory to establish scaling laws from statistical distributions [29]. These orders of magnitude have been widely described in the literature in extensional [17,20,30] and trans-tensional [17] contexts. It consists of: (1) first order scale related to the crustal faults larger than 100 km length, (2) second order scale refers to the faults comprised between 20 and 30 km length, (3) third order scale refers to faults around 10 km length, (4) and the fourth order refers to faults under 1 km length [20]. In the extensional regime, [30] having defined a spacing characteristic for the two first order scales, with a 10 to 15 km spacing for first order and 3 to 8 km for the second order scale; while [20] have defined 0.8 to 1.5 km spacing for the third order scale. However, the fourth order spacing characteristic is not defined in the literature.
Fracture networks impact the fluid flow in reservoirs [23]. The 2D/3D seismic lines and 1D borehole data cannot detect respectively the fracture geometries and the spatial arrangement at the reservoir scale due to the lack of information [31]. Then, the spatial arrangement of fracture networks are widely studied from field analogues [16,23,29,32], as they give access to 2D and 3D distributions. In geothermal basement setting, the analogues are chosen according to the lithology and geological context to get closer to the reservoir conditions. Sometimes, the analogue is chosen in desert conditions, without vegetation, perfectly suited for realistic multiscale fracture network reconstructions in 2D, and in 3D in case of modeling canyons with photogrammetric [33] or lidar [34] approaches.
The present work is part of the MEET project (Multidisciplinary and multi-context demonstration of EGS exploration and Exploitation Techniques and potentials, [35]), which aims to develop geothermal exploitation at European scale by applying Enhanced Geothermal System (EGS) technology to different geological contexts. This study aims to propose geometric description and quantify the multiscale network organization and its effect on connectivity. A wide-ranging scale analysis from the microscopic scale to the regional scale was conducted in the desert environment of Noble Hills (NH) fractured granitic basement. It is located in the southern termination of Death Valley (DV, California, USA) and assimilated to a paleo geothermal analogue. The NH range is considered as analogue to the Soultz-sous-Forêts (SsF) geothermal electricity producing system, due to the granitic nature, the alteration and the trans-tensional tectonic setting of the DV region [36,37].
Measurements have been performed at various scales using the DV regional map [38] at 1:250,000, NH regional map based on previous studies undertaken by [37,39] and orthophoto images taken for the present day. At outcrop scale, fractures are digitized thanks to the photogrammetric models. Several 2D fracture maps are also used, as well as additional scales on samples and in thin sections. This allows to integrate fracture lengths ranging from micrometer to kilometer scales.
In this study, the multiscale approach is used to better understand the spatial arrangement of the fracture networks which aims at producing the necessary data for DFN modeling. This helps to better characterize reservoirs in response to the developing geothermal exploration and exploitation by EGS. This study is conducted through:
  • a 2D characterization of the NH fracture network;
  • a multiscale evolution of length distributions;
  • evaluate the fracture system in the complex tectonic and geometrical setting;
  • present a conceptual scheme of the NH fracture network organization, and the role of each fracture order of magnitude on the connectivity.

2. Geological Setting

The present study takes place in the NH fractured granitic zone, located at the southern termination of the Death Valley (DV, California, USA) (Figure 1a). The NH range is assimilated to a paleo geothermal analogue [37]. Indeed, Reference [37] confirmed the analogy between the DV region and Soultz-sous-Forêts reservoir (Rhine graben, East of France), with many similarities, especially: (1) the trans-tensional tectonic setting of the DV, and (2) the granitic nature and hydrothermal alteration of the central part of the NH range. Furthermore, the desert conditions of the NH range make this analogue perfectly suited for multiscale characterization of fracture networks dedicated to the global understanding of the spatial arrangement in granitic reservoir affected by trans-tensional tectonics [35].
The DV region has been characterized by a complex structural and tectonic history which includes the overprinting of Mesozoic to early Cenozoic contractional structures by late Cenozoic extensional and trans-tensional features [40,41,42]. The northwest trending contractional structures of the DV are at the origin of the Cordilleran orogenic belt of North America, which extends more than 6000 km from southern Mexico to the Canadian Arctic and Alaska [43]. Their age is estimated around 100 Ma and coincides with the Sevier orogenic belt [43,44]. The northeast trend is related to a thrust faults system [41].
The Mesozoic period was marked by the beginning of pluton emplacement in DV along the development of contractional structures. Then, during the Cenozoic period, the DV extension episode occurred [45,46], but there is no general agreement about its timing, e.g. [45,47]. The Miocene period was characterized by a trans-tensional regime. The opening of the DV region as a pull-apart basin began around 5 Ma [41,48,49,50]. A recent study done by [51] challenges this, mentioning that the opening of DV region into pull-apart basin started around 12 Ma ago.
Located in the southernmost part of the DV, the NH range trends parallel to, and then forms, the main topographic features aligned with components of the right-lateral Southern Death Valley Fault Zone (SDVFZ) [37] (Figure 1b). This SDVFZ is part of the Death Valley fault system (DVFS) [52], and its net dextral strike-slip displacement has been estimated around 40–41 km [51]. The northeast-vergent contractional deformation has been characterized along the length of the NH and constitutes the dominant structural style [48,53,54]. In the NH foreland basin, compressional structures have been characterized by [39] near the Canadian Club Wash (Figure 1c). An entire compressional region has also been created by the interaction between the SDVFZ and the GF zone, which is responsible for shortening within the Avawatz Mountains [55,56]. Furthermore, the reverse displacement of the GF was identified in the front of the Avawatz [57]. The E/W fractures observed mainly in the southeast end of the NH show an identical orientation to GF. Given this similarity in orientation and the close vicinity to the GF, it is tempting to relate the E/W trending fracturing to GF zone activity.
Recent work by [37] using high-resolution digital mapping techniques reveals the dominance of basement rocks in the central part of the NH (Figure 1c). Indeed, the granitic rocks are mostly represented and related to the Mesozoic granitic intrusion (Mzla, Figure 1c) [58]. Proterozoic formations characterized by gneiss in the bottom have been defined in the center part and the southeast end of the NH (pCgn, Figure 1c). The Proterozoic Crystal Spring sedimentary series defined in the northwestern part of the NH are mainly composed of carbonates and quartzites facies (pCu, Figure 1c). Some tertiary volcanic series have also been mapped in the southeastern end of the NH.
Outside the center part, Reference [39] has widely studied the Cenozoic NH formations mainly composed of Fanglomerate and alluvial fan deposits.

3. Materials and Methods

3.1. Materials

3.1.1. Large Scale Characterization

The analysis of large scale fracture attributes was performed on fractures digitized from DV regional map at 1:250,000 scale (geological map of California, Trona Sheet [38]) (Figure 2a). In the central part of the NH range, the main structures were mapped during 2018 and 2019 field campaigns published by Klee et al. [37]. In addition, in this present study, orthophoto images of 1 m resolution were used to digitalize and then complete the fractures sampling (Figure 2b).
With the aim of pinpointing the likely fracture variability, the NH range map has been divided into three domains (Figure 3). The sampling strategy along domains is detailed below. In total, 1013 fractures are extracted from the DV geological map, 1434 fractures from the NH map with 306 from domain A, 522 from domain B, and 606 from domain C.
Orientation and length distributions were collected and 1D/2D densities were calculated from them. All of these data are summarized in Table 1.

3.1.2. Photogrammetric Study/Analysis

In order to combine the widest fracture network analysis, three photogrammetric models, localized only in the granitic facies and alongside the major faults that structure the NH range (see Figure 1 for the location), are considered in this study to extract the fractures ranging approximatively from 10−2 m to 20 m. A photogrammetric campaign was carried out in October 2018 with a high-resolution 3D point cloud and large collection of photographs.
Drone model 1 is sized approximately 350 m per 46 m and is located in the granitic facies (Figure 1); 1271 fractures are traced. Drone model 2 is located in the granitic facies within a high deformation zone, and is sized approximately 172 m per 44 m (Figure 1). In total, 4196 fractures are traced. Finally, drone model 3 is located in the southeast termination of NH, and is sized approximately 280 m per 70 m. 15,594 fractures are traced.
The main statistical characteristics are summarized in Table 1.

3.1.3. Fracture Map Characterization

To complete the multiscale analysis with the small fractures, fracture maps were created with a resolution of 2 × 10−4 m. The fracture map 1 (see Figure 1c for location) is sized at 3.4 m per 3.1 m and is located between the granitic facies and the tertiary sediments, near the influence of the SDVFZ (see Figure 1b for the SDVFZ location). It is composed of quartzite boudin facies (part of Crystal Spring series) and granitic rocks, which respectively represent approximately 20% and 80% of occurrences.
In order to include the very small fractures in this study, additional fracture sets were collected from this fracture map with sample 1-1 sized 17 cm per 12 cm (resolution of 10−4 m) and thin sections 1-1 and 1-2 (resolution of 10−5 m), both sized 3.5 per 2.5 cm (see Figure 1c for location). Both sections are composed mainly of Plagioclase, Quartz, K-Feldspar, and Biotite representing respectively 35%, 30%, 25%, and 10% of occurrences.
Fracture map 2 (Figure 1c) is sized 1.7 m per 1.6 m and is located in the granitic facies, near the SDVFZ deformation corridor. This map includes sample 2-1 and thin section 2-1 which size respectively 15 cm per 5.2 cm and 3.5 cm per 2.5 cm. Thin section 2-1 represents the same mineral composition as thin sections 1-1 and 1-2 with approximately the same occurrences. Fracture map 3 (Figure 1c) is sized 1.8 m per 1.7 m and is located also in the granitic facies.
Table 2 summarizes the main statistical characteristics.

3.2. Methods

3.2.1. Fractures Acquisition

In this study, fracture digitization was performed manually by tracing every fracture segment from entire 2D maps in QGIS® software v.2.18.17. Only fractures reported as full solid lines on the DV geological map were considered for statistical analysis (Figure 2a).
Regarding the procedure of fracture digitization, the fractures extending out of the sampling domain were considered as one continuous feature [16,23,59] (Figure 2b). The digitization of fractures consists of an extraction of the end point coordinates of each fracture using the QGIS® software v.2.18.17. Each extracted fracture is characterized by the X and Y coordinates of each of the two end points, which help to compute the orientations and the length of segments. In case of curved fractures, a straight segment line was automatically traced between the end of point coordinates, and then the mean directions and lengths were computed.
As described above, the NH fracture data were acquired during the field mapping campaign and then completed by orthophoto image analysis. The data were analyzed in the entire area (Figure 2b). However, the complexity in loading history within NH widely discussed in the literature [48,54,60] makes the analysis of the fracture geometries difficult. Furthermore, the field observations and the new geological map done by [37] reveal additional complexities inside this area, and show a stacking of different Crystal Spring series (pCu, Figure 1c), intruded by the Mesozoic granite (Mzla, Figure 1c). This observation was highlighted in the northwest part of the NH. In center part, Crystal Spring series thicknesses were reduced, dragged, and stretched against the granite due to the SDVFZ activity (pCu, Figure 1c). The southeast of the NH is characterized by the absence of the Crystal Spring series. To better characterize the fracture variability, it is prime of interest to consider the facies variability and the deformation intensity within NH, because they influence the fracture evolution [23,59]. In this sense, we decided to divide the NH range into three domains according to the facies variability and change in range trend orientation variation (Figure 3): (1) Domain A is located northwestward, highlighted by thick Crystal Spring sediments and granitic rocks; (2) Domain B is in the central part of NH, highlighted by reduced thickness of Crystal Spring sediments, granitic and gneissic rocks, and (3) Domain C is located in the southeastern part of the NH and is characterized by granite, gneiss, and Tertiary volcanism. Note that Domain B and C are composed approximately of the same facies. However, range orientation in domain B is NW/SE, while in domain C it is toward E/W. This general E/W trend is puzzling as it is similar to the GF (see Figure 1b for location). Therefore, this difference in orientation constitutes an additional argument to better delimitate domain B and C. Figure 3 shows the fracture distributions within each domain. Some more work based on field analyses could more precisely delimitate the domains.
The photogrammetric models undertaken in this work were performed using a 3DR Solo drone with 4k cameras and DJI Phantom drone provided by University of Texas at El Paso (UTEP), Texas, USA. The videos were recorded between the late morning and the early afternoon during seven days with a manual mode camera setting to reduce the effects of lighting condition. Pictures were then extracted every second from the recorded drone videos using ffmpeg software v.4.5. The extracted pictures with a sufficient overlapping were aligned in Agisoft Metashape software (2020, Version 1.6.5). The obtained 3D models are georeferenced and then imported in CloudCompare software (version 2.9.1; [GPL software] (2017)) to begin the fracture extraction process. A workflow explaining the procedure of the models construction and the fractures extraction is detailed in [36]. In this study, the digitized fractures are projected on a 2D map to make the work only in 2D in order to keep data homogenous at different scales.
The 2D fracture maps at outcrop scale were performed in the field using a DSLR high resolution camera provided by UniLaSalle (Beauvais, France), with a 50 mm focal lens to minimize distortion. Pictures were taken vertically, with the same distance, and in the absence of sunlight to avoid the light effects in the fracture digitization [12]. From each fracture map, several pictures were taken with a sufficient overlapping. Then, pictures were aligned using the Agisoft Metashape software with the same procedure detailed in [36]. The maps are georeferenced and then used to extract the fractures in QGIS® with the same technique as for large scale maps.
Additional fracture datasets are used in this study by adding samples. These samples were taken directly from fracture maps. Then, a high-resolution picture was taken for each sample using a DSLR camera. With the same procedure as large-scale fractures acquisition, the sample was added in QGIS® to extract the fractures.
Thin section mosaics are also added to this study, made from samples as described earlier to keep a consistent sampling strategy. These mosaics were taken under an optical microscope Leica DM4500-P provided also by UniLaSalle (Beauvais, France), using a ×5 magnification and polarized non-analyzed light mode. A Leica DFC450C high resolution camera provided also by UniLaSalle (Beauvais, France) and Leica application Suite v.4.11.0 were used to take pictures. Every mosaic was relatively oriented using the corresponding sample. Then, with the same fracture digitization procedure described earlier, fracture parameters were extracted under QGIS® v.2.18.17.

3.2.2. Fractures Analysis

Different geometrical parameters were then collected from each fracture database at different scales. Detailed orientation distributions and classification into fracture sets were performed using the mixture of von Mises distribution (MvM) [61]. This approach consists of a semi-automated procedure based on appraisal tests in order to avoid any subjectivity in fracture sets analysis. For each fracture set, three output parameters were considered: (1) mean orientation (µ) around which the distribution is centered, (2) kappa (κ) which controls the concentration of the orientation’s values around the mean, and (3) weight (ω) corresponding to the relative contribution of each fracture set to the model. Then, we are able to check the best number of fracture sets from the distributions using the goodness of fit parameters (e.g., Likelihood). For more details, see [62] who describe and adapt the methodology for structural data. The standard of deviation of +/−10° was calculated for each given mean orientation value in this study.
Fracture length is the most used geometrical parameter to characterize the spatial organization in the natural fracture networks [4,25,63]. This characterization is performed using a statistical distribution as the Power law distributions widely used in structural data from field analogue [4,25,26,63,64]. The power law is often used to describe the distribution of fracture parameters such as length and aperture [25]. It is recognized that power law and fractal geometry provide widely applicable descriptive tools for fracture system characterization. This is due to the absence of characteristic length scales in the fracture growth process. The power law exponent α provides a real significance on the fracture connectivity. Indeed, for an exponent comprised between 2 and 3, fracture connectivity is ruled by both small and large fractures [65]. In addition, fractal analyses using Cantor’s dust method allow the quantification of fracture distribution in clusters or, in the opposite, with a homogeneous distribution [66] and prediction of the fracture occurrence [7]. The exponential law is also used to describe the size of discontinuities in rocks [67,68,69], and to incorporate a characteristic scale that reflects a physical length in the system, such as thickness of a sedimentary layer [70].
However, fitting the geometric attributes to the statistical distributions suffers from a lot of biases, such as truncation and censoring biases [25]. Truncation effects are caused by resolution limitations of a field observation such as from satellite images, the human eye, or microscopes [63]. Censoring effects are associated with the probability that a long fracture intersecting the boundary of the sampling area is not sampled, and to the subjective choice of the sampling area which tends to exclude very long fractures [63,71]. Then, censoring effects cause an overestimation of fracture density. In this study, the truncation and censoring effects were automatically excluded from the distributions. Length distribution in Figure 4 shows the data excluded from the distribution (grey color) due to the impact of truncation and censoring effects.
The fracture length distributions are analyzed using the cumulative distribution. Statistical distributions used in this study were adjusted after corrections from the truncated and censoring effects. Research for truncation and censoring thresholds was performed using the « poweRlaw: Analysis of Heavy Tailed Distributions » package from Rstudio® v.1.3.1056 [72]. We also used the coefficient of determination (R²) to estimate the goodness of fit of the power law to the length distribution. This coefficient is comprised between 0 and 1. A high R² for a given number of degrees of freedom means that the regression is a statistically meaningful description of the data.
Fracture densities are computed in this study. They consist of fracture density (P10), defined as the number of fracture intersections along a 1D virtual scanline traced on every analyzed 2D map [59,73]. The scanline methodology is widely used to describe the fracture variability in 1D [73]. In this study, the linear fracture density P10 was obtained from two virtual scanlines, orientated perpendicular to the main structures.
Finally, the surface fracture density (P21) is defined as the total sum of fracture lengths within the area [59,73].

4. Results

4.1. Large Scale Domains

The mean orientation (µ) N095° (E/W trend) and N132° (NW/SE trend) trending fractures occur at the largest length scale, with a 20 and 24% of whole fractures, and about 3300 to 4400 m mean length (Figure 2a). Both directions are well expressed following the DV and Garlock strike slip trend faults (See Figure 1b for location) [39,48]. The largest fracture length is recorded within the NE/SW fracture set with 65 km length. The other recorded fracture sets are relatively equivalent (around 20%), except for the N025° fracture set which is less dominant, with 13% and 1900 m mean length.
At NH scale, the same dominance of N090° and N126° fracture sets with respectively 37% and 31% are observed (Figure 2b). The other fracture sets are poorly expressed (<15%). The boxplot distribution in Figure 2b showed also the dominance of the E/W and NW/SE fracture sets with respectively 80 m and 125 m mean length. The other fracture sets did not exceed the 50 m mean length.
The occurrence of two prominent fracture sets is shown in the NH domains A and B (Figure 3a,b). Domain A is characterized by two main fracture sets striking N091° and N132° representing respectively 29% and 55% of occurrences (Figure 3b). The N091° fracture set lengths range from 30 m to 300 m, while the N132° fracture set length ranges from 5 m to 800 m, meaning that the NW/SE is the most dominant fracture set in domain A (Figure 3b).
Orientation and length data of domain B shows an equivalent distribution as in domain A (Figure 3b). Indeed, two main fracture sets striking also N088° and N128° are mostly representative with respectively 45% and 31%. The fractures are much longer within NW/SE trend, ranging from 2 m to 1300 m (mean is of 108 m). The other fracture sets show an intermediate length with a 50 m mean value.
Fracture geometry in Domain C shows immediately a different distribution with four main fracture sets striking N050° (19%), N085° (31%), N111° (20%), and N141° (17%) (Figure 3b). The NW/SE fracture set mainly sampled and representative in the domain A and B is split into N111° and N141° fracture sets in domain C, with respective lengths ranging from 3 to 1600 m (mean is 190 m) and from 8 m to 730 m (mean is 65 m).
The fracture densities are increasing considerably from domain A to C with 2 × 10−2/3 × 10−2 m/m² in the domain A and B, and 5 × 10−2 m/m² in the domain C.

4.2. Photogrammetric Models

NH canyons modeled with photogrammetric method provide fractures from centimetric to decametric scale. Fracture distributions are displayed by drone model 1 for both sides of the canyon walls (Figure 4a). Six fracture sets are recorded and strike N025°, N055°, N085°, N115°, N142°, and N174°. The N142° is also the most dominated fracture set with 22%. The E/W fracture set is the less expressed (14%) at outcrop scale. An equivalent mean length of fractures is shown by the boxplot distribution graphic with 2.3 m, whatever the fracture set (Figure 4a).
The exponent of power law (red line in the length distribution, Figure 4) is of α = −2.4 for length distribution of the drone model 1, outside lengths affected by truncation and censoring bias (data mentioned in the length distribution graphic with grey color, Figure 4). The range of length values performed by the power law is 1.85 m to 25 m.
Finally, fracture densities P21 and P10 are of respectively 2 × 10−1 m/m² and 6.5 × 10−1 frac/m.
Fractures from drone model 2 are mainly distributed along the left side of the canyon (Figure 4b). The same fracture sets as drone model 1 are recorded with an equivalent percentage (between 15 and 18%) (Figure 4b). Fracture lengths are highlighted by the boxplot distribution and are also equivalent with 1 m mean length, whatever the fracture set. The largest fractures are recorded within the NW/SE fracture set (maximum of 8.5 m), and then confirm the consistency of the NW/SE direction at outcrop scale.
The fracture length range modeled by the power law is of 0.69 m to 8.5 m, for exponent α = −2.5 and R² = 0.97 (Figure 4b). Fracture lengths under 0.69 m are excluded automatically from the distribution (truncation effects).
Fracture densities are quite high in comparison with Drone model 1, with 7 × 10−1 m/m² and 1.28 frac/m for respectively P21 and P10.
Drone model 3 is the largest studied model with 15594 traced fractures (Figure 5). Six fracture sets are highlighted also in this canyon. Their proportions range from 13% (N079° and N109°), 14–16% (N140° and N038°), to 19–20% (N018 and N169°). The fracture lengths are equivalent, once again, with a 1.2 m mean length.
The power law exponent for drone model 3 length distribution is of α = −2, outside lengths affected by truncation and censoring effects (Figure 5). R² value is of 0.97, indicating a good fit of the power law to the data. Fracture density P21 is of 1 m/m², increasing by a factor 5 compared to drone model 1 fracture density.

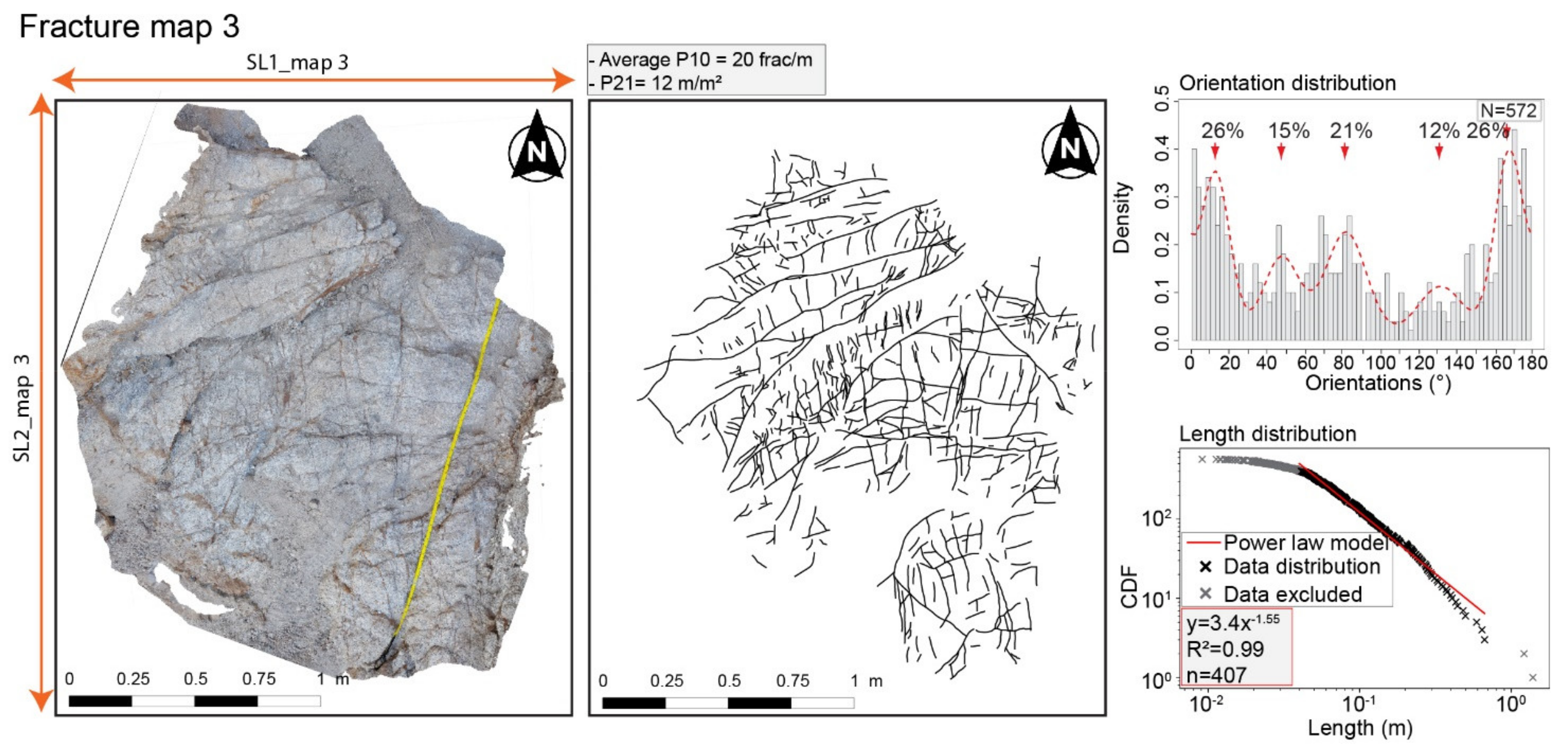
4.3. Fracture Maps

Fracture map 1 is characterized by intense fracture areas, especially along the center part (Highly fractured area, Figure 6). The high fracture density is located mainly in the quartzite boudin, while the less fractured zone is related to the granitic rocks.
For the rest of the fracture map, average P10 of 12 frac/m is computed from two scanlines (SL1_map1 and SL2_map 2, Figure 6), while P21 is of 10 m/m². Two main fracture sets are highlighted: N005° and N083°, with respectively 57% and 32% (Figure 6). Outside fracture lengths affected by truncation and censoring bias, the power law exponent is of α = −1.7 for values ranging from 6 × 10−2 m to 1.2 m.
Sample 1-1 is characterized by homogeneous fracture distribution with four main fracture sets: N018°, N053°, N090°, and N126° representing respectively 27%, 30%, 30%, and 13% (Figure 7a). The largest veins visible in the sample map are characterized by carbonate mineralizations in two directions: N053° and N126°. P10 and P21 fracture densities are of 184 frac/m and 118 m/m² respectively. Regarding the length distribution, the power law exponent is of α = −1.43, with thresholds of 3 × 10−3 m and 7 × 10−2 m.
Four main fracture sets are highlighted in thin section 1-1: N018°, N053°, N090°, and N126° with a comparable fracture proportion (around 25%). Additional fracture set is detected in thin section 1-2: N162°. Regarding the densities, P21 is of 715 m/m² and 702 m/m², while P10 is of 5140 frac/m and 4525 frac/m respectively for thin section 1-1 and 1-2 (Figure 7b,c). The power law exponents are quite higher with α = −1.95 (modeled range from 2.2 × 10−4 m to 4.63 × 10−3 m) and α = −1.7 (modeled range from 2.2 × 10−4 m to 7 × 10−3 m) respectively for thin section 1-1 and 1-2.
Fracture densities of fracture map 2 are comparable with fracture map 1 with average P10 = 18 frac/m and P21 = 13 m/m² (Figure 8a). Five fracture sets are highlighted: N005°, N038°, N070°, N110°, and N145°. The N070° and N145° are the most recorded fracture sets with respectively 32% and 27%.
The power law exponent is also comparable to that of fracture map 1 (α = −1.59), with the thresholds of 8 × 10−2 m and 1.43 m (Figure 8a).
Sample 2-1 is characterized by a fracture density of P10 = 177 frac/m and P21 = 240 m/m² (Figure 8b). In total, five fracture sets are highlighted: N017°, N057°, N092°, N130°, and N157°. Three fracture sets are the most recorded: N057°, N130° and N157°, with 20% to 25%. The power law exponent is of α = −1.66, thresholds from 1.6 × 10−3 m to 3.33 × 10−2 m.
Thin section 2-1 trans-cutting a large carbonate vein in the central part (Figure 8c), is characterized by a fracture density P21 = 1064 m/m² higher than in thin section 1-1 and 1-2. Only four fracture sets are highlighted: N014°, N059°, N097° and N140°, with an equivalent fracture proportion. Outside the lengths affected by sampling bias, the exponent is of α = −2, thresholds of 7 × 10−4 m to 3.5 × 10−2 m.
Finally, fracture map 3 is characterized by a comparable fracture density as in fracture map 2 with P10 = 20 frac/m and P21 = 12 m/m² (Figure 9). Five fracture sets are also detected with a high proportion of 26% for N009° and N149°. Fracture sets N033°, N077°, N104° showed an abundance of 15%, 21%, and 12% respectively. The power law exponent is of α = −1.53 for lengths data ranging from 4 × 10−2 m to 1.21 m.

5. Discussion

The combination of data at various scales in this study allowed to propose a new interpretation of the fracture network in the NH range, based on multiscale evolution of fractures length and orientation. A conceptual scheme of the NH structuration is created and discussed in terms of fracture network connectivity and its influence of fluid flow.

5.1. Multiscale Length Characterization

The cumulative length distributions of each fracture map from the DV regional map scale to thin section scale are plotted in Figure 10. All length datasets have been fitted to the power law distribution, outside lengths affected by truncation and censoring bias.
DV regional map exponent is quite low, around α = −1.40, and gradually increase to around α = −1.62 in NH map (Figure 10a,b). The division of the NH into 3 domains according to the facies variability and the change in range trend orientation showed a disparity in power law exponent values. Indeed, the exponent α = −0.83 in the domain A (values ranging from 21 m to 230 m), while α = −1.42 (values ranging from 25 m to 1283 m) and α = −1.52 (values ranging from 70 m to 1500 m) respectively in domain B and C (Figure 10c–e). The lowest α value in domain A can be explained by the dependence of fracture lengths on scale of observation for fractures ranging from 5 m to 870 m. In addition, the domain A is composed of granitic rocks and Crystal Spring sedimentary series with carbonates and quartzites (Figure 1), meaning that the sedimentary rocks can have a different behavior from that of basement rocks during the fracture growth and propagation process.
Cumulative distribution of fracture lengths in the domain A showed also two different trend slopes (Figure 10c), with a failure slope quantified around 230 m. Distribution into two slopes has been largely discussed in the literature [25,67,70], and can be explained by the fracture growth process which has been divided into two trends. However, this result and interpretation cannot allow to determine if these two trends correspond to a single or to two different regional directions. Cumulative distribution of fracture lengths according to their orientations and the nature of rocks could help to resolve the episodes of deformation challenge, together with some more work in the field (e.g., looking for evidences of displacement).
The cumulative fracture length from all maps has been plotted in a single graphic, normalized by surface area of each map [63] (Figure 10f). The power law distribution included fracture lengths from 2.2 × 10−4 m to 65 km scale. Power law distribution was performed over 6 orders of magnitude. Two length ranges were not represented in this study. The first one corresponds to the fracture lengths over 100 km and related to the first order fracture defined by [30]. This absence can be explained by: (1) a different evolution stage and opening mechanism of faults [30,74], (2) a structural heritage which controls the reactivation during the DV trans-tensional tectonic setting. The second one corresponds to the length ranging from 1 km to 5 km length (Figure 10f). The Basin and Range regional map and the geological map at 1:25,000 scale could help to resolve both gaps.
The power law distribution gives an exponent α = −2 for the whole 2D fracture lengths analyzed in this study (Figure 10f), which suggests the 2D representation is self-similar [4,16,23,26]. The probability to detect fracture of the size of the sampling window is the same at all scales. Then, the fracture connectivity is ruled by the small and large fractures [65], meaning that the large fractures detected and studied at large scale in the NH play the same role as any fracture at millimeter scale in fracture network connectivity.

5.2. Spatial Organization of NH Fracture Network

The fracture densities and the main dominant orientations on the regional maps show the control of NH geometry by NW/SE and E/W trends. Both trends are associated to the second order scale faults over 20 km length, well expressed in terms of abundance (DV regional map, Figure 11). The third order scale detected along NE/SW trend is characterized by faults around 10 km length. Spacing values were computed and correspond to 5 km and 1 km respectively for the second and the third order scale (Figure 12a). The same geometrical characteristics (detailed in the introduction) were approved in the extensional regime [20,30], meaning that the second and third order scale spacing classification can be generalized to the trans-tensional regime studied in the present work.
At NH scale, the fracture densities and the main dominant orientations approve the separation of the NH into three domains:
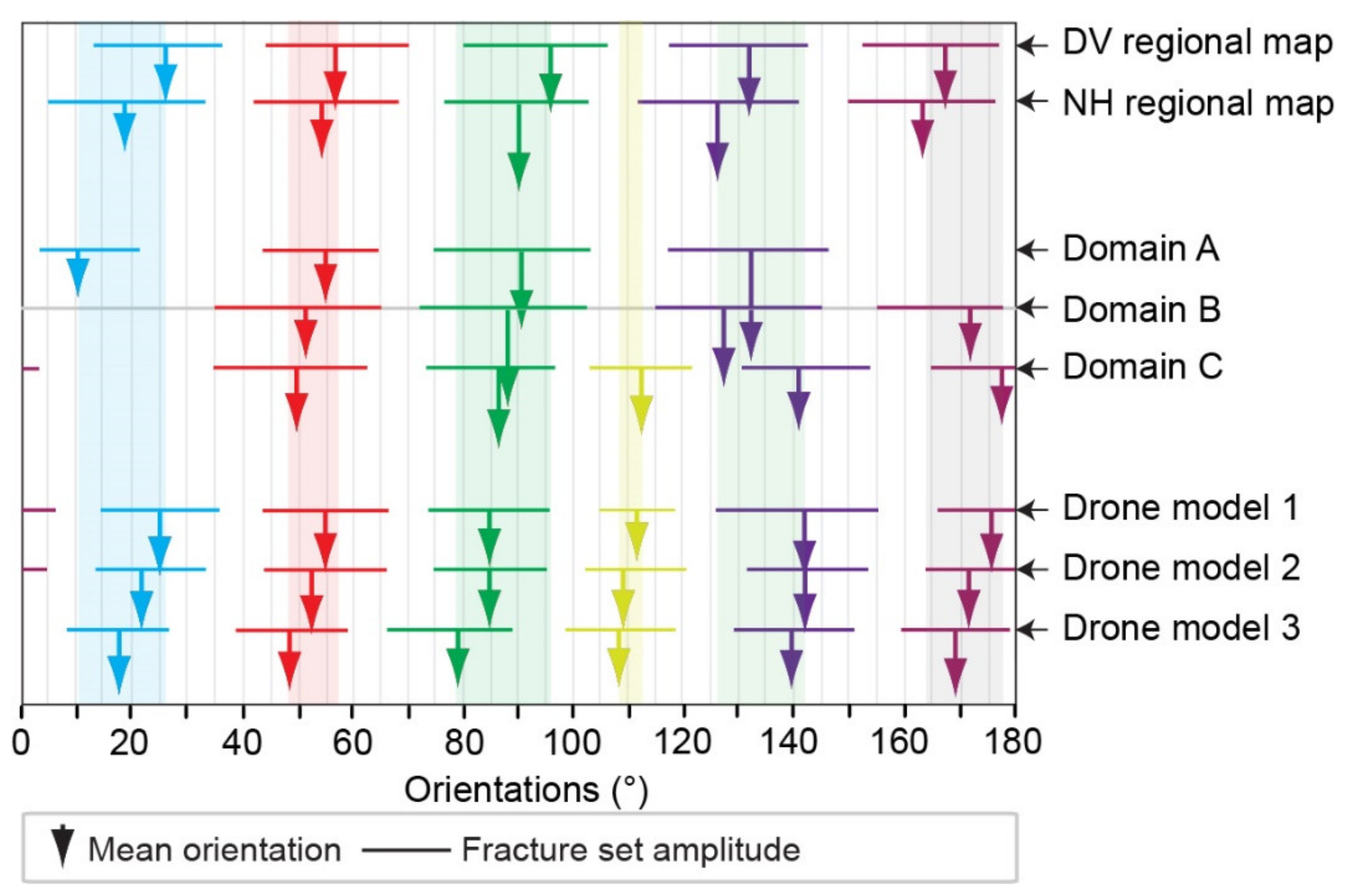
  • The first domain referred to the NH domain A is characterized by a specific spatial arrangement with a NW/SE direction dominance (Domain A, Figure 11). This direction is marked by the SDVFZ bordering fault of the strike-slip corridor, and is mostly dominated the NH fracture network in terms of length and abundance. It approved the importance of the NW/SE deformation episode at the fourth order scale. These fractures are the longest ones and also control the internal structuration inside the domain (Figure 12b). The E/W direction is less represented in comparison with domains B and C (Figure 11), but still the second most dominated fracture set, with less control on the NH geometry. Regarding the spacing characteristics, the NW/SE fractures set are regularly spaced from 0.1 to 0.2 km, while the E/W fractures set did not exceed 0.1 km spacing (Figure 12b).
  • The central domain (domain B, Figure 3) is characterized by several short segments of fractures. Indeed, the E/W direction is also dominated by short fractures with 60 m mean length, while the NW/SE direction is the second dominated system with long fracture of 100 m mean length (Figure 11). Then, NW/SE and E/W directions control the NH geometry respectively following the third and fourth order scale length. In this case, the spacing related to the third order scale is around 1 km between the SDVFZ bordering faults and regularly spaced at 0.2 km (Figure 12b). A spacing of 0.05 km is defined along the E/W fracture set (Figure 12b).
  • The southeastern end area corresponding to the domain C (Figure 3) highlights a specific spatial arrangement with an additional fracture set (yellow color, Figure 11), the longest one with 200 m mean length. Indeed, the NW/SE direction is split into N111° and N141° fracture sets thus highlighting the influence of both NW/SE and E/W deformation episodes in this area. Once again, the E/W direction is more expressed, with a 100 m mean length (Figure 11). The ENE/WSW, E/W and also NW/SE directions control the NH geometry and structuration respectively following the third and fourth order scale. The spacing of 0.3 km defined for the third order scale in domain C between the SDVFZ bordering faults is under the third order spacing characteristic. Indeed, the NW/SE direction has been deviated and then the relative spacing is reduced. Regarding the internal organization, the NW/SE and E/W fractures are also regularly spaced with 0.1–0.2 km and 0.05 km, respectively (Figure 12b).
In the present work, the spacing characteristics of 0.05 km to 0.1–0.2 km computed in the three internal domains are attributed to the fourth order scale (Figure 12b). These values vary according to their directions and also lengths. Two spacing characteristics can be highlighted from this study: (1) spacing of 0.05 km corresponding to the fractures comprised between 0.1 and 0.35 km (percentile 90 values), (2) spacing of 0.1–0.2 m corresponding to the fractures comprised between 0.35 and 0.5 km. Further work on the fourth order scale spacing characteristics will obviously be needed in order to generalize them to the trans-tensional regime.
At outcrop scale, the drone models highlighted the reproducibility and the consistency of the whole fracture sets defined at large scale (Figure 11). However, N111° fracture set, detected only in domain C, is less expressed in domain A (drone model 1, 9%) (Figure 11). The E/W direction trend is more expressed in the drone models 2 and 3 respectively in the domain B and C. This observation is confirmed by the fracture maps 2 and 3, sample 2-1 and thin section 2-1 (Figure 8 and Figure 9), highlighting a consistent fracturing episode. In the previous works, [39,55,56,57] mentioned the presence of the compression signature at the southeastern end of the NH and the front of the Avawatz mountains. According to these studies and our current observations, a hypothesis of fracturing intensity which affected up to the internal domain can explain the consistency of the E/W direction.
A special fracture arrangement was observed in fracture map 1 (Figure 6). The length distribution is characterized by a high density of short fractures in the quartzite boudin rocks, while the granitic part is characterized by a lower density of long fractures. This leads to a change in the power law and orientation distributions and then makes a bias. Indeed, only N/S and E/W directions are recorded, while the sample 1-1, thin sections 1-1 and 1-2 have recorded the whole fracture sets.
Fractures are organized along SDVFZ direction as fault zone segments with a highly mineralized (clay minerals) fault core (FC) which can act as a barrier and damage zone (DZ), acting as a conduit (Figure 12c). A complex joint network that can play a key role in the fracture connectivity is highlighted in the host rock. A petrographic study focusing on these fault zones is required to better characterize the fluid circulation potential.
The N/S to NNE/SSW and the NE/SW fracture sets are less expressed and are attributed to the fourth order scale with 40 m mean length on NH map, while they are still very important and consistent at outcrop, sample, and thin section scales, regardless of domain (Figure 2, Figure 3, Figure 4 and Figure 5). These trends are highly dependent on the scale of observation and have no influence on the NH geometry.
To summarize, a new spatial organization of the NH range based on second, third, and fourth order scales has been proposed with length, spacing, density, and orientation distributions. Each NH domain shows its own internal organization. Variability in between recorded fracture sets from different areas is a marker of a complex tectonic and geometrical setting. One main deformation episode played a key role in the NH structuration: SDVFZ trending NW/SE affected whole NH and then controlled its geometry. The second main deformation episode is in the GF system trending E/W, likely responsible for E/W fracturing episode, and controlled the NH geometry mostly in its internal part and the southeastern end.
The identical orientation of GF and the E/W structures could suggest that the GF was responsible for the E/W fracturing in the internal and southeastern end domains (Figure 12b). Furthermore, the E/W structures are characterized by a sinistral strike-slip displacement, highlighted by the movement of the tertiary volcanic blocks in the back of the NH. This sinistral strike-slip movement has been characterized along the GF zone, widely described in the literature [55,57]. The similarities on the strike-slip nature can help to consider that the E/W fractures are related to GF activity which plays a key role on the NH geometry. In addition, the lower dominance of the NW/SE direction in the central and the southeastern end of the NH can be explained by the overprinting of the E/W fracturing, highlighting that these structures are posterior to the SDVFZ system (Figure 12c).
Regarding the fracture distributions, the fracture density is higher in the domain C with a factor 2.5 and 1.5, in comparison respectively with domain A and B (Figure 3). At outcrop scale, fracture densities raise from domains A and B to domain C with a factor 05 and 1.4, approving the localization of the fracture intensity in this area due to the complex tectonic setting [39]. Furthermore, a gradient of deformation has been observed in the field along the entire NH length with evidence of extreme shearing, notably in the internal domain. Boudinage structures and brittle shearing are prevalent within Crystal Spring series. A future publication will be planned to better characterize this deformation.

5.3. Fracture Network Impact on Flow

The deformation occurred with a different intensity at the whole NH scale. This can influence the fluid circulation through the fracture network following the domains. Even if the connectivity in the reservoir analogue is ruled by the large and small fractures (Figure 10f), some domains, such as domain A, had a different behavior insofar as the connectivity was ruled by only the large fractures. A complex joint network is highlighted at outcrop scale in the host rock and plays a key role in the fracture connectivity leading the fluid supply toward the fault zone.
The fluid flow modeling in this reservoir analogue should consider that the orientation parameter depends on scale observation and then should be modeled differently at each scale, while the length parameter is independent of the observation scale in the case of NH geothermal reservoir analogue.
Flow simulations will be planned in the future publications, based on photogrammetric models acquired from different NH domains. This study can help to approve the sensitivity of the fluid circulations to the gradient of strike-slip deformation and the spatial arrangement of NH fracture network. The sensitivity of the deterministic models on resulting permeability will be tested according to the directional dependence and their corresponding length distribution.

6. Conclusions

This study is part of the MEET project (Multidisciplinary and multi-context demonstration of EGS exploration and Exploitation Techniques and potentials), aiming at developing geothermal exploitation at European scale by applying Enhanced Geothermal System (EGS) technology to different geological settings. NH range, assimilated to a paleo geothermal reservoir analogue, gives an opportunity to study the basement rocks in trans-tensional context. This study proposes geometric description and quantifies the multiscale network organization and its effect on connectivity using a wide-ranging analysis scale from the microscopic scale to the regional scale. We used 2D fracture maps at different scales. We have shown a power law distribution for six orders of scales. Then, a power law exponent of α = −2 was computed by combining the whole datasets, meaning that the connectivity is ruled by the small and the large fractures.
A new spatial arrangement of the fracture network at different scales has been proposed for the NH range, based on densities, spacings, orientations, and length distributions. The SDVFZ controls the NH geometry at large scale within the second order scale, while the E/W directions—whose origin remains to be determined—controls the NH geometry within the third order scale. The spacing characteristics are of 5 and 1 km for respectively the second and the third order scale, and correspond to the spacings highlighted in the extensional regime.
The division into three domains according to the facies variability and the change in range trend orientation has been approved by statistical analysis. Indeed, domain A is characterized by a dominance of the NW/SE direction in terms of length and abundance at the fourth order scale with a regular fracture spacing of 0.1–0.2 km. Then, NW/SE direction controls the internal structuration of this domain. Domain B is structured by the second and third orders of fractures scales following the E/W and NW/SE direction with regular spacing of 0.2 km and 0.005 km, respectively. Domain C was also characterized by the structuration of a specific spatial arrangement with the dominance of short fractures following E/W direction, which highlight the persistence of the E/W fracturing episode. The ENE/WSW, E/W, and also NW/SE directions control the NH geometry and structuration in this area. A regular spacing of 0.2 km and 0.005 km is computed inside the domain at fourth order scale. Therefore, two spacing characteristics have been highlighted in this study at fourth order scale: 0.1–0.2 km and 0.05 km spacing for fractures length of 0.1–0.35 km and 0.005 km, respectively.
Each internal domain described in this study proposes its own spatial arrangement of fracture network. Indeed, two main deformation episodes referring to the SDVFZ striking NW/SE and fractures system striking E/W play a key role in the structuration of the NH range. However, the SDVFZ deformation affected the whole NH, whereas the E/W fracturing affected only the central and the southeastern area.
Fluid flow modeling will be planned and will take into consideration that orientation parameters should be modelled differently at each scale, while length parameters modelled by the power law should be considered as homogenous at different scales.

Author Contributions

Conceptualization, A.C., G.T. and B.A.L.; methodology, A.C.; software, A.C.; validation, G.T., B.A.L. and J.K.; formal analysis, A.C.; investigation, A.C., G.T., B.A.L. and J.K.; resources, A.C.; data curation, A.C.; writing—original draft preparation, A.C.; writing—review and editing, G.T., B.A.L. and H2020 MEET consortium; visualization, G.T., B.A.L. and J.K.; supervision, G.T.; project administration, G.T.; funding acquisition, G.T. and H2020 MEET consortium. All authors have read and agreed to the published version of the manuscript.

Funding

This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 792037 (MEET project).

Data Availability Statement

Not applicable.

Acknowledgments

This work is part of postdoctoral contribution, prepared at Institut Polytechnique UniLaSalle Beauvais, which was funded by European Union’s Horizon 2020 research (H2020 MEET project). We are grateful to Armand Pomart and Ruben Attali for their help for analyses. We also wish to thank the H2020 MEET consortium for their helpful comments and manuscript validation. We also thank the Assistant Editor Sorin Hadrian Petrescu and the anonymous reviewers for the relevant remarks that significantly approved the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bour, O.; Davy, P. Connectivity of Random Fault Networks Following a Power Law Fault Length Distribution. Water Resour. Res. 1997, 33, 1567–1583. [Google Scholar] [CrossRef]
  2. Gillespie, D.T. Approximate Accelerated Stochastic Simulation of Chemically Reacting Systems. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
  3. Berkowitz, B. Characterizing Flow and Transport in Fractured Geological Media: A Review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
  4. Odling, N.E.; Gillespie, P.; Bourgine, B.; Castaing, C.; Chiles, J.P.; Christensen, N.P.; Fillion, E.; Genter, A.; Olsen, C.; Thrane, L. Variations in Fracture System Geometry and Their Implications for Fluid Flow in Fractured Hydrocarbon Reservoirs. Pet. Geosci. 1999, 5, 373–384. [Google Scholar] [CrossRef]
  5. Johnston, J.D.; McCaffrey, K.J.W. Fractal Geometries of Vein Systems and the Variation of Scalingrelationships with Mechanism. J. Struct. Geol. 1996, 18, 349–358. [Google Scholar] [CrossRef]
  6. Geiger, S.; Emmanuel, S. Non-Fourier Thermal Transport in Fractured Geological Media. Water Resour. Res. 2010, 46, W07504. [Google Scholar] [CrossRef]
  7. Ledésert, B.; Dubois, J.; Genter, A.; Meunier, A. Fractal Analysis of Fractures Applied to Soultz-Sous-Forets Hot Dry Rock Geothermal Program. J. Volcanol. Geotherm. Res. 1993, 57, 1–17. [Google Scholar] [CrossRef]
  8. Dezayes, C.; Genter, A.; Valley, B. Structure of the Low Permeable Naturally Fractured Geothermal Reservoir at Soultz. Comptes Rendus Géosciences 2010, 343, 517–530. [Google Scholar] [CrossRef] [Green Version]
  9. Valley, B.; Dezayes, C.; Genter, A.; Maqua, E.; Syren, G. Main Fracture Zones in GPK3 and GPK4 and Cross-Hole Correlations. In Proceedings of the EHDRA Scientific Conference, Soultz-sous-Forêts, France, 17–18 March 2005. [Google Scholar]
  10. Bour, O.; Davy, P. On the Connectivity of Three-dimensional Fault Networks. Water Resour. Res. 1998, 34, 2611–2622. [Google Scholar] [CrossRef]
  11. Darcel, C.; Bour, O.; Davy, P.; de Dreuzy, J.R. Connectivity Properties of Two-Dimensional Fracture Networks with Stochastic Fractal Correlation: Connectivity of 2D Fractal Fracture Networks. Water Resour. Res. 2003, 39, 1272. [Google Scholar] [CrossRef]
  12. Odling, N.E. Scaling and Connectivity of Joint Systems in Sandstones from Western Norway. J. Struct. Geol. 1997, 19, 1257–1271. [Google Scholar] [CrossRef]
  13. Castaing, C.; Halawani, M.A.; Gervais, F.; Chilès, J.P.; Genter, A.; Bourgine, B.; Ouillon, G.; Brosse, J.M.; Martin, P.; Genna, A. Scaling Relationships in Intraplate Fracture Systems Related to Red Sea Rifting. Tectonophysics 1996, 261, 291–314. [Google Scholar] [CrossRef]
  14. Marrett, R.; Ortega, O.J.; Kelsey, C.M. Extent of Power-Law Scaling for Natural Fractures in Rock. Geology 1999, 27, 799–802. [Google Scholar] [CrossRef]
  15. Soliva, R.; Schultz, R.A.; Benedicto, A. Three-dimensional Displacement-length Scaling and Maximum Dimension of Normal Faults in Layered Rocks. Geophys. Res. Lett. 2005, 32, L16302. [Google Scholar] [CrossRef] [Green Version]
  16. Bertrand, L.; Géraud, Y.; Le Garzic, E.; Place, J.; Diraison, M.; Walter, B.; Haffen, S. A Multiscale Analysis of a Fracture Pattern in Granite: A Case Study of the Tamariu Granite, Catalunya, Spain. J. Struct. Geol. 2015, 78, 52–66. [Google Scholar] [CrossRef]
  17. Bertrand, L.; Jusseaume, J.; Géraud, Y.; Diraison, M.; Damy, P.-C.; Navelot, V.; Haffen, S. Structural Heritage, Reactivation and Distribution of Fault and Fracture Network in a Rifting Context: Case Study of the Western Shoulder of the Upper Rhine Graben. J. Struct. Geol. 2018, 108, 243–255. [Google Scholar] [CrossRef]
  18. Ehlen, J. Fractal Analysis of Joint Patterns in Granite. Int. J. Rock Mech. Min. Sci. 2000, 37, 909–922. [Google Scholar] [CrossRef]
  19. Genter, A.; Castaing, C. Effets d’échelle Dans La Fracturation Des Granites. Comptes Rendus de l’Académie des Sci. Ser. IIA Earth Planet. Sci. 1997, 325, 439–445. [Google Scholar] [CrossRef]
  20. Le Garzic, E.; de L’Hamaide, T.; Diraison, M.; Géraud, Y.; Sausse, J.; De Urreiztieta, M.; Hauville, B.; Champanhet, J.-M. Scaling and Geometric Properties of Extensional Fracture Systems in the Proterozoic Basement of Yemen. Tectonic Interpretation and Fluid Flow Implications. J. Struct. Geol. 2011, 33, 519–536. [Google Scholar] [CrossRef]
  21. De Dreuzy, J.-R.; Davy, P.; Bour, O. Hydraulic Properties of Two-dimensional Random Fracture Networks Following Power Law Distributions of Length and Aperture. Water Resour. Res. 2002, 38, 12-1–12-9. [Google Scholar] [CrossRef]
  22. Davy, P.; Le Goc, R.; Darcel, C.; Bour, O.; de Dreuzy, J.R.; Munier, R. A Likely Universal Model of Fracture Scaling and Its Consequence for Crustal Hydromechanics. J. Geophys. Res. 2010, 115, B10411. [Google Scholar] [CrossRef]
  23. Hardebol, N.J.; Maier, C.; Nick, H.; Geiger, S.; Bertotti, G.; Boro, H. Multiscale Fracture Network Characterization and Impact on Flow: A Case Study on the Latemar Carbonate Platform. J. Geophys. Res. Solid Earth 2015, 120, 8197–8222. [Google Scholar] [CrossRef]
  24. McCaffrey, K.J.W.; Sleight, J.M.; Pugliese, S.; Holdsworth, R.E. Fracture Formation and Evolution in Crystalline Rocks: Insights from Attribute Analysis. Geol. Soc. Lond. Spec. Publ. 2003, 214, 109–124. [Google Scholar] [CrossRef]
  25. Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of Fracture Systems in Geological Media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
  26. Bour, O.; Davy, P.; Darcel, C.; Odling, N. A Statistical Scaling Model for Fracture Network Geometry, with Validation on a Multiscale Mapping of a Joint Network (Hornelen Basin, Norway). J. Geophys. Res. Solid Earth 2002, 107, ETG 4-1–ETG 4-12. [Google Scholar] [CrossRef]
  27. Bonneau, F.; Caumon, G.; Renard, P.; Sausse, J. Stochastic Sequential Simulation of Genetic-like Discrete Fracture Networks. Proceeding 32nd Gocad Meeting, Nancy, France. 2012. Available online: https://www.ring-team.org/component/liad/?view=pub&id=2214 (accessed on 3 July 2021).
  28. de Dreuzy, J.-R.; Méheust, Y.; Pichot, G. Influence of Fracture Scale Heterogeneity on the Flow Properties of Three-Dimensional Discrete Fracture Networks (DFN): 3D Fracture Network Permeability. J. Geophys. Res. 2012, 117, B11207. [Google Scholar] [CrossRef] [Green Version]
  29. Chabani, A. Analyse Méthodologique et Caractérisation Multi-Échelle Des Systèmes de Fractures à l’interface Socle/Couverture Sédimentaire Application à La Géothermie (Bassin de Valence, SE France). These de Doctorat, Paris Sciences et Lettres (ComUE), Paris, France, 2019. Available online: http://www.theses.fr/2019PSLEM046 (accessed on 3 July 2021).
  30. Morellato, C.; Redini, F.; Doglioni, C. On the Number and Spacing of Faults. Terra Nova 2003, 15, 315–321. [Google Scholar] [CrossRef]
  31. Bourbiaux, B.; Basquet, R.; Daniel, J.M.; Hu, L.Y.; Jenni, S.; Lange, G.; Rasolofosaon, P. Fractured Reservoirs Modelling: A Review of the Challenges and Some Recent Solutions. First Break 2005, 23. [Google Scholar] [CrossRef]
  32. Gillespie, P.; Monsen, E.; Maerten, L.; Hunt, D.; Thurmond, J.; Tuck, D.; Martinsen, O.J.; Pulham, A.J.; Haughton, P.D.W.; Sullivan, M.D. Fractures in Carbonates: From Digital Outcrops to Mechanical Models. Outcrops Revital.—Tools Tech. Appl. Tulsa Okla. SEPM Concepts Sedimentol. Paleontol. 2011, 10, 137–147. [Google Scholar]
  33. Vollgger, S.A.; Cruden, A.R. Mapping Folds and Fractures in Basement and Cover Rocks Using UAV Photogrammetry, Cape Liptrap and Cape Paterson, Victoria, Australia. J. Struct. Geol. 2016, 85, 168–187. [Google Scholar] [CrossRef]
  34. Biber, K.; Khan, S.D.; Seers, T.D.; Sarmiento, S.; Lakshmikantha, M.R. Quantitative Characterization of a Naturally Fractured Reservoir Analog Using a Hybrid Lidar-Gigapixel Imaging Approach. Geosphere 2018, 14, 710–730. [Google Scholar] [CrossRef]
  35. Trullenque, G.; Genter, A.; Leiss, B.; Wagner, B.; Bouchet, R.; Léoutre, E.; Malnar, B.; Bär, K.; Rajšl, I. Upscaling of EGS in Different Geological Conditions: A European Perspective. In Proceedings of the Proceedings 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018. [Google Scholar]
  36. Chabani, A.; Trullenque, G.; Rishi, P.; Pomart, A.; Attali, R.; Sass, I. Modelling of Fractured Granitic Geothermal Reservoirs: Use of Deterministic and Stochastic Methods in Discrete Fracture Networks and a Coupled Processes Modeling Framework. In Proceedings of the Extended Abstract, Reykjavik, Iceland, 2 May 2021. [Google Scholar]
  37. Klee, J.; Trullenque, G.; Ledésert, B.; Potel, S.; Hébert, R.; Chabani, A.; Genter, A. Petrographic Analyzes of Fractured Granites Used as An Analogue of the Soultz-Sous-Forêts Geothermal Reservoir: Noble Hills, CA, USA. In Proceedings of the Extended Abstract, Reykjavik, Iceland, 26 May 2021. [Google Scholar]
  38. Jennings, C. Geologic Map of California, Scale 1: 250,000. Olaf P. Jenkins Edition, Long Beach Sheet. Calif. Div. Mines Geol, Serie No 33, List No 6347.033; CA, USA, 1962. Available online: https://www.davidrumsey.com/luna/servlet/detail/RUMSEY~8~1~324920~90093990:Geologic-Map-of-California,-Long-Be?sort=Pub_List_No_InitialSort%2CPub_Date%2CPub_List_No%2CSeries_No (accessed on 3 July 2021).
  39. Niles, J.H. Post-Middle Pliocene Tectonic Development of the Noble Hills, Southern Death Valley, California. Doctoral Dissertation, San Francisco State University, San Francisco, CA, USA, 2016. [Google Scholar]
  40. Miller, M.; Pavlis, T. The Black Mountains Turtlebacks: Rosetta Stones of Death Valley Tectonics. Earth-Sci. Rev. 2005, 73, 115–138. [Google Scholar] [CrossRef]
  41. Pavlis, T.L.; Rutkofske, J.; Guerrero, F.; Serpa, L.F. Structural Overprinting of Mesozoic Thrust Systems in Eastern California and Its Importance to Reconstruction of Neogene Extension in the Southern Basin and Range. Geosphere 2014, 10, 732–756. [Google Scholar] [CrossRef] [Green Version]
  42. Snow, J.K.; Wernicke, B. Uniqueness of Geological Correlations: An Example from the Death Valley Extended Terrain. Geol. Soc. Am. Bull. 1989, 101, 1351–1362. [Google Scholar] [CrossRef]
  43. DeCelles, P.G. Late Jurassic to Eocene Evolution of the Cordilleran Thrust Belt and Foreland Basin System, Western U.S.A. Am. J. Sci. 2004, 304, 105–168. [Google Scholar] [CrossRef]
  44. Walker, J.D.; Burchfiel, B.; Davis, G.A. New Age Controls on Initiation and Timing of Foreland Belt Thrusting in the Clark Mountains, Southern California. Geol. Soc. Am. Bull. 1995, 107, 742–750. [Google Scholar] [CrossRef]
  45. Stewart, J.H. Possible Large Right-Lateral Displacement along Fault and Shear Zones in the Death Valley-Las Vegas Area, California and Nevada. Geol. Soc. Am. Bull. 1967, 78, 131–142. [Google Scholar] [CrossRef]
  46. Stewart, J.H. Extensional Tectonics in the Death Valley Area, California: Transport of the Panamint Range Structural Block 80 Km Northwestward. Geology 1983, 11, 153–157. [Google Scholar] [CrossRef]
  47. Snow, J.K. Cenozoic Tectonism in the Central Basin and Range; Magnitude, Rate, and Distribution of Upper Crustal Strain. Am. J. Sci. 2000, 300, 659–719. [Google Scholar] [CrossRef]
  48. Brady, R. Cenozoic Geology of the Northern Avawatz Mountains in Relation to the Intersection of the Garlock and Death Valley Fault Zones, San Bernardino County, California. Doctoral Dissertation, University of California, Davis, CA, USA, 1987. [Google Scholar]
  49. Norton, I. Two-Stage Formation of Death Valley. Geosphere 2011, 7, 171–182. [Google Scholar] [CrossRef]
  50. Burchfiel, B.C.; Stewart, J.H. “Pull-Apart” Origin of the Central Segment of Death Valley, California. Geol. Soc. Am. Bull. 1966, 77, 439–442. [Google Scholar] [CrossRef]
  51. Pavlis, T.L.; Trullenque, G. Evidence for 40–41 Km of Dextral Slip on the Southern Death Valley Fault: Implications for the Eastern California Shear Zone and Extensional Tectonics. Geology 2021, 49, 767–772. [Google Scholar] [CrossRef]
  52. Machette, M.N.; Klinger, R.E.; Knott, J.R.; Wills, C.J.; Bryant, W.A.; Reheis, M.C. A Proposed Nomenclature for the Death Valley Fault System. Quaternary and Late Pliocene Geology of the Death Valley Region: Recent Observations on Tectonics, Stratigraphy, and Lake Cycles (Guidebook for the 2001 Pacific Cell—Friends of the Pleistocene Fieldtrip); US Department of the Interior, US Geological Survey: Reston, VA, USA, 2001; p. 173.
  53. Troxel, B.W.; Butler, P.R. Rate of Cenozoic Slip on Normal Faults, South-Central Death Valley, California. Doctoral Dissertation, Departement of Geology, University of California, Office of Scholarly Communication (OSC), Irvine, CA, USA, 1979. [Google Scholar]
  54. Brady III, R.H. Neogene Stratigraphy of the Avawatz Mountains between the Garlock and Death Valley Fault Zones, Southern Death Valley, California: Implications as to Late Cenozoic Tectonism. Sediment. Geol. 1984, 38, 127–157. [Google Scholar] [CrossRef]
  55. Reinert, E. Low Temperature Thermochronometry of the Avawatz Mountians, California: Implications for the Inception of the Eastern California Shear Zone. Doctoral Dissertation, University of Washington, Washington, DC, USA, 2004. Available online: https://www.ess.washington.edu/content/people/student_publications_files/reinert--erik/Reinert_2004.pdf (accessed on 3 July 2021).
  56. Spencer, J.E. Late Cenozoic Extensional and Compressional Tectonism in the Southern and Western Avawatz Mountains, Southeastern California. Basin and Range Extensional Tectonics near the Latitude of Las Vegas, Nevada: Geological Society of America Memoir; Geological Society of America: Las Vegas, NV, USA, 1990; Volume 176, pp. 317–333. [Google Scholar] [CrossRef]
  57. Chinn, L.D. Low-Temperature Thermochronometry of the Avawatz Mountains; Implications for the Eastern Terminus and Inception of the Garlock Fault Zone; University of Washington: Washington, DC, USA; Available online: https://www.ess.washington.edu/content/people/student_publications_files/chinn--logan/chinn--logan_ms_2013.pdf (accessed on 3 July 2021).
  58. Rämö, T.O.; Calzia, J.P.; Kosunen, P.J. Geochemistry of Mesozoic Plutons, Southern Death Valley Region, California: Insights into the Origin of Cordilleran Interior Magmatism. Contrib. Mineral. Petrol. 2002, 143, 416–437. [Google Scholar] [CrossRef]
  59. Bisdom, K.; Gauthier, B.D.M.; Bertotti, G.; Hardebol, N.J. Calibrating Discrete Fracture-Network Models with a Carbonate Threedimensional Outcrop Fracture Network: Mplications for Naturally Fractured Reservoir Modeling. AAPG Bull. 2014, 98, 13511376. [Google Scholar] [CrossRef]
  60. Brady, R.H.; Troxel, B.W.; Wright, L.A. The Miocene Military Canyon Formation: Depocenter Evolution and Constraints on Lateral Faulting, Southern Death Valley, California. Spec. Pap. Geol. Soc. Am. 1999, 277–288. [Google Scholar] [CrossRef]
  61. von Mises, R. Uber Die “Ganzzahligkeit” Der Atomgewicht Und Verwandte Fragen. Physikal. Z. 1918, 19, 490–500. [Google Scholar]
  62. Chabani, A.; Mehl, C.; Cojan, I.; Alais, R.; Bruel, D. Semi-Automated Component Identification of a Complex Fracture Network Using a Mixture of von Mises Distributions: Application to the Ardeche Margin (South-East France). Comput. Geosci. 2020, 137, 104435. [Google Scholar] [CrossRef]
  63. Pickering, G.; Bull, J.M.; Sanderson, D.J. Sampling Power-Law Distributions. Tectonophysics 1995, 248, 1–20. [Google Scholar] [CrossRef] [Green Version]
  64. Pickering, G.; Peacock, D.C.; Sanderson, D.J.; Bull, J.M. Modeling Tip Zones to Predict the Throw and Length Characteristics of Faults. AAPG Bull. 1997, 81, 82–99. [Google Scholar]
  65. Davy, P.; Bour, O.; De Dreuzy, J.-R.; Darcel, C. Flow in Multiscale Fractal Fracture Networks. Geol. Soc. Lond. Spec. Publ. 2006, 261, 31–45. [Google Scholar] [CrossRef]
  66. Ledésert, B.; Dubois, J.; Velde, B.; Meunier, A.; Genter, A.; Badri, A. Geometrical and Fractal Analysis of a Three-Dimensional Hydrothermal Vein Network in a Fractured Granite. J. Volcanol. Geotherm. Res. 1993, 56, 267–280. [Google Scholar] [CrossRef]
  67. Cruden, D.M. Describing the Size of Discontinuities; Elsevier: Amsterdam, The Netherlands, 1977; Volume 14, pp. 133–137. [Google Scholar]
  68. Priest, S.D.; Hudson, J.A. Estimation of Discontinuity Spacing and Trace Length Using Scanline Surveys; Elsevier: Amsterdam, The Netherlands, 1981; Volume 18, pp. 183–197. [Google Scholar]
  69. Priest, S.D.; Hudson, J.A. Discontinuity Spacings in Rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1976, 13, 135–148. [Google Scholar] [CrossRef]
  70. Cowie, P.A.; Sornette, D.; Vanneste, C. Multifractal Scaling Properties of a Growing Fault Population. Geophys. J. Int. 1995, 122, 457–469. [Google Scholar] [CrossRef] [Green Version]
  71. Priest, S.D. Discontinuity Analysis for Rock Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
  72. Gillespie, C.S. The PoweRlaw Package: A General Overview. Newcastle, UK. Available online: https://cran.r-project.org/web/packages/poweRlaw/vignettes/a_introduction.pdf (accessed on 3 July 2021).
  73. Gillespie, P.A.; Howard, C.B.; Walsh, J.J.; Watterson, J. Measurement and Characterisation of Spatial Distributions of Fractures. Tectonophysics 1993, 226, 113–141. [Google Scholar] [CrossRef]
  74. Bertrand, L. Etude Des Réservoirs Géothermiques Développés Dans Le Socle et à l’interface Avec Les Formations Sédimentaires. Doctoral Dissertation, Université de Lorraine, Lorraine, France, April 2017; p. 492. [Google Scholar]
Geosciences 11 00280 g001 550
Figure 1. (a,b) Location and geological setting of DV, NDVFZ: Northern Death Valley Fault Zone, SDVFZ: Southern Death Valley Fault Zone; (c) Structural scheme of the NH range built using high-resolution digital mapping techniques modified after [37,39]. Additional digitized fractures were performed using orthophotos. The aerial picture in (b) was extracted from Google Earth®. The samples location was reported in the structural scheme. FM: fracture map.
Figure 1. (a,b) Location and geological setting of DV, NDVFZ: Northern Death Valley Fault Zone, SDVFZ: Southern Death Valley Fault Zone; (c) Structural scheme of the NH range built using high-resolution digital mapping techniques modified after [37,39]. Additional digitized fractures were performed using orthophotos. The aerial picture in (b) was extracted from Google Earth®. The samples location was reported in the structural scheme. FM: fracture map.
Geosciences 11 00280 g001
Geosciences 11 00280 g002 550
Figure 2. Fracture traces, orientation, and boxplot distributions from (a) DV geological map and (b) NH range map (in red rectangle for large scale location). The order of fractures magnitude were referred to the classification detailed in [30]. The first order referred to the faults larger 100 km length is not detected in this study. Each fracture map dataset is expressed in histogram for orientation distribution, and into boxplot for length distribution, according to the fracture orientations. Two scanlines (SL) were taken for every map.
Figure 2. Fracture traces, orientation, and boxplot distributions from (a) DV geological map and (b) NH range map (in red rectangle for large scale location). The order of fractures magnitude were referred to the classification detailed in [30]. The first order referred to the faults larger 100 km length is not detected in this study. Each fracture map dataset is expressed in histogram for orientation distribution, and into boxplot for length distribution, according to the fracture orientations. Two scanlines (SL) were taken for every map.
Geosciences 11 00280 g002
Geosciences 11 00280 g003 550
Figure 3. Fracture traces from the NH range divided into 3 domains. (a) NH domains: A, B, and C, (b) orientation distributions, and (c) boxplot of length distributions according to the fracture orientations. Two scanlines (SL) were taken for every domain. For boxplot and orientation distribution legend, see Figure 2.
Figure 3. Fracture traces from the NH range divided into 3 domains. (a) NH domains: A, B, and C, (b) orientation distributions, and (c) boxplot of length distributions according to the fracture orientations. Two scanlines (SL) were taken for every domain. For boxplot and orientation distribution legend, see Figure 2.
Geosciences 11 00280 g003
Geosciences 11 00280 g004 550
Figure 4. Fracture traces, orientation, boxplot length distributions from (a) drone model 1 and (b) drone model 2. Each fracture map data is expressed into histogram for orientation distribution, boxplot of length distribution according to the fracture orientations, and cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken along the left and the right side of the canyon. For the boxplots and orientation distributions legend, see Figure 2.
Figure 4. Fracture traces, orientation, boxplot length distributions from (a) drone model 1 and (b) drone model 2. Each fracture map data is expressed into histogram for orientation distribution, boxplot of length distribution according to the fracture orientations, and cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken along the left and the right side of the canyon. For the boxplots and orientation distributions legend, see Figure 2.
Geosciences 11 00280 g004
Geosciences 11 00280 g005 550
Figure 5. Fracture traces, orientation, boxplot length distributions from drone model 3. Different Datasets are expressed into histogram for orientation distribution, boxplot of length distribution according to the fracture orientations, and cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken along the left and the right side of the canyon. For Boxplot and orientation distribution legend, see Figure 2.
Figure 5. Fracture traces, orientation, boxplot length distributions from drone model 3. Different Datasets are expressed into histogram for orientation distribution, boxplot of length distribution according to the fracture orientations, and cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken along the left and the right side of the canyon. For Boxplot and orientation distribution legend, see Figure 2.
Geosciences 11 00280 g005
Geosciences 11 00280 g006 550
Figure 6. Fracture traces, orientation and length distributions from fracture map 1. Different datasets are expressed into histogram for orientations distribution, and into cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken for every domain. For orientation distribution legend, see Figure 2.
Figure 6. Fracture traces, orientation and length distributions from fracture map 1. Different datasets are expressed into histogram for orientations distribution, and into cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken for every domain. For orientation distribution legend, see Figure 2.
Geosciences 11 00280 g006
Geosciences 11 00280 g007 550
Figure 7. Fracture traces, orientation and length distributions from (a) sample 1-1, (b) thin section 1-1, and (c) thin section 1-2 sampled from fracture map 1. Different datasets are expressed into histograms for orientations distribution, and into cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken for each map. For orientation distribution legend, see Figure 2.
Figure 7. Fracture traces, orientation and length distributions from (a) sample 1-1, (b) thin section 1-1, and (c) thin section 1-2 sampled from fracture map 1. Different datasets are expressed into histograms for orientations distribution, and into cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken for each map. For orientation distribution legend, see Figure 2.
Geosciences 11 00280 g007
Geosciences 11 00280 g008 550
Figure 8. Fracture traces, orientation, and length distributions from (a) fracture map 2, (b) sample 2-1, and (c) thin section 2-1, located in sample 2-1. Different datasets are expressed into histogram for orientations distribution, and into cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken for each map. For orientation distribution legend, see Figure 2.
Figure 8. Fracture traces, orientation, and length distributions from (a) fracture map 2, (b) sample 2-1, and (c) thin section 2-1, located in sample 2-1. Different datasets are expressed into histogram for orientations distribution, and into cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken for each map. For orientation distribution legend, see Figure 2.
Geosciences 11 00280 g008
Geosciences 11 00280 g009 550
Figure 9. Fracture traces, orientation and length distributions from fracture map 3. The computed dataset is expressed into histogram for orientations distribution, and into cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken. For orientation distribution legend, see Figure 2.
Figure 9. Fracture traces, orientation and length distributions from fracture map 3. The computed dataset is expressed into histogram for orientations distribution, and into cumulative distribution function (CDF) of lengths. Two scanlines (SL) were taken. For orientation distribution legend, see Figure 2.
Geosciences 11 00280 g009
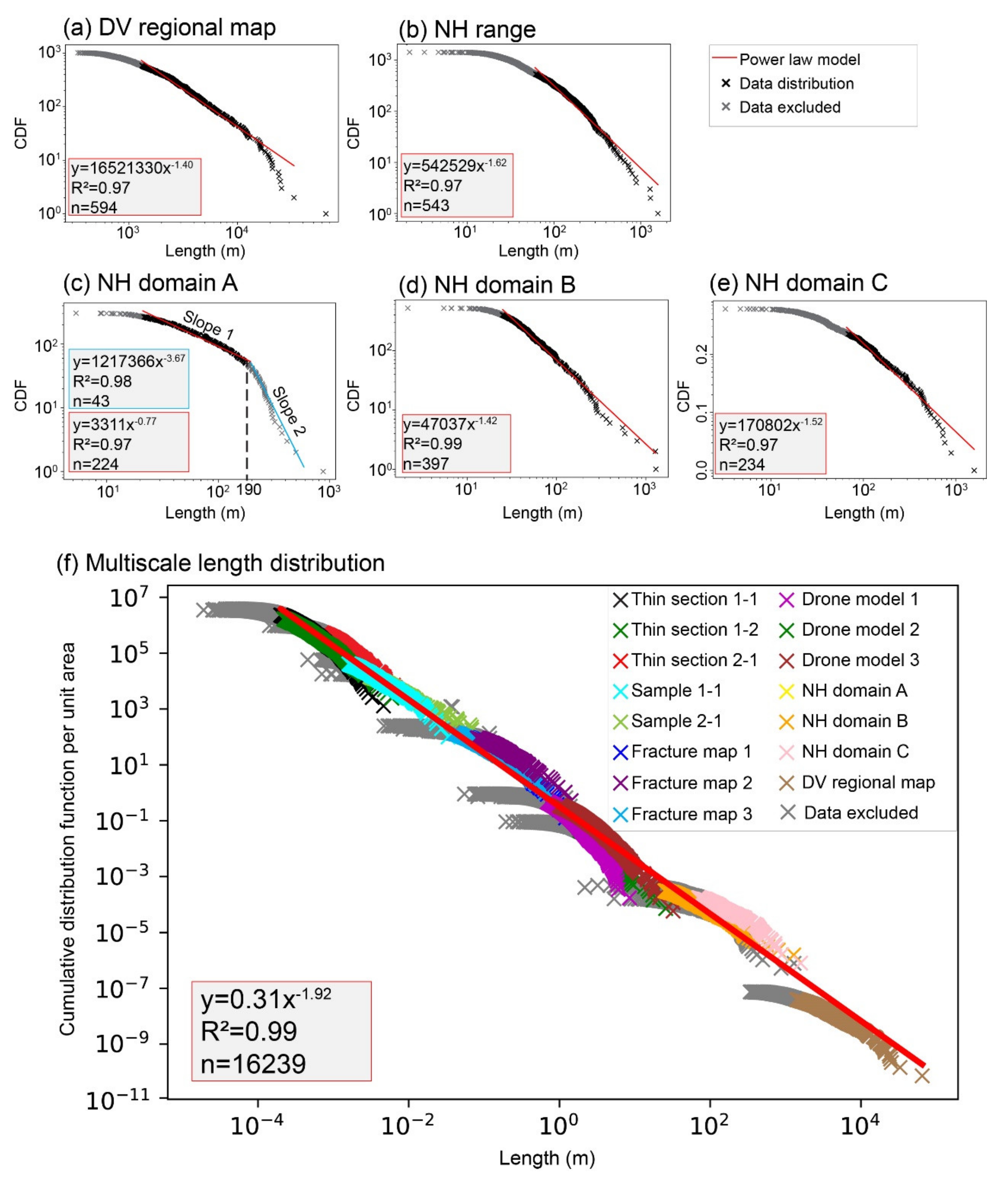
Geosciences 11 00280 g010 550
Figure 10. Fracture length distribution from (a) DV geological map, (b) NH range, (c) NH map domain A, (d) NH map domain B, and (e) NH map domain C, and (f) Multiscale length distribution obtained from the combination of the whole data.
Figure 10. Fracture length distribution from (a) DV geological map, (b) NH range, (c) NH map domain A, (d) NH map domain B, and (e) NH map domain C, and (f) Multiscale length distribution obtained from the combination of the whole data.
Geosciences 11 00280 g010
Geosciences 11 00280 g011 550
Figure 11. Orientation plot representing mean orientation of each fracture set from DV regional map, NH regional map, NH domains and drone models at outcrop scale. Each arrow corresponds to the mean orientation. The length of each arrow corresponds to the fracture set abundance. The horizontal line above each arrow corresponds to the fracture set standard deviation within an interval of confidence of 75% (see [62] for more explanations). Each color arrow corresponds to fracture set: Blue arrow corresponds to NNE/SSW fracture set, red arrow corresponds to the NE/SW fracture set, green arrow corresponds to the E/W fracture set, yellow arrow corresponds to the NNW/SSE fracture set, purple arrow corresponds to the NW/SE fracture set, and marron arrow corresponds to the N/S fracture set.
Figure 11. Orientation plot representing mean orientation of each fracture set from DV regional map, NH regional map, NH domains and drone models at outcrop scale. Each arrow corresponds to the mean orientation. The length of each arrow corresponds to the fracture set abundance. The horizontal line above each arrow corresponds to the fracture set standard deviation within an interval of confidence of 75% (see [62] for more explanations). Each color arrow corresponds to fracture set: Blue arrow corresponds to NNE/SSW fracture set, red arrow corresponds to the NE/SW fracture set, green arrow corresponds to the E/W fracture set, yellow arrow corresponds to the NNW/SSE fracture set, purple arrow corresponds to the NW/SE fracture set, and marron arrow corresponds to the N/S fracture set.
Geosciences 11 00280 g011
Geosciences 11 00280 g012 550
Figure 12. Conceptual scheme presenting the spatial arrangement of the NH fracture network at (a) regional scale, (b) NH scale, and (c) outcrop scale. The organization is based on scale orders referring to the [16,17,20,30] classification, and their associated spacing characteristics referring to [20,30]. The picture presented in (c) is provided by GoogleEarth®.
Figure 12. Conceptual scheme presenting the spatial arrangement of the NH fracture network at (a) regional scale, (b) NH scale, and (c) outcrop scale. The organization is based on scale orders referring to the [16,17,20,30] classification, and their associated spacing characteristics referring to [20,30]. The picture presented in (c) is provided by GoogleEarth®.
Geosciences 11 00280 g012
Table
Table 1. Spatial statistics of 2D samples acquired at large scale (DV and NH regional maps) and outcrop scale (Drone models). Two Scanlines (SL) at least were generated for calculating the fracture density (P10). The length average is provided.
Table 1. Spatial statistics of 2D samples acquired at large scale (DV and NH regional maps) and outcrop scale (Drone models). Two Scanlines (SL) at least were generated for calculating the fracture density (P10). The length average is provided.
Nb of FracturesMean OrientationAverage SL Length (m)/Area (m²)Fracture Density (P10) (frac/m)Fracture Density (P21) (m/m²)
DV regional map133N025105/1.3 × 10102 × 10−43 × 10−4
188N058
199N096
248N132
197N167
NH regional map97N0204.7 × 103/4.4 × 1062.6 × 10−4 3 × 10−4
168N054
535N090
441N126
192N163
NH domain A13N0101.5 × 103/1.9 × 1062 × 10−22 × 10−2
26N055
89N091
168N132
NH domain B43N0501.7 × 103/1.2 × 1064 × 10−23 × 10−2
233N088
164N128
59N171
NH domain C113N0492 × 103/1.2 × 1065 × 10−25 × 10−2
191N085
119N111
103N141
77N177
Drone model 1235N0253.5 × 102/1.4 × 1046.5 × 10−12 × 10−1
208N055
183N085
112N115
281N142
214N174
Drone model 2681N0221.7 × 102/5.8 × 1031.287 × 10−1
767N043
642N085
616N108
722N142
637N171
Drone model 32968N0182.8 × 102/1.7 × 1049 × 10−11
2531N038
1993N079
2127N109
2232N140
3084N169
Table
Table 2. Spatial statistics of 2D samples acquired from outcrop scale (fracture maps) to thin section scale. Two Scanlines (SL) at least were generated for calculating the fracture density (P10); the length average is provided.
Table 2. Spatial statistics of 2D samples acquired from outcrop scale (fracture maps) to thin section scale. Two Scanlines (SL) at least were generated for calculating the fracture density (P10); the length average is provided.
Nb of FracturesMean OrientationAverage SL Length (m)/Area (m²)Fracture Density (P10) (frac/m)Fracture Density (P21) (m/m²)
Fracture map 11133N0053.1/7.941212
631N083
Sample 1-1104N01815 × 10−2/2.2 × 10−2184118
115N053
117N090
51N126
Thin section 1-1723N0183 × 10−2/8 × 10−45140715
754N053
751N090
730N126
Thin section 1-2612N0203 × 10−2/8 × 10−44525702
659N051
444N088
512N128
623N162
Fracture map 236N0051.7/1.911813
34N038
98N070
32N110
83N145
Sample 2-175N01710−1/10−2177240
145N057
101N092
116N130
135N157
Thin section 2-1201N0143 × 10−2/8 × 10−45171064
213N059
170N097
221N140
Fracture map 3149N0091.7/32012
88N033
119N071
70N104
146N149
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Chabani, A.; Trullenque, G.; Ledésert, B.A.; Klee, J. Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), Application to Geothermal Reservoirs. Geosciences 2021, 11, 280. https://doi.org/10.3390/geosciences11070280

AMA Style

Chabani A, Trullenque G, Ledésert BA, Klee J. Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), Application to Geothermal Reservoirs. Geosciences. 2021; 11(7):280. https://doi.org/10.3390/geosciences11070280

Chicago/Turabian Style

Chabani, Arezki, Ghislain Trullenque, Béatrice A. Ledésert, and Johanne Klee. 2021. "Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), Application to Geothermal Reservoirs" Geosciences 11, no. 7: 280. https://doi.org/10.3390/geosciences11070280

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop