Preferential Localization of the Bacterial Nucleoid
Abstract
:1. Introduction
2. Materials and Methods
3. Results
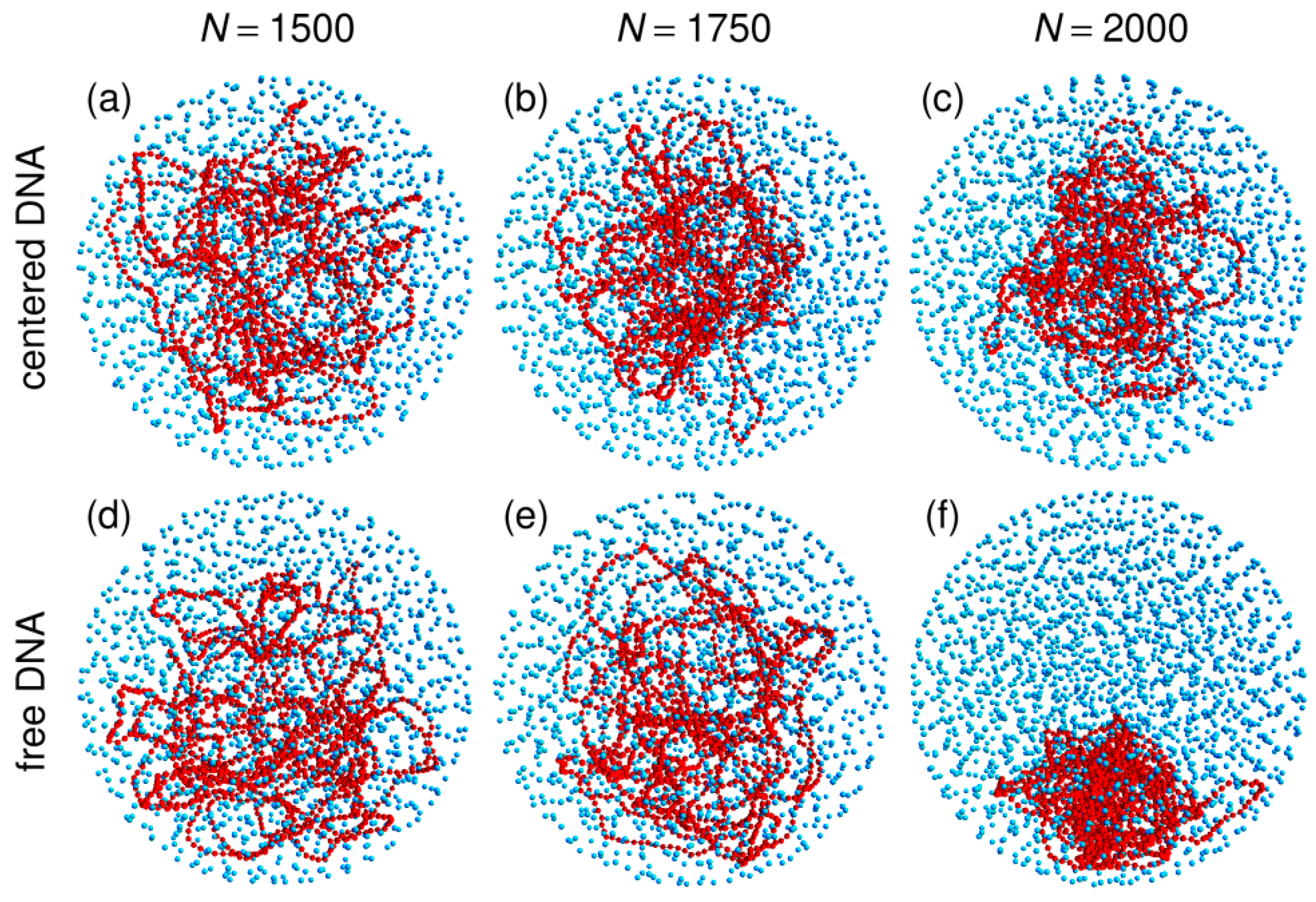
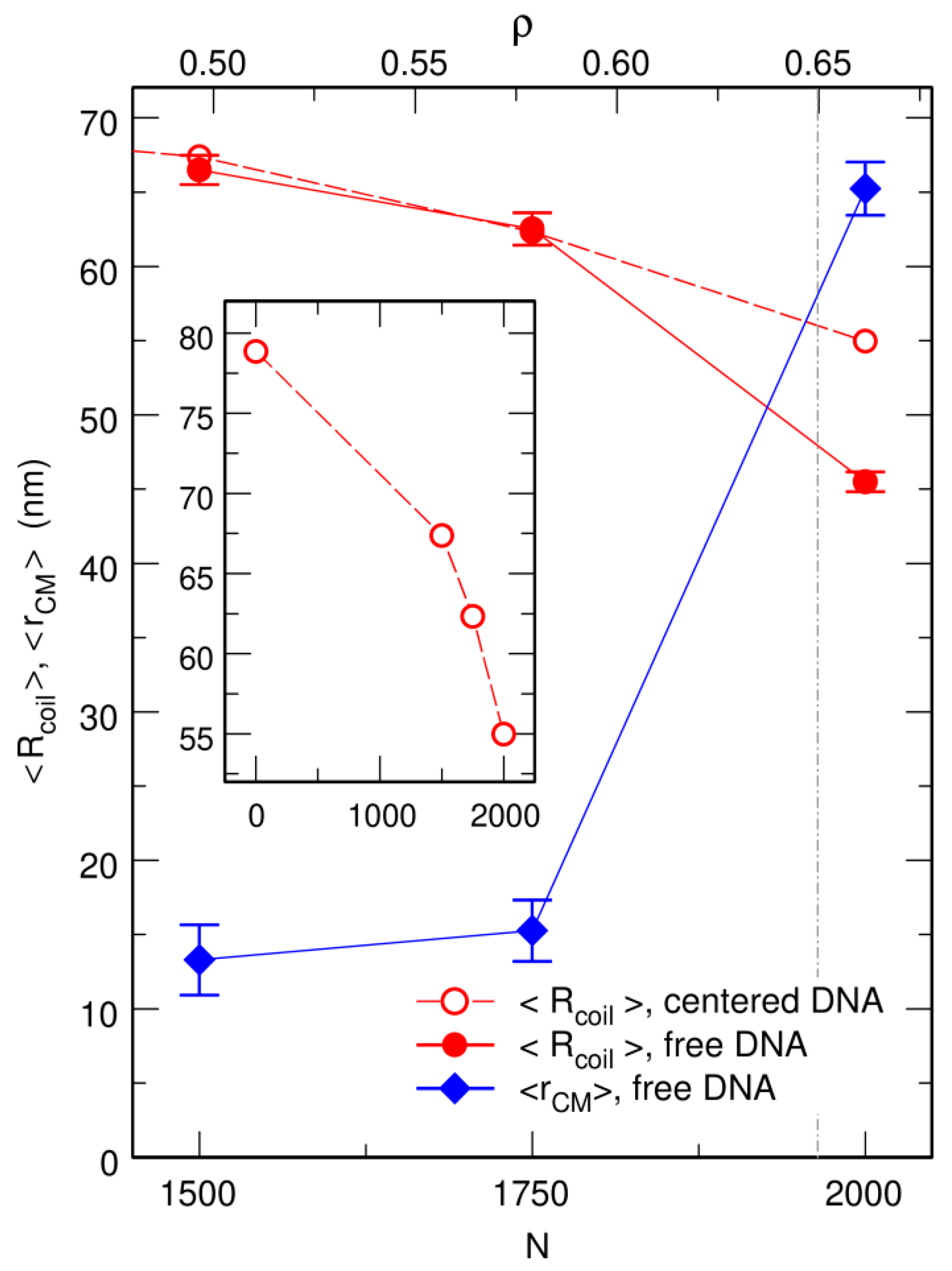
3.1. Compaction of DNA Coils with Increasing Crowder Density
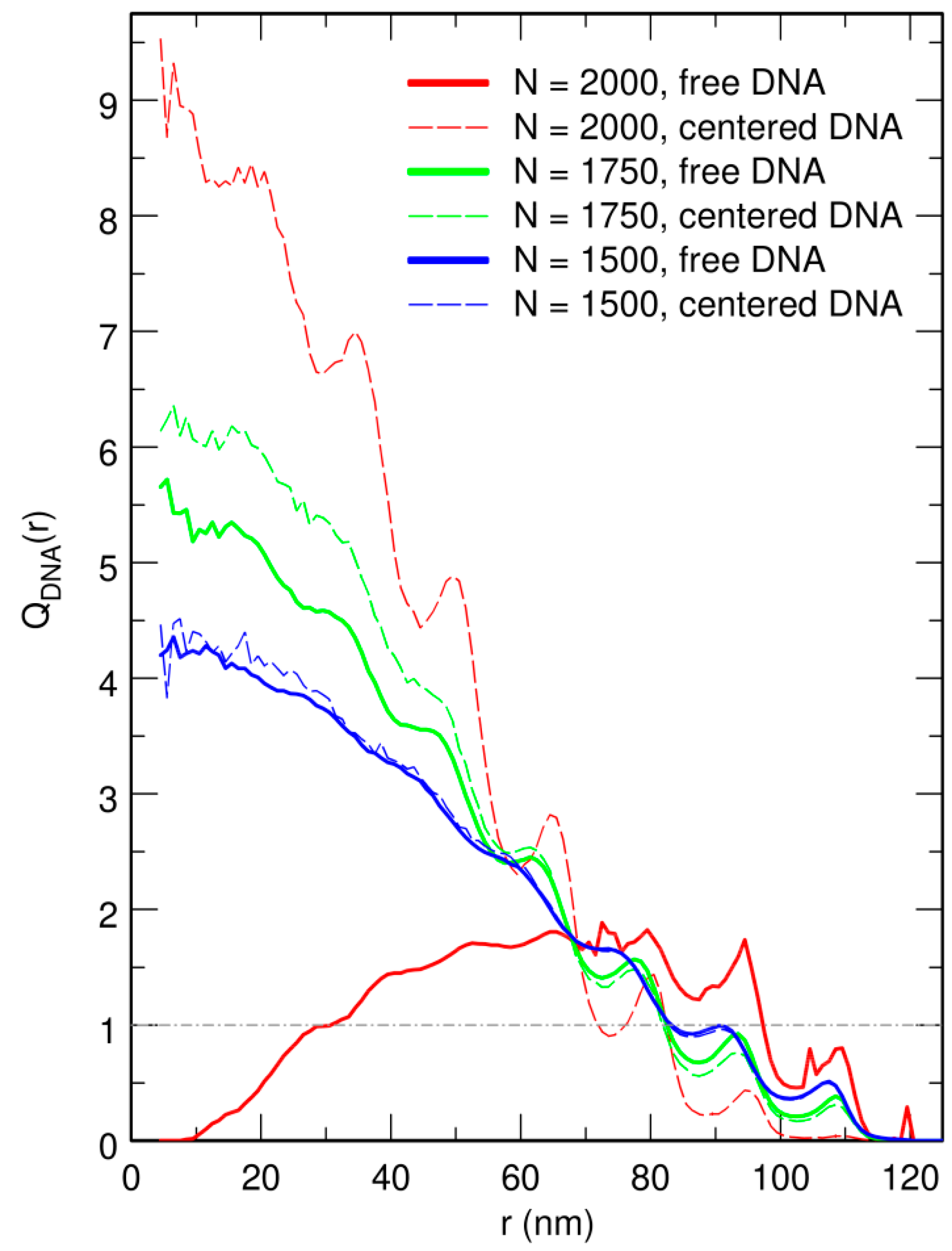
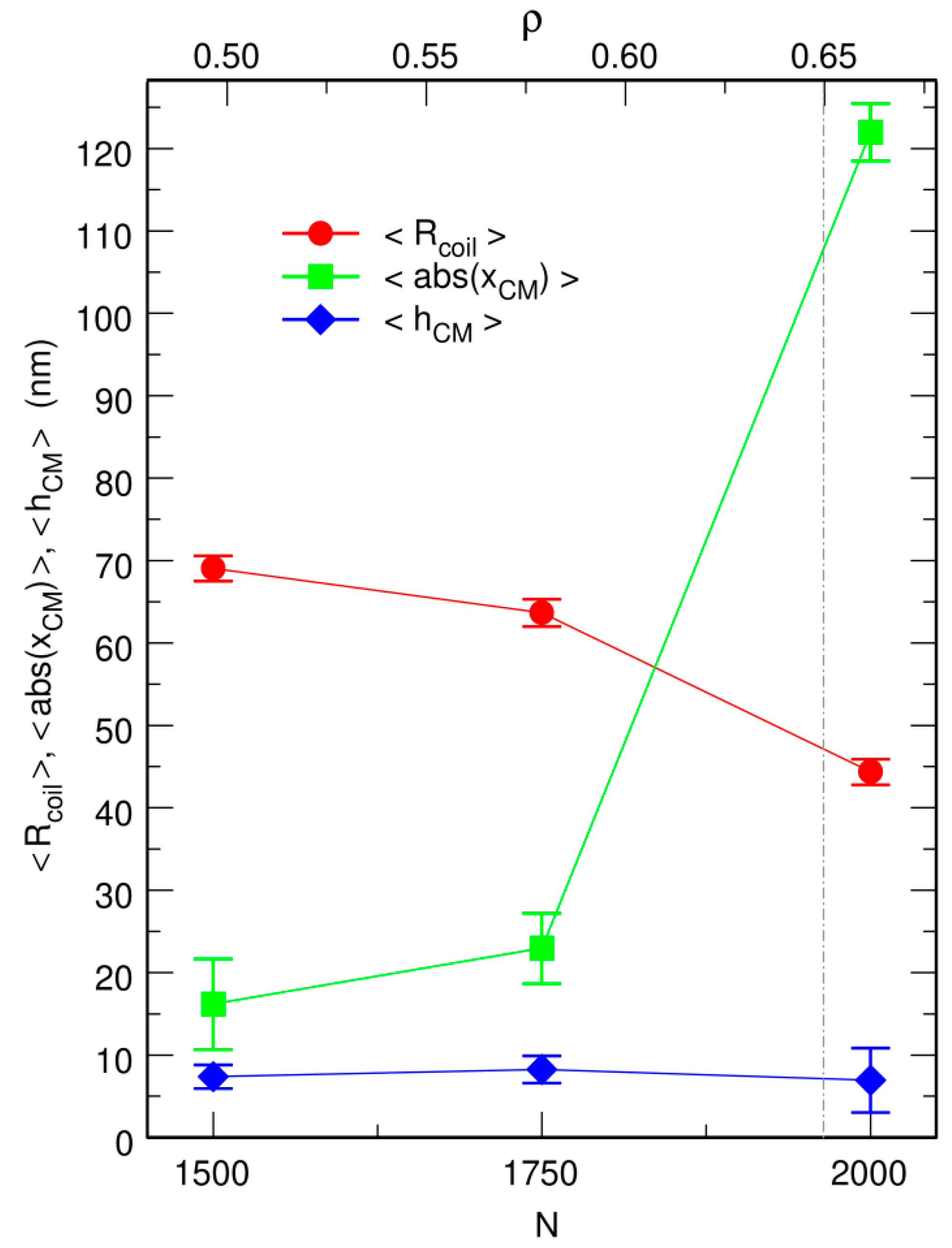
3.2. Free DNA Coils Acquire the Localization Properties of Solid Spheres at Large Crowder Density
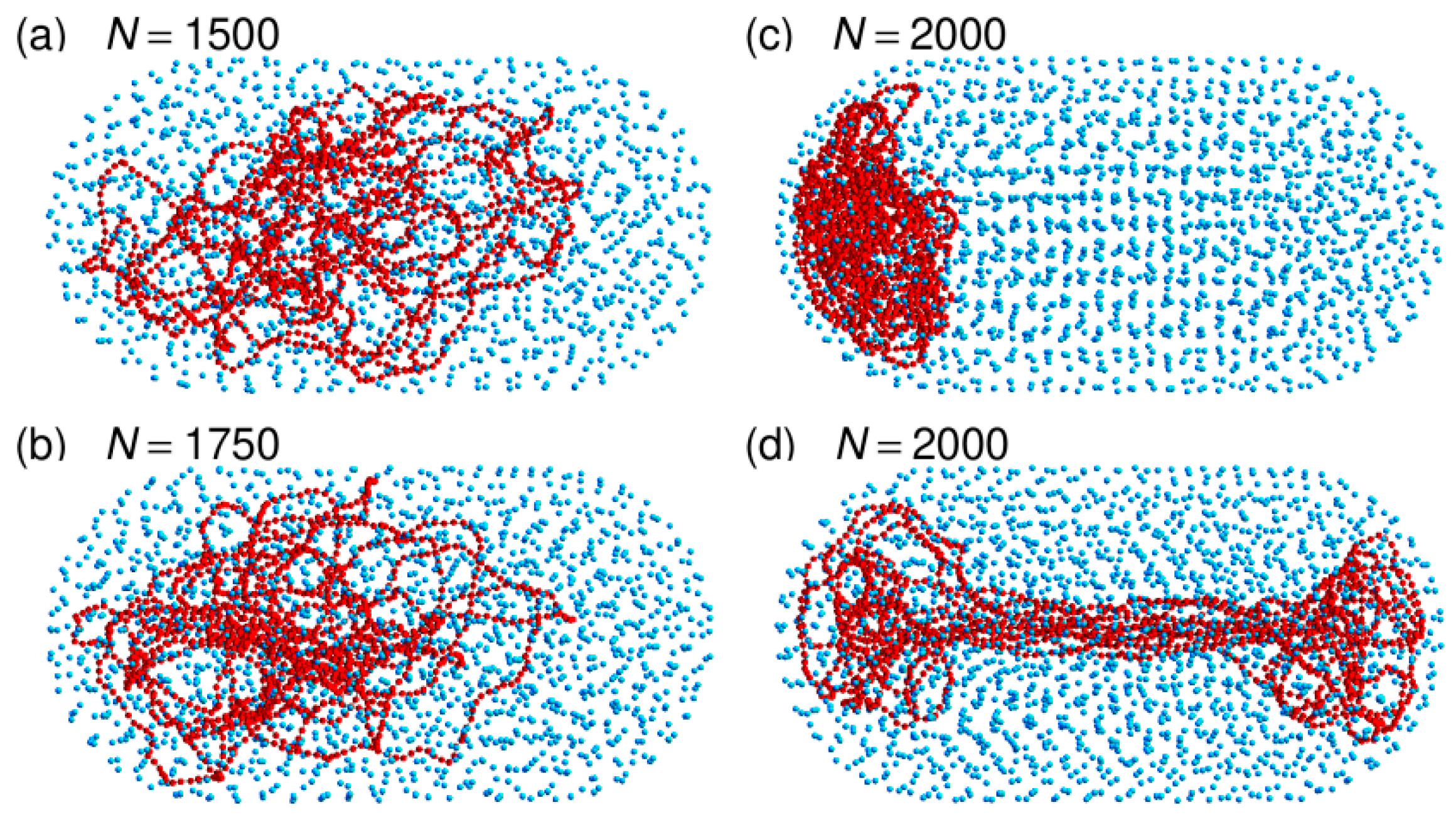
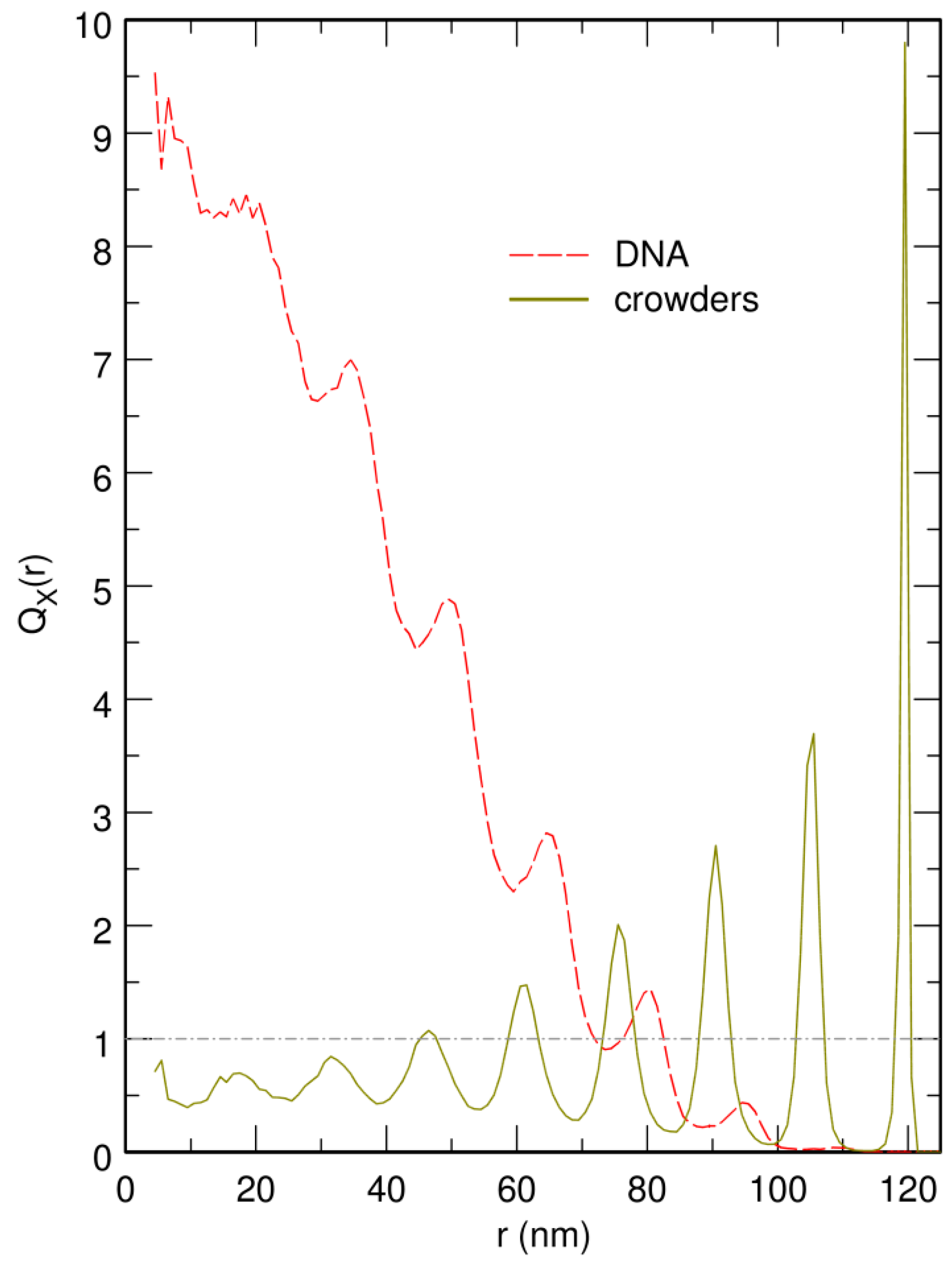
3.3. Localization of Compact DNA Coils in the Regions with Largest Boundary Curvature
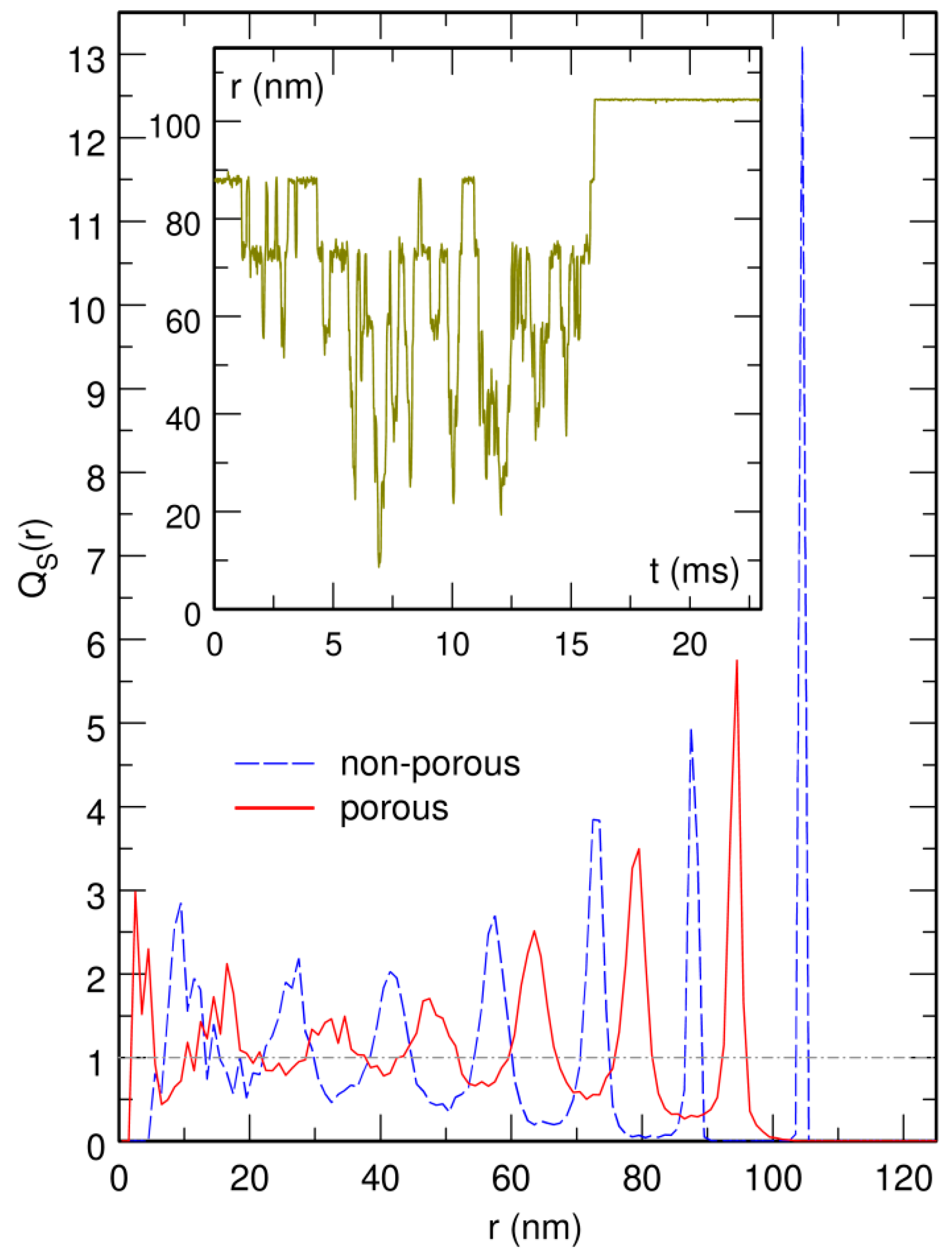
3.4. The Bacterial Nucleoid Does Not Behave Like A “Soft Sphere”
4. Discussion
Funding
Conflicts of Interest
References
- Sherratt, D.J. Bacterial chromosome dynamics. Science 2003, 301, 780–785. [Google Scholar] [CrossRef] [PubMed]
- Badrinarayanan, A.; Le, T.B.K.; Laub, M.T. Bacterial chromosome organization and segregation. Annu. Rev. Cell Dev. Biol. 2015, 31, 171–199. [Google Scholar] [CrossRef] [PubMed]
- Endesfelder, U.; Finan, K.; Holden, S.J.; Cook, P.R.; Kapanidis, A.N.; Heilemann, M. Multiscale spatial organization of RNA polymerase in Escherichia coli. Biophys. J. 2013, 105, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Yazdi, N.H.; Guet, C.C.; Johnson, R.C.; Marko, J.F. Variation of the folding and dynamics of the Escherichia coli chromosome with growth conditions. Mol. Microbiol. 2012, 86, 1318–1333. [Google Scholar] [CrossRef] [PubMed]
- Jin, D.J.; Cagliero, C.; Martin, C.M.; Izard, J.; Zhou, Y.N. The dynamic nature and territory of transcriptional machinery in the bacterial chromosome. Front. Microbiol. 2015, 6, 497. [Google Scholar] [Green Version]
- Jin, D.J.; Cagliero, C.; Zhou, Y.N. Role of RNA polymerase and transcription in the organization of the bacterial nucleoid. Chem. Rev. 2013, 113, 8662–8682. [Google Scholar] [CrossRef] [PubMed]
- Stracy, M.; Lesterlin, C.; de Leon, F.G.; Uphoff, S.; Zawadzki, P.; Kapanidis, A.N. Live-cell superresolution microscopy reveals the organization of RNA polymerase in the bacterial nucleoid. Proc. Natl. Acad. Sci. USA 2015, 112, E4390–E4399. [Google Scholar] [CrossRef] [Green Version]
- Spahn, C.; Endesfelder, U.; Heilemann, M. Super-resolution imaging of Escherichia coli nucleoids reveals highly structured and asymmetric segregation during fast growth. J. Struct. Biol. 2014, 185, 243–249. [Google Scholar] [CrossRef]
- Fisher, J.K.; Bourniquel, A.; Witz, G.; Weiner, B.; Prentiss, M.; Kleckner, N. Four-dimensional imaging of E. coli nucleoid organization and dynamics in living cells. Cell 2013, 153, 882–895. [Google Scholar] [CrossRef]
- Cagliero, C.; Jin, D.J. Dissociation and re-association of RNA polymerase with DNA during osmotic stress response in Escherichia coli. Nucleic Acids Res. 2013, 41, 315–326. [Google Scholar] [CrossRef]
- Cabrera, J.E.; Cagliero, C.; Quan, S.; Squires, C.L.; Jin, D.J. Active transcription of rRNA operons condenses the nucleoid in Escherichia coli: Examining the effect of transcription on nucleoid structure in the absence of transertion. J. Bacteriol. 2009, 191, 4180–4185. [Google Scholar] [CrossRef] [PubMed]
- Bakshi, S.; Choi, H.; Weisshaar, J.C. The spatial biology of transcription and translation in rapidly growing Escherichia coli. Front. Microbiol. 2015, 6, 636. [Google Scholar] [CrossRef] [PubMed]
- Bakshi, S.; Siryaporn, A.; Goulian, M.; Weisshaar, J.C. Superresolution imaging of ribosomes and RNA polymerase in live Escherichia coli cells. Mol. Microbiol. 2012, 85, 21–38. [Google Scholar] [CrossRef] [PubMed]
- Bakshi, S.; Choi, H.; Mondal, J.; Weisshaar, J.C. Time-dependent effects of transcription- and translation-halting drugs on the spatial distributions of the Escherichia coli chromosome and ribosomes. Mol. Microbiol. 2014, 94, 871–887. [Google Scholar] [CrossRef] [PubMed]
- Götzelmann, B.; Roth, R.; Dietrich, S.; Dijkstra, M.; Evans, R. Depletion potential in hard-sphere fluids. Europhys. Lett. 1999, 47, 398–404. [Google Scholar] [CrossRef] [Green Version]
- Roth, R.; Götzelmann, B.; Dietrich, S. Depletion forces near curved surfaces. Phys. Rev. Lett. 1999, 83, 448–451. [Google Scholar] [CrossRef]
- Roth, R.; Evans, R.; Dietrich, S. Depletion potential in hard-sphere mixtures: Theory and applications. Phys. Rev. E 2000, 62, 5360–5377. [Google Scholar] [CrossRef] [Green Version]
- Pagonabarraga, I.; Cates, M.E.; Ackland, G.J. Local size segregation in polydisperse hard sphere fluids. Phys. Rev. Lett. 2000, 84, 911–914. [Google Scholar] [CrossRef]
- Li, W.; Ma, H.R. Depletion potential near curved surfaces. Phys. Rev. E 2002, 66, 061407. [Google Scholar] [CrossRef]
- Buzzacchi, M.; Pagonabarraga, I.; Wilding, N.B. Polydisperse hard spheres at a hard wall. J. Chem. Phys. 2004, 121, 11362–11373. [Google Scholar] [CrossRef]
- Donachie, W.D.; Begg, K.J. Chromosome partition in Escherichia coli requires postreplication protein synthesis. J. Bacteriol. 1989, 171, 5405–5409. [Google Scholar] [CrossRef]
- Hiraga, S.; Ogura, T.; Niki, H.; Ichinose, C.; Mori, H. Positioning of replicated chromosomes in Escherichia coli. J. Bacteriol. 1990, 172, 31–39. [Google Scholar] [CrossRef]
- Robinow, C.; Kellenberger, E. The bacterial nucleoid revisited. Microbiol. Rev. 1994, 58, 211–232. [Google Scholar]
- Seto, S.; Miyata, M. Partitioning, movement, and positioning of nucleoids in Mycoplasma capricolum. J. Bacteriol. 1999, 181, 6073–6080. [Google Scholar]
- Chai, Q.; Singh, B.; Peisker, K.; Metzendorf, N.; Ge, X.; Dasgupta, S.; Sanyal, S. Organization of ribosomes and nucleoids in Escherichia coli cells during growth and in quiescence. J. Biol. Chem. 2014, 289, 11342–11352. [Google Scholar] [CrossRef]
- Mohapatra, S.; Weisshaar, J.C. Functional mapping of the E. coli translational machinery using single-molecule tracking. Mol. Microbiol. 2018, 110, 262–282. [Google Scholar] [CrossRef]
- Azam, T.A.; Hiraga, S.; Ishihama, A. Two types of localization of the DNA-binding proteins within the Escherichia coli nucleoid. Genes Cells 2000, 5, 613–626. [Google Scholar] [CrossRef]
- Shew, C.-Y.; Oda, S.; Yoshikawa, K. Localization switching of a large object in a crowded cavity: A rigid/soft object prefers surface/inner positioning. J. Chem. Phys. 2017, 147, 204901. [Google Scholar] [CrossRef] [Green Version]
- Mondal, J.; Bratton, B.P.; Li, Y.; Yethiraj, A.; Weisshaar, J.C. Entropy-based mechanism of ribosome-nucleoid segregation in E. coli cells. Biophys. J. 2011, 100, 2605–2613. [Google Scholar] [CrossRef]
- Roggiani, M.; Goulian, M. Chromosome-membrane interactions in bacteria. Annu. Rev. Genet. 2015, 49, 115–129. [Google Scholar] [CrossRef]
- Toro, E.; Shapiro, L. Bacterial chromosome organization and segregation. Cold Spring Harb. Perspect. Biol. 2010, 2, a000349. [Google Scholar] [CrossRef]
- Wang, X.; Rudner, D.Z. Spatial organization of bacterial chromosomes. Curr. Opin. Microbiol. 2014, 22, 66–72. [Google Scholar] [CrossRef] [Green Version]
- Yamaichi, Y.; Bruckner, R.; Ringgaard, S.; Möll, A.; Cameron, D.E.; Briegel, A.; Jensen, G.J.; Davis, B.M.; Waldor, M.K. A multidomain hub anchors the chromosome segregation and chemotactic machinery to the bacterial pole. Genes Dev. 2012, 26, 2348–2360. [Google Scholar] [CrossRef] [Green Version]
- Crawford, J.A.; Krukonis, E.S.; DiRita, V.J. Membrane localization of the ToxR winged-helix domain is required for TcpP-mediated virulence gene activation in Vibrio cholerae. Mol. Microbiol. 2003, 47, 1459–1473. [Google Scholar] [CrossRef]
- Dalia, A.B.; Lazinski, D.W.; Camilli, A. Identification of a membrane-bound transcriptional regulator that links chitin and natural competence in Vibrio cholerae. mBio 2014, 5, e01028-13. [Google Scholar] [CrossRef]
- Tetsch, L.; Koller, C.; Haneburger, I.; Jung, K. The membrane-integrated transcriptional activator CadC of Escherichia coli senses lysine indirectly via the interaction with the lysine permease LysP. Mol. Microbiol. 2008, 67, 570–583. [Google Scholar] [CrossRef]
- Adams, D.W.; Wu, L.J.; Errington, J. Nucleoid occlusion protein Noc recruits DNA to the bacterial cell membrane. EMBO J. 2015, 34, 491–501. [Google Scholar] [CrossRef]
- Lutkenhaus, J. Assembly dynamics of the bacterial MinCDE system and spatial regulation of the Z Ring. Annu. Rev. Biochem. 2007, 76, 539–562. [Google Scholar] [CrossRef]
- Teraoka, I. Polymer Solutions: An Introduction to Physical Properties; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Zimmerman, S.B. Shape and compaction of Escherichia coli nucleoids. J. Struct. Biol. 2006, 156, 255–261. [Google Scholar] [CrossRef]
- De Vries, R. DNA condensation in bacteria: Interplay between macromolecular crowding and nucleoid proteins. Biochimie 2010, 92, 1715–1721. [Google Scholar] [CrossRef]
- Benza, V.G.; Bassetti, B.; Dorfman, K.D.; Scolari, V.F.; Bromek, K.; Cicuta, P.; Lagomarsino, M.C. Physical descriptions of the bacterial nucleoid at large scales, and their biological implications. Rep. Prog. Phys. 2012, 75, 076602. [Google Scholar] [CrossRef]
- Joyeux, M. Compaction of bacterial genomic DNA: Clarifying the concepts. J. Phys. Condens. Matter 2015, 27, 383001. [Google Scholar] [CrossRef]
- Joyeux, M. In Vivo compaction dynamics of bacterial DNA: A fingerprint of DNA/RNA demixing? Curr. Opin. Colloid Interface Sci. 2016, 26, 17–27. [Google Scholar] [CrossRef]
- Sear, R.P. Coil-globule transition of a semiflexible polymer driven by the addition of spherical particles. Phys. Rev. E 1998, 58, 724–728. [Google Scholar] [CrossRef] [Green Version]
- Van der Schoot, P. Protein-induced collapse of polymer chains. Macromolecules 1998, 31, 4635–4638. [Google Scholar] [CrossRef]
- Odijk, T. Osmotic compaction of supercoiled DNA into a bacterial nucleoid. Biophys. Chem. 1998, 73, 23–29. [Google Scholar] [CrossRef]
- Castelnovo, M.; Gelbart, W.M. Semiflexible chain condensation by neutral depleting agents: Role of correlations between depletants. Macromolecules 2004, 37, 3510–3517. [Google Scholar] [CrossRef]
- de Vries, R. Depletion-induced instability in protein-DNA mixtures: Influence of protein charge and size. J. Chem. Phys. 2006, 125, 014905. [Google Scholar] [CrossRef]
- Krotova, M.K.; Vasilevskaya, V.V.; Makita, N.; Yoshikawa, K.; Khokhlov, A.R. DNA compaction in a crowded environment with negatively charged proteins. Phys. Rev. Lett. 2010, 105, 128302. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Hirota, S.; Makita, N.; Yoshikawa, Y. Compaction of DNA induced by like-charge protein: Opposite salt-effect against the polymer-salt-induced condensation with neutral polymer. J. Phys. Chem. Lett. 2010, 1, 1763–1766. [Google Scholar] [CrossRef]
- Zinchenko, A.; Tsumoto, K.; Murata, S.; Yoshikawa, K. Crowding by anionic nanoparticles causes DNA double-strand instability and compaction. J. Phys. Chem. B 2014, 118, 1256–1262. [Google Scholar] [CrossRef]
- Kim, J.; Jeon, C.; Jeong, H.; Jung, Y.; Ha, B.-Y. A polymer in a crowded and confined space: Effects of crowder size and poly-dispersity. Soft Matter 2015, 11, 1877–1888. [Google Scholar] [CrossRef]
- Jeon, C.; Jung, Y.; Ha, B.-Y. Effects of molecular crowding and confinement on the spatial organization of a biopolymer. Soft Matter 2016, 12, 9436–9450. [Google Scholar] [CrossRef] [Green Version]
- Jeon, C.; Hyeon, C.; Jung, Y.; Ha, B.-Y. How are molecular crowding and the spatial organization of a biopolymer interrelated. Soft Matter 2016, 12, 9786–9796. [Google Scholar] [CrossRef] [Green Version]
- Jeon, C.; Jung, Y.; Ha, B.-Y. A ring-polymer model shows how macromolecular crowding controls chromosome-arm organization in Escherichia coli. Sci. Rep. 2017, 7, 11896. [Google Scholar] [CrossRef]
- Joyeux, M. Coarse-grained model of the demixing of DNA and non-binding globular macromolecules. J. Phys. Chem. B 2017, 121, 6351–6358. [Google Scholar] [CrossRef]
- Joyeux, M. A segregative phase separation scenario of the formation of the bacterial nucleoid. Soft Matter 2018, 14, 7368–7381. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, T.; Manjunath, G.P.; Habib, F.; Chatterji, A. Bacterial chromosome organization. I. Crucial role of release of topological constraints and molecular crowders. J. Chem. Phys. 2019, 150, 144908. [Google Scholar] [CrossRef]
- Agarwal, T.; Manjunath, G.P.; Habib, F.; Chatterji, A. Bacterial chromosome organization. II. Few special cross-links, cell confinement, and molecular crowders play the pivotal roles. J. Chem. Phys. 2019, 150, 144909. [Google Scholar] [CrossRef]
- Hsu, C.C.; Prausnitz, J.M. Thermodynamics of polymer compatibility in ternary systems. Macromolecules 1974, 7, 320–324. [Google Scholar] [CrossRef]
- Liu, A.J.; Nagel, S.R. The jamming transition and the marginally jammed solid. Annu. Rev. Condens. Matter Phys. 2010, 1, 347–369. [Google Scholar] [CrossRef]
- Mutch, K.J.; van Duijneveldt, J.S.; Eastoe, J. Colloid-polymer mixtures in the protein limit. Soft Matter 2007, 3, 155–167. [Google Scholar] [CrossRef]
- Sear, R.P. Phase separation in mixtures of colloids and long ideal polymer coils. Phys. Rev. Lett. 2001, 86, 4696–4699. [Google Scholar] [CrossRef]
- Odijk, T. Many-body depletion interactions among protein spheres in a semidilute polymer solution. J. Chem. Phys. 1997, 106, 3402–3406. [Google Scholar] [CrossRef] [Green Version]
- Dijkstra, M.; van Roij, R.; Roth, R.; Fortini, A. Effect of many-body interactions on the bulk and interfacial phase behavior of a model colloid-polymer mixture. Phys. Rev. E 2006, 73, 041404. [Google Scholar] [CrossRef] [Green Version]
- Bolhuis, P.G.; Louis, A.A.; Hansen, J.-P. Influence of polymer-excluded volume on the phase-behavior of colloid-polymer mixtures. Phys. Rev. Lett. 2002, 89, 128302. [Google Scholar] [CrossRef]
- Aarts, D.G.A.L.; Tuinier, R.; Lekkerkerker, H.N.W. Phase behaviour of mixtures of colloidal spheres and excluded-volume polymer chains. J. Phys. Condens. Matter 2002, 14, 7551–7561. [Google Scholar] [CrossRef] [Green Version]
- Fleer, G.J.; Tuinier, R. Analytical phase diagram for colloid-polymer mixtures. Phys. Rev. E 2007, 76, 041802. [Google Scholar] [CrossRef] [Green Version]
- Bolhuis, P.G.; Meijer, E.J.; Louis, A.A. Colloid-Polymer Mixtures in the Protein Limit. Phys. Rev. Lett. 2003, 90, 068304. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, M.; Schweizer, K.S. Structure of colloid-polymer suspensions. J. Phys. Condens. Matter 2002, 14, R239–R269. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, M.; Schweizer, K.S. Structure and thermodynamics of colloid-polymer mixtures: A macromolecular approach. Europhys. Lett. 2000, 51, 621–627. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, M.; Schweizer, K.S. Macromolecular theory of salvation and structure in mixtures of colloids and polymers. Phys. Rev. E 2001, 64, 021514. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Schweizer, K.S. Depletion interactions in suspensions of spheres and rod-polymers. J. Chem. Phys. 2002, 117, 1351–1362. [Google Scholar] [CrossRef]
- Kulkarni, A.M.; Chatterjee, A.P.; Schweizer, K.S.; Zukowski, C.F. Depletion interactions in the protein limit: Effects of polymer density fluctuations. Phys. Rev. Lett. 1999, 83, 4554–4557. [Google Scholar] [CrossRef]
- Woodward, C.E.; Forsman, J. A many-body Hamiltonian for nanoparticles immersed in a polymer solution. Langmuir 2015, 31, 22–26. [Google Scholar] [CrossRef]
- Florescu, A.-M.; Joyeux, M. Description of nonspecific DNA-protein interaction and facilitated diffusion with a dynamical model. J. Chem. Phys. 2009, 130, 015103. [Google Scholar] [CrossRef] [Green Version]
- Florescu, A.-M.; Joyeux, M. Dynamical model of DNA-protein interaction: Effect of protein charge distribution and mechanical properties. J. Chem. Phys. 2009, 131, 105102. [Google Scholar] [CrossRef] [Green Version]
- Florescu, A.-M.; Joyeux, M. Comparison of kinetic and dynamical models of DNA-protein interaction and facilitated diffusion. J. Phys. Chem. A 2010, 114, 9662–9672. [Google Scholar] [CrossRef]
- Joyeux, M.; Vreede, J. A model of H-NS mediated compaction of bacterial DNA. Biophys. J. 2013, 104, 1615–1622. [Google Scholar] [CrossRef]
- Joyeux, M. Equilibration of complexes of DNA and H-NS proteins on charged surfaces: A coarse-grained model point of view. J. Chem. Phys. 2014, 141, 115102. [Google Scholar] [CrossRef] [Green Version]
- Joyeux, M. Role of salt valency in the switch of H-NS proteins between DNA-bridging and DNA-stiffening modes. Biophys. J. 2018, 114, 2317–2325. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, M.D.; Lukashin, A.V.; Anshelevich, V.V. Torsional and bending rigidity of the double helix from data on small DNA rings. J. Biomol. Struct. Dyn. 1985, 2, 1005–1012. [Google Scholar] [CrossRef]
- Vologodskii, A.; Cozzarelli, N. Modeling of long-range electrostatic interactions in DNA. Biopolymers 1995, 35, 289–296. [Google Scholar] [CrossRef]
- Manning, G.S. Limiting laws and counterion condensation in polyelectrolyte solutions I. Colligative properties. J. Chem. Phys. 1969, 51, 924–933. [Google Scholar] [CrossRef]
- Oosawa, F. Polyelectrolytes; Marcel Dekker: New York, NY, USA, 1971. [Google Scholar]
- Gorle, A.K.; Bottomley, A.L.; Harry, E.J.; Collins, J.G.; Keene, F.R.; Woodward, C.E. DNA condensation in live E. coli provides evidence for transertion. Mol. BioSyst. 2017, 13, 677–680. [Google Scholar] [CrossRef]
- Ingraham, J.L.; Maaloe, O.; Neidhardt, F.C. Growth of the Bacterial Cell; Sinauer Associates: Sunderland, MA, USA, 1983. [Google Scholar]
- Mika, J.T.; Poolman, B. Macromolecule diffusion and confinement in prokaryotic cells. Curr. Opin. Biotechnol. 2011, 22, 117–126. [Google Scholar] [CrossRef]
- Wu, L.J.; Errington, J. Coordination of cell division and chromosome segregation by a nucleoid occlusion protein in Bacillus subtilis. Cell 2004, 117, 915–925. [Google Scholar] [CrossRef]
- Bernhardt, T.G.; de Boer, P.A.J. SlmA, a nucleoid-associated, FtsZ binding protein required for blocking septal ring assembly over chromosomes in E. coli. Mol. Cell 2005, 18, 555–564. [Google Scholar] [CrossRef]
- Nielsen, H.J.; Ottesen, J.R.; Youngren, B.; Austin, S.J.; Hansen, F.G. The Escherichia coli chromosome is organized with the left and right chromosome arms in separate cell halves. Mol. Microbiol. 2006, 62, 331–338. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Possoz, C.; Sherratt, D.J. The two Escherichia coli chromosome arms locate to separate cell halves. Genes Dev. 2006, 20, 1727–1731. [Google Scholar] [CrossRef]
- Ryter, A. Association of the nucleus and the membrane of bacteria: A morphological study. Bacteriol. Rev. 1968, 32, 39–54. [Google Scholar]
- Leibowitz, P.J.; Schaechter, M. The attachment of the bacterial chromosome to the cell membrane. In International Review of Cytology; Academic Press: Cambridge, MA, USA, 1975; Volume 41, pp. 1–28. [Google Scholar]
- Hendrickson, W.G.; Kusano, T.; Yamaki, H.; Balakrishnan, R.; King, M.; Murchie, J.; Schaechter, M. Binding of the origin of replication of Escherichia coli to the outer membrane. Cell 1982, 30, 915–923. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joyeux, M. Preferential Localization of the Bacterial Nucleoid. Microorganisms 2019, 7, 204. https://doi.org/10.3390/microorganisms7070204
Joyeux M. Preferential Localization of the Bacterial Nucleoid. Microorganisms. 2019; 7(7):204. https://doi.org/10.3390/microorganisms7070204
Chicago/Turabian StyleJoyeux, Marc. 2019. "Preferential Localization of the Bacterial Nucleoid" Microorganisms 7, no. 7: 204. https://doi.org/10.3390/microorganisms7070204
APA StyleJoyeux, M. (2019). Preferential Localization of the Bacterial Nucleoid. Microorganisms, 7(7), 204. https://doi.org/10.3390/microorganisms7070204




