1. Introduction
Structural testing of machine tools to evaluate their static and dynamic characteristics involves loading the machine with scenarios experienced under real cutting conditions. Since real loading conditions often involve a periodic force that modulates about a non-zero mean, and since commonly used modal hammers and/or electrodynamic shakers cannot provide such excitations, this paper reports on the characteristics of a newly developed high-performance electro-hydraulic actuator to evaluate its suitability for its use in machine tool structural testing applications.
Electro-hydraulic actuators, because of their high stiffness-to-weight ratios, their high force capabilities, their large strokes, and their relatively quick response, have found applications across many engineering domains. Applications include their use in manufacturing and industrial machinery [
1,
2,
3], farm and earth moving equipment [
4], machine tools [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15], testing equipment [
16,
17], flight simulation and control [
18,
19], automotive and robotics [
20], and in numerous other domains. Since actuators are designed and characterized as per their applications, and since this paper is concerned with electro-hydraulic actuators for their use in the static and dynamic testing of machine tool structural systems, discussions herein are circumscribed by the application of interest.
Even though electro-hydraulic actuators have found use in machine tools, their use has mainly been limited to provide motion to the table and/or the tool [
5,
6,
7,
8], to effectively damp machine tool vibrations [
9,
10,
11], and to isolate machines from ground vibrations [
12,
13,
14]. Though machine tool structural testing using electro-hydraulic actuators is routine across many research labs, oddly, besides the study reporting the design and development of actuators for vibration testing [
15], there appear no other reports discussing the characteristics of electro-hydraulic actuators for machine tools.
Furthermore, despite the wide use of electro-hydraulic actuators across domains, and despite of the advantages they offer over other kinds of actuators, the static and dynamic characteristics of these electro-hydraulic systems are nonlinear, and understanding and characterizing these nonlinearities are essential to enable effective use and control of the actuators. Typical nonlinearities arise due to electrical hysteresis in the torque motor of the servo valve [
1,
2,
21,
22,
23], due to dead-band related nonlinearities in the servo valve [
1,
2,
21,
24,
25,
26], due to pressure drops on account of leakages in actuator-servo valve assembly [
1,
2,
23,
24,
27,
28,
29,
30,
31], due to friction present in the piston-cylinder arrangement [
1,
2,
23,
25,
26,
27,
28,
29,
32,
33,
34,
35,
36], and due to variations in the operating fluid temperature [
2,
25,
37].
Even though these nonlinearities exist, some reported work of the use of electro-hydraulic actuators across other engineering domains have assumed a linearized model of the system [
1,
2,
12,
13,
14,
15,
23,
38,
39,
40,
41], while some other reports for actuators used across other engineering domains have characterized some of these nonlinearities [
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37]. However, there are no reports detailing the nonlinear behavior of electro-hydraulic actuators used in machine tools. Furthermore, even though there are some reports on the static and dynamic characteristics of electro-hydraulic actuators used across other engineering domains [
1,
2,
23,
24,
29,
31,
39,
40], there are no such reports for actuator behavior for testing of machine tools. Moreover, since the actuator and the machine tool to be tested, both exhibit nonlinear behavior, it is paramount to decouple the nonlinear characteristics of the actuator from that of the machine. To do so, the nonlinear static and dynamic behavior of the electro-hydraulic actuator must be characterized separately and systematically.
Seeing that there is a need for an electro-hydraulic actuator that can apply periodic forces modulating about a non-zero mean for the static and dynamic testing of machine tool behavior under realistic loading scenarios, and that there exist no detailed reports characterizing the actuator behavior, this paper reports on the characteristics of the newly developed high-performance electro-hydraulic actuator to assess its suitability for its use in machine tool structural testing applications.
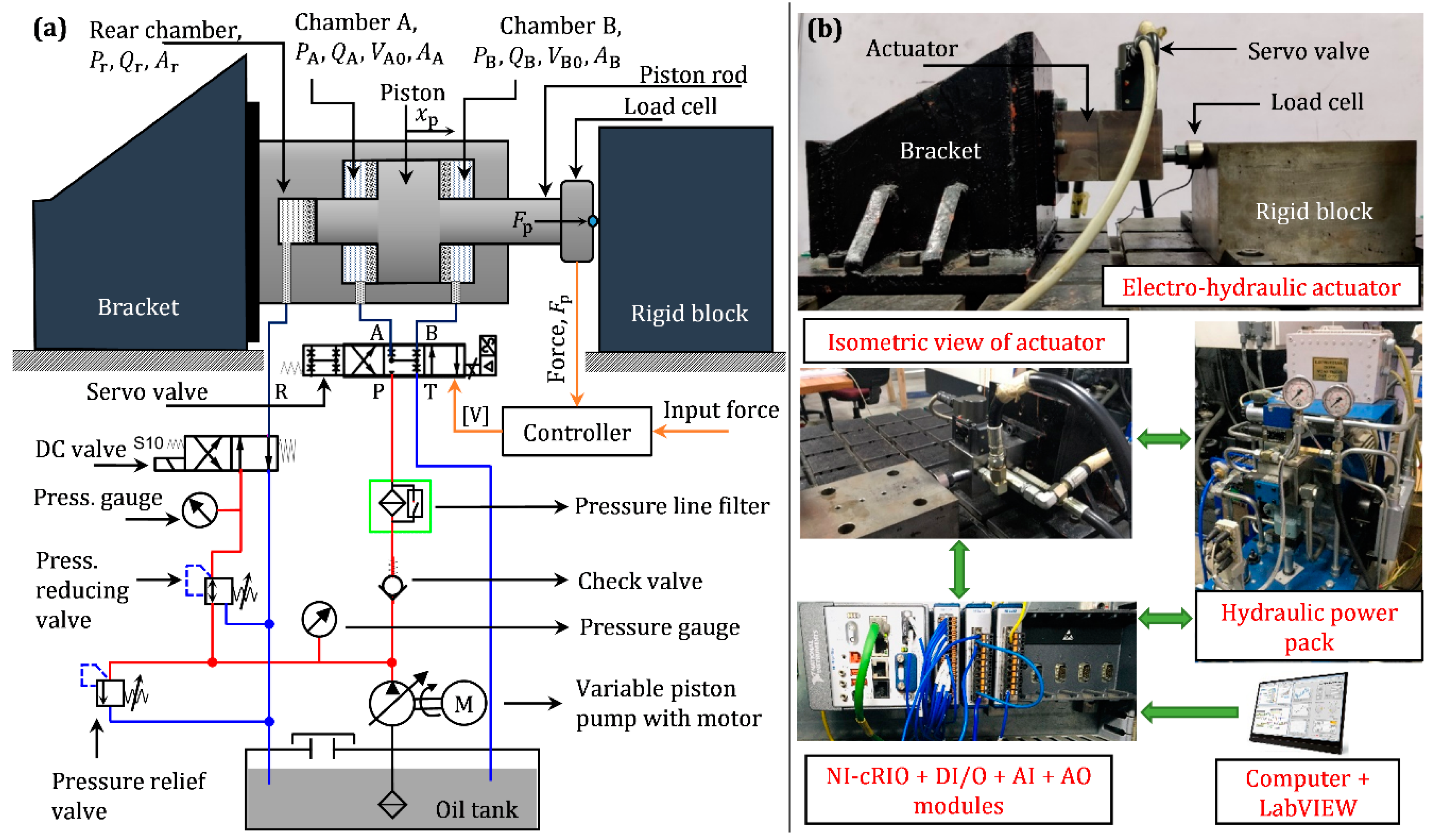
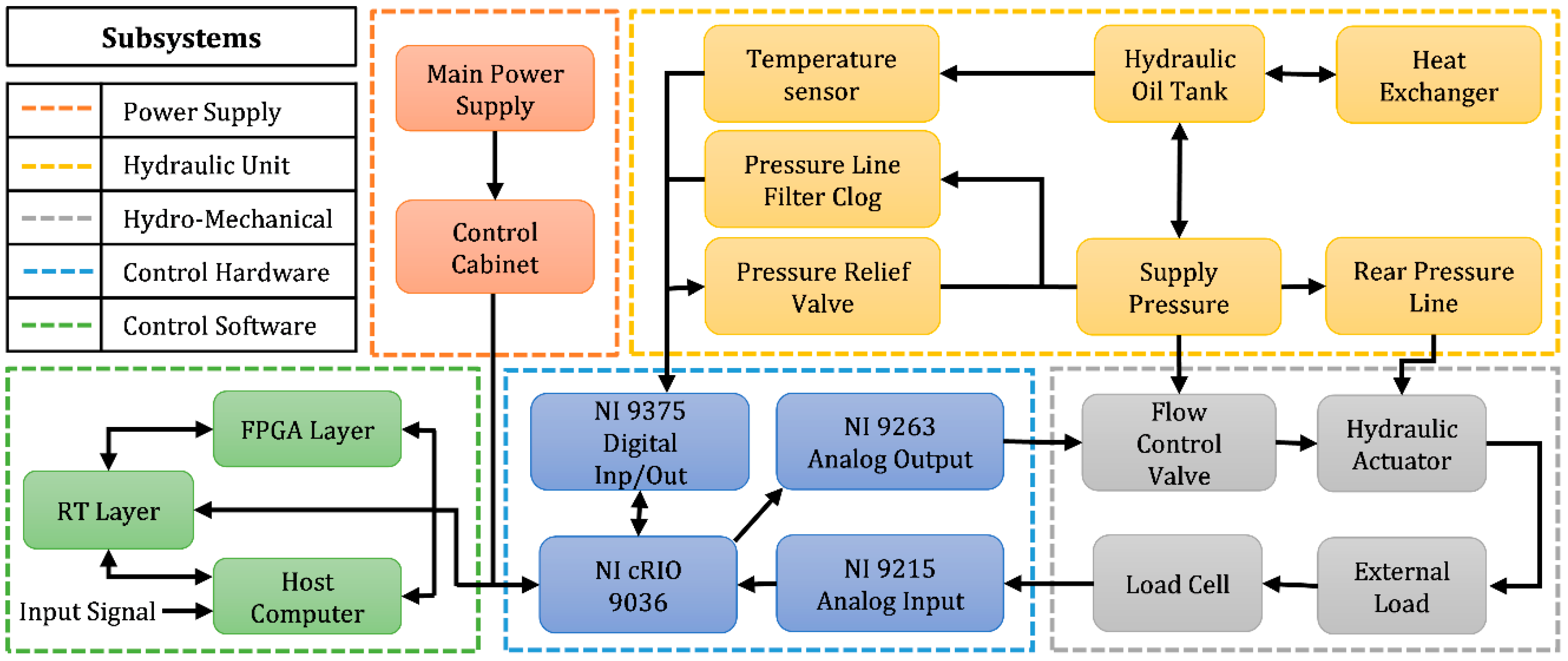
The constructional details of the newly developed composite and compact actuator are presented in
Section 2 of the paper. The actuator consists of a double-acting piston and cylinder arrangement controlled by a servo valve, and a separate rear chamber controlled by a separate valve that are designed to work in conjunction to generate static forces up to 7000 N that can be superposed with dynamic forces of up to ±1500 N with a targeted operational bandwidth of 200 Hz. The superposition of static and dynamic forces meets the machine tool requirement of generating periodic forces with a non-zero mean, and the bandwidth of 200 Hz will enable excitation of the low frequency global structural modes of machine tools [
42]. Though the composite design of the actuator is like that reported in [
15,
39,
40], the force capacity, the bandwidth, and the expanded model-based systematic analysis presented in
Section 3 and
Section 4 in this paper is unlike any in the literature.
Experiments in
Section 4 of the paper for different voltages and pressures show the static behavior of the electro-hydraulic actuator to be nonlinear. Characterization of the nonlinear static behavior of the actuator is separately presented for flow control by the servo valve to the main piston chambers, and separately for the pressure reducing valve controlling flow to the rear chamber. Static models for both cases are expanded to include the nonlinear flow characteristics of the servo valve and actuator assembly. These include accounting for the presence of dead-bands, for friction and frictional hysteresis, for leakages, for saturation behavior, and for even the effects of fluid temperature on the force response. Unknown model parameters in each case are identified from experiments, and the expanded nonlinear static model is observed to capture experimentally observed behavior very well, as is also discussed in
Section 4. Such expanded and comprehensive modelling of all the key nonlinearities observed in typical electro-hydraulic actuators, as is done in this paper, we believe, is unlike any other investigation reported in the literature. Furthermore, characterization of the actuator’s behavior under pressurized flow to the rear chamber, as is presented in this paper, is new, and has not been reported on by others.
Dynamic experimental characteristics are discussed in
Section 5 of the paper. Those experiments include a dynamic force component superposed with a static component. The dynamic model is also updated by identifying unknown model parameters from experiments. Following the reports in [
39,
40], herein too, we assume that since most nonlinearities are accounted for in the static model, and since nonlinearities are due to the static friction, due to variations in the flow-pressure coefficient of the servo valve, due to leakages causing pressure drops, and due to that valve overlaps do not strongly depend on the operating frequency, the updated dynamic model remains linear, and results with it are found to reasonably agree with experiments–as is also discussed in
Section 5.
Models and experiments presented in
Section 3,
Section 4 and
Section 5 are all for the open-loop configuration of the electro-hydraulic actuator, with closed-loop control being separately addressed in
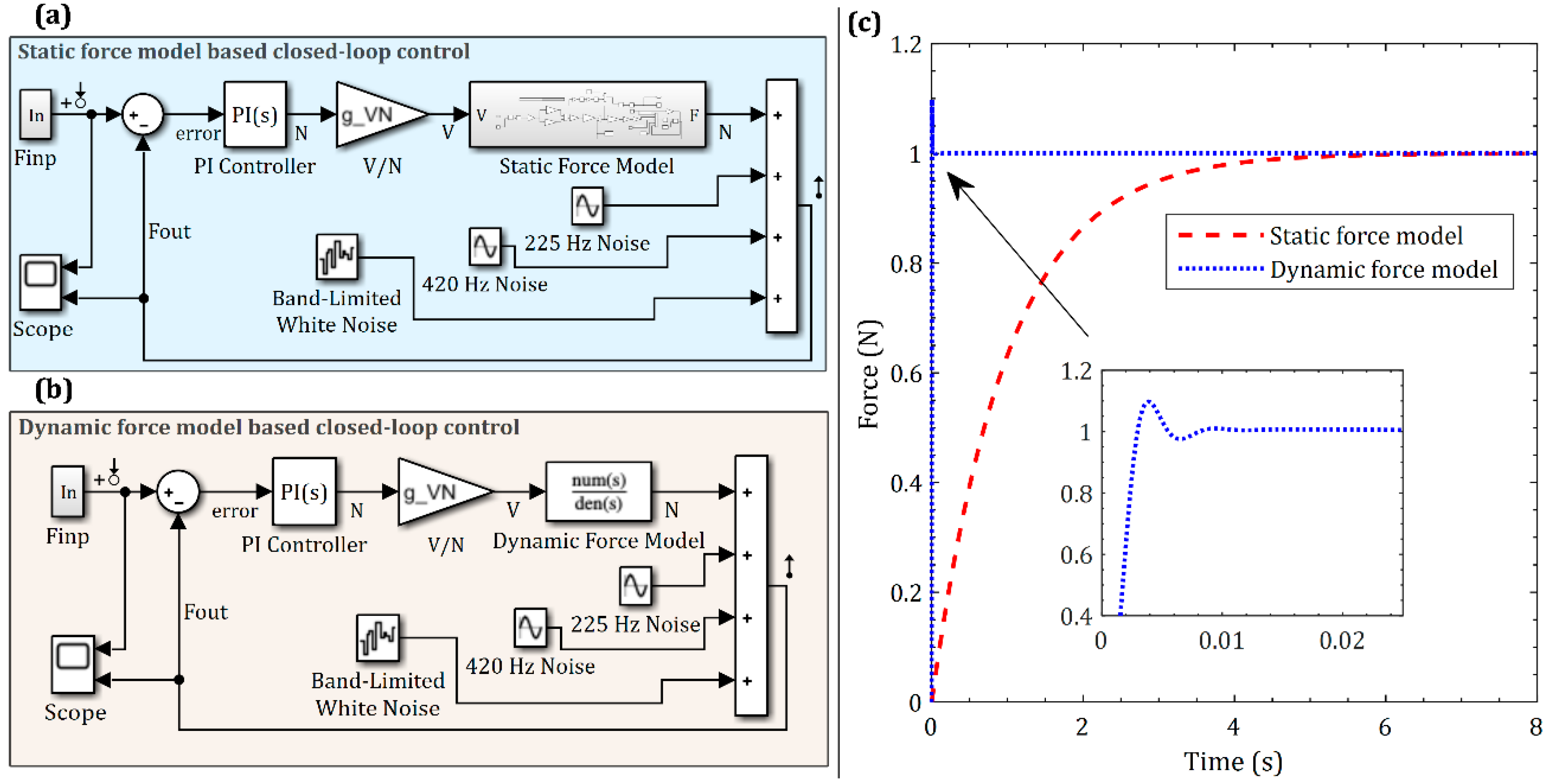
Section 6 of the paper. Closed-loop control is based on force feedback, such as reported in [
28,
43,
44,
45,
46,
47]. Since the objective of closed-loop control is to target a bandwidth of 200 Hz, a simple proportional-integral (PI) controller is preferred herein. The validated static and dynamic models are used to tune gains for the closed-loop control strategy, and the model-based tuning in turn guides appropriate closed-loop control of the actuator. On having systematically characterized the nonlinear static and dynamic behavior of the actuator and its control, the paper is finally concluded.
4. Static Force Characterization of the Electro-Hydraulic Actuator
This section first discusses the static behavior controlled by the servo valve followed by the static behavior controlled by the pressure in the rear chamber. This is followed by characterizing the superposed static behavior with flow controlled with the servo valve and with pressurized fluid being supplied to the rear chamber. In each case, experiments exhibit nonlinearities, and hence the linearized static models presented in
Section 3 are expanded herein to include nonlinearities.
4.1. Static Force Characterization of Actuator with Flow Control via Servo Valve
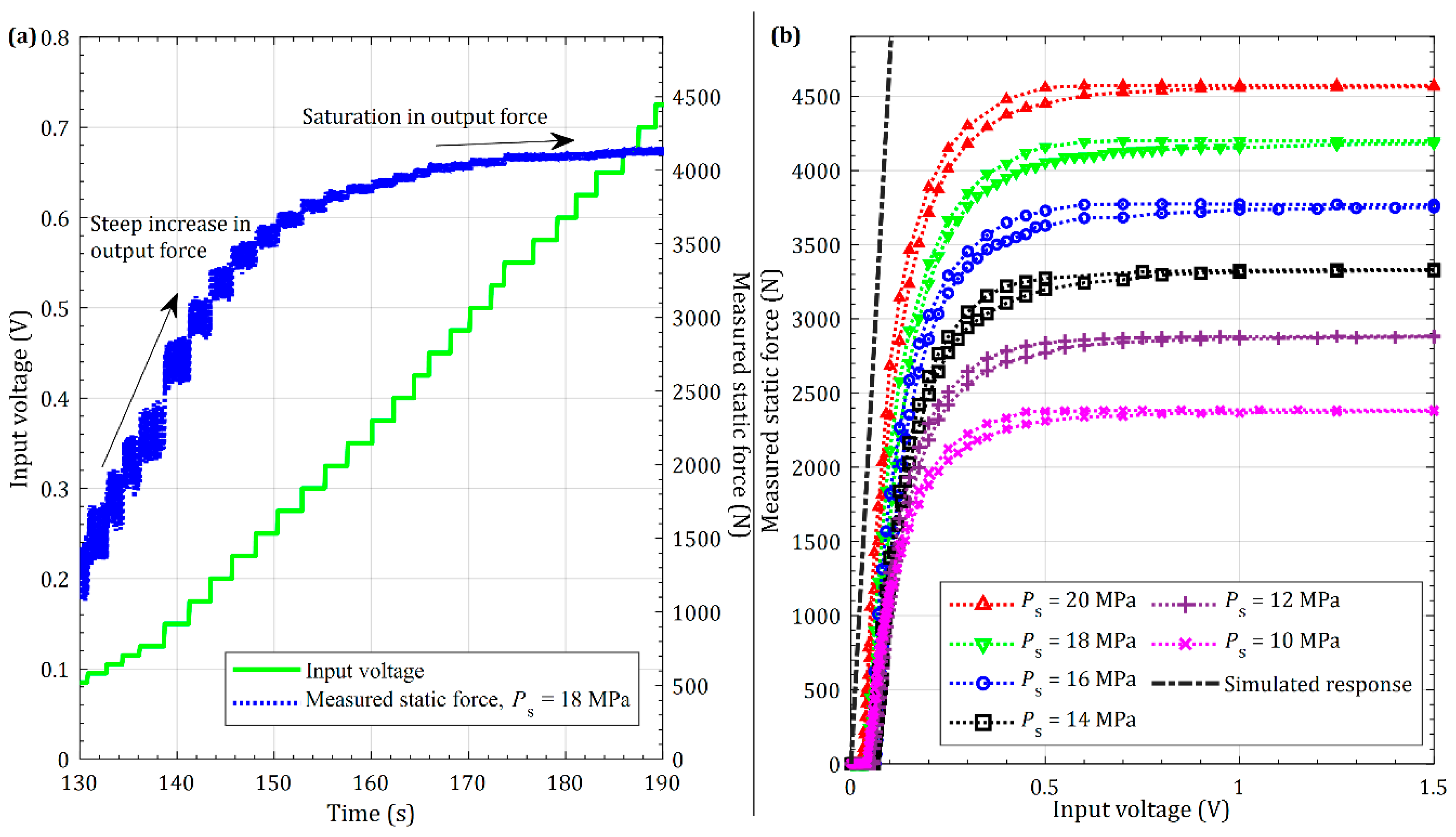
Experiments were conducted at different levels of voltages and supply pressures to understand the dependence of force on these parameters. Input voltage was varied from 0 to 2.5 V in steps of ~0.05 V, and the supply pressure was varied from 10 to 20 MPa in steps of 2 MPa. For each supply pressure, the voltage was first increased in steps until the forces stabilize and then decreased until the forces reduce to zero. An example of how the forces change with an increase in voltage for a supply pressure of 18 MPa is shown in
Figure 4a and changing force characteristics with changes in voltages and pressures are summarized in
Figure 4b. These experiments were all conducted with no fluid being supplied to the rear chamber.
Figure 4b also shows the model predicted forces using the linearized static force model discussed in
Section 3.2.1. For model predictions, the servo valve gain,
was calculated to be
, the valve flow coefficient,
was calculated to be
, and the area of the piston,
was estimated from the computer-aided design (CAD) model of the actuator to be
. For the linearized static force model, if we ignore the leakages in piston-cylinder arrangement, the net flow-pressure coefficient,
is replaced by
–the flow-pressure coefficient of the servo valve, which was evaluated from the flow-pressure curve for a differential pressure of 7–21 MPa [
12], and was taken to be
The servo valve gain, the valve flow coefficient, and the flow-pressure coefficient were all evaluated from the valve manufacturer’s data sheet [
48].
As is evident from
Figure 4a, forces increase with increasing voltages, and then saturate, i.e., when forces reach their saturation limits, a further increase in the voltage does not increase the force.
Figure 4a only shows representative results for a fixed supply pressure of 18 MPa and for the forward path, and as is evident from
Figure 4b which summarizes results for other pressures, and also for the reverse path—the force characteristics are similar to the case shown in
Figure 4a, i.e., forces always saturate. As is also amply evident from the comparisons in
Figure 4b, the linearized static force model cannot capture the measured behavior. The model suggests a linear relationship between the force and the voltage with the coefficients contributing to the slope. The model also is not dependent on the supply pressure. Experiments on the other hand suggest that forces change with supply pressure, and that forces are nonlinearly dependent on the supply voltage. Experiments also suggest that there is a certain threshold voltage that must be reached before the actuator applies a force, and that forces saturate after a certain other threshold voltage is reached. Experiments further demonstrate hysteresis in the measured forces changing with increasing and decreasing levels of voltages. All these observations clearly demonstrate that the linearized static model is inadequate.
The observed dead band region, i.e., the threshold voltage that must be reached before the actuator applies a force may be attributed to servo valve behavior [
1,
2,
21,
24], and also potentially due to the static friction that needs to be overcome [
1,
2,
21,
23,
25,
26]. The nonlinear force-voltage characteristics and their dependence on supply pressure may be attributed to the nonlinear characteristics of the flow-pressure coefficient [
1,
2], and to the leakages across the piston, and across the relief valve [
1,
2,
23,
24,
27,
28,
29,
30,
31], and also to the nonlinear Coulombic and viscous friction behavior [
1,
2,
23,
25,
26,
27,
28,
29,
32,
33,
34,
35,
36]. The observed hysteresis is also attributable to frictional hysteresis of the actuator [
23], and to a lesser extent, to the electrical hysteresis caused by the inductance of the torque motor in the servo valve [
1,
2,
21,
22,
23], and to yet a lesser extent due to temperature related effects that change the viscosity and the bulk modulus of the oil in use [
2,
25,
37]. The nonlinear saturation behavior is attributable to the saturation of the servo valve and the actuator [
1,
2,
23,
27,
39,
40]. Though some of the above observed nonlinearities have been characterized separately using models and/or experiments for the use of electro-hydraulic actuators across other engineering domains, there appears no report characterizing the cumulative influence of these nonlinearities, and none whatsoever in the context of electro-hydraulic actuators for use in machine tool structural testing applications. Each of the observed nonlinearities is included in an expanded static model—as is described next.
4.2. Modelling of Nonlinearities in the Static Force Model for Flow Control via Servo Valve
This section expands the linear static model to include nonlinearities due to flow, due to leakages and pressure drops, due to saturation, and due to friction and frictional hysteresis. Each of these effects is characterized in separate subsections as follows.
4.2.1. Nonlinearities Due to Flow and Leakages
The linear static model (see Equation (18)) suggests a linear relationship between the output force and the input voltage, with the flow coefficient (
) and the flow-pressure coefficient (
) contributing to the slope. These coefficients, though nonlinear (see Equation (6)), were linearized assuming that they do not change with operating conditions. However, since the static characteristics evident in
Figure 4 clearly exhibit nonlinearities, the dependence of these coefficients on operating parameters must be accounted for. Since the flow coefficient depends on the spool displacements (see Equations (6)–(8)), which does not change much for static experiments, the flow coefficient can be assumed to remain constant. The flow-pressure coefficient on the other hand is a function of the load pressure. This dependence is valve specific and is usually described by valve manufacturers’ in terms of variations in the valve flow (Q) with the pressure differential (
) across the servo valve. In the present case, we characterize this relationship by fitting a curve to the data provided by the valve manufacturer [
48]. The data and the fitted relationship in logarithmic scales are shown in
Figure 5.
Because of the logarithmic nature of the plot, the relationship between Q and
appears linear, when in fact an exponential fit characterizes the relationship as:
where
is in MPa. Using the Equation (20) and Equation (4) and taking into account the unit conversion of
into Pa, the nonlinear flow-pressure coefficient, denoted by
, can be calculated as follows:
Equation (21) clearly shows the flow-pressure coefficient to be a nonlinear function of the pressure differential across the valve. This pressure differential, in the absence of leakages, is equal to the difference of supply pressure on the input end and the load pressure on the output end of the servo valve. However, since leakages are inadvertently present in any hydro-mechanical system, we account for them by considering leakages from the pressure relief valve, leakages in the return line, and internal leakages across the two chambers of the actuator piston. Since leakages from the relief valve feed into the main supply line leading to the servo valve, these leakages might additively contribute to the input supply pressure, and we denote this pressure by
. The leakages in the return line result in a pressure drop across the servo valve equal to the tank pressure (denoted by
). The internal leakages also result in a pressure drop, but across the piston chambers. This pressure drop is proportional to the differential pressure across the piston chambers and is here denoted by
. Accounting for these leakages, the resultant pressure differential across the valve becomes:
where
remains the supply pressure. Substituting this expression for the pressure differential within Equation (21), the flow-pressure coefficient can be rewritten as:
Having accounted for nonlinearities due to the servo-valve characteristics and pressure drops due to leakages, we next discuss characterization of saturation of the force.
4.2.2. Characterizing the Saturation of the Force Response
Saturation in the actuator response occurs when the load pressure achieves its limiting value of the supply pressure. Noting the linear dependence of static force (
) on the load pressure (
), the inverse relation between the slope of
curve and
from the static force model presented in
Section 3.2 and the hyperbolic relation between
and the load pressure (
) as shown in Equation (23), it is easy to deduce that as the static force and hence the load pressure increases with the input voltage, so does the value of
resulting in a corresponding decrease in the slope of
curve. As the load pressure (
) converges to its limiting value of supply pressure (
), the slope tends to zero and a constant force value is achieved, which is termed as the
Saturated Force (
). The voltage value at this saturation point is correspondingly termed as the
Saturation Voltage (
). Beyond the
Saturation Voltage (
), the static force is constant and independent of the input voltage. Hence, the net saturated force (
) can be expressed using the Pascal’s law as the product of the saturated load pressure (
) and the area of the central annulus of the piston, while also accounting for the pressure drop due to internal leakages across the piston chambers (
) as follows:
where
is a cumulative coefficient of internal leakages. External leakages in the piston-cylinder assembly are neglected in the present analysis. At the saturated condition,
and hence,
, which makes the saturation force to be:
Equation (25) can be rewritten in a more convenient form as:
This re-arrangement suggests that the slope of the relationship between
and
must be equal to
, and the intercept must be equal to
. Since
is a design parameter and is known beforehand, and the tank pressure
can be taken to be the atmospheric pressure (
), the coefficient of internal leakages,
and the pressure leakage from the pressure reducing valve,
can be easily estimated by fitting a line to the measured relationship between
and
based on the characteristic behavior in
Figure 4. The resulting linear fit is shown in
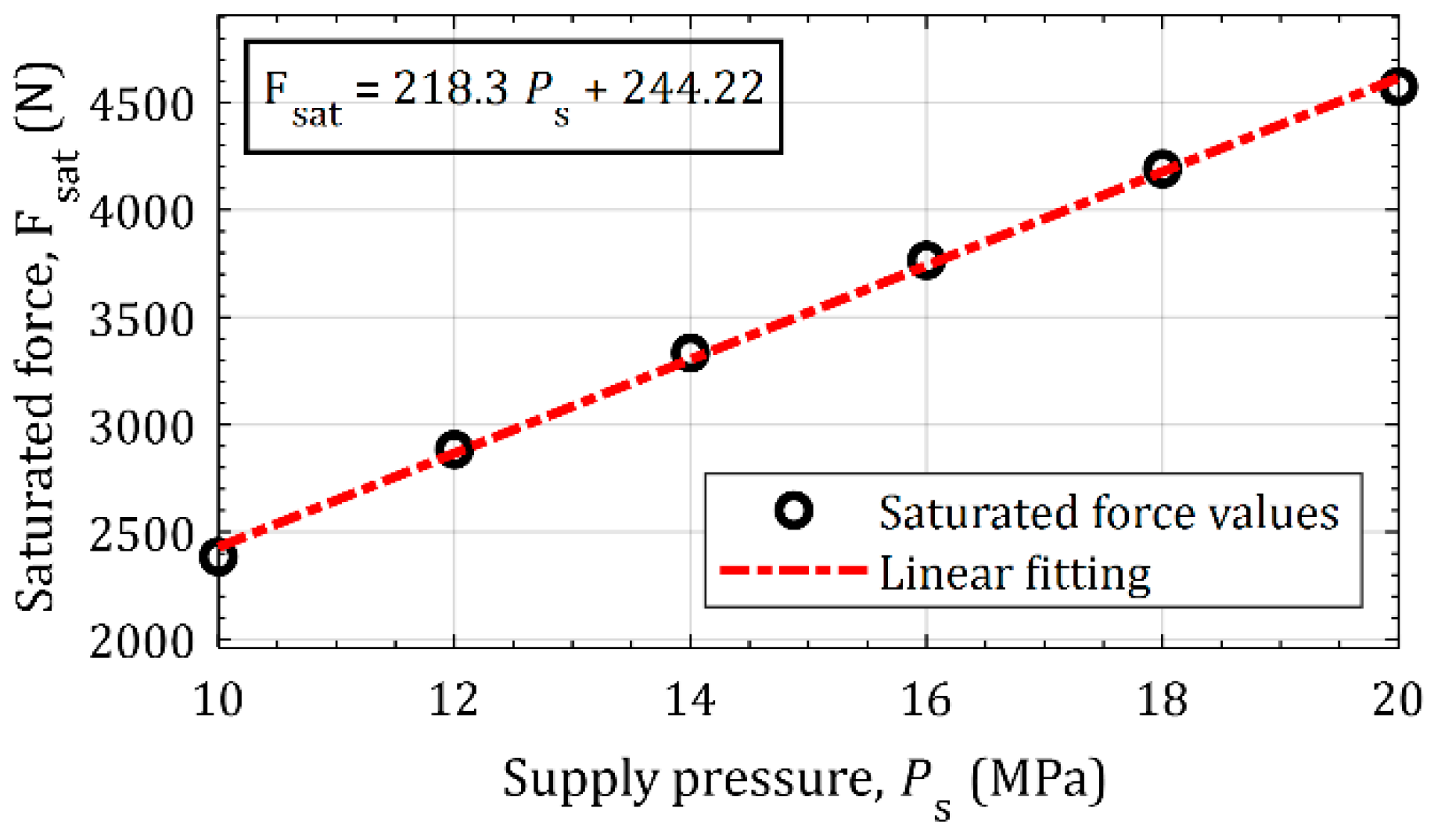
Figure 6.
Using the linear fit equation in conjunction with Equation (26), the coefficient of internal leakage and the pressure leakage form the pressure reducing valve can be identified to be = 0.0680 and = 1.1157 MPa respectively.
Having characterized the saturated force behavior and having systematically identified the unknown model parameters including the flow coefficients, leakage coefficients and the pressure drops, we re-define the static force model (Equation (18)) as:
where
is a constant value.
Having characterized the nonlinearities which directly influence the force generation within the system, we next discuss frictional nonlinearities that are external to the source of force application but still influence the static force characteristics and contribute to the hysteresis in the system.
4.2.3. Nonlinearities Due to Friction and Frictional Hysteresis
To better understand the influence of frictional nonlinearities on the static force response of the system, consider the partitioning of force–voltage behavior for a representative supply pressure of 20 MPa into the four regions as shown in
Figure 7. These four regions are classified as the no-force region, the linear region, the transition region, and the saturation region.
As is evident from
Figure 7, in the no-force region, even as the voltage is increased, there is no force until point ‘A’ is reached (denoted by the
Onset Voltage). This suggests that for the piston to move and exert a force, it must overcome some static friction, and hence this region must be characterized by a static friction model. As the voltage is increased beyond the point ‘A’, the piston breaks away the static friction and starts to slide, and consequently the output force increases. The linear increase in the static force is bounded by the Coulombic friction force and hence, the Coulombic friction model defines the friction behavior in the linear region. The transition region defines the transition from the linear force profile to the start of the force saturation region, i.e., point ‘B’. The slope of the force-voltage plot slowly tends towards zero, and so does the velocity of the piston. As the velocity tends to zero, the friction value goes below the maximum friction defined by the Coulombic friction model, and the viscous friction model comes into action. Hence, the friction in this nonlinear steady transition region is possibly governed by a viscous friction model. Since the viscous friction has a strong dependence on the piston velocity, it plays a major role in the frictional hysteresis—which appears to be dominant only in the transition region—see
Figure 7. Beyond point ‘B’, which marks the
Saturation Voltage, the force saturates suggesting that the piston velocity becomes zero, and since there is no relative motion, friction plays no role in the saturation region.
The characteristic behavior of the static force suggests that the frictional effects can be modelled by a static friction model in the ‘no-force’ region, by a Coulombic friction model in the linear region, and by a viscous friction model in the transition region. These models are formulated as under.
The static frictional force,
that must be overcome for the piston to slide and for the actuator to apply a force can be characterized by:
where
is the maximum static friction value,
denotes the piston velocity, and
is the output static force of the actuator. This static frictional force was estimated using the setup as shown in
Figure 8. As shown, the actuator was placed with the piston facing upwards, and different calibrated weights were placed incrementally on the piston, and the weight under which the piston moved downwards was recorded as the weight which equates the static frictional force. The static frictional force was hence experimentally calibrated to be ~44 N.
The frictional force behavior in the linear region is characterized by the Coulomb friction model which suggests the friction force to be a constant beyond the threshold value of maximum Coulombic friction as follows:
where
denotes the Coulombic frictional force,
denotes the maximum Coulomb sliding friction value, and
denotes the output static force. The value of
is found experimentally using similar methodology as reported in [
23,
32]. The piston was manually pulled via a digital force gauge (Make: Eagle, Model number: EEL6001A), and the corresponding pull force, just sufficient to make the piston slide, was recorded. Three sets of experiments were carried out and an average pull force value of ~39 N was taken as the maximum Coulomb sliding friction value,
.
To characterize the frictional behavior in the transition region, the piston-velocity dependent viscous friction model is considered:
where in
denotes the viscous friction force, and
is the same viscous coefficient of friction as described in Equation (12). Since this coefficient is to be calibrated through experiments, and since we do not explicitly measure the velocity of the piston, we instead rewrite the viscous friction force to be dependent on the change in the force with voltage. To do so, we rewrite the static force in Equation (12) under no external load (i.e.,
) to change with voltage as:
where
is the overall stiffness of the piston along with the load cell, and
is the position of the piston. Since experiments involve ramping the input voltage (at a constant slope) with time, hence, the time derivative of voltage comes out to be the constant slope value from which we get the time derivative of the piston displacement in terms of the output force as follows:
where in
is the slope of the ramped input voltage and hence, a model-dependent factor. Since, for a simulation time of 10 s, the voltage signal was ramped from 0 to 2.5 V and back from 2.5 to 0 V, hence, the slope value which gives the time derivative of the voltage signal (
), was calculated to be 0.5 V/s for increasing force values and −0.5 V/s for decreasing force values. Now, substituting Equation (32) into Equation (30), we get the modified viscous friction model as:
where
is defined as the cumulative coefficient of viscous friction, which can be calibrated to fit the observed behavior in the transition region. The calibrated cumulative coefficient of viscous friction was found to be 0.2 V.
Combining the static friction model, the Coulombic frictional model, and the viscous frictional model, we get the net frictional force behavior modelled as follows:
4.2.4. Nonlinearities Due to Dead bands, Electrical Hysteresis, and the Effect of Temperature
The no-force region of the force-voltage curve shown in
Figure 7 is generally caused by the combined effects of the static friction, spool overlaps and zero offsets in the spool of the servo valve. Static frictional effects have already been accounted for as discussed in
Section 4.2.3, and since the valve under use has a critically centered spool and the zero offsets specified in the valve datasheet are less than 1%, their influence is expected to be negligible. Similarly, for the servo valve under use, the specified electrical hysteresis as per the valve datasheet is also less than 1.5% over the operating range of the system, and its effect is also expected to be negligible. Though negligible, the effects of spool overlaps, zero offsets, and electrical hysteresis are accounted for by introducing an ‘
Offset Voltage’ in the model, which is estimated to be ~1.5% of the operating voltage range, i.e., 0.0375 V.
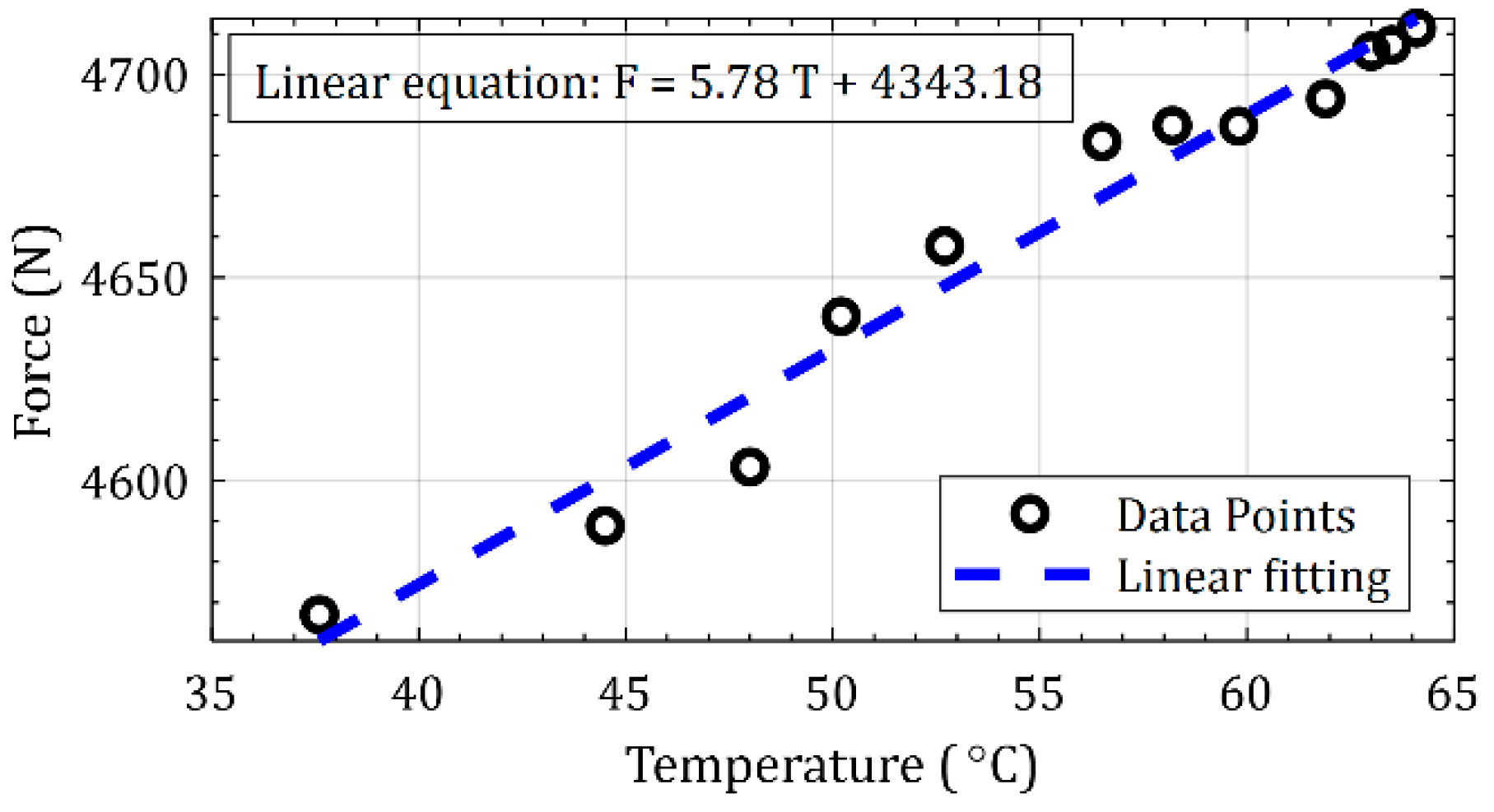
Although temperature is not a control parameter of the system, to understand its influence on the force, experiments were performed with the system kept in continuous operation at a supply pressure of 20 MPa, with the oil temperature of the hydraulic tank and the force applied being recorded at periodic intervals of 10 min. These measurements shown in
Figure 9, show the forces increasing with an increase in temperature–which is consistent with trends reported in [
37]. Since forces only increase by 3% for a 30 °C increase in temperature, and since all experiments for all analysis in this paper were performed only when the oil temperature was consistently between 30 °C to 50 °C, for which range the change in forces is negligible, hence, effects of temperature are ignored in this analysis.
Having characterized the nonlinearities due to flow and leakages, and due to friction, and having also accounted for the saturation behavior, the static model for force application by controlling the servo valve is updated to include the nonlinear characteristics—as discussed next.
4.3. Expanded Nonlinear Static Force Model Obtained by Actuating the Servo Valve
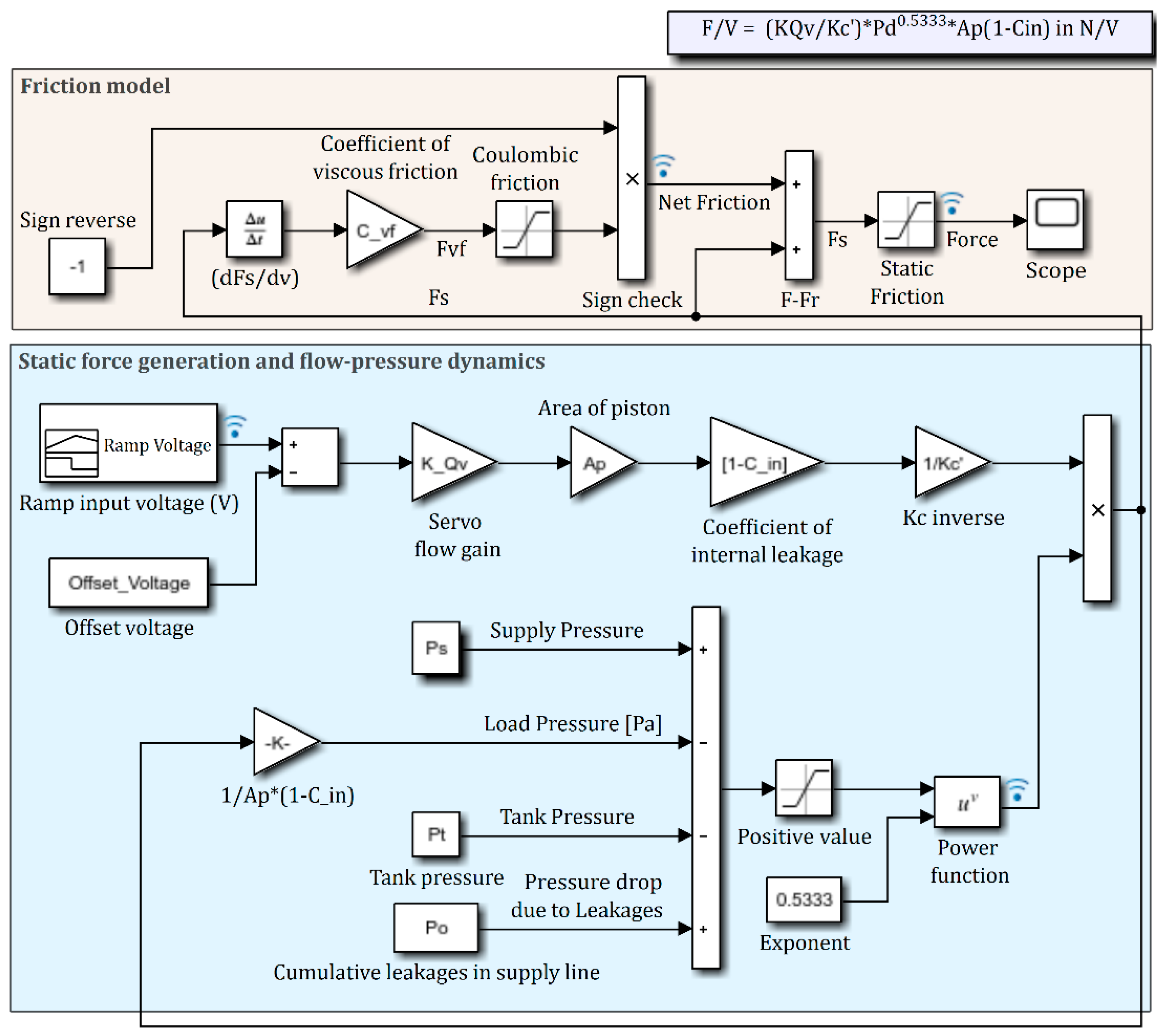
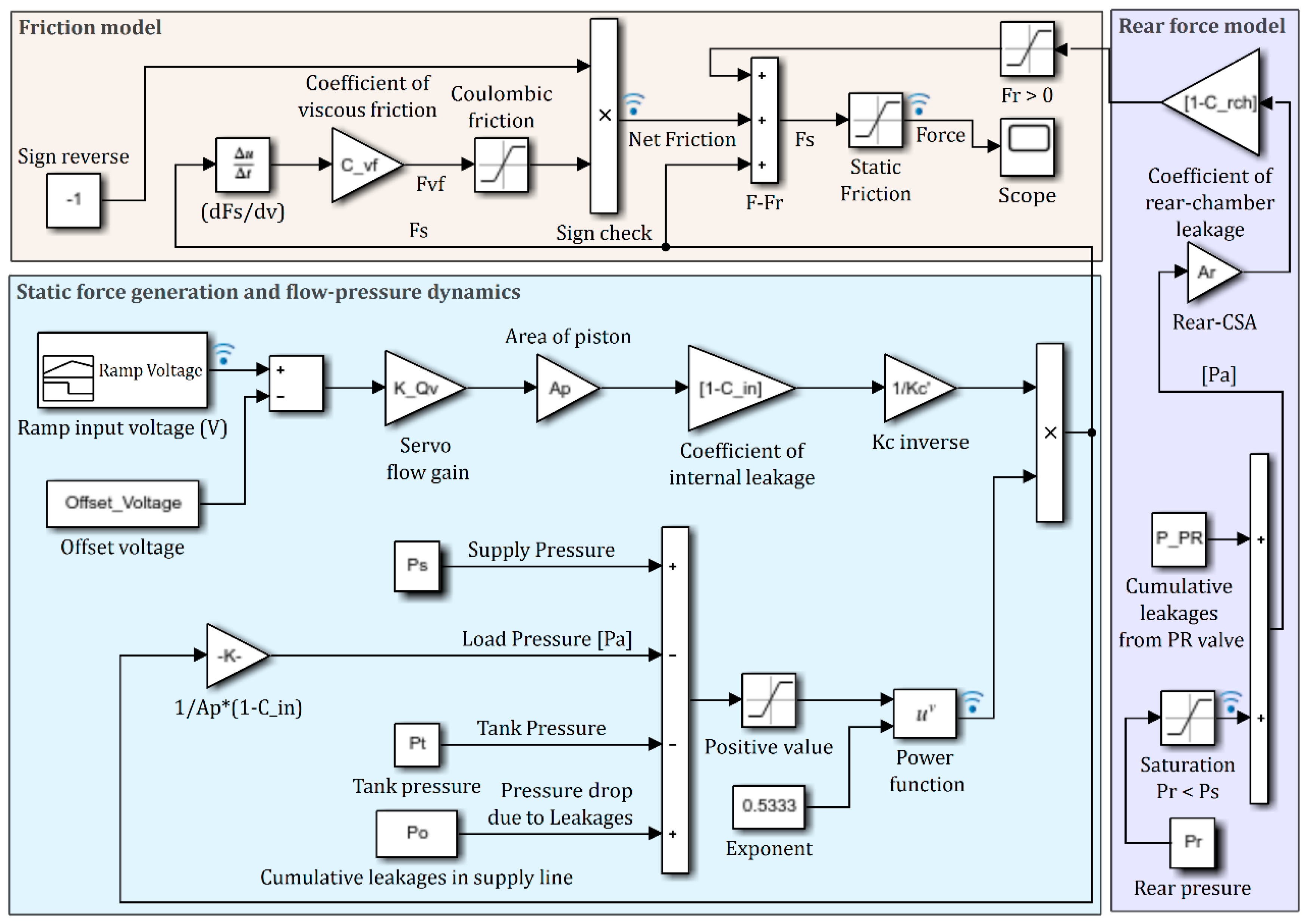
The major nonlinearities in the static response of the system were identified and modelled using a block-diagram approach using Simulink
®-as shown in
Figure 10. The model comprises of two sections. The section on ‘
Force generation and flow-pressure dynamics’ includes the model for nonlinear servo valve characteristics, pressure drops across the servo valve and internal leakages across the piston; and the section on the ‘
Friction model’ accounts for the influence of the friction on the static force. To mimic experimental procedures, the input voltage is ramped to increase and then, decrease. To account for the nonlinearities due to dead-bands and electrical hysteresis—as discussed in
Section 4.2.3 and in
Section 4.2.4, an
Offset Voltage is subtracted from the input signal—which results in a positive shift in the voltage axis of the force curve to help characterize the ‘no-force’ region. The ‘servo flow gain’ shown in
Figure 10 is a product of the servo gain (
) and of the flow coefficient (
). All other parameters shown in
Figure 10 are the same as described in
Section 4.2. The load pressure is recursively calculated from the output force using Pascal’s law. This is achieved using a force feedback-loop as shown in
Figure 10. For the friction model, the measured output force is differentiated with respect to the input voltage to compute the viscous friction force as per Equation (33), and a saturation block is used to model the Coulombic friction force. Another saturation block is used to set a lower bound on the output force as defined by the static friction model, which ensures that the output force remains zero until the threshold limit defined by the static friction is achieved.
Using the expanded nonlinear static model, force predictions for different supply pressures are compared with experimental results in
Figure 11. As is amply evident, model predictions can faithfully capture all observed behavior for different supply pressures of interest. The no-force region is captured well, as is the nonlinear transition from the linear region to the saturation region. Seeing how the expanded model accounts for nonlinearities due to flow and leakages, and due to friction and frictional hysteresis, as well as for the saturation behavior, it is reasonable to conclude that the expanded nonlinear static force model of the actuator with flow controlled with the servo valve is validated. Such systematic characterization of all major nonlinearities included in a single expanded static model for electro-hydraulic actuators is a new contribution to the literature on modelling, characterizing, and understating the nonlinear behavior of servo valve controlled electro-hydraulic actuators.
Similar analysis as was presented herein for flow controlled by the servo valve is presented in the next section to characterize the static force obtained by controlling pressure in the rear chamber.
4.4. Static Force Characterization of the Actuator by Controlling Pressure in the Rear Chamber
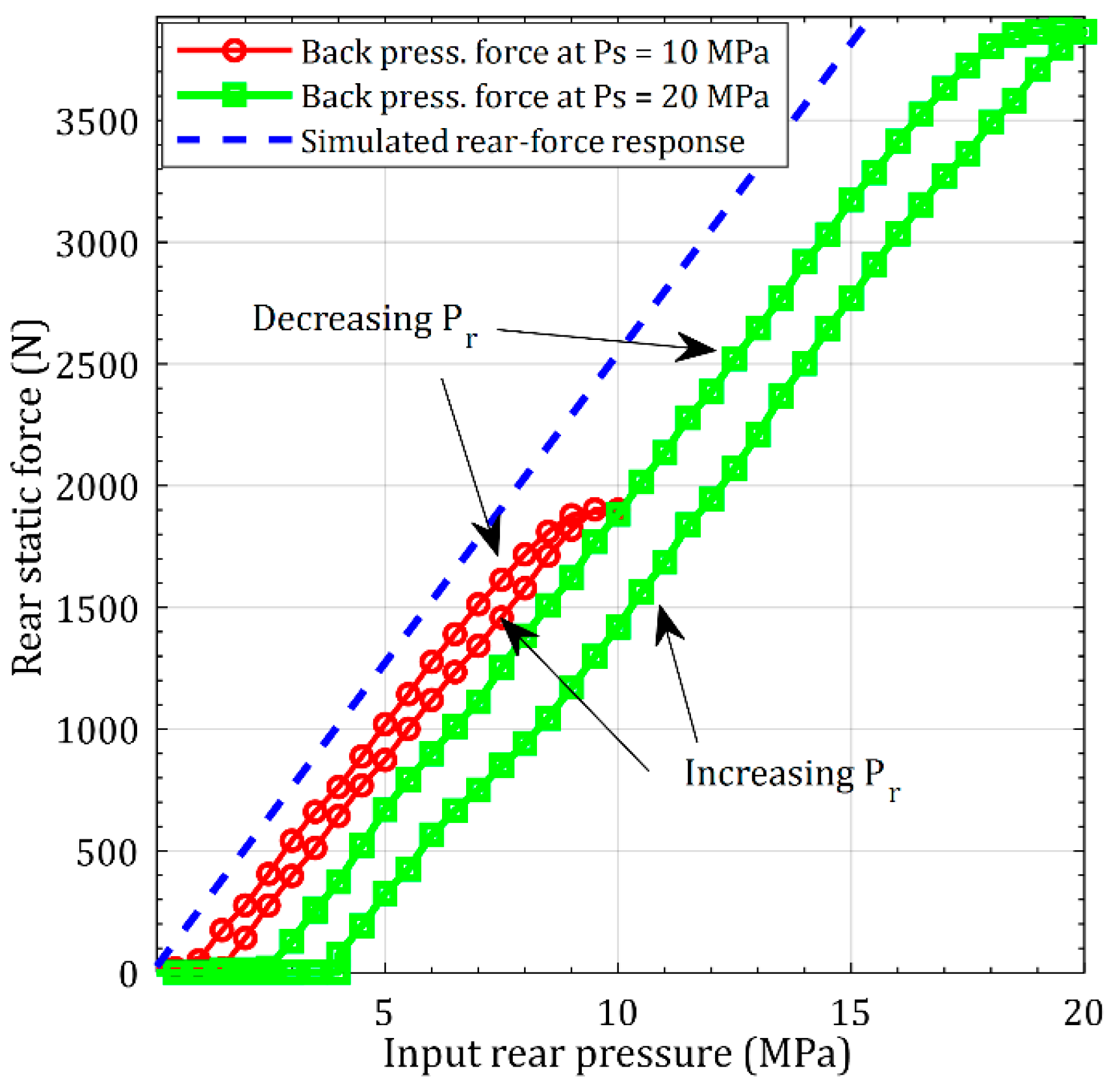
Experiments were conducted by regulating the pressure in the rear chamber by using the pressure reducing valve. To isolate these experiments from the influence of the servo valve, the servo valve was turned off. The pressure reducing valve was used to increase the pressure in the rear chamber in steps of 1 MPa until the pressure in the rear chamber equaled the supply pressure, which was controlled independently. Two separate experiments with two different supply pressures were conducted. On reaching the saturation limit (when pressure in the rear chamber equaled the supply pressure), the pressure in the rear chamber was decreased in steps of 1 MPa. The pressure across the pressure reducing valve was monitored using a pressure gauge, and the force was measured using the same load cell. The resulting measured forces changing with pressures in the rear chamber are shown in
Figure 12. For comparison purposes, the predicted static forces using the linear rear-force model (Equation (19)) described in
Section 3.2.2 are also shown in
Figure 12. For model predictions,
was identified from the CAD model of the actuator and was taken to be
m
2.
As is evident from
Figure 12, the measured force characteristics are very different than model predictions, and are also very different than the measured force characteristics for force applied by controlling flow to the servo valve (see
Figure 4). Even though the force model for pressurized flow in the rear chamber is linear, experiments are not. The measured output force clearly saturates at pressures in the rear chamber equaling the supply pressure. Measured characteristics also suggest that there is certain threshold value of the pressure in the rear chamber that must be reached before which the actuator can exert a force. Measurements also exhibit hysteresis. Though the model predicted slope is like that of the measurements, the model is clearly inadequate, and it must hence be expanded to include the experimental observations.
The observed dead band region, i.e., the threshold pressure in the rear chamber that must be reached before the actuator applies a force may be attributed to the servo valve behavior, even when it is off, and can be explained by the accounting for the ‘no-load’ leakages [
1,
21,
23,
27,
48]. Even when the servo valve is turned off, there is some fluid flowing into both the piston chambers and further, back to the tank via the return line. This fluid-flow at zero voltage, termed as the ‘no-load’ leakage in the servo valve maintains the piston chambers at a certain pressure value termed as the no-load chamber pressure (
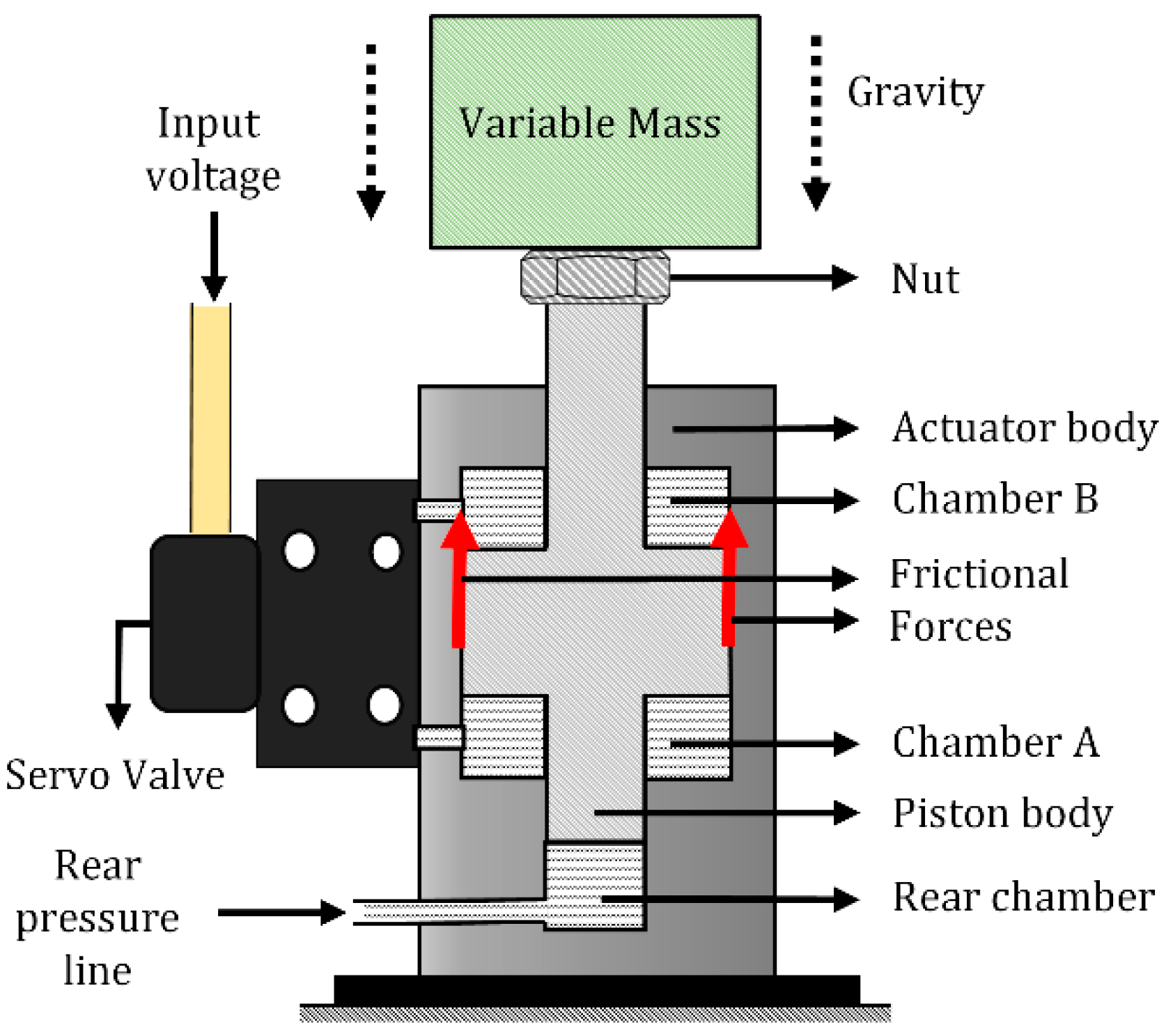
). The fluid in the main piston chambers A and B (see
Figure 1) potentially obstructs the sliding motion of the piston, and hence may influence the force response due to pressurized flow supplied to the rear-chamber. This no-load chamber pressure was inactive in the previous static-force analysis via the servo valve, because at no load, the pressure in both the chambers are equal and hence cancel each other out. However, in the present case, the chamber pressure is potentially responsible for resisting the motion of the piston until some threshold rear chamber pressure is achieved.
The no-load chamber pressure in that sense, acts like friction resisting motion, and may also help explain the large hysteresis that is observed, and can be explained as follows: as the piston slides ahead, the fluid in the piston chamber B (at front) is compressed and exerts an opposite pressure on the piston reducing the net force. However, during the backward motion of the piston, the fluid in the chamber A undergoes compression, and exerts a similar force but in the forward direction, thus resisting the motion of the piston. This velocity-dependent behavior is like the friction model proposed in
Section 4.2.3 and may help explain the observed hysteresis. The dependence of this hysteresis behavior on the supply pressure can be attributed to the fact that the no-load chamber pressure in the servo valve is known to be proportional to the supply pressure acting on the input end of the servo valve [
21,
27,
48]. For similar reasons, the threshold pressure that must be reached in the rear chamber before the actuator exerts a force must also be a function of the supply pressure.
Though there has been some reporting and characterization of the nonlinearities due to servo valve-controlled actuators, there appear no reports explaining and/or modelling the above described force nonlinearities due to pressurized flow in the rear chamber. Each of the observed nonlinearities are included in an expanded static model for the actuator of interest—as is described next.
4.5. Modelling of Nonlinearities in the Static Force Model for Pressurized Flow to the Rear Chamber
This section expands the static force model for force obtained by supplying pressurized flow to the rear chamber by including nonlinearities due to no-load leakages, due to friction, and due to hysteresis. Each of these nonlinearities are characterized separately in the subsections discussed next.
4.5.1. Nonlinearities Due to Leakages in the System
Three basic leakages are considered in the present analysis, namely the leakages from the pressure reducing valve in the rear pressure line, the leakages from the rear chamber of the piston, and the leakages from the servo valve to the main piston chambers. The leakages in the rear pressure line occur through the pressure reducing valve, which is connected to the high-pressure main supply line. These leakages seep into the high-pressure supply line and add to the rear pressure and are denoted by
. The drop in pressure due to internal leakages from the rear chamber of the piston (
) is similar to that considered across the main piston chambers in the static force analysis with the servo valve. They are, hence, similarly modelled as a linear function of the rear-pressure (
) of the actuator as follows:
where
is the constant of proportionality which is equal to the coefficient of rear-chamber leakage and
denotes the net rear pressure including the leakages, as defined ahead in Equation (37).
As discussed in
Section 4.4, the no-load chamber pressure acts like friction and resists the sliding motion of the piston. Thus, as the rear pressure is gradually increased, the piston tends to slide ahead, but the pressure in chamber B resists this force till a threshold value of rear pressure is reached. This threshold pressure, denoted by
, is modelled as a linear function of the supply pressure as:
where
is the coefficient of the threshold pressure value,
and
are the cross-sectional areas of the piston’s central annulus and the rear-surface, respectively, and
is the supply pressure. Since the threshold pressure is defined in terms of the rear pressure which acts on the rear surface, and since the chamber pressure acts on the central annulus area (
), the factor
is included in Equation (36) to maintain force equivalence in the system.
Including the influence of leakages in the rear chamber based static force model, we get:
where
is defined in Equation (35), in which the net rear pressure,
, and the threshold pressure,
is defined in Equation (36). Substituting for these, and rearranging the resulting equation in a more convenient form, we get:
This force equation represents the equation for a line, and knowing
and
, the unknown
,
and
can be found from the measured characteristics of
vs
for different known values of
–as is shown in
Figure 12. The unknowns are hence estimated as:
= 0.03623;
= 0.6 MPa;
= 0.184. Having thus characterized the nonlinearities due to leakages, we now turn our attention to characterizing nonlinearities due to friction and due to frictional hysteresis.
4.5.2. Nonlinearities Due to Friction and Frictional Hysteresis
The friction model developed previously in the case of static force characterization with the servo valve was largely defined by the characteristics of the piston. Since the hydraulic piston and the actuation manner remains the same, hence, the same friction model is considered here as well. Similar to the friction model discussed in
Section 4.2.3, the net frictional force is defined by the combination of the static friction model, the viscous friction model and the Coulombic friction model. The parameters of the static friction model and the Coulombic friction model are piston-dependent and hence, remain the same. However, the viscous friction model is a function of the piston velocity, which was earlier (in
Section 4.2.3) expressed in terms of the slope of the output force plot with the input voltage. In a similar fashion, the slope of the rear force plot with the rear pressure is used to estimate the piston velocity, as shown below:
where in
denotes the stiffness of the piston, and
denotes the slope of the ramped input signal, i.e., the rear chamber pressure, and is a model-dependent factor. Since the rear pressure signal was ramped from 0 to 20 MPa and back within a simulation time of 10 s,
was estimated to be 4 MPa/s. Using Equation (39), the viscous friction model becomes:
where in
is the cumulative coefficient of viscous friction and is identified to be 0.2 V in
Section 4.2.3.
The only modification from the friction model described in
Section 4.2.3, is the change in the control parameter which was the input voltage in the case of the servo valve and is the rear pressure herein. However, both are ramped with a constant slope with respect to time, hence mathematically, both models are equivalent.
4.5.3. Hysteretic Nonlinearities Due to the No-Load Chamber Pressures
Hysteresis in the system can be attributed to the no-load chamber pressure generated in the piston chambers due to leakages or no-load flow in the servo valve. Such leakages in the servo valve are proportional to the supply pressure of the system acting on the input end of the servo valve. Just like friction, the no-load chamber pressures would exert an opposite force on the piston, thus reducing the net output force in the case of forward motion of the piston, while increasing the same in the case of backward movement of the piston. Thus, the model for no-load chamber pressures should depend on the direction of motion of the piston, which can be directly related to the sliding velocity of the piston. Using the same modelling strategy as that for modelling of friction, the direction of sliding motion of the hydraulic piston is calculated and then used to determine the direction of the resistive force due to the piston chamber pressure. Based on the above discussions, the no-load chamber pressure,
is modelled to be proportional to the supply pressure and to the piston velocity, as:
where
denotes the piston displacement and
is the coefficient of no-load chamber pressure. The velocity term in Equation (41) can again be replaced with the slope of the rear force plot, as described in Equation (39). Since
and
are both positive quantities, therefore the sign of the displacement gradient of the hydraulic piston
is same as the sign of the slope of the force curve
, and the no-load chamber pressure can hence be rewritten as:
The corresponding force due to the no-load chamber pressure becomes:
Since the resultant force due to the chamber pressure, as formulated above is proportional to the supply pressure, therefore, at lower supply pressure values the amount of hysteresis is low, and at higher supply pressures, the hysteresis is high. Additionally, the change in the sign of the slope of the curve changes the sign of the force as well, and hence, the ideal force curve (without hysteresis) is displaced equally about its mean position i.e., it is shifted downwards with increasing rear pressures, and shifted upwards with decreasing rear pressures. The unknown gain
in Equation (43) is identified by equating the magnitude of hysteresis in the experimental plot (see
Figure 12) for a known supply pressure value with that of the hysteresis model as in Equation (43), and it comes out to be
.
Having characterized the nonlinearities due to leakages, and due to friction, and having also accounted for hysteretic behavior, the static model for force application by controlling the pressure in the rear chamber is updated to include the nonlinear characteristics—as discussed next.
4.6. Expanded Nonlinear Static Model for Pressurized Flow Supplied to the Rear Chamber
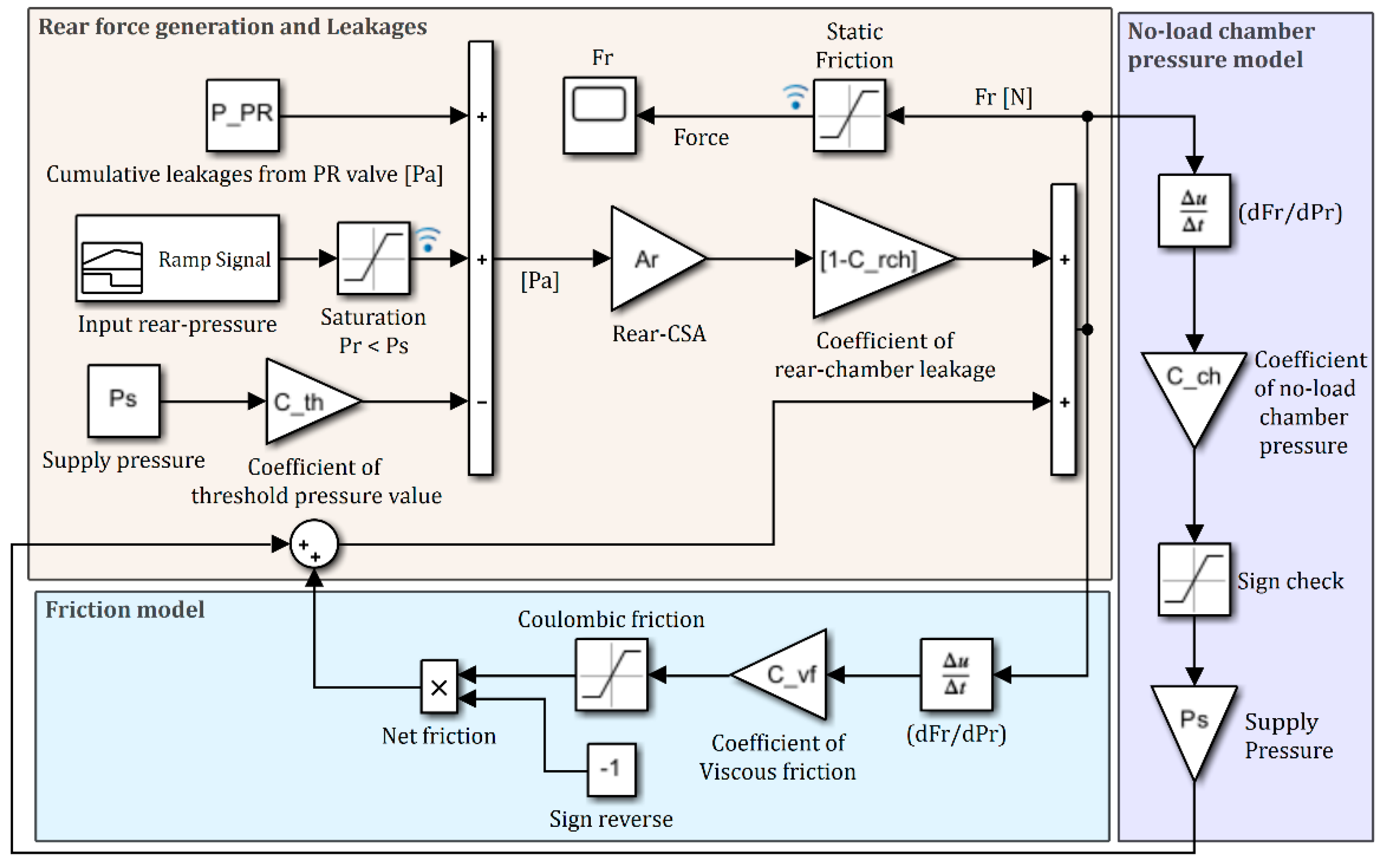
The major nonlinearities in the static response of the system due to pressurized flow supplied to the rear chamber were identified and modelled using a block-diagram representation using Simulink
®-as shown in
Figure 13. The model comprises of three sections, each separately accounting for the influence of non-linearities in the three distinct components of the system, namely, the rear pressure chamber, the servo valve, and the piston.
The section on ‘
Rear force generation and leakages’ models the forces in the rear pressure chamber and the associated non-linearities due to leakages. Similar to the experimental procedures, the input rear pressure is modelled as a ramped signal followed by a saturation block that has an upper threshold equal to the supply pressure value to ensure that the rear pressure does not exceed the supply pressure. Leakages due to pressure reducing valve are modelled as constant pressure drops while the no-load chamber pressure is modelled as a function of the supply pressure. The section on the ‘
Friction model’ accounts for nonlinearities due to mechanical characteristics of piston-cylinder. The piston velocity is evaluated by the derivative of the rear force with respect to the input rear pressure. The cumulative viscous friction is modelled as a product of rear force-pressure gradient and cumulative coefficient of viscous friction. The Coulombic model is captured using a saturation block as in
Section 4.3. The static friction model is also represented by a saturation block just prior to the final force output to keep a check on the lower threshold value of force output. The section on ‘
No-load chamber Leakages’ models the hysteretic behavior due to the no-load chamber pressure as per Equation (43). The piston velocity is evaluated as in the section on the ‘
Friction model’. The signum function is implemented as shown and the leakage coefficient and the supply pressure are modelled as gains.
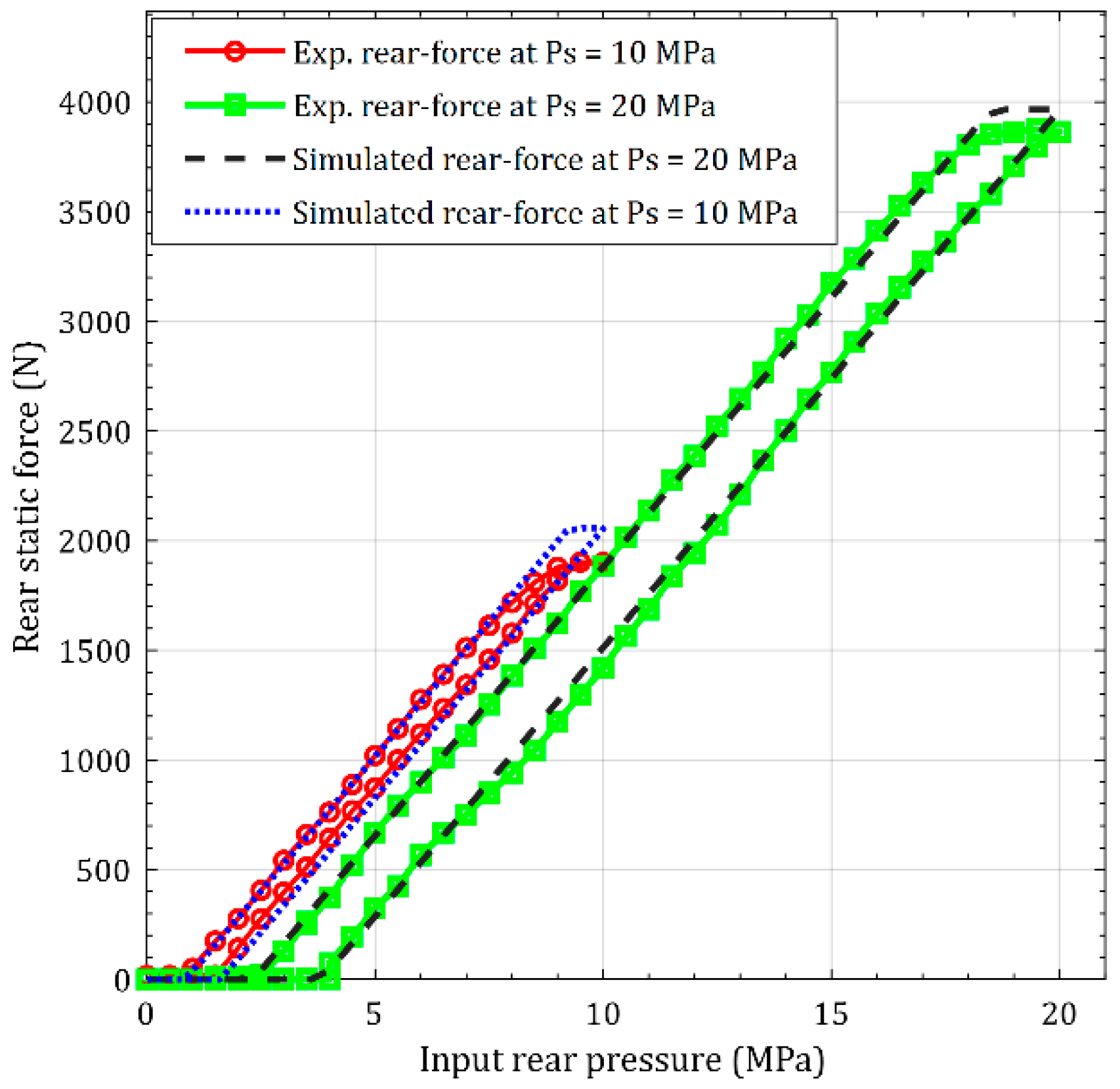
The algebraic sum of the rear force, the friction force, and the force due to the no-load chamber leakages, results in effective force output by supplying pressurized fluid to the rear chamber. Using this expanded nonlinear static model, force predictions for different supply pressures are compared with experimental results in
Figure 14.
As is amply evident from
Figure 14, predictions using the expanded nonlinear static model can faithfully capture all observed behavior for different supply pressures of interest. The no-force region is captured well, as is the hysteretic behavior. Seeing how the expanded model accounts for nonlinearities due to leakages, and due to friction and frictional hysteresis, as well as for the saturation behavior, it is reasonable to conclude that the expanded nonlinear static force model of the actuator with pressurized flow supplied to the rear chamber is also validated. Such systematic characterization of all major nonlinearities included in an expanded static force model for pressurized flow supplied to the rear chamber is a new contribution to the literature.
Seeing how the expanded nonlinear static force models for the valve-controlled actuator and for the case of pressurized fluid supplied to the rear chamber have both been validated separately, and since the actuator is designed such that the pressurized fluid in the rear chamber can be supplied over and above the flow through the servo valve such that higher forces may be applied to structure being tested, characteristic behavior for the superposition of these forces is described next.
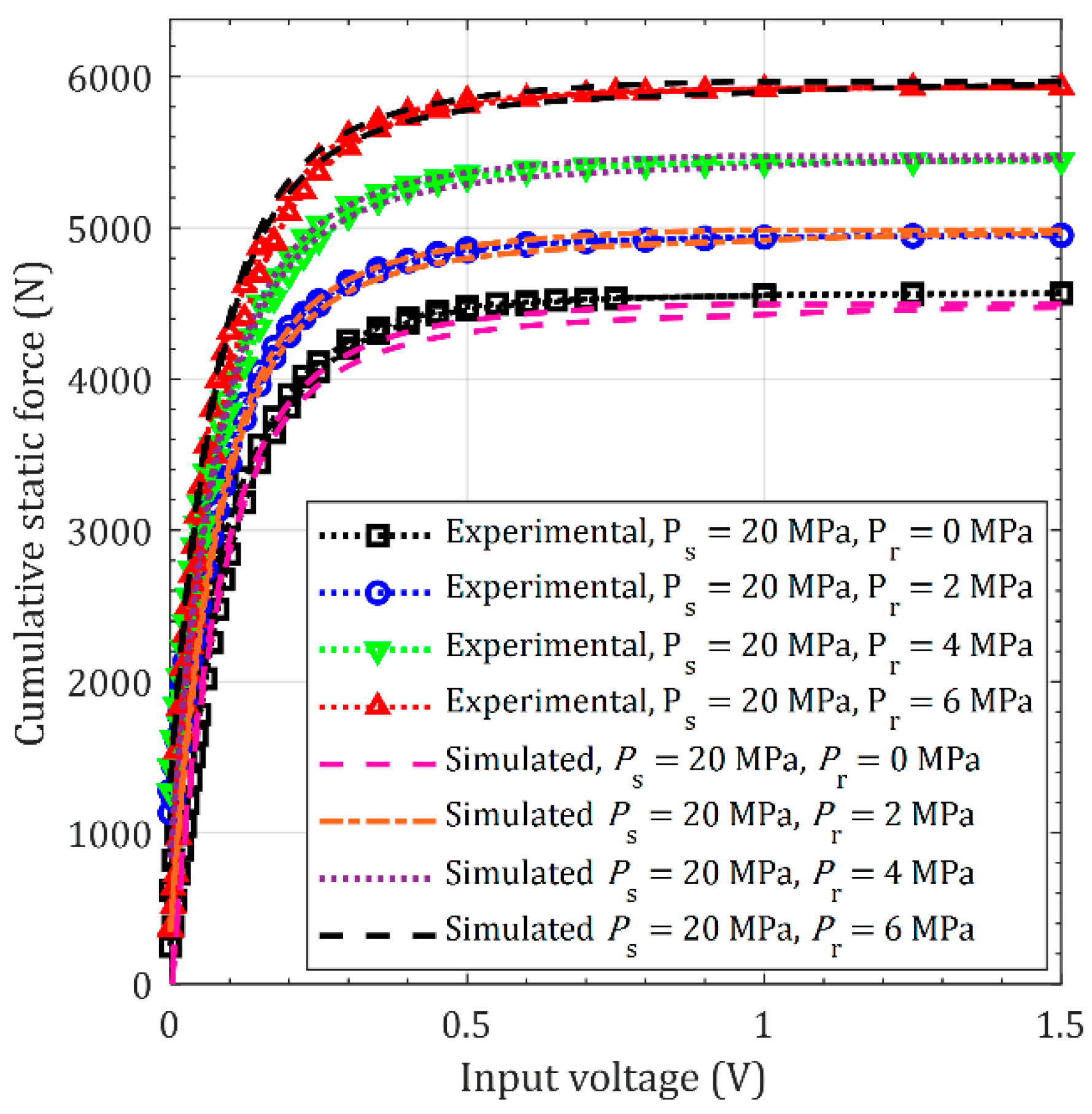
4.7. Static Force Characteristics for Superposition of Forces Obtained from Controlling the Servo Valve and from Supplying Pressurized Flow to the Rear Chamber
To characterize the static behavior of the actuator when forces obtained from controlling the servo valve are superposed with those obtained from controlling pressure in the rear chamber, experiments were performed at different values of the rear chamber pressure and with different values of input voltages being supplied to the servo valve at a constant supply pressure of 20 MPa. For pressure in the rear chamber being 0, 2, 4 and 6 MPa, respectively, the input voltage was increased from 0 to 2.5 V and then decreased back from 2.5 to 0 V, in steps of 0.05 V for each rear pressure value. The output forces were recorded and compared with model predictions that account for all the nonlinearities characterized in
Section 4.1,
Section 4.2,
Section 4.3,
Section 4.4,
Section 4.5 and
Section 4.6.
The block-diagram representation of the static model that superposes forces obtained from controlling the servo valve with those obtained from controlling pressure in the rear chamber is shown in
Figure 15. Since the characterization of the valve controlled force behavior was carried out with no pressurized fluid supplied to the rear chamber in
Section 4.1,
Section 4.2 and
Section 4.3, and since characterization of the force behavior for pressurized flow to the rear chamber was carried out with the servo valve being turned ‘off’ (
Section 4.4,
Section 4.5 and
Section 4.6), the model in
Figure 15 is a modified version of the models presented in
Figure 10 and
Figure 13. For example, the characterization of the force behavior with pressurized fluid in the rear chamber with the servo valve turned ‘off’ accounted for the no-load chamber leakages which would not have existed had the servo valve been in operation. Since the servo valve is ‘on’ when things work in conjunction, the no-load leakages can be neglected as the no-load chamber pressure in both the piston chambers cancel out each other. Furthermore, since the friction model is present in both cases, and since they are essentially the same, only one friction model is retained as shown in
Figure 15.
The model shown in
Figure 15 has three parts. The sections on ‘
Force generation and flow-pressure dynamics’, and the section on the ‘
Friction model’ are essentially the same as in
Figure 10, and the section on the ‘
Rear force model’ essentially reduces to a rear force, with the internal leakages and leakages through pressure reducing valve already being accounted for. Parameters shown in the model in
Figure 15 remain the same as those identified and reported in
Section 4.1,
Section 4.2,
Section 4.3,
Section 4.4,
Section 4.5 and
Section 4.6.
Model predicted behavior for the superposed forces are compared with experiments in
Figure 16. As is amply evident, model predictions can faithfully capture all observed behavior for different rear pressures and input voltages to the servo valve. Additionally, it is evident that the superposed force output is greater than the force output by controlling either the flow through the servo valve (see
Figure 11) or flow to the rear chamber (see
Figure 14). Seeing how the superposed response of both the models accounts for nonlinearities in the resulting static force behavior of the actuator, it is reasonable to conclude that both the expanded nonlinear static force models of the actuator are validated. Furthermore, such systematic characterization of superposed behavior is also a new contribution to the literature.
Having characterized the static behavior and having presented expanded models to describe the observed nonlinearities, we now move our attention to characterizing the dynamic behavior of the valve-controlled actuator.
7. Conclusions
This paper discussed the characterization of the static, dynamic, and closed-loop control behavior of a newly developed compact electro-hydraulic actuator that consists of a double-acting piston and cylinder arrangement controlled by a servo valve, and a separate rear chamber controlled by a separate valve that are designed to work in conjunction to generate static forces up to 7000 N that can be superposed with dynamic forces of up to 1500 N. The actuator was characterized to evaluate its suitability for machine tool structural testing, and the actuator’s ability to superpose periodic forces over a non-zero mean makes it capable of applying realistic loading conditions like those experienced by machines during cutting processes.
Experiments to characterize the static behavior of the actuator show it to exhibit nonlinearities for when the actuator is controlled by the servo valve, and separately for when pressurized flow is supplied to the rear chamber. Static experiments that superpose forces obtained from controlling the servo valve with those obtained from controlling pressure in the rear chamber also exhibit nonlinearities. Since linearized static models were found to be inadequate to capture the observed nonlinear behavior, the static force models were expanded to include nonlinearities due to dead-bands, nonlinearities due to hysteresis of the electrical and mechanical kinds, nonlinearities in the flow-pressure characteristics, nonlinearities due to static, Coulombic and viscous friction, nonlinearities causing saturation of forces, and nonlinearities due to no-load flow and leakages in the system. Predictions with the expanded nonlinear static force models were found to agree with experimental observations for the valve controlled actuator and for the case of pressurized fluid supplied to the rear chamber, as well as for the case of forces being a superposition of those obtained from controlling the servo valve with those obtained from controlling pressure in the rear chamber. Such expanded model-based characterization of all the major nonlinearities in the system for such electro-hydraulic actuators is thought to be a new contribution to the literature.
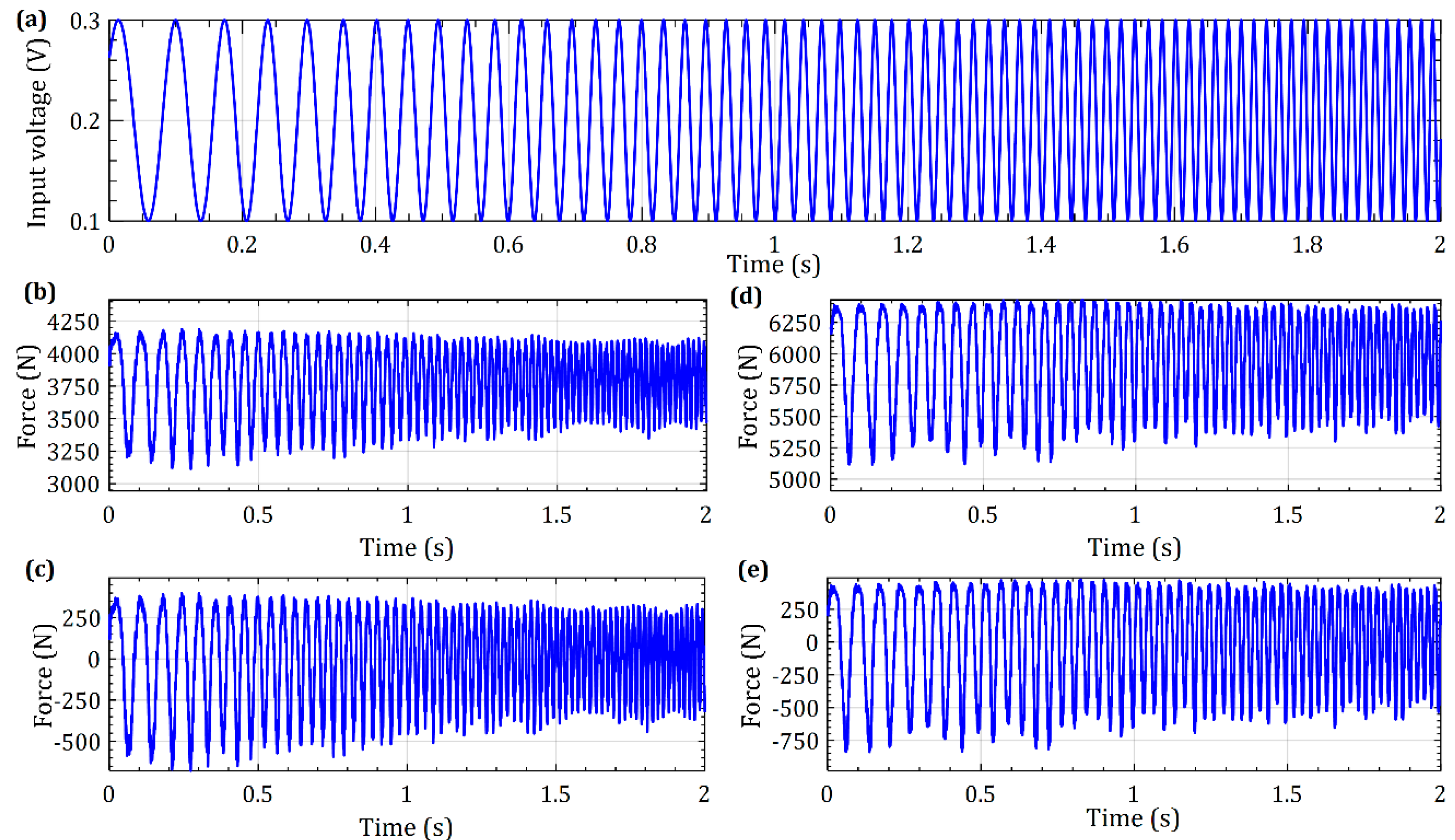
Experiments to characterize the dynamical behavior of the actuator under different loading scenarios, i.e., by superimposing dynamic forces over static forces, including superposition of dynamic forces over valve-controlled static forces and over the superposition of static forces applied through flow to the servo valve and with pressurized flow to the rear chamber—showed the actuator to behave linearly, which suggested that the proposed linear model adequately describes the actuator’s dynamic response. Such systematic model-based characterization supported by experiments of the static and dynamic behavior of electro-hydraulic actuators to evaluate their suitability for machine tool structural testing is also a new contribution to the literature.
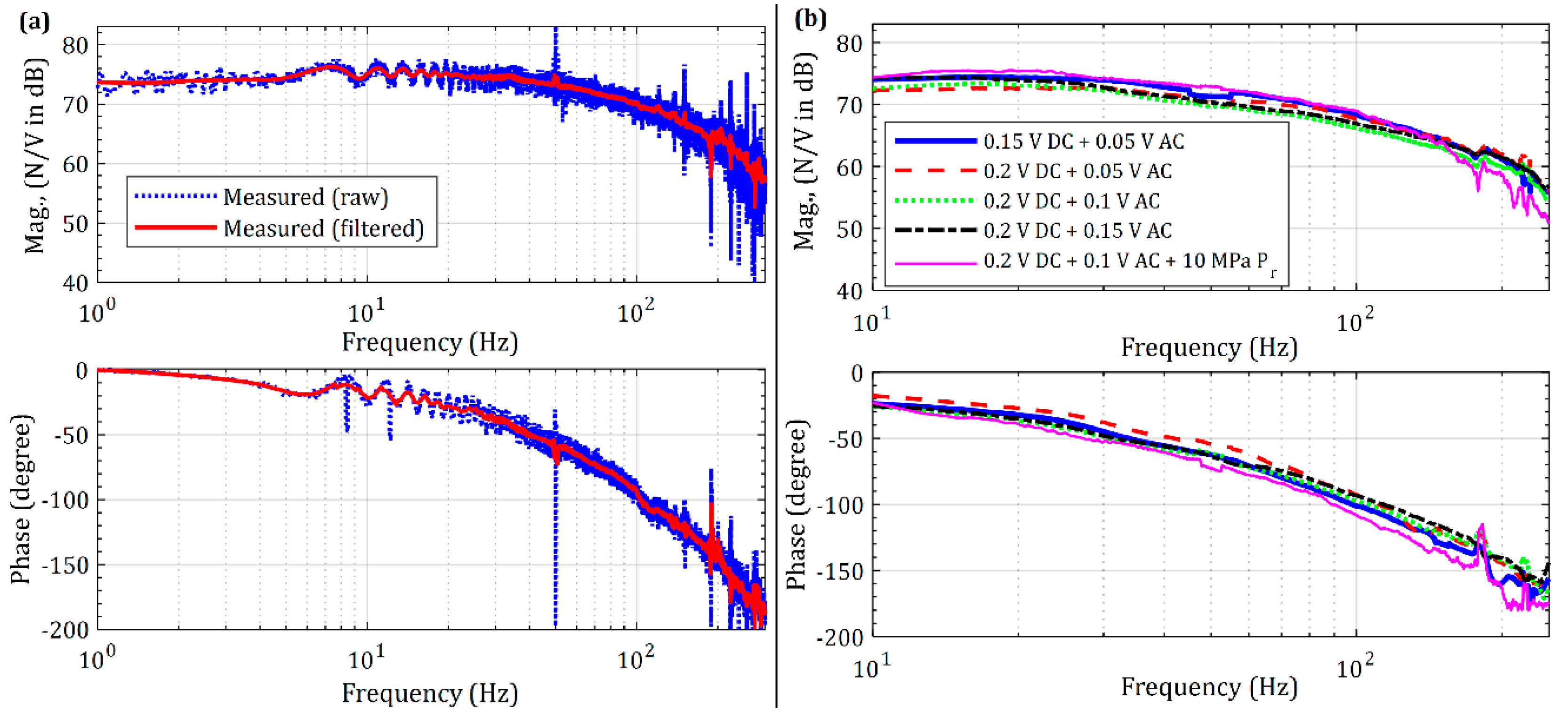
Since the open-loop dynamic behavior of the actuator was observed to have a high gain, and a bandwidth of less than 50 Hz, the validated static and dynamic force models were used to develop a model-based tuning strategy, which in turn guided the closed-loop experiments. Closed-loop control based on tuning a simple proportional-integral (PI) controller increased the bandwidth up to 200 Hz–making the actuator more suitable for its intended application of machine tool structural testing. Though closed-loop control increased the bandwidth significantly, yet issues related to the observed phase lags at higher frequencies still need to be addressed.
The validated models presented herein can instruct the design and development of other higher-performance electro-hydraulic actuators—even for other applications, and, can also guide the conversion of the actuator into a damper, and to also test other advanced control strategies to further improve actuator performance.