1. Introduction
Semi-hard magnetic materials (SHMMs) are of great interest for high- and ultra-high-speed rotating electric machines because of their elevated mechanical strength and advantageous magnetic features. The magnetic hysteresis loop of these materials can be activated to yield mechanical torque. This principle is narrowed nowadays to very few motor applications due to the limited power density with respect to other electric machine solutions. However, at high speed, the simple structure and rotordynamic features of hysteresis motors allow unmatchable power density [
1,
2]. The magnetic behavior of SHMMs can also be used to achieve levitating forces, leading to magnetic bearing applications. In most turbomachinery, levitating journals require an electric machine to provide rotation. Active Magnetic Bearings (AMBs) and electric motors have very similar construction. Therefore, they can be combined into one single device: the bearingless drive. Its main advantages are lower component count and more compact layout than common solutions with separate electric motor and bearing system [
3,
4,
5,
6]. Furthermore, magnetic levitation is an advantageous solution for high-speed applications. Attractive features for high-speed machines are bearing losses lower than in conventional ball or journal bearings, lubrication-free operation, low maintenance costs along with the possibility to control the dynamics of the hovering [
4,
7,
8,
9]. These features motivated a wide use of AMBs in industrial applications such as compressors, turbines and flywheels. Nowadays, the research effort focuses on the control and hardware improvement [
10,
11,
12,
13,
14] along with the system identification [
15,
16]. Usually, the rotating part of magnetic bearings is made of soft magnetic material with high magnetic permeability, which leads to low reluctance of the magnetic path, as well as a fairly linear behavior in a large operational range.
Bearingless hysteresis drives are a novel field of research where very few works have been published in the last years. Noh et al. [
17] propose the comparison between hysteresis and reluctance bearingless motors. The rotor robustness and easier manufacturing of hysteresis drives along with their inherently smooth torque make them clearly advantageous. From the motor perspective, the coated solid rotor induction machine is a valid solution for high speed applications [
18]. Its drawback is related to the overheating due to the eddy currents, which is significant at high speed. Conversely, the magnetic hysteresis phenomenon enables synchronous operation with respect to the rotating magnetic field, thus making hysteresis drives advantageous with respect to the asynchronous motors. Moreover, the rotor strength allows for reaching higher peripheral speed limits when compared to permanent-magnet-equipped technologies [
19] and induction motors [
20].
The available literature on bearingless hysteresis drives focuses mostly on the torque generation. On the bearing side, the design and the performance assessment have been carried out by neglecting the hysteretic behavior of the rotor materia [
17,
21]. In those cases, this assumption is justified since the energy dissipation due to hysteresis is rather low. Imani-Nejad [
20] investigated the force generation by considering the magnetic hysteresis of the material through a one-dimensional approach. The hysteresis does not affect significantly the bearing performance since the employed material (D2 steel) exhibits a poor hysteretic behavior. Furthermore, only the minor hysteresis loops are activated. Hence, the magnetic capability of the material is not fully exploited since the achieved magnetic flux densities are significantly below the saturation value.
Additional efforts have investigated the magnetic hysteresis effect on the force generation of reluctance actuators for high-precision applications. One-dimensional analyses can be found in [
22,
23], whereas 2D and 3D finite element (FE) approaches have been also proposed [
24]. All of these works address the hysteresis phenomenon exclusively on soft magnetic materials. Therefore, the magnetic hysteresis slightly affects the actuator performance.
In literature so far, no work has been conducted to study the force capability of electromagnetic actuators based on materials of large magnetic hysteresis behavior. To fulfill this gap, this paper presents the force characterization of an electromagnetic actuator based on FeCrCo 48/5 SHMM. In contrast to the above-mentioned literature, the applied magnetic fields are significant and, consequently, the nonlinear hysteretic behavior of the material needs to be considered. This work intends to build and experimentally validate a FE model able to capture the force generation phenomenon on SHMM-based AMBs.
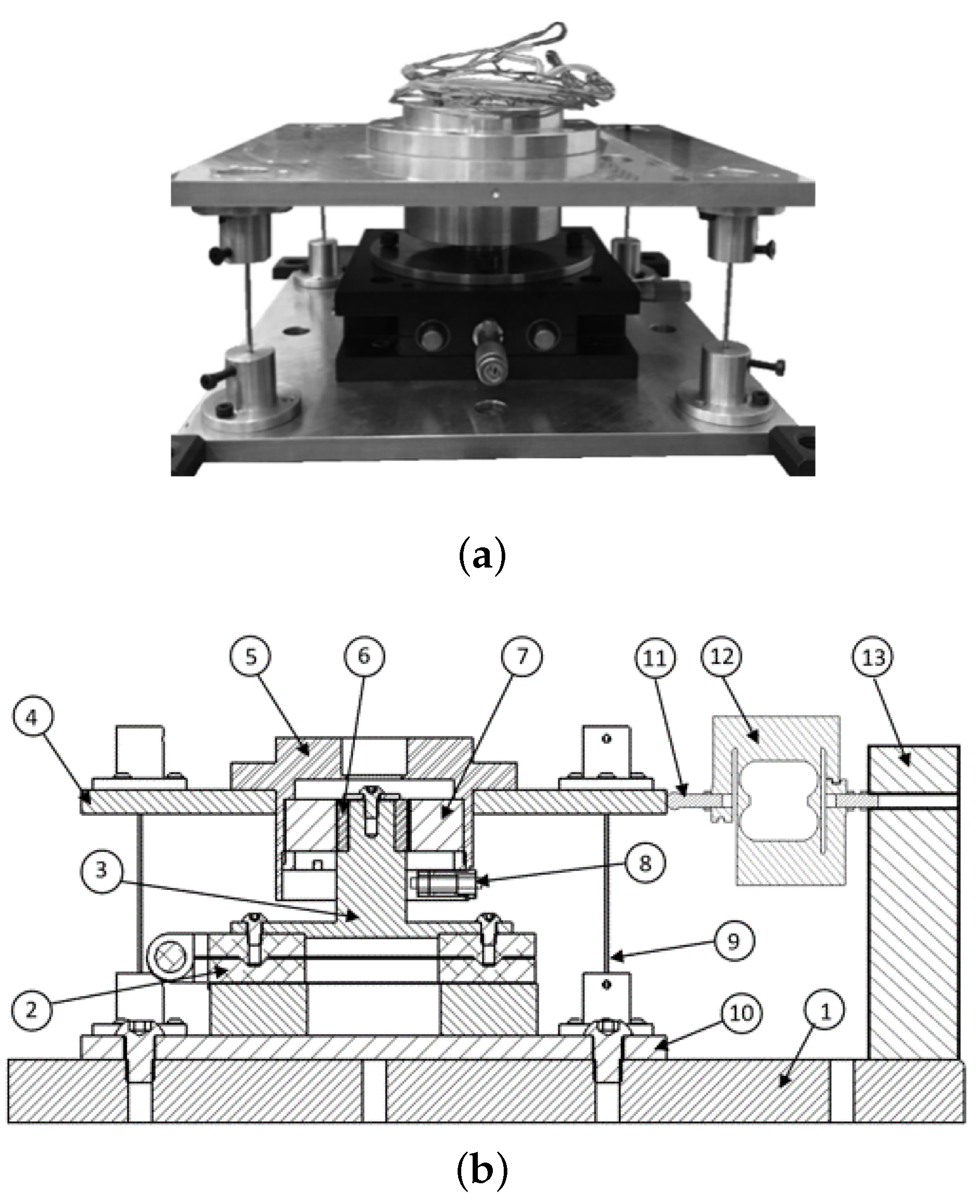
The present work is structured as follows. The experimental setup is introduced in
Section 2.
Section 3 presents the numerical modeling. For comparison purposes, a system with the journal made of soft magnetic material and another one based on the SHMM are presented. The latter adopts the Jiles–Atherton model to reproduce the hysteresis behavior of the FeCrCo 48/5 SHMM. Afterwards, the experimental procedure is described in
Section 4. Finally,
Section 5 shows the comparison between numerical results and experimental data for both of the systems. In this regard, the results achieved from the system based on the soft magnetic material are used to identify the stator inner diameter. Then, the results obtained from the system based on the SHMM validate the proposed numerical model and lead to important considerations on the behavior of such systems.
Section 6 presents the conclusions.
3. Numerical Modeling
The force generation phenomenon on the SHMM-based AMB is numerically investigated through the finite element method by means of a COMSOL Multiphysics model. The electromagnetic problem is formulated through the Magnetic Fields Interface under the AC/DC Module of the software solving the following electromagnetic problem formulation in terms of the magnetic vector potential
A over a discretized domain
H being the magnetic field vector,
J the current density,
B the magnetic flux density vector, σ the electrical conductivity,
v the velocity of the conductor (which is null in the present analyses),
Je an externally generated current density and
E the electric field. This simulation can be executed either in stationary mode or, as in this study, in time-stepping mode. Further details about the implemented formulation can be found in [
25].
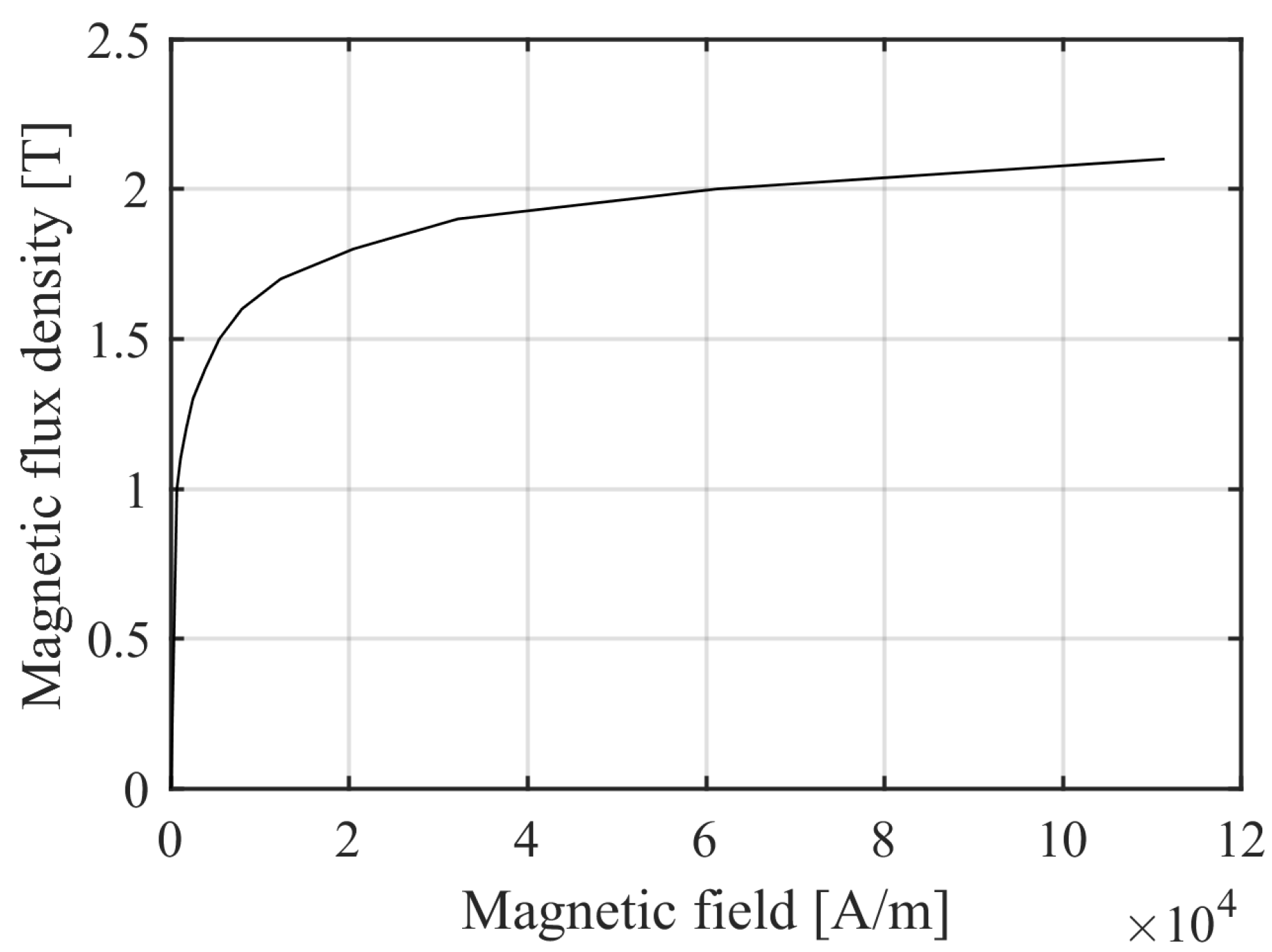
The simulation tool requires boundary conditions and material constitutive relations to fully define the problem. The following nonlinear constitutive relation (whose reciprocal is taken from the software library and plotted in
Figure 2), based on the nonlinear function
, is adopted to consider the iron saturation in the static part of the actuator and the soft iron journal
The hysteretic behavior of the FeCrCo 48/5 alloy is modeled through a vector generalization of the Jiles–Atherton model [
26]. It is implemented in the software to describe the anisotropic magnetic behavior of the material. In this case, the magnetic constitutive relation is
where
is the permeability of free space and
is the magnetization vector. It is calculated by solving the main equation of the Jiles–Atherton model
where
and
are the anhysteretic and the irreversible magnetization terms, respectively,
is the identity matrix and
is the reversibility tensor. For the
ith vector component, the Langevin function is used to express the anhysteretic behavior
where
is the saturation magnetization and
the Langevin slope for the
ith component. The effective magnetic field is
where
is the interdomain coupling tensor. The irreversible magnetization vector is obtained from the nonlinear equation
being the pinning tensor and
the reversible magnetization vector.
The parameters needed to represent the radial and tangential characteristics (
Table 2) have been identified by means of the least-squares optimization method proposed by Kis and Iványi [
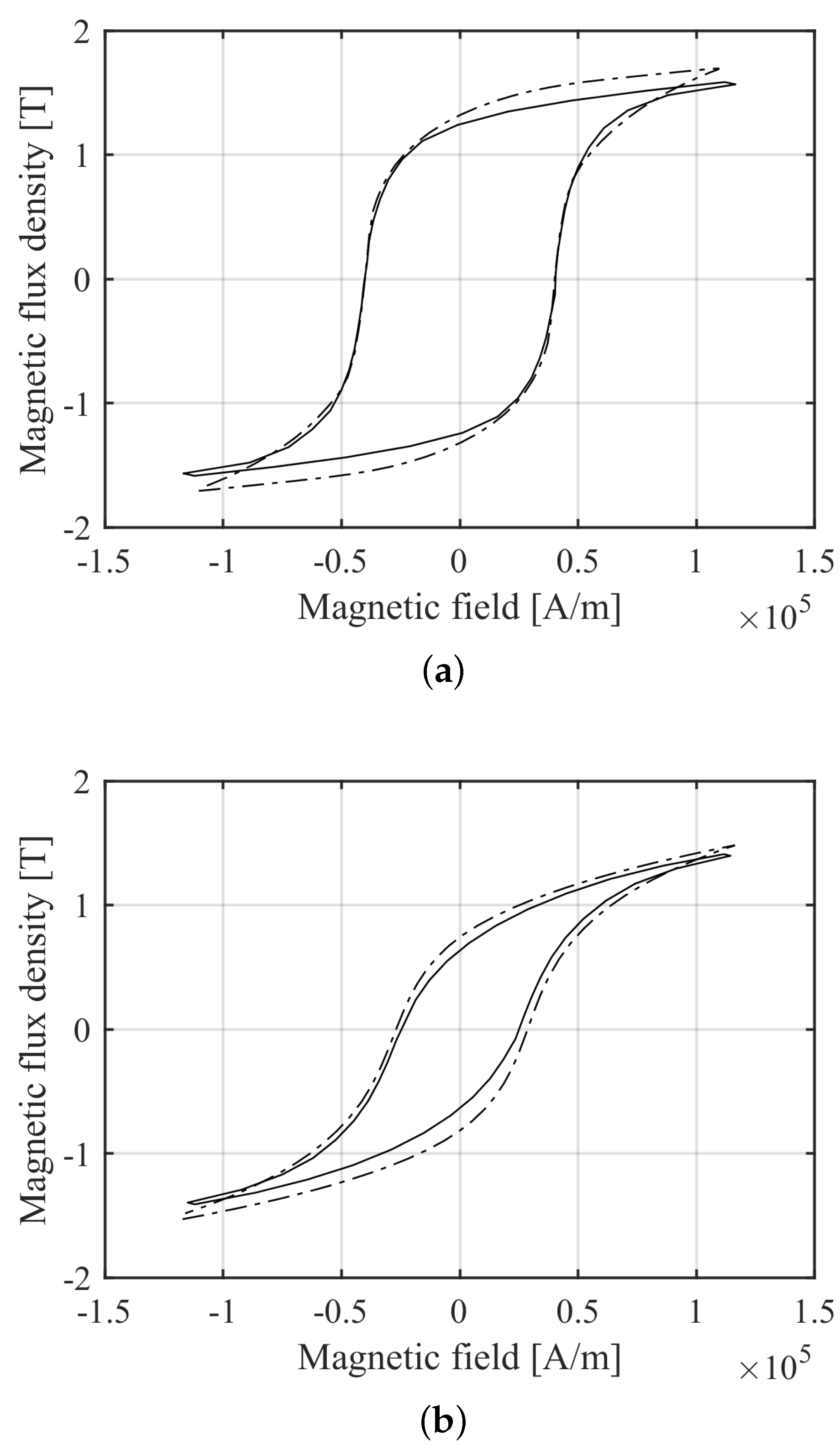
27]. The identification is based on the material radial and tangential hysteresis loops measured on FeCrCo 48/5 SHMM samples by means of a vibrating-sample magnetometer.
Figure 3a,b show the comparison between the experimental and the numerical hysteresis loops.
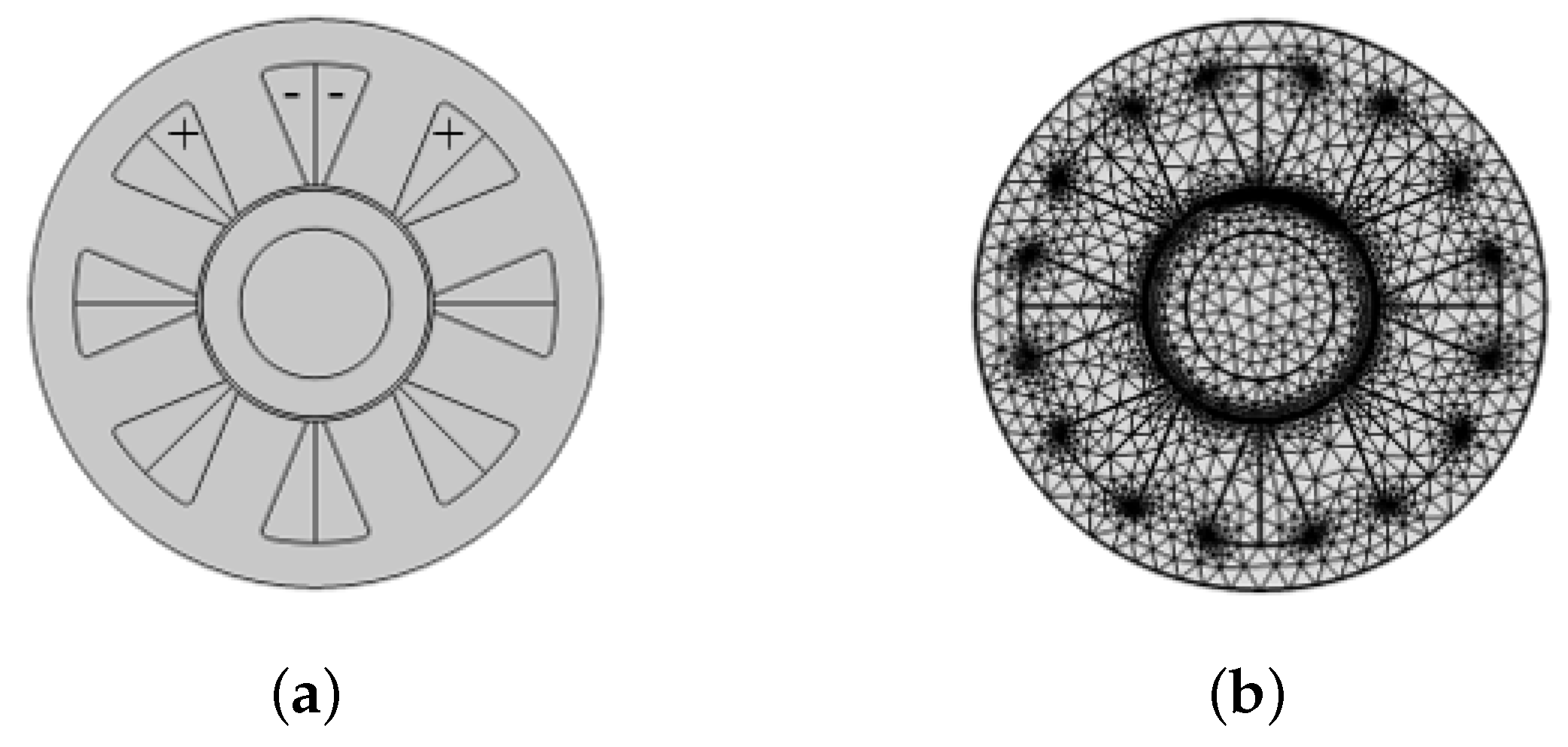
Both 2D and 3D finite element models are proposed. The 2D model (
Figure 4a) assumes the vector potential with a single component normal to the plane of interest. This approach enables a significant reduction in the size of the problem but cannot consider possible effects of the end fields along the axial direction. The domain is discretized using quadratic triangular elements. The convergence study leads to the selection of the meshes constituted by 3438 elements for the model with the soft magnetic journal and 4420 elements for the one with the semi-hard magnetic journal (
Figure 4b). The homogeneous Dirichlet’s condition on the magnetic vector potential is applied to the external edge of the stator. It imposes all the magnetic flux lines tangent to the boundary. The coil is modeled as external current densities
normal to the domains surrounding the stator poles as shown in
Figure 4a.
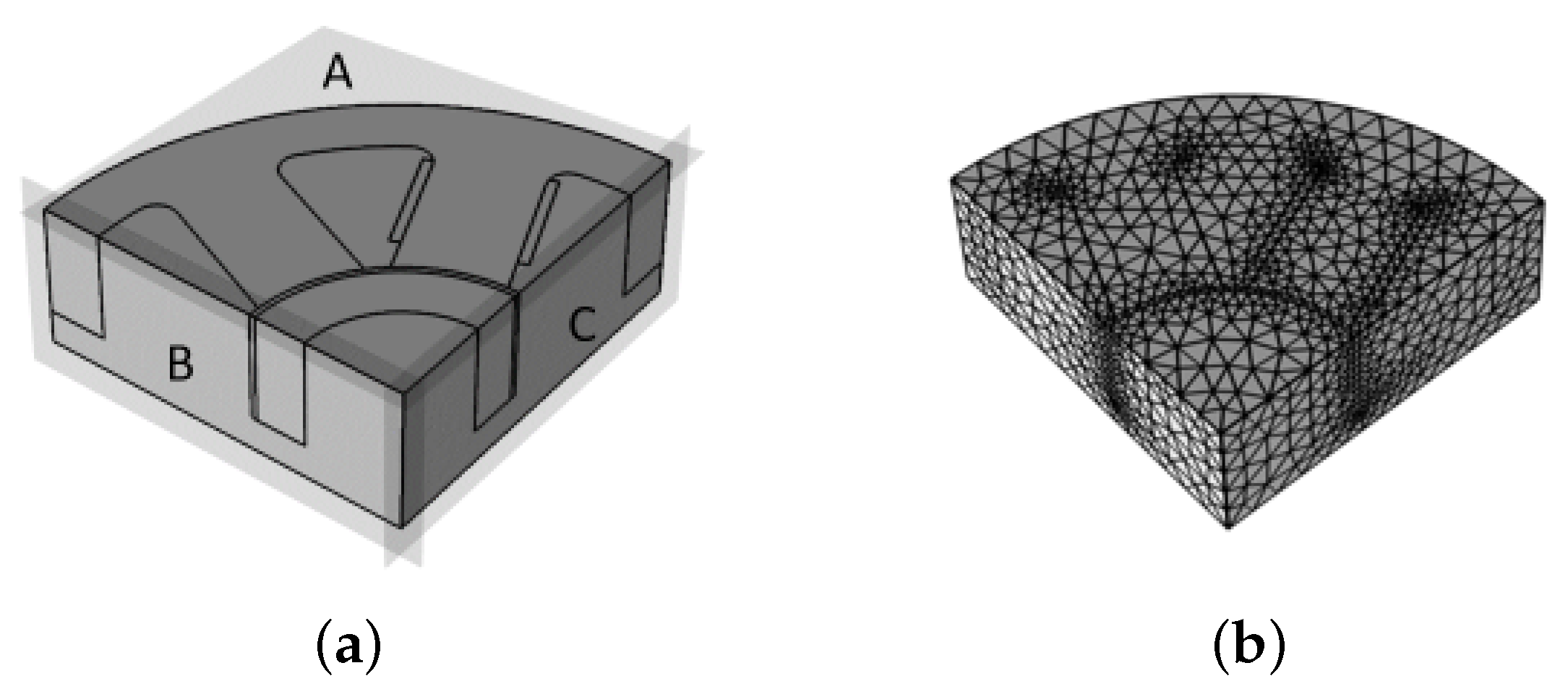
The 3D model captures the effect of the end fields but is computationally more expensive than the 2D approach. It presents some issues in the convergence of the numerical solution. To improve the convergence robustness and obtain an efficient solving, linear tetrahedral elements are selected. Furthermore, symmetries of the geometry are exploited to reduce the size of the model. The symmetry with respect to the plane A (
Figure 5a) is modeled by applying the homogeneous Dirichlet’s condition on the component of the magnetic vector potential lying on the plane. The symmetry with respect to plane C (
Figure 5a) is given by the homogeneous Neumann’s condition on the component of the magnetic vector potential lying on the plane. It imposes the magnetic field perpendicular to the surfaces where the condition is applied. A further reduction of the model is achieved by considering that the magnetic flux is restricted in half of the model and does not cross the plane B (
Figure 5a). This is modeled with the homogeneous Dirichelet’s condition on the component of the magnetic vector potential lying on the plane B. Therefore, the model geometry is reduced to one eighth of its original size. The homogeneous Dirichlet’s condition on the component of the magnetic vector potential lying on the boundary is applied to the external boundaries of the stator as well as the domain of air surrounding the tip of the magnetic bearing. The coil is modeled through the coil domain feature of the software. It implements a multi-wire coil by applying the main features of the coil (number of turns, wire cross-section, electrical conductivity of the material) to the interested domain. By defining the input and output boundaries of the coil, one preliminary analysis is needed to determine the local direction of the current flow in the domain. The convergence study leads to the selection of the meshes constituted by 44,906 elements for the model with the soft magnetic journal and 45,618 elements for the one with the semi-hard magnetic journal (
Figure 5b).
The generated force is computed by integrating the Maxwell’s stress tensor over the boundary surface of the journal domain. For the 3D case, this computation is proportionally corrected by a factor four to account for the model reduction due to symmetry.
Since the Jiles–Atherton model is available mainly for time-dependent studies, the analysis in time is carried out. The input current follows a slow profile to reproduce the quasi-static nature of the test. Therefore, there is no dynamic effect in Equation (
1) and the influence of the electrical conductivity becomes negligible.
A modified version of the proposed model can be adopted to conduct a complete dynamic analysis. In this case, the main dynamic contribution is related to the SHMM losses. Eddy current effects are already accounted by the time stepping solver, as seen in Equation (
1). In addition, rate-dependent hysteresis models [
28] can be implemented in COMSOL Multiphysics either through partial differential equations or as a C-compiled external material. More details regarding these two implementation methods can be found in the software manual [
25].
4. Test Procedure
The test procedure is the same for both the setups with the soft and the semi-hard magnetic journals. Some preliminary steps are needed before the test:
The system is preloaded by unscrewing the fastener interfacing the load cell and the upper plate. This operation causes a relative displacement between the upper and the lower plates. Therefore, the preload is produced by the compliant beams.
The journal is moved by means of the sliding micrometer to approach the actuator edge. This position is identified as soon as the preload changes.
The journal is moved through the sliding micrometer to set the desired nominal air gap. The output of the eddy current sensor is recorded as reference.
After this preliminary procedure, the actuator coils are powered to achieve the needed current step-profile. The current is varied by small steps: each current step leads to a force variation
which causes a change in the air gap because of the load cell compliance. Hence, the nominal air gap has to be restored: the journal is moved by a quantity
through the sliding micrometer to restore the reference output of the eddy current sensor. Note that, after this operation, the relative position between the upper and the lower plates has changed by a quantity
and, consequently, the preload is different with respect to the previous current step. Now, the force measured by the load cell
is read, so the electromagnetic net force
is computed:
in which the superscripts
i and
refer to the present and the previous current steps, respectively.
is the net preload that considers the change in the relative position
between the upper and the lower plates, which is the quantity the journal needs to be moved through the sliding micrometer to restore the nominal air gap:
where
k is the mechanical stiffness of the compliant beams. It has been identified by manually varying the preload and measuring the resulting displacement through the eddy current sensor. The identified stiffness is 59.8
. Note that a current increase leads to
, which, in turn, yields
and thus the preload decreases. The opposite is true if the current decreases.
Then, the current can be varied for the next current step. At the end of the test, the journal is degaussed through an alternating magnetic field with decreasing amplitude, achieved by supplying the actuator coil with a 25 AC current with 5 initial amplitude. This step is needed to start the successive test with no residual magnetization, which would have a significant influence in the case of the semi-hard magnetic journal.
5. Results
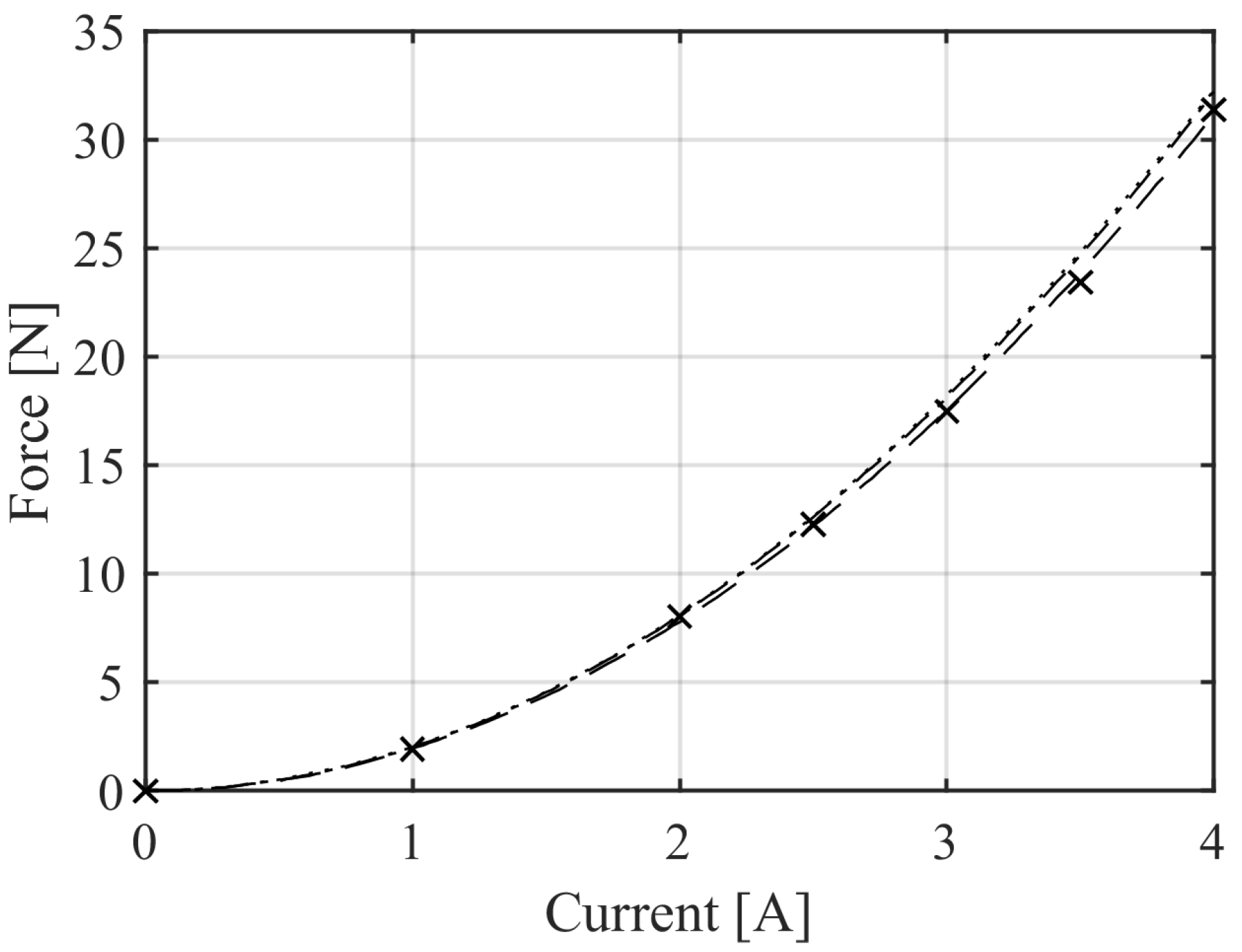
The system with the soft magnetic journal is investigated firstly. The numerical-experimental comparison of the force produced at 0.55
air gap is reported in
Figure 6. The experimental data are achieved by increasing the current from 0 to 4
. The maximum current is limited by the mechanical instability of the test rig. This occurs because the mechanical stiffness that the load cell and the compliant beams provide is not sufficient to balance the negative stiffness introduced by the electromagnet. The numerical results are obtained with an input current ramp from 0 to 4
. At first, the geometric air gap is considered. The comparison between 2D and 3D results shows that there is no influence of the end-field effects; therefore, the 2D model can be used for further analyses. The model with the geometric air gap overestimates the experimental force. This is due to the difference between the geometric and the magnetic air gap, which can be completely attributed to the stator [
29]. In order to achieve the best fit, the stator inner diameter is increased by 0.06% to 31.42
(the identified non-magnetic layer is 0.02
).
The experimental tests on the system based on the SHMM at three different air gap values (0.55
, 0.50
and 0.45
) are carried out by increasing the current from 0 to 6
and then reducing it to 0
. The maximum current is limited to 6
to avoid the overheating of the electromagnet coils. The numerical results consider the stator inner diameter identified through the analysis with the soft magnetic journal.
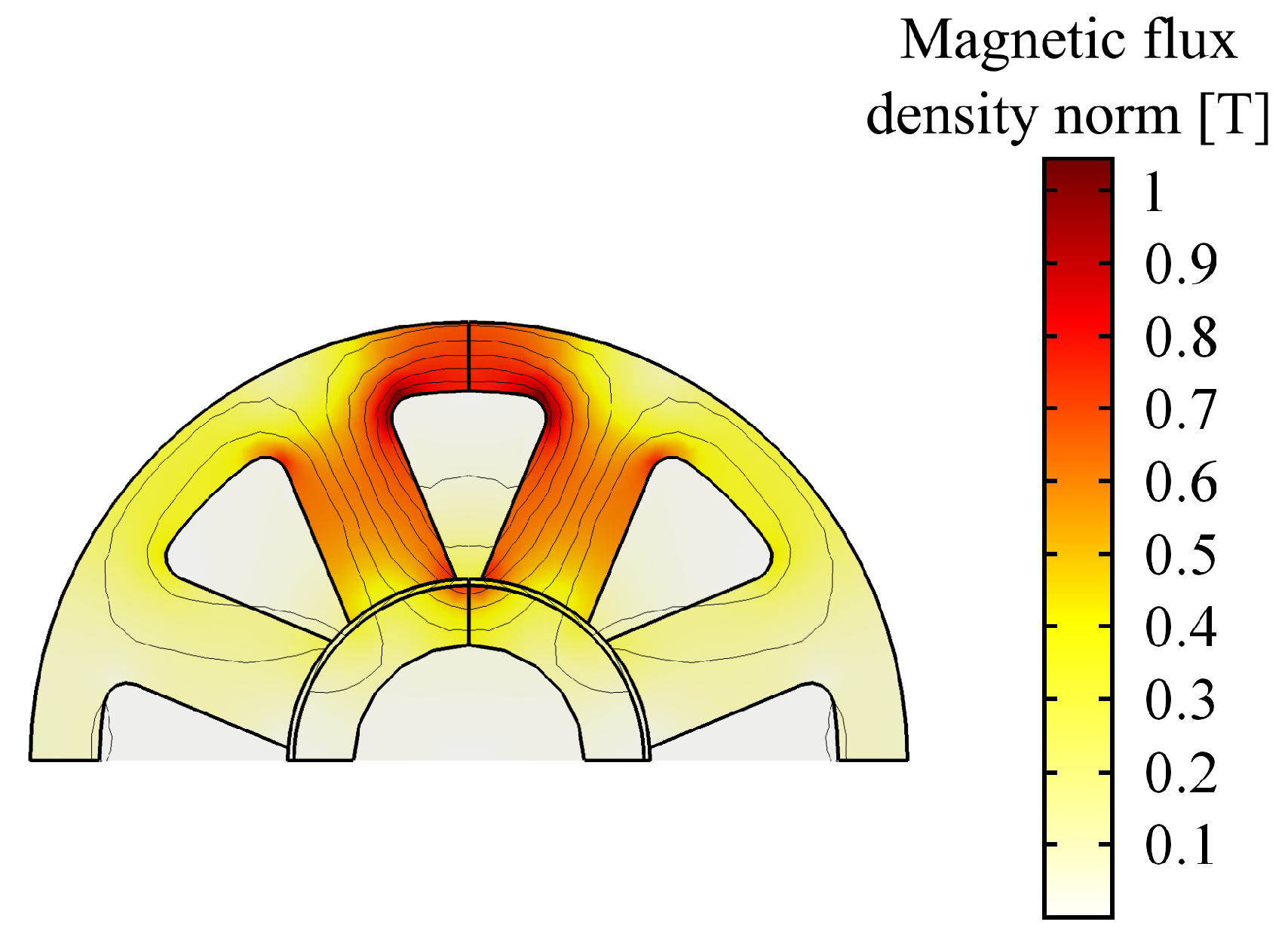
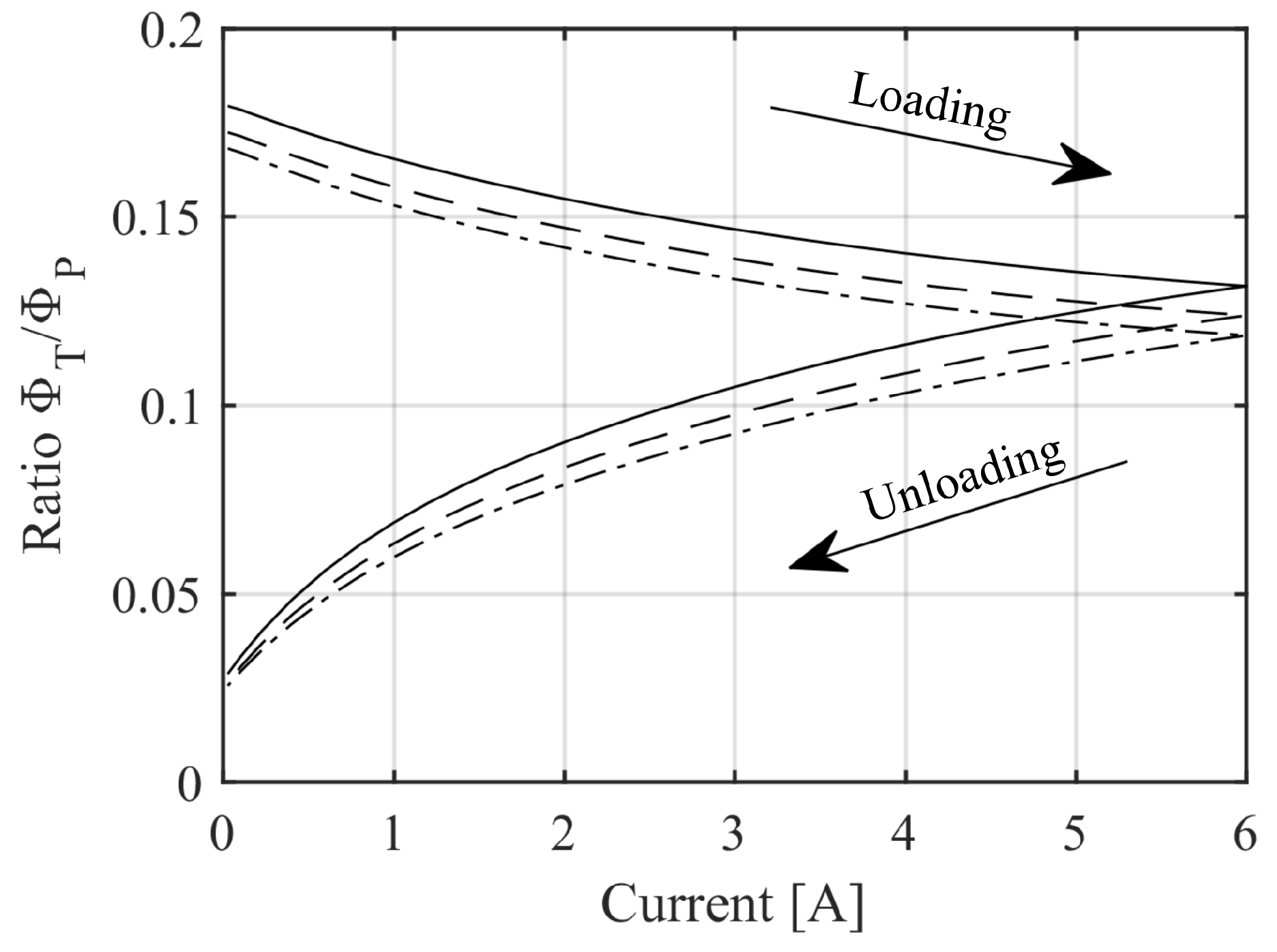
Figure 7 shows the magnetic flux density distribution over the cross-section of the 3D model with 0.55
air gap at the maximum current. The contours of the normal component of the vector potential are plotted as well. These can be interpreted as magnetic flux lines and show how the flux is inclined to bypass the journal and tries to follow the shortest path across the journal. This is due to the low permeability of the FeCrCo 48/5 and led to a quite unbalanced flux distribution in the air gap. The flux leakages are also responsible for the mismatch between the 2D and the 3D force prediction (
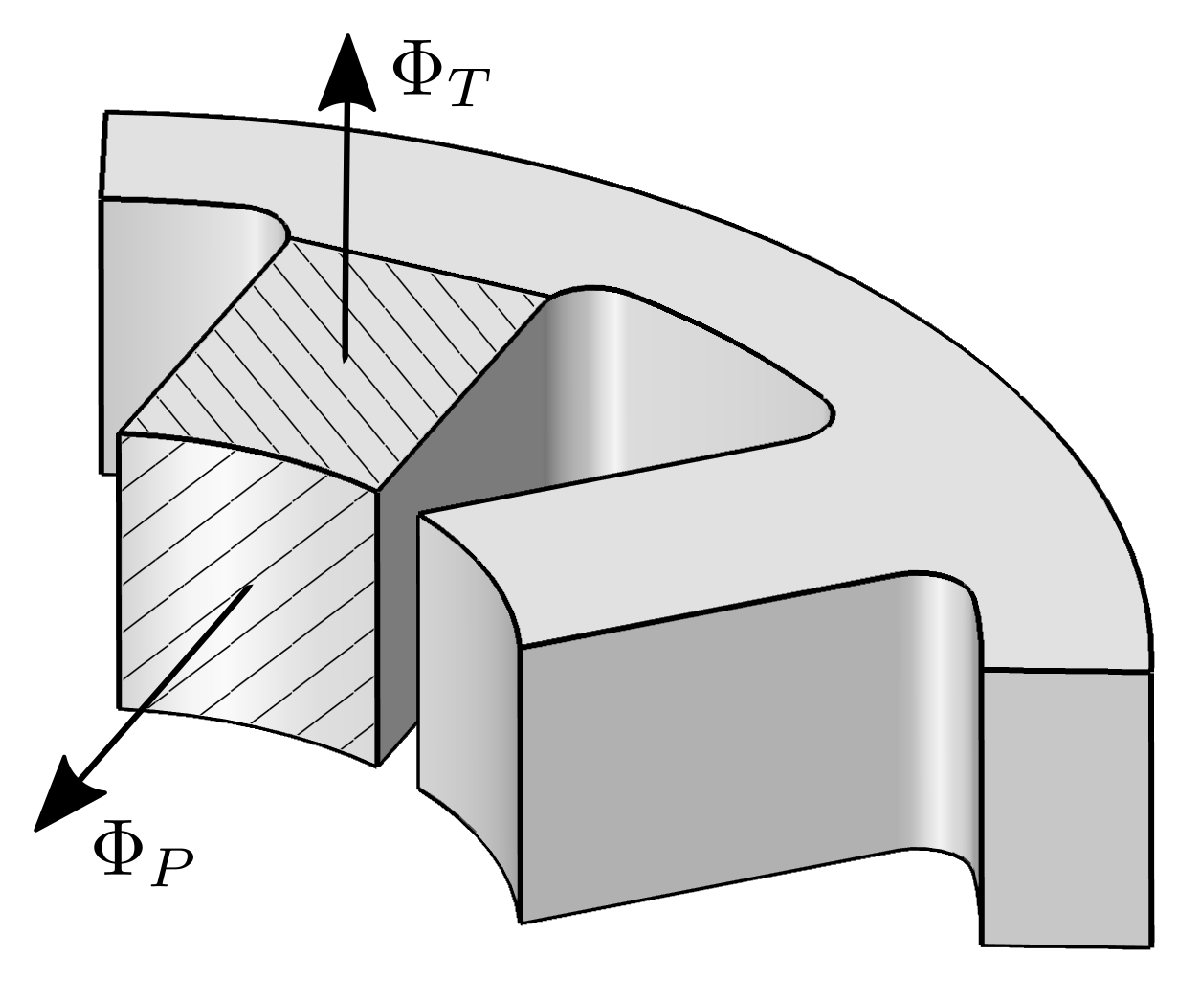
Figure 8). To investigate more deeply this effect, the magnetic flux straying through the top face of one polar expansion
(
Figure 9) is computed. It is compared to the magnetic flux
(
Figure 9) flowing through the polar area, that is the flux responsible for the force generation. The ratio
is plotted for the three different air gap values (
Figure 10). It is observed that the flux leakage in axial direction is not negligible with respect to the useful flux, thus explaining why the 2D model overestimates the generated force. The ratio decreases at smaller air gaps since the flux paths crossing the journal imply a lower reluctance and, consequently, the leakage decreases.
Figure 8 shows a comparison between the 3D force prediction and the experimental results at the three different air gaps. The maximum error of the predicted force at the different air gaps is reported in
Table 3. The influence of the measurement error, which is related to the accuracy of the sensors (see
Section 2), is negligible. The results show that the numerical model overestimates the experimental force. This behavior can be ascribed to the numerical representation of the FeCrCo 48/5. The Jiles–Atherton model is usually employed to represent the magnetic behavior of soft magnetic alloys, which exhibit a narrow coercive magnetic fields when compared to SHMMs. In such applications, this model is demonstrated to be accurate [
27,
30,
31]. Conversely, in this case, the SHMM presents a high coercive field and the Jiles–Atherton approach does not perfectly reproduce the magnetic behavior of the material, as illustrated in
Figure 4. This limitation can be ascribed to the pinning parameter
k, which is assumed constant during the magnetization process [
28,
30].
The influence of the magnetic hysteresis on the force generation of the SHMM-based system is evident. The difference between the loading and the unloading force profiles at the three air gap values (
Figure 8) is significant. Note that after the tests the residual forces are 1.47
, 2.08
and 2.59
at 0.55
, 0.50
and 0.45
air gap, respectively. By comparing the force generated by the systems based on the soft magnetic journal (
Figure 6) and the FeCrCo 48/5 journal (
Figure 8a) at 0.55
air gap, it is clear that the SHMM magnetic behavior significantly lowers the force capability of the electromagnetic actuator. A quantitative analysis of this comparison is reported in
Table 4 from 0 A to 4 A in loading and unloading conditions. If analyzed in loading conditions, the ratio between the two forces (
) tends to be smaller at higher supplied currents mainly because of the above-mentioned flux leakage reduction in the SHMM electromagnet. On the other hand, the ratio in unloading conditions is lower than in the previous case because of the higher level of magnetization in the SHMM. These results demonstrate that the effects of previous magnetization in SHMMs represent a potential improvement in the force capability of the studied system. However, this aspect goes beyond the purpose of the present research.