Abstract
Axial magnetic bearing actuators often lack the bandwidth necessary to achieve the desired closed loop performance due to their nonlaminated construction. Since bandwidth can be directly related to actuator material and geometric properties, an opportunity exists to improve closed loop performance through the optimization of these properties. This prospect is exploited herein, both to demonstrate the improvements that can be obtained and to illustrate the relationship between various parameters and dynamic performance. For the latter, Pareto-optimal curves are generated exploring the influence that disk outer radius, peak force, axial gap, and magnetic permeability have upon actuator bandwidth.
1. Introduction
Interest in the use of active magnetic bearings (AMBs) for the support of rotors in turbomachinery and machine tools has increased over the last two decades. Such machines typically use two radial AMBs to control transverse motions of the rotor and a single thrust magnetic bearing to control axial motion. Both the rotating component (journal) and the stationary component (stator) of radial AMBs are constructed from soft magnetic laminations to reduce eddy currents within the ferromagnetic material (referred to as the ‘iron’) induced by changing electromagnetic fields. This manufacture is quite similar to the construction of induction motors. The rotating and stationary components of the thrust actuator (thrust disk and stator, respectively), however, are rarely composed of laminations due to the great difficulty and cost of such construction and the poor resulting mechanical strength, particularly problematic for high rotational speed machines. Instead, these components are made of solid ferromagnetic materials (i.e., nonlaminated), with little attempt made to reduce eddy currents. Since the electromagnetic field for the thrust components does not change due to rotation of the shaft, eddy currents are due only to changing coil currents. For most applications, eddy currents within the thrust bearing are inconsequential from a thermal or rotating loss viewpoint. However, they are very important in determining the dynamic performance of the axial magnetic suspension since they result in a much lower actuator bandwidth (<50 Hz) than that enjoyed by radial AMBs (>1000 Hz).
Because of the importance of eddy currents to thrust AMB dynamic performance, significant efforts have been made to develop useful, analytic models that predict actuator frequency response from geometry and material properties. Zmood et al. [1] first proposed a dynamic model for a nonlaminated actuator, a C-core electromagnet. Feeley [2] also analyzed a C-core actuator and proposed a fractional-order transfer function model. The dynamics of a nonlaminated cylindrical magnetic actuator were first examined by Kucera and Ahrens [3]. All of these works assumed that the air gap flux density was uniformly distributed and was independent of the frequency of the harmonic field. In Zhu et al. [4] this assumption was shown to be the source of significant modeling errors. Zhu developed a high-fidelity analytic model of axisymmetric cylindrical electromagnetic actuators by dividing the actuator into six parts and finding the frequency-dependent reluctance of each part. From this model, a simple fractional order model was derived, which was explicitly dependent on actuator material and geometric properties. The accuracy of this model was demonstrated via extensive comparison to the frequency response obtained from finite-element analysis. Later, Zhu et al. [5] examined how to extend this model to incorporate time-varying rotor axial position and voltage-mode operation of the magnetic suspension. Experimental results were also presented that demonstrate the accuracy of this modeling approach. In [6], Knospe and Zhu examined the limits to the performance of nonlaminated magnetic suspension systems. The sensitivity integral constraint condition was formulated for the fractional order closed loop system. Expressions were obtained that relate achievable closed loop performance to actuator model parameters. Sun et al. [7] examined the modeling of conventional thrust AMBs. The reluctance of the gap elements was treated as frequency independent. More recently, Whitlow [8] extended the work of Zhu to the conventional geometry and treated the gap elements as dynamic. Whitlow also examined the dynamics of segmented thrust stator designs [9].
From a mechatronic viewpoint, the task of developing an axial magnetic suspension system for a rotating machine consists of (I) designing the AMB thrust actuator and (II) designing the feedback controller. Since the thrust actuator transfer function has significant phase lag in the frequency band of interest, the feedback controller design cannot proceed until actuator design has been completed. The actuator design strongly impacts the ultimate performance of the magnetic suspension. It is critical to take this impact into account when designing the actuator. That is, actuator design both depends upon the feedback control objectives and dictates the feedback control design. The theory of performance limitations for nonlaminated magnetic suspension [6] provides an approach for resolving this design interdependence.
In contrast to finite element models, which might require hours or days of computation to find the actuator bandwidth, analytic models can be readily employed within optimization algorithms so as to tailor actuator geometry to maximize bandwidth. Furthermore, such optimization can take into account constraints imposed by the application (e.g., maximum thrust disk radius, shaft diameter, etc.).
2. Thrust Magnetic Bearing Model and Performance
2.1. Axial Actuator Model
Most magnetic bearing applications rely upon two opposing stators to control rotor axial motion with each stator providing an equal and opposite force to the rotor when no external force is to be applied. Thus, coils in both stators are energized with a bias current in the absence of any applied external force. In response to any measured displacement the feedback controller alters the coil currents in the two stators, decreasing that on the same side as the displacement and increasing that in the opposing coil. Often, the decrease and increase in the coil currents are the same and this quantity is referred to as the perturbation current. While the relationship between the force produced by a stator electromagnet and the coil current that induced it is quadratic, the relationship between the net force () applied to the rotor (from the opposing pair of electromagnets) and the perturbation current () is quite linear. Furthermore, the relationship between axial displacement () and the magnetic force induced by the rotor displacement alone (i.e., with coil currents fixed) may also be treated as linear if the displacement is significantly smaller than the nominal gap () between rotor and stator. Hence, for laminated actuators (without the dynamics produced by eddy currents) the relationship between force, perturbation current, and displacement is commonly written as
(We assume throughout this presentation that the active magnetic bearing is operated with transconductance amplifiers—i.e., “current-mode”. We plan to address “voltage-mode” operation in a sequel to this paper.) For nonlaminated AMBs this relationship is modified because of the presence of actuator dynamics. Because the relationship between signals is no longer memoryless, it is best to express it after taking the Laplace transform of the signals involved. Let , , and denote the Laplace transforms of , , and , respectively. The relationships between these variables may then be modeled as
Here, is the actuator’s transfer function
where is the frequency-dependent effective reluctance of the magnetic flux path, as derived by Whitlow [8] and summarized in Appendix A. This effective reluctance is explicitly dependent on the actuator’s geometric parameters (), shown in Figure 1, and the conductivity () and relative permeability () of its ferromagnetic material.
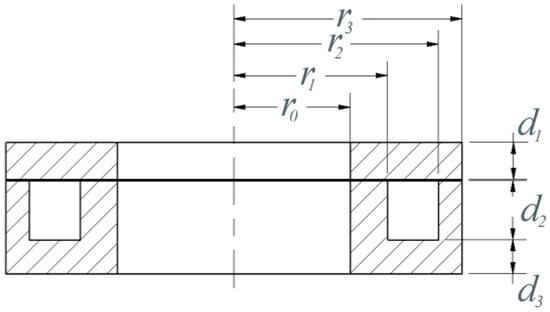
Figure 1.
Axisymmetric geometry of thrust disk and stator electromagnet of an axial magnetic bearing. Only one electromagnet of the opposing pair shown (flux-carrying path in iron cross hatched).
2.2. The Importance of Magnetic Actuator Bandwidth
Here we review and expand upon the relevant previous results on performance limitations of magnetic suspension systems presented by Zhu et al. [5]. These results rigorously demonstrate that magnetic actuator bandwidth is a critical parameter in the performance of magnetic suspension systems. This theory is based upon an approximate fractional-order transfer function model of the magnetic actuator:
where is the static reluctance of the electromagnet (i.e., at zero frequency) and c is a parameter that governs the importance of eddy currents ( corresponds to no eddy currents). Such approximate models have been shown to well represent the actual transfer function of magnetic suspension actuators [4,5].
In [4,5,8,9] analytic expressions for and are provided for a variety of actuator geometries. These expressions are functions of only material and geometric properties. Of greatest interest to this investigation are the expressions developed by Whitlow [8] for the conventional AMB thrust bearing geometry (see Figure 1):
where is the iron’s conductivity, is its relative permeability, is the permeability of free space.
The bandwidth of a low pass filter is typically specified as the frequency at which the filter’s gain is that of the DC value (i.e., −3 dB). This corresponds to −45° for a first order system. For the actuator transfer function (Equation (4)) the bandwidth is related to the transfer function coefficients via
where . This frequency corresponds to that where the phase lag is −15°.
It is assumed now that axial motion of the rotor may be described via a 2nd order rigid body model. Then, the transfer function of the rotor/actuator system (i.e., plant) is
where m is the rotor mass [5].
The first limitation we examine is the feedback controller gain that may be employed. The allowable controller gain for an application is dependent on many factors such as sensor noise, the power amplifiers used, and the accuracy of the model used in controller synthesis. A constraint on the gain of the controller’s transfer function, C(s), may be written as
where the units are those of force/displacement, hence may be interpreted as the maximum dynamic stiffness at a high frequency. (Note that there is no bound imposed on low-frequency gain and the controller may, thus, contain an integrator.) The parameter will be referred to as the control effort. Define the magnetic suspension loop gain transfer function as . We will introduce a constraint on this transfer function in a similar fashion to that of Freudenberg and Looze [10]:
where is an upper bound on the loop crossover frequency, and and are constants describing the rate of attenuation (“roll-off”) of the loop gain with frequency ( and is a positive fraction). This is essentially a constraint upon the gain–bandwidth product of the loop transfer function since the crossover frequency will be near to the closed loop bandwidth of the magnetic suspension system. This specification ensures that any closed loop design considered in evaluating achievable performance would not demand unreasonable performance from the sensor or power amplifier hardware.
With these constraints defined for open loop transfer functions, we turn our attention to specifications on closed loop performance. These specifications may be written in terms of the gain of the sensitivity function, :
In the first constraint, is the required sensitivity attenuation and is the attenuation bandwidth—that is, the range of low frequencies where the sensitivity gain is required to be small. Small sensitivity is necessary to achieve good rejection of disturbance forces that act along the thrust axis in this frequency band. It is also required if the levitated rotor’s position is to track a reference signal that has this frequency content. The second sensitivity constraint provides a bound, , on the peak sensitivity (). Limiting the maximum sensitivity requires the magnetic suspension to be robust to destabilizing, unmodeled dynamics. These sensitivity constraints are illustrated in Figure 2.
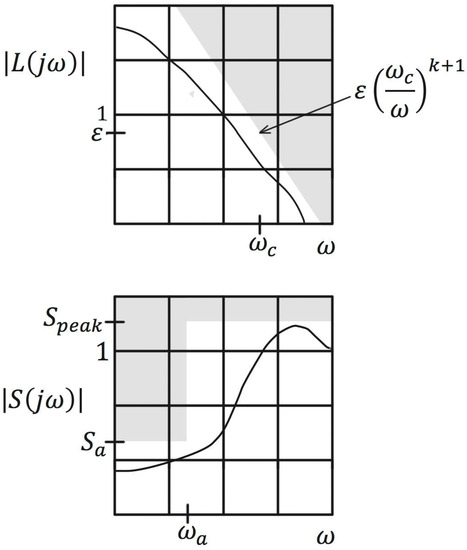
Figure 2.
Loop gain and sensitivity constraints (Equations (9) and (10)) for performance limitations analysis.
We now define a magnetic suspension performance metric:
where . Since , . In general, the designer seeks smaller values of (hence more negative values of ) and, therefore, larger values of . If the value of were increased (an undesirable result) then the value of would be reduced (all other factors unchanged). As before, larger values of are preferable.
In [6] it was shown that a necessary condition for an actuator with the transfer function to achieve a specified attenuation bandwidth (), with a given control effort () and magnetic suspension performance metric (), is
All terms on the left-hand side of the inequality are parameters of the actuator design, while those on the right are properties of the control system requirements. Since must be greater than zero, we can define an upper bound on achievable attenuation bandwidth for any magnetic suspension where the control effort () and performance metric () have been prescribed:
As Equation (12) indicates, when eddy currents become more significant (greater c) either the attenuation bandwidth and/or the magnetic suspension performance metric must decrease. Using Equation (6), this condition may be rewritten as an inequality dictating the required actuator bandwidth necessary to achieve given magnetic suspension’s performance specifications:
This result indicates that increasing either the specification on attenuation bandwidth () or magnetic suspension performance metric () would require that the actuator bandwidth () be increased as well. This could be offset if greater control effort () were possible. This result shows the critical importance of achieving higher actuator bandwidth to improving the behavior of nonlaminated magnetic suspension systems.
3. Optimization
3.1. Design Constraints
There are five specified geometric inequality constraints that must be satisfied when optimizing a thrust magnetic actuator design so as to maximize its bandwidth:
- Outer radius constraint—the outer radius () must not exceed a bound determined either by the available space within the housing or the allowable hoop stress in the thrust disk at maximum speed;
- Inner radius constraint—the inner radius () must be sufficient to accommodate the shaft and allow for assembly;
- Axial length constraint—the total length of the actuator must not exceed a bound determined from the machine design and its rotordynamics;
- Peak force constraint—adequate pole face area must be provided so as to generate the specified maximum force. Furthermore, the cross-sectional area of all segments of the flux path must be greater than or equal to that of the pole face, thus, ensuring that the material’s saturation flux density can be achieved at the pole face;
- Continuous force constraint—the cross-sectional area of the coil must be sufficiently large so as to provide the number of ampere-turns required to generate the specified continuous force without causing coil overheating.
In addition to these, there are several intrinsic geometric constraints that must be enforced in optimization: .
Table 1 provides the mathematical expressions for these constraints. The derivation of the continuous force constraint can be found in Appendix B.

Table 1.
Constraints present in axial magnetic actuator optimization problem.
3.2. Optimization Method
The performance index for optimization was the −3 dB bandwidth as calculated from the actuator frequency response as described by Equation (3) and Appendix A. Constrained optimization of actuator geometry was carried out via MATLAB’s fmincon function, which uses an interior-point algorithm to find the set of decision variables that maximize the performance index, while satisfying the geometric constraints in Table 1. The optimization algorithm cannot be guaranteed to find the global maximum of the performance index. However, repeated executions of the algorithm were carried out with random starting points to examine the quality and uniqueness of the solution found. In each case, the algorithm returned the same optimal set of decision variables, suggesting that the values found do indeed represent the global maximum within the constraints.
3.3. Pareto-Optimal Curves
Optimization is not only useful for finding the best actuator for a given set of constraints. It also may be used to determine the relationship between design specifications (e.g., peak actuator force) and the achievable actuator bandwidth. That is, optimization may be used to define Pareto-optimal curves. Such curves can be informative to the system designer. For example, when given a particular thrust actuator design, it is often possible to alter the design to increase its peak force without necessarily modifying its bandwidth. That is, the peak force does not directly dictate the bandwidth, making it difficult to understand the relationship between these two variables. However, if a thrust actuator design has been developed to maximize actuator bandwidth, any modification of the design to increase its peak force must result in a change in the achievable bandwidth. Thus, the salient relationship between the variables is revealed by the Pareto-optimal curve.
Using Pareto-optimization, the relationships between the maximum achievable bandwidth and four design specifications were evaluated. The design specifications examined were the maximum force, size of the gap between disk and stator, thrust disk outer radius, and actuator magnetic permeability.
4. Results
4.1. Design Example
For all design results examined, nominal values of the parameters and constraints were based upon the thrust magnetic actuator presented in [11]—see Table 2. The dimensions describing the original magnetic bearing design and those of the optimized design are listed in Table 3. This table also includes the bandwidth values before and after optimization, as calculated from the model in Appendix A. The reader will note that the optimization has pushed the stator/thrust disk outer diameter up to the constraint on its value. This increase in diameter has allowed the radial width of the pole faces (i.e., , and ) to be significantly decreased without sacrificing the peak force. Their circumferences have also grown by nearly 50%. The thrust disk and back iron dimensions (), like the pole faces, have been made much narrower by the optimization. The coil slot radial width () and depth () have remained largely unchanged, thus providing the coil area necessary for achieving the required continuous force. The combination of geometric changes results in a substantial increase in actuator bandwidth, from 51.8 to 206.5 Hz. To provide context, this change in bandwidth would allow the disturbance rejection metric to be more than doubled for one example problem studied, from before optimization to after. (For this calculation kg, Hz, , N/m, and were used.)

Table 2.
Nominal values of parameters and constraints for design optimization.

Table 3.
Dimensions and performance characterization variables for axial magnetic actuator designs. Nominal (starting) values and values after optimization.
4.2. Pareto-Optimal Results
As the previous example illustrates, increasing the constraint on outer radius allows a significant improvement in actuator bandwidth. In Figure 3, this trend is illustrated in the Pareto-optimal curves for this constraint. Each curve in the figure illustrates the maximum achievable actuator bandwidth as a function of the allowable disk outer radius. Curves are presented for varying peak force, from 7000 N to 8500 N. Bearings with larger peak force have lower bandwidth, as the required increase in pole faces result in greater pole face radial widths and smaller circumferences. The results indicate that substantial improvements in bandwidth (>2x) can be achieved with moderate increases in disk radius.
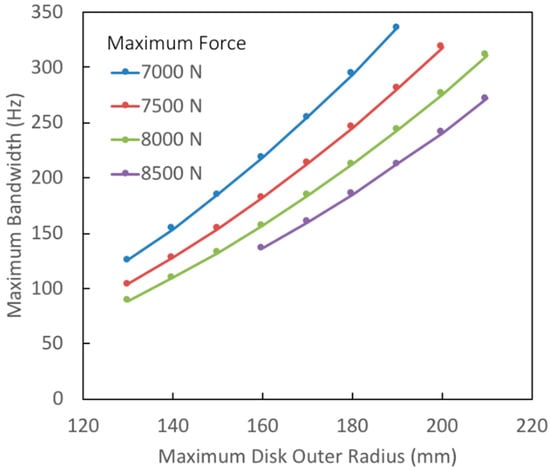
Figure 3.
Pareto-optimal curves showing maximum achievable actuator bandwidth as a function of the maximum allowable disk outer radius for various values of maximum force.
Figure 4 illustrates the effect that peak force has upon maximum achievable bandwidth. Pareto-optimal curves are shown for various values of the axial gap ranging from the nominal value of 1.158 mm to 1.758 mm. (In each case the maximum disk outer radius was set to 150 mm.) The reader will note that the maximum achievable bandwidth is strongly dependent on the peak force of the thrust bearing. A 30% increase in peak force cut the maximum bandwidth in half.
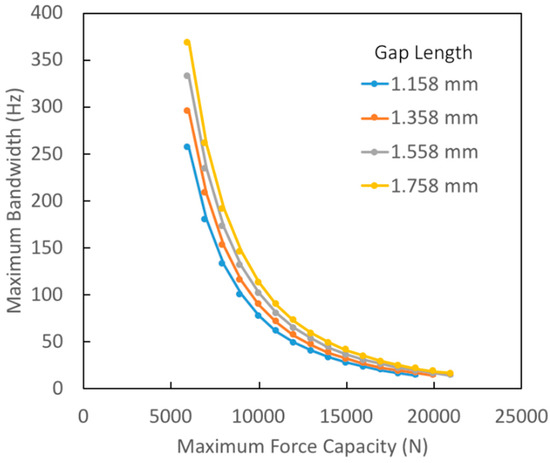
Figure 4.
Pareto-optimal curves showing maximum achievable actuator bandwidth as a function of maximum force for various values of axial gap.
A similar Pareto-optimal investigation of peak force is shown in Figure 5. Here, curves of maximum achievable bandwidth are shown for three values of disk outer radius constraint: 100 mm, 150 mm (nominal), and 200 mm. In each case, results show that the maximum achievable bandwidth scales as .
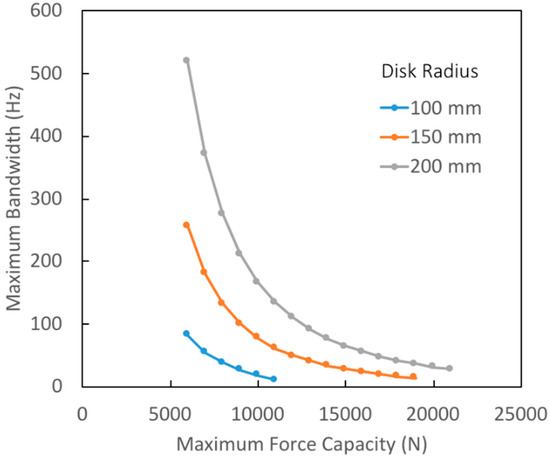
Figure 5.
Pareto-optimal curves showing maximum achievable actuator bandwidth as a function of maximum force for various values of the maximum allowable disk outer radius.
An investigation of the effect of axial gap upon maximum achievable bandwidth yielded an unexpected result: increasing the gap between stator and disk resulted in an increase in achievable actuator bandwidth—see Figure 6. This trend is counterintuitive since a larger gap requires a larger coil area to supply the increased number of ampere-turns necessary to energize the gap. A larger coil area will typically result in a decrease in the circumference of the inner pole face, which will tend to increase eddy currents within it and thus increase the eddy current parameter . But, as Equation (6) states, actuator bandwidth depends on both and the static reluctance . In the instance of increasing axial gap, the increase in is more significant than the increase in the parameter . Thus, actuator bandwidth improves as gap size is increased. (The reader should note that this analysis assumes that the gap is small enough that flux leakage and fringing are not significant factors.)
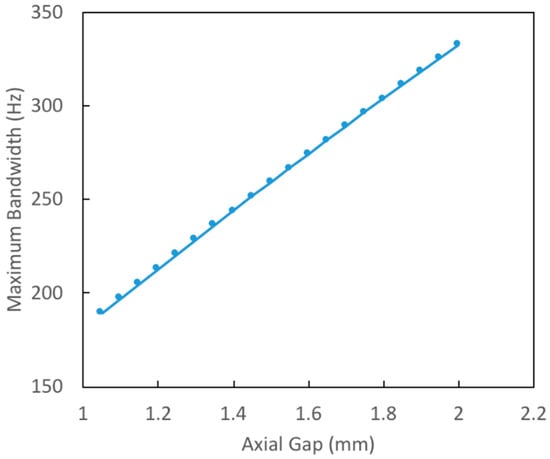
Figure 6.
Pareto-optimal curve showing maximum achievable bandwidth as a function of axial gap.
In Figure 7 the impact of iron permeability on achievable bandwidth is depicted. The Pareto-optimal curve shows that actuator bandwidth can be significantly improved through the use of higher permeability materials. This might at first seem surprising as the optimized geometry of the actuator designed with is almost the same as that designed with . Thus, the increase in bandwidth is almost entirely due to the direct effect of on bandwidth as predicted by Equations (5) and (6), and not upon changes to geometry enabled by the use of a higher permeability material. From Equation (5), the dependence of dynamic parameters and on relative permeability can be captured by the relationships
where coefficients are independent of , and therefore bandwidth scales as
(see Equation (6)). Thus, for sufficiently large the bandwidth will increase linearly in (and it will never increase at a rate greater than linear). It is this linear scaling behavior that is evident in Figure 7.
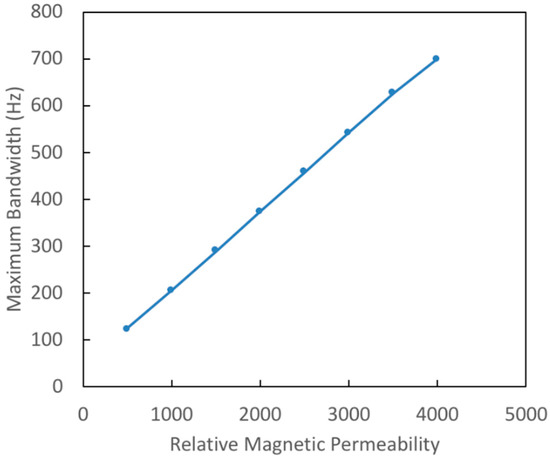
Figure 7.
Pareto-optimal curve showing maximum achievable bandwidth as a function of relative magnetic permeability of the actuator’s ferromagnetic material.
5. Discussion
One of the primary features of optimized designs is the increase of the disk and stator radius to the outer radius constraint. This allows the pole faces to be made radially thinner, in a certain sense approximating a (thick) circumferential lamination. In applications, the maximum diameter of the thrust actuator is constrained both by required housing dimensions and the hoop stress that is induced within the disk at the maximum operating speed. In optimized designs, the inner pole face radii (,), as well as those of the outer, are increased. We note that the inner radii could be further increased if the coil slot radial width () was made smaller and the coil slot depth () was made larger (so as to preserve coil slot area). This tactic, however, is not typically pursued by the optimization algorithm for the examples studied. We posit that this is due to a bandwidth cost of high aspect ratio (i.e., ) coils: the increased length of the iron path increases the eddy currents in the poles and, thus, the eddy current parameter (see Equation (5b)). It is likely that this cost offsets any benefit from increasing the inner pole radii.
To the authors’ knowledge, the effectiveness of increasing gap length as a means to improve thrust bearing actuator bandwidth has not been previously noted. Of course, a larger gap would result in greater flux leakage and fringing and, thus, impact peak force. Nevertheless, this avenue for improved performance is one that merits careful examination by practitioners when designing AMB systems for rotating machinery.
Increasing permeability offers another avenue for improving actuator bandwidth. In general, strength properties of ferromagnetic materials must be compromised in order to achieve greater permeability. As the stator is not subject to the same stress as the disk, this suggests that particular attention be paid to the selection of ferromagnetic material for the stator so as to maximize both and (see Equations (5a) and (5b)). For example, while cobalt-iron has high strength (e.g., 500 MPa for Carpenter Hiperco 50HS), it has a much lower permeability (). In contrast, nickel-iron’s strength is much lower (e.g., 150 MPa for Carpenter HyMu 80) but its permeability is exceptional (). Since the length of the flux path in the disk is much shorter than in the stator, a combination of these materials should permit high bandwidth and adequate disk strength. We note here that silicon-iron is not particularly well-suited to either the stator or the disk as its strength is lower than cobalt-iron and its permeability is less than nickel-iron.
It is intriguing to consider whether an E-core design for the actuator stator might offer any benefit for improving bandwidth. Since only half the flux would pass through the inner and outer pole faces, they could be made with less radial width, enhancing bandwidth. However, the overall iron path lengths might be longer, penalizing bandwidth. This analysis would make a worthwhile study.
6. Conclusions
The problem of maximizing axial magnetic bearing actuator bandwidth through the choice of geometric and material properties was mathematically formulated. Optimal designs were shown to have significantly larger bandwidth than nominal designs. This is a previously unexploited direction for improving the dynamic performance of rotating machinery supported by active magnetic bearings. The use of this bandwidth optimization approach to determine Pareto-optimal curves for the axial actuator design problem was introduced. Such curves were developed for an example problem with several variables investigated. The Pareto-optimal curves show that bandwidth may be significantly improved by increasing disk outer diameter, axial gap, and magnetic permeability. Actuator bandwidth was found to have an inverse-square relationship with peak force.
Author Contributions
Conceptualization, R.F. and C.K.; formal analysis, C.K.; investigation, H.S.; methodology, R.F. and C.K.; Software, H.S.; Supervision, R.F. and C.K.; writing—original draft, C.K.; writing—review and editing, H.S. and R.F.
Funding
This work was supported by the Rotating Machinery and Controls (ROMAC) Industrial Consortium at the University of Virginia.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The frequency-dependent effective reluctance of the thrust magnetic actuator is:
where
and
The actuator’s geometric parameters () are as indicated in Figure 1. In these equations and are the conductivity and relative permeability of the ferromagnetic material. The constant is the permeability of free space.
Appendix B
Consider a magnetic thrust bearing consisting of opposing electromagnets, labeled “u” and “d”. Let and denote the inner and outer pole face areas of each electromagnet. The attractive force produced by “u” and “d” electromagnets are, respectively:
Here, is the permeability of free space and , are the fluxes in the electromagnets. These fluxes can be related to the coil currents in the opposing coils (,) and the static reluctance of each electromagnet, , (assuming centered operation) via:
The nominal reluctances are from the nonlaminated actuator model and are dependent on the nominal value of gap. The net force () produced by the pair of opposing electromagnets is:
The bias flux is related to the bias current in the coils via:
which can be determined from the desired bias flux density () for operation:
where . Simplifying this:
The currents in the two opposing electromagnets can be written in terms of bias and perturbation currents:
And therefore:
and
Since
we can simplify:
Solving for the perturbation ampere-turns such that the net force equals the desired continuous force () yields:
Assuming (without loss of generality) that the continuous force acts in the “u” direction, the ampere-turns in the “u” coil are:
To prevent overheating of the coil we require that the coil slot area satisfy:
where is the coil area and is the coil current density. Therefore, the coil size needed to provide the constant force is:
For calculations, we will assume that Tesla and A/m2.
References
- An, D.K.; Zmood, R.B.; Kirk, J.A. The influence of eddy currents on magnetic actuator performance. Proc. IEEE 1987, 75, 259–260. [Google Scholar]
- Feeley, J. A simple dynamic model for eddy currents in a magnetic actuator. IEEE Trans. Magn. 1996, 32, 453–458. [Google Scholar] [CrossRef]
- Kucera, L.; Ahrens, M. A model for axial magnetic bearings including eddy currents. In Proceedings of the Third International Symposium on Magnetic Suspension Technology, Tallahassee, FL, USA, 13–15 December 1995; pp. 421–438. [Google Scholar]
- Zhu, L.; Knospe, C. Modeling of nonlaminated electromagnetic suspension systems. IEEE/ASME Trans. Mechatron. 2010, 15, 59. [Google Scholar]
- Zhu, L.; Knospe, C.; Maslen, E. Analytic model for a nonlaminated cylindrical magnetic actuator including eddy currents. IEEE Trans. Magn. 2005, 41, 1248–1258. [Google Scholar]
- Knospe, C.; Zhu, L. Performance Limitations of Non-laminated Magnetic Suspension Systems. IEEE Trans. Control Syst. Technol. 2010, 19, 327–336. [Google Scholar] [CrossRef]
- Sun, Y.; Ho, Y.-S.; Yu, L. Dynamic stiffnesses of active magnetic thrust bearing including eddy-current effects. IEEE Trans. Magn. 2009, 45, 139–149. [Google Scholar] [CrossRef]
- Whitlow, Z.W. Modeling and Control of Non-Laminated Active Magnetic Thrust Bearings. Master’s Thesis, University of Virginia, Charlottesville, VA, USA, 2014. [Google Scholar]
- Whitlow, Z.; Fittro, R.; Knospe, C. Dynamic Performance of Segmented Active Magnetic Thrust Bearings. IEEE Trans. Magn. 2016, 52, 1–11. [Google Scholar] [CrossRef]
- Freudenberg, J.; Looze, D. A sensitivity tradeoff for plants with time delay. IEEE Trans. Autom. Control 1987, 32, 99–104. [Google Scholar] [CrossRef]
- Yoon, S.; Lin, Z.; Allaire, P. Control of Surge in Centrifugal Compressors by Active Magnetic Bearings; Springer: London, UK, 2013. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).