Abstract
The evolution of microelectronic technologies is giving constant impulse to advanced micro-scaled systems which perform complex operations. In fact, the actual micro and nano Electro-Mechanical Systems (MEMS/NEMS) easily integrate information-gathering and decision-making electronics together with all sorts of sensors and actuators. Mechanical manipulation can be obtained through microactuators, taking advantage of magnetostrictive, thermal, piezoelectric or electrostatic forces. Electrostatic actuation, more precisely the comb-drive approach, is often employed due to its high versatility and low power consumption. Moreover, the device design and fabrication process flow can be simplified by compliant mechanisms, avoiding complex elements and unorthodox materials. A nano-scaled rotary comb drive is herein introduced and obtained using NEMS technology, with an innovative design which takes advantages of the compliant mechanism characteristics. A theoretical and numerical study is also introduced to inspect the electro-mechanical behavior of the device and to describe a new technological procedure for its fabrication.
1. Introduction
The end of the 1960s has witnessed the rise and consolidation of semiconductor fabrication technologies leading, together with the first microchip developments, to the evolution of increasingly complex systems able to connect advanced electronics and engineering systems with the physical world [1]. This process was made possible due to the development of MEMS sensors and actuators, that are currently an essential part of our daily life, being present in information-communication, electromechanical, optical, chemical and biological devices [2,3,4,5]. Moreover, the scaling phenomenon from macro- to micro-actuators led to a drastic change in the influence of individual parameters and opened new perspectives with innovative mechanical designs.
MEMS actuators and sensors are many and different. Micromachined structures movimentation can be carried out using various approaches: such as magnetostrictive, thermal, piezoelectric or electrostatic [6]. In this work, attention is given to work-producing actuators, with silicon being the key material, by an electrical and mechanical point of view. State-of-the-art MEMS devices are often actuated taking advantage of electrostatic forces between charged surfaces at a distance. Electrostatic actuation combines high versatility, fast dynamic response and low power consumption with a simplified design and a fabrication process flow which is made possible by avoiding complex elements like coils or cores and unorthodox materials like shape-memory-alloys or piezoelectric ceramics [7]. It exploits the relation of surface to spacing (not volume to spacing), therefore its force is less affected by scaling [8].
Among all the possible electrostatic actuation techniques, the comb-drive approach is one of the most employed [9], with different possibilities in terms of out-of-plane [10] or in-plane [11] motion.
Moreover, Compliant mechanisms have been successfully adopted to develop MEMS devices in order to replace hinges and improve motion properties: the incorporation of the Conjugate Surfaces Flexure Hinges (CSFH) mechanism into the MEMS technology has opened up new perspectives for a completely new class of microdevices, characterized by a neutral stable configuration with a stationary pose, avoiding lubrication due to the absence of mechanical backlash, and easier to actuate [12]. The outcome is not a combination of different layers and sub-parts, the whole device can be made of a monolithic body of a single material, obtained by a highly simplified fabrication procedure, being at the same time extremely versatile in terms of integration in complex systems and structures for different applications, such as compliant 3 D.O.F. microrobots [13,14,15,16], micromechanisms [17,18], micro hinges [19,20,21] and microgrippers [22,23,24,25,26,27].
The drastic reduction of complexity made possible by the CSFH principle, together with its minimization of internal stresses and its robustness in operation, can facilitate the scaling process from a Micro-Electro-Mechanical System to a Nano-Electro-Mechanical System (NEMS), with new challenges in terms of mechanical movement, actuation possibilities and applications [28,29,30]. In this work, the properties of a NEMS rotary comb-drive nano-scaled actuator is introduced, its design is inspected, its electro-mechanical behaviour is theoretically and numerically studied and a new technological procedure for its fabrication is described, making it able to integrate in standard systems as well as in wearable/flexible systems, polymer substrates or in glass devices, with a variety of applications in the field of mechanical manipulation, such as nano-surgery, lab-on-chip bimolecular analysis, or nano-movimentation in space environment.
2. A Nano-Scaled Rotary Comb-Drive Electrostatic Actuator
The presented structure covers a total area of 120 × 75 m and is made of 2 main components, as depicted in Figure 1:
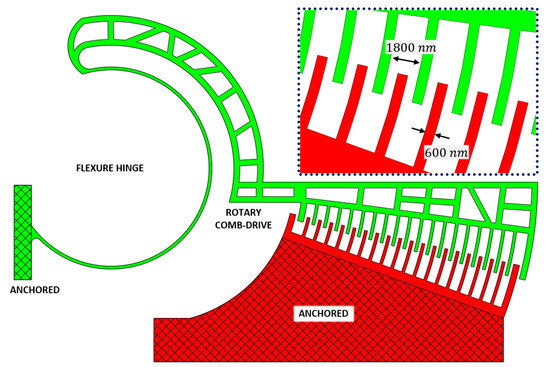
Figure 1.
Top view of the proposed device.
- A fixed part (red colored), with interdigitated fingers;
- A suspended part (green colored), composed by a mobile rigid body with interdigitated fingers and a flexure hinge with an anchored part on the left.
The system can be moved by changing the voltage between the static and movable part, which generates an alteration in the electrostatic forces between the two components, which are proportional to the capacitance between the two interdigitated structures: the result is a variation of the gap between the comb fingers and a movement of the rigid suspended body, made possible by the flexible hinge. Figure 2 shows a 3D sketch of the system.
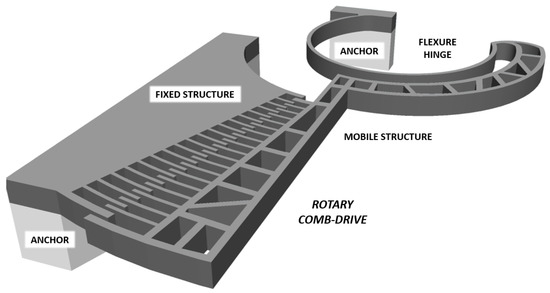
Figure 2.
Three-D sketch of the proposed device.
The actual comb-drive mechanism is 50 × 25 m, the smallest size ever presented in literature (to the best of the authors’ knowledge), and has two arrays of 18,600 nm-wide and 1800 nm-spaced fingers, with a length which changes from 4 m up to 9 m; the first and last finger of each array is 1200 nm-wide. The whole suspended part is able to move due to a 600 nm wide curved beam flexure hinge, with a circular shape and a radius of 20 m. The curved beam is considered as a revolute joint, centered in correspondence of the center of the beam elastic weight.
3. Microelectromechanical Simulation
The response of the comb drive to the application of a voltage on the pads connected to the fixed and mobile sets of fingers has been simulated in two steps.
Firstly, considering the geometry of the systems, the number of fingers and the dielectric characteristics of the gap, an elementary force F has been calculated as acting on each one of the n fingers. Force F has the line of action perpendicular to the finger free-end section and can be calculated as [31]
where is the vacuum permittivity ( Fm), is the air relative permittivity (1.00058), h is the thickness of the finger, g is the radial distance between the movable and fixed finger, and V is the applied voltage.
Then, a static force analysis has been performed by means of the commercial Finite Elements Analysis software ANSYS© (Canonsburg, PA, USA). Polycrystalline silicon has been considered as structural material, with Young’s modulus equal to 164 GPa and Poisson’s ratio equal to 0.22 [32]. Isotropic material formulation and nonlinearity due to large deflections were also considered. A fixed support was introduced to simulate the anchor constraint at the flexure end–section.
Two different layouts for the comb drives have been considered.
3.1. First Layout
For the first layout, fingers, a thickness nm and a gap nm have been considered. The forces were calculated for an applied voltage ranging from 1 to 14 V, with steps of 1 V.
Figure 3 shows the generated mesh, composed of 9484 nodes and 7594 elements, and refined in correspondence to the flexible beam and to the comb-drive fingers.
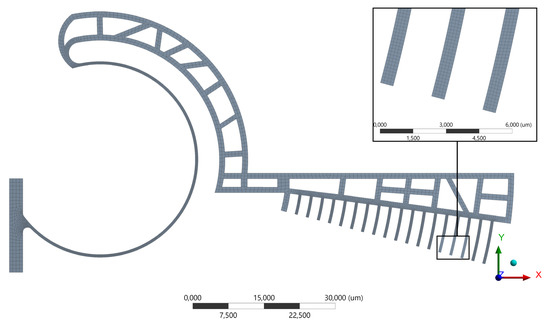
Figure 3.
First layout: mesh of the floating structure and detail of the comb-drive fingers.
The rotation of the floating part and the maximum value of the maximum principal stress (MPS), for increasing values of the applied voltage, are reported in Figure 4. The value of 14 V corresponds a rotation of 4.85°, close to the maximum rotation permitted by the comb-drive geometry (5°). This case is represented in Figure 5, showing the deformed and neutral configurations of the structure and the stress distribution on the flexure. The maximum MPS value is equal to 66.7 MPa. Yield strength of polycrystalline silicon is equal to 1.2 GPa [33,34].
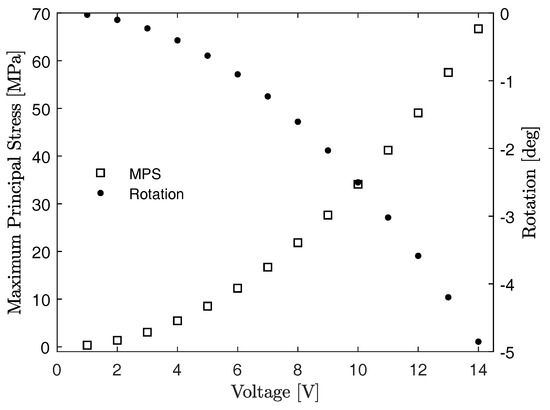
Figure 4.
First layout: maximum values of the MPS and rotation angle of the movable fingers for increasing values of the applied voltage V.

Figure 5.
First layout: neutral and deformed configurations, and stress distribution on the flexure.
A modal analysis has been performed with ANSYS to evaluate the dynamic performance of the actuator. The first resonant mode, occurring at 16.5 kHz, corresponds to an out-of-plane motion characterized by an axis of rotation parallel to the y-axis (see Figure 5). This occurrence is not really critical for the fingers which are subject locally to a relative translation with no problems for fingers interference.
The second mode occurs at 18.3 kHz, and it is associated to an in-plane oscillation with an axis of rotation parallel to the z-axis. This mode corresponds, actually, to the designed working motion for the mobile fingers and therefore there are no interference problems.
The third and sixth modes, corresponding to out-of plane motions, are characterized by natural frequencies equal to 41.6 kHz and 149.3 kHz, respectively.
The fourth and fifth modes, occurring at 56.5 kHz and 126.9 kHz, respectively, are attributed to in-plane motions that could be detrimental because of the possible contact among floating and anchored fingers. Finally, higher order modes have been neglected because the natural frequencies are very high.
3.2. Second Layout
After the former simulation, a second case has been studied with a gap g between the fingers larger than in the first case. In fact, the gap has been increased by the 30%, in order to avoid surface sticking during the fabrication and the releasing of the device. Furthermore, this could help operational performances during actuation.
To model the comb drive action in this second layout, the force F has been applied to each one of the fingers. The thickness of the finger h remained 500 nm, as well as the radial distance between the movable and fixed finger (1.2 m), while the range of applied voltage spans from 1 to 24 V, with 1 V steps.
Figure 6 reports the generated mesh, composed of 8065 nodes and 6423 elements, and refined in correspondence to the flexible beam and to the comb drive fingers.
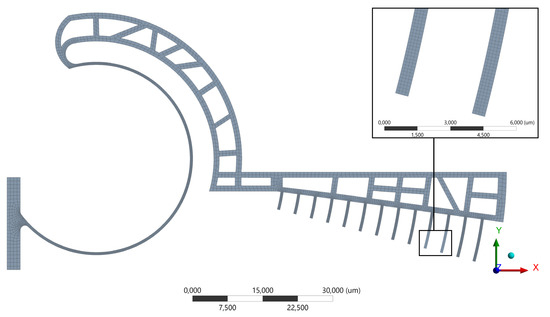
Figure 6.
Second layout: mesh of the floating structure and detail of the comb-drive fingers.
The rotation of the floating part and the maximum value of the maximum principal stress (MPS), for increasing values of the applied voltage, are reported in Figure 7. The value of 24 V corresponds to a rotation of 4.88°, close to the maximum rotation permitted by the comb-drive geometry (5°). As for the previous layout, the limit case is reported in Figure 8, that shows the deformed and neutral configurations and the stress distribution. The maximum MPS value is equal to 66.7 MPa.
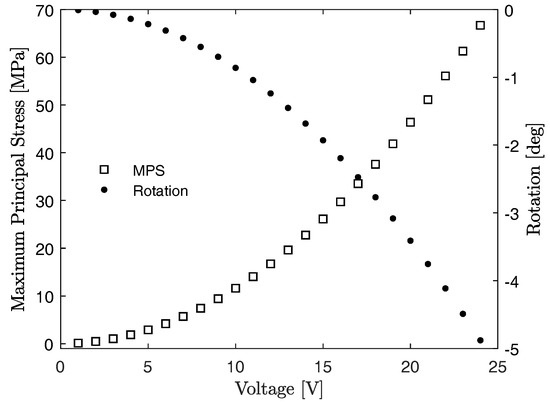
Figure 7.
Second layout: maximum values of the MPS and rotation angle of the movable fingers for increasing values of the applied voltage.
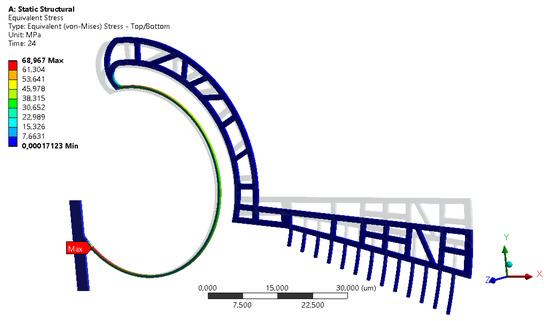
Figure 8.
Second layout: neutral and deformed configurations, and stress distribution on the flexure.
As for the first layout, modal analysis has been conducted to calculate the most affecting natural modes and so the first six natural frequencies have been considered, having, respectively, values equal to 16.7, 18.6, 40.4, 57.7, 127.1 and 147.9 kHz. The corresponding modes are similar to the ones described in the previous case.
4. Fabrication
Microelectronic manufacturing technologies, and its constant evolution in time, opened new possibilities for the fabrication of micro- and nano-scaled electro-mechanical systems, allowing to obtain a highly complex mechanism through a sequence of iterations of simple steps:
- Deposition/growth of a chosen material on a substrate in form of thin/thick film, using various kinds of methods, such as Physical or Chemical Vapor Deposition (PVD/CVD), Atomic Layer Deposition (ALD) and Epitaxy;
- Geometry definition of the latter, usually via lithographic techniques or similar;
- Material patterning, via wet/dry etching procedures.
The result is a device assembled by a composition of different layers overlapped, each shaped with the corresponding geometry [35,36].
MEMS manufacturing and production, for this kind of devices, usually employs a standard Silicon-on-Insulator (SOI) stack. For this work, an unconventional material stack is designed, as sketched in Figure 9.
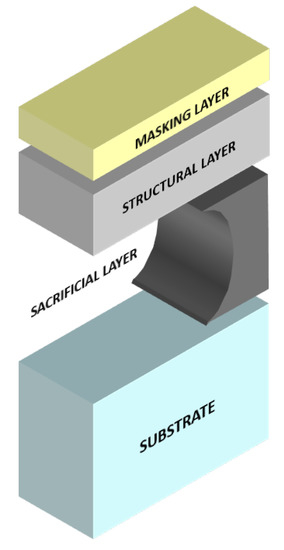
Figure 9.
Three-D sketch of the proposed device.
In particular, the stack is composed by:
- A glass substrate;
- A Ti/W metallic alloy as intermediate sacrificial layer;
- Doped hydrogenated amorphous silicon (a-Si:H) as structural layer: a highly versatile material, suitable for large-area and low-cost electronic devices, biologically compatible, while monolithically integrable on rigid or flexible, metallic, dielectric or polymeric substrates [37,38,39,40,41,42]. It also shows interesting mechanical features and was chosen to build bridge-like structures and cantilevers based devices [43].
- Chromium as masking layer for the structure patterning.
The fabrication procedure was carried out as follows:
- PVD of the sacrificial layer;
- CVD of the amorphous silicon layer;
- Geometry definition on a PVD obtained chromium film by lithographic technique: in particular, Electron Beam Lithography (EBL) was required, in order to obtain submicrometric resolution, on an electron-sensible polymeric film [44];
- Structure patterning by Reactive Ion Etching (RIE) technique, with the previously shaped chromium film as masking layer;
- Structure releasing via isotropic and selective removal of the intermediate layer, in a wet etching solution. Etch holes in the rigid suspended bodies were considered in order to promote the under-etching phenomenon and optimize the releasing process.
Figure 10 shows first examples of the nanoscaled rotary comb-drive during its fabrication process. Since the structure geometries reach the sub-micrometric scale, it was impossible to appropriately identify and discern all the features of our device with an optical microscope: therefore Scanning Electron Microscope (SEM) pictures were taken.

Figure 10.
SEM pictures of the nano comb-drive during its fabrication process: top view of the whole patterned device (a) with a 30° tilted enlargement on the comb-drive fingers (b); 45° tilted view of an anchored flexure hinge (c) and fingers (d) released from the glass substrate and suspended. These images were taken with an accelerating voltage (EHT) of 10 kV, 10 kV, 2 kV and 5 kV respectively; a magnification of 2630×, 8630×, 8000× and 2281×, respectively; a working distance of 5.5 mm, 10 mm, 5.9 mm and 10.0 mm, respectively, and a beam current of 10 pA.
Figure 10a,b show a top view (top left) of the whole device during the structure patterning phase, with an enlargement on the comb fingers (top right). Figure 10c,d show the crucial parts of the device suspended and detached from the substrate after the releasing process: the attachment between the hinge of the actuator and the anchor (bottom left), and the comb-drive fingers (bottom right). The displayed devices have n-doped a-Si:H, deposited by Plasma Enhanced Chemical Vapour Deposition (PECVD), as structural layer, with the following parameters:
- A substrate temperature of 200 °C;
- A SiH4 flow of 45 sccm and a PH3 flow of 10 sccm into the process chamber, with a process pressure of 0.3 Torr;
- A glow discharge with a power density of 25 mW/cm2, for 1 h.
5. Conclusions
This paper has shown the feasibility of a new nano fabrication process to build nano actuators, based on electrostatic actuation. The construction process has been applied to a rotary comb-drive which appears promising as a tool for microactuation and micromanipulation. Furthermore, the numerical simulations gave also encouraging results in terms of operational capability. Two models have been studied with different characteristics and the results showed that operational capabilities can be increased by reducing the gap between the fingers and their size, which makes the systems less robust. Therefore, an optimal design should find a balance of mediation between the two different factors. The developed actuator seems to be one of the smallest actuators available as state-of-the-art, and this could lead to new applications, especially in the biomedical field.
Author Contributions
A.V., A.B., M.H., and E.G. were involved in the fabrication and design of the rotary comb drives; M.V. and N.P.B. have performed the numerical analysis and design; F.F., G.d.C. and N.P.B coordinated the work and supervised the project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gardner, J.W.; Varadan, V.K.; Awadelkarim, O.O. Microsensors. In Microsensors, MEMS, and Smart Devices; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001; pp. 227–302. [Google Scholar]
- Bhushan, B. Nanotribology and nanomechanics of MEMS/NEMS and BioMEMS/BioNEMS materials and devices. In Nanotribology and Nanomechanics; Springer: Cham, Switzerland, 2017; pp. 797–907. [Google Scholar]
- Grayson, A.C.R.; Shawgo, R.S.; Johnson, A.M.; Flynn, N.T.; Li, Y.; Cima, M.J.; Langer, R. A BioMEMS review: MEMS technology for physiologically integrated devices. Proc. IEEE 2004, 92, 6–21. [Google Scholar] [CrossRef]
- Tilmans, H.A.; De Raedt, W.; Beyne, E. MEMS for wireless communications: From RF-MEMS components to RF-MEMS-SiP. J. Micromech. Microeng. 2003, 13, S139. [Google Scholar] [CrossRef]
- Saxena, V.; Plum, T.J.; Jessing, J.R.; Baker, R.J. Design and fabrication of a MEMS capacitive chemical sensor system. In Proceedings of the 2006 IEEE Workshop on Microelectronics and Electron Devices, WMED’06, Boise, ID, USA, 14 April 2006. [Google Scholar]
- Bell, D.J.; Lu, T.; Fleck, N.A.; Spearing, S.M. MEMS actuators and sensors: Observations on their performance and selection for purpose. J. Micromech. Microeng. 2005, 15, S153. [Google Scholar] [CrossRef]
- Del Corro, P.G.; Imboden, M.; Pérez, D.J.; Bishop, D.J.; Pastoriza, H. Single ended capacitive self-sensing system for comb drives driven XY nanopositioners. Sens. Actuators A Phys. 2018, 271, 409–417. [Google Scholar] [CrossRef]
- Thielicke, E.; Obermeier, E. Microactuators and their technologies. Mechatronics 2000, 10, 431–455. [Google Scholar] [CrossRef]
- Legtenberg, R.; Groeneveld, A.; Elwenspoek, M. Comb-drive actuators for large displacements. J. Micromech. Microeng. 1996, 6, 320. [Google Scholar] [CrossRef]
- Xie, H.; Pan, Y.; Fedder, G.K. A CMOS-MEMS mirror with curled-hinge comb drives. J. Microelectromech. Syst. 2003, 12, 450–457. [Google Scholar]
- Yi, B.J.; Chung, G.B.; Na, H.Y.; Kim, W.K.; Suh, I.H. Design and experiment of a 3-DOF parallel micromechanism utilizing flexure hinges. IEEE Trans. Robot. Autom. 2003, 19, 604–612. [Google Scholar]
- Belfiore, N.P.; Scaccia, M.; Ianniello, F.; Presta, M. Selective Compliance Hinge. U.S. Patent 8,191,204 B2, 6 May 2012. [Google Scholar]
- Balucani, M.; Belfiore, N.P.; Crescenzi, R.; Genua, M.; Verotti, M. Developing and modeling a plane 3 DOF compliant micromanipulator by means of a dedicated MBS code. In Proceedings of the 2011 NSTI Nanotechnology Conference and Expo, Boston, MA, USA, 13–16 June 2011; Volume 2, pp. 659–662. [Google Scholar]
- Balucani, M.; Belfiore, N.P.; Crescenzi, R.; Verotti, M. The development of a MEMS/NEMS-based 3 D.O.F. compliant micro robot. Int. J. Mech. Control 2011, 12, 3–10. [Google Scholar]
- Belfiore, N.P.; Balucani, M.; Crescenzi, R.; Verotti, M. Performance analysis of compliant mems parallel robots through pseudo-rigid-body model synthesis. In Proceedings of the ASME 2012 11th Biennial Conference on Engineering Systems Design and Analysis, Nantes, France, 2–4 July 2012; Volume 3, pp. 329–334. [Google Scholar]
- Belfiore, N.P.; Emamimeibodi, M.; Verotti, M.; Crescenzi, R.; Balucani, M.; Nenzi, P. Kinetostatic optimization of a MEMS-based compliant 3 DOF plane parallel platform. In Proceedings of the ICCC 2013–IEEE 9th International Conference on Computational Cybernetics, Tihany, Hungary, 8–10 July 2013; pp. 261–266. [Google Scholar]
- Sanò, P.; Verotti, M.; Bosetti, P.; Belfiore, N.P. Kinematic Synthesis of a D-Drive MEMS Device with Rigid-Body Replacement Method. J. Mech. Des. Trans. ASME 2018, 140, 075001. [Google Scholar] [CrossRef]
- Verotti, M.; Crescenzi, R.; Balucani, M.; Belfiore, N.P. MEMS-based conjugate surfaces flexure hinge. J. Mech. Des. Trans. ASME 2015, 137, 012301. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Broggiato, G.; Verotti, M.; Balucani, M.; Crescenzi, R.; Bagolini, A.; Bellutti, P.; Boscardin, M. Simulation and construction of a MEMS CSFH based microgripper. Int. J. Mech. Control 2015, 16, 21–30. [Google Scholar]
- Belfiore, N.P.; Broggiato, G.; Verotti, M.; Crescenzi, R.; Balucani, M.; Bagolini, A.; Bellutti, P.; Boscardin, M. Development of a MEMS technology CSFH based microgripper. In Proceedings of the 23rd International Conference on Robotics in Alpe-Adria-Danube Region (RAAD), Smolenice, Slovakia, 3–5 September 2014. [Google Scholar]
- Crescenzi, R.; Balucani, M.; Belfiore, N.P. Operational characterization of CSFH MEMS technology based hinges. J. Micromech. Microeng. 2018, 28. [Google Scholar] [CrossRef]
- Di Giamberardino, P.; Bagolini, A.; Bellutti, P.; Rudas, I.; Verotti, M.; Botta, F.; Belfiore, N. New MEMS tweezers for the viscoelastic characterization of soft materials at the microscale. Micromachines 2017, 9, 15. [Google Scholar] [CrossRef]
- Bagolini, A.; Ronchin, S.; Bellutti, P.; Chistè, M.; Verotti, M.; Belfiore, N.P. Fabrication of Novel MEMS Microgrippers by Deep Reactive Ion Etching With Metal Hard Mask. J. Microelectromech. Syst. 2017, 26, 926–934. [Google Scholar] [CrossRef]
- Dochshanov, A.; Verotti, M.; Belfiore, N. A Comprehensive Survey on Microgrippers Design: Operational Strategy. J. Mech. Des. Trans. ASME 2017, 139, 070801. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. A Comprehensive Survey on Microgrippers Design: Mechanical Structure. J. Mech. Des. Trans. ASME 2017, 139, 060801. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. Compliance Synthesis of CSFH MEMS-Based Microgrippers. J. Mech. Des. Trans. ASME 2017, 139. [Google Scholar] [CrossRef]
- Potrich, C.; Lunelli, L.; Bagolini, A.; Bellutti, P.; Pederzolli, C.; Verotti, M.; Belfiore, N.P. Innovative silicon microgrippers for biomedical applications: Design, mechanical simulation and evaluation of protein fouling. Actuators 2018, 7, 12. [Google Scholar] [CrossRef]
- Veroli, A.; Buzzin, A.; Crescenzi, R.; Frezza, F.; de Cesare, G.; D’Andrea, V.; Mura, F.; Verotti, M.; Dochshanov, A.; Belfiore, N.P. Development of a NEMS-Technology Based Nano Gripper. In Proceedings of the International Conference on Robotics in Alpe-Adria Danube Region, Torino, Italy, 21–23 June 2017; Springer: Cham, Switzerland, 2017; pp. 601–611. [Google Scholar]
- Buzzin, A.; Veroli, A.; de Cesare, G.; Belfiore, N. Nems-Technology based nano gripper for mechanic manipulation in space exploration mission. Adv. Astronaut. Sci. 2018, 163, 61–67. [Google Scholar]
- Nascetti, A.; Caputo, D.; Scipinotti, R.; de Cesare, G. Technologies for autonomous integrated lab-on-chip systems for space missions. Acta Astronaut. 2016, 128, 401–408. [Google Scholar] [CrossRef]
- Hou, M.T.K.; Huang, J.Y.; Jiang, S.S.; Yeh, J.A. In-plane rotary comb-drive actuator for a variable optical attenuator. J. Micro/Nanolithogr. MEMS MOEMS 2008, 7, 043015. [Google Scholar]
- Cho, S.; Chasiotis, I. Elastic properties and representative volume element of polycrystalline silicon for MEMS. Exp. Mech. 2007, 47, 37–49. [Google Scholar] [CrossRef]
- Sharpe, W.N.; Yuan, B.; Vaidyanathan, R.; Edwards, R.L. Measurements of Young’s modulus, Poisson’s ratio, and tensile strength of polysilicon. In Proceedings of the IEEE The Tenth Annual International Workshop on Micro Electro Mechanical Systems. An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Nagoya, Japan, 26–30 January 1997; pp. 424–429. [Google Scholar]
- Sharpe, W.N., Jr.; Yuan, B.; Vaidyanathan, R.; Edwards, R.L. New test structures and techniques for measurement of mechanical properties of MEMS materials. In Proceedings of the Micromachining and Microfabrication, Austin, TX, USA, 13 September 1996; Volume 2880, pp. 78–91. [Google Scholar]
- Volland, B.; Heerlein, H.; Rangelow, I. Electrostatically driven microgripper. Microelectr. Eng. 2002, 61, 1015–1023. [Google Scholar] [CrossRef]
- Caputo, D.; Ceccarelli, M.; de Cesare, G.; Nascetti, A.; Scipinotti, R. Lab-on-glass system for DNA analysis using thin and thick film technologies. MRS Online Proc. Libr. Arch. 2009, 1191, 53–58. [Google Scholar] [CrossRef]
- De Cesare, G.; Gavesi, M.; Palma, F.; Riccò, B. A novel a-Si: H mechanical stress sensor. Thin Solid Films 2003, 427, 191–195. [Google Scholar] [CrossRef]
- Caputo, D.; de Cesare, G.; Nardini, M.; Nascetti, A.; Scipinotti, R. Monitoring of temperature distribution in a thin film heater by an array of a-Si: H temperature sensors. IEEE Sens. J. 2012, 12, 1209–1213. [Google Scholar] [CrossRef]
- De Cesare, G.; Nascetti, A.; Caputo, D. Amorphous silicon pin structure acting as light and temperature sensor. Sensors 2015, 15, 12260–12272. [Google Scholar] [CrossRef] [PubMed]
- Tucci, M.; Serenelli, L.; Salza, E.; De Iuliis, S.; Geerligs, L.; Caputo, D.; Ceccarelli, M.; de Cesare, G. Back contacted a-Si: H/c-Si heterostructure solar cells. J. Non-Cryst. Solids 2008, 354, 2386–2391. [Google Scholar] [CrossRef]
- Caputo, D.; de Cesare, G. New a-Si: H two-terminal switching device for active display. J. Non-Cryst. Solids 1996, 198, 1134–1136. [Google Scholar] [CrossRef]
- Asquini, R.; Buzzin, A.; Caputo, D.; de Cesare, G. Integrated Evanescent Waveguide Detector for Optical Sensing. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 1180–1186. [Google Scholar] [CrossRef]
- Gaspar, J.; Chu, V.; Conde, J. Amorphous silicon electrostatic microresonators with high quality factors. Appl. Phys. Lett. 2004, 84, 622–624. [Google Scholar] [CrossRef]
- Veroli, A.; Mura, F.; Balucani, M.; Caminiti, R. Dose influence on the PMMA e-resist for the development of high-aspect ratio and reproducible sub-micrometric structures by electron beam lithography. AIP Conf. Proc. 2016, 1749, 020010. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).