A Rotational Order Vibration Reduction Method Using a Regular Non-Circular Pulley
Abstract
1. Introduction
1.1. Motivations
1.2. Literature Reviews and Objectives
2. Modeling and Solution of the Timing Belt System with a Non-Circular Pulley
2.1. Modeling of Timing Drive System with Elliptical Pulley
2.1.1. Modeling of Belt Drive System with Elliptical Pulley
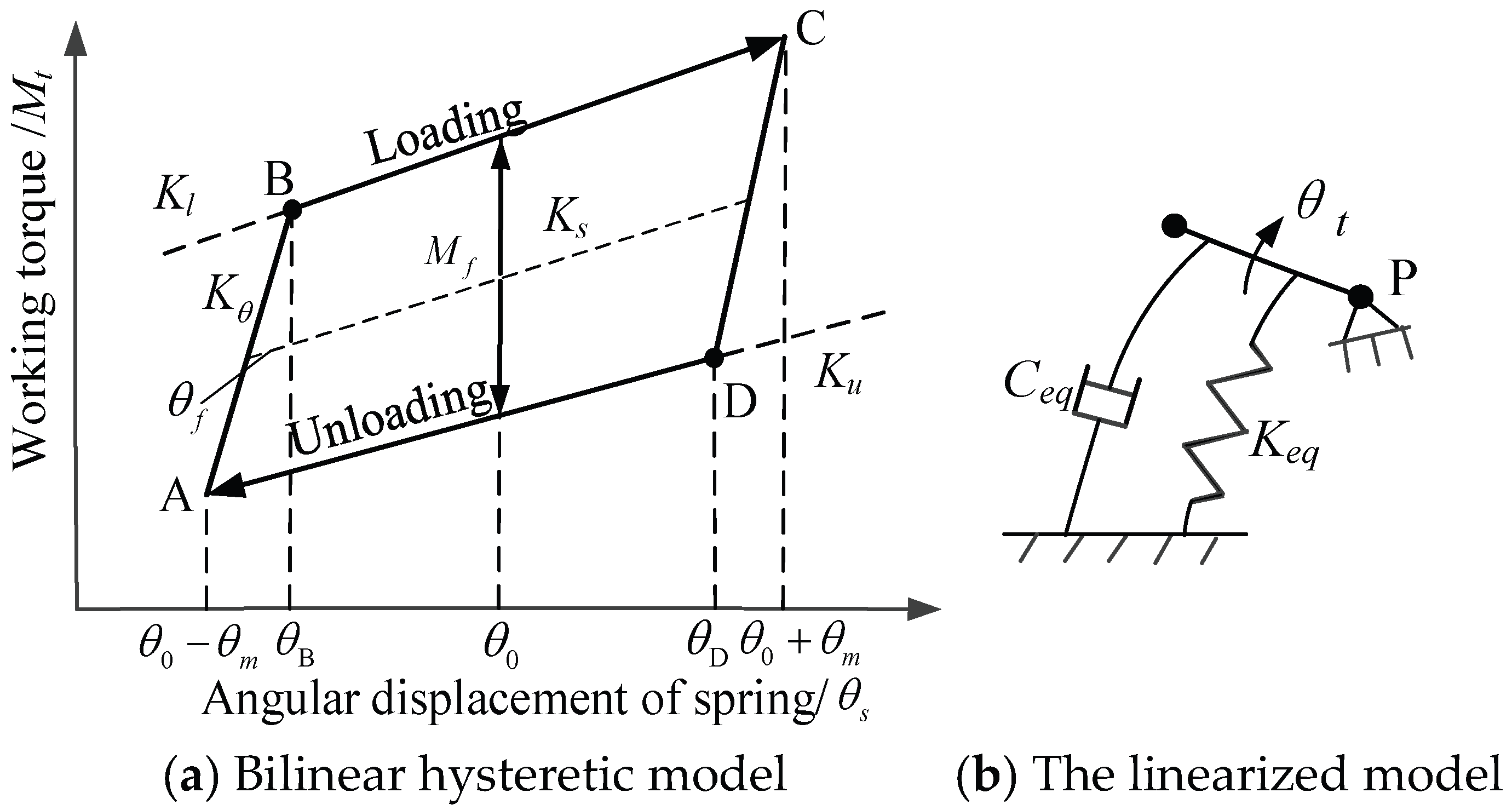
2.1.2. Hysteretic Model of the Tensioner
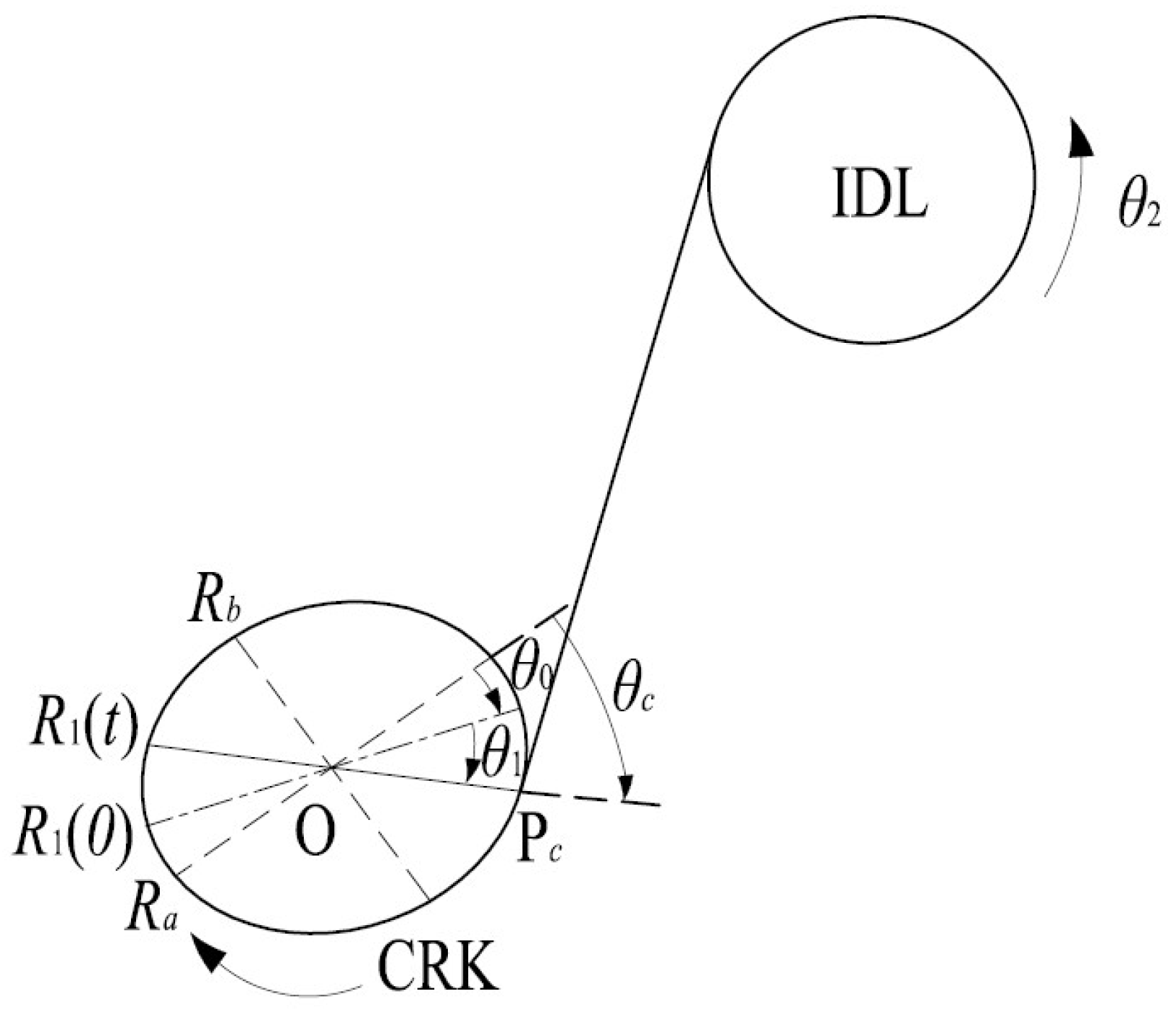
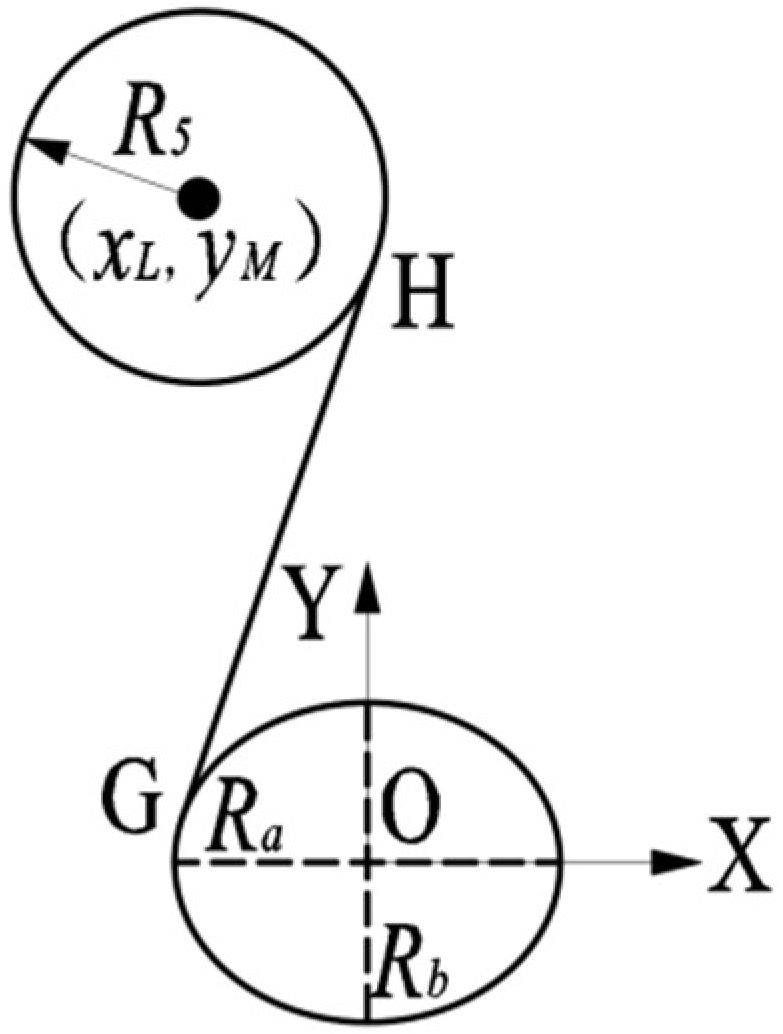
2.2. Method for Calculating Tangent Point and Tangent Length of Rotating Elliptical Pulley
2.2.1. The Definition and Parameters of Elliptical Pulley
2.2.2. Method for Calculating Tangent Points Between Elliptical Pulley and Circular Pulley
2.2.3. Method for Calculating Arc Length of Elliptical Pulley in Any Phase and Rotational Angle
2.3. Vibration Response Solution of Belt Drive System
3. Analysis of Dynamic Performance of System with Elliptical Pulley
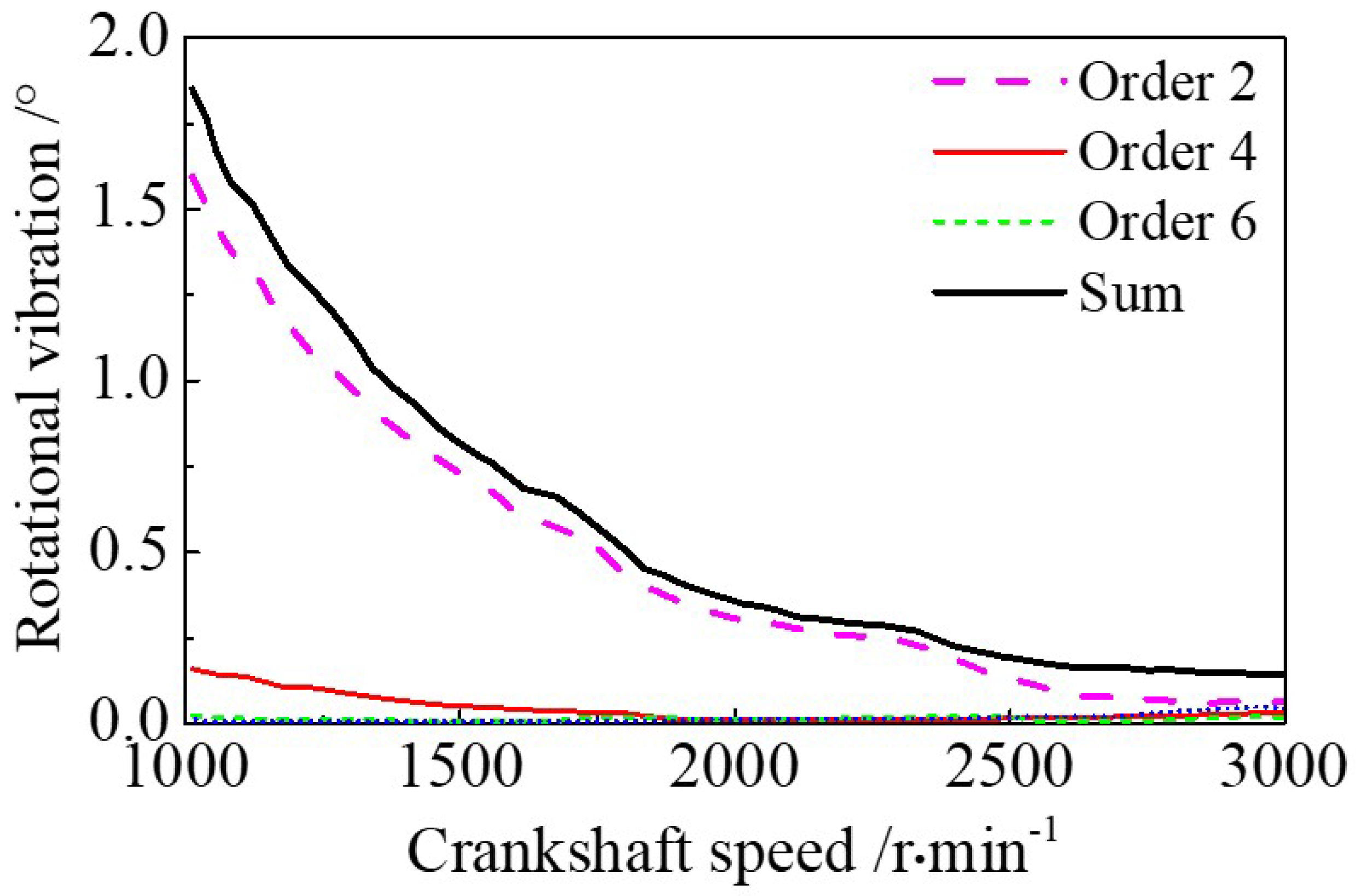
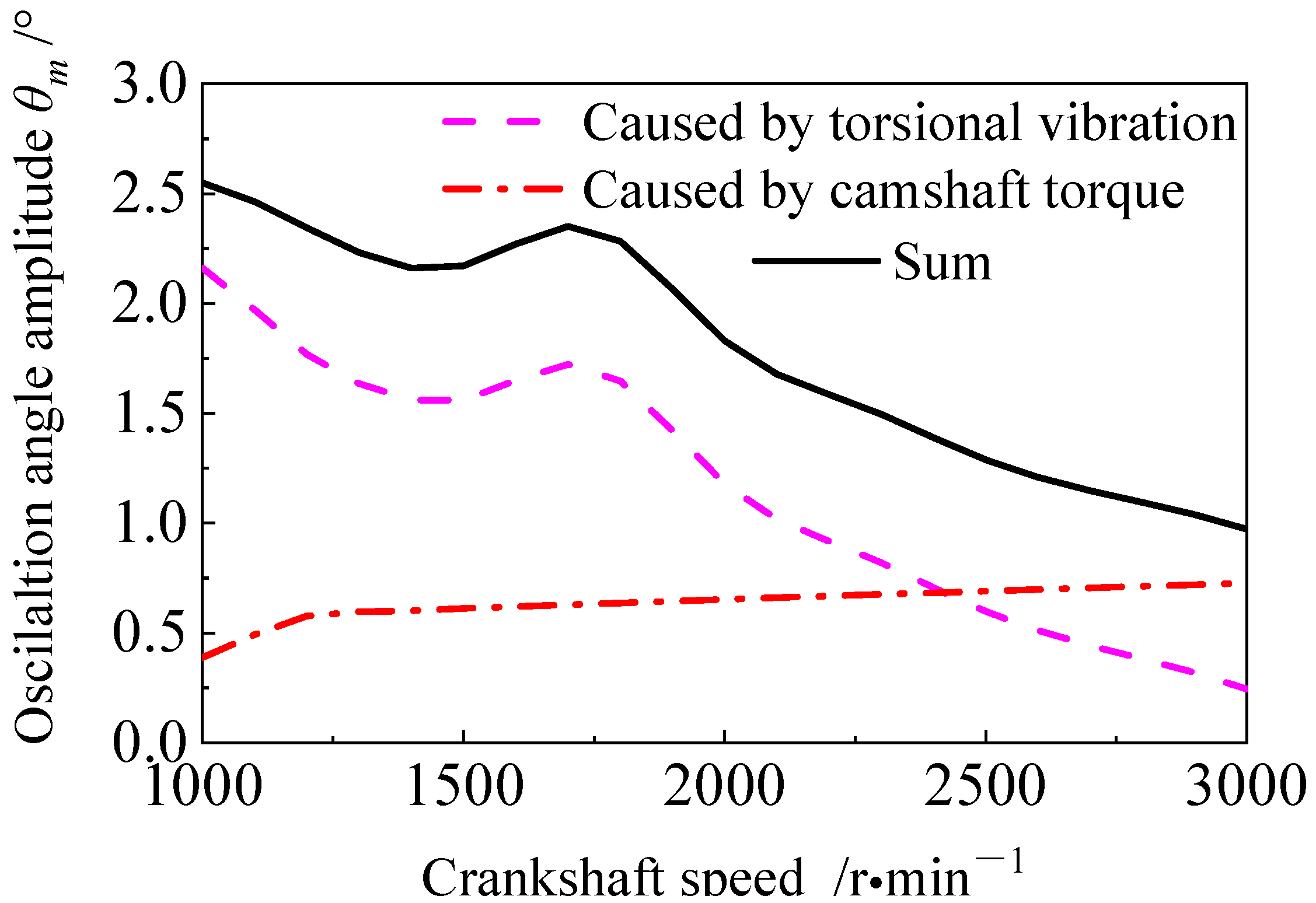
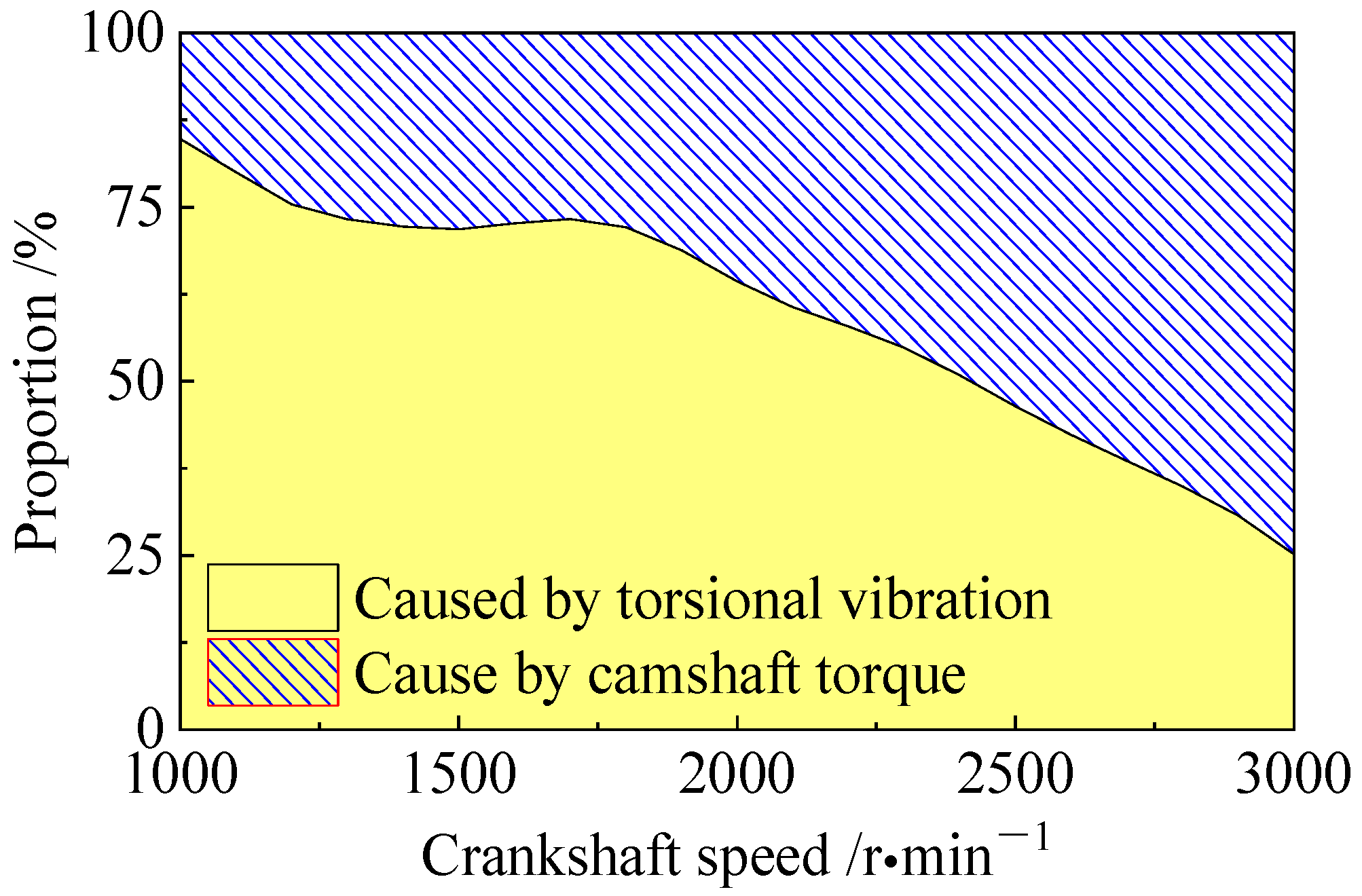
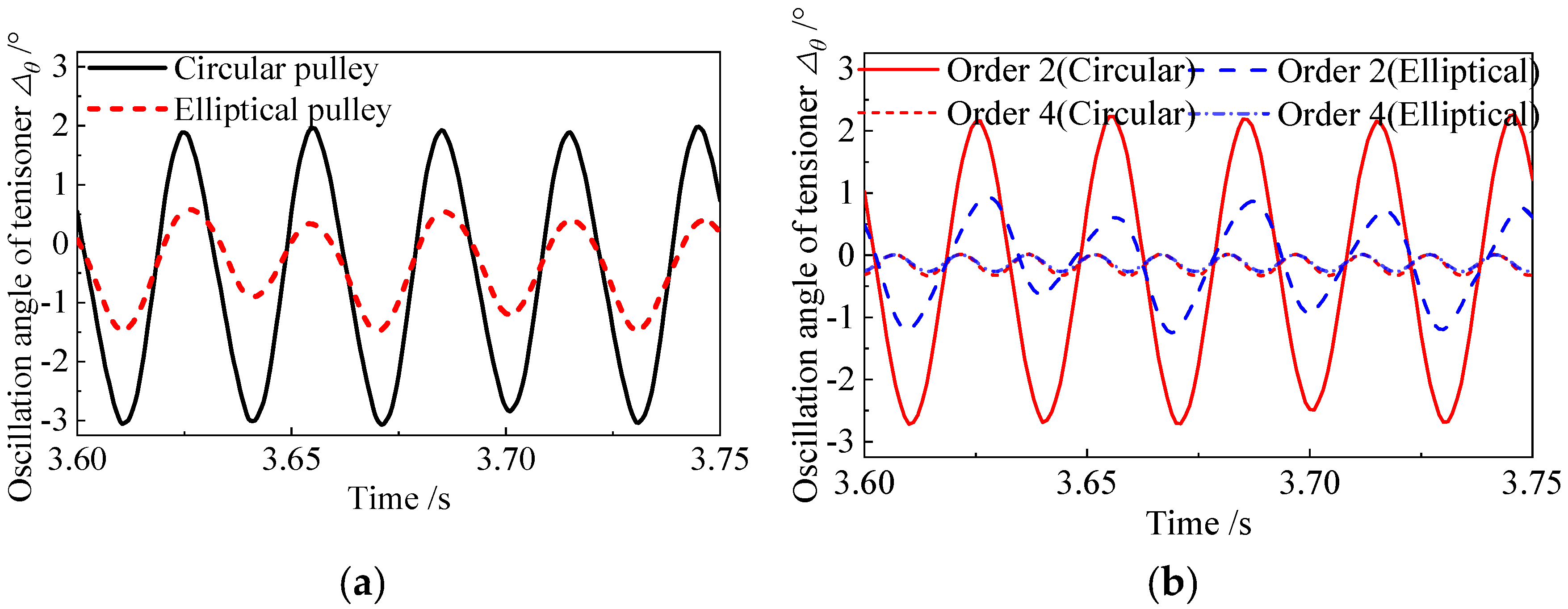
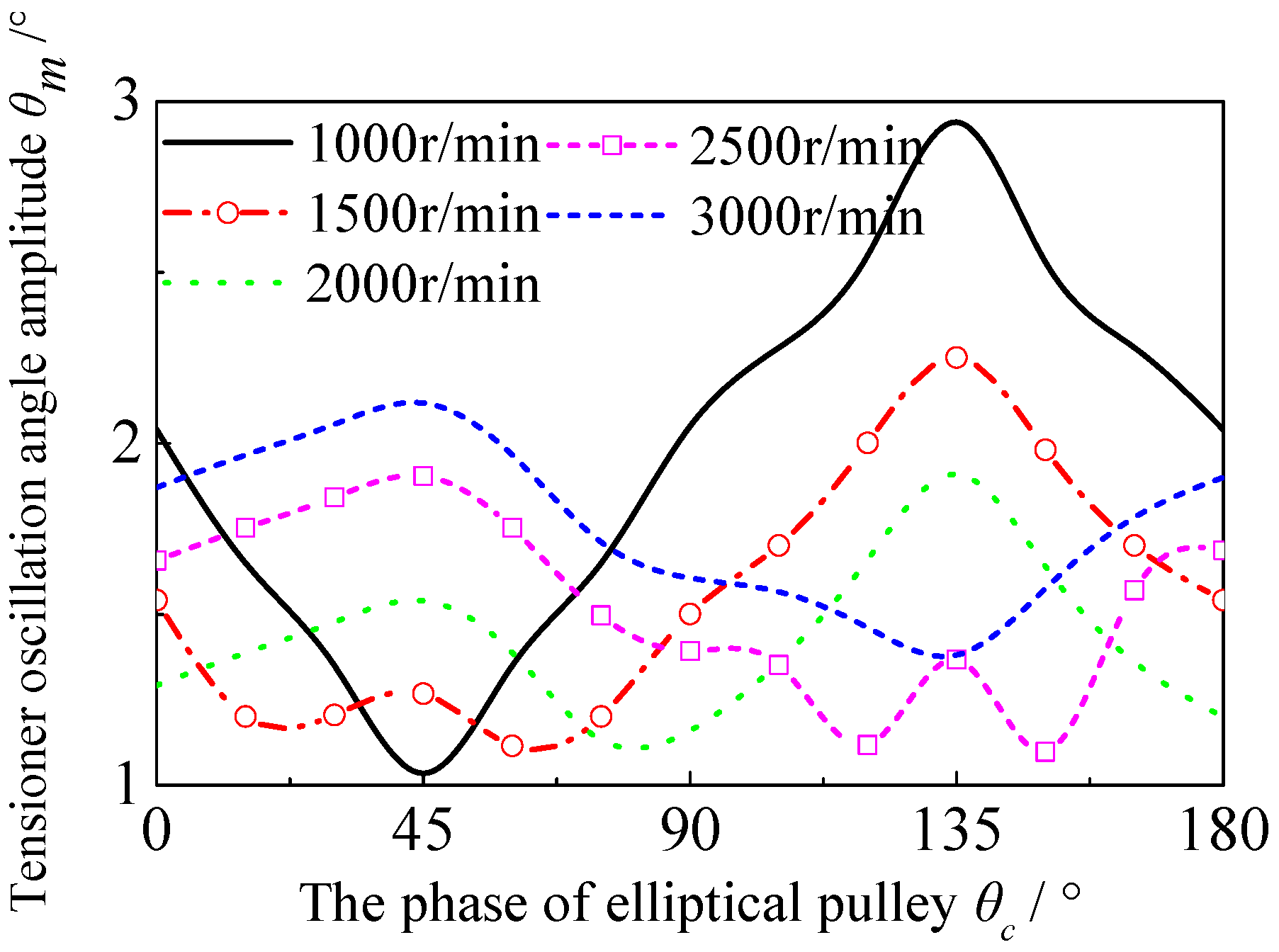
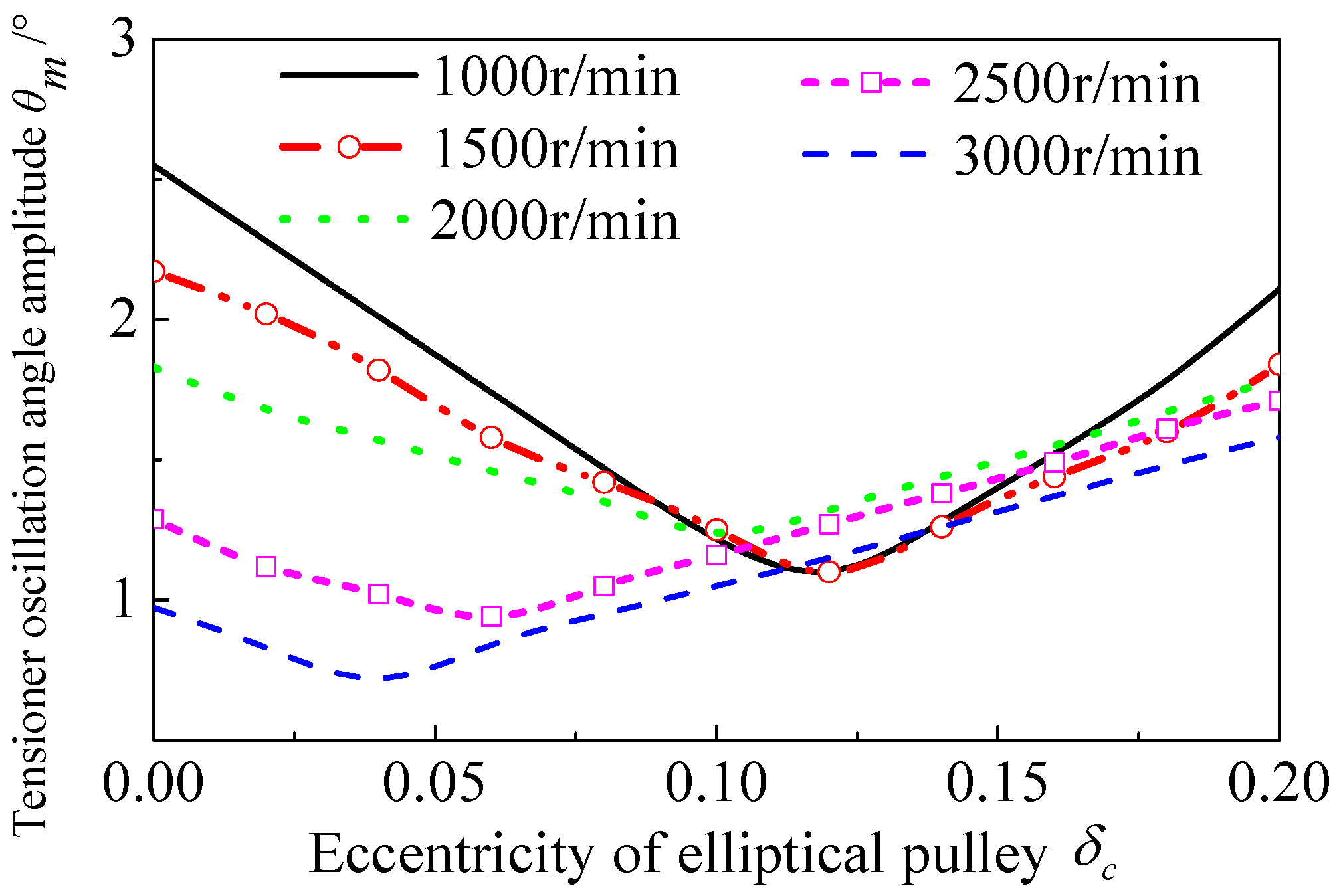
3.1. The Component Analysis of Oscillation Angle Amplitude of Tensioning Arm
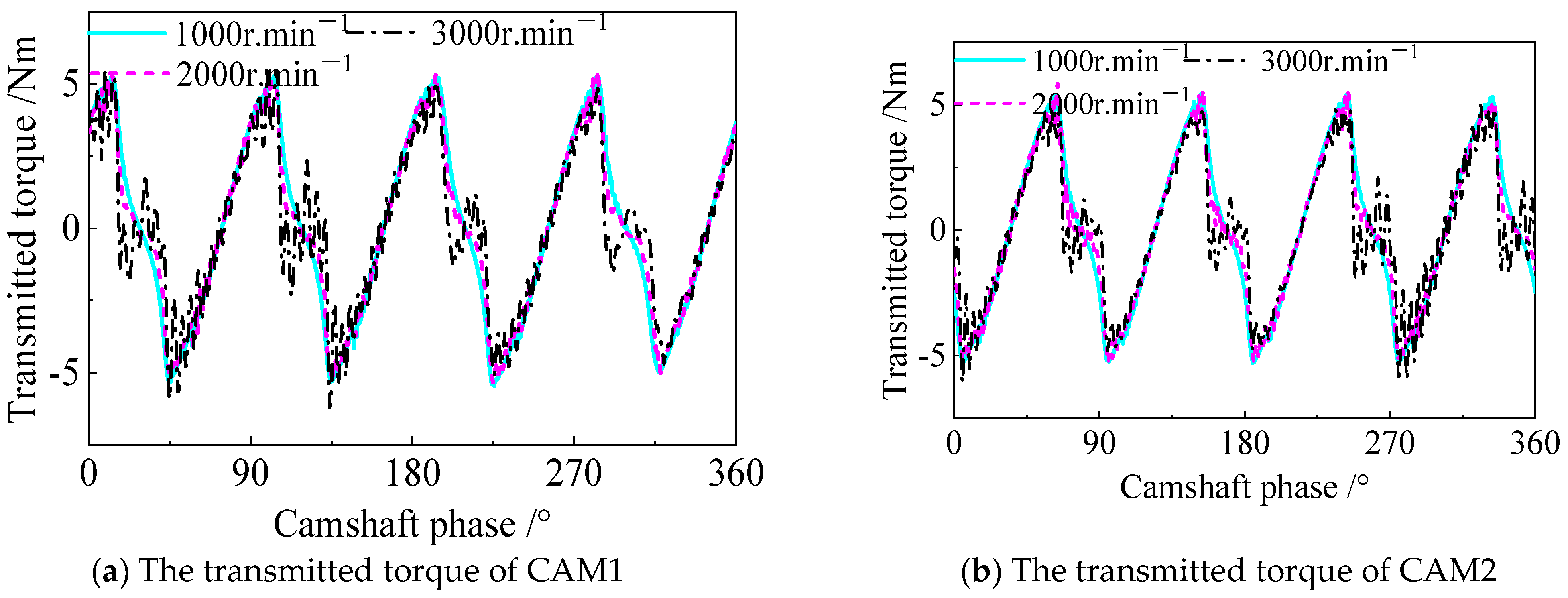
3.2. The Analysis Results of System Dynamic Response at the Typical Speed
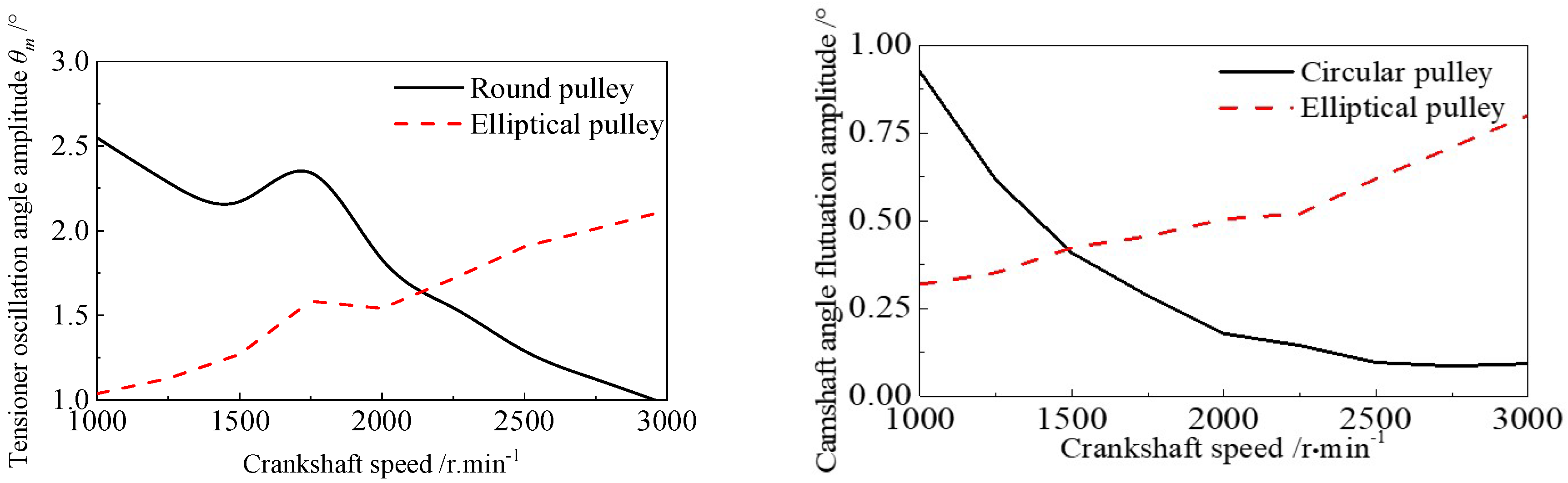
3.3. The Analysis Results of System Dynamic Response Versus Different Speeds
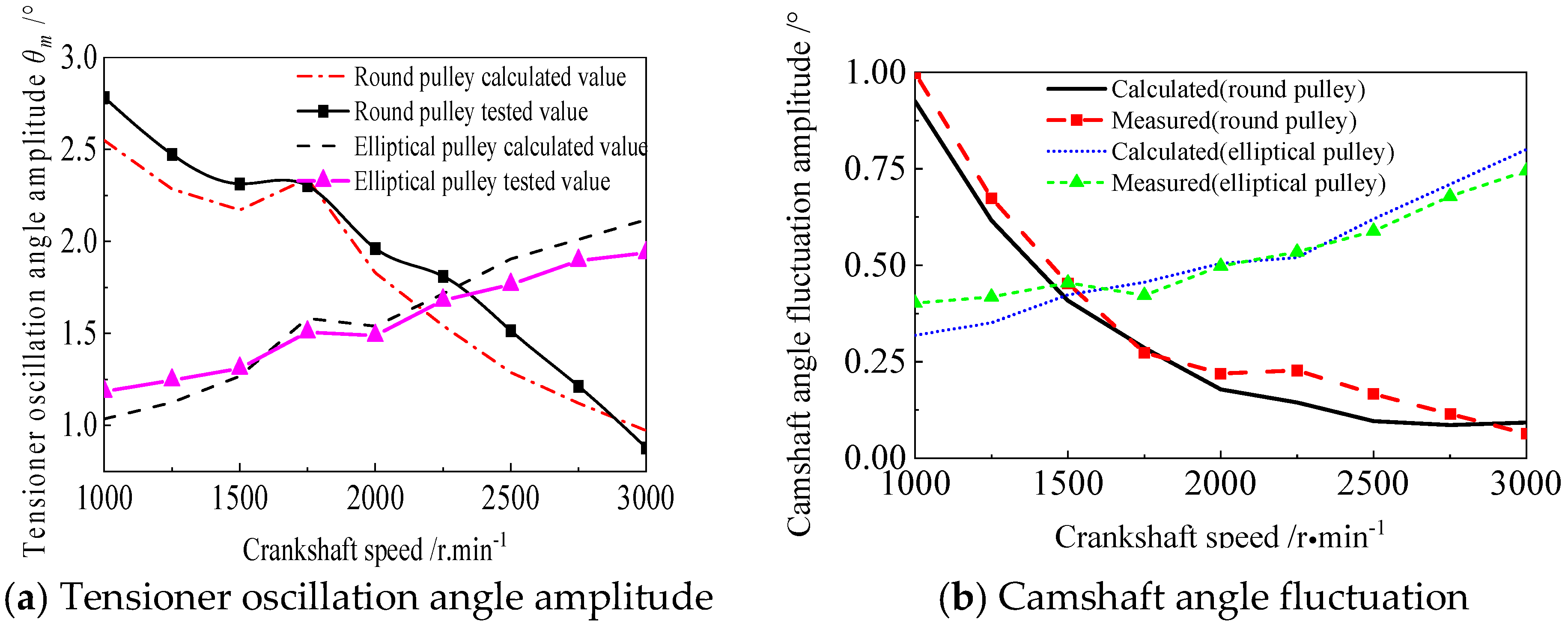
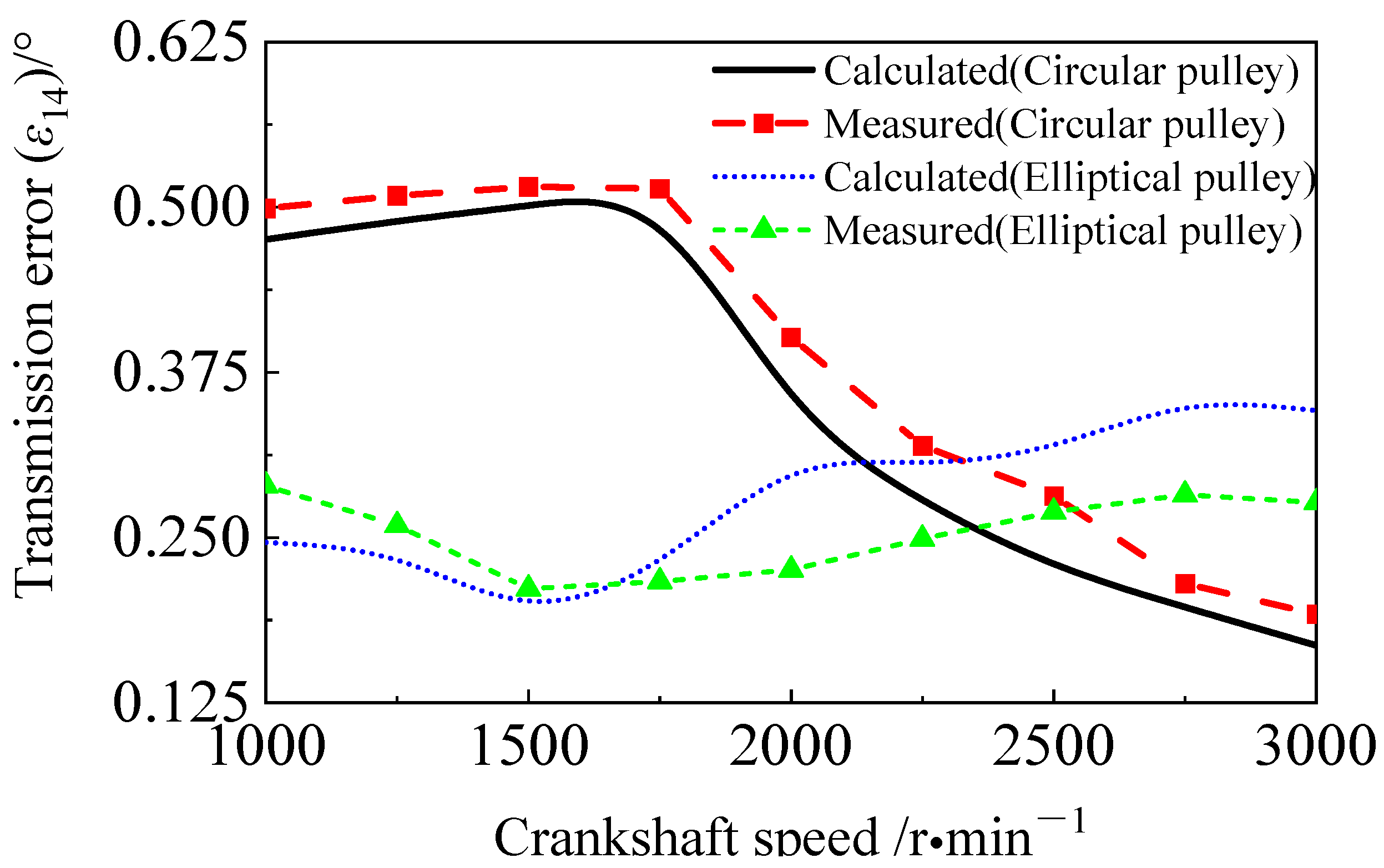
4. System Vibration Response Test and Verification of the Method
4.1. Test Rig for Dynamic Response of System
4.2. Verification for Dynamic Response of System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| (xp, yp) | Pivot position | (−7.976, 159.114) | mm |
| Tensioning arm’s length | 5 | mm | |
| Angular displacement of the tensioning arm in the initial equilibrium position | 75.82 | ° | |
| Zero torque angular displacement of tensioning arm | 0.80 | ° | |
| Moment of inertial for the tensioning arm turning around the pivot | 7.9 × 10−6 | kg·m2 |
| Type | (mm) | (mm) | (kg·m2) | (Nms/°) |
|---|---|---|---|---|
| CRK | (0, 0) | 28.803 (Circular) | 0.0276 | 0.0001 |
| CAM1 | (55.40, 321.25) | 57.606 | 0.002 | 0.0001 |
| CAM2 | (−62.50, 321.25) | 57.606 | 0.002 | 0.0001 |
| TEN | - | 32.700 | 0.000417 | 0.0001 |
| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| Elasticity modulus | 5107 | MPa | |
| The belt pretension | 215 | N | |
| Angle between belt tensions and | 162.81 | ° | |
| Angle from the fourth belt span to the negative X-axis in anticlockwise orientation | 220.67 | ° | |
| Angle from the fifth belt span to the negative X-axis in the anticlockwise orientation | 110.96 | ° |
| Symbol | Parameter | Measurement | Unit |
|---|---|---|---|
| Loading stiffness | 0.0218 | Nm/° | |
| Unloading stiffness | 0.0133 | Nm/° | |
| Spring stiffness | 0.00165 | ||
| Lag stiffness | 0.612 | Nm/° | |
| Lag angle | 0.518 | ° | |
| Friction torque | 0.317 | Nm |
References
- Long, S.; Zhao, X.; Shangguan, W.B.; Zhu, W. Modeling and Validation of Dynamic Performances of Timing Belt Driving Systems. Mech. Syst. Signal Process. 2020, 144, 106910. [Google Scholar] [CrossRef]
- Long, S.; Huang, W.; Wang, J.; Liu, J.; Gu, Y.; Wang, Z. A Fixed-Time Consensus Control with Prescribed Performance for Multi-Agent Systems Under Full-State Constraints. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6398–6407. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Chen, C.L.P.; Liu, Z.; Wu, W. Adaptive PI Event-Triggered Control for MIMO Nonlinear Systems with Input Delay. Inf. Sci. 2024, 677, 120817. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Wu, Y.; Liu, Z.; Chen, K.; Chen, C.L.P. Fixed-Time Formation Control for Uncertain Nonlinear Multi-Agent Systems with Time-Varying Actuator Failures. IEEE Trans. Fuzzy Syst. 2024, 32, 1965–1977. [Google Scholar] [CrossRef]
- Shangguan, W.B.; Zeng, X. Modeling and validation of rotational vibration responses for accessory drive system-Part II: Simulations and Analyses. ASME J. Vib. Acoust. 2013, 135, 031003. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, W.; Fan, W. Dynamics modeling, simulation and experiment of power transmission belt drives: A systematic review. J. Sound Vib. 2020, 491, 115759. [Google Scholar] [CrossRef]
- Liu, X.; Tan, J.; Long, S. Multi-axis fatigue load spectrum editing for automotive components using generalized S-transform. Int. J. Fatigue 2024, 188, 108503. [Google Scholar] [CrossRef]
- Ding, H.; Li, D. Static and dynamic behaviors of belt-drive dynamic systems with a one-way clutch. Nonlinear Dyn. 2014, 78, 1553–1575. [Google Scholar] [CrossRef]
- Bastien, J.; Michon, G.; Manin, L.; Dufour, R. An analysis of the modified Dahl and Masing models: Application to a belt tensioner. J. Sound Vib. 2007, 302, 841–864. [Google Scholar] [CrossRef]
- Wan, J.; Gong, Q.; Huang, K.; Liu, Z.; Chen, C.L.P.; Liu, J. Event-Triggered Prescribed Settling Time Consensus Compensation Control for a Class of Uncertain Nonlinear Systems with Actuator Failures. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5590–5600. [Google Scholar]
- Zhu, F.; Parker, R.G. Non-linear dynamics of a one-way clutch in belt–pulley systems. J. Sound Vib. 2005, 279, 285–308. [Google Scholar] [CrossRef]
- Zhu, F.; Parker, R.G. Influence of Tensioner Dry Friction on the Vibration of Belt Drives With Belt Bending Stiffness. ASME J. Vib. Acoust. 2008, 130, 1161–1171. [Google Scholar] [CrossRef]
- Ludovico, D.; Guardiani, P.; Lasagni, F.; Lee, J.; Cannella, F.; Caldwell, D.G. Design of Non-Circular Pulleys for Torque Generation: A Convex Optimisation Approach. IEEE Robot. Autom. Lett. 2021, 6, 958–965. [Google Scholar] [CrossRef]
- Cheng, G.; Zu, J.W. Nonstick and stick-slip motion of a coulomb-damped belt drive system subjected to multifrequency excitations. ASME J. Appl. Mech. 2003, 70, 871–884. [Google Scholar] [CrossRef]
- Long, S.; Zhao, X.; Shangguan, W.B. Method for estimating vibration responses of belt drive systems with a nonlinear tensioner. Nonlinear Dyn. 2020, 100, 2315–2335. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, Y.; Zhu, W. Modification of natural frequencies of an automotive belt drive system based on eigen-sensitivity analysis of its configuration parameters. Eur. J. Mech.-A/Solids 2018, 67, 137–156. [Google Scholar] [CrossRef]
- Hou, Z.; Wang, X.; Lao, Y. Frequency Sensitivity Analysis of Multi-ribbed Belt Drive System. J. Mech. Eng. 2009, 45, 235–239. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, Y.; Zhu, W.; Pi, Y. Optimal design of an autotensioner in an automotive belt drive system via a dynamic adaptive PSO-GA. ASME J. Mech. Des. 2017, 139, 093302. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, Y.; Zhu, W.; Fan, W.; Zhou, B.W. Multi-objective design optimization of an engine accessory drive system with a robustness analysis. Appl. Math. Model. 2020, 77, 1564–1581. [Google Scholar] [CrossRef]
- Coppola, G.; Boyes, A.M.; Spicer, G. Synchronous drive apparatus with adjustable non-circular drive elements. U.S. Patent 10,767,516, 8 September 2020. [Google Scholar]
- Wölfle, F.; Kaufhold, T.; Hagemann, K.; Maier, S. Simulationsprogramm zur Vorhersage der dynamischen Vorgänge in Nebenaggregate-Antrieben mit Keilrippenriemen. MTZ-Mot. Z. 2003, 64, 414–421. (In German) [Google Scholar] [CrossRef]
- Wang, X.; Zhu, W. Dynamic analysis of an automotive belt-drive system with a noncircular sprocket by a modified incremental harmonic balance method. ASME J. Vib. Acoust. 2017, 139, 011009. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, W.; Hu, Y. Periodic response of a timing belt drive system with an oval cogged pulley and optimal design of the pitch profile for vibration reduction. ASME J. Comput. Nonlinear Dyn. 2018, 13, 011014. [Google Scholar] [CrossRef]
- Li, J. Eccentric sprocket technology applied to engine timing system. Intern. Combust. Engine Power Plant 2018, 35, 39–44. (In Chinese) [Google Scholar]
- Liang, S.; Li, Z.; Li, Y.; Hu, J.; Yang, W.; Lan, J.; Wang, R. Non circle belt pulley dynamic calculate by EXCITE_TD. Automob. Appl. Technol. 2017, 2, 29–31. (In Chinese) [Google Scholar]
- Chen, J.; Ye, J.; Wang, Y.; Sun, X.; Xia, X.; He, X. Design, modeling and experiment of a novel synchronous belt drive with noncircular pulleys. Iran. J. Sci. Technol. Trans. Mech. Eng. 2020, 44, 533–542. [Google Scholar] [CrossRef]
- Long, S.; Wang, W.; Yue, X.; Zhang, C. Dynamic modeling of the belt drive system with an equivalent tensioner model. J. Vib. Eng. Technol. 2022, 10, 511–525. [Google Scholar] [CrossRef]
- Barnard, R.W.; Pearce, K.; Richards, K.C. A Monotonicity Property Involving 3 F 2 and Comparisons of the Classical Approximations of Elliptical Arc Length. SIAM J. Math. Anal. 2000, 32, 403–419. [Google Scholar] [CrossRef]
- Feng, Y. Series expansion and approximate treatment for elliptic arc length. Coll. Math. 2018, 195, 110–114. (In Chinese) [Google Scholar]









| Order | (N)/° | Phase (N)/° |
|---|---|---|
| 2 | 1.60 | 45.18 |
| 4 | 0.16 | −22.48 |
| 6 | 0.02 | −11.56 |
| Symbol | Description |
|---|---|
| Case I | The viscous damping decreases by a value of 20%. Here, the loading and unloading directions of the tensioner are each reduced by 10%. |
| Case II | The belt tension decreases by a value of 20%. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, S.; Zhu, Y.; Zhou, Z.; Chen, F.; Li, Z. A Rotational Order Vibration Reduction Method Using a Regular Non-Circular Pulley. Actuators 2025, 14, 371. https://doi.org/10.3390/act14080371
Long S, Zhu Y, Zhou Z, Chen F, Li Z. A Rotational Order Vibration Reduction Method Using a Regular Non-Circular Pulley. Actuators. 2025; 14(8):371. https://doi.org/10.3390/act14080371
Chicago/Turabian StyleLong, Shangbin, Yu Zhu, Zhihong Zhou, Fangrui Chen, and Zisheng Li. 2025. "A Rotational Order Vibration Reduction Method Using a Regular Non-Circular Pulley" Actuators 14, no. 8: 371. https://doi.org/10.3390/act14080371
APA StyleLong, S., Zhu, Y., Zhou, Z., Chen, F., & Li, Z. (2025). A Rotational Order Vibration Reduction Method Using a Regular Non-Circular Pulley. Actuators, 14(8), 371. https://doi.org/10.3390/act14080371






