Robust Attitude Stabilization of Rigid Bodies Based on Control Lyapunov Function: Experimental Verification on a Quadrotor Testbed
Abstract
1. Introduction
- We construct a quadrotor testbed integrating a self-developed flight controller to implement the proposed controller.
- Through real-time flight experiments, we confirm that the proposed controller can achieve attitude stabilization.
- To validate the importance of disturbance attenuation, we also conduct comparative experiments using a PID-type controller and a non-robust (i.e., without disturbance attenuation) controller.
Notation
- A continuous function is said to belong to class () if it is strictly increasing and . A function is said to belong to class () if and .
- A continuous function is said to belong to class () if, for each fixed s, the mapping belongs to class with respect to r, and for each fixed r, the mapping is decreasing with respect to s and .
2. Input-to-State Stability (ISS) and ISS Control Lyapunov Function (ISS-CLF) for Nonlinear Systems [19]
- (A1)
- V is proper, i.e., the sublevel set is compact for every ;
- (A2)
- V is positive definite, i.e., and ;
- (A3)
- there exist a class function ρ such that
3. Problem Formulation
4. Controller Design [21]
4.1. ISS-CLF Design for System (15)
4.2. Extension to the Robust Adaptive Controller
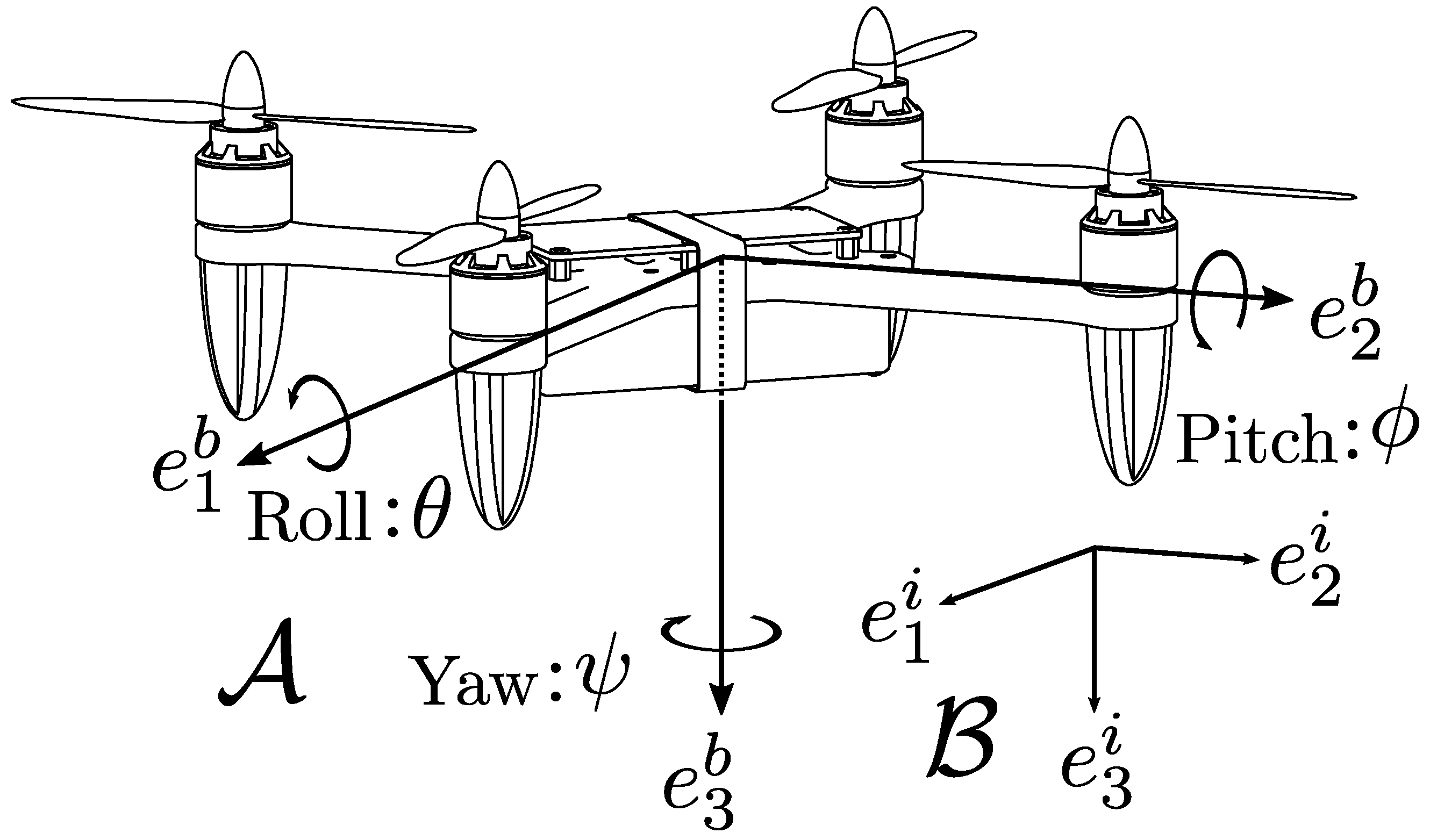
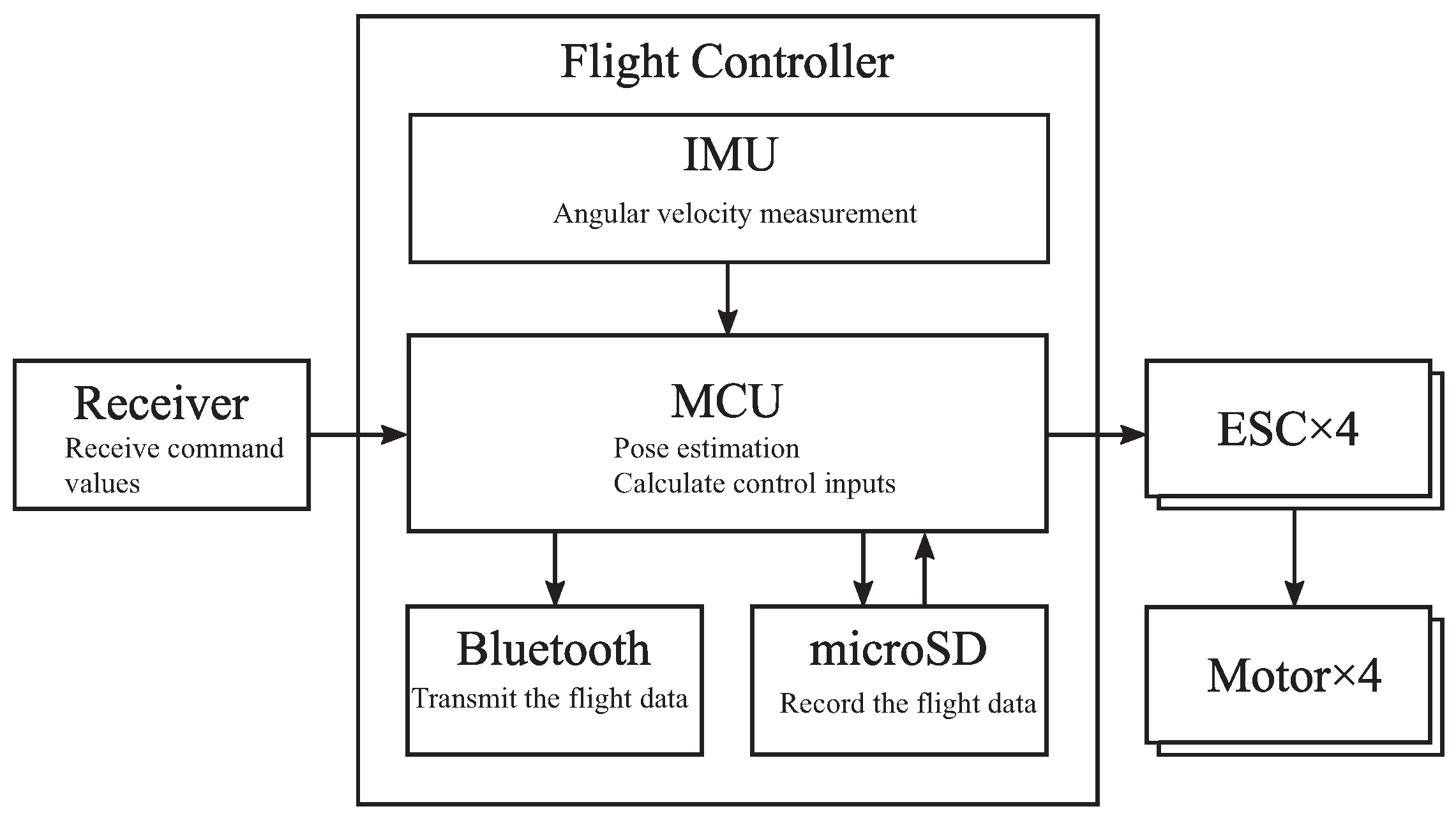
5. Development of a Quadrotor Testbed
5.1. Configuration of the Quadcopter
5.2. Conversion of Input Torque to a PWM Signal
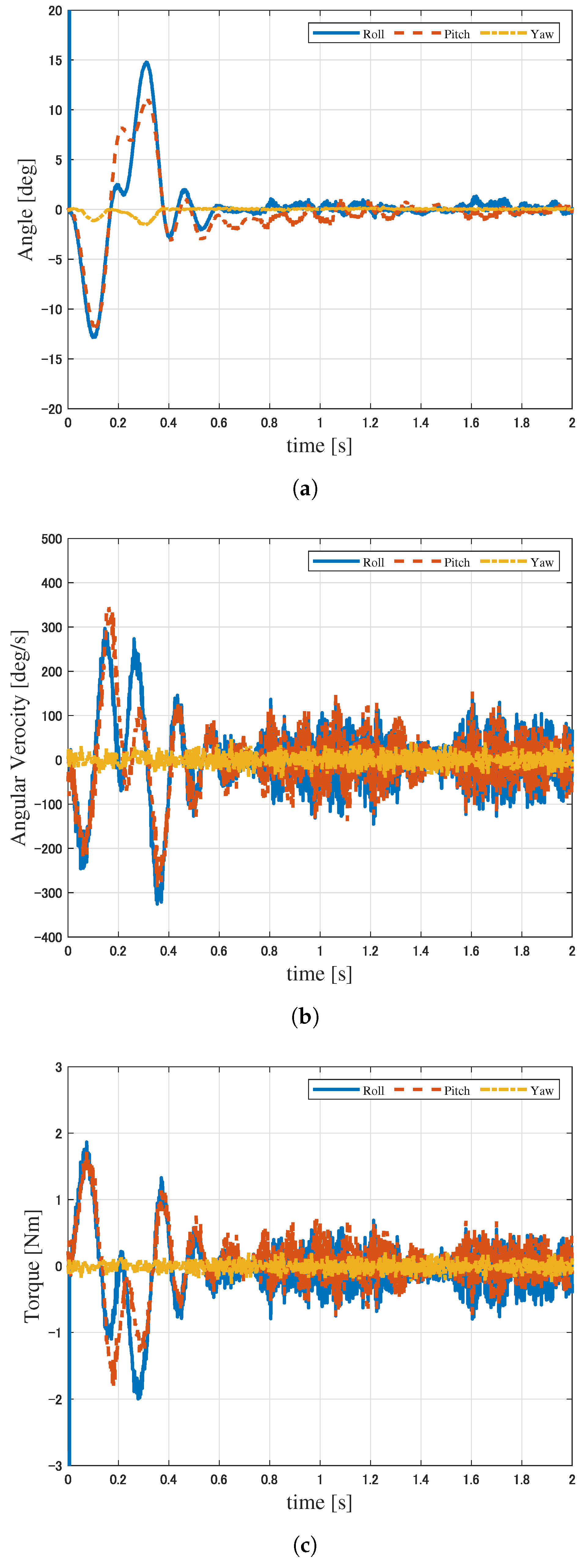
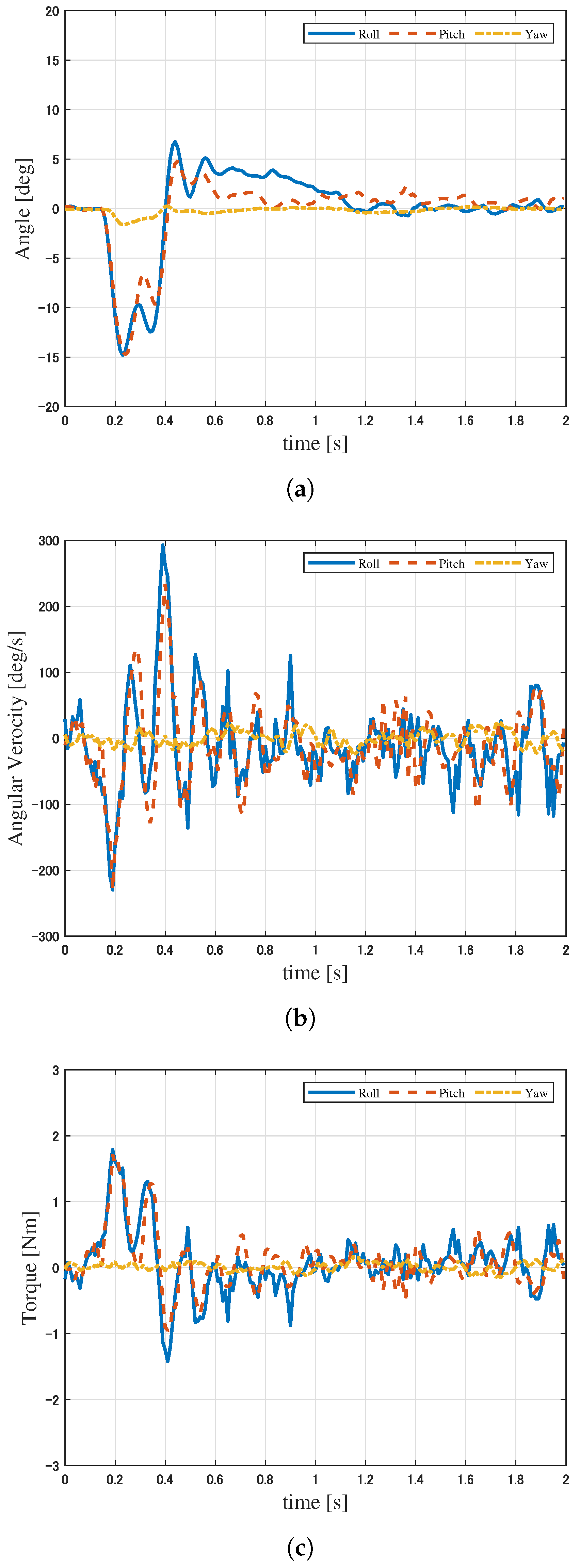
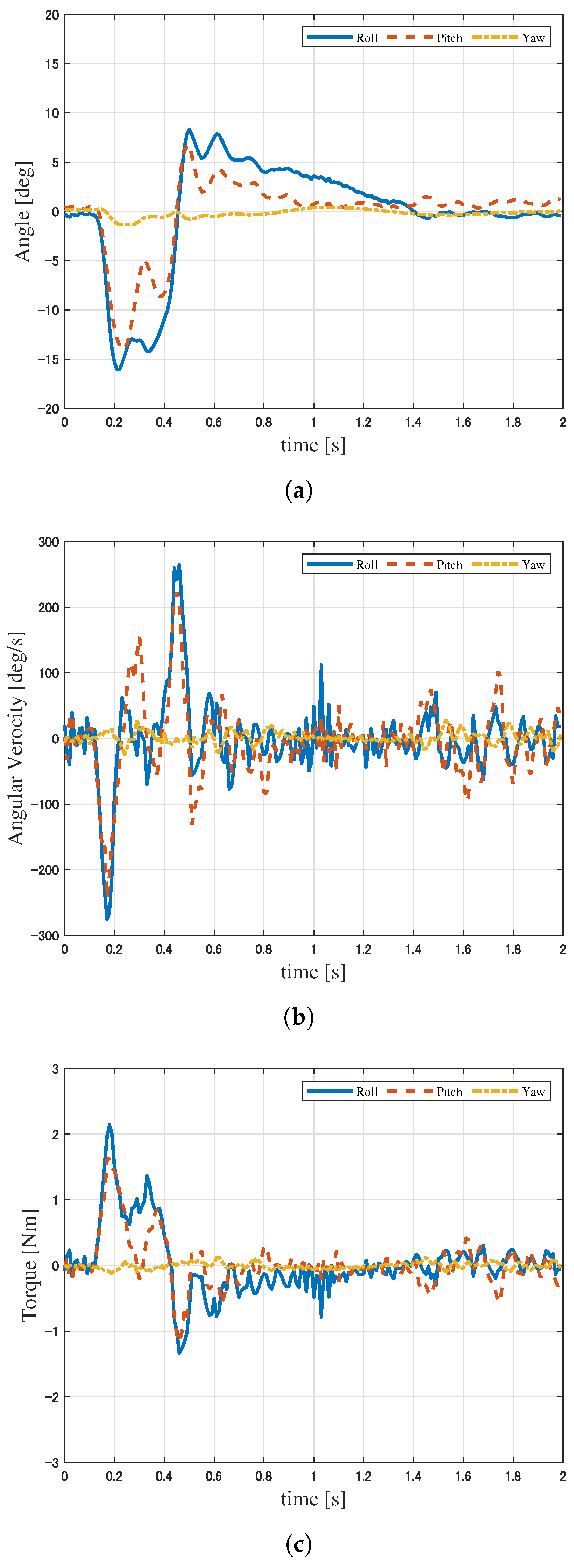
6. Experimental Verification
6.1. Experimental Conditions
- Experiment 1.
- Comparison with a PID-type controller.
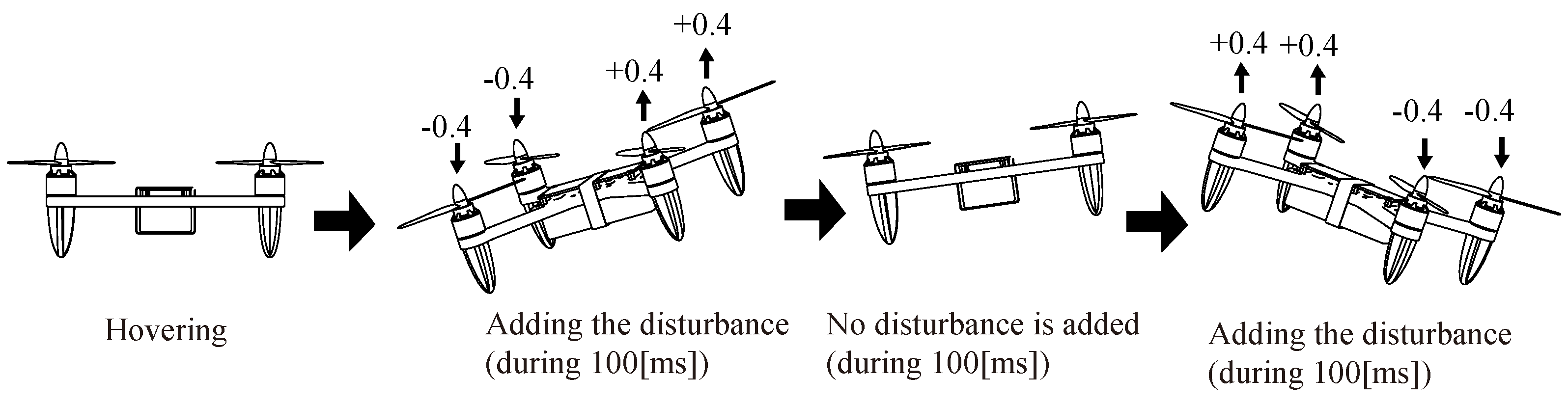
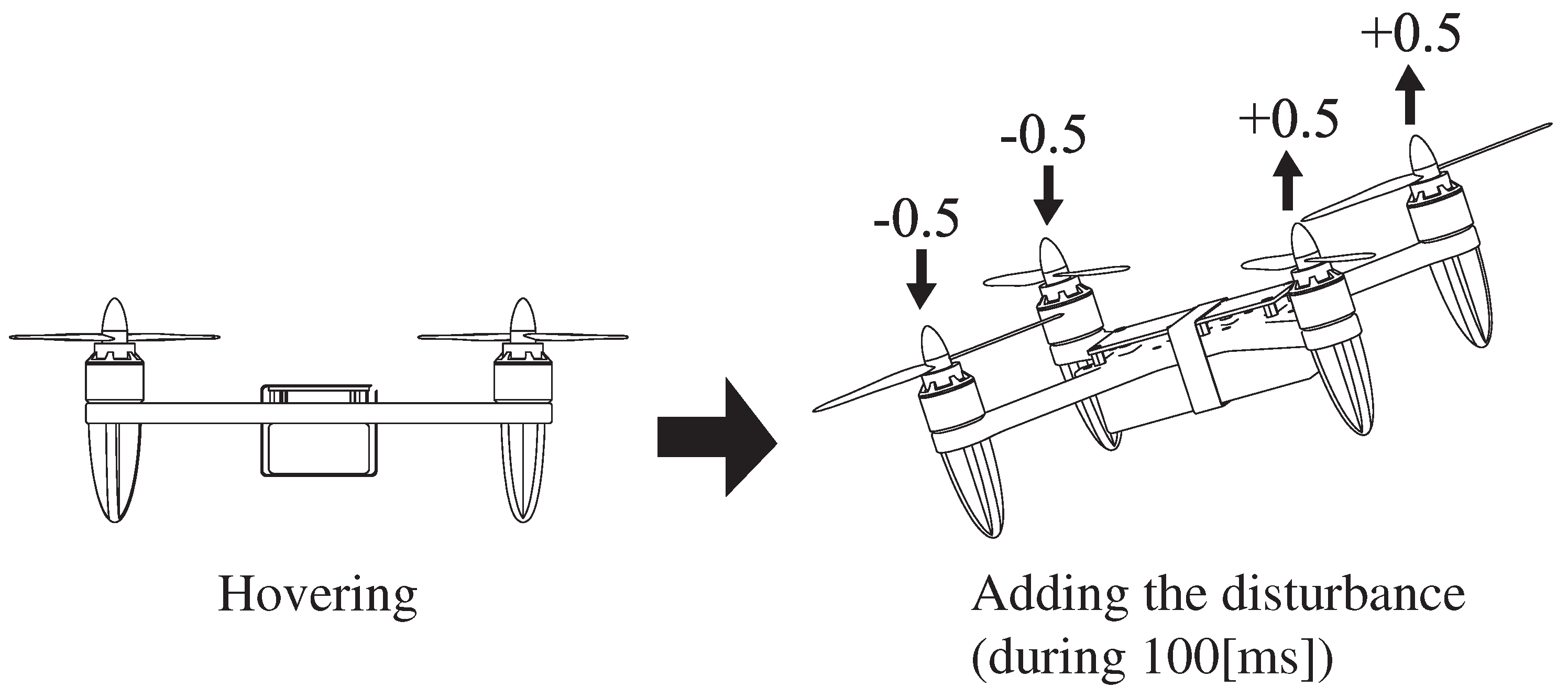
- Experiment 2.
- Evaluation of disturbance attenuation performance.
6.2. Results of Experiment 1
6.3. Results of Experiment 2
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nonami, K. Drone Technology, Cutting-Edge Drone Business, and Future Prospects. J. Robot. Mechatron. 2016, 28, 262–272. [Google Scholar] [CrossRef]
- Nascimento, T.P.; Saska, M. Position and attitude control of multi-rotor aerial vehicles: A survey. Annu. Rev. Control 2019, 48, 129–146. [Google Scholar] [CrossRef]
- Marshall, J.A.; Sun, W.; L’Afflitto, A. A survey of guidance, navigation, and control systems for autonomous multi-rotor small unmanned aerial systems. Annu. Rev. Control 2021, 52, 390–427. [Google Scholar] [CrossRef]
- Castillo, A.; Sanz, R.; Garcia, P.; Qiu, W.; Wang, H.; Xu, C. Disturbance observer-based quadrotor attitude tracking control for aggressive maneuvers. Control Eng. Pract. 2019, 82, 14–23. [Google Scholar] [CrossRef]
- Xie, W.; Yu, G.; Cabecinhas, D.; Cunha, R.; Silvestre, C. Global Saturated Tracking Control of a Quadcopter with Experimental Validation. IEEE Control Syst. Lett. 2021, 5, 169–174. [Google Scholar] [CrossRef]
- Azid, S.I.; Kumar, K.; Cirrincione, M.; Fagiolini, A. Robust Motion Control of Nonlinear Quadrotor Model with Wind Disturbance Observer. IEEE Access 2021, 9, 149164–149175. [Google Scholar] [CrossRef]
- Kazim, M.; Azar, A.T.; Koubaa, A.; Zaidi, A. Disturbance-Rejection-Based Optimized Robust Adaptive Controllers for UAVs. IEEE Syst. J. 2021, 15, 3097–3108. [Google Scholar] [CrossRef]
- Wang, F.; Gao, H.; Wang, K.; Zhou, C.; Zong, Q.; Hua, C. Disturbance Observer-Based Finite-Time Control Design for a Quadrotor UAV with External Disturbance. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 834–847. [Google Scholar] [CrossRef]
- Mechali, O.; Xu, L.; Huang, Y.; Shi, M.; Xie, X. Observer-based fixed-time continuous nonsingular terminal sliding mode control of quadrotor aircraft under uncertainties and disturbances for robust trajectory tracking: Theory and experiment. Control Eng. Pract. 2021, 111, 104806. [Google Scholar] [CrossRef]
- Shao, X.; Sun, G.; Yao, W.; Liu, J.; Wu, L. Adaptive Sliding Mode Control for Quadrotor UAVs with Input Saturation. IEEE/ASME Trans. Mechatron. 2022, 27, 1498–1509. [Google Scholar] [CrossRef]
- Lian, S.; Meng, W.; Lin, Z.; Shao, J.; Zheng, J.; Li, H. Adaptive Attitude Control of a Quadrotor Using Fast Nonsingular Terminal Sliding Mode. IEEE Trans. Ind. Electron. 2022, 6, 3769–3776. [Google Scholar] [CrossRef]
- Torrente, G.; Kaufmann, E.; Föhn, P.; Scaramuzza, D. Data-Driven MPC for Quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 3769–3776. [Google Scholar] [CrossRef]
- Sun, S.; Romero, A.; Foehn, P.; Kaufmann, E.; Scaramuzza, D. A Comparative Study of Nonlinear MPC and Differential-Flatness-Based Control for Quadrotor Agile Flight. IEEE Trans. Robot. 2022, 38, 3357–3373. [Google Scholar] [CrossRef]
- Xu, Z.; Fan, L.; Qiu, W.; Wen, G.; He, Y. A Robust Disturbance-Rejection Controller Using Model Predictive Control for Quadrotor UAV in Tracking Aggressive Trajectory. Drones 2023, 7, 557. [Google Scholar] [CrossRef]
- Sontag, E.D. A ‘Universal’ Construction of Artstein’s Theorem on Nonlinear Stabilization. Syst. Control Lett. 1989, 13, 117–123. [Google Scholar] [CrossRef]
- Sepulchre, R.; Janković, M.; Kokotović, P.V. Constructive Nonlinear Control; Springer: London, UK, 1997. [Google Scholar]
- Krstić, M.; Kanellakopoulos, I.; Kokotović, P. Nonlinear and Adaptive Control Design; John Wiley and Sons: New York, NY, USA, 1995. [Google Scholar]
- Freeman, R.A.; Kokotović, P. Robust Nonlinear Control Design: State-Space and Lyapunov Techniques; Birkhäuser: Boston, MA, USA, 1996. [Google Scholar]
- Krstić, M.; Deng, H. Stabilization of Nonlinear Uncertain Systems; Springer: London, UK, 1998. [Google Scholar]
- Hatayama, T.; Nakamura, H. Discontinuous Adaptive Control of Attitude of Rigid Body by Using Minimum Projection Method. In Proceedings of the SICE Annual Conference 2014, Sapporo, Japan, 9–12 September 2014; pp. 1424–1429. [Google Scholar]
- Ohno, K.; Satoh, Y.; Nakamura, H.; Kato, K. Disturbance rejection control of rigid body attitude based on nonsmooth control Lyapunov function. In Proceedings of the 44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 2293–2298. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer: London, UK, 2010. [Google Scholar]
- Wie, B. Space Vehicle Dynamics and Control, 2nd ed.; American Institute of Aeronautics: Reston, VA, USA, 2008. [Google Scholar]
- Madgwick, S.O.H. An efficient orientation filter for inertial and inertial/magnetic sensor arrays. Rep. x-io Univ. Bristol (UK) 2010, 25, 763–775. [Google Scholar]
- Jardin, M.R.; Mueller, E.R. Optimized Measurements of UAV Mass Moment of Inertia with a Bifilar Pendulum. J. Aircr. 2009, 46, 763–775. [Google Scholar] [CrossRef]
- Nonami, K.; Kendoul, F.; Suzuki, S.; Wang, W.; Nakazawa, D. Autonomous Flying Robots: Unmanned Aerial Vehicles and Micro Aerial Vehicles; Springer: Tokyo, Japan, 2014. [Google Scholar]




| Parameter | Explanation | Value |
|---|---|---|
| [m] | Arm length | |
| [kg] | Mass of the quadrotor | |
| [] | Roll axis rotational inertia | |
| [] | Pitch axis rotational inertia | |
| [] | Yaw axis rotational inertia | |
| [] | Drag coefficient | |
| [] | Rotational coefficient |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satoh, Y.; Ohno, K. Robust Attitude Stabilization of Rigid Bodies Based on Control Lyapunov Function: Experimental Verification on a Quadrotor Testbed. Actuators 2025, 14, 509. https://doi.org/10.3390/act14100509
Satoh Y, Ohno K. Robust Attitude Stabilization of Rigid Bodies Based on Control Lyapunov Function: Experimental Verification on a Quadrotor Testbed. Actuators. 2025; 14(10):509. https://doi.org/10.3390/act14100509
Chicago/Turabian StyleSatoh, Yasuyuki, and Kota Ohno. 2025. "Robust Attitude Stabilization of Rigid Bodies Based on Control Lyapunov Function: Experimental Verification on a Quadrotor Testbed" Actuators 14, no. 10: 509. https://doi.org/10.3390/act14100509
APA StyleSatoh, Y., & Ohno, K. (2025). Robust Attitude Stabilization of Rigid Bodies Based on Control Lyapunov Function: Experimental Verification on a Quadrotor Testbed. Actuators, 14(10), 509. https://doi.org/10.3390/act14100509






