New Tuning Rules of PI+CI Controllers for First-Order Systems
Abstract
1. Introduction
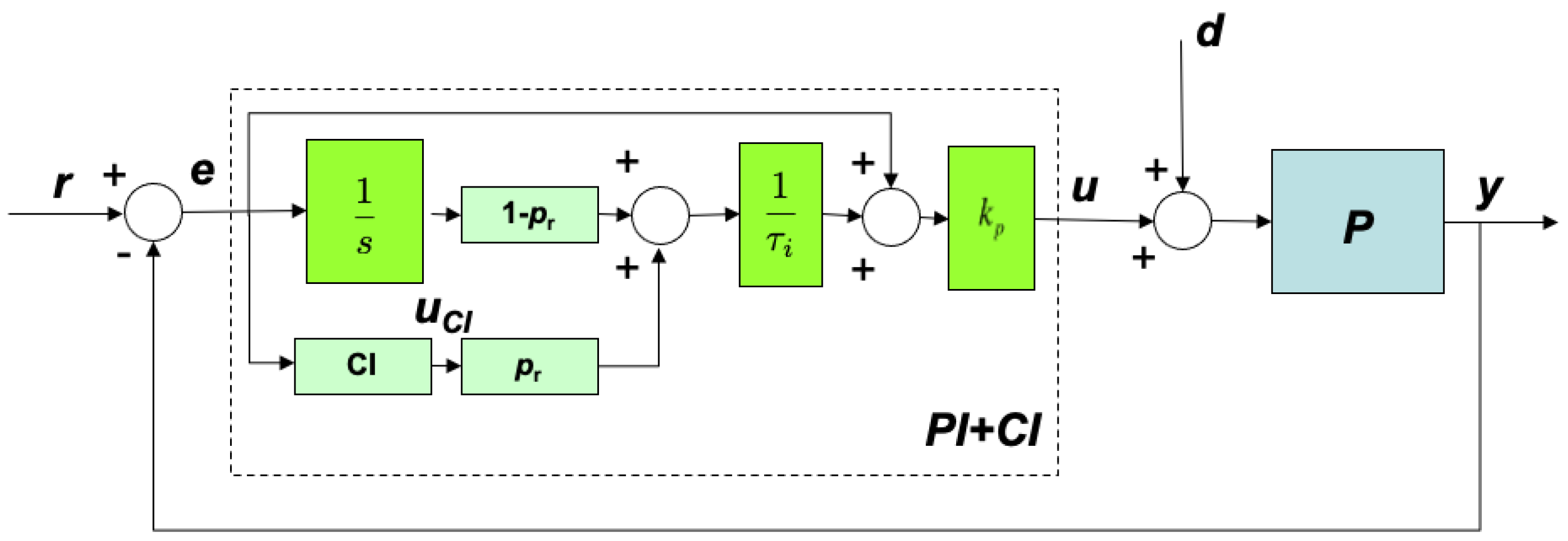
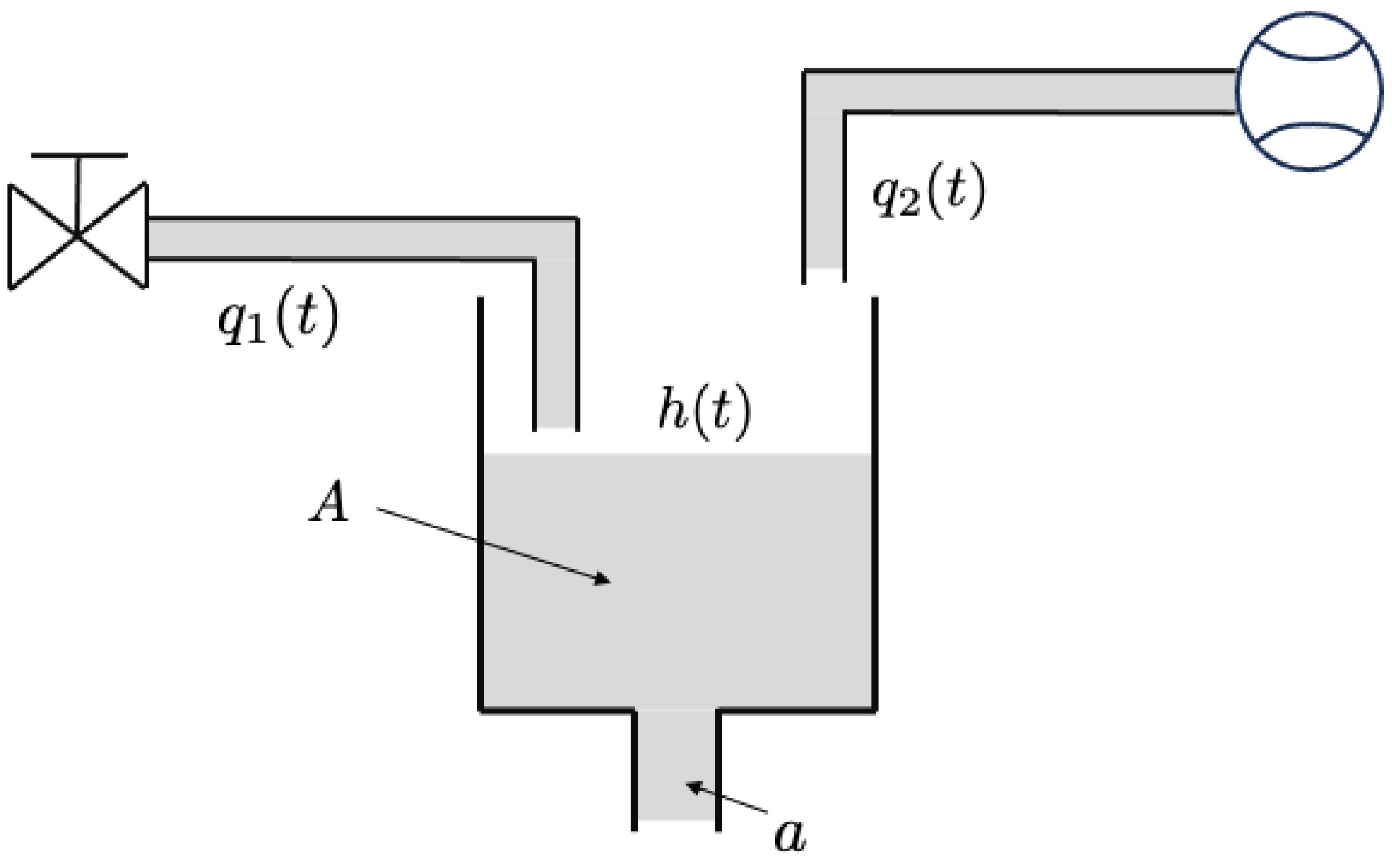
2. Fundamentals of PI+CI Controller
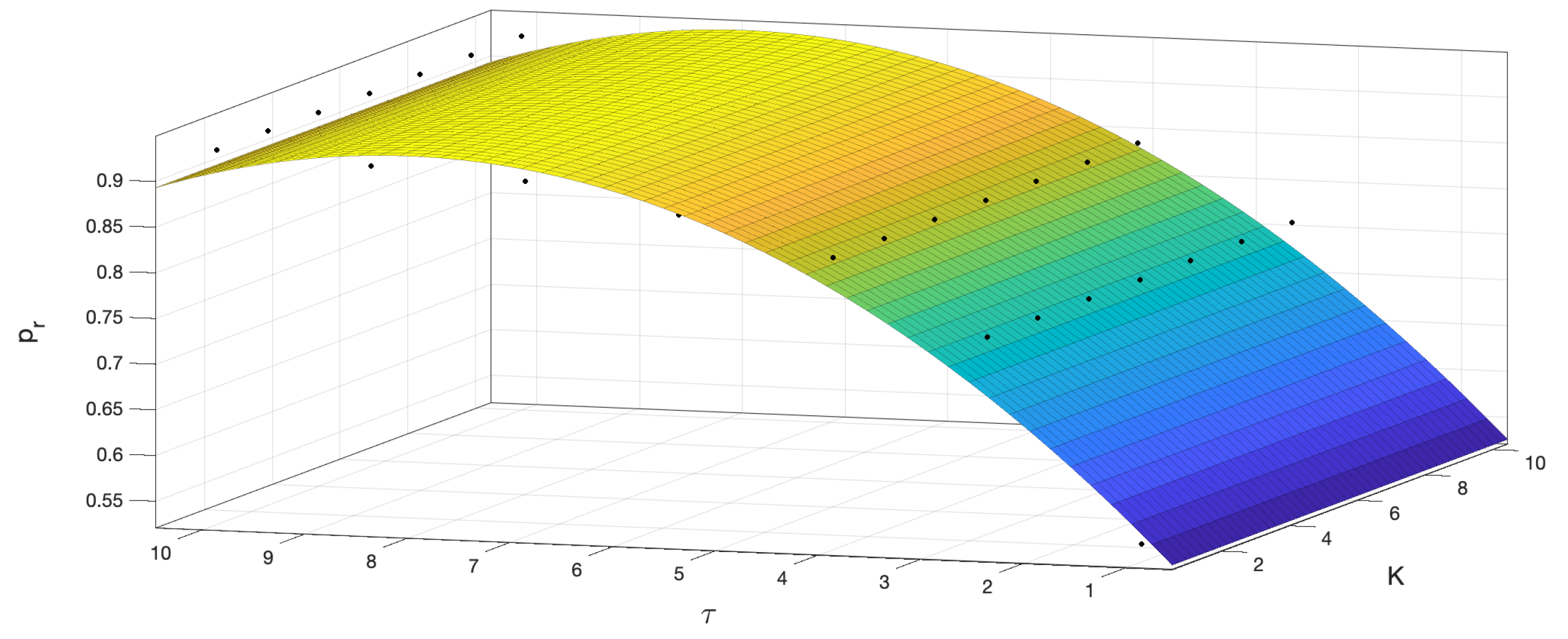
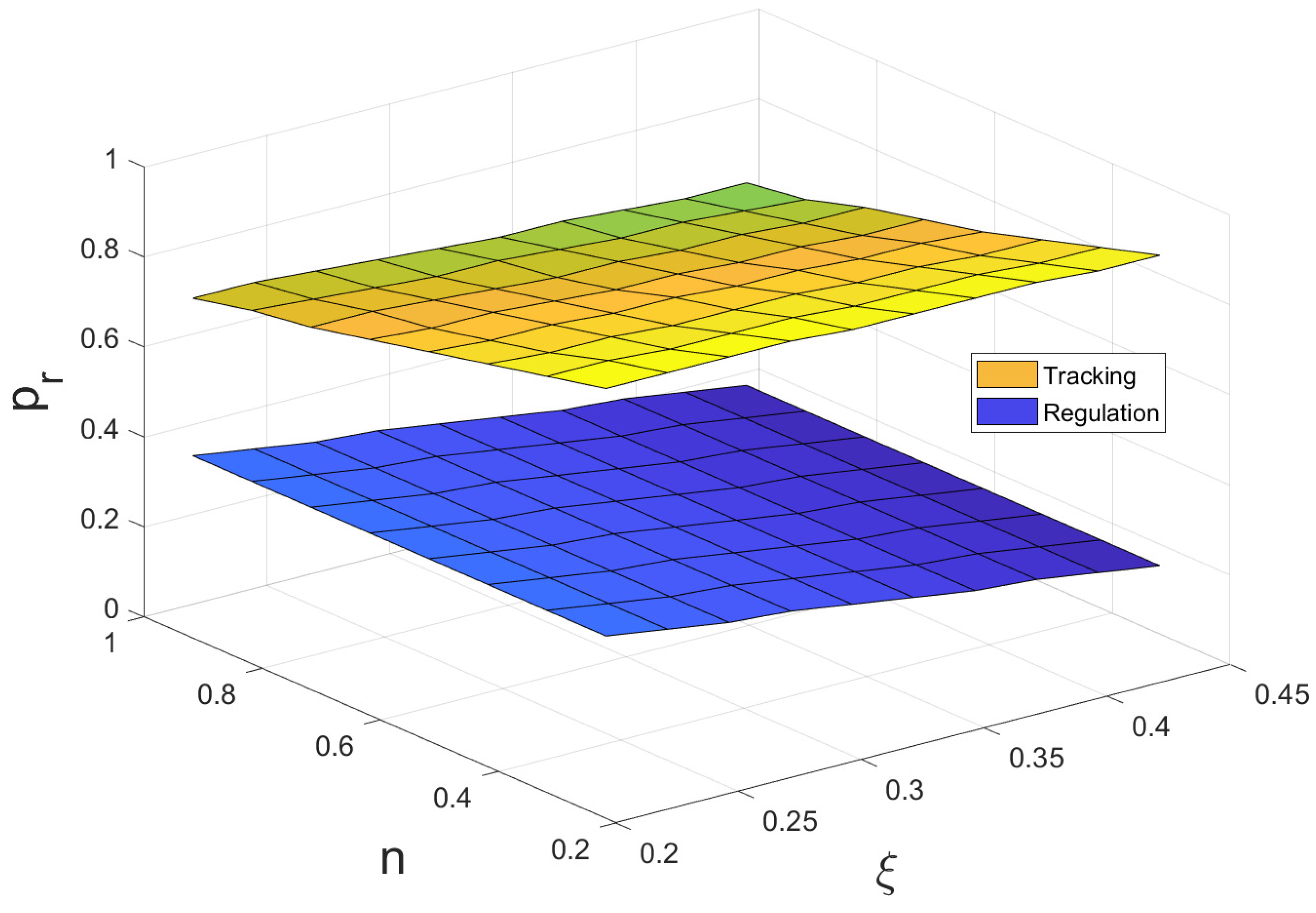
3. New Tuning Rules for PI+CI
3.1. Tracking Problem
3.2. Regulation Problem
3.3. Combined Tracking and Regulation Problems
| Algorithm 1: Control algorithm |
|
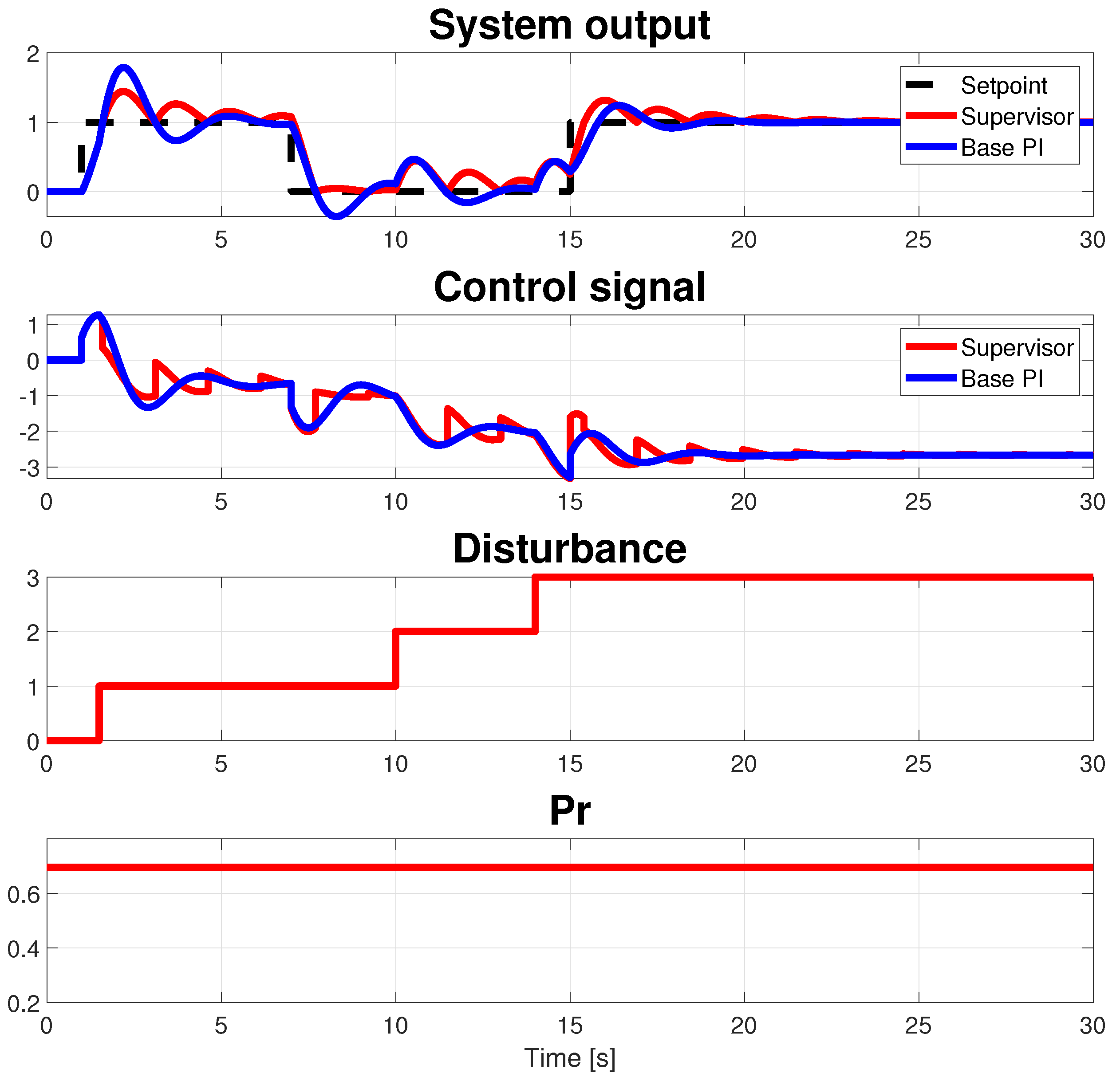
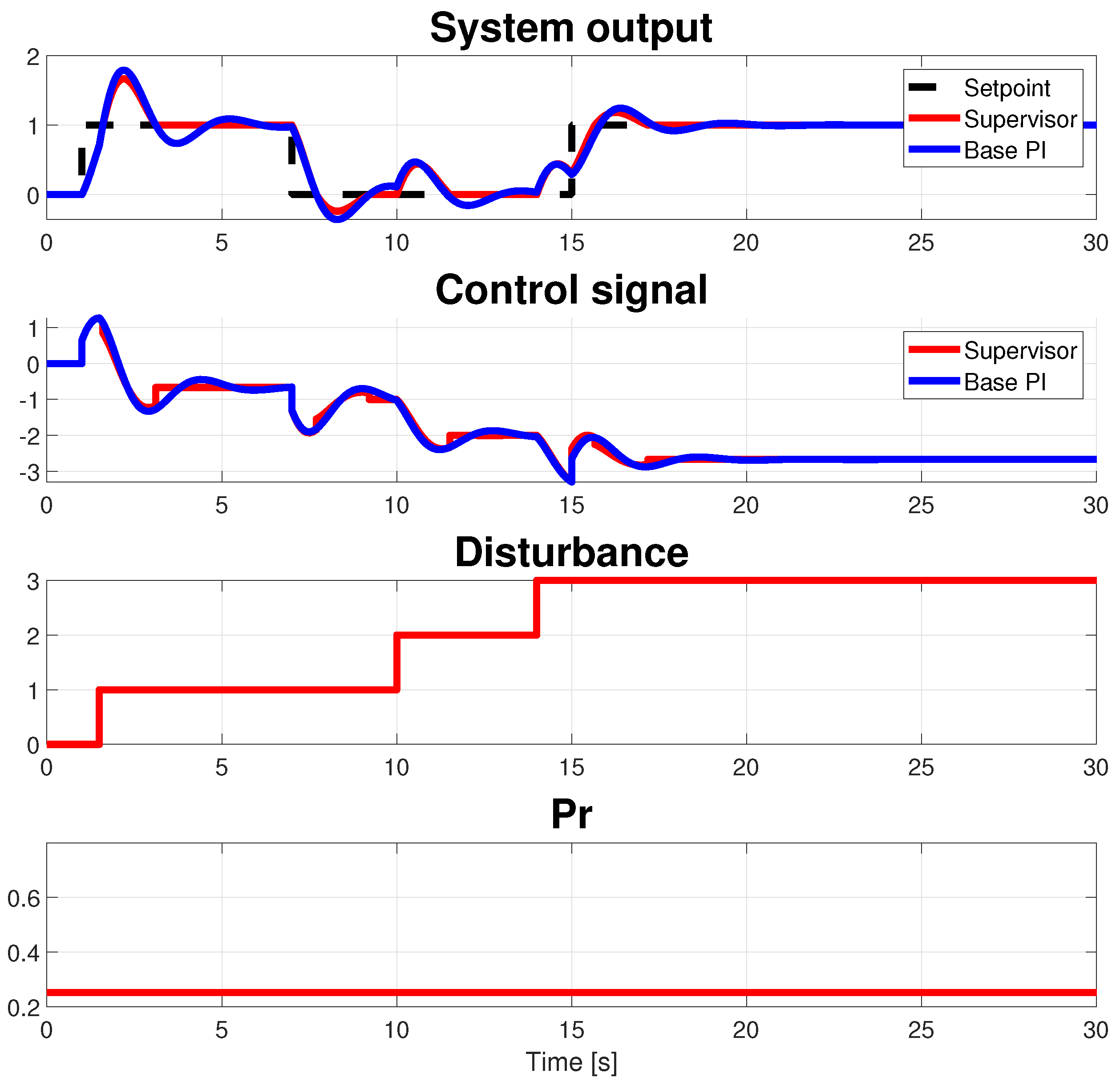
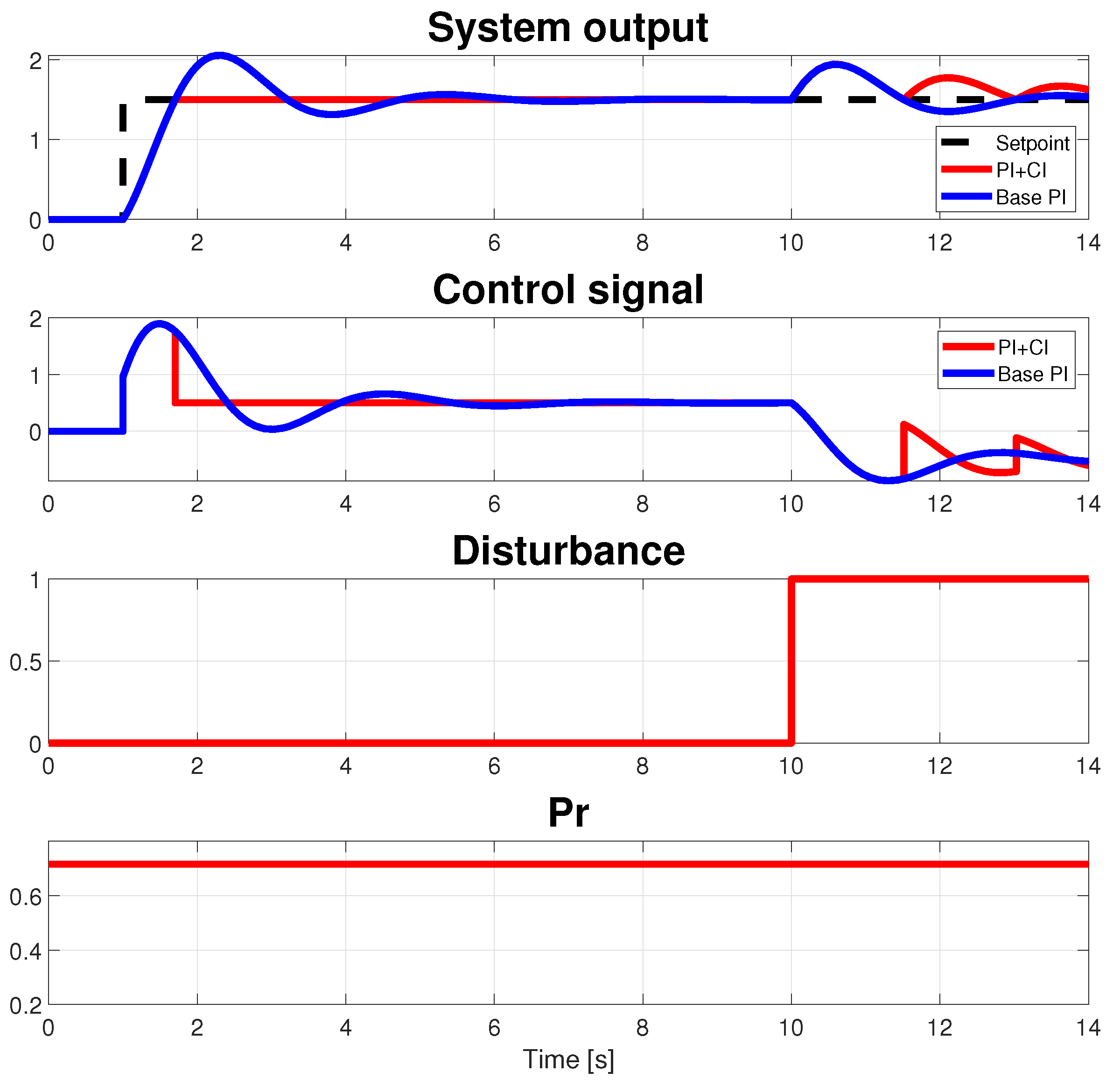
4. Discussion
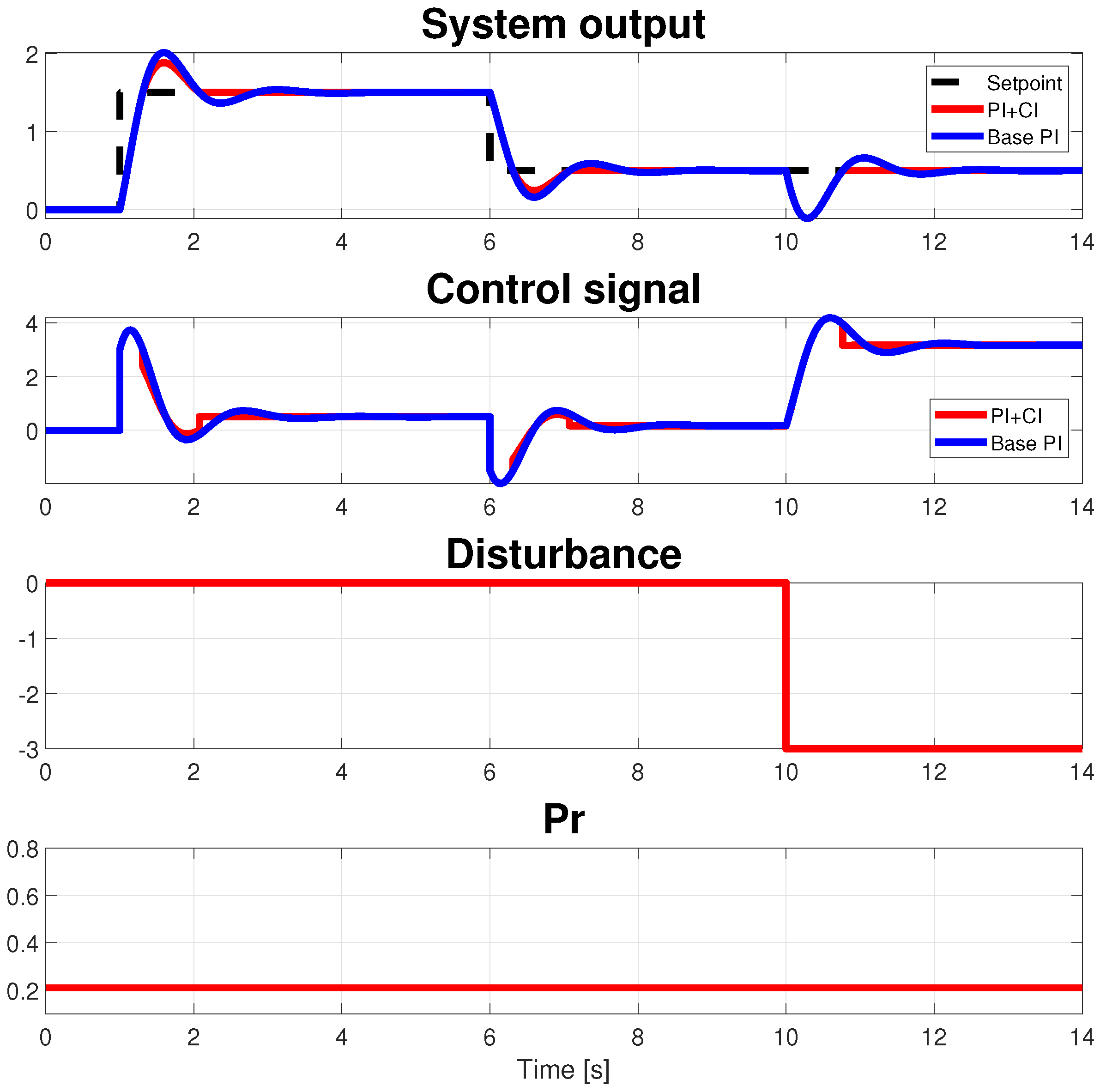
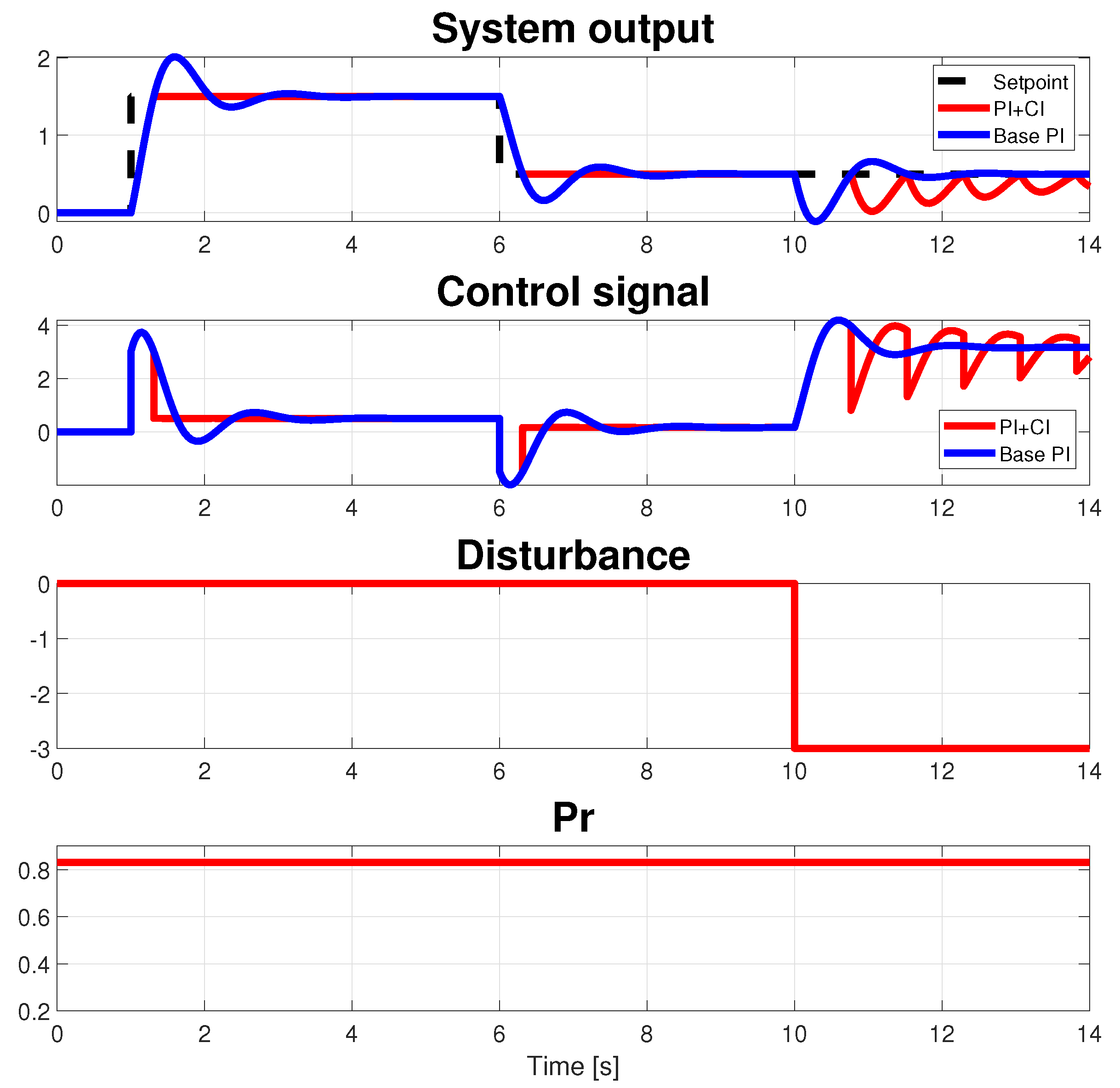
5. An Example
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Clegg, J.C. A nonlinear integrator for servomechanisms. Trans. Am. Inst. Electr. Eng. Part II Appl. Ind. 1958, 77, 41–42. [Google Scholar] [CrossRef]
- Horowitz, I.; Rosenbaum, P. Non-linear design for cost of feedback reduction in systems with large parameter uncertainty. Int. J. Control 1975, 21, 977–1001. [Google Scholar] [CrossRef]
- Krishnan, K.R.; Horowitz, I.M. Synthesis of a non-linear feedback system with significant plant-ignorance for prescribed system tolerances†. Int. J. Control 1974, 19, 689–706. [Google Scholar] [CrossRef]
- Bainov, D.D.; Simeonov, P.S. Systems with Impulse Effect: Stability, Theory, and Applications; Ellis Horwood Series in Mathematics and Its Applications; Wiley Online Library: Hoboken, NJ, USA, 1989; p. 255. [Google Scholar]
- Sáez, J.F. Reset Control of Multiple-Input Single-Output Systems. Ph.D. Thesis, University of Murcia, Murcia, Spain, 2023. [Google Scholar]
- Baños, A.; Barreiro, A. Reset Control Systems; Springer: London, UK, 2012. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. The future of PID control. Control Eng. Pract. 2001, 9, 1163–1175. [Google Scholar] [CrossRef]
- Beker, O. Analysis of Reset Control Systems. Ph.D. Thesis, University of Massachusetts, Amherst, MA, USA, 2001. [Google Scholar]
- Vidal, A.; Baños, A. Reset compensation for temperature control: Experimental application on heat exchangers. Chem. Eng. J. 2010, 159, 170–181. [Google Scholar] [CrossRef]
- Davó, M.A.; Baños, A. Delay-dependent stability of reset control systems with input/output delays. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 2018–2023. [Google Scholar]
- Nair, U.R.; Costa-Castelló, R.; Baños, A. Grid voltage regulation using a reset PI+CI controller for Energy storage systems. IFAC-PapersOnLine 2018, 51, 226–231. [Google Scholar] [CrossRef]
- Mulero-Martínez, J.I.; Baños, A.; Moreno, J.C.; Guzmán, J.L. Hybrid Controller for an Industrial Raceway Photobioreactor. In Proceedings of the 2023 IEEE 28th International Conference on Emerging Technologies and Factory Automation (ETFA), Sinaia, Romania, 12–15 September 2023. [Google Scholar] [CrossRef]
- Baños, A.; Vidal, A. Design of reset control systems: The PI+CI compensator. J. Dyn. Syst. Meas. Control. Trans. ASME 2012, 134, 051003. [Google Scholar] [CrossRef]
- Joraked, S.; Pongyart, W.; Angkeaw, K. Design and implementation of a FPAA based PI+CI reset controller Emulator. In Proceedings of the ISCIT 2018—18th International Symposium on Communication and Information Technology, Bangkok, Thailand, 26–29 September 2018; pp. 408–411. [Google Scholar] [CrossRef]
- Doktian, J.; Pongyart, W.; Vanichchanunt, P. Development of a Semi Auto-Tuning Algorithm for PI+CI Reset Controller. In Proceedings of the 2019 1st International Symposium on Instrumentation, Control, Artificial Intelligence, and Robotics, ICA-SYMP 2019, Bangkok, Thailand, 16–18 January 2019; pp. 155–158. [Google Scholar] [CrossRef]
- Banki, T.; Faghihi, F.; Soleymani, S. Robust Frequency Control of Provisional Microgrid by Using of a Combined Fuzzy Reset Approach. J. Electr. Eng. Technol. 2023, 19, 125–132. [Google Scholar] [CrossRef]
- Shakibjoo, A.D.; Vasegh, N. Method for Analytically Obtaining Reset Ratio in Non-Minimum Phase Systems with PI+CI Controller in order to Improve Performance. Int. J. Mechatronics Electr. Comput. Technol. 2014, 4, 1880–1899. [Google Scholar]
- Baños, A.; Davó, M.A. Tuning of reset proportional integral compensators with a variable reset ratio and reset band. IET Control Theory Appl. 2014, 8, 1949–1962. [Google Scholar] [CrossRef]
- Bakkeheim, J.; Smogeli, O.N.; Johansen, T.A.; Sorensen, A.J. Improved transient performance by lyapunov-based integrator reset of PI thruster control in extreme seas. In Proceedings of the IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 4052–4057. [Google Scholar] [CrossRef]
- Wu, D.; Guo, G.; Wang, Y. Reset integral-derivative control for HDD servo systems. IEEE Trans. Control Syst. Technol. 2007, 15, 161–167. [Google Scholar] [CrossRef]
- Aangenent, W.H.; Witvoet, G.; Heemels, W.P.; Van De Molengraft, M.J.; Steinbuch, M. Performance analysis of reset control systems. Int. J. Robust Nonlinear Control 2010, 20, 1213–1233. [Google Scholar] [CrossRef]
- Nešić, D.; Zaccarian, L.; Teel, A.R. Stability properties of reset systems. Automatica 2008, 44, 2019–2026. [Google Scholar] [CrossRef]
- Nešić, D.; Teel, A.R.; Zaccarian, L. On necessary and sufficient conditions for exponential and L2 stability of planar reset systems. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 4140–4145. [Google Scholar] [CrossRef]
- Åström, K.; Hägglund, T. Advanced PID Control; ISA—The Instrumentation, Systems and Automation Society: Research Triangle Park, NC, USA, 2006. [Google Scholar]
- Dorf, R.; Bishop, R. Modern Control Systems, 12th ed.; Pearson: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
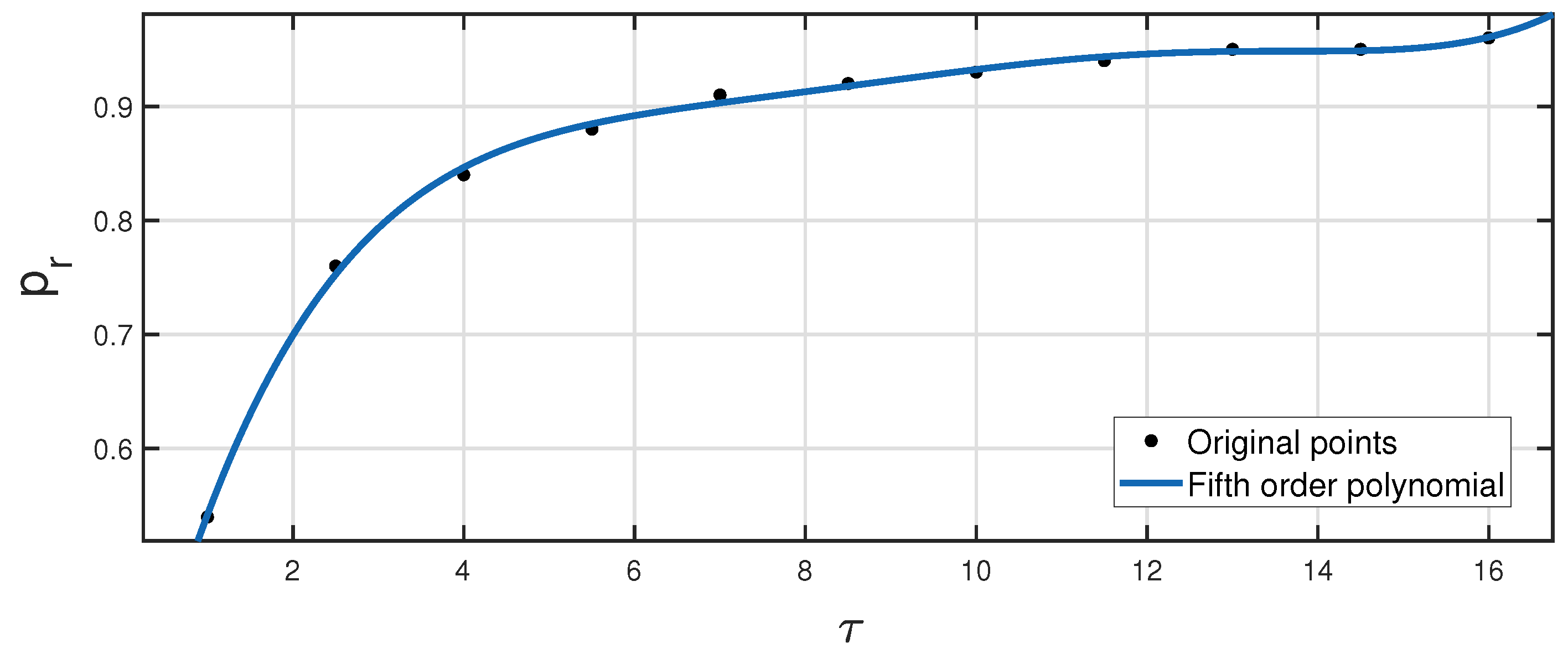

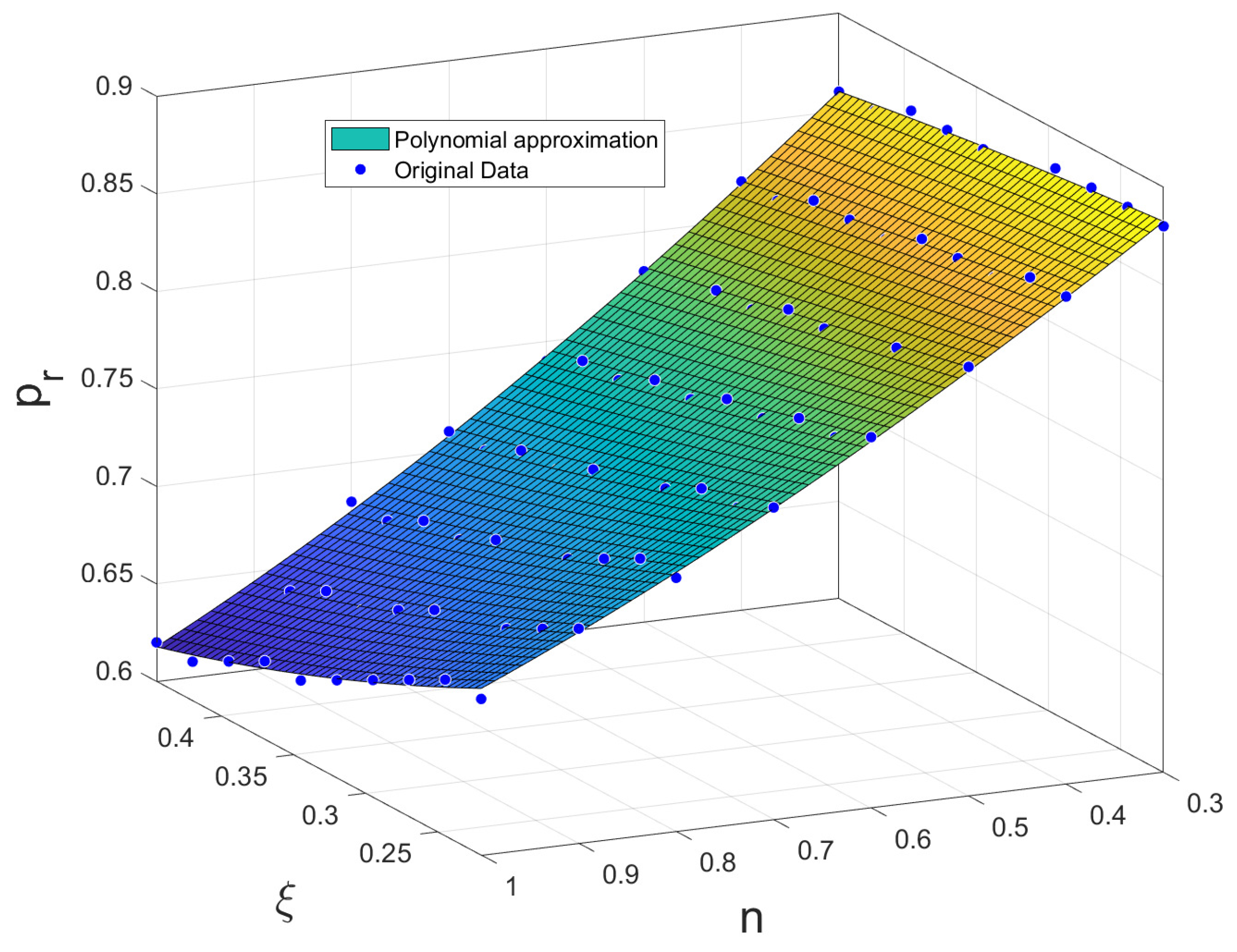
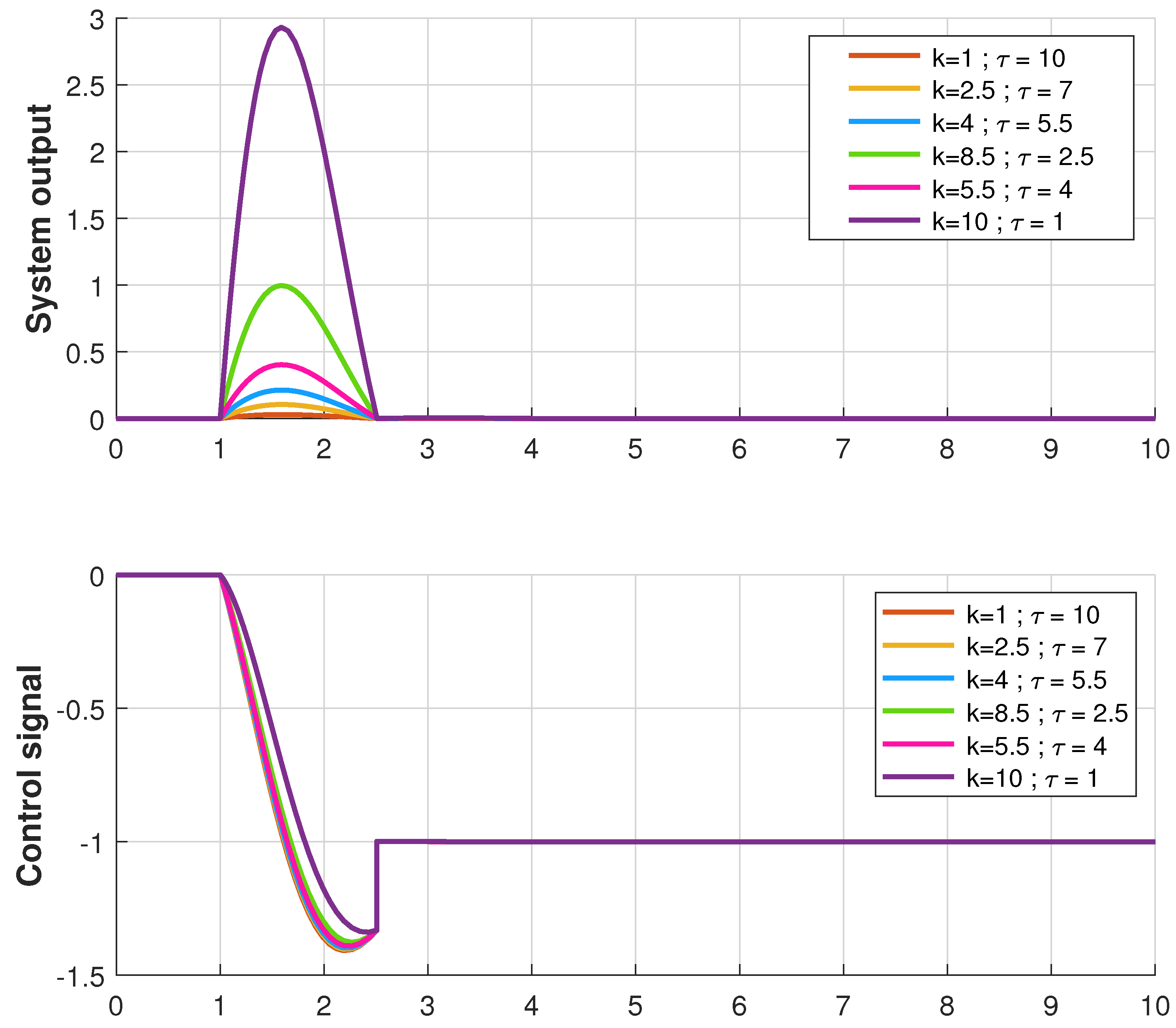
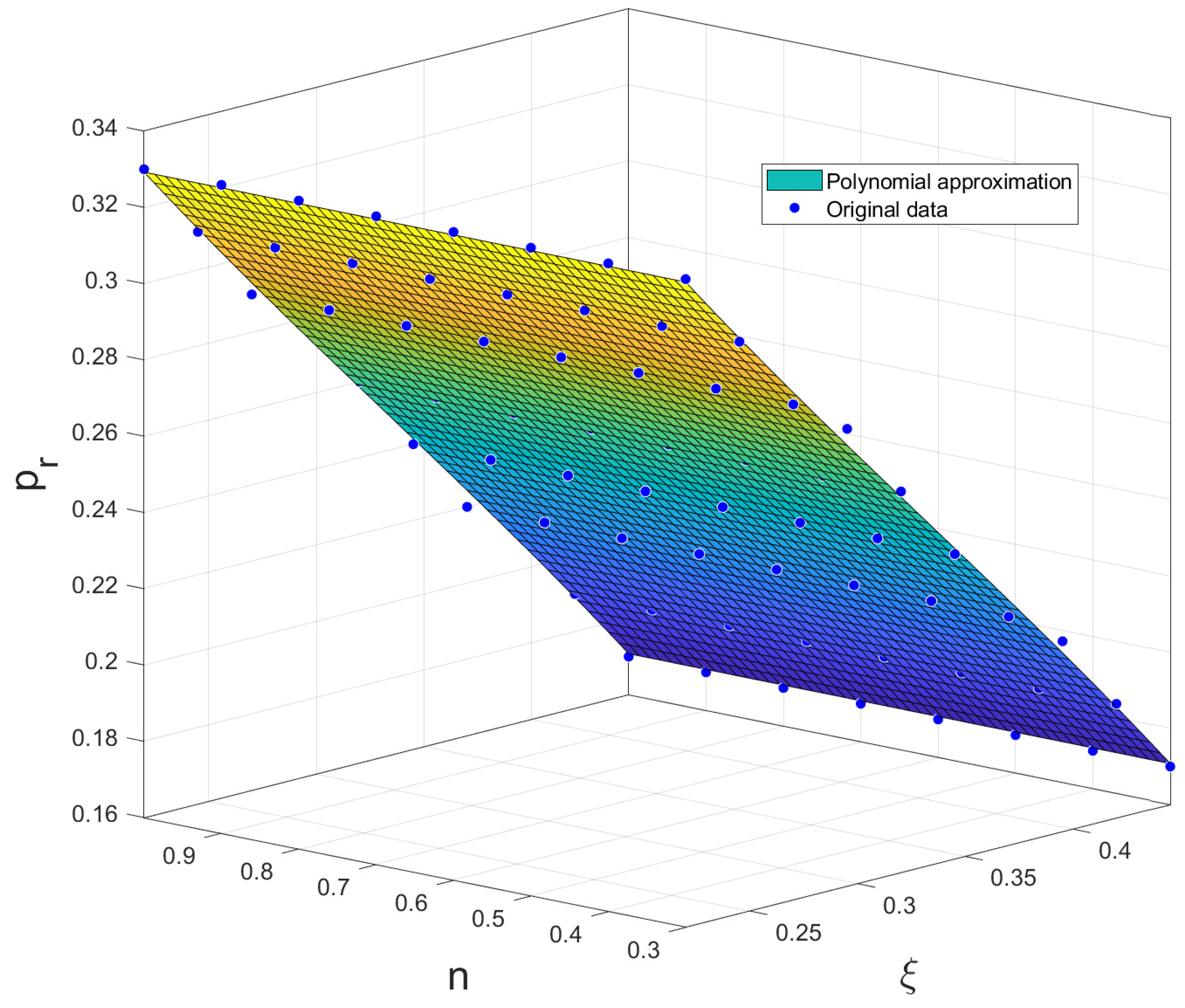


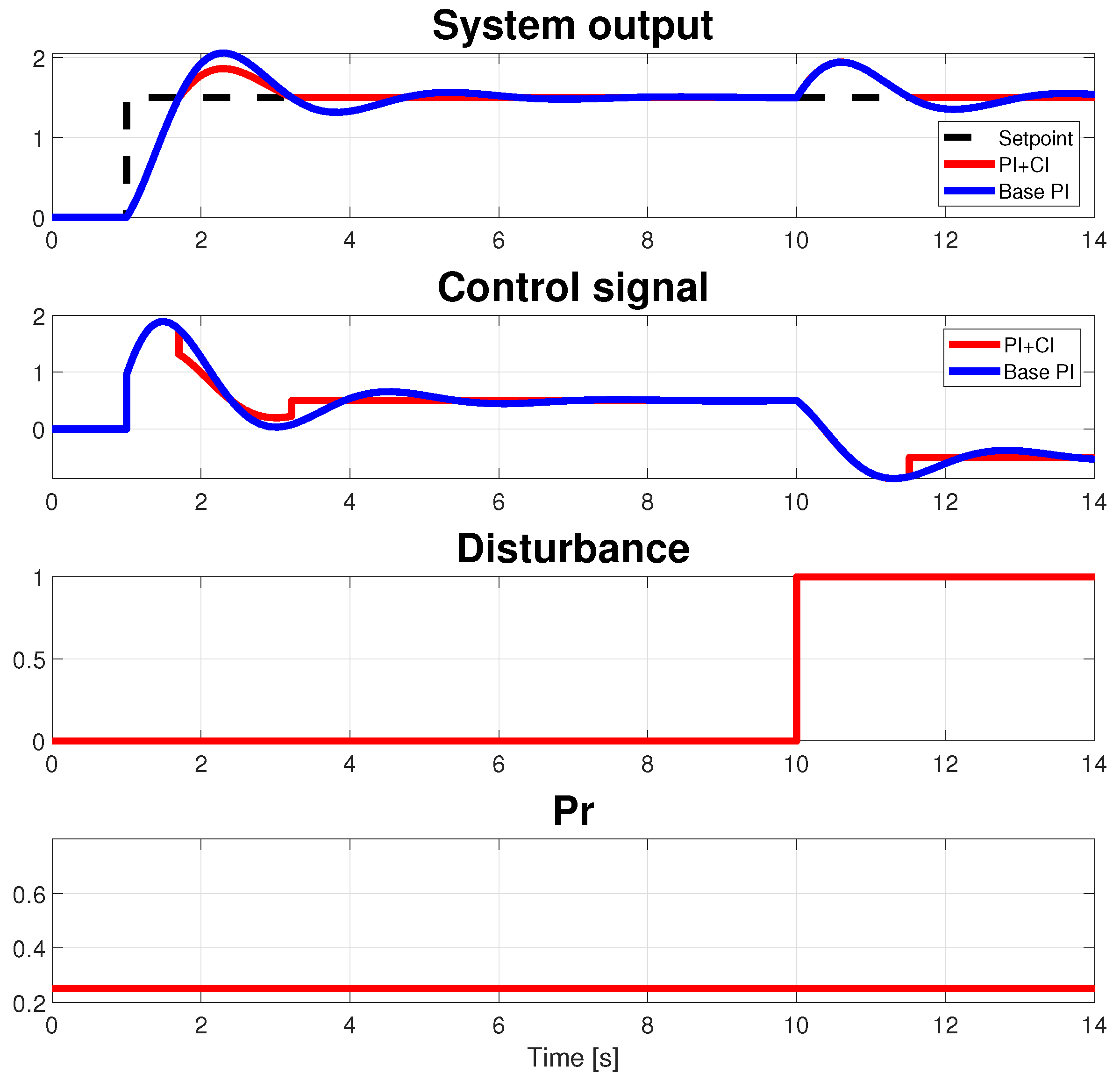

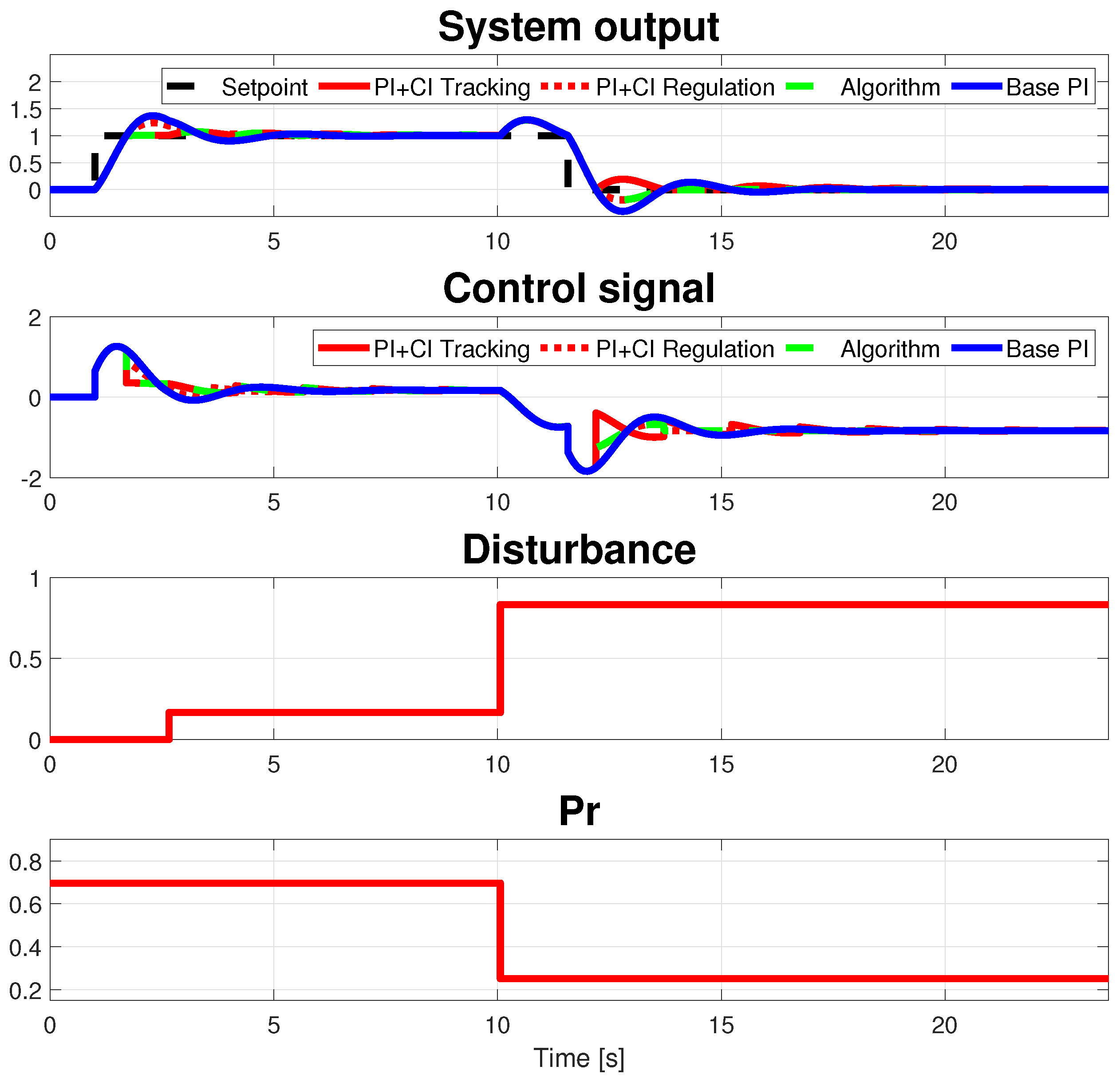

| Plant | PI+CI Tracking | PI+CI Regulation | Algorithm | Base PI |
|---|---|---|---|---|
| 107.86 | 54.44 | 51.258 | 81.861 | |
| 104.98 | 50.046 | 48.156 | 75.231 | |
| 6.0852 | 8.9267 | 5.8518 | 13.424 | |
| 0.3595 | 0.18146 | 0.16609 | 0.27284 | |
| 0.15212 | 0.22319 | 0.14634 | 0.335759 | |
| 0.037044 | 0.047396 | 0.032019 | 0.0713055 | |
| 0.11145 | 0.078324 | 0.06304 | 0.1178 | |
| 1.5213 | 2.2319 | 1.463 | 3.3584 | |
| 17.976 | 9.0733 | 8.344 | 13.642 | |
| 22.293 | 15.665 | 12.589 | 23.569 |
| Plant | PI+CI Tracking | PI+CI Regulation | Algorithm 1 | Base PI |
|---|---|---|---|---|
| 23.455 | 21.355 | 19.485 | 30.551 | |
| 15.637 | 14.236 | 13.04 | 20.325 | |
| 15.634 | 14.235 | 13.053 | 20.36 | |
| 0.078188 | 0.071176 | 0.065103 | 0.10183 | |
| 0.39087 | 0.35589 | 0.32611 | 0.50932 | |
| 0.078163 | 0.071173 | 0.065253 | 0.10182 | |
| 0.078162 | 0.071173 | 0.065217 | 0.10169 | |
| 3.9077 | 3.5589 | 3.2627 | 5.0921 | |
| 3.9092 | 3.5592 | 3.2354 | 5.0909 | |
| 15.638 | 14.236 | 12.991 | 20.365 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, J.C.; González, J.; Navarro, A.; Guzmán, J.L. New Tuning Rules of PI+CI Controllers for First-Order Systems. Actuators 2024, 13, 67. https://doi.org/10.3390/act13020067
Moreno JC, González J, Navarro A, Guzmán JL. New Tuning Rules of PI+CI Controllers for First-Order Systems. Actuators. 2024; 13(2):67. https://doi.org/10.3390/act13020067
Chicago/Turabian StyleMoreno, José Carlos, José González, Ana Navarro, and José Luis Guzmán. 2024. "New Tuning Rules of PI+CI Controllers for First-Order Systems" Actuators 13, no. 2: 67. https://doi.org/10.3390/act13020067
APA StyleMoreno, J. C., González, J., Navarro, A., & Guzmán, J. L. (2024). New Tuning Rules of PI+CI Controllers for First-Order Systems. Actuators, 13(2), 67. https://doi.org/10.3390/act13020067








