Distributed Fixed-Time Formation Tracking Control for the Multi-Agent System and an Application in Wheeled Mobile Robots
Abstract
1. Introduction
2. Preliminaries and Problem Statements
2.1. Graph Theory Preliminaries
2.2. Mathematical Preliminaries
2.3. HMAS Model Descriptions
3. Fixed-Time ISMC-Based Formation Control for HMASs
3.1. Fixed-Time Disturbance Observer
3.2. Fixed-Time Formation Control Protocol
4. Fixed-Time Formation Control for a Multi-WMR System
4.1. Fixed-Time Disturbance Observers
4.2. Distributed Formation Control for the Second-Order Subsystem
4.3. Distributed Formation Control for the Third-Order Subsystem
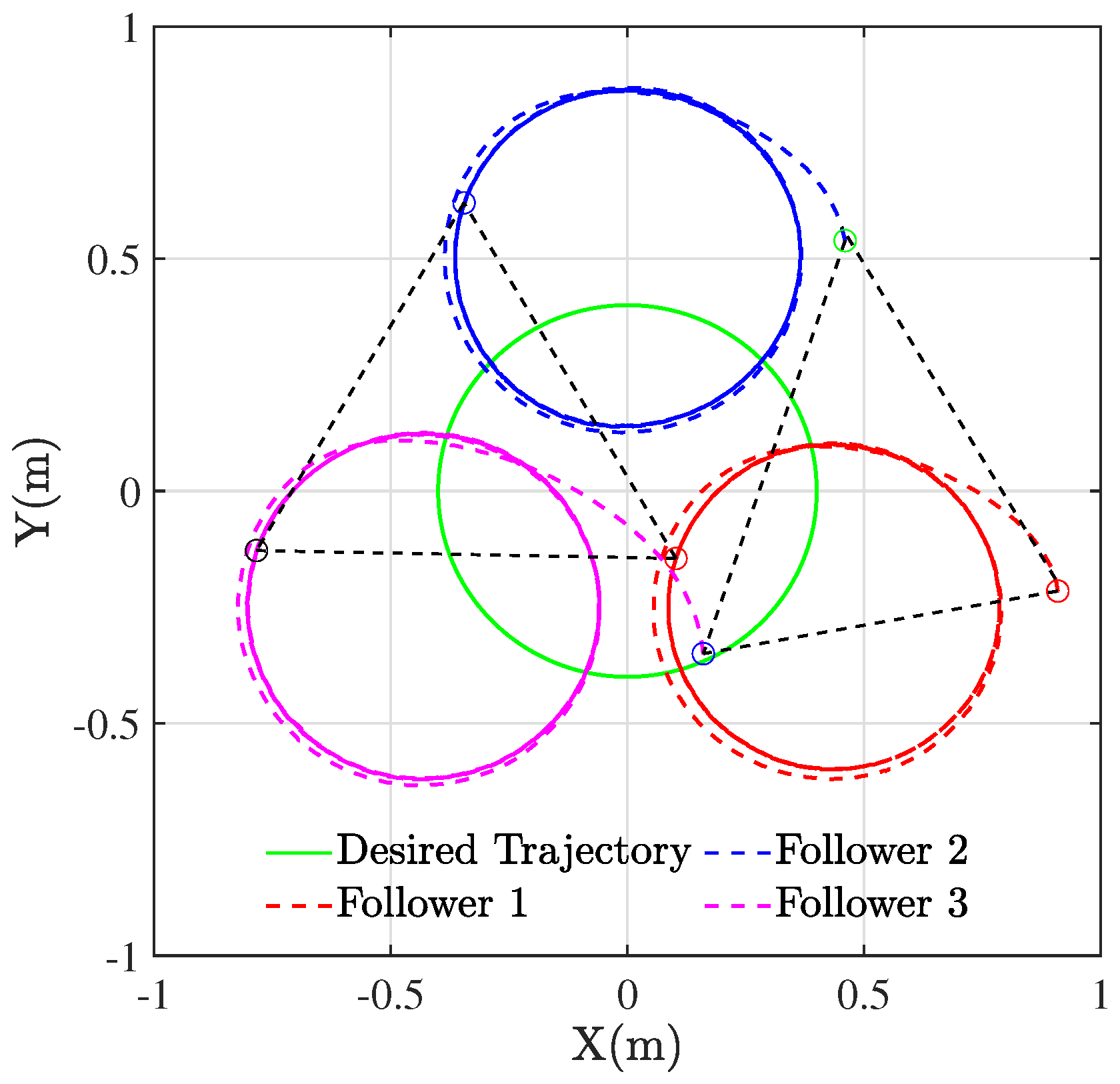
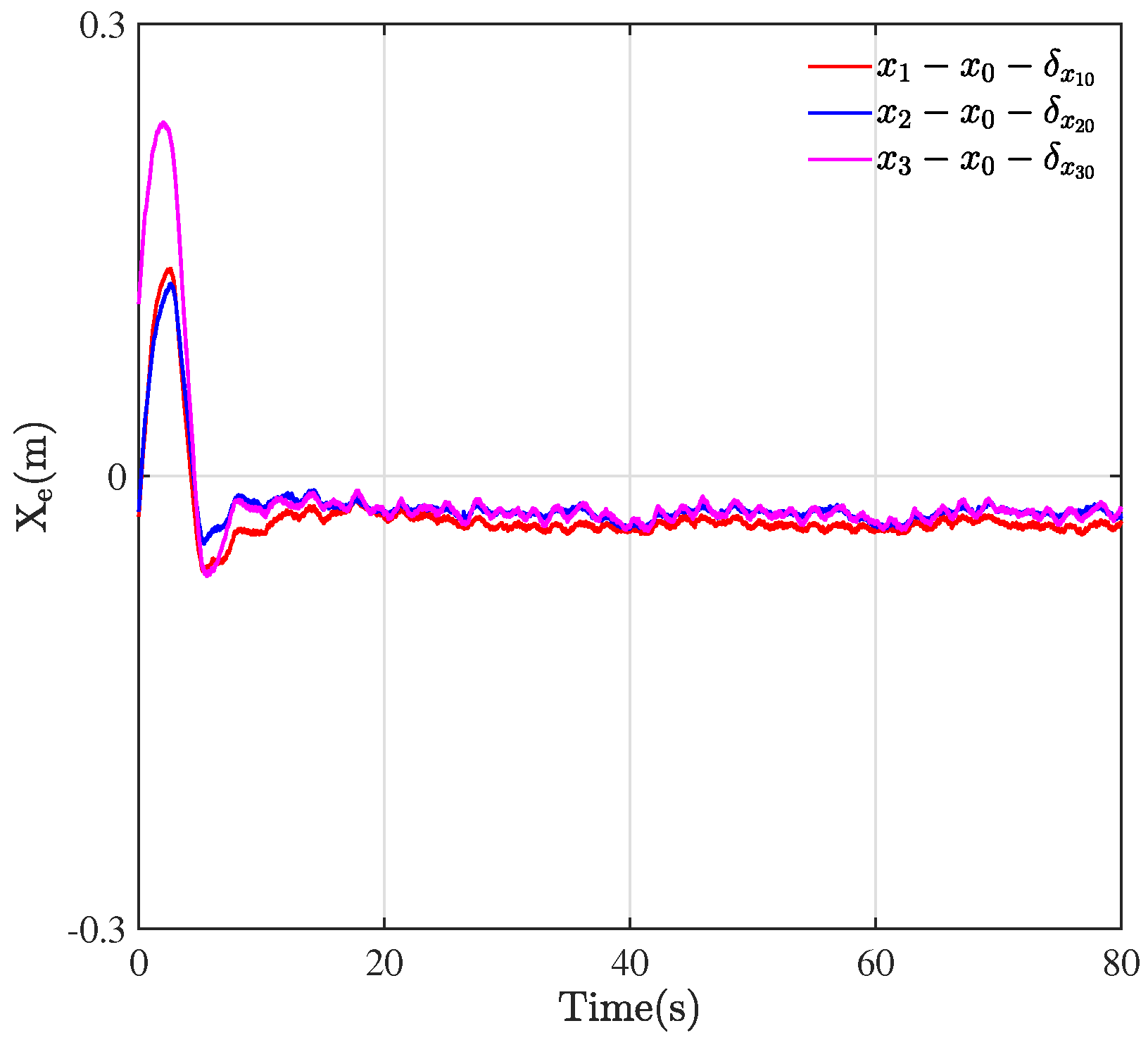
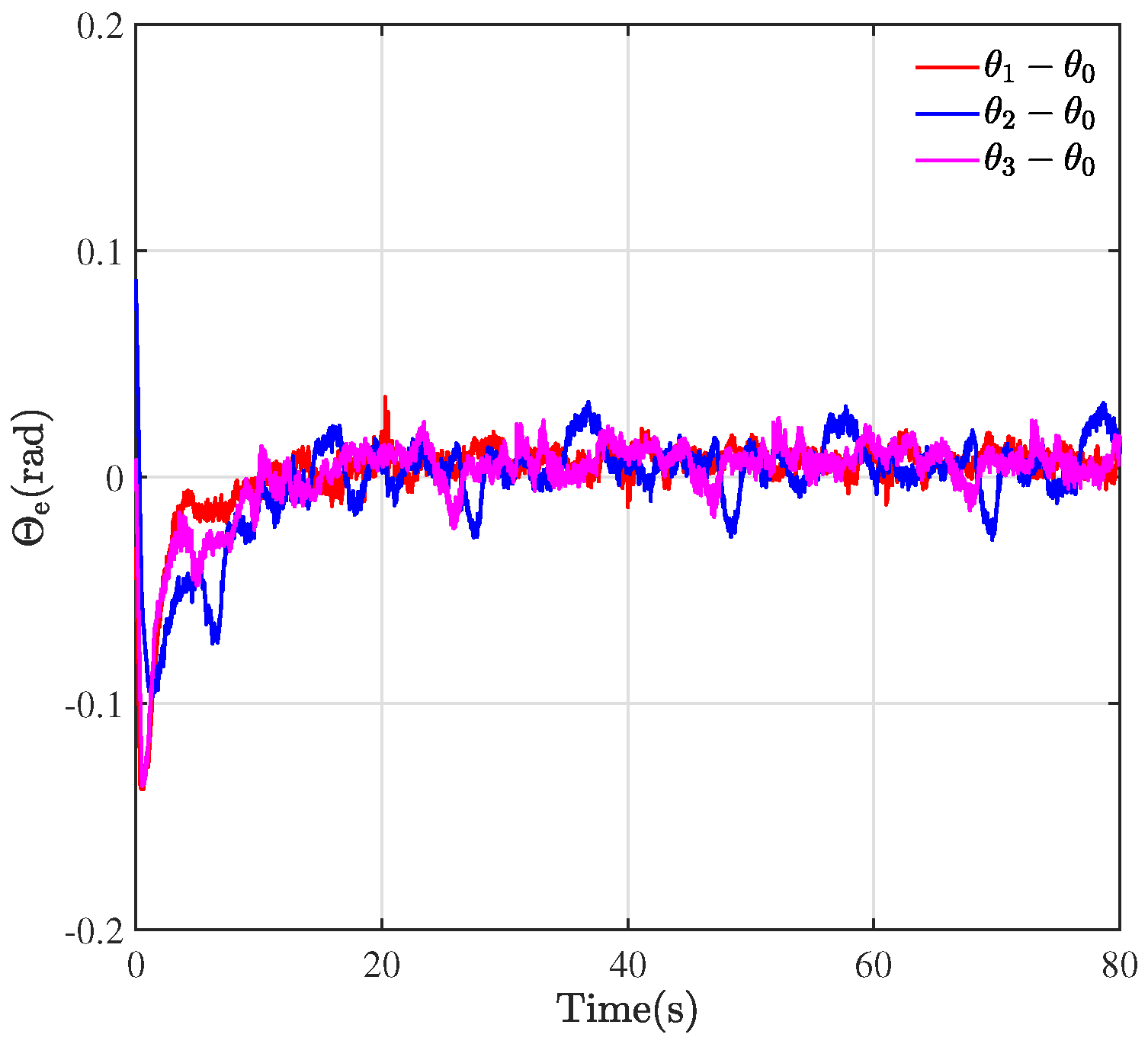
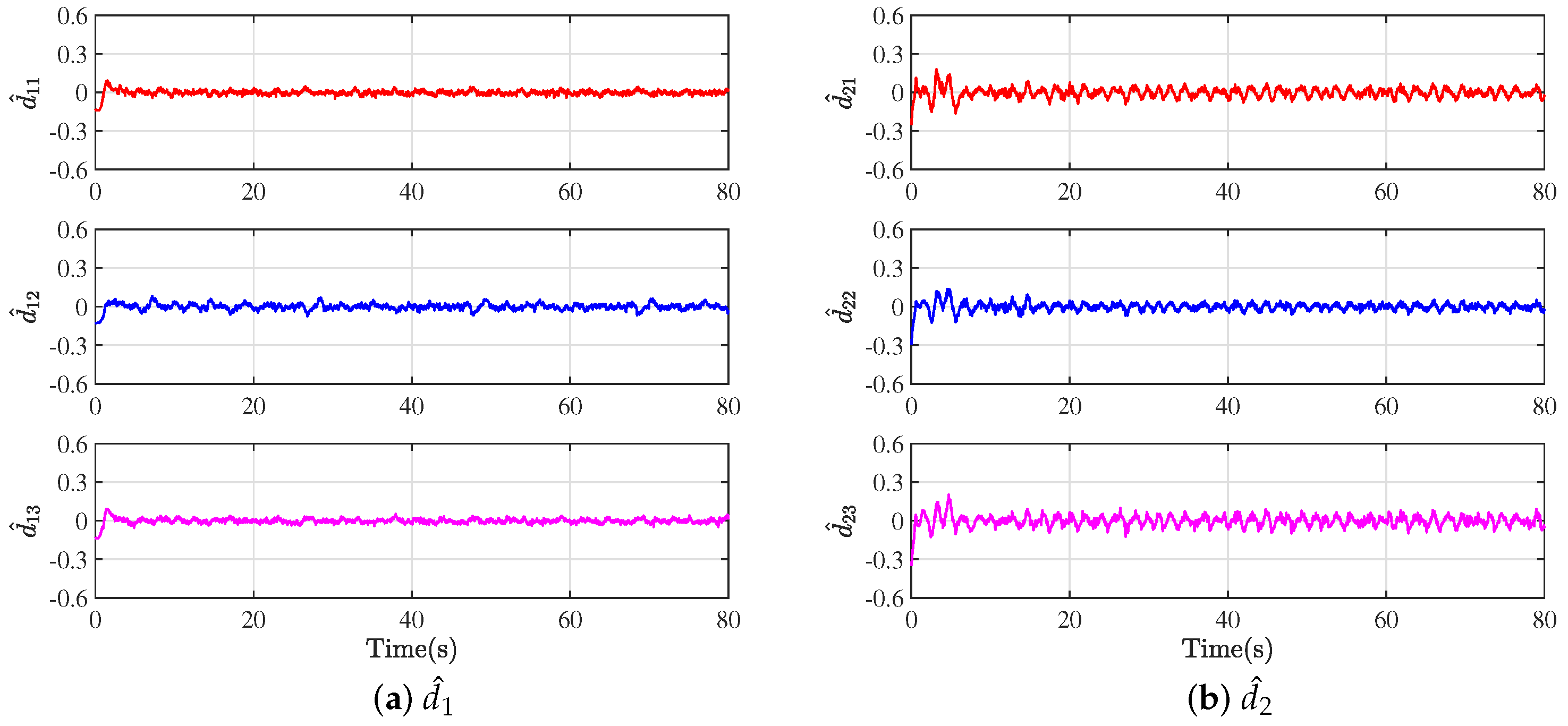
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAS | Multi-agent system |
| WMR | Wheeled mobile robot |
| HMAS | High-order multi-agent system |
References
- Hu, Q.; Shi, Y.; Wang, C. Event-based formation coordinated control for multiple spacecraft under communication constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3168–3179. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Yang, Y.; Xiao, B.; Ran, D. Leader-following output-feedback consensus for second order multiagent systems with arbitrary convergence time and prescribed performance. ISA Trans. 2023, 141, 251–260. [Google Scholar] [CrossRef]
- Li, B.; Liu, H.; Ahn, C.K.; Gong, W. Optimized intelligent tracking control for a quadrotor unmanned aerial vehicle with actuator failures. Aerosp. Sci. Technol. 2024, 144, 108803. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, Q.; Huang, N.; Yu, C.; Anderson, B.D.O. Cooperative event-based rigid formation control. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4308–4320. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, M.; Zhang, C.; Zeng, J. Decentralized formation trajectory tracking control of multi-AUV system with actuator saturation. Ocean Eng. 2022, 255, 111423. [Google Scholar] [CrossRef]
- Maghenem, M.; Loria, A.; Nuno, E.; Panteley, E. Consensus-based formation control of networked nonholonomic vehicles with delayed communications. IEEE Trans. Autom. Control 2021, 66, 2242–2249. [Google Scholar] [CrossRef]
- Liang, D.; Wang, C.; Cai, X.; Li, Y.; Xu, Y. Distributed fixed-time leader-following consensus tracking control for nonholonomic multi-agent systems with dynamic uncertainties. Neurocomputing 2021, 430, 112–120. [Google Scholar] [CrossRef]
- Cui, Y.; Cao, L.; Gong, X.; Basin, M.V.; Shen, J.; Huang, T. Resilient output containment control of heterogeneous multiagent systems against composite attacks: A digital twin approach. IEEE Trans. Cybern. 2023. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Gong, W.; Yang, Y.; Xiao, B. Distributed fixed-time leader-following formation control for multi-quadrotors with prescribed performance and collision avoidance. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7281–7294. [Google Scholar] [CrossRef]
- Bhat, S.; Bernstein, D. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. A new class of finite-time nonlinear consensus protocols for multi-agent systems. Int. J. Control. 2014, 87, 363–370. [Google Scholar] [CrossRef]
- Du, H.; Wen, G.; Cheng, Y.; He, Y.; Jia, R. Distributed finite-time cooperative control of multiple high-order nonholonomic mobile robots. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2998–3006. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, Y.; Fu, J. Adaptive finite-time optimal formation control for second-order nonlinear multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6132–6144. [Google Scholar] [CrossRef]
- Wei, C.; Li, Y.; Yin, Z.; Liang, Z.; Feng, J. On finite-time anti-saturated proximity control with a tumbling non-cooperative space target. Space Sci. Technol. 2023, 3, 0045. [Google Scholar] [CrossRef]
- Ou, M.; Du, H.; Li, S. Finite-time tracking control of multiple nonholonomic mobile robots. Int. J. Robust Nonlinear Control 2012, 349, 2834–2860. [Google Scholar] [CrossRef]
- Tran, Q.V.; Trinh, M.H.; Zelazo, D.; Mukherjee, D.; Ahn, H.S. Finite-time bearing-only formation control via distributed global orientation estimation. IEEE Trans. Control Netw. Syst. 2019, 6, 702–712. [Google Scholar] [CrossRef]
- Wang, D.; Zong, Q.; Tian, B.; Wang, F.; Dou, L. Finite-time fully distributed formation reconfiguration control for UAV helicopters. Int. J. Robust Nonlinear Control 2018, 28, 5943–5961. [Google Scholar] [CrossRef]
- Zhu, C.; Huang, B.; Su, Y.; Zhou, B.; Zhang, E. Finite-time time-varying formation control for marine surface vessels. Ocean. Eng. 2021, 239, 109817. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Liu, H.; Li, B.; Xiao, B.; Ran, D.; Zhang, C. Reinforcement learning-based tracking control for a quadrotor unmanned aerial vehicle under external disturbances. Int. J. Robust Nonlinear Control 2023, 33, 10360–10377. [Google Scholar] [CrossRef]
- Jiang, B.; Hu, Q.; Friswell, M.I. Fixed-time rendezvous control of spacecraft with a tumbling target under loss of actuator effectiveness. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1576–1586. [Google Scholar] [CrossRef]
- Liu, J.; Sun, M.; Chen, Z.; Sun, Q. Output feedback control for aircraft at high angle of attack based upon fixed-time extended state observer. Aerosp. Sci. Technol. 2019, 95, 105468. [Google Scholar] [CrossRef]
- Ye, D.; Zou, A.M.; Sun, Z. Predefined-time predefined-bounded attitude tracking control for rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 464–472. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, B.; Golestani, M.; Ran, D. Faster fixed-time control of flexible spacecraft attitude stabilization. IEEE Trans. Ind. Inform. 2020, 16, 1281–1290. [Google Scholar] [CrossRef]
- An, S.; Wang, L.; He, Y. Robust fixed-time tracking control for underactuated AUVs based on fixed-time disturbance observer. Ocean Eng. 2022, 266, 112567. [Google Scholar] [CrossRef]
- Zuo, Z.; Tian, B.; Defoort, M.; Ding, Z. Fixed-time consensus tracking for multiagent systems with high-order integrator dynamics. IEEE Trans. Autom. Control 2018, 63, 563–570. [Google Scholar] [CrossRef]
- Ou, M.; Sun, H.; Zhang, Z.; Li, L. Fixed-time trajectory tracking control for multiple nonholonomic mobile robots. Trans. Inst. Meas. Control 2021, 43, 1596–1608. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, F.; Huang, P.; Lu, Y. Fixed-time consensus tracking for second-order multiagent systems under disturbance. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4883–4894. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, B. Distributed fixed-time control of high-order multi-agent systems with non-holonomic constraints. J. Franklin Inst. 2021, 358, 2948–2963. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Y.L.; Fei, M.R.; Pan, Q.K. Cross-dimensional formation control of second-order heterogeneous multi-agent systems. ISA Trans. 2022, 127, 188–196. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Y.; Wang, J.; Chen, J.; Qian, D. Disturbance observer–based super-twisting sliding mode control for formation tracking of multi-agent mobile robots. Meas. Control 2020, 53, 908–921. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, K.; Jiang, B.; Ding, S.X. Fixed-time fault-tolerant formation control for heterogeneous multi-agent systems with parameter uncertainties and disturbances. IEEE Trans. Circuits Syst. I Reg. Pap. 2021, 68, 2121–2133. [Google Scholar] [CrossRef]
- Jenabzadeh, A.; Safarinejadian, B. Distributed estimation and control for nonlinear multi-agent systems in the presence of input delay or external disturbances. ISA Trans. 2020, 98, 198–206. [Google Scholar] [CrossRef] [PubMed]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Polycarpou, M.; Ioannou, P. A robust adaptive nonlinear control design. Automatica 1996, 32, 423–427. [Google Scholar] [CrossRef]
- Chevillard, S. The functions erf and erfc computed with arbitrary precision and explicit error bounds. Inf. Comput. 2012, 216, 72–95. [Google Scholar] [CrossRef]
- Bagul, Y.J.; Chesneau, C. Sigmoid functions for the smooth approximation to the absolute value function. Moroccan J. Pure Appl. Anal. 2021, 7, 12–19. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Gao, Y.; Li, B. Distributed Fixed-Time Formation Tracking Control for the Multi-Agent System and an Application in Wheeled Mobile Robots. Actuators 2024, 13, 68. https://doi.org/10.3390/act13020068
Ma L, Gao Y, Li B. Distributed Fixed-Time Formation Tracking Control for the Multi-Agent System and an Application in Wheeled Mobile Robots. Actuators. 2024; 13(2):68. https://doi.org/10.3390/act13020068
Chicago/Turabian StyleMa, Ling, Yufeng Gao, and Bo Li. 2024. "Distributed Fixed-Time Formation Tracking Control for the Multi-Agent System and an Application in Wheeled Mobile Robots" Actuators 13, no. 2: 68. https://doi.org/10.3390/act13020068
APA StyleMa, L., Gao, Y., & Li, B. (2024). Distributed Fixed-Time Formation Tracking Control for the Multi-Agent System and an Application in Wheeled Mobile Robots. Actuators, 13(2), 68. https://doi.org/10.3390/act13020068




