Computational Control Strategy for Reducing Medial Compartment Load in Knee Bracing with Embedded Actuator
Abstract
1. Introduction
- Step 1: We present an efficient unloading strategy based on penetration depth reduction to avoid lateral compartment overloading along with adequate medial compartment unloading.
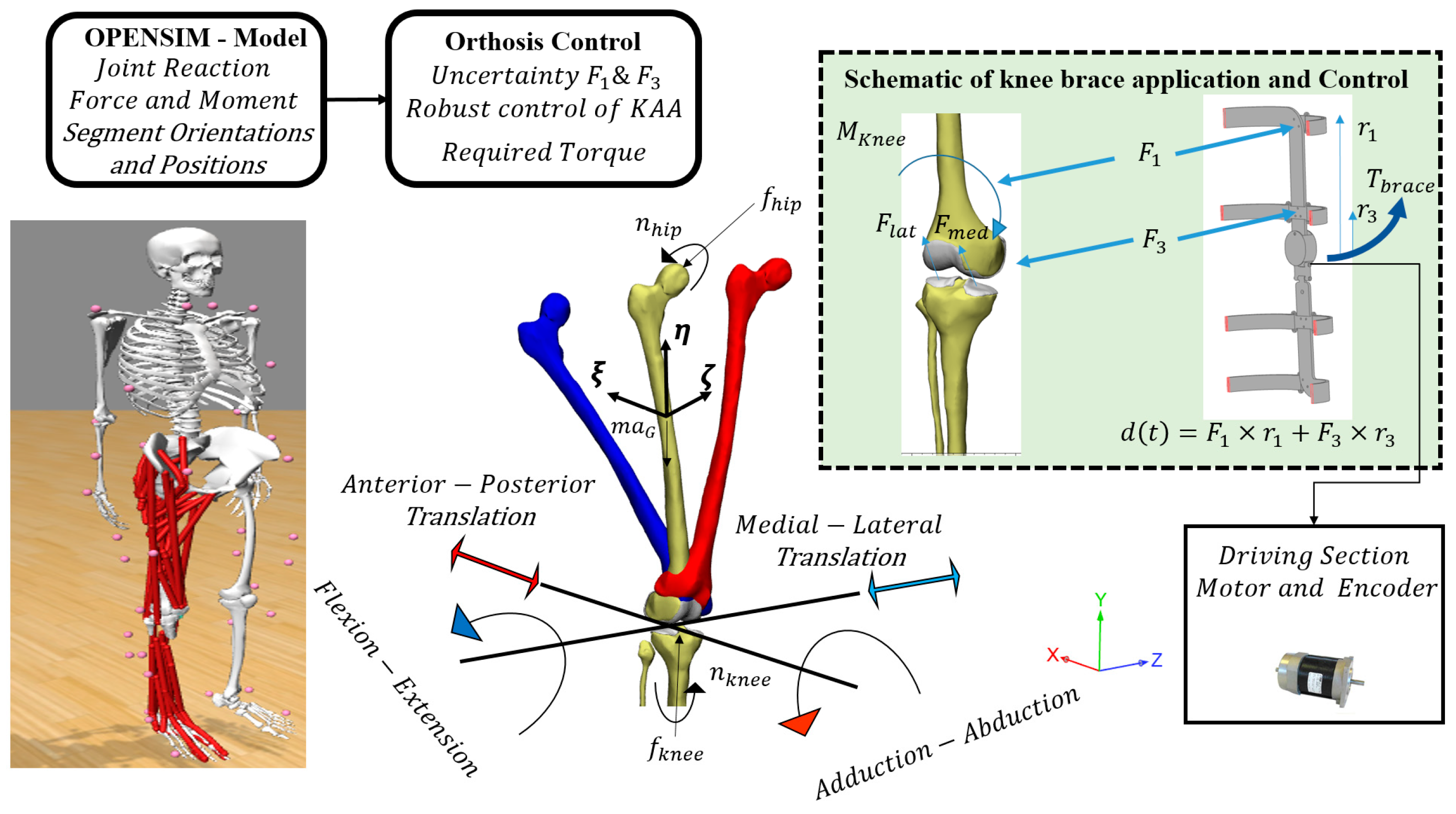
- Step 2: We calculate robust abduction torque to alter the adduction angle in the presence of interaction force uncertainty between the orthosis and the user.
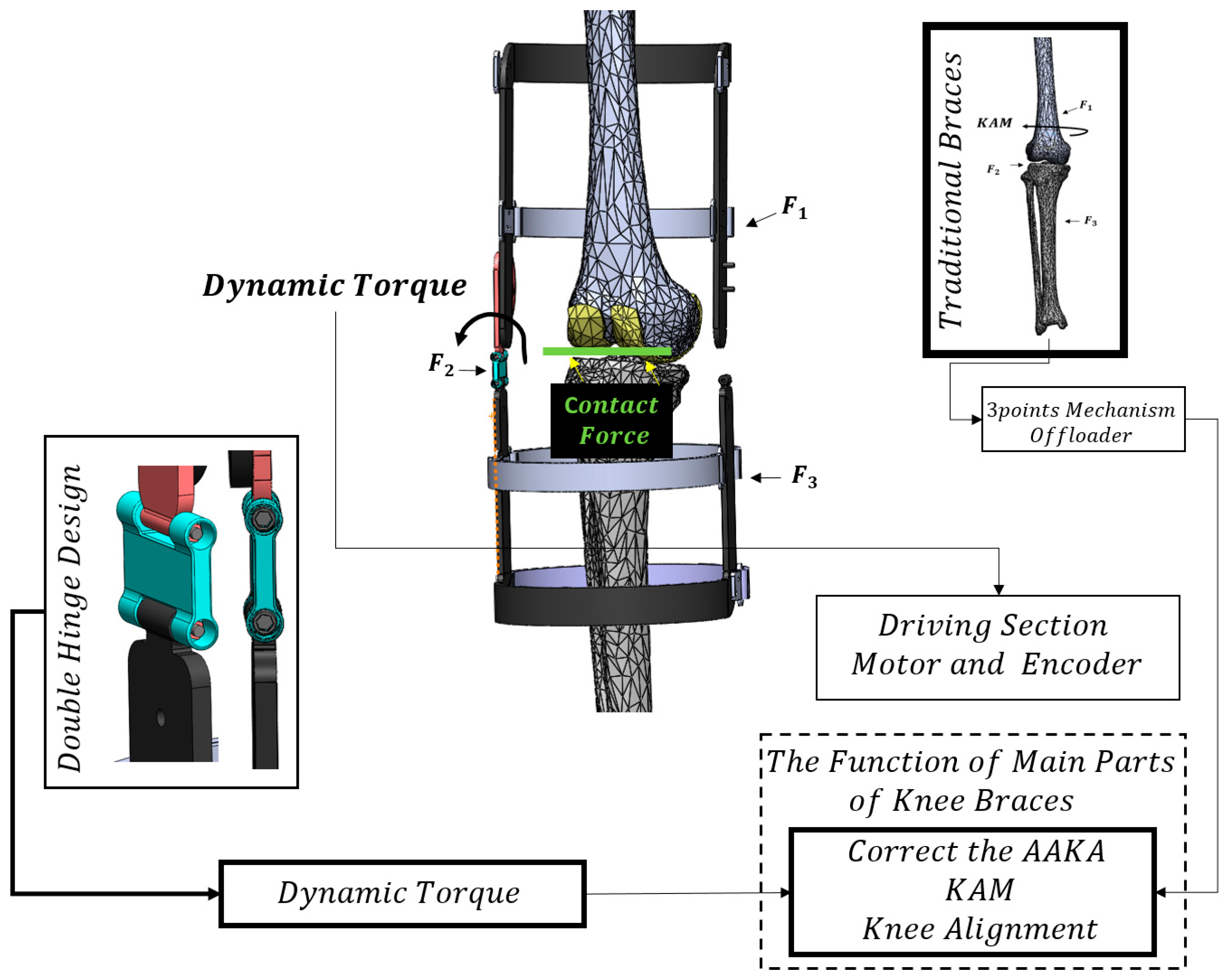
- Step 3: We design the embedded actuator hinge for the knee brace to control the adduction angle.
- Step 4: The nonlinear position controller design according to a robust inverse dynamic method adjusts the abduction torque to track the desired adduction angle.
2. Materials and Methods
2.1. Related Work
2.2. Hypothesis
- Medial unloader braces, although commonly used for KOA, can lead to lateral overloading due to neglecting the phenomenon of unwarranted rotation from adduction to abduction.
- The new embedded actuation mechanism in the proposed unloader brace aims to correct the knee adduction angle (KAA) actively, thereby addressing the issue of lateral compartment overload.
- The computational procedure used in the design of the brace takes into account factors such as cartilage penetration depth, contact force, and contact point, which are surrogate parameters for determining pain and damage in KOA.
- Through simulation and analysis, it is hypothesized that by controlling the KAA and applying external abduction torque, the proposed unloader brace can effectively reduce medial compartment load and prevent excessive lateral compartment loading.
2.3. Problem Statement
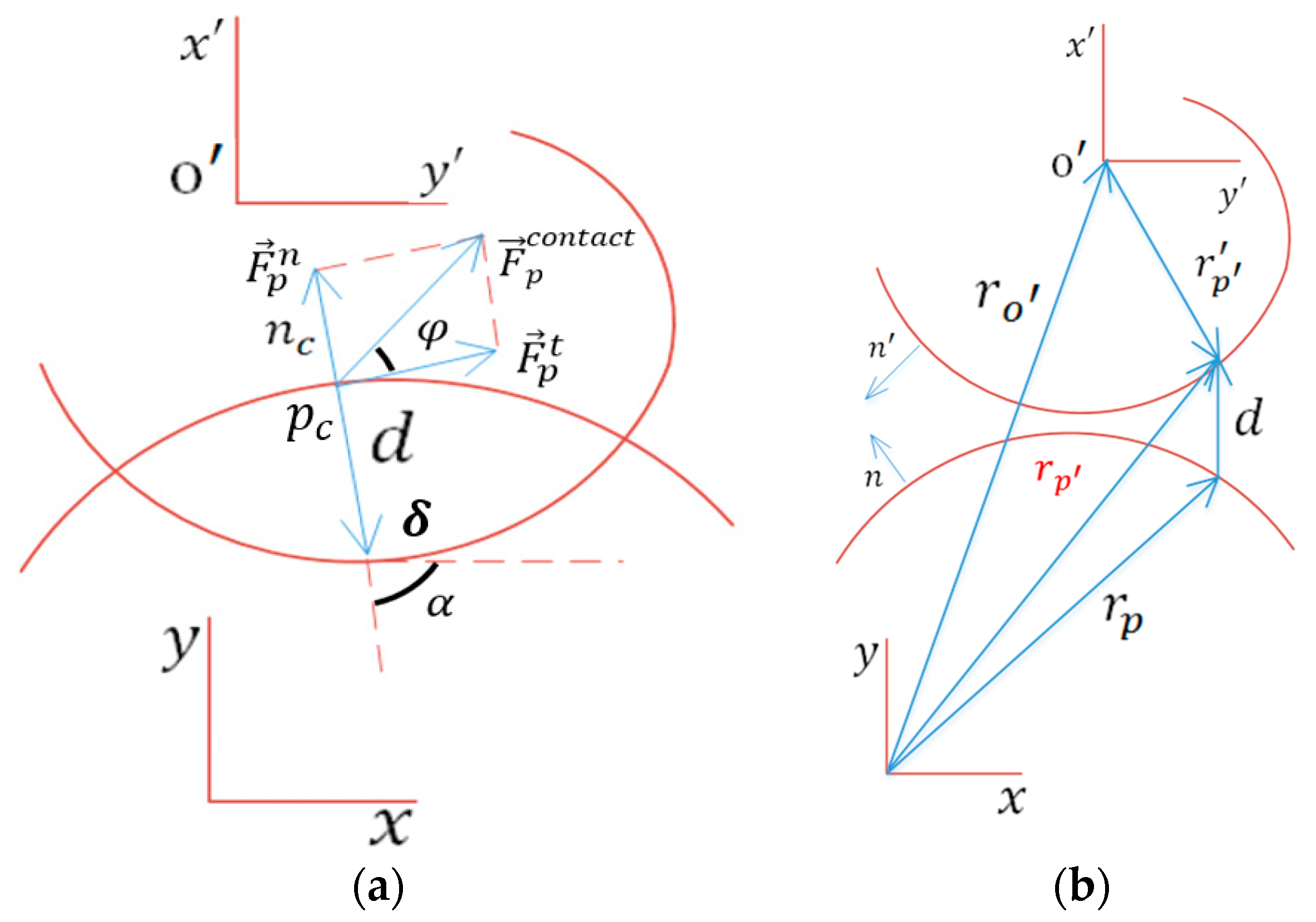
2.4. Knee Joint Model
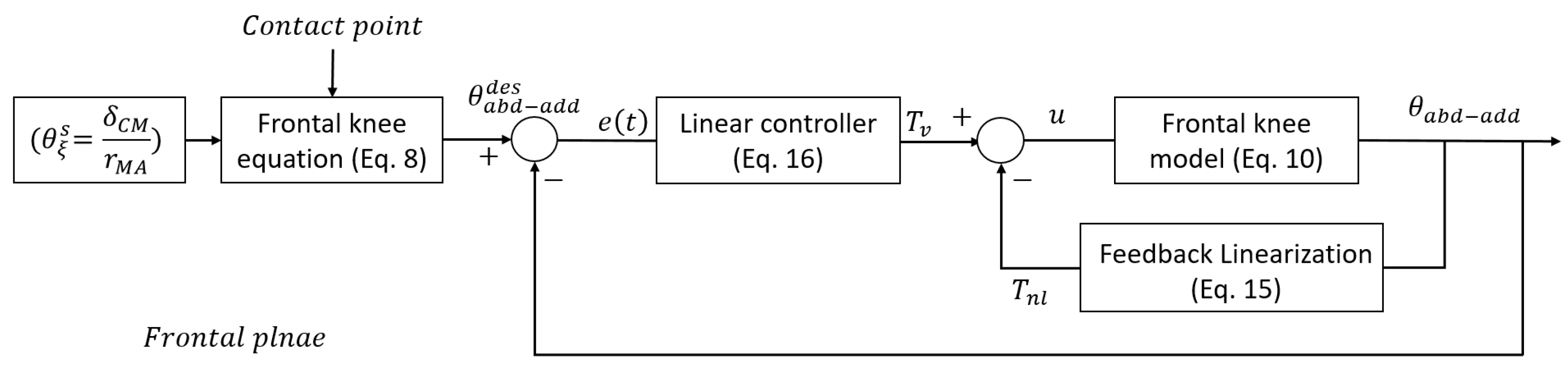
2.5. Dynamic and Control Modeling
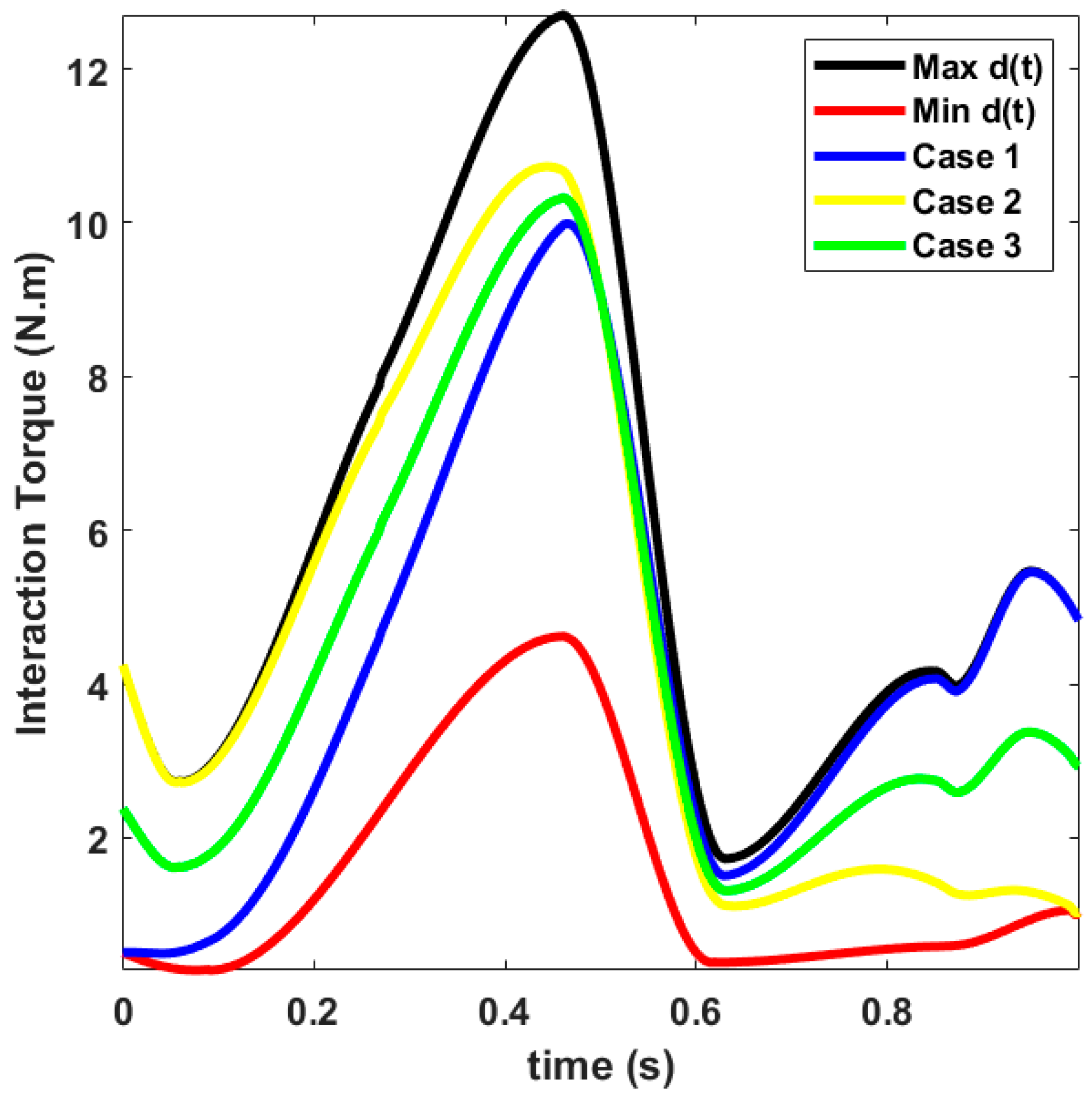
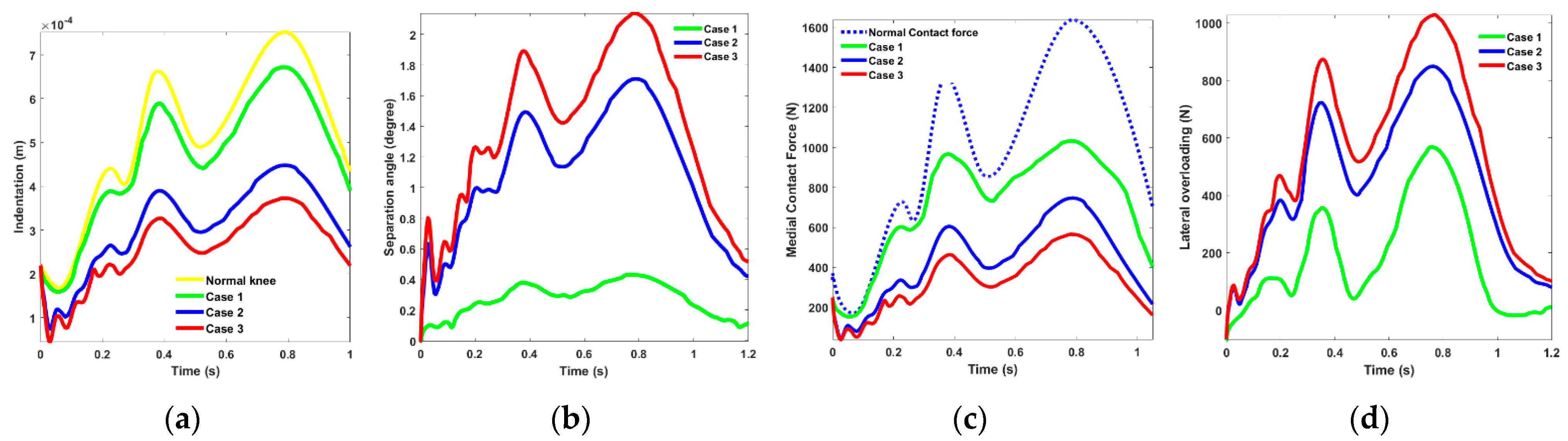
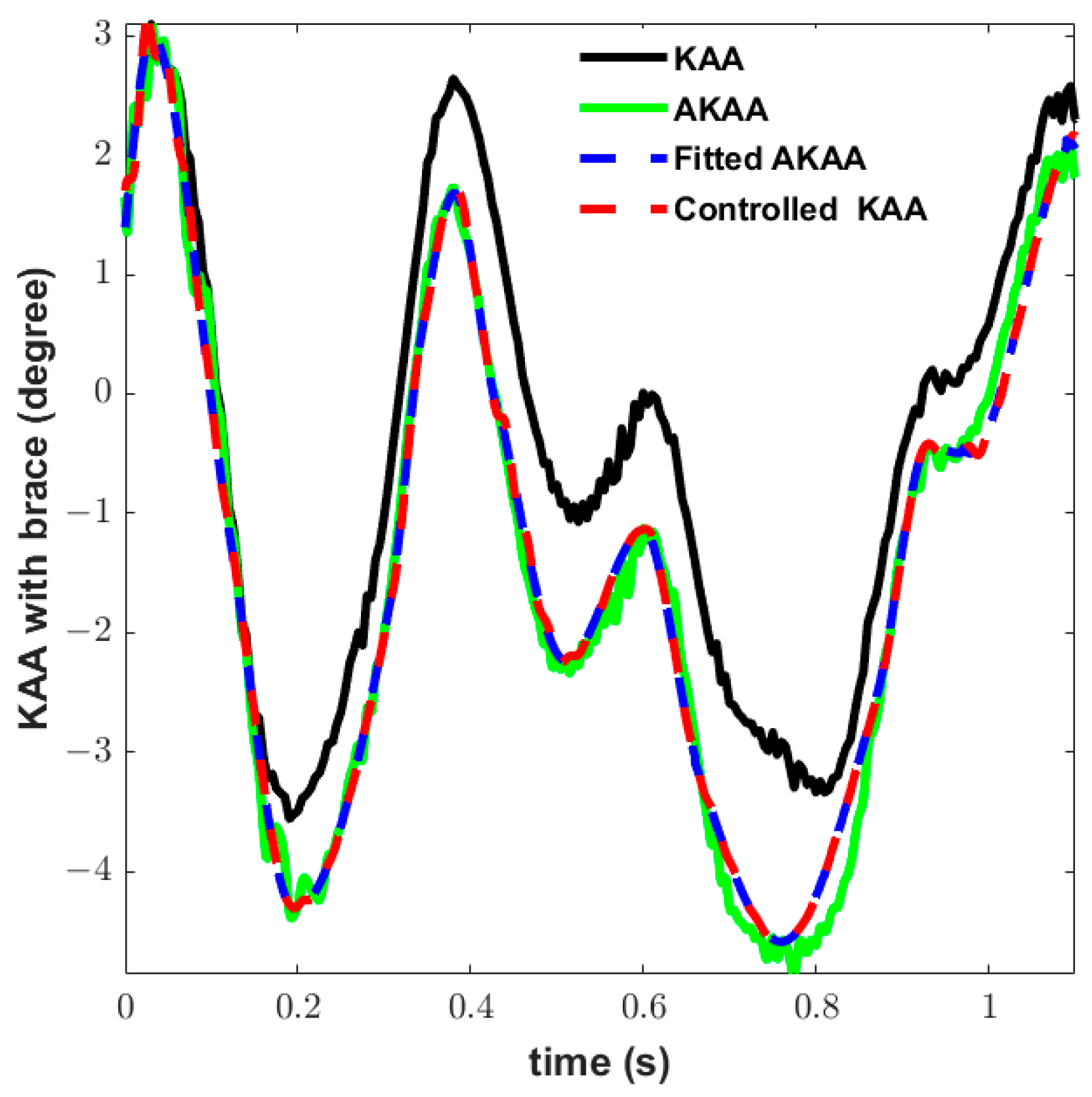
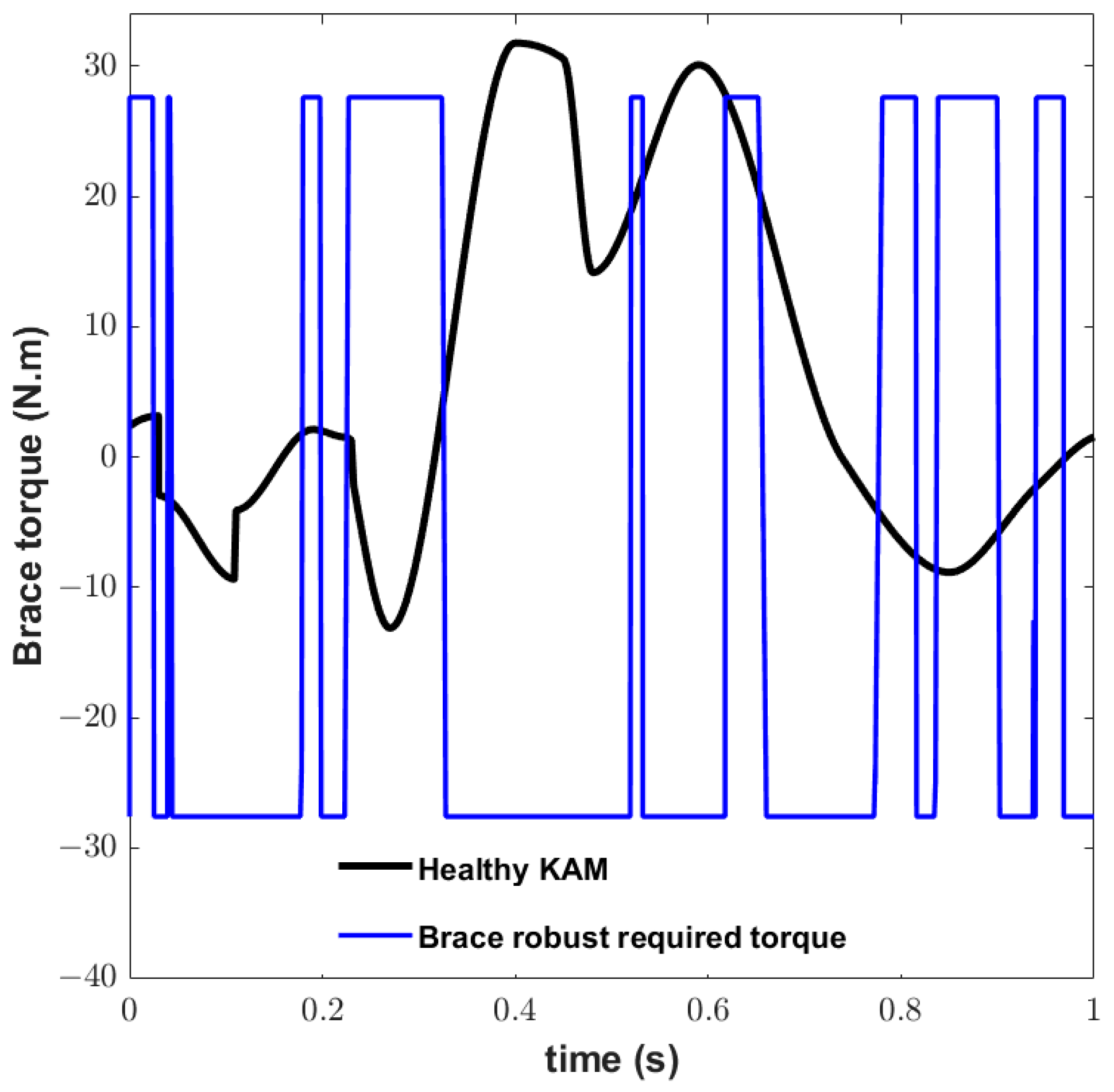
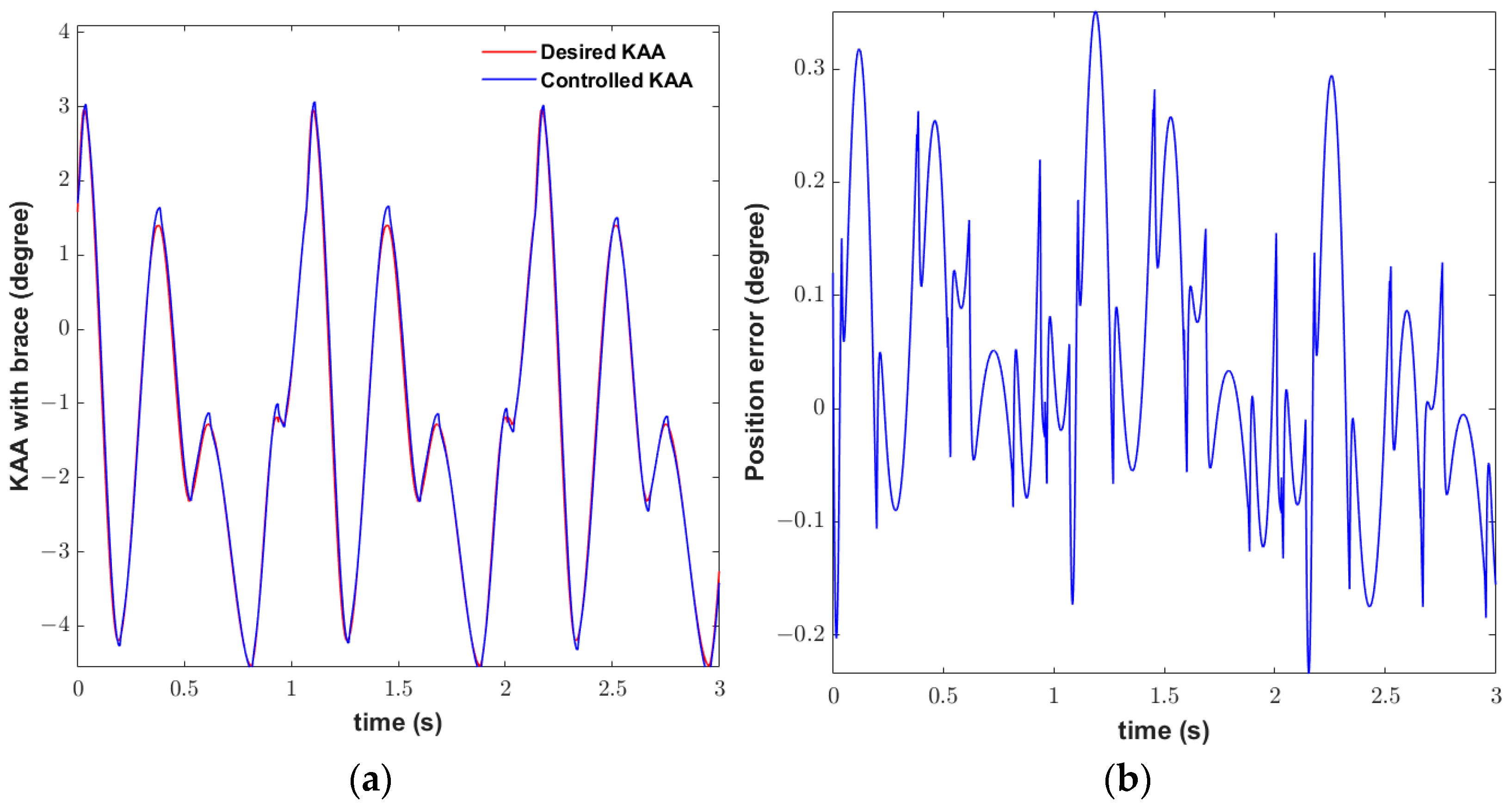
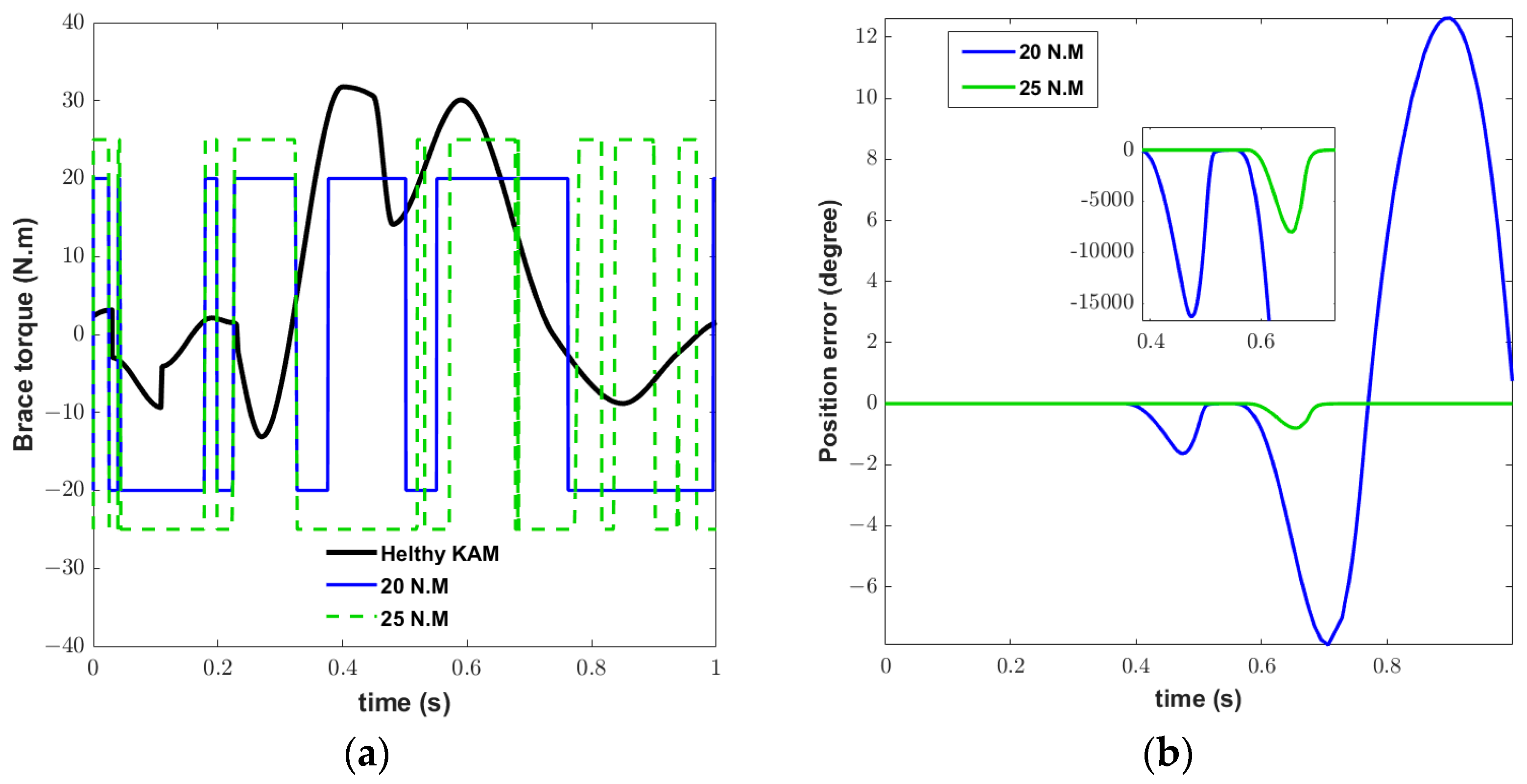
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MCF | Medial contact force |
| KOA | Knee osteoarthritis |
| CF | Contact forces |
| KAM | Knee adduction moment |
| KFM | Knee flexion moment |
| KAA | Knee adduction angle |
| LCF | Lateral contact force |
| MCF | Medial contact force |
| δ | Cartilage penetration depth |
| AKAA | Altered adduction knee angle |
Appendix A
References
- Dieppe, P.; Cushnaghan, J.; Young, P.; Kirwan, J. Prediction of the progression of joint space narrowing in osteoarthritis of the knee by bone scintigraphy. Ann. Rheum. Dis. 1993, 52, 557–563. [Google Scholar] [CrossRef] [PubMed]
- Koshino, T.; Murase, T.; Saito, T. Medial opening-wedge high tibial osteotomy with use of porous hydroxyapatite to treat medial compartment osteoarthritis of the knee. J. Bone Jt. Surg. 2003, 85, 78–85. [Google Scholar] [CrossRef]
- Javanfar, A.; Bamdad, M. (Eds.) Knee brace control for reduction of medial compartment load. In Proceedings of the 10th RSI International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 15–17 November 2022. [Google Scholar]
- Herscovici, D., Jr.; Sammarco, G.J.; Sammarco, V.J.; Scaduto, J.M.; Scaduto, J.M. Pantalar arthrodesis for post-traumatic arthritis and diabetic neuroarthropathy of the ankle and hindfoot. Foot Ankle Int. 2011, 32, 581–588. [Google Scholar] [CrossRef] [PubMed]
- Karatsidis, A. Kinetic Gait Analysis Using Inertial Motion Capture: New Tools for Knee Osteoarthritis. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Su, Q.; Pei, Z.; Tang, Z.; Liang, Q. Design and Analysis of a Lower Limb Loadbearing Exoskeleton. Actuators 2022, 11, 285. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Z.; Liu, J.; Xu, Y. Cost-Effectiveness Analysis Based on Intelligent Electronic Medical Arthroscopy for the Treatment of Varus Knee Osteoarthritis. J. Healthc. Eng. 2021, 2021, 5569872. [Google Scholar] [CrossRef] [PubMed]
- Machado, M.M.F. A Multibody Approach to the Contact Dynamics: A Knee Joint Application. Ph.D. Thesis, Universidade do Minho, Braga, Portugal, 2013. [Google Scholar]
- Lee, P.Y.; Winfield, T.G.; Harris, S.R.; Storey, E.; Chandratreya, A. Unloading knee brace is a cost-effective method to bridge and delay surgery in unicompartmental knee arthritis. BMJ Open Sport Exerc. Med. 2017, 2, e000195. [Google Scholar] [CrossRef]
- Lacquaniti, F.; Maioli, C. Independent control of limb position and contact forces in cat posture. J. Neurophysiol. 1994, 72, 1476–1495. [Google Scholar] [CrossRef] [PubMed]
- Harrington, I.J. Static and dynamic loading patterns in knee joints with deformities. J. Bone Jt. Surg. 1983, 65, 247–259. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, B.W. Gait Modification to Reduce Peak Knee Abduction Moment. Ph.D. Thesis, George Mason University, Fairfax, VA, USA, 2021. [Google Scholar]
- Bowd, J. Does Gait Retraining Have the Potential to Slow Osteoarthritis Development and Prolong the Benefits of Knee Realignment Surgery? Ph.D. Thesis, Cardiff University, Cardiff, UK, 2022. [Google Scholar]
- Rynne, R.; Le Tong, G.; Cheung, R.T.; Constantinou, M. Effectiveness of gait retraining interventions in individuals with hip or knee osteoarthritis: A systematic review and meta-analysis. Gait Posture 2022, 95, 164–175. [Google Scholar] [CrossRef]
- Walter, J.P.; D’Lima, D.D.; Colwell, C.W., Jr.; Fregly, B.J. Decreased knee adduction moment does not guarantee decreased medial contact force during gait. J. Orthop. Res. 2010, 28, 1348–1354. [Google Scholar] [CrossRef]
- Stoltze, J.S.; Rasmussen, J.; Andersen, M.S. On the biomechanical relationship between applied hip, knee and ankle joint moments and the internal knee compressive forces. Int. Biomech. 2018, 5, 63–74. [Google Scholar] [CrossRef]
- Kumar, V.; Hote, Y.V.; Jain, S. (Eds.) Review of exoskeleton: History, design and control. In Proceedings of the 2019 3rd International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 10–11 October 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Mahdi, S.M.; Yousif, N.Q.; Oglah, A.A.; Sadiq, M.E.; Humaidi, A.J.; Azar, A.T. Adaptive Synergetic Motion Control for Wearable Knee-Assistive System: A Rehabilitation of Disabled Patients. Actuators 2022, 11, 176. [Google Scholar] [CrossRef]
- McGibbon, C.A.; Brandon, S.C.; Brookshaw, M.; Sexton, A. Effects of an over-ground exoskeleton on external knee moments during stance phase of gait in healthy adults. Knee 2017, 24, 977–993. [Google Scholar] [CrossRef] [PubMed]
- Walsh, C.J.; Endo, K.; Herr, H.M. A Quasi-passive leg exoskeleton for load-carrying augmentation. Int. J. Hum. Robot. 2007, 4, 487–506. [Google Scholar] [CrossRef]
- Shamaei, K.; Adams, A.A.; Cenciarini, M.; Gregorczyk, K.N.; Dollar, A.M. (Eds.) Preliminary investigation of effects of a quasi-passive knee exoskeleton on gait energetics. In Proceedings of the 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Ramsey, D.K.; Russell, M.E. Unloader Braces for Medial Compartment Knee Osteoarthritis: Implications on Mediating Progression. Sport. Health 2009, 1, 416–426. [Google Scholar] [CrossRef] [PubMed]
- Budarick, A.R.; MacKeil, B.E.; Fitzgerald, S.; Cowper-Smith, C.D. Design Evaluation of a Novel Multicompartment Unloader Knee Brace. J. Biomech. Eng. 2019, 142, 014502. [Google Scholar] [CrossRef]
- Parween, R.; Shriram, D.; Mohan, R.E.; Lee, Y.H.D.; Subburaj, K. Methods for evaluating effects of unloader knee braces on joint health: A review. Biomed. Eng. Lett. 2019, 9, 153–168. [Google Scholar] [CrossRef]
- Shriram, D.; Yamako, G.; Chosa, E.; Lee, Y.H.D.; Subburaj, K. Effects of a valgus unloader brace in the medial meniscectomized knee joint: A biomechanical study. J. Orthop. Surg. Res. 2019, 14, 44. [Google Scholar] [CrossRef]
- Pollo, F.E.; Otis, J.C.; Backus, S.I.; Warren, R.F.; Wickiewicz, T.L. Reduction of Medial Compartment Loads with Valgus Bracing of the Osteoarthritic Knee. Am. J. Sport. Med. 2002, 30, 414–421. [Google Scholar] [CrossRef]
- Cusin, E.; Honeine, J.; Schieppati, M.; Rougier, P. A Simple Method for Measuring the Changeable Mechanical Action of Unloader Knee Braces for Osteoarthritis. IRBM 2018, 39, 136–142. [Google Scholar] [CrossRef]
- Brandon, S.C.; Brown, M.J.; Clouthier, A.L.; Campbell, A.; Richards, J.D.; Deluzio, K.J. Contributions of muscles and external forces to medial knee load reduction due to osteoarthritis braces. Knee 2019, 26, 564–577. [Google Scholar] [CrossRef]
- Adouni, M.; Shirazi-Adl, A. Partitioning of knee joint internal forces in gait is dictated by the knee adduction angle and not by the knee adduction moment. J. Biomech. 2014, 47, 1696–1703. [Google Scholar] [CrossRef]
- Zeighami, A. Tibiofemoral Contact Areas and Contact Forces in Healthy and Osteoarthritic Subjects. Ph.D. Thesis, École de Technologie Supérieure, Montreal, QC, Canada, 2018. [Google Scholar]
- Javanfar, A.; Bamdad, M. Development of a planar multibody model of the knee joint with contact mechanics. Iran. J. Biomed. Eng. 2022, 16, 111–120. [Google Scholar]
- Zhou, X.; Chen, X. Design and Evaluation of Torque Compensation Controllers for a Lower Extremity Exoskeleton. J. Biomech. Eng. 2020, 143, 011007. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, Y.; Wang, R.; Smith, C.; Gutierrez-Farewik, E.M. Modeling and simulation of a human knee exoskeleton’s assistive strategies and interaction. Front. Neurorobot. 2021, 15, 620928. [Google Scholar] [CrossRef]
- Jerbi, H.; Al-Darraji, I.; Tsaramirsis, G.; Ladhar, L.; Omri, M. Hamilton–Jacobi Inequality Adaptive Robust Learning Tracking Controller of Wearable Robotic Knee System. Mathematics 2023, 11, 1351. [Google Scholar] [CrossRef]
- Richards, R.E.; Andersen, M.S.; Harlaar, J.; Van Den Noort, J.C. Relationship between knee joint contact forces and external knee joint moments in patients with medial knee osteoarthritis: Effects of gait modifications. Osteoarthr. Cartil. 2018, 26, 1203–1214. [Google Scholar] [CrossRef] [PubMed]
- Reeves, N.D.; Bowling, F.L. Conservative biomechanical strategies for knee osteoarthritis. Nat. Rev. Rheumatol. 2011, 7, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef]
- Bingham, J.T.; Papannagari, R.; Van de Velde, S.K.; Gross, C.; Gill, T.J.; Felson, D.T.; Rubash, H.E.; Li, G. In vivo cartilage contact deformation in the healthy human tibiofemoral joint. Rheumatology 2008, 47, 1622–1627. [Google Scholar] [CrossRef]
- Javanfar, A.; Bamdad, M. A developed multibody knee model for unloading knee with cartilage penetration depth control. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2022, 236, 1528–1540. [Google Scholar] [CrossRef]
- Bamdad, M.; Zarshenas, H. Robotic rehabilitation with the elbow stiffness adjustability. Modares Mech. Eng. 2015, 14, 151–158. [Google Scholar]
- Gross, K.D.; Hillstrom, H.J. Noninvasive Devices Targeting the Mechanics of Osteoarthritis. Rheum. Dis. Clin. N. Am. 2008, 34, 755–776. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, X.; Huang, T.-H.; Yu, S.; Li, Y.; Chen, T.; Carriero, A.; Oh-Park, M.; Su, H. Comfort-Centered Design of a Lightweight and Backdrivable Knee Exoskeleton. IEEE Robot. Autom. Lett. 2018, 3, 4265–4272. [Google Scholar] [CrossRef]
- Lenhart, R.L.; Kaiser, J.; Smith, C.; Thelen, D.G. Prediction and Validation of Load-Dependent Behavior of the Tibiofemoral and Patellofemoral Joints During Movement. Ann. Biomed. Eng. 2015, 43, 2675–2685. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Robertson, D.G.E.; Caldwell, G.E.; Hamill, J.; Kamen, G.; Whittlesey, S. Research Methods in Biomechanics; Human kinetics: Champaign, IL, USA, 2013. [Google Scholar]
- Wu, J.; Gao, J.; Song, R.; Li, R.; Li, Y.; Jiang, L. The design and control of a 3DOF lower limb rehabilitation robot. Mechatronics 2016, 33, 13–22. [Google Scholar] [CrossRef]
- Bamdad, M.; Parivash, F. Integrated active and passive gravity compensation method for a cable-actuated elbow rehabilitation robot. In Proceedings of the 2015 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7 October 2015; pp. 79–84. [Google Scholar]
- Roodsari, R.B.; Esteki, A.; Aminian, G.; Ebrahimi, I.; Mousavi, M.E.; Majdoleslami, B.; Bahramian, F. The effect of orthotic devices on knee adduction moment, pain and function in medial compartment knee osteoarthritis: A literature review. Disabil. Rehabil. Assist. Technol. 2016, 12, 441–449. [Google Scholar] [CrossRef] [PubMed]
- Komistek, R.D.; Dennis, D.A.; Northcut, E.J.; Wood, A.; Parker, A.W.; Traina, S.M. An in vivo analysis of the effectiveness of the osteoarthritic knee brace during heel-strike of gait. J. Arthroplast. 1999, 14, 738–742. [Google Scholar] [CrossRef] [PubMed]
- Segal, N.A. Bracing and Orthoses: A Review of Efficacy and Mechanical Effects for Tibiofemoral Osteoarthritis. PMR 2012, 4, S89–S96. [Google Scholar] [CrossRef]
- Neville, S.R.; Brandon, S.C.; Brown, M.J.; Deluzio, K.J. Validation of method for analysing mechanics of unloader brace for medial knee osteoarthritis. J. Biomech. 2018, 76, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Kutzner, I.; Küther, S.; Heinlein, B.; Dymke, J.; Bender, A.; Halder, A.M.; Bergmann, G. The effect of valgus braces on medial compartment load of the knee joint—In vivo load measurements in three subjects. J. Biomech. 2011, 44, 1354–1360. [Google Scholar] [CrossRef] [PubMed]
- Koo, S.; Andriacchi, T.P. A comparison of the influence of global functional loads vs. local contact anatomy on articular cartilage thickness at the knee. J. Biomech. 2007, 40, 2961–2966. [Google Scholar] [CrossRef] [PubMed]





| OA Brace Type/ Research | Medial Unloading (BW) | Lateral Overloading (BW) | Abduction Torque (Nm/kg) | Separation Angle (Degree) | |
|---|---|---|---|---|---|
| Valgus Brace Alignment 8° in [25] | 0.82 (600 N/74 Kg) | 0.55 (400 N/74 Kg) | - | 1 | |
| Three-Point Bending Double Upright in [28] | 0.3 | 0.2 | 0.1 | - | |
| Unloader Brace Present study | Case I | 0.8 | 0.76 | 0.25 | 0.43 |
| Case II | 1.18 | 1.14 | 0.36 | 1.7 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bamdad, M.; Javanfar, A. Computational Control Strategy for Reducing Medial Compartment Load in Knee Bracing with Embedded Actuator. Actuators 2023, 12, 256. https://doi.org/10.3390/act12060256
Bamdad M, Javanfar A. Computational Control Strategy for Reducing Medial Compartment Load in Knee Bracing with Embedded Actuator. Actuators. 2023; 12(6):256. https://doi.org/10.3390/act12060256
Chicago/Turabian StyleBamdad, Mahdi, and Amirhosein Javanfar. 2023. "Computational Control Strategy for Reducing Medial Compartment Load in Knee Bracing with Embedded Actuator" Actuators 12, no. 6: 256. https://doi.org/10.3390/act12060256
APA StyleBamdad, M., & Javanfar, A. (2023). Computational Control Strategy for Reducing Medial Compartment Load in Knee Bracing with Embedded Actuator. Actuators, 12(6), 256. https://doi.org/10.3390/act12060256





