Fault Detection and Reliable Controller Design for Fractional-Order Systems Based on Dynamic Observer

Abstract

In this paper, the problem of the fractional-order linear systems’ simultaneous fault detection and reliable control (SFDC) in the finite frequency domain is investigated. A dynamic observer aimed at detecting faults is designed, which also generates state estimation signals. In particular, it is found that the proposed dynamic-observer-based controller can achieve a better $H_{\infty }$ performance. We derived the detector and controller’s design conditions to achieve $H_{-}$ fault sensitivity performance and $H_{\infty }$ interference attenuation performance in the limited frequency domain based on the generalized KYP lemma, which can achieve a better disturbance attenuation performance and fault sensitivity performance. Finally, the simulation results show the designed method’s effectiveness.

1. Introduction

Fractional-order theory has successfully solved many non-classical problems in practical systems, which makes it an important branch of mathematics. It has been proved that fractional calculus can more accurately describe the actual models in the fields of network control, structural mechanics, biological genetics, economics and so on [1,2,3]. Due to their special properties, fractional-order systems (FOSs) have received increasing attention in recent years. The main feature of a fractional derivative equation is its ability to model real-word physical systems very well, with postponement and memory. Moreover, its extra degree of freedom is conducive to improving the performance of control systems [4,5,6]. Nowadays, the fractional-order system theory has been widely used in the field of engineering control.

Stability is an important concept in control theory, and the analysis of system stability is the primary task of control system research. To date, the research on the stability theory of fractional-order systems is still undergoing continuous improvement, and is far from reaching a mature level [7,8,9]. The stability analyses of fractional-order control systems were considered in [10,11,12]. As is well known, external disturbances, as well as plant uncertainties, inevitably occur in real-world applications. Therefore, the corresponding $H_{\infty }$ optimal control theory must be developed for FOSs. Similarly, many useful analysis and synthesis results about the $H_{\infty }$ control problem for FOSs have been presented [13,14,15]. With the theoretical development of fractional controllers, and fractional differential equations including the CRONE principle [16], the fractional lead-lag compensator [17] has been put forward, which possess more robustness and flexibility.

Considering the complex working conditions and mechanical fatigue, the occurrence of system failure is often difficult to avoid. It is known that faults could degrade system performance, and in the worst cases can cause serious destruction. Therefore, it is very meaningful to reduce the fault’s impact so as to accurately detect the fault and take measures. In recent years, for integer-order systems, there exist some monographs involving fault-tolerant control (FTC) [18,19,20]. Note that, for the fault detection (FD) of an integer-order linear system, the definition of the $H_{-}$ index was used in [21] to estimate fault sensitivity. With the performance indicators defined in this way, we have transformed the design problem of fault detection observers in [22] into a multi-target optimization problem, and by using the $H_{-}/H_{\infty }$ techniques, have also produced many results about how to design fault detectors [23,24]. However, system failure usually occurs in low-frequency bands.This is why the finite-frequency FD design method is more reasonable and meaningful. Fortunately, in [25] the developed generalized Kalman–Yakubovich–Popov (KYP) lemma is proposed, and linear matrix inequalities (LMI) are used to describe the $H_{-}$ index at a finite frequency. For strictly correct systems, the matrix can obtain a true minimum singular value. Considering this method, many important results on the FD problem are put forward in the literature [26,27,28].

For most of the above results, we usually assumed that the system is open-loop stable or that the original control strategy can still ensure the stability of the system when faults occur, which is too strict for most practical closed-loop feedback control systems. Therefore, in the last few years, the SFDC problem has attracted widespread notice. Compared with the separate design’s case, its complexity is lower and this is a reasonable approach, because each unit’s design should consider another unit. According to different performance requirements, many SFDC methods have been proposed. For example, the authors in [29] investigated the SFDC problem in the multi-object robust control framework. In [30], the SFDC problem is converted into a $H_{\infty }$ filtering problem. We can address the SFDC problem in [31] by introducing the $H_2/H_{\infty }$ optimization technique.

With the fractional-order models’ increasing application in actual control systems and the importance of actual system reliability, people are becoming increasingly interested in fault-tolerant control, including fractional-order systems and diagnosis. In [32], a robust FTC method aimed at uncertainties and actuator failure was raised for FOSs. A fractional high-gain observer and a reduced-order fractional proportional integral observer were put forward to design a class of FTC schemes in [33] for fractional nonlinear systems. In [34], taking fuzzy T-S fractional-order systems with actuator failures and saturation into consideration, a flexible fault-tolerant controller was designed. In [35], the second-order sliding pattern approach was able to address the FOSs’ fault detection problem. Moreover, the design method of the $H_{-}/H_{\infty }$ fault detection observer was raised in [36] to address the faults and the sensitivity of the robustness to disturbances.

Motivated by the above analysis, this paper investigated the fractional-order linear systems’ SFDC problem, where the fault is considered to be in the finite-frequency range. A composite unit based on a fractional-order dynamic observer is designed to generate a detection signal and a control signal, which are useful to detect faults and ensure some control objectives. To guarantee the ideal interference attenuation performance and the fault sensitivity performance, one new bounded real lemma for fractional-order systems is presented by introducing the generalized KYP Lemma. In order to ensure the solvability of the observer and the controller, a linearizing change-of-variables and a tangent hyperplane technique are adopted to transform the sufficient conditions into a series of LMI. Furthermore, the comparison simulation test shows that the proposed approach for FOS has better $H_{\infty }$ performance.

The organization of the article is as follows. In Section 2, we give the problem statements and preliminaries. In Section 3, we present solutions to the SFDC problem for a linear fractional-order system. In order to prove the the proposed approach’s effectiveness, we give a numerical example in Section 4, and present our conclusions in Section 6.

Notations: The complex number and real number are represented by $\mathbb{C}$ and $\mathbb{R}$, respectively. We define $He\left(A\right):=A+A^T$ for any matrix $A\in {\mathbb{R}}^{n\times n}$. ${\mathbb{H}}_n$ represents the whole set of $n\times n$ Hermitian matrices. For any matrix $Z\in {\mathbb{C}}^{n\times n}$, the matrix’s real and imaginary part of the Z are $Re\left(Z\right)$ and $Im\left(Z\right)$, respectively. The conjugate transposition matrix of Z is $Z^{\ast }$. For matrices $X\in {\mathbb{C}}^{n\times m}$ and $Y\in {\mathbb{H}}_{n+m}$, we define a function $\sigma (X,Y):=[X,I]Y{[X,I]}^{\ast }$, where $\sigma$ : ${\mathbb{C}}^{n\times m}\times {\mathbb{H}}_{n+m}$→${\mathbb{H}}_m$.

2. Problem Formulation

Consider the following fractional linear system:

$$\left\{\begin{array}{c}{D}^{\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+B_{d}d\left(t\right)+B_{f}f\left(t\right)\hfill \\ y\left(t\right)=C_{1}x\left(t\right)\hfill \\ z\left(t\right)=C_{2}x\left(t\right)+Du\left(t\right)+D_{d}d\left(t\right)\hfill \end{array}\right.$$

(1)

where the fractional proportional order is $\alpha$ and $0<\alpha <1$. $x\left(t\right)\in R^n$ is the pseudo state, and the control output and input are $y\left(t\right)\in R^p$ and $u\left(t\right)\in R^m$, respectively. A, $B_d$, B, $C_1$, $B_f$, $C_2$, D and $D_d$ are system-constant matrices which have proper dimensions. The transfer function matrix from $d\left(t\right)$ to $z\left(t\right)$ is as follows, assuming the pairs $(A,B)$ and $(A,C_1)$ are detectable and stabilizable.

$$\begin{array}{c}\hfill G\left(s\right)=C_2{(s^{\alpha }I-A)}^{-1}{B}_d+D_d\end{array}$$

(2)

The use and definition of the Caputo fractional-order derivative [3] are as follows:

$$\begin{array}{c}\hfill D^{\alpha }f\left(t\right)=\frac{1}{\Gamma (m-\alpha )}{\int }_0^t\frac{f^{\left(m\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha +1-m}}d\tau \end{array}$$

where $f\left(t\right)$ is a function that changes over time, $\alpha$ represents the derivative’s order ($m\in N$ and $m-1<\alpha \le m$), and the Gamma function of $\Gamma$ is $\Gamma \left(s\right)={\int }_0^{\infty }{t}^{s-1}{e}^{-t}dt$.

Generally, we regard the frequency ranges as some complex numbers [25,37] if the matrices meet $\Phi ,\Psi \in H_2$:

$$\begin{array}{c}\hfill \Lambda (\Phi ,\Psi ):=\{\lambda \in \mathbb{C}|\sigma (\lambda ,\Phi )=0,\sigma (\lambda ,\Psi )\ge 0\},\end{array}$$

(3)

Then, in a certain range, $\Lambda (\Phi ,\Psi )$ can represent the frequency curve by selecting the appropriate matrices, $\Phi$ and $\Psi$. For FOSs, we choose

$$\begin{array}{c}\hfill \Phi =\left[\begin{array}{cc}0& r\\ ★& 0\end{array}\right]\end{array}$$

(4)

to describe the curve $\Lambda =\left\{{\left(j\omega \right)}^{\alpha }\right|\omega \in \Omega \}$, where $r=e^{j\theta }$, $\theta =(\alpha -1)\pi /2$, and the additional choice of $\Psi$ is used to choose a subset of real numbers $\Omega$. An example is listed in Table 1, where ${\omega }_c=({\omega }_l^{\alpha }+{\omega }_h^{\alpha })/2$, ${\omega }_h\ge 0$, and ${\omega }_l\ge 0$, the low-, middle- and high-frequency ranges, are expressed by LF, MF, and HF, respectively.

Definition 1.

For the FOS (1), we defined the transfer function $G\left(s\right)$’s index $H_{-}$ in a limited frequency domain, as shown below:

$$\begin{array}{c}\hfill {\Vert G\left(s\right)\Vert }_{-}:=\underset{\omega }{inf}{\sigma }_{min}\left(G\left({\left(j\omega \right)}^{\alpha }\right)\right),\forall \omega \in \Omega ,\end{array}$$

(5)

where ${\sigma }_{min}$ represents the smallest singular value.

Remark 1.

In fact, we use the $H_{-}$ index given in the first definition to evaluate the fault sensitivity in the worst case. By comparing it with the $H_{-}$ index defined in [36], it is seen to be more general, where the frequency spectrum is $[0,\infty )$.

Remark 2.

In actual engineering, the controlled object usually has nonlinearity, and some real systems cannot be described by linear models, so it is of significance to conduct fault diagnosis and control research for fractional-order nonlinear systems at the same time. From the perspective of the transfer function matrix, this paper conducts fault diagnosis research on a fractional-order system based on the fractional-order generalized KYP lemma. There is no transfer function for fractional-order nonlinear systems, so the proposed method cannot be directly applied to nonlinear systems. Therefore, the problem of fault diagnosis and control of fractional-order nonlinear systems is also very challenging.

Table 1. Different limited frequency ranges.

	LF	MF	HF
$\Omega$	$\omega \le {\omega }_l$	${\omega }_l\le \omega \le {\omega }_h$	$\omega \ge {\omega }_h$
$\Psi$	$\left[\begin{array}{cc}-1& 0\\ ★& {\omega }_l^{2\alpha }\end{array}\right]$	$\left[\begin{array}{cc}-1& jr{\omega }_c\\ ★& -{\omega }_l^{\alpha }{\omega }_h^{\alpha }\end{array}\right]$	$\left[\begin{array}{cc}-1& 0\\ ★& {\omega }_l^{2\alpha }\end{array}\right]$

Inspired by the dynamic observers form of integer-order linear systems [38,39,40], the controller’s design based on the fractional-order dynamic observer is as follows:

$$\left\{\begin{array}{c}{D}^{\alpha }\widehat{x}=A\widehat{x}+Bu+\eta \hfill \\ \widehat{y}=C\widehat{x}\hfill \\ D^{\alpha }\xi =A_L\xi +B_L(y-\widehat{y})\hfill \\ \eta =C_L\xi +D_L(y-\widehat{y})\hfill \\ u=K\widehat{x}\hfill \end{array}\right.$$

(6)

The design of matrices $A_L$, $B_L$, $C_L$, $D_L$ and K is uncertain. The system state and observer output’s estimation are $\widehat{x}\left(t\right)$ and $\widehat{y}\left(t\right)$, respectively. The auxiliary state is $\xi \left(t\right)$ and $\eta \left(t\right)$ is the calibration signal.

Defining $e=x-\widehat{x}$ and $\overline{x}={[x^T,e^T,{\xi }^T]}^T$, from (1) and (6), we obtained the following augmented system:

$$\left\{\begin{array}{c}{D}^{\alpha }\overline{x}=\overline{A}\overline{x}+{\overline{B}}_{f}f+{\overline{B}}_{d}d\hfill \\ r={\overline{C}}_1\overline{x}\hfill \\ z={\overline{C}}_2\overline{x}+D_{d}d\hfill \end{array}\right.$$

(7)

where

$$\begin{array}{cc}\hfill & \overline{A}=\left[\begin{array}{ccc}BK+A& -BK& 0\\ 0& -D_{L}C+A& -C_L\\ 0& B_{L}C& A_L\end{array}\right]\hfill \\ \hfill & {\overline{B}}_f=\left[\begin{array}{c}{B}_f\\ B_f\\ 0\end{array}\right],{\overline{B}}_d=\left[\begin{array}{c}{B}_d\\ B_d\\ 0\end{array}\right]\hfill \\ \hfill & {\overline{C}}_1=[V-V0],{\overline{C}}_2=[DK+C_2-DK0]\hfill \end{array}$$

(8)

Remark 3.

The dynamic observer (6) can reduce to the Luenberger-type fractional-order observer when setting $A_L=B_L=C_L=0$ and $D_L=L$. Therefore, it can be seen that a dynamic observer’s (6) special case is a Luenberger-type fractional-order observer in [10,12].

SFDC problem: For FOS (7), the design of the detector/controller (6) should be such that

1. For control objectives, the augmented system (7) is stable and the influence of disturbances and faults on regulation output $z\left(t\right)$ is minimized. Then, for the performance indexes ${\gamma }_1$ and ${\gamma }_2$, the performance requirements are formulated as follows:

$$\begin{array}{cc}\hfill & \underset{\omega }{sup}{\sigma }_{max}\left(G_{zf}{\left(j\omega \right)}^{\alpha }\right)<{\gamma }_1,\forall 0<\omega <{\omega }_1\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \underset{\omega }{sup}{\sigma }_{max}\left(G_{zd}{\left(j\omega \right)}^{\alpha }\right)<{\gamma }_2,\forall \omega \in (-\infty ,+\infty )\hfill \end{array}$$

(10)

where ${\omega }_1$ is a positive scalar, and we define the transfer functions from $f\left(t\right)$ and $d\left(t\right)$ to $z\left(t\right)$ as follows:

$$\begin{array}{cc}\hfill & G_{zf}={\overline{C}}_2{\left(j\omega \right)}^{\alpha }I-\overline{A}{)}^{-1}{\overline{B}}_f\hfill \\ \hfill & G_{zd}={\overline{C}}_2{\left(j\omega \right)}^{\alpha }I-\overline{A}{)}^{-1}{\overline{B}}_d+D_d\hfill \end{array}$$

2. For detection targets, the fault’s impact on the regulated output $r\left(t\right)$ is expected to be as small as possible when the fault has the greatest impact on the residual signal $r\left(t\right)$. Then, for performance indexes ${\gamma }_3$ and $\beta$, the performance requirements are formulated as follows:

$$\begin{array}{cc}\hfill & \underset{\omega }{inf}{\sigma }_{min}\left(G_{rf}{\left(j\omega \right)}^{\alpha }\right)>\beta ,\forall 0<\omega <{\omega }_1\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & \underset{\omega }{sup}{\sigma }_{max}\left(G_{rd}{\left(j\omega \right)}^{\alpha }\right)<{\gamma }_3,\forall \omega \in (-\infty ,+\infty )\hfill \end{array}$$

(12)

where the transfer functions from $f\left(t\right)$ and $d\left(t\right)$ to $r\left(t\right)$ are $G_{rf}$ and $G_{rd}$, respectively, defined as follows:

$$\begin{array}{cc}\hfill & G_{zf}={\overline{C}}_2({(G_{rf}{\left(j\omega \right)}^{\alpha }I-\overline{A})}^{-1}{\overline{B}}_f\hfill \\ \hfill & G_{zd}={\overline{C}}_2({(G_{rd}{\left(j\omega \right)}^{\alpha }I-\overline{A})}^{-1}{\overline{B}}_d+D_d\hfill \end{array}$$

The performance requirements (9), (10) and (12) are $H_{\infty }$ optimization problems which can attenuate the disturbance influence on the residual $r\left(t\right)$ signal and regulated output $z\left(t\right)$, being also able to attenuate the fault effects on the regulated output $z\left(t\right)$. Furthermore, to guarantee the residuals’ sensitivity to the faults, we use the $H_{-}$ index. The performance requirement (11) is an $H_{-}$ optimization problem, and by increasing the positive real number $\beta$, it will also enhance the sensitivity. Hence, our problem is a mixed $H_{-}/H_{\infty }$ SFDC (detector/controller) design.

The following lemmas play an important role in our main results:

Lemma 1

([41]). With $0<\alpha <1$, the system (1) is asymptotically stable and satisfies the condition $\parallel T_{zd}{\left(s\right)\parallel }_{\infty }\le \gamma$ in the presence of a positive definite Hermitian matrix $X=X^{\ast }\in C^{n\times n}>0$ and a positive real number γ such that

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}He\left(A(rZ+\overline{r}\overline{Z})\right)& \ast & \ast \\ C_2(rZ+\overline{r}\overline{Z})& -\gamma I& \ast \\ B^T& D_d^T& -\gamma I\end{array}\right]<0\end{array}$$

(13)

where $r=e^{j(1-\alpha )\pi /2}.$

Lemma 2

([42]). Assuming γ is a positive scalar, we can derive the following equivalent statements:

(i) 

There is a Hermitian matrix $X=X^{\ast }\in C^{n\times n}>0$ such that

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}He\left(A(rX+\overline{r}\overline{X})\right)& \ast & \ast \\ C(rX+\overline{r}\overline{X})& -\gamma I& \ast \\ B^T& D^T& -\gamma I\end{array}\right]<0\end{array}$$

(14)

where $r=e^{j\theta }$, $\theta =(1-\alpha )\pi /2$.

(ii) 

There is a matrix variable $P\in R^{n\times n}$ such that

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}{\varphi }_{p2}& \ast & \ast \\ CP& -\gamma I& \\ B^T& D^T& -\gamma I\end{array}\right]<0\end{array}$$

(15)

$$\begin{array}{c}\hfill \left[\begin{array}{cc}(P+P^T)/\left(4cos\theta \right)& \left({\varphi }_{p1}\right)/\left(4sin\theta \right))\\ {\left({\varphi }_{p1}\right)}^T/\left(4sin\theta \right)& (P+P^T)/\left(4cos\theta \right)\end{array}\right]>0\end{array}$$

(16)

where ${\varphi }_{p1}=P^T-P$, $\theta =(1-\alpha )\pi /2$, ${\varphi }_{p2}={\left(AP\right)}^T+AP$.

Lemma 3

(Projection Lemma [43]). Given two matrices Γ and Π, as well as a symmetric matrix Ξ, there is a matrix satisfying Θ

$$\begin{array}{c}\Xi +\Gamma \Theta \Pi +{(\Gamma \Theta \Pi )}^T<0\hfill \end{array}$$

(17)

if and only if

$$\begin{array}{c}{\Gamma }^{\perp }\Xi {\Gamma }^{\perp T}<0\hfill \end{array}$$

(18)

$$\begin{array}{c}{\Pi }^{T\perp }\Xi {\Pi }^{T\perp T}<0\hfill \end{array}$$

(19)

Lemma 4.

Given a symmetric matrix Π and the appropriately dimensioned matrices A, B, C, and D, we derive the following equivalent LMI conditions:

(i) 

For $G\left({\left(j\omega \right)}^{\alpha }\right)=C{({\left(j\omega \right)}^{\alpha }I-A)}^{-1}B+D$, the following LMI holds

$$\begin{array}{c}\hfill \left[\begin{array}{cc}G\left({\left(j\omega \right)}^{\alpha }\right)& I\end{array}\right]\Pi \left[\begin{array}{c}G{\left({\left(j\omega \right)}^{\alpha }\right)}^{\ast }\\ I\end{array}\right]<0,\forall \omega \in \Omega \end{array}$$

(20)

(ii) 

There must be s Hermitian matrices P and $Q>0$ such that

$$\begin{array}{c}{\kappa }_1({\Phi }_i\otimes P+{\Psi }_i\otimes Q){\kappa }_1^T+{\kappa }_2\Pi {\kappa }_2^T<0\hfill \end{array}$$

(21)

where ${\kappa }_1=\left[\begin{array}{cc}A& I\\ C& 0\end{array}\right]$, ${\kappa }_2=\left[\begin{array}{cc}B& 0\\ D& I\end{array}\right]$. In Table 1, we define ${\Phi }_i,{\Psi }_i(i=LF,MF,HF)$.

Proof. 

The proof is related and similar to the IOSs’ GKYP lemma in [25], so the proof of this lemma is omitted. □

3. Main Results

In the previous section, we described how addressing SFDC problem can be used to design a controller/detector unit so as to make the augmented system (7) stable and satisfy all mixed $H_{-}/H_{\infty }$ performance indexes simultaneously. In this section, for solving this problem, the purpose is to provide new sufficient conditions. Theorems 1–4 are given. After that, we provide the SFDC problem with a feasible solution by using Theorems 1–4 in Corollary 1.

First, in the following theorem, we propose an LMI condition about how to design the observer and controller’s gains of the augmented FOS (7) so as to minimize the interference’s influence on regulated output.

Theorem 1.

Given a scalar $0<\alpha <1$ and defining $r=e^{j\theta }$ with $\theta =(1-\alpha )\pi /2$, if there exist matrices ${\mathcal{P}}_1$, H, X, Z, M, E, G, Y, and L with appropriate dimensions, the system (7) is asymptotically stable and meets condition (9) such that the following inequalities hold:

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}He\left(\mathcal{A}\right)& {\mathcal{P}}_1-{\mathcal{W}}^T+\mathcal{A}& {\mathcal{C}}_2^T& {\mathcal{B}}_d\\ \ast & -{\mathcal{W}}^T-\mathcal{W}& {\mathcal{C}}_2^T& 0\\ \ast & \ast & -{\gamma }_{1}I& D_d\\ \ast & \ast & \ast & -{\gamma }_{1}I\end{array}\right]<0\end{array}$$

(22)

$$\begin{array}{c}\hfill \left[\begin{array}{cc}({\mathcal{P}}_1+{\mathcal{P}}_1^T)/\left(4cos\theta \right)& ({\mathcal{P}}_1-{\mathcal{P}}_1^T)/\left(4sin\theta \right)\\ ({\mathcal{P}}_1^T-{\mathcal{P}}_1)/\left(4sin\theta \right)& ({\mathcal{P}}_1+{\mathcal{P}}_1^T)/\left(4cos\theta \right)\end{array}\right]>0\end{array}$$

(23)

where

$$\begin{array}{cc}\hfill \mathcal{A}& =\left[\begin{array}{cc}{\mathcal{A}}_{11}& {\mathcal{A}}_{12}\\ {\mathcal{A}}_{21}& {\mathcal{A}}_{22}\end{array}\right],{\mathcal{A}}_{11}=\left[\begin{array}{cc}AX& -BE\\ 0& G_3\end{array}\right],{\mathcal{A}}_{12}=\left[\begin{array}{c}A\\ A-L{C}_1\end{array}\right]\hfill \\ \hfill {\mathcal{A}}_{21}& =\left[\begin{array}{cc}0& M\end{array}\right],{\mathcal{A}}_{22}=\left[\begin{array}{c}G{C}_1+YA\end{array}\right],{\mathcal{B}}_d^T=\left[\begin{array}{c}{B}_d\\ B_d\\ Y{B}_d\end{array}\right],\mathcal{W}=\left[\begin{array}{ccc}X& 0& I\\ 0& X& I\\ 0& Z& Y\end{array}\right]\hfill \\ \hfill {\mathcal{C}}_2& =\left[\begin{array}{ccc}{\varphi }_{p3}& -DE& 0\end{array}\right],{\varphi }_{p3}=DE+C_{1}X,G_3=AX-H\hfill \end{array}$$

(24)

Proof. 

It can be seen from Lemma 2 that if there exists a matrix variable $P_1$, the augmented system (7) is asymptotically stable and the condition (9) holds such that

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}He\left\{\overline{A}{P}_1\right\}& P_1^T{\overline{C}}_2^T& {\overline{B}}_d\\ \ast & -{\gamma }_{1}I& D_d\\ \ast & \ast & -{\gamma }_{1}I\end{array}\right]<0\end{array}$$

(25)

$$\begin{array}{c}\hfill \left[\begin{array}{cc}(P_1+P_1^T)/\left(4cos\theta \right)& (P_1^T-P_1)/\left(4sin\theta \right))\\ (P_1-P_1^T)/\left(4sin\theta \right)& (P_1+P_1^T)/\left(4cos\theta \right)\end{array}\right]>0\end{array}$$

(26)

Let

$$\begin{array}{cc}\hfill {\rm Y}& =\left[\begin{array}{cccc}0& P_1^T& 0& {\overline{B}}_d\\ P_1& 0& 0& 0\\ 0& 0& -{\gamma }_{1}I& D_d\\ {\overline{B}}_d^T& 0& D_d^T& -{\gamma }_{1}I\end{array}\right]\hfill \end{array}$$

(27)

Then, (25) can be rewritten as follows:

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}I& \overline{A}& 0& 0\\ 0& {\overline{C}}_2& I& 0\\ 0& 0& 0& I\end{array}\right]{\rm Y}{\left[\begin{array}{cccc}I& \overline{A}& 0& 0\\ 0& {\overline{C}}_2& I& 0\\ 0& 0& 0& I\end{array}\right]}^T<0\end{array}$$

(28)

which has the same form as inequality (18).

On the other hand,

$$\begin{array}{c}\hfill {\kappa }_3{\rm Y}{\kappa }_3^T<0\end{array}$$

(29)

which has the same form as inequality (19), where ${\kappa }_3=\left[00I0\right]$.

The calculations of explicit null space bases yield

$$\begin{array}{c}\hfill {\left[\begin{array}{c}\overline{A}\\ -I\\ {\overline{C}}_2\\ 0\end{array}\right]}^{\perp }=\left[\begin{array}{cccc}I& \overline{A}& 0& 0\\ 0& {\overline{C}}_2& I& 0\\ 0& 0& 0& I\end{array}\right],{\left[\begin{array}{c}I\\ I\\ 0\\ 0\end{array}\right]}^{\perp }=\left[00I0\right]\end{array}$$

(30)

According to Lemma 3, the following inequality is equivalent to (25):

$$\begin{array}{c}\hfill {\rm Y}+\left[\begin{array}{c}\overline{A}\\ -I\\ {\overline{C}}_2\\ 0\end{array}\right]W{\kappa }_4+{\kappa }_4^T{W}^T{\left[\begin{array}{c}\overline{A}\\ -I\\ {\overline{C}}_2\\ 0\end{array}\right]}^T\end{array}$$

(31)

where W is an additional matrix variable ${\kappa }_4=\left[II00\right]$. Then, the following inequality can be obtained:

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}He\left\{\overline{A}W\right\}& P_1^T-{\kappa }_w& W^T{\overline{C}}_2^T& {\overline{B}}_d\\ \ast & -He\left(W\right)& W^T{\overline{C}}_2^T& 0\\ \ast & \ast & -{\gamma }_{1}I& D_d\\ \ast & \ast & \ast & -{\gamma }_{1}I\end{array}\right]<0\end{array}$$

(32)

where ${\kappa }_w=W^T-\overline{A}W$

It can be found that (32) is not a strict LMI. Based on the method proposed in [39], the problem is converted into a standard LMI problem. Firstly, we design W and $W^{-1}$ as follows:

$$\begin{array}{cc}\hfill W& =\left[\begin{array}{ccc}X& 0& {\left(V^T\right)}^{-1}\\ 0& X& {\varphi }_{p5}{V}^{-T}\\ 0& U& {\varphi }_{p6}\end{array}\right]\hfill \\ \hfill W^{-1}& =\left[\begin{array}{ccc}{X}^{-1}& -X^{-1}& U^{-1}\\ 0& Y^T& {\varphi }_{p5}{U}^{-1}\\ 0& V^T& -V^{T}X{U}^{-1}\end{array}\right]\hfill \end{array}$$

(33)

where V, X, and U are invertible, ${\varphi }_{p5}=I-X{Y}^T$, and ${\varphi }_{p6}=-U{Y}^T{V}^{-T}$. Then, the observer and controller variables are expressed as follows:

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}E& 0& 0\\ 0& M& G\\ 0& H& L\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& YAX& 0\\ 0& 0& 0\end{array}\right]+G_2\left[\begin{array}{ccc}K& 0& 0\\ 0& A_L& B_L\\ 0& C_L& D_L\end{array}\right]G_1\end{array}$$

(34)

where $G_1=\left[\begin{array}{ccc}X& 0& 0\\ 0& U& 0\\ 0& CX& I\end{array}\right]$, and $G_2=\left[\begin{array}{ccc}I& 0& 0\\ 0& V& -Y\\ 0& 0& I\end{array}\right]$. Denoting $Z=YX+VU$, and letting

$$\begin{array}{c}\hfill T=\left[\begin{array}{ccc}I& 0& 0\\ 0& I& 0\\ 0& Y& V\end{array}\right]\end{array}$$

(35)

one has

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}\mathcal{A}& {\mathcal{B}}_d\\ {\mathcal{C}}_2& 0\end{array}\right]& =\left[\begin{array}{cc}{\varphi }_{p7}& T{\overline{B}}_d\\ CW{T}^T& 0\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cccc}AX& -G_5& A& B_d\\ 0& G_3& -L{C}_1+A& B_d\\ 0& M& G_4+G{C}_1& Y{B}_d\\ {\varphi }_{p4}& -DE& 0& \end{array}\right]\hfill \end{array}$$

(36)

where ${\varphi }_{p4}=DE+C_{2}X$, $G_5=BE$, $G_4=YA$, ${\varphi }_{p7}=T\overline{A}W{T}^T$ and

$$\begin{array}{cc}\hfill {\mathcal{P}}_1& =T{P}_1{T}^T=\left[\begin{array}{ccc}X& 0& I\\ 0& X& I\\ 0& Z& Y\end{array}\right]\hfill \end{array}$$

(37)

Pre-and post-multiplying (32) by $diag\{T,T,I,I\}$ and its transpose, we have

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}\mathcal{A}+{\mathcal{A}}^T& {\mathcal{P}}_1-{\mathcal{W}}^T+\mathcal{A}& {\mathcal{C}}_2^T& {\mathcal{B}}_d\\ \ast & -{\mathcal{W}}^T-\mathcal{W}& {\mathcal{C}}_2^T& 0\\ \ast & \ast & -{\gamma }_{1}I& D_d\\ \ast & \ast & \ast & -{\gamma }_{1}I\end{array}\right]<0\end{array}$$

(38)

Furthermore, pre-multiplying and post-multiplying (26) by $diag\{T,T\}$ and its transpose yield

$$\begin{array}{c}\hfill \left[\begin{array}{cc}F(P_1+P_1^T)F^T/(4cos\theta )& F(P_1^T-P_1)F^T/(4sin\theta ))\\ F(P_1-P_1^T)F^T/(4sin\theta )& F(P_1+P_1^T)F^T/(4cos\theta )\end{array}\right]>0\end{array}$$

(39)

After a short calculation, it follows

$$\begin{array}{c}\hfill \left[\begin{array}{cc}({\mathcal{P}}_1+{\mathcal{P}}_1^T)/(4cos\theta )& ({\mathcal{P}}_1^T-{\mathcal{P}}_1)/(4sin\theta ))\\ ({\mathcal{P}}_1-{\mathcal{P}}_1^T)/(4sin\theta )& ({\mathcal{P}}_1+{\mathcal{P}}_1^T)/(4cos\theta )\end{array}\right]>0\end{array}$$

(40)

In this way, the proof is finished. □

Theorem 2.

Given a scalar $0<\alpha <1$ and defining $r=e^{j\theta }$ with $\theta =(1-\alpha )\pi /2$, the system (7) satisfies condition (10) if there exist matrices X, E, M, Z, Y, G, H, L, $V_1$ and ${\mathcal{P}}_2$, and the dimensions are appropriate, such that the following inequalities hold:

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}He\left(\mathcal{A}\right)& {\mathcal{P}}_2-{\mathcal{W}}^T+\mathcal{A}& {\mathcal{C}}_1^T& {\mathcal{B}}_d\\ \ast & -{\mathcal{W}}^T-\mathcal{W}& {\mathcal{C}}_1^T& 0\\ \ast & \ast & -{\gamma }_{2}I& 0\\ \ast & \ast & \ast & -{\gamma }_{2}I\end{array}\right]<0\end{array}$$

(41)

$$\begin{array}{c}\hfill \left[\begin{array}{cc}({\mathcal{P}}_2+{\mathcal{P}}_2^T)/\left(4cos\theta \right)& ({\mathcal{P}}_2-{\mathcal{P}}_2^T)/\left(4sin\theta \right)\\ ({\mathcal{P}}_2^T-{\mathcal{P}}_2)/\left(4sin\theta \right)& ({\mathcal{P}}_2+{\mathcal{P}}_2^T)/\left(4cos\theta \right)\end{array}\right]>0\end{array}$$

(42)

where ${\mathcal{C}}_1={[V_1-V_{1}0]}^T$, $\mathcal{A}$, ${\mathcal{B}}_d$, and $\mathcal{W}$ are defined in (24).

Proof. 

The proof is similar to the proof of Theorem 1, the difference being

$$\begin{array}{c}\hfill {\mathcal{C}}_1={\overline{C}}_{1}W{T}^T=[VX-VX0]=[V_1-V_{1}0]\end{array}$$

(43)

Contrary to conditions (10) and (12) in the full domain, we define the performance index (9) in the limited frequency domain. Subsequently, achieving an LMI condition for (9) is possible based on Lemma 2. □

Theorem 3.

Given a scalar $0<\alpha <1$ and defining $r=e^{j\theta }$ with $\theta =(1-\alpha )\pi /2$, the system (7) satisfies condition (12) if there exist matrices X, E, Y, M, H, G, Z, L, ${\mathcal{P}}_3$ and ${\mathcal{Q}}_3$ such that the following inequalities hold:

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}-{\mathcal{Q}}_3& r{\mathcal{P}}_3-\mathcal{W}& 0& 0\\ \ast & {\omega }_1^2{\mathcal{Q}}_3+{\mathcal{A}}^T+\mathcal{A}& {\mathcal{C}}_2^T& {\mathcal{B}}_f\\ \ast & \ast & -{\gamma }_3^{2}I& 0\\ \ast & \ast & \ast & -I\end{array}\right]<0\end{array}$$

(44)

where ${\mathcal{Q}}_3$ is a positive definite Hermitian matrix, $\mathcal{A}$, ${\mathcal{C}}_2$, and $\mathcal{W}$ are defined in (24), and ${\mathcal{B}}_f={\left[B_f^T{B}_f^T{B}_f^T{Y}^T\right]}^T$.

Proof. 

Now, condition (9) is equivalent to

$$\begin{array}{c}\hfill G_{zf}{\left(jw\right)}^{\alpha }{G}_{zf}{\left({\left(jw\right)}^{\alpha }\right)}^T-{\gamma }_3^{2}I<0,for0<\omega <{\omega }_1\end{array}$$

(45)

According to Lemma 3, (45) is equivalent to

$$\begin{array}{c}\hfill \left[\begin{array}{cc}\overline{A}& I\\ {\overline{C}}_2& 0\end{array}\right]\left[\begin{array}{cc}-Q_3& r{P}_3\\ \overline{r}{P}_3& {\omega }_1^{2\alpha }{Q}_3\end{array}\right]{\left[\begin{array}{cc}\overline{A}& 0\\ {\overline{C}}_2& 0\end{array}\right]}^T+\left[\begin{array}{cc}{\overline{B}}_f& 0\\ 0& I\end{array}\right]{\Pi }_1{\left[\begin{array}{cc}{\overline{B}}_f& 0\\ 0& I\end{array}\right]}^T<0\end{array}$$

(46)

where ${\Pi }_1=\left[\begin{array}{cc}I& 0\\ 0& -{\gamma }_3^{2}I\end{array}\right]$.

Let

$$\begin{array}{c}\hfill \overline{{\rm Y}}=\left[\begin{array}{cc}\left[\begin{array}{cc}-Q_3& r{P}_3\\ \overline{r}{P}_3& {\omega }_1^{2\alpha }{Q}_3\end{array}\right]& 0\\ 0& \left[\begin{array}{cc}{\overline{B}}_f& 0\\ 0& I\end{array}\right]{\Pi }_1\left[\begin{array}{cc}{\left({\overline{B}}_f\right)}^T& 0\\ 0& I^T\end{array}\right]\end{array}\right]\end{array}$$

(47)

Then, (46) can be reformulated as

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}\overline{A}& I& 0\\ {\overline{C}}_2& 0& I\end{array}\right]\left(\mu \overline{{\rm Y}}{\mu }^T\right)\left[\begin{array}{cc}{\overline{A}}^T& {\overline{C}}_2^T\\ I& 0\\ 0& I\end{array}\right]<0\end{array}$$

(48)

where $\mu =\left[\begin{array}{ccc}I& 0& 0\\ 0& I& 0\\ 0& I& 0\\ 0& 0& I\end{array}\right]$, which has the same form as inequality (18) with

$$\begin{array}{cc}\hfill \overline{\Theta }& ={\mu }^T\overline{{\rm Y}}\mu =\left[\begin{array}{ccc}-Q_3& r{P}_3& 0\\ \overline{r}{P}_3& {\omega }_1^{2\alpha }{Q}_3+{\overline{B}}_f{\overline{B}}_f^T& 0\\ 0& 0& -{\gamma }_3^{2}I\end{array}\right]\hfill \end{array}$$

(49)

On the other hand,

$$\begin{array}{c}\hfill {\left[\begin{array}{cc}I& 0\\ 0& 0\\ 0& I\end{array}\right]}^T\overline{\Theta }\left[\begin{array}{cc}I& 0\\ 0& 0\\ 0& I\end{array}\right]=\left[\begin{array}{cc}-Q_3& 0\\ 0& -{\gamma }_3^{2}I\end{array}\right]\end{array}$$

(50)

which has the same form as inequality (19).

The calculations of explicit null space bases yield

$$\begin{array}{c}\hfill {\left[\begin{array}{c}-I\\ \overline{A}\\ {\overline{C}}_2\end{array}\right]}^{\perp }=\left[\begin{array}{ccc}\overline{A}& I& 0\\ {\overline{C}}_2& 0& I\end{array}\right],{\left[\begin{array}{c}0\\ I\\ 0\end{array}\right]}^{\perp }=\left[\begin{array}{ccc}I& 0& 0\\ 0& 0& I\end{array}\right]\end{array}$$

(51)

From Lemma 3, (46) is equivalent to the following inequality:

$$\begin{array}{c}\hfill \overline{\Theta }+\left[\begin{array}{c}-I\\ \overline{A}\\ {\overline{C}}_2\end{array}\right]W_1\left[0I0\right]+{\left[0I0\right]}^T{W}_1^T{\left[\begin{array}{c}-I\\ \overline{A}\\ {\overline{C}}_2\end{array}\right]}^T<0\end{array}$$

(52)

where $W_1$ is an additional matrix variable. Recalling (21)–(23), and choosing $W_1=W$, then we have

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}\mathcal{A}& {\mathcal{B}}_f\\ {\mathcal{C}}_2& 0\end{array}\right]& =\left[\begin{array}{cc}T\overline{A}{W}_1{T}^T& {\varphi }_{p8}\\ {\overline{C}}_2{W}_1{T}^T& 0\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cccc}{G}_3+H& -G_5& A& B_f\\ 0& G_3& -L{C}_1+A& B_f\\ 0& M& G{C}_1+G_4& Y{B}_f\\ {\varphi }_{p4}& -DE& 0& \end{array}\right]\hfill \end{array}$$

(53)

where ${\varphi }_{p8}=T{\overline{B}}_f$.

It can be proved that inequality (52) multiplied by the full rank matrix $diag(T,T,I)$ on the left-hand side and multiplied by $diag(T^T,T^T,I)$ on the right-hand side results in the following inequality:

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}-Q_3& r{P}_3& 0\\ \overline{r}{P}_3& {\omega }_1^{2\alpha }{Q}_3& 0\\ 0& 0& -{\gamma }_3^{2}I\end{array}\right]+He\left(\left[\begin{array}{c}-\mathcal{W}\\ \mathcal{A}\\ {\mathcal{C}}_2\end{array}\right]\left[0I0\right]\right)<0\end{array}$$

(54)

After some manipulations, one can rewrite (54) as

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}-Q_3& r{P}_3-\mathcal{W}& 0\\ \overline{r}{P}_3& {\omega }_1^{2\alpha }{Q}_3+He\left(\mathcal{A}\right)& {\mathcal{C}}_2^T\\ 0& 0& -{\gamma }_3^{2}I\end{array}\right]+\left[\begin{array}{c}0\\ {\mathcal{B}}_f\\ 0\end{array}\right]{\left[\begin{array}{c}0\\ {\mathcal{B}}_f\\ 0\end{array}\right]}^T<0\end{array}$$

(55)

It is known that (54) is equivalent to (44) using the Schur complement lemma, so we complete the proof. □

In the following theorem, we give sufficient conditions of LMIs, aimed at designing the controller/detector unit. This will enhance the stability of the augmented system (7) to obtain the $H_{-}$ performance defined in (11). Finally, we maximize the faults’ influence on the residuals.

Theorem 4.

Given a scalar $0<\alpha <1$ and defining $r=e^{j\theta }$ with $\theta =(1-\alpha )\pi /2$, the system (7) satisfies condition (11) if there exist matrices L, X, E, Y, Z, M, H, G, $V_1$, ${\mathcal{P}}_4$ and ${\mathcal{Q}}_4$, as well as a positive scalar ϵ, such that the following inequalities hold

$$\begin{array}{cc}\hfill & \left[\begin{array}{ccc}-{\mathcal{Q}}_4& r{\mathcal{P}}_4-\mathcal{W}& -\mathcal{W}V\\ \ast & {\omega }_1^2{\mathcal{Q}}_4+{\mathcal{A}}^T+\mathcal{A}-{ϵ}^{2}I& \mathcal{A}V+{\mathcal{C}}_1^T\\ \ast & \ast & {\beta }^{2}I+He\left({\mathcal{C}}_{1}V\right)\end{array}\right]<0\hfill \end{array}$$

(56)

$$\begin{array}{c}\hfill {ϵ}^2-B_f^T{T}_1<0\end{array}$$

(57)

where ${\mathcal{Q}}_4$ is a positive definite Hermitian matrix, ${\mathcal{B}}_f^T=\left[B_f^T{B}_f^T{\left(B_{f}Y\right)}^T\right]$, $\mathcal{A}$, and $\mathcal{W}$ are defined in (24) and ${\mathcal{C}}_1$ is defined in (43). $V={\left[{\nu }^{T}00\right]}^T$ and ν are matrices we should give in advance.

Proof. 

Based on the proof of Theorem 3, the following inequality is equivalent to the condition (11):

$$\begin{array}{c}\hfill \left[\begin{array}{cc}\overline{A}& I\\ {\overline{C}}_1& 0\end{array}\right]\left[\begin{array}{cc}-Q_4& r{P}_4\\ \overline{r}{P}_4& {\omega }_1^{2\alpha }{Q}_4\end{array}\right]{\left[\begin{array}{cc}\overline{A}& 0\\ {\overline{C}}_1& 0\end{array}\right]}^T+\left[\begin{array}{cc}{\overline{B}}_f& 0\\ 0& I\end{array}\right]{\Pi }_2{\left[\begin{array}{cc}{\overline{B}}_f& 0\\ 0& I\end{array}\right]}^T<0\end{array}$$

(58)

where ${\Pi }_2=\left[\begin{array}{cc}-I& 0\\ 0& {\beta }^{2}I\end{array}\right]$.

Let

$$\begin{array}{c}\hfill \widetilde{{\rm Y}}=\left[\begin{array}{cc}\left[\begin{array}{cc}-Q_4& r{P}_4\\ \overline{r}{P}_4& {\omega }_1^{2\alpha }{Q}_4\end{array}\right]& 0\\ 0& \left[\begin{array}{cc}{\overline{B}}_f& 0\\ 0& I\end{array}\right]{\Pi }_2{\left[\begin{array}{cc}{\overline{B}}_f& 0\\ 0& I\end{array}\right]}^T\end{array}\right]\end{array}$$

(59)

Then, (58) can be reformulated as

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}\overline{A}& I& 0\\ {\overline{C}}_1& 0& I\end{array}\right]\left({\mu }^T\widetilde{{\rm Y}}\mu \right)\left[\begin{array}{cc}{\overline{A}}^T& {\overline{C}}_1^T\\ I& 0\\ 0& I\end{array}\right]<0\end{array}$$

(60)

which has the same form as inequality (18) with

$$\begin{array}{cc}\hfill \tilde{\Theta }& ={\mu }^T\widetilde{{\rm Y}}\mu =\left[\begin{array}{ccc}-Q_4& r{P}_4& 0\\ \overline{r}{P}_4& {\omega }_1^{2\alpha }{Q}_4-{\overline{B}}_f{\overline{B}}_f^T& 0\\ 0& 0& {\beta }^{2}I\end{array}\right]\hfill \end{array}$$

(61)

On the other hand,

$$\begin{array}{c}\hfill {\left[\begin{array}{c}I\\ 0\\ 0\end{array}\right]}^T\tilde{\Theta }\left[\begin{array}{c}I\\ 0\\ 0\end{array}\right]=-Q_4<0\end{array}$$

(62)

which has the same form as inequality (19).

The calculations of explicit null space bases yield

$$\begin{array}{c}\hfill {\left[\begin{array}{c}-I\\ \overline{A}\\ {\overline{C}}_1\end{array}\right]}^{\perp }=\left[\begin{array}{ccc}\overline{A}& I& 0\\ {\overline{C}}_1& 0& I\end{array}\right],{\left[\begin{array}{cc}0& 0\\ I& 0\\ 0& I\end{array}\right]}^{\perp }={\left[\begin{array}{c}I\\ 0\\ 0\end{array}\right]}^T\end{array}$$

(63)

Based on Lemma 3, (58) is equivalent to the following inequality:

$$\begin{array}{c}\hfill \tilde{\Theta }+\nu +{\nu }^T<0\end{array}$$

(64)

where $W_2$ is an additional matrix variable, $\nu =\left[\begin{array}{c}-I\\ \overline{A}\\ {\overline{C}}_1\end{array}\right]W_2\left[\begin{array}{ccc}0& I& 0\\ 0& 0& I\end{array}\right]$.

Note that the terms $-{\overline{B}}_f{\overline{B}}_f^T$ and ${\beta }^{2}I$ of $\tilde{\Theta }$ caused the key technical difficulty of linearizing the inequality (64). We partition $W_2$ as $W_2=\left[WWV\right]$ to make the inequality (64) feasible, with ${\beta }^{2}I>0$, where W is chosen as one of (33), $V={\left[{\nu }^{T}00\right]}^T$, and $\nu$ should be given in advance. Recalling (35), it is proved that inequality (64) multiplied by $diag(T^T,T^T,I)$ on the right and multiplied by the full-rank matrix $diag(T,T,I)$ on the left results in the following inequality:

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}-Q_4& r{P}_4& 0\\ \overline{r}{P}_4& -{\overline{B}}_f{\overline{B}}_f^T+{\omega }_1^{2\alpha }{Q}_4& 0\\ 0& 0& {\beta }^{2}I\end{array}\right]+He\left(\left[\begin{array}{c}-\mathcal{W}\\ \mathcal{A}\\ {\mathcal{C}}_1\end{array}\right]\left[0IV\right]\right)<0\end{array}$$

(65)

By simple calculation, one can rewrite (65) as

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}-{\mathcal{Q}}_4& r{\mathcal{P}}_4-\mathcal{W}& -\mathcal{W}V\\ \ast & {\omega }_1^2{\mathcal{Q}}_4-{\overline{B}}_f{\overline{B}}_f^T+{\mathcal{A}}^T+\mathcal{A}& \mathcal{A}V+{\mathcal{C}}_1^T\\ \ast & \ast & {\beta }^{2}I+He\left({\mathcal{C}}_{1}V\right)\end{array}\right]<0\end{array}$$

(66)

In order to solve the non-linearity, we can impose an upper bound on the coupled term $-{\overline{B}}_f{\overline{B}}_f^T$. Hence, we can guarantee (66) by inequality (56) and

$$\begin{array}{c}\hfill {\overline{B}}_f{\overline{B}}_f^T>{ϵ}^{2}I\end{array}$$

(67)

where $ϵ$ is a given scalar. In fact, (67) represents the radius of the outer area of a ball $ϵ$ in the target variable ${\overline{B}}_f$; in other words, the feasible set is non-convex. In order to solve this problem, we introduce the result in [44]. Note that ${\overline{B}}_f$ in (66) is a row vector, and that it is easy to find that ${\overline{B}}_f$ in (67) is also a row vector. So, ${\overline{B}}_f^T{T}_1-{\parallel T_1\parallel }_2^2=0$ with $\parallel T_1{\parallel }_2^2=ϵ$ is the ball’s (67) hyperplane tangent, and we can achieve a convex feasible subset of (67)’s search by imposing the following constraint, ${ϵ}^{2}I-{\overline{B}}_f^T{T}_1<0$, which is the condition (57). □

Remark 4.

It should be pointed out that due to the introduction of a finite-frequency $H_{-}$ performance, (56) is non-convex. Given the design parameters ϵ, $T_1$, and ν of equation A in advance, then (56) and (57) can be solved using the LMI Toolbox.

Remark 5.

In the above proof, the matrix $W_2$ is decomposed to linearize (64). In addition, the W after decomposition has a special structure, so a certain degree of conservatism is introduced in the process of obtaining solvable design conditions.

The following corollary unifies Theorems 1–4 and gives a process for solving the SFDC problem.

Corollary 1.

Given system (1), there exist a weighting matrix V and a dynamic-observer-based controller (6) such that if the LMI conditions (22), (23), (41), (42), (44), (56), and (57) hold, the augmented system model (7) satisfies the performance indexes (9)–(12).

Therefore, we can solve the SFDC problem as follows:

Given positive scalars ${\gamma }_1$, ${\gamma }_2$, and ${\gamma }_3$, we can obtain the observer and controller gains by solving the following convex optimization problem

$$\begin{array}{c}max\beta \hfill \\ s.t.\left(22\right),\left(23\right),\left(41\right),\left(42\right),\left(44\right),\left(56\right),\left(57\right)\hfill \end{array}$$

(68)

4. Detection Threshold Design

Aimed at fault detection, a widely used method is as follows. First, we define a threshold $J_{th}>0$ and use the logic unit, and then follow the results in [45]. Based on the above, we can define the residual evaluation function $J_r\left(t\right)$ as follows:

$$\begin{array}{c}\hfill J_r\left(t\right)=\sqrt{\frac{1}{t}{\int }_0^t{r}^T\left(\tau \right)r\left(\tau \right)d\tau }\end{array}$$

(69)

where t represents the detection time range. We determine the threshold $J_{th}$ by

$$\begin{array}{c}\hfill J_{th}=\underset{f\left(t\right)=0,d\left(t\right)\in L_2,}{sup}{J}_r\left(t\right)\end{array}$$

(70)

and faults can be detected by

$$\begin{array}{c}\hfill J_r>J_{th}\Rightarrow \mathrm{alarm},J_r\le J_{th}\Rightarrow \mathrm{no}\mathrm{faults}.\end{array}$$

(71)

5. Examples

In this section, we will show the effectiveness of the proposed approach with two examples. The first example aims to compare the proposed method with existing results. The second example is used to demonstrate the proposed method’s capabilities and effectiveness.

5.1. Example 1

The fractional-order model of a permanent magnet synchronous motor (PMSM) velocity control system has the following form:

$$\begin{array}{c}\hfill G\left(s\right)=\frac{6.28}{0.00078s^{1.74}+0.097s^{0.87}+1}\end{array}$$

(72)

The $G\left(s\right)$’s pseudo-state space is expressed as follows:

$$\left\{\begin{array}{c}{D}^{\alpha }{x}_s\left(t\right)=A_s{x}_s\left(t\right)+B_{s}y\left(t\right)\hfill \\ u\left(t\right)=C_s{x}_s\left(t\right)\hfill \end{array}\right.$$

(73)

With the fractional order $\alpha =0.87$, the fractional-order system (73) can be obtained as follows:

$$\begin{array}{cc}\hfill A_s& =\left[\begin{array}{cc}100& -3.07\\ 7723.85& -224.36\end{array}\right],B_s=\left[\begin{array}{c}1\\ -1\end{array}\right],\hfill \\ \hfill C_s& =\left[11\right],D_s=0\hfill \end{array}$$

(74)

where ${{\omega }_r}^{\ast }$ is the given velocity and ${\omega }_r$ is the feedback value. K is the gain matrix, and $W_1$ and $W_2$ are weighted values. Experimental verification is achieved through the block diagram displayed in Figure 1. For the complementary sensitivity function $T\left(s\right)$ from w to y and the closed-loop sensitivity function $S\left(s\right)$ from w to $\epsilon$, we consider $W_1\left(s\right)$ and $W_2\left(s\right)$. The sensitivity functions of the closed-loop system must be verified

$$\begin{array}{c}\hfill \parallel W_1{S\parallel }_{\infty }<1,{\parallel W_{2}T\parallel }_{\infty }<1\end{array}$$

(75)

which are equivalent to

$$\begin{array}{c}\hfill {\parallel S\parallel }_{\infty }<\parallel W_1^{-1}{S\parallel }_{\infty }{,\parallel T\parallel }_{\infty }<{\parallel W_2^{-1}S\parallel }_{\infty }\end{array}$$

(76)

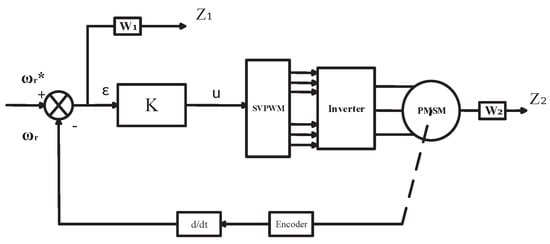
Figure 1. Block diagram of the experimental validation.

In order to eliminate the closed-loop static error, we have to make the constraint $W_1^{-1}$ low enough. In order to attenuate the resonance of $T\left(s\right)$, constraint $W_2^{-1}$ is chosen. The transfer function is

$$\begin{array}{c}\hfill W_1^{-1}\left(s\right)=3.15\times \frac{s^{0.87}+5.6\times {10}^{-4}}{s^{0.87}+1}\end{array}$$

(77)

$$\begin{array}{c}\hfill W_2^{-1}\left(s\right)=1.98\times {10}^{-5}\times \frac{s^{0.87}+1.8\times {10}^5}{s^{0.87}+1}\end{array}$$

(78)

For system (1) without an actuator fault, we consider the general control configuration of this $H_{\infty }$ problem.

Furthermore, we consider the PMSM velocity control system’s integer-order model as

$$\begin{array}{c}\hfill G\left(s\right)=\frac{6.25}{0.0001s^2+0.067s+1}\end{array}$$

(79)

According to (79), with an integer order $\alpha =1$, we have

$$\begin{array}{cc}\hfill A_s& =\left[\begin{array}{cc}-262.6& 1\\ 41667& -184\end{array}\right],B_s=\left[\begin{array}{c}1\\ 0\end{array}\right],\hfill \\ \hfill C_s& =\left[01\right],D_s=0\hfill \end{array}$$

(80)

In [46], a real-time PMSM velocity servo plant, the fractional-order model is identified according to the experimental tests. The fact that the fractional model is more accurate than the traditional integer-order model is substantiated, and then according to the identified fractional-order model and the traditional integer-order one, two $H_{\infty }$ stabilizing output feedback controllers are designed, respectively. The experimental test performance is compared to demonstrate the advantage of the proposed fractional-order model of the PMSM velocity system.

The following optimization problem is solved for the two above-mentioned models:

$$\begin{array}{cc}\hfill min{\gamma }_1& \\ \hfill s.t\left(22\right),& \left(23\right)\hfill \end{array}$$

The performance bounds are given in Table 2 as follows:

Table 2. Comparison of the $H_{\infty }$ performance ${\gamma }_1$.

	Fractional Order	Integer Order
${\gamma }_1$	4.0339	4.0366

In this paper, the fractional-order dynamic observer-based controller is proposed. Considering the results given in Table 2, it can be found that the proposed method in this paper for FOSs has a better $H_{\infty }$ performance than the method in [39] for integer-order systems.

5.2. Example 2

Consider the following fractional-order systems

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{D}^{\alpha }x\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+B_{w}w\left(t\right)\hfill \\ z\left(t\right)=C_{z}x\left(t\right)\hfill \end{array}\right.\end{array}$$

with the order $\alpha =0.5$

$$\begin{array}{cc}\hfill & A=\left[\begin{array}{cc}-0.2& 0.4\\ -0.4& -0.2\end{array}\right],B_s=\left[\begin{array}{c}1\\ 1\end{array}\right]\hfill \\ \hfill & B_w=\left[\begin{array}{c}1\\ 0\end{array}\right],C_z=\left[10\right].\hfill \end{array}$$

(81)

The open-loop transfer function is

$$\begin{array}{c}\hfill T_{zw}=\frac{s^{0.5}+0.2}{s+0.4s^{0.5}+0.2}\end{array}$$

(82)

It is assumed that $B_f=\left[\begin{array}{c}-1\\ -0.3\end{array}\right]$, and the measurement output $y\left(t\right)=\left[10\right]x\left(t\right)$.

In this paper, we investigated the fault in a limited frequency range $[0,0.1)$, assuming that the disturbance belongs to a finite frequency range $[0,3)$. To avoid high gains in terms of the observer and controller, two constraints, $H^{T}H<10000I$ and $G^{T}G<10000I$, are added to the optimization problem (68). Given $ϵ=1$, $T_1=[00000.5-0.3]$, $\nu =[-3.701;-0.078]$, ${\gamma }_1=1.3178$, ${\gamma }_2=1.3761$, and ${\gamma }_3=1.32$, by using the LMI toolbox in Matlab, we can solve the optimization problem (68), and we obtain $\beta =1.1195$. Furthermore, we finally obtain the controller and observer gains, as follows:

$$\begin{array}{c}\hfill f\left(t\right)=\left\{\begin{array}{c}0,0<t<6\hfill \\ 0.2,otherwise\hfill \end{array}\right.\end{array}$$

$$\begin{array}{cc}\hfill & A_L=\left[\begin{array}{cc}-19.3983& -1.0708\\ 27.7707& -54.8427\end{array}\right],B_L=\left[\begin{array}{c}-56.9595\\ 10.3892\end{array}\right]\hfill \\ \hfill & C_L=\left[\begin{array}{cc}-18.8641& 33.8935\\ 13.8016& -7.7066\end{array}\right],D_L=\left[\begin{array}{c}48.6071\\ 48.0950\end{array}\right]\hfill \\ \hfill & K=[-0.6653-0.2052]\hfill \end{array}$$

(83)

Then, the simulation results are given as follows. $x\left(0\right)=[0;0]$ is the initial system condition and $\widehat{x}\left(0\right)=[0;0]$, $\xi \left(0\right)=[0;0]$ is the initial observer condition. Moreover, the disturbance is assumed to be $d\left(t\right)=0.1e^{-0.2t}cos\left(0.3\pi t\right)$ and the fault signal is chosen.

Figure 2 displays the residual signal $r\left(t\right)$. It can be found from Figure 2 that the residual signal has large discrepancies when the fault occurs. Figure 3 shows the regulation output of the augmented system (7). From Figure 3, we can see that the influence of the disturbance and fault on the output has been weakened. Furthermore, Figure 4 plots the residual evaluation function. By using a threshold test $J_{th}=0.3$, we can effectively detect the fault $f\left(t\right)$ at approximately $t=7s$.

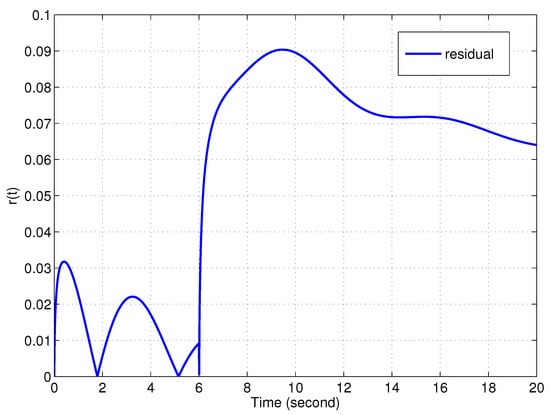
Figure 2. Residual output $\left|r\right(t\left)\right|$.

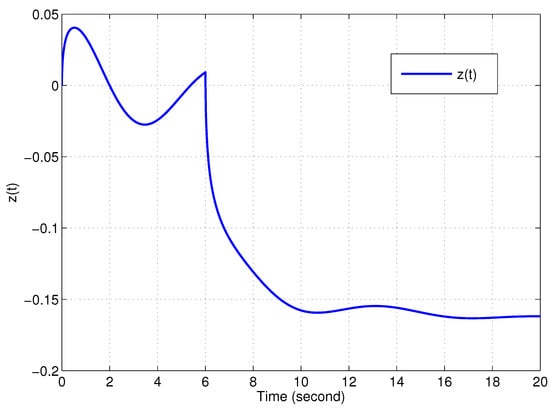
Figure 3. The performance output $z\left(t\right)$ of the augmented system.

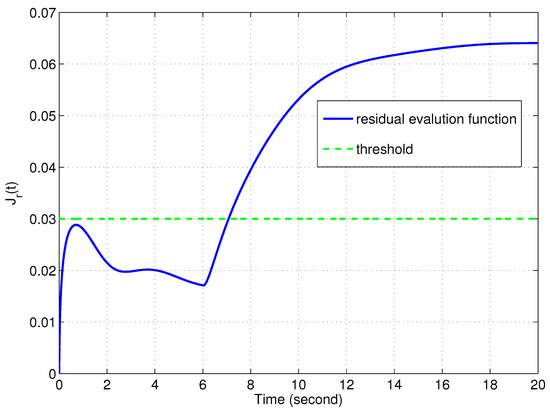
Figure 4. Dashed line: threshold; solid line: residual evaluation function.

6. Conclusions

In this paper, we study the SFDC problem in FOSs. We give the new bounded real lemma related to the FOSs’ $H_{\infty }$ norm so as to assess the disturbance attenuation performance. Moreover, we introduce the GKYP lemma directly to address the finite-frequency performance indexes. Then, we applied a linearizing change-of-variables and a tangent hyperplane technique to convert the design conditions into a class of LMI. Finally, the numerical examples demonstrate the proposed approach’s effectiveness. Future work will consider the fault detection problem in a finite-frequency domain for fractional-order Lipschitz non-linear systems and fractional-order singular systems.