Path Planning for Automatic Guided Vehicles (AGVs) Fusing MH-RRT with Improved TEB
Abstract
:1. Introduction
- A multiple heuristic strategy is designed for the RRT to solve the problems of non-optimality, including collision detection, goal-biased guidance, bidirectional extension, goal-point attempt and branch pruning.
- An improved multiobjective local path topology optimization method based on the TEB is put forward to reduce the run time with better path smoothness simultaneously, which divides the process into path decision-making and speed decision-making.
2. Preliminaries
2.1. Path Planning Problem
2.2. Rapidly Exploring Random Tree (RRT)
2.3. Timed Elastic Band (TEB)
3. Methodology
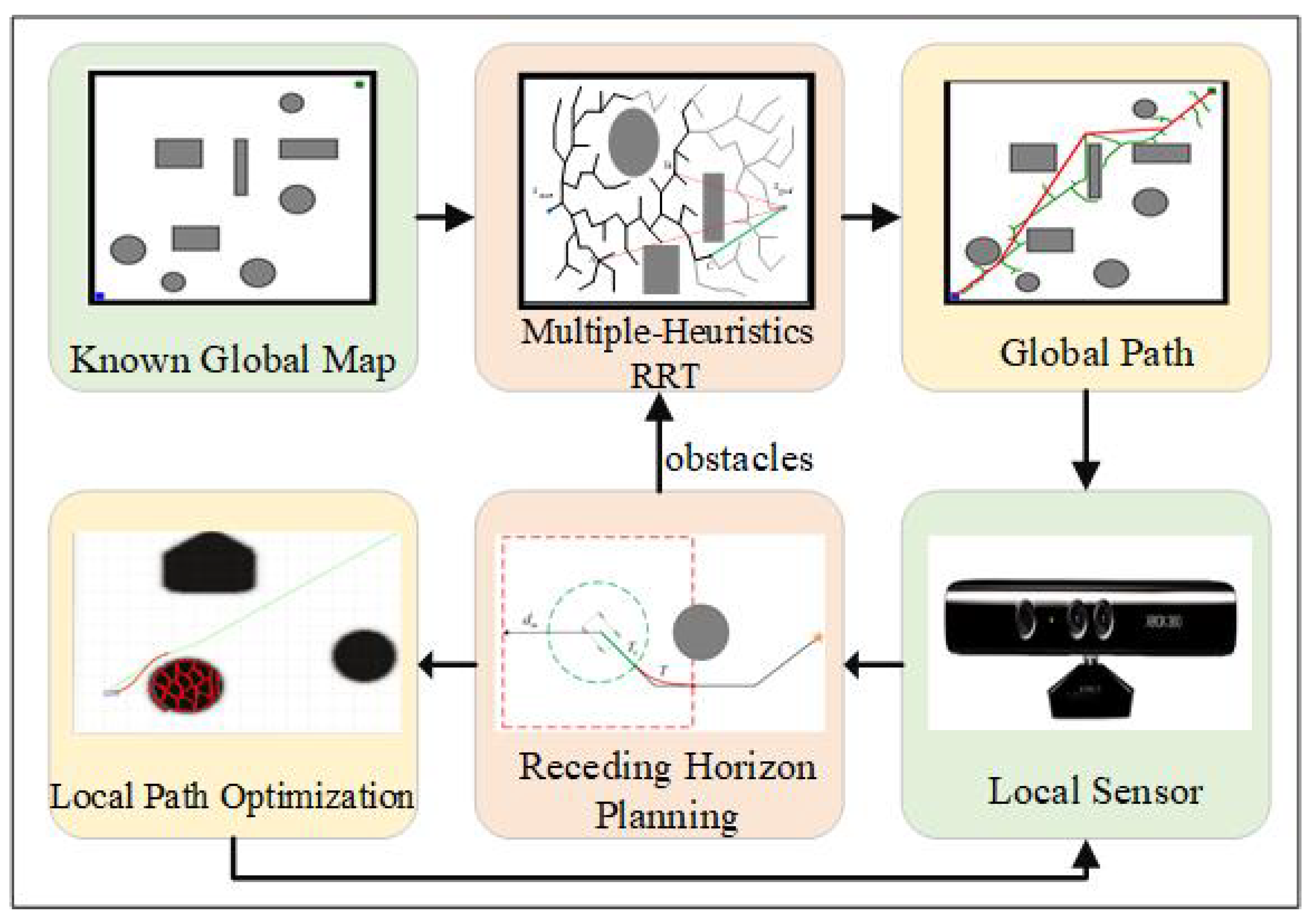
3.1. System Overview
3.2. Mutiple-Heuristics-RRT
| Algorithm 1: Multiple-Heuristics-RRT |
 |
3.2.1. Collision Detection
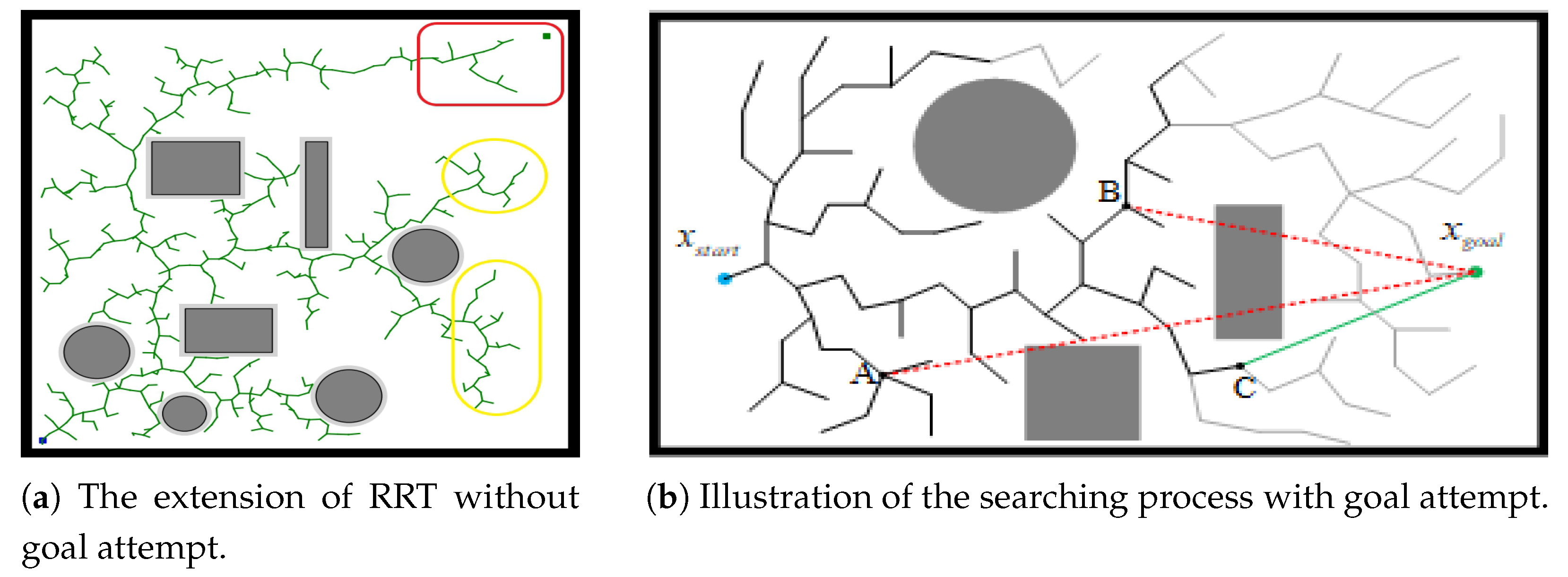
3.2.2. Goal-Biased Guidance
3.2.3. Bi-Direction Extension
3.2.4. Goal-Point Attempt
3.2.5. Branch Pruning
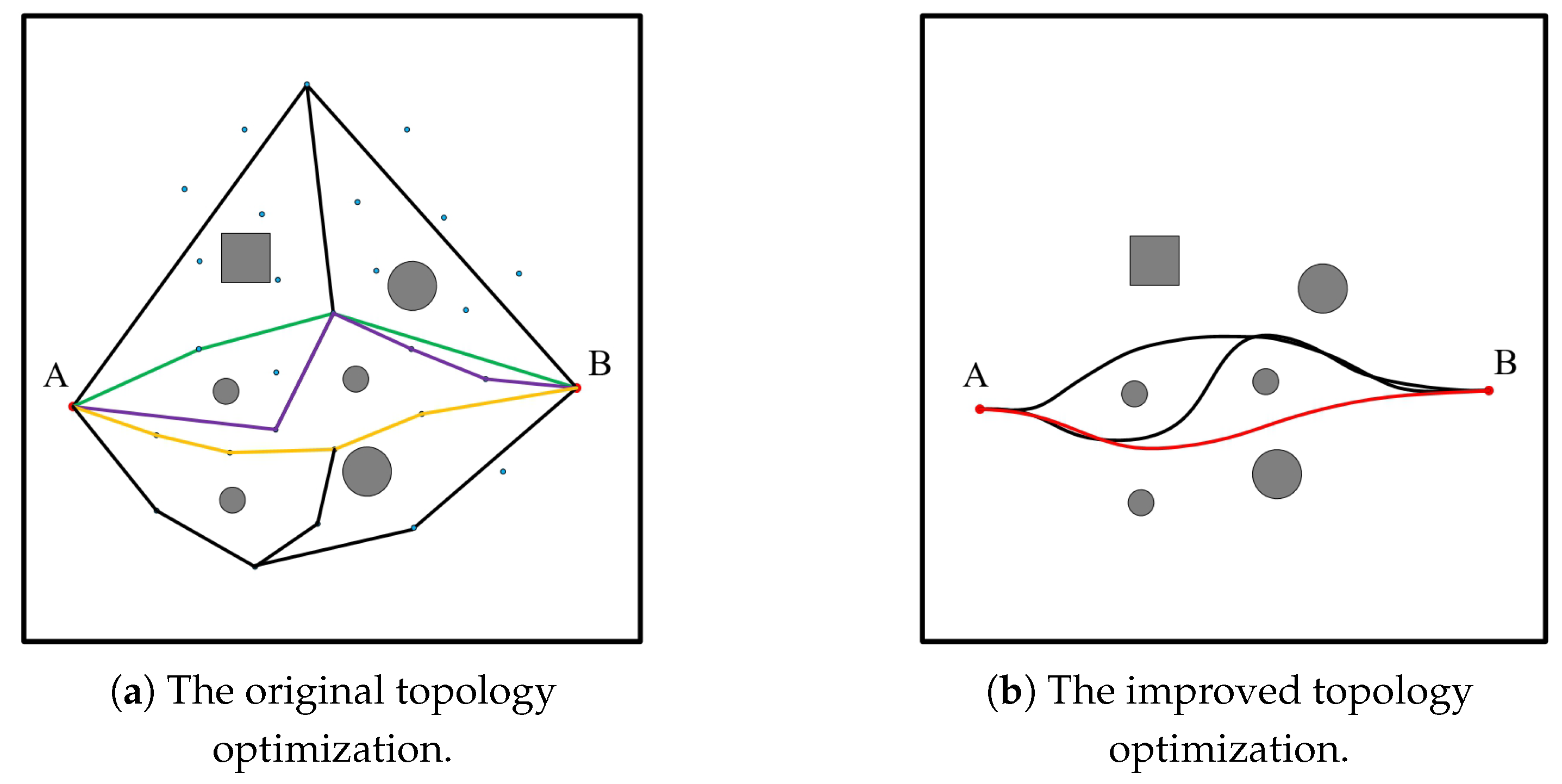
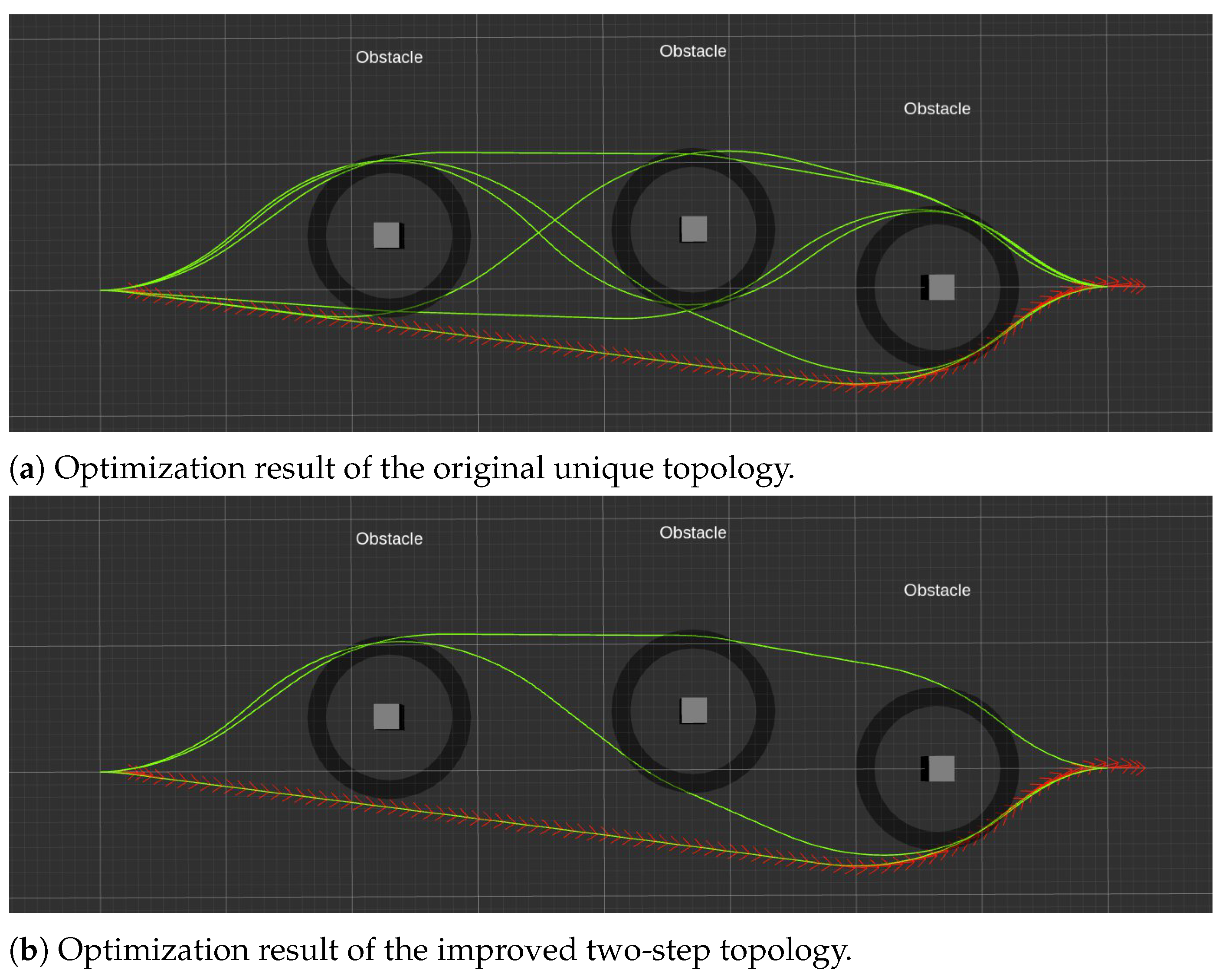
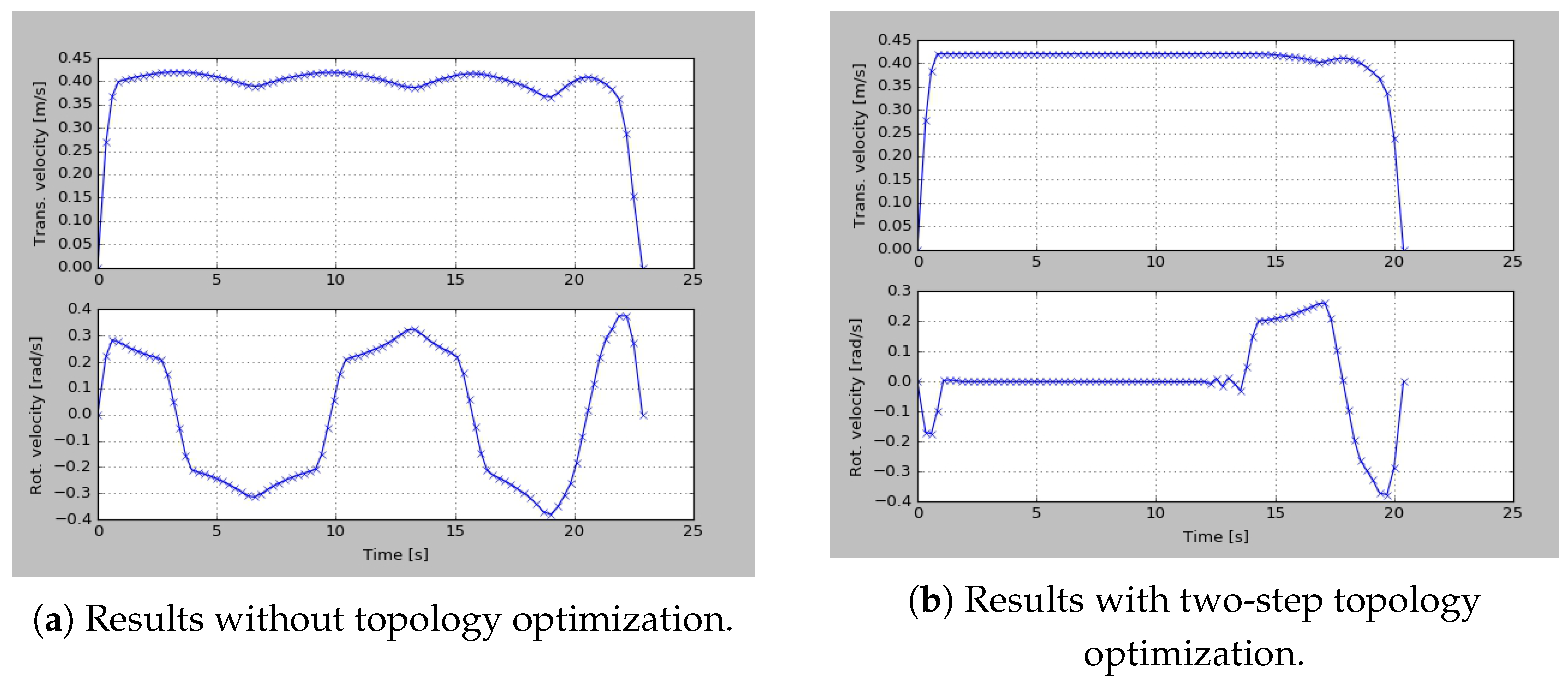
3.3. The Improved Two-Step TEB
| Algorithm 2: Two-step Optimization |
 |
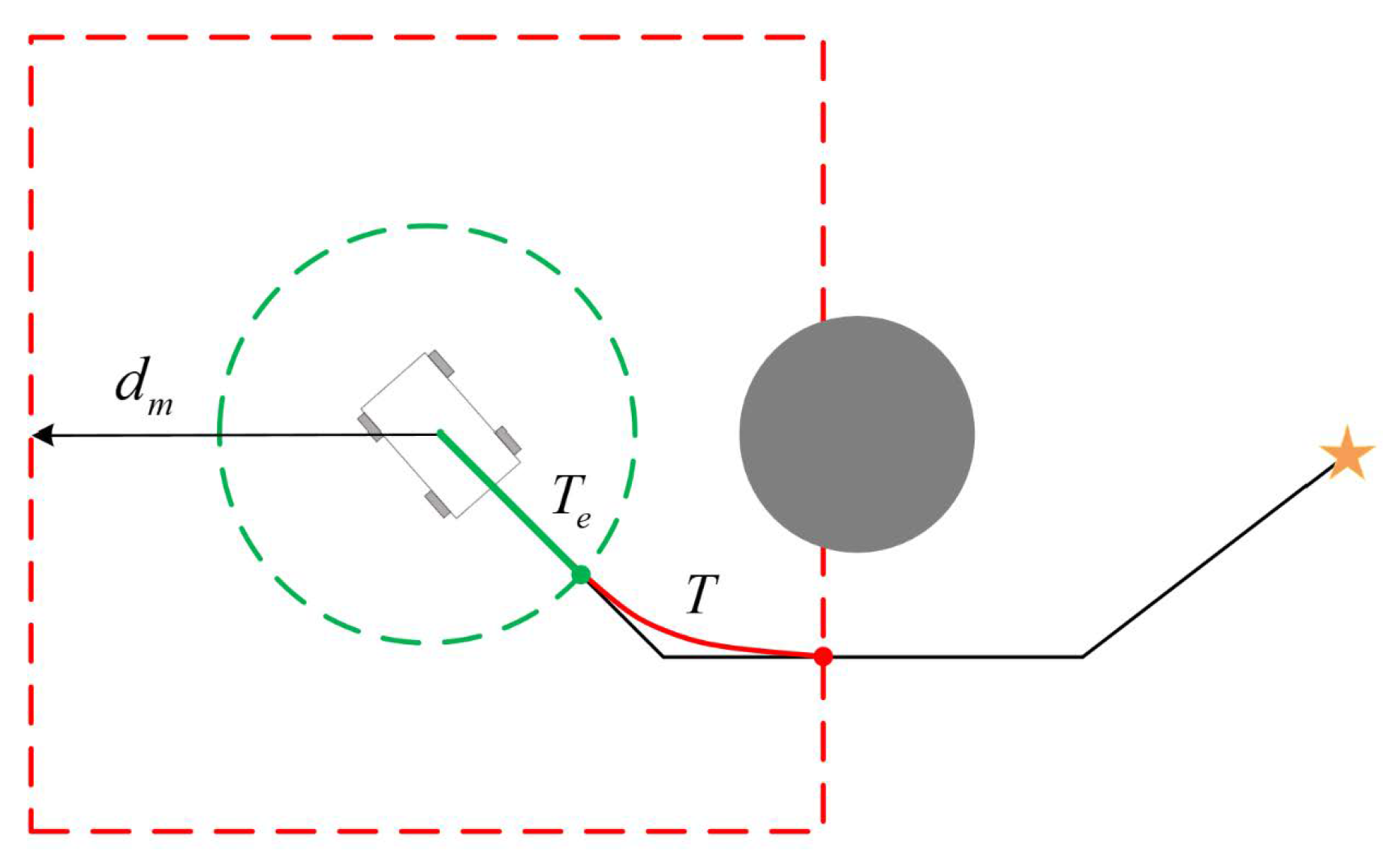
3.4. Receding Horizon Planning
4. Simulation and Experiment
4.1. Comparison in Global Path Planning
4.1.1. Simulation in Different Maps
4.1.2. Comparison in Global Path
4.2. Comparison in Local Path Planning
4.3. Results of the Proposed Fusion Algorithm
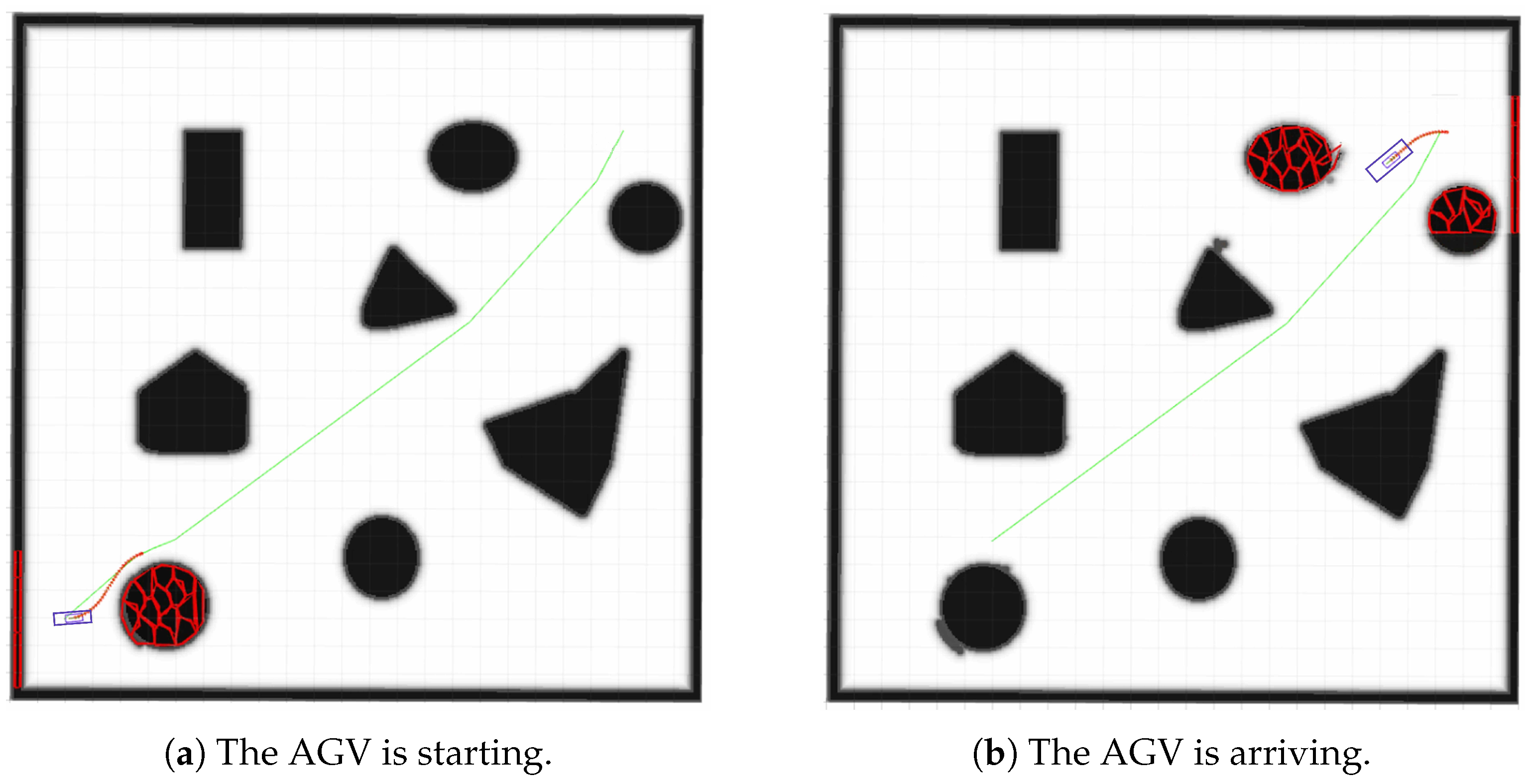
4.3.1. Simulation Results in Static Environment
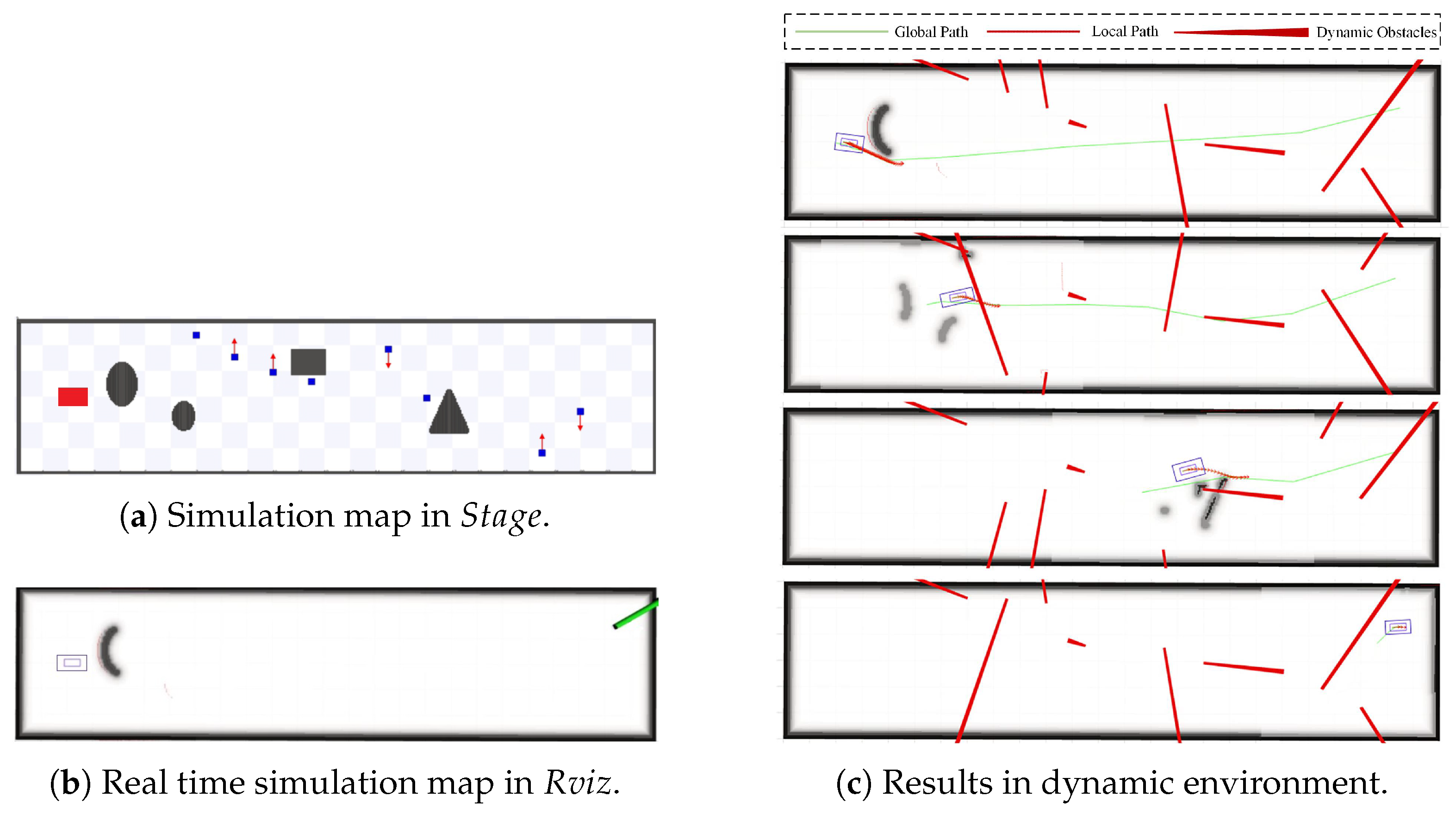
4.3.2. Simulation Results in Dynamic Environment
4.3.3. Real Experiment Results in Complex Dynamic Environments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ryck, M.; Versteyhe, M.; Debrouwere, F. Automated guided vehicle systems, state-of-the-art control algorithms and techniques. J. Manuf. Syst. 2020, 54, 152–173. [Google Scholar] [CrossRef]
- Moshayedi, A.J.; Jinsong, L.; Liao, L. AGV (automated guided vehicle) robot: Mission and obstacles in design and performance. J. Simul. Anal. Nov. Technol. Mech. Eng. 2019, 12, 5–18. [Google Scholar]
- Zhang, B.; Tang, L.; Decastro, J.; Roemer, M.J.; Goebel, K. A Recursive Receding Horizon Planning for Unmanned Vehicles. IEEE Trans. Ind. Electron. 2015, 62, 2912–2920. [Google Scholar] [CrossRef]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Reis, W.; Junior, O.M. Sensors applied to automated guided vehicle position control: A systematic literature review. Int. J. Adv. Manuf. Technol. 2021, 113, 21–34. [Google Scholar] [CrossRef]
- Guang, X.; Guan, S.; Song, H. Research on Path Planning Based on Artificial Potential Field Algorithm. In Proceedings of the 2nd International Conference on Artificial Intelligence and Advanced Manufacture, Manchester, UK, 23–25 October 2020; pp. 125–129. [Google Scholar]
- Sabudin, E.N.; Omar, R.; Joret, A.; Ponniran, A.; Debnath, S.K. Improved Potential Field Method for Robot Path Planning with Path Pruning. In Proceedings of the 11th National Technical Seminar on Unmanned System Technology 2019; Springer: Singapore, 2021. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 2007, 4, 100–107. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Svestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic Roadmaps for Path Planning in High-Dimensional Configuration Spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef] [Green Version]
- Lavalle, S.M. Rapidly Exploring Random Trees: A New Tool for Path Planning. 1998. Available online: https://www.cs.csustan.edu/~xliang/Courses/CS4710-21S/Papers/06%20RRT.pdf (accessed on 18 November 2021).
- Lin, H.I. 2D-Span Resampling of Bi-RRT in Dynamic Path Planning. Int. J. Autom. Smart Technol. 2015, 4, 39–48. [Google Scholar] [CrossRef]
- Qi, J.; Yang, H.; Sun, H. MOD-RRT*: A Sampling-Based Algorithm for Robot Path Planning in Dynamic Environment. IEEE Trans. Ind. Electron. 2020, 68, 7244–7251. [Google Scholar] [CrossRef]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the 2000 ICRA Millennium Conference, IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 995–1001. [Google Scholar]
- Wang, J.; Meng, Q.H.; Khatib, O. EB-RRT: Optimal Motion Planning for Mobile Robots. IEEE Trans. Autom. Sci. Eng. 2020, 17, 2063–2073. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based Algorithms for Optimal Motion Planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Chen, L.; Shan, Y.; Tian, W.; Li, B.; Cao, D. A fast and efficient double-tree RRT*-like sampling-based planner applying on mobile robotic systems. IEEE/ASME Trans. Mechatron. 2018, 23, 2568–2578. [Google Scholar] [CrossRef]
- Wang, J.; Li, B.; Meng, M.Q.H. Kinematic Constrained Bi-directional RRT with Efficient Branch Pruning for robot path planning. Expert Syst. Appl. 2021, 170, 114541. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Trajectory modification considering dynamic constraints of autonomous robots. In Proceedings of the 7th German Conference on Robotics, Munich, Germany, 21–22 May 2012; pp. 1–6. [Google Scholar]
- Bhattacharya, S. Topological and Geometric Techniques in Graph Search-Based Robot Planning; University of Pennsylvania: Philadelphia, PA, USA, 2012. [Google Scholar]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Wen, J.; Wang, R.; Chen, X. Goal-biased Bidirectional RRT based on Curve-smoothing. IFAC-PapersOnLine 2019, 52, 255–260. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]


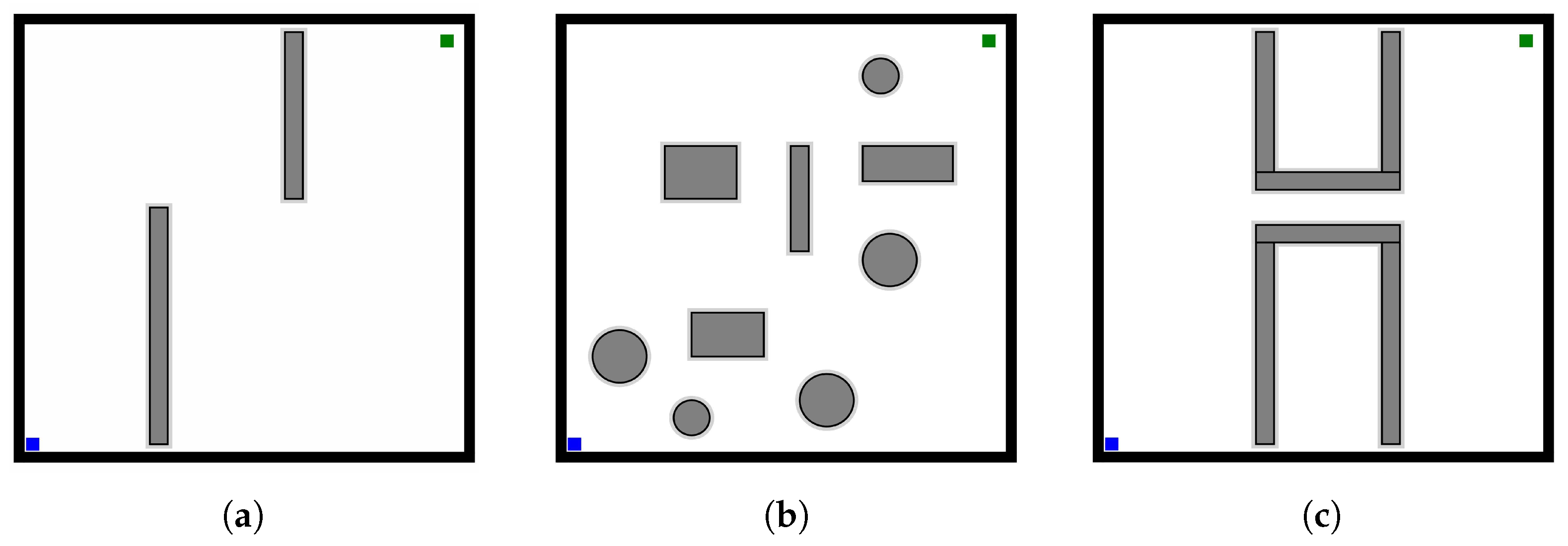
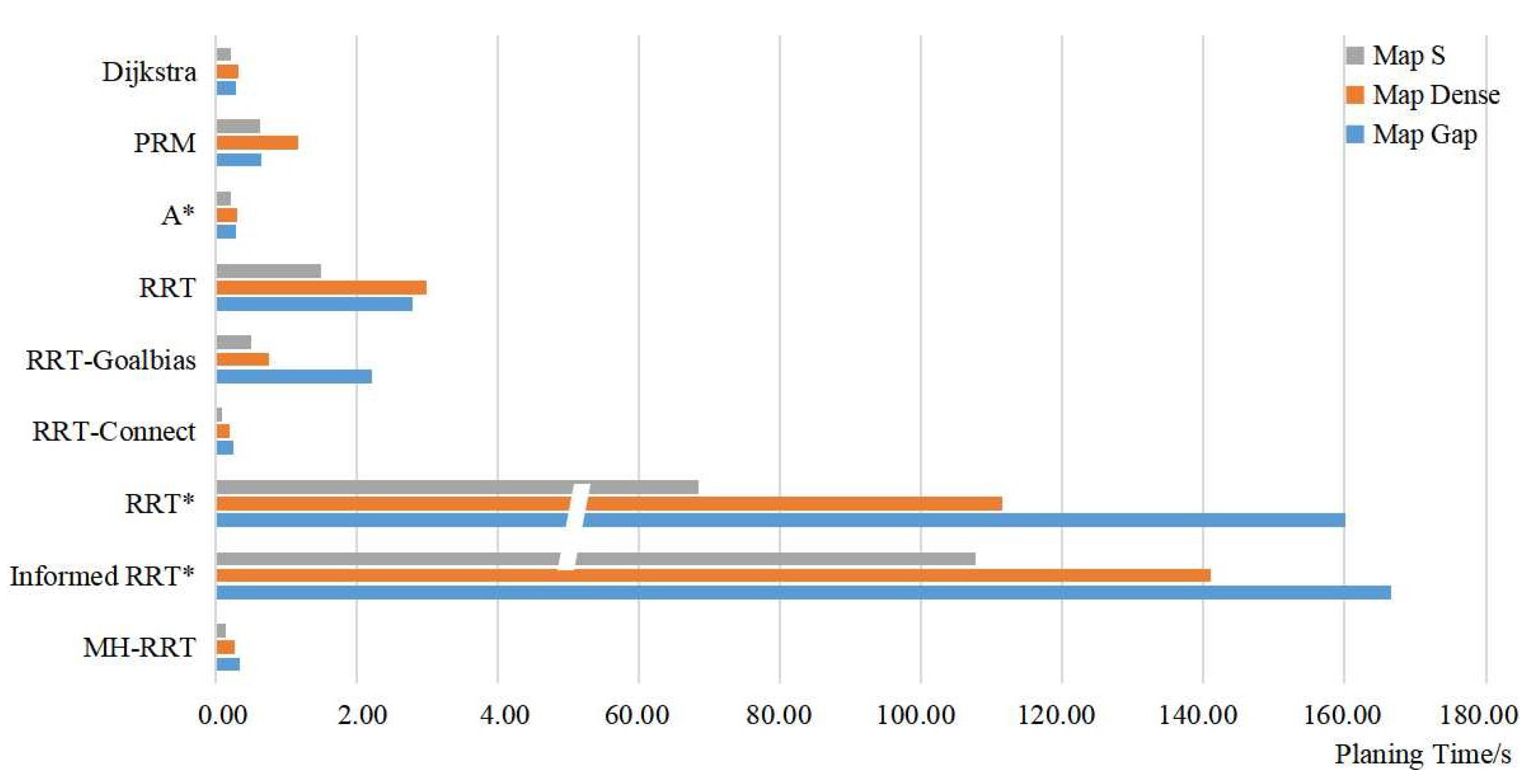
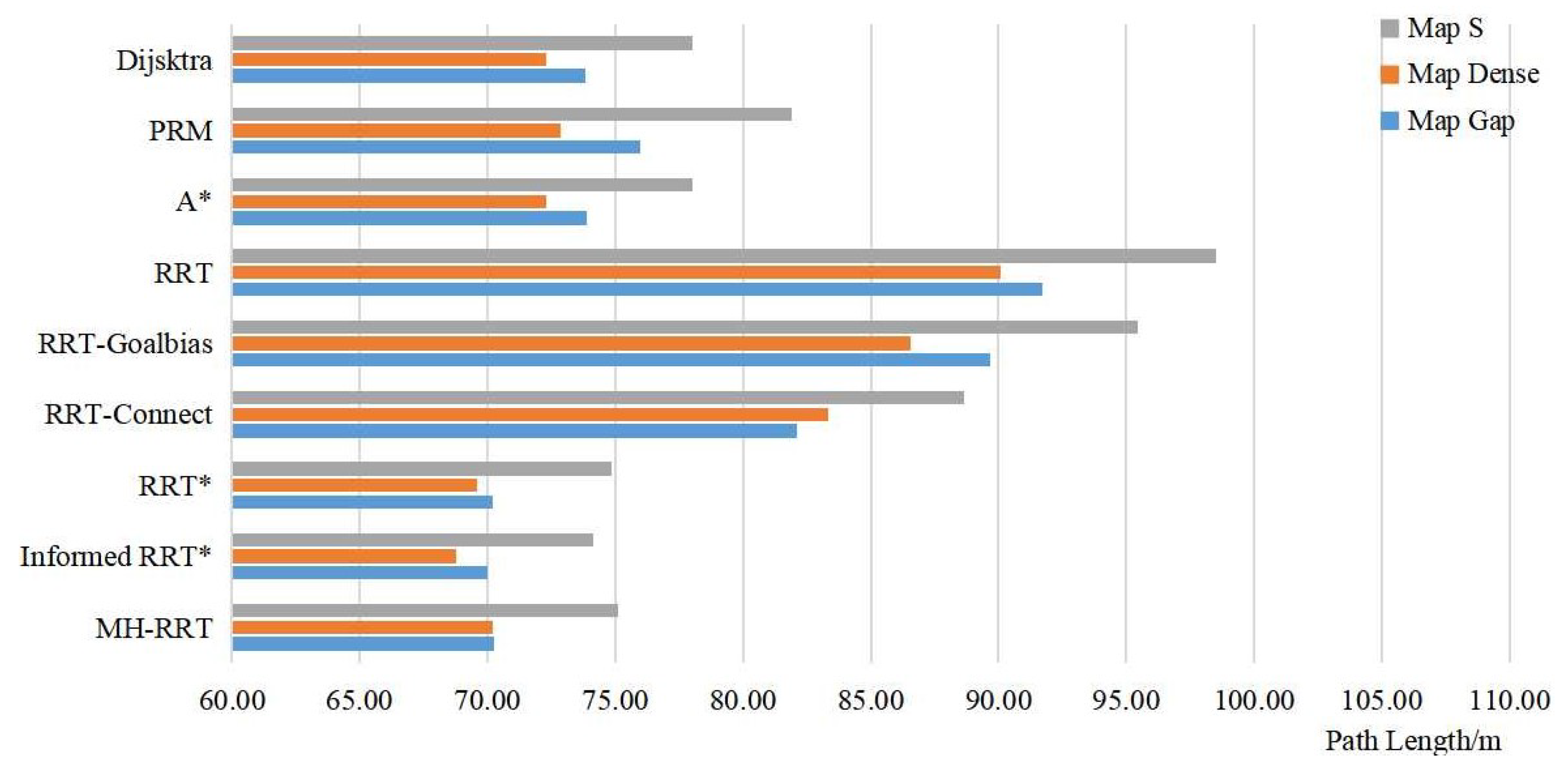




| Planning | Path | Iteration | Valid | Success | |
|---|---|---|---|---|---|
| Time (s) | Length (m) | Times | Nodes | Rate | |
| RRT | 3.00 | 90.09 | 2271.63 | 92.13 | 100% |
| RRT-Goalbias | 0.76 | 86.54 | 848.90 | 87.99 | 100% |
| RRT-Connect | 0.20 | 83.35 | 216.66 | 84.04 | 100% |
| RRT* | 111.46 | 69.57 | 5000.00 | 29.10 | 100% |
| Informed RRT* | 140.98 | 68.76 | 5000.00 | 27.13 | 100% |
| Dijkstra | 0.32 | 72.29 | 100% | ||
| A* | 0.31 | 72.29 | - | - | 100% |
| PRM | 1.17 | 72.86 | - | - | 100% |
| MH-RRT (ours) | 0.28 | 70.19 | 208.70 | 6.70 | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Luo, Y.; Tan, X. Path Planning for Automatic Guided Vehicles (AGVs) Fusing MH-RRT with Improved TEB. Actuators 2021, 10, 314. https://doi.org/10.3390/act10120314
Wang J, Luo Y, Tan X. Path Planning for Automatic Guided Vehicles (AGVs) Fusing MH-RRT with Improved TEB. Actuators. 2021; 10(12):314. https://doi.org/10.3390/act10120314
Chicago/Turabian StyleWang, Jiayi, Yonghu Luo, and Xiaojun Tan. 2021. "Path Planning for Automatic Guided Vehicles (AGVs) Fusing MH-RRT with Improved TEB" Actuators 10, no. 12: 314. https://doi.org/10.3390/act10120314
APA StyleWang, J., Luo, Y., & Tan, X. (2021). Path Planning for Automatic Guided Vehicles (AGVs) Fusing MH-RRT with Improved TEB. Actuators, 10(12), 314. https://doi.org/10.3390/act10120314







