A Multi-Curvature, Variable Stiffness Soft Gripper for Enhanced Grasping Operations

Abstract

For soft grippers to be applied in atypical industrial environments, they must conform to an object’s exterior shape and momentarily change their stiffness. However, many of the existing grippers have limitations with respect to these functions: they grasp an object with only a single curvature and a fixed stiffness. Consequently, those constraints limit the stability of grasping and the applications. This paper introduces a new multicurvature, variable-stiffness soft gripper. Inspired by the human phalanx and combining the phalanx structure and particle jamming, this work guarantees the required grasping functions. Unlike the existing soft pneumatic grippers with one curvature and one stiffness, this work tries to divide the pressurized actuating region into three parts to generate multiple curvatures for a gripper finger, enabling the gripper to increase its degrees of freedom. Furthermore, to prevent stiffness loss at an unpressurized segment, this work combines divided actuation and the variable-stiffness capability, which guarantee successful grasping actions. In summary, this gripper generates multiple grasping curvatures with the proper stiffness, enhancing its dexterity. This work introduces the new soft gripper’s design, analytical modeling, and fabrication method and verifies the analytic model by comparing it with FEM simulations and experimental results.

1. Introduction

Typical robotic tasks have recently changed from repetitive tasks in fixed environments to performing tasks in various atypical environments. Furthermore, there are many automated tasks where human–robot interactions are the norm. Therefore, existing robots made of rigid materials require sophisticated control, cannot quickly adapt to atypical environments, and are difficult to use in situations requiring human–robot interaction due to safety issues. To solve this, research on alternative robots made of soft materials has been actively conducted.

Most of the early versions of soft robots could move in a primitive actuation mode, driven by simple pneumatics or using soft active materials. However, they have evolved into systems that can hold objects using the actuators, though their functions remain limited [1,2,3]. Furthermore, soft robotic actuation [4,5,6,7,8] has been actively adopted in general soft robotic mechanisms, including manipulators [9,10], soft actuators [11], soft grippers [12,13,14], and rotating soft actuator systems [15].

Among various soft robots, the demand in fields where it is difficult to apply the current technology is increasing, and research on soft grippers is being actively conducted. In particular, it is challenging to use existing grippers in, for example, the agricultural product, confectionery, and bakery industries because their products are soft and fragile. The condition of the surface of a product has a significant influence on its marketability. Furthermore, since the product’s shape is usually rather random, there is a need for grippers that can be applied directly to an irregular shape. Therefore, it is essential to have a gripper that does not damage the surface of the product and can change its curvature according to the irregular shape of the product (multiple curvatures), by adjusting its stiffness (variable stiffness). In

Table 1. Comparison of soft gripper in terms of multi-curvature and variable stiffness.

Author	Multi-Curvature	Variable Stiffness
Group #1
(a) Loai A.T. Al Abeach [16]	×	◯
(b) Jihong Yan [17]	◯	◯
(c) Yufei Hao [18,19]	×	×
(d) Yeunhee Kim [20]	×	×
(e) Guoliang Zhong [21,22]	×	×
(f) Guoli Wang [23]	×	×
Group #2
(g) Loai Al Abeach [24]	×	◯
(h) Amir Firouzeh [25]	◯	◯
Group #3
(i) Zhijie Tang [26]	×	◯
Group #4
(j) Wei Wang [27]	◯	◯

, various types of grippers developed so far are compared regarding their abilities to address multiple curvatures and variable stiffness, which are essential requirements of soft grippers. The grippers’ driving method is divided into Group 1, driven by pneumatics, Group 2, driven by tendons, Group 3, driven by motors, and Group 4, driven by shape memory polymers (SMP), respectively.

In Group 1, grippers driven by pneumatic pressure, the most commonly used driving methods of soft robots, are collected. In (c), (d), and (e) of Group 1, the compliance increases by making the gripper from silicon. However, producing multiple curvatures and variable stiffness, which are the essential requirements mentioned earlier, is impossible. In (f), the actuating method is unique in that it uses negative pressure. However, it cannot realize multiple curvatures and variable stiffness. In the case of (a), although the gripper’s rigidity was adjusted using McKibben muscles, it has difficulty gripping objects of various sizes because it is impossible for it to adjust its curvature. Next, in (b), a low-melting-point alloy (LMPA) enables multiple curvatures and variable stiffness. The LMPA is inserted under the soft gripper and transfers heat using conductive Ni-Cr to melt the desired part to increase the desired curvature’s stiffness. Since these methods adjust the stiffness using phase changes through temperature, they are difficult to control, and it is very slow to heat them up and cool them down. One of the other problems is that the robot could be damaged due to heat.

Group 2 uses tendons to drive soft grippers. In the case of (g) of Group 2, variable stiffness was enabled using particle jamming. The particle jamming method uses the jamming effect in which a membrane and the particles are stuck to increase the stiffness upon applying negative air pressure. However, as multiple curvatures are not available, the gripper cannot grasp various objects. In (h), the gripper was bent into the desired shape using a tendon, and the stiffness was regulated by adding a shape memory alloy (SMP) layer to the joint. Therefore, the gripper in (h) has multiple curvatures and variable stiffness; however, similar to the LMPA, the SMP also uses heat to change the stiffness, so it is difficult to control, and the increasing and decreasing of the temperature is slow. As a result, its application to agriculture and food product handling may be limited.

Group 3 is a motor-driven method. In Group 2, a tendon is attached to the gripper, and a motor controls the tendon. However, in Group 3, a link mechanism is connected to the motor, and a thin-walled hollow structure is attached to the end of the link mechanism to drive it. In (i), the stiffness is regulated by applying pneumatic pressure to the thin-walled hollow structure, but multiple curvatures are impossible.

Group 4 is driven by SMP. For the case of (j), although the gripper finger is divided into three independent sections and individually heated for finger curvature change, it can not maintain enough stiffness when a particular section is not activated. Therefore it can not sustain stiffness for holding a heavy object, and it is not practical apparatus despite its capability for stiffness change. In addition, it is activated with heat input, and it is relatively slow such as it needs about 90 s for the stiffness transition.

In summary, the grasping operation time is concerned with the pneumatic driven gripper is the fastest mechanism compared to SMP and tendon wired motor drive. For the pneumatic gripper, it can be driven up to 1 Hz with moderate phase delay [20]. However, the tendon-driven soft gripper works at 0.33 Hz [24] whereas the SMP needs at least 90 s for changing its curvature [27]. For the stiffness transition speed, the pneumatic grippers need about 5 s to change their stiffness, whereas LMPA requires about 50 s and SMP needs even more time [17,27].

Noting the motivation of a new gripper design that adapts to various object shapes and multiple weights, the present work tries to deliver a Multi-curvature variable stiffness soft gripper that can change its stiffness and bending curvature. By dividing a pneumatic actuation chamber for creating pseudo-independent joints and combining them with a particle jamming-based variable stiffness mechanism, this work enables the new soft gripper to have expanded DOF and enhanced dexterity. In addition, with a newly developed segmented-core-frame, the particle jamming is more stabilized even for tasks requiring a curved finger shape. A new soft gripper could stably grasp objects of various shapes, sizes, and weights.

This article is organized as follows. Section 2 describes a new variable stiffness mechanism inspired by the human phalanx, and Section 3 proposes a multicurvature design using ecofriendly and highly stable fluidic actuation with an air supply panel. In Section 4, the analytical model of the new soft gripper was obtained, and the result was compared with simulation and experiment to verify the analytical model. Section 5 explains the manufacturing process of the new soft gripper and the connection to a robotic arm. In Section 6, the performance of the new soft gripper is evaluated through four types of experiments. Our conclusions are presented in Section 7.

2. Variable Stiffness Mechanism Inspired by the Human Phalanx

As mentioned earlier, the demand for structures that can change their stiffness at the desired moment increases. Therefore, this paper proposes a new variable stiffness mechanism inspired by the human phalanx, adjusting its stiffness at the designated structure curvature. In other words, the proposed method should provide a stable stiffened structure for a given shape. The soft-and-stiff hybrid feature enables a better soft gripper design for holding and handling various objects. Furthermore, it would be one of the technical contributions of this work.

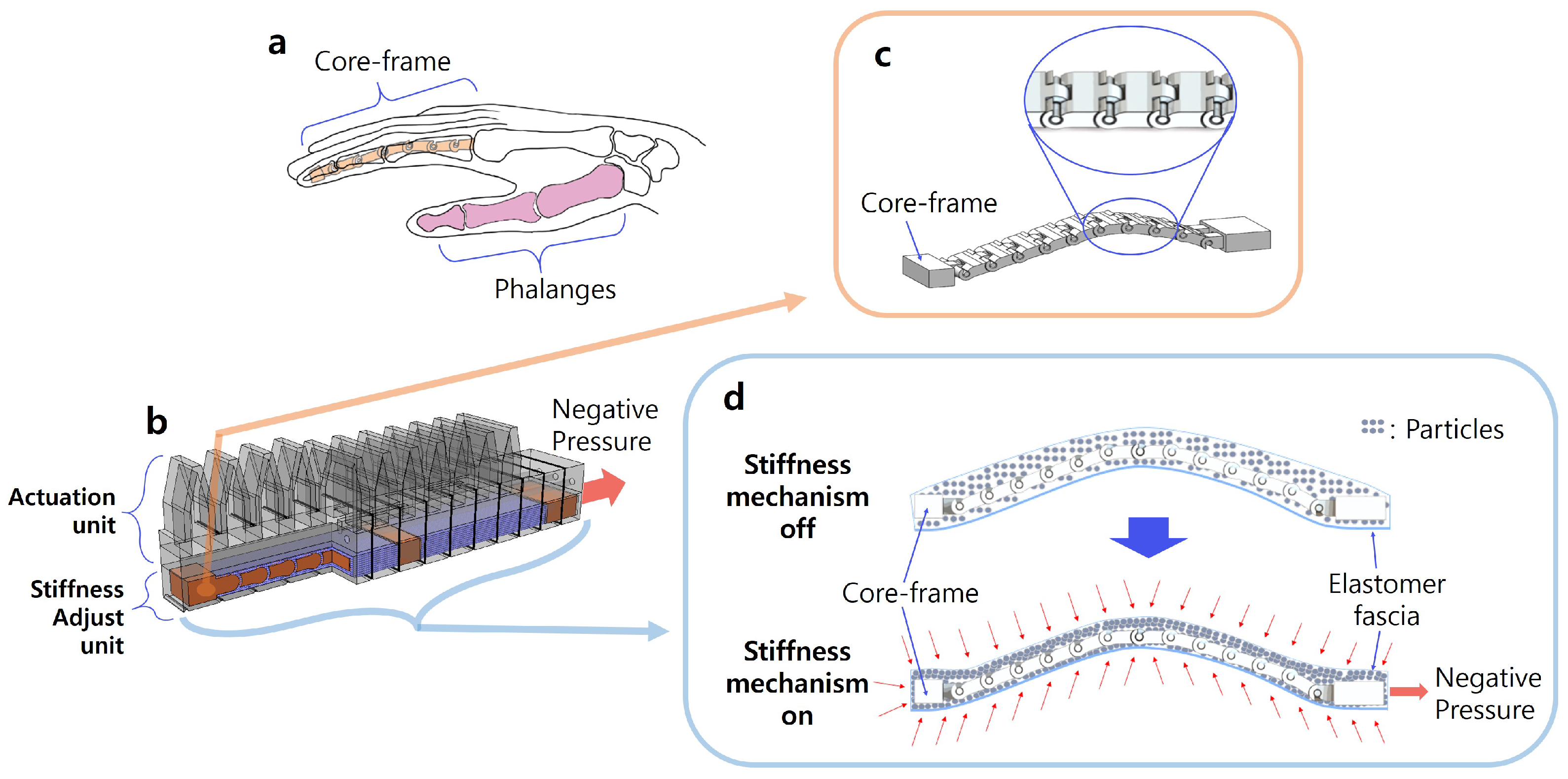
Humans can handle various objects more freely than any other creature on the Earth, as shown in Figure 1. It is accomplished by muscles that bend the finger joints to form a shape suitable for the object, phalanges that can maintain that shape, and sensory nerves that measure the proper grasping force. Anatomically analyzed, we focused on the phalanges that support the desired finger muscles and nerves to enable a proper grip. The phalanges forming the fingers consist of the distal, middle, and proximal phalanx [28], as in Figure 1b. The phalanx aspect ratio is relatively large, with a much longer length than the width or radius. Moreover, its grasping stability increase by holding the object in the longitudinal direction of the phalange. Additionally, phalanges are connected by hinge-like inter-phalangeal joints, so there are no obstacles to bending grasping motion.

Our phalanx-inspired variable stiffness mechanism is presented in Figure 2. This mechanism consists of two major parts, core-frame and particle jamming, to comply with the previously mentioned physical description.

In an actual finger, the phalanx position adapts to the object using muscles, and then that shape is maintained. To simulate this, particle jamming, which is widely used in soft robots, was applied here. The jamming refers to the effect of increasing stiffness by collecting thin wafers or small particles in a thin membrane container and then applying a negative air pressure across the container so that the membrane container and the structure stick together. Although there are many advantages to the jamming method in designing a soft robot since it helps maintain a required stiffness, there are also notable drawbacks to the typical jamming method. One of the disadvantages is structural stability issues, especially when their force chain is broken with an impulsive force input. In other words, when a jamming mechanism is organized with only particles encapsulated with a thin container, the jamming structures are weak for a particular type of abrupt force inputexternal force, which may induce buckling of the entire structure and fail to maintain the proper stiffness. Especially when a curved shape is required, the conventional particle jamming method could not guarantee to maintaining maintain both the desired stiffness and the curved shape.

A study combining layer and particle jamming was conducted to improve this drawback [29]. Furthermore, a study in which the entire soft gripper was composed of particle jamming was conducted [30]. However, as the stiffness enhancement mechanism was bulky, there was a disadvantage that it could not stably grip by making point contact with an object. Another study was conducted to solve the problem by connecting a bell-shaped object (so-called backbone) located in the middle of the particles. Still, the system itself became bulky and was not suitable for the gripper fingers [31].

Recognizing the prerequisite for stabilizing the force chain, which is crucial for the jamming method to guarantee effective stiffness management even when bent, this work tries to propose a new mechanism inspired by the phalanx architecture. The mechanism preserves the force chains created when negative pressure is applied. Hence the mechanism should support the grasping action and at the same time maintain the desired shape so as not to interfere.

From the human anatomy shown in Figure 2, since the fingers are connected by hinge-type joints so that they can be freely deformed without interfering with the grasping action, our core frame mimics the advantages of the phalanx joint. Unlike the previously introduced mechanism, this work constructed it by connecting small thin plates with 1-DOF pivot joints (Figure 2b) [31]. Furthermore, to take advantage of phalanx for stable grasping, the aspect ratio of the core-frame is large (Figure 2a). In other words, our new variable stiffness mechanism, which is inspired by human phalanx, consists of core-frame and particle jamming (Figure 2d). As Figure 2c, a new variable stiffness mechanism called stiffness adjust unit is located underneath the pentagonal shape actuation unit. Stiffness adjust unit works based upon constructing many force chains between neighboring particles. In addition, when a solid structure is packed with those particles, it works as a core for securing the stiffness by supporting the forces chains and eliminating unstable structural configuration. This work assembles particles and core-frame in a thin elastomer fascia like Figure 2d, and negative pressure is applied through the vent so that the stiffness increases using the jamming effect. It is stabilized with the core-frame even when a gripper finger is bent.

Even though adding the core frame into a particle jamming increases the jamming mechanism’s stability, particularly when it should maintain a bent shape, it still has room to be further optimized. This study proposes a design that can withstand a larger load by dividing the core-frame. As shown in Figure 3a, a divided core-frame named segmented-core-frame shows much better performance. The segmented-core-frame divides one membrane into two sections by inserting a connector in the middle of the core-frame. Furthermore, it sustains the force chain more effectively. Furthermore, by drilling a hole in the connector, air flows through increases the stiffness of the whole unit with one vacuum source. Although we have to admit the absence of the closed-form mathematical model, which could be used for optimization, we do not limit the possibility of extending this work for the future goal.

Stiffness testings with and without the connector were performed by fixing both ends with a curved shape of the phalanx jamming structure, and negative pressure (70 kPa) was applied to them, as demonstrated in Figure 3b. Next, a linear stage carrying the force measurement unit is installed perpendicular to the center of the curvature. Furthermore, the force is measured by moving the force measurement module from 1 to 10 mm by 1 mm increment. Each measurement was repeated ten times for an average. The standard deviation is in

Table 2. The standard deviation of stiffness test.

Displacement	1	2	3	4	5	6	7	8	9	10
Segmented-core	0.0017	0.0016	0.0018	0.0019	0.0020	0.0023	0.0022	0.0020	0.0019	0.0022
Core	0.0016	0.0019	0.0021	0.0023	0.0019	0.0020	0.0022	0.0022	0.0021	0.0020

. Figure 3c shows that the segmented-core-frame provides much better performances by 65% stiffer than the unsegmented one, core-frame; accordingly, segmented-core-frame is applied to this work.

3. Multi-Curvature Pneumatic Gripper Finger Design

Most soft grippers work with single-curvature fingers, as shown in Figure 4a. Therefore if the shape is irregular or large, objects are held with a point contact using the ends of the gripper’s finger. When the gripper holds an object in such a point contact, it may damage an object having a weak, soft surface, such as agricultural products or food products. It is degrading the market value, and the grasping stability against external forces is significantly reduced. As a result, to handle objects of various sizes having an atypical shape or a soft surface, the gripper’s shape must be changed according to the object’s shape. That is our motivation for designing a pneumatic actuator that can create multiple curvatures to conform to an object’s profile and maximize its bending range, as shown in Figure 4b.

The primary driving principle of the typical soft gripper fingers is as follows. First, several inflatable chambers are sitting on a beam supplying air through engraved channels, which also works as a finger frame. When pressurized airflow is given to the inflatable chamber through the beam, they are inflated and cause contact to neighboring ones. Then it generates a bending of the beam that can be used for grasping. However, as mentioned above, the existing grippers have all chambers connected to each other, so only one curvature can be produced; this means that atypical objects of various sizes are gripped using a point contact thus cannot be stably held. 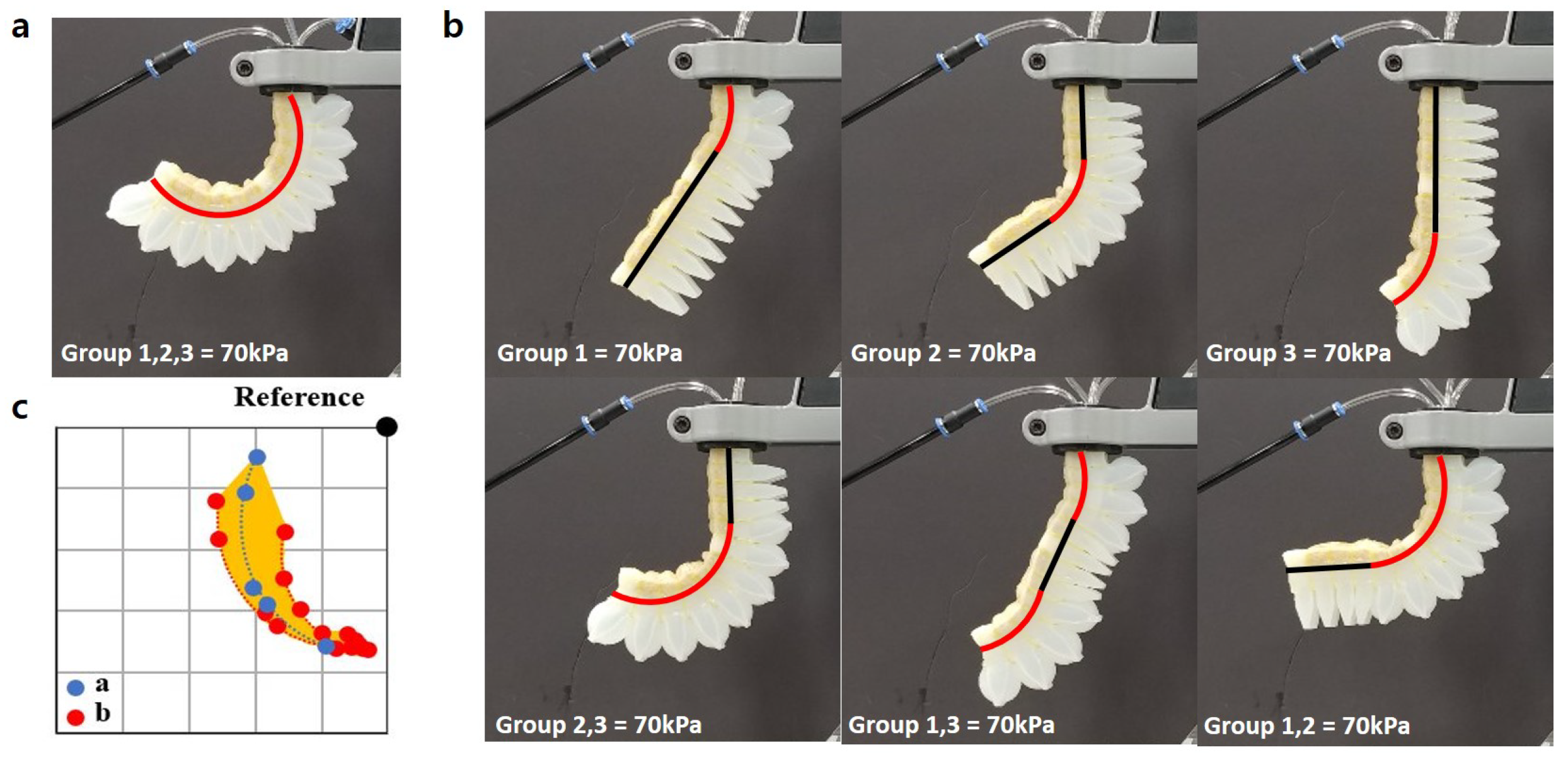This work changes the actuation scheme by dividing the air flows into three sections to resolve this problem, as depicted in Figure 5. The proposed design divided a gripper finger into three independent sections, proximal, middle, and distal. In addition, the air supply panel provides airflow to each section. The segmented configuration enables the gripper to produce many different shapes like human fingers since it is possible to apply different pneumatic pressures to each group 1 (proximal), 2 (middle), and 3 (distal) independently, as shown in Figure 5. This function will be tested, and the results will be elaborated in Section 6.

In addition to the separated airflow scheme for each group, the geometry of the individual inflating chamber might affect the gripper’s performance. Figure 6 shows finger cross-section view and its design parameters. The parameters are (a) the profile shape of the chamber, which affects swelling patterns, (b) the number of chambers for a certain finger length, (c) the height of the base, which is the overlapped section between the chamber root and the base and it becomes the constraint of the finger bending.

Most of the existing pneumatic soft grippers adopt a rectangular cube-type inflating chamber. Then it collides to adjacent inflated chambers to generate gripper finger bending. However, the rectangular cube shape chambers might have three disadvantages. First, producing a negative bending curvature is ineffective as the cubic profile limits the inverse bending motion. Second, when the same positive pressure is applied, it bends less than the pentagonal shape chamber, confirmed in the following discussions. Finally, the stress is concentrated at the corners of the chamber that does not contribute to bending operation and may raise reliability concerns. Therefore, this work uses a modified pentagonal shape inflating chambers. Figure 7, Figure 8 and Figure 9 will explain how the proposed chamber design works better.

First, the gripper’s workspace could be enlarged since the proposed chamber design provides better gripper finger curvatures. In Figure 7a, the proposed chamber design called Case 1 makes contacts to neighboring ones at closer locations to the air supply panel compared to the traditional squared chambers called Case 2. This feature produces a much shorter bending radius than Case 2 and provides an extended bending range for a positive curvature, as shown in Figure 7b. Along with the curvature geometry analysis, a FEM simulation confirmed the extended range, as shown in Figure 7c. In the FEM analysis, material properties, wall thicknesses, stand-off distances between chambers, and given air pressures of the two cases are identical. No gravitation is considered. Second, the proposed chamber design alleviates stress concentrations when pressurized. As a result, it enhances the life cycle, especially when it works at heavy-duty tasks. A FEM stress analysis shown in the Figure 8 supports the results. The maximum von Mises stress of the proposed design is about 87% of the typical design. Third, equipped with the modified pentagonal shape inflation chambers, the gripper finger could be bent with negative curvatures, expanding the gripper’s workspace. Figure 9 shows the advantages of the proposed design in terms of the expanded workspace when controlled with a negative air pressure input. This example could be one of the representative cases that confirms the advantages of an inflation chamber’s modified pentagonal profile.

To study the effect of the number of chambers when a certain finger length is fixed for the given grasping tasks, the bending curvature was measured with the same pressure (70 kPa) while increasing the number of chambers from 7 to 11 as shown in Figure 10. In the provided FEM result, the bending curvature increases as the number of chambers increases. Moreover, the gripper’s workspace could be enlarged.

Next is the height of the finger base that is the overlapped section between the chamber root and finger base. Furthermore, the role of the overlapped region should be answered for the finger design improvement. Figure 11 shows the analysis results. One can notice that the overlapped section works as a bending constraint, and as expected, less overlap produces more bending. It can be confirmed by comparing the “height 0” and “10” cases. Moreover, the “0” seems to be the best in terms of producing large bending deformation. However, it has a critical disadvantage in terms of loading capacity or grasping force. From the color legends that represent deformation stress, since the “0” case does not accrue proper stress on its structure, the case does not provide usable finger stiffness. On the other hand, the other extremity of the test “10” builds much higher stiffness when inflated. Therefore, selecting base height “2.5” or “5” would be the best solution.

In order to investigate the constructed bending geometry, curvatures of the bent fingers are considered. We can notice that the bent fingers could have multiple curvatures. Furthermore, the simple bent geometry of one finger section might be more beneficial when we expand our design to a three-independent-section multiple curvature finger. The “2.5” case has a more significant difference between the minimum and the maximum curvatures than the case of “5”. Consequently, base height “5” has been selected for this work.

4. Analytical Modeling

This section describes the analytical modeling process for chamber inflation ($\delta$) by pneumatic pressure (Pa) to expect the New soft gripper’s bending displacement, and it will confirm the results provided in Figure 7. First, by assuming the problem with two dimensions, free body diagrams are provided for each chamber of Case 1 and Case 2 mentioned in Figure 7 that determine the forces applied to the chamber and calculate the stress applied to the inflated chamber. Then, a constitutive equation is established to connect the pressure and displacement. Details are as follows.

4.1. Free Body Diagram and Force Equilibrium Condition

Figure 12 provides the initial and inflated configuration of Case 1 and Case 2 chambers. It is assumed that chamber bottom width d is not changed during the operation. The axis in the chamber’s height direction is called h that also plays a role in symmetry, and the axis in the chamber’s swelling direction is called $\delta$. $Pa$ is the applied air pressure, and $F/2$ is the reaction force acting at the end of the chamber to balance the force when d is unchanged. In summary, the force equilibrium of Case 1 and Case 2 is as follows.

$$F=Pa·l$$

(1)

where l is the length of the arc of the inflated chamber. Furthermore, since F is equal to the value obtained by integrating the stress of the chamber in the (h) direction of the chamber, the force balance equation can be established as follows. T is stress.

$$\begin{array}{c}\hfill \int Tdh=P_a·l\end{array}$$

(2)

4.2. Solving Constructed Equations

4.2.1. Case 1

In order to obtain the inflated length of the chamber solving Equation (2) derived from Section 4.1, l must be obtained.

From the Figure 12, due to the discontinuity of the structure geometry at the point ‘b’, the deflection of the rod must be calculated by dividing it into two. Since the point ‘b’ has two degrees of freedom in this two-dimensional representation, it is assumed that spring is attached to the tip of the rod to realize a convex downward elastic curve without restricting the vertical and horizontal movement of ‘b’ (Figure 13a). These boundary conditions make the analysis result similar to the FEM analysis to be compared.

The moments for each of the two sections are considered for a compatibility conditions. Using Figure 13, $M_1$ and $M_2$ are explained. At this time, each range is $0\le x_1<\alpha$ and $0\le x_2<\beta$. $x_2$ is set from the right end of the rod to where the spring is located $R_a$ is the reaction force at the pin.

$$\begin{array}{ccc}{M}_1\hfill & =& R_a{x}_1+P_a\alpha (\frac{\alpha }{2}-x_1)\hfill \\ M_2\hfill & =& P_a\beta (\frac{\beta \alpha }{2}-x_2)\hfill \end{array}$$

(3)

Next, by integrating the moment, the deflected curves of the $x_1$ section ($v_1$) and the $x_2$ section ($v_2$) are calculated as following.

$$\begin{array}{ccc}\hfill v_1& =& \frac{1}{EI}[\frac{R_a}{6}{x_1}^3+P_a\alpha (\frac{\alpha }{4}{x_1}^2-\frac{1}{6}{x_1}^3)+c_1{x}_1]\hfill \\ \hfill c_1& =& \frac{P_a{\beta }^2\alpha -2P_a{\alpha }^3}{12}-\frac{P_a{L}^2}{2\alpha k}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill v_2& =& \frac{1}{EI}[P_a\beta (\frac{\beta }{4}{x_2}^2-\frac{1}{6}{x_2}^3)+c_2{x}_2+c_3]\hfill \\ \hfill c_2& =& \frac{R_a{\alpha }^2}{2}+c_1\hfill \\ \hfill c_3& =& \frac{-P_a{L}^2}{2\alpha k}-\frac{P_a{\beta }^4}{12}-c_2\beta \hfill \end{array}$$

(5)

where k is the spring constant, E is the modulus of elasticity, and I is the moment of inertia, respectively.

4.2.2. Case 2

The deflection shape of Case 2 could be obtained likewise. Since point ‘a’ of Case 2 moves only vertically, a roller could represent the boundary condition. Afterward, through the same calculation procedure as Case 1, the deflected curve of Case 2 can be determined as,

$$\begin{array}{c}v=\frac{-P_{a}x}{24EI}(x^3-2L{x}^2+L^3)\end{array}$$

(6)

Equation (2) must be solved to determine the maximum inflated length of the chamber (${\delta }_{max}$) versus the pressure applied to the chamber ($P_a$). Moreover, we know that l is equal to the length of the deflected curve. In this case, by using the relationship between the length of the function (curve) and the derivative of the function, the l of the equation can be obtained using the deflected curves obtained from Section 4.2.1 and Section 4.2.2. Furthermore, since the force applied to the chamber is the sum of the stresses in the $xx$ direction, Equation (2) can be written as follows.

$$\begin{array}{c}\hfill {\int }_0^h{T}_{xx}dh=P_a·{\int }_0^h\sqrt{1+({v^{\prime }\left(h\right))}^2}dh\end{array}$$

(7)

4.3. Constitutive Equations

To solve the force balance equation derived above, the stress value of the inflated part of the chamber must be known. Furthermore, the Cauchy-stress for it is as follows.

$$\mathbf{T}=\mu \mathbf{F}{\mathbf{F}}^{\mathbf{T}}-p_h\mathbf{I}$$

(8)

where $\mathbf{F}$ is the deformation gradient, and $\mu$ is the modulus of the elastomer. $p_h$ is the hydraulic pressure, and $\mathbf{I}$ is the identity tensor. Therefore, $\mathbf{F}$ must be determined first to obtain the stress of the chamber. In Figure 12, $(X,Y)$ is the global coordinate and $(x,y)$ is the rotating one. Moreover, as explained in Figure 14, the coordinate rotation is by $\omega$. Therefore, the relation between the segment’s initial length of $dX,dY$, and the post-deformation length $dx,dy$ is as follows.

$$\begin{array}{c}\hfill dY=dycos\omega -dxsin\omega \end{array}$$

(9)

$$\begin{array}{c}\hfill dX=dysin\omega +dxcos\omega \end{array}$$

Therefore, by substituting Equation (9) to $\mathbf{F}$, the deformation gradient for the chamber can be obtained as

$$\mathbf{F}=\left(\begin{array}{cc}\frac{\partial y}{\partial Y}& \frac{\partial y}{\partial X}\\ \frac{\partial x}{\partial Y}& \frac{\partial x}{\partial X}\end{array}\right)=\left(\begin{array}{cc}cos\omega & sin\omega \\ -sin\omega & cos\omega \end{array}\right)$$

(10)

Furthermore, substituting Equation (10) into Equation (8), the Cauchy stress tensor is determined as follows.

$$\begin{array}{ccc}\hfill T_{yy}& =& -p_h+\mu {cos}^2\omega +\mu {sin}^2\omega \hfill \\ \hfill T_{yx}& =& -p_h\hfill \\ \hfill T_{xy}& =& -p_h\hfill \\ \hfill T_{xx}& =& -p_h+\mu {cos}^2\omega +\mu {sin}^2\omega \hfill \end{array}$$

(11)

At this time, in the case of $T_{xx}$, it is possible to know that it is a function of $P_h$ and $\mu$ through Equation (11), and because h is a known value, $T_{xx}$ can be calculated. Therefore, using Equation (7), the value of l according to $P_a$ is obtained. Calculation results are provided in Figure 15 for Case 1 and Figure 16 for Case 2. For Case 1, as shown in Figure 12, only the section ‘b-c’ is shown because the chamber inflates to the maximum at this section. Furthermore, one can find in the figures, the chamber’s vertical height becomes shorter as the pressure increases, and the $\delta$ increases as the pressure increases are very similar to the actual situation.

4.4. Comparative Study for Analytical Modeling, FEM, and Experiments

In this section, using the presented analytical model of Section 4, the inflation versus pressure for single chamber Case 1 and 2 are calculated and compared with the FEM (Dassault Systems Abaqus) simulation results. Besides, the motion of a gripper finger is compared with the analytic model and FEM. Furthermore, those are also confirmed with tests. Figure 17 compares the analytic model and FEM simulation results for the chamber’s inflation. In the figure, both results are matched well. Next, Figure 18 shows the volumetric strain and inflation $\delta$ of one chamber for various inputs. According to Figure 18, the volumetric strain of Case 2 is larger than Case 1 at low pressure, 20 kPa. However, the volumetric strain of Case 1 becomes larger than Case 2 at higher pressure. The results confirm that the deflection and volumetric strain of Case 1 is greater than that of Case 2 at the same input, although the reason should be further studied.

Next is a comparison between the analytical model, FEM simulation, and experimental results for the multicurvature configuration. The pressure is applied equally to 70 kPa, and all seven curvatures that the new soft gripper can produce are compared by applying pneumatic pressure to Groups 1, 2, and 3 described in Figure 5. As shown in Figure 19, it can be seen that the analytic model, simulation, and experimental results are all well-matched. For the analytic model, a result for a single chamber is extrapolated to construct gripper bending. In this situation, the physical interaction between inflated chambers is ignored, and it might be a leading source of the error.

5. Fabrication Procedures

Detailed fabrication procedures of the new soft gripper are provided in this section. Two major functional parts, the actuation unit for multicurvature and the stiffness adjust unit for variable stiffness, consist of the gripper.

As mentioned, the gripper finger has eleven inflating chambers, and those are grouped into three. Moreover, each group is independently connected to an air pressure source through an air supply panel. In this work, most flexible soft parts are made with silicon (Dragon Skin 30 and Ecoflex 00-30). Figure 20 shows schematics of the fabrication procedures. First, the inflating chambers are built with the Dragon Skin using Fused Filament Fabrication (FFF) 3D printed molds. The mold filled with Dragon Skin has to stay in a hot chamber for curing. The air supply panel is made with the same method adopted for the inflating chambers. Once the chamber and panel are cured, they are assembled with silicone adhesive (Sil-Poxy).

For the Stiffness adjust unit fabrication, a Stereo Lithography Apparatus (SLA)3D printing is adopted to construct segmented-core-frames. Its elastomer fascia (container) is made with the same procedure as the inflating chambers. Once the core-frame and the fascia are combined, small polymer particles are poured into the fascia. When the two units are finished, they are glued with a silicone adhesive (Sil-Poxy) and cured.

6. Testings and Discussions

In this section, the proposed new soft gripper is tested for the verification of its functionality. Emphases are given on the following. The first functional element confirmed is whether the gripper could produce several different finger shapes and grasp various objects. The second, whether it could maintain proper finger stiffness and carry various weights. Last, whether the finger could maintain the designated shape even after loading. In addition, various experimental videos that can show the enhanced functions of the new soft gripper are attached.

Note on the third item since it has not been elaborated on before. Suppose all of the inflating chambers of a gripper finger are connected and pressurized simultaneously, which is a norm for the existing grippers. In that case, the gripper finger will create one curvature and be stiffened. On the other hand, this proposed design has separated inflating chambers grouped into three and can be pressurized independently to create many different shapes. In this case, if one of the inflating chamber groups is not pressurized to produce a local strait shape, that portion may have less stiffness since the pressurized chambers do not support it. Consequently, the intended finger shape could be distorted and may be difficult to work correctly when it is heavily loaded. One of the essential motivations of this work is to combine multicurvature creation and the jamming-based stiffness adjustment.

6.1. Multicurvature Bending Shape Test

Experiments are conducted to see the difference between multi and single-curvature. The 70 kPa air is applied to the finger using a pump (JUN-AIR) and a regulator (SMC Pneumatics) for the experiments. In Figure 21, the red line indicates the chamber group to which pneumatic pressure is applied. Figure 21a shows a single curvature posture as all chamber groups are pressurized, whereas Figure 21b presents multiple curvatures with six different actuation combinations. In order to check the finger workspace, another test is carried out using a vision camera following the fingertip when the finger is pressurized with 0 to 80 kPaa increasing air supplies. Furthermore, the results are provided in Figure 21c. In the graph, the fingertip of the single curvature moves along with the blue line dotted with ‘a’ whereas the multicurvature moves on the yellow area with extreme cases are marked with red `b’ dots. The results confirm that the multicurvature guarantees a better dexterity of the manipulation.

6.2. Variable Stiffness Test

In this test, the second feature of this work will be verified in terms of load sustainability when partially pressurized. First, as shown in Figure 22a, the finger is not pressurized, but the segmented core frame reinforced jamming is operated on and off. Here the ‘on’ represents that air inside the elastomer fascia is drained with a vacuum pump (Rocker 300) by negative 70 kPa. Under the condition, the finger is pushed with a force gauge guided by a linear motion stage, and the reaction force is measured. By the same token, Figure 22b shows a situation for a 90-degree bent finger test. Note that the proximal and middle inflating chamber groups are pressurized for the 90-degree bent shape. The finger’s reaction force was measured every 1 mm by changing the force gauge position from 1 mm to 10 mm, repeated ten times for each of the four states to derive an average value for each location. The standard deviation is in

Table 3. The standard deviation of variable stiffness test.

Displacement	1	2	3	4	5	6	7	8	9	10
Figure 22c
Stiffness on	0.0019	0.0017	0.0027	0.0030	0.0018	0.0023	0.0023	0.0019	0.0019	0.0021
Stiffness off	0.0026	0.0036	0.0023	0.0024	0.0033	0.0026	0.0023	0.0027	0.0019	0.0015
Figure 22d
Stiffness on	0.0023	0.0022	0.0031	0.0032	0.0020	0.0029	0.0023	0.0028	0.0024	0.0033
Stiffness off	0.0035	0.0032	0.0027	0.0038	0.0029	0.0016	0.0024	0.0021	0.0027	0.0043

. As a result, as shown in Figure 22c,d, when the stiffness adjust unit is on, the stiffness was improved by about 30%.

6.3. Grasping Stability Test

In this subsection, two tests are carried out to verify the grasping stability of the new soft gripper. The first test is shown in Figure 23, where the gripper is given three different spheres, and they are tangerine, tomato, and orange. Figure 23a shows the typical grasping operation of the existing pneumatic grippers. Since the gripper has to grasp the object with one curvature, some objects should be held with a point contact pinch grasping. With this grasping condition, the gripper may lose its grip because of external force.

On the other hand, Figure 23b bends the gripper finger according to the shape of the object and increases the stiffness using a variable stiffness mechanism (using negative pressure 70 kPa). For verifying the grasping quality, the gripper is shaken. As a result, Those different objects are firmly held with proper finger posture adjustments, and it successfully maintains the grip even when it is shaken.

The second test shown in Figure 24 demonstrates the grasping capability of the new soft gripper that can reliably grasp objects of various sizes, weights, and shapes using its multicurvature and variable stiffness mechanism. Figure 24a,b verify that the new soft gripper successfully changes its shape to fit the various objects’ profile and increases the contact area for more secure grasping. As a result, it can grasp tiny soft blueberries, raw eggs, tomatoes, and even heavy pomegranates. In addition, a cylinder shape object can be effectively held, as shown in Figure 24b,e,h. Moreover, the gripper also easily holds a hammer (1.7 kg) by increasing its stiffness, as shown in Figure 24j.

In all tests, one can verify that an inflating chamber group that is not pressurized can sustain its designated shape thanks to the jamming support. Authors have to admit that the postures of each grasping are not optimized in the present tests, and it should be further elaborated in the following work.

7. Conclusions

The soft robot could soon play an important role in general robotics technology fields by extending the application area to many industrial problems. For example, industries where soft or malleable products are the mainstream, such as agriculture, bakery, or cosmetics, will need soft grippers for their automated manufacturing. Although many soft grippers are made with many different materials, most focus on delivering softness characteristics to switch current rigid gripper-dominated application areas. However, few of them are concentrating on the enhancement of the soft gripper’s manipulation dexterity. This work proposed a new soft pneumatic gripper that can change its finger bending curvature and stiffness.

The variable stiffness mechanism combines the particle jamming and the segmented-core-frame inspired by the human phalanx. It is designed to effectively adjust stiffness without disturbing the soft gripper to achieve multicurvature grasping actions. Furthermore, the multicurvature gripper design proves its contribution to enhancing dexterity. The new soft gripper successfully expands its workspace and can grasp objects with improved stability by reconstructing the expansion chamber profile into a modified pentagonal shape Analytical modeling of the new soft gripper is established to analyze the bending motion. Modeling is compared with FEM simulation and Experiment.

Although the combination of the segmented-core-frame based particle jamming and the multicurvature finger was not an option for an accurate gripper operation, both ideas could be independently used for soft robot manipulation. In this work, even though the presented soft gripper is believed to outperform the typical pneumatic soft grippers in terms of both dexterity and stability, authors have to admit that its design is not elaborated for optimized performance. Moreover, although the present work does not quantitatively measure the gripper’s capability to maintain grasping quality, it does not limit its application to complicated grasping tasks requiring precise objects handling. In summary, the presented soft gripper can adapt to the object’s profile to achieve a secure hold, and it maintains the condition even with an abrupt external shaking. Moreover, the gripper could be effectively used for many industrial applications if further improved with embedded sensors and proper control.