Analysis of Multi-Physics Thermal Response Characteristics of Anchor Rod and Sealant Systems Under Fire Scenarios

Abstract

During on-site welding operations, the sealant coated on anchor bolt surfaces can be ignited by hot particles or localized sparks, potentially triggering a fire hazard. This combustion process involves a complex multi-physics coupling among sealant combustion, convective and radiative heat transfer, and three-dimensional heat conduction in solids. To resolve this coupling, a simulation strategy is proposed that correspondingly integrates the Fire Dynamics Simulator (FDS, version 6.7.6) for modeling combustion and radiation with ABAQUS (2024) for simulating conductive heat transfer in solids. The proposed method is validated against experimental measurements, showing close agreement in temperature evolution. It also demonstrates robustness across varying geometric scales, thereby confirming its reliability for predicting thermal response. Using this validated method, simulations are performed to analyze the fire behavior of an anchor rod-sealant system. Results show that the burning sealant can raise anchor rod temperatures above 900 °C and lead to rapid flame spread between adjacent rods. Furthermore, a sensitivity analysis of thermophysical parameters identifies critical thresholds for fire safety optimization: sealants with an ignition temperature > 280 °C and thermal conductivity ≥ 0.26 W/(m·K) demonstrate effective self-extinguishing properties, while specific heat capacity can retard flame growth. These findings provide a robust numerical framework and quantitative guidelines for the fire-safe design of bridge anchorage systems.

1. Introduction

In the anchorage systems of suspension bridges, applying a sealant layer to steel anchor rods serves as a critical technical measure to enhance structural durability and mechanical performance. The sealant layer not only forms a dense protective barrier that effectively blocks the intrusion of corrosive media such as chloride ions, moisture, and oxygen, thereby slowing down the electrochemical corrosion of steel anchor rods [1], but also fills the interfacial gaps between the rod body and the concrete bore wall. This action allows the load to be uniformly transferred as shear stress, thereby preventing stress concentration. However, this type of organic sealing material is typically flammable. During on-site welding construction, hot particles or localized sparks can easily ignite the sealant, consequently causing a fire and posing a potential threat to the safety of the anchorage system [2].

The thermal response characteristics of steel structures and ancillary materials under fire scenarios constitute an important research topic in the field of engineering safety. Compared to experimental tests, numerical fire simulation is favored by researchers due to its advantages in saving time and labor. At the single-physics field analysis level, the Fire Dynamics Simulator (FDS), which is based on Computational Fluid Dynamics (CFD), is widely used to describe fluid behavior during a fire [3]. For instance, Wahlqvist [4] validated the reliability of FDS in predicting smoke movement, temperature distribution, and thermal radiation in large confined spaces through numerical simulation. Regarding the single-physics field analysis of solid structure thermal response, ABAQUS, a general-purpose simulation platform based on the Finite Element Method (FEM), possesses excellent capabilities for structural thermal analysis. Previous studies have used ABAQUS to construct three-dimensional thermo-mechanical coupling models, successfully capturing the nonlinear deformation of steel beams at high temperatures [5,6]. This highlights the importance of 3D numerical modeling in structural fire resistance analysis.

The thermal behavior of steel structures and ancillary materials in fire scenarios involves a complex coupling among sealant combustion, convective and radiative heat transfer, and solid heat conduction, which is a typical multi-physics transient response process. Therefore, accurately describing its thermal behavior remains challenging using only traditional single analysis methods. Multi-physics coupled simulation provides a critical tool for the in-depth revelation of structural behavior under fire [7,8]. With the deepening of research, the coupled simulation of CFD and FEM has become a key means to achieve refined analysis of fire–structure interaction. Zhang et al. [9] proposed a one-way coupling method based on FDS and ABAQUS, which effectively evaluated the thermodynamic response of steel structures under localized fires by using the adiabatic surface temperature as the thermal boundary condition. Furthermore, Chen et al. [10] utilized the coupling of FDS and ABAQUS to reveal the significant effect of non-uniform temperature fields on the distribution of internal forces in structures, thereby promoting the in-depth application of multi-physics coupling in structural fire resistance research.

In addition, in the field of bridge fire safety, scholars have conducted systematic research focusing on the thermodynamic behavior of key components, localized fire effects, and the optimization of fire protection design [11,12,13,14]. Du et al. [15] combined small-scale tests with FDS simulation to reveal the temperature distribution pattern of a suspension bridge main cable under vehicular fire. For composite structures containing polymer materials, Park [16] systematically analyzed the fire behavior of steel–polymer composite slabs, clarifying the influence of parameters such as steel plate and polymer layer thickness on fire resistance, which provides a basis for the fire protection design of conventional composite systems.

However, existing research primarily focuses on specific standardized components such as beams and slabs, and a thorough investigation into the heat transfer path and safety implications of the steel anchor rod–organic sealant system under fire conditions is still lacking. Particularly when specialized sulfurized sealants for bridges are involved, the mechanism by which their key thermophysical parameters (such as ignition temperature, thermal conductivity, and specific heat capacity) affect the system’s overall fire risk remains unclear. Furthermore, under transient high-temperature fire sources induced by welding construction, the ignition characteristics of the sealant, its flame propagation behavior, and its thermal feedback mechanism to the anchor rod have not been systematically revealed. This gap restricts the safety assessment and the formulation of control strategies for such structures in real fire scenarios.

This study investigates the thermal response of the anchor rod-sealant system in the Shiziyang Bridge under construction-phase fire exposure. To address the limitations of conventional simulation methods, a coupled FDS–ABAQUS framework is developed, enabling integrated analysis of fire dynamics and three-dimensional heat transfer in solids. Using this approach, the combustion process within the system is analyzed, and the risk of flame propagation between adjacent anchor rods is evaluated. Furthermore, the effects of three key material parameters—ignition temperature, thermal conductivity, and specific heat capacity—on the fire-induced thermal behavior are quantitatively examined. The findings provide both a validated simulation methodology and practical insights for the fire-safe design of sealants in critical bridge components.

2. Methodology

2.1. Coupled FDS–ABAQUS Simulation

The process of sealant combustion and anchor rod heat conduction under fire conditions involves multi-physics coupling problems, specifically fluid combustion, thermal radiation transfer, and three-dimensional heat conduction in solids. A single simulation software tool cannot simultaneously meet the accuracy requirements of each stage. Based on an assessment of software functional complementarity, this study established a coupled strategy of FDS providing the thermal load and ABAQUS resolving the temperature field, in order to overcome the limitation of FDS’s one-dimensional simplification in solid heat conduction and the deficiency of ABAQUS in fire fluid simulation. The specific procedure includes the following two steps:

(1)

Establish an FDS fire model consistent with actual working conditions to simulate the smoke flow and thermal radiation distribution characteristics during the sealant combustion process, focusing on extracting the time-history data of the heat flux on the anchor rod structure’s surface.

(2)

Establish a three-dimensional solid ABAQUS model of the anchor rod that corresponds exactly to the geometric dimensions of the FDS model, apply the pre-processed heat flux as a surface load to the model’s surface, and perform transient heat conduction calculations to obtain the detailed temperature field distribution inside the anchor rod and its time evolution.

2.2. Validation of the Framework

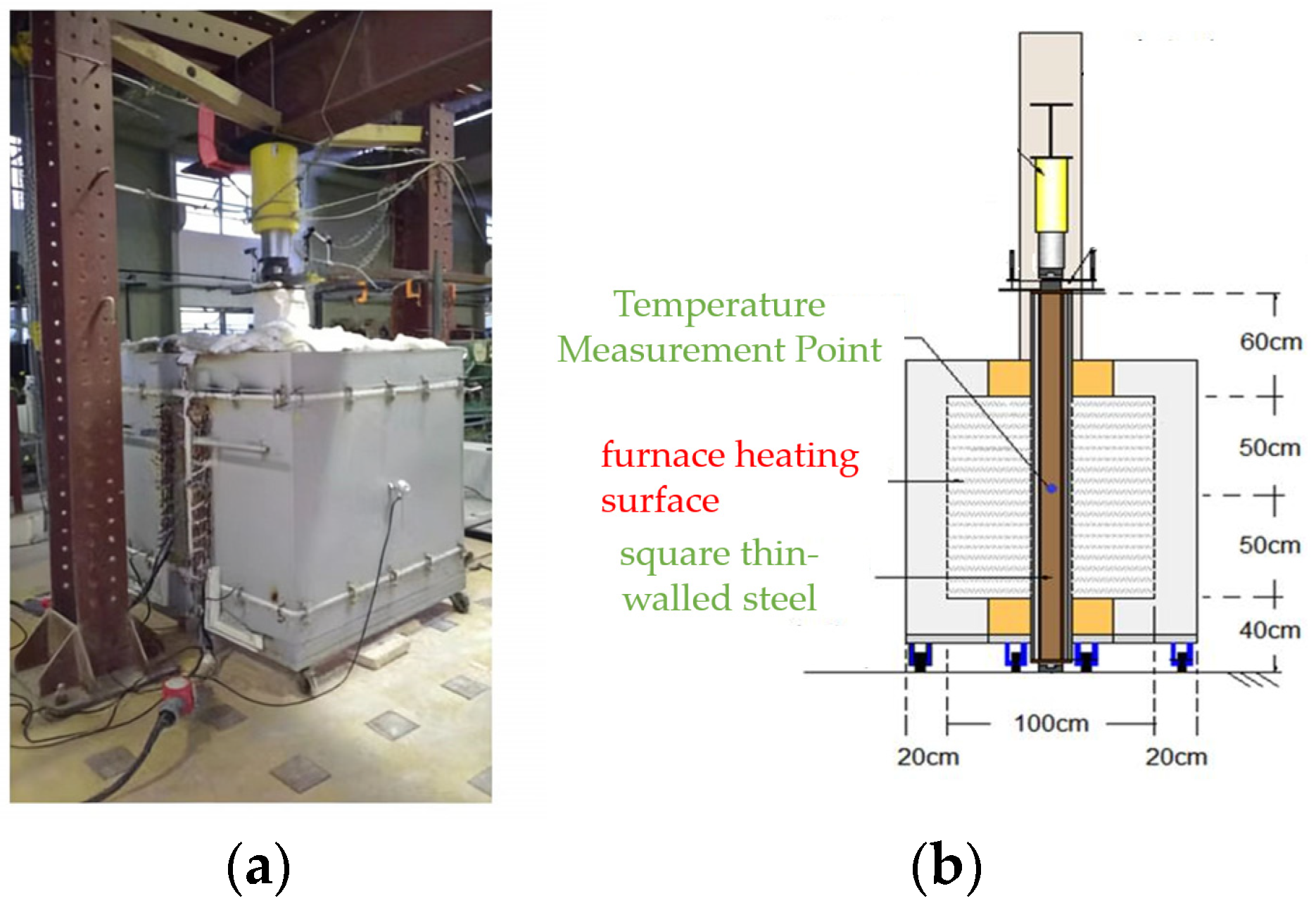
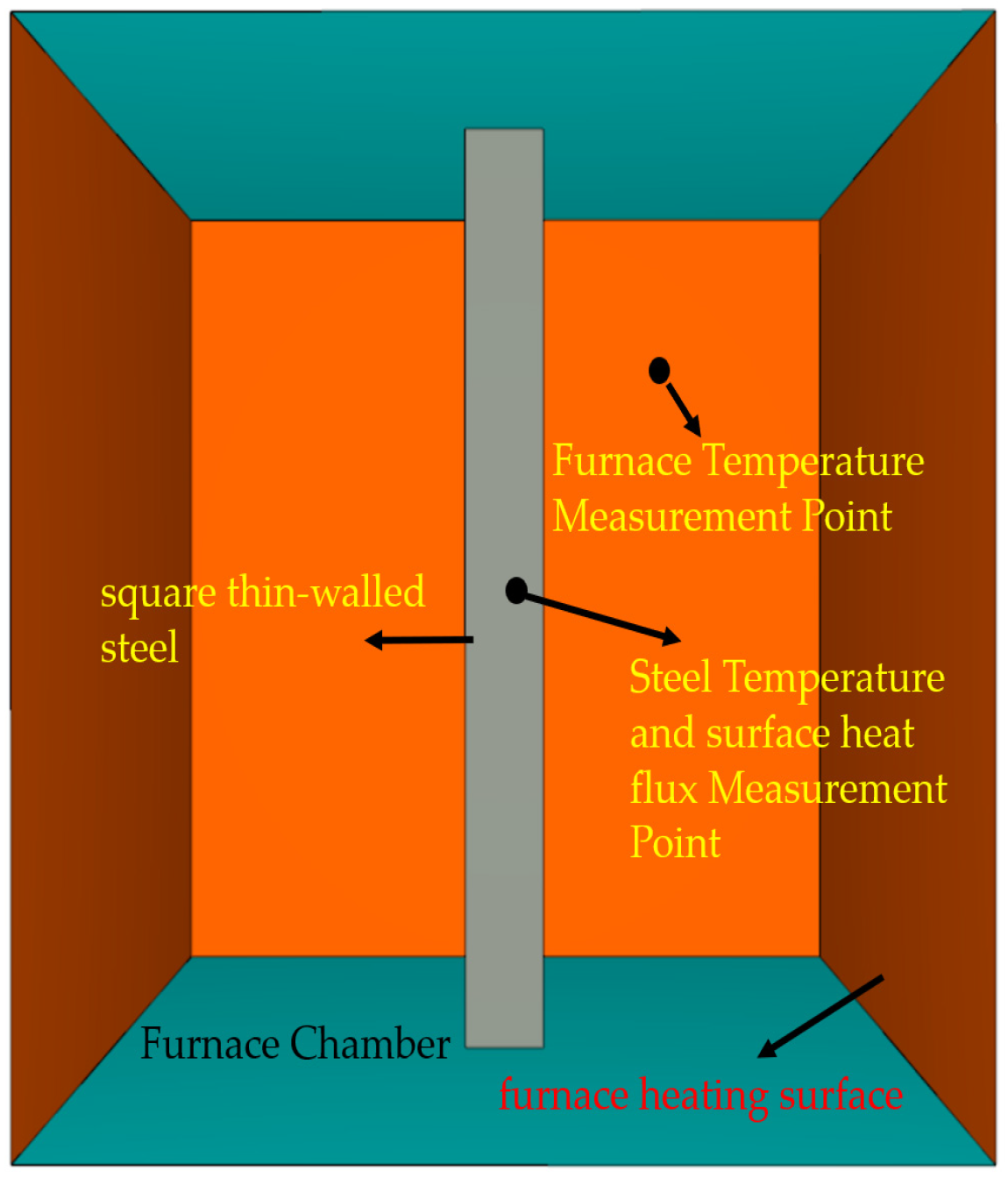
2.2.1. Experimental Configuration

To validate the coupled calculation method, the fire resistance test data for square thin-walled steel members from Ref. [17] were used. As shown in Figure 1a,b, the experiment was conducted in a furnace with an internal chamber measuring 1 m × 1 m × 1 m. Heat was supplied through the four walls of the furnace, following the ISO 834 [18] standard temperature–time curve, to heat a vertically placed thin-walled square steel tube positioned at the center of the chamber. The tube had a cross-section of 0.1 m × 0.1 m and a wall thickness of 0.003 m. During heating, temperatures of the specimen and the furnace environment were simultaneously recorded using K-type thermocouples installed on the specimen surface and inside the furnace chamber.

2.2.2. Numerical Modeling

1.

FDS Model for Fire and Thermal Loads

Based on the experimental configuration, a three-dimensional numerical model was developed in FDS. The internal geometry of the model is illustrated in Figure 2. Time-varying thermal boundary conditions conforming to the ISO 834 standard fire curve were imposed on the heated surfaces. The density of steel was taken as 7850 kg/m³, while specific heat and thermal conductivity were assigned as temperature-dependent functions, with values provided in

Table 1. Thermal parameters of the steel.

Temperature (°C)	Specific Heat Capacity (kJ/(kg·K))	Thermal Conductivity (W/(m·K))
20	0.5	54
100	0.52	50
200	0.55	48
400	0.62	43
600	0.7	38
800	0.8	33

. These parameter selections ensure that the thermal boundary conditions and material properties in the simulation accurately represent those of the physical experiment.

To achieve an optimal balance between computational resources and analytical precision, the mesh size for the bridge fire computational domain is typically selected within the range of $1/5$ to $1/20$ of the characteristic fire diameter. The characteristic fire diameter, $D^{*}$, is calculated as follows:

$$D^{*}={\left({\displaystyle \frac{Q}{{\rho }_{\infty }{c}_p{T}_{\infty }\sqrt{g}}}\right)}^{2/3}$$

(1)

where $D^{*}$ is the characteristic fire diameter (m); $Q$ is the heat release rate of the fire, taken as 340 kW; ${\rho }_{\infty }$ is the air density, taken as $1.293 {\mathrm{kg}/\mathrm{m}}^3$; $c_p$ is the specific heat of air, taken as $1.005 \mathrm{kJ}/(\mathrm{kg}·\mathrm{K})$; $T_{\infty }$ is the ambient temperature, taken as 293 K; and $g$ is the acceleration of gravity, taken as $9.8 {\mathrm{m}/\mathrm{s}}^2$.

Based on the above formula, $D^{*}$ is calculated to be 0.43 m, suggesting a maximum allowable mesh size of 0.086 m for the computational domain. Consequently, a mesh size of $0.08\times 0.08\times 0.08 \mathrm{m}$ was adopted.

Heat generated by the fire is transferred to the sealant surface via radiation, convection, and conduction. The nonlinear heat conduction differential equation for the components is given by

$${\rho }_s{c}_s{\displaystyle \frac{\partial T_s}{\partial t}}={\displaystyle \frac{\partial }{\partial n}}\left({\lambda }_s{\displaystyle \frac{\partial T_s}{\partial n}}\right)+q_s^{‴}$$

(2)

where $T_s$ is the material temperature (°C), ${\rho }_s$ is the component density (${\mathrm{kg}/\mathrm{m}}^3$), $c_s$ is the component specific heat capacity ($\mathrm{J}/(\mathrm{kg}·\mathrm{K})$), ${\lambda }_s$ is the thermal conductivity coefficient ($\mathrm{W}/(\mathrm{m}·\mathrm{K})$), $n$ is the normal direction to the component surface, and $q_s^{‴}$ is the heat source term.

The thermal analysis boundary conditions are defined as:

$$-k_s{\displaystyle \frac{\partial T_s}{\partial x}}\left(0,t\right)=q_r^{″}+q_c^{″}$$

(3)

$$q_r^{″}={\epsilon }_s\sigma \left(T_g^4-T_s^4\right)$$

(4)

$$q_c^{″}=h\left(T_g-T_s\right)$$

(5)

where $q_r^{″}$ is the radiative heat flux (${\mathrm{W}/\mathrm{m}}^2$); $q_c^{″}$ is the convective heat flux (${\mathrm{W}/\mathrm{m}}^2$); ${\epsilon }_s$ is the emissivity coefficient, set to a default of 0.89; $\sigma$ is the Stefan-Boltzmann constant, $5.67\times {10}^{-8}{ \mathrm{W}/(\mathrm{m}}^2·{\mathrm{K}}^4)$; $T_g$ is the gas temperature at the object surface (K); $T_s$ is the object surface temperature (K); and $h$ is the convective heat transfer coefficient (${\mathrm{W}/(\mathrm{m}}^2·\mathrm{K})$).

The coefficient $h$ is determined by

$$h=\mathrm{m}\mathrm{a}\mathrm{x}\left[C_1\Delta T^{1/3},{\displaystyle \frac{k}{L}}{C}_{2}R{e}^{4/5}P{r}^{1/3},{\displaystyle \frac{k}{\delta n}}\right]$$

(6)

where $C_1$ is the natural convection coefficient (1.52 for horizontal surfaces and 1.31 for vertical surfaces), $\Delta T$ represents the temperature difference between the object and the ambient airflow, $k$ is the thermal conductivity of the ambient air, $L$ is the characteristic length (taken as 1 m), $C_2$ is the forced convection coefficient (taken as 0.037), and $Re$ and $Pr$ are the Reynolds and Prandtl numbers, respectively, which are related to the flow velocity surrounding the object.

In the explicit time-advancement scheme of FDS, the time step $\Delta t$ is not a constant value but is dynamically set based on the ratio of the minimum mesh size to the characteristic flow velocity to satisfy the CFL (Courant-Friedrichs-Lewy) stability condition. During the calculation process, the time step is automatically monitored and corrected: following the first stage of the explicit predictor-corrector time update, the system verifies the time step to ensure it remains within a reasonable stability interval. If the step size exceeds this interval, it is adjusted by 10% (or iteratively adjusted until within the allowable range), and the predictor calculation for that step is re-executed. Specifically, $\Delta t$ is determined by the following formula:

$$\Delta t={\displaystyle \frac{5(\delta x\delta y\delta z{)}^{1/3}}{\sqrt{gH}}}$$

(7)

where $\delta x$, $\delta y$, and $\delta z$ are the dimensions of the smallest mesh unit, $H$ is the height of the computational domain, and $g$ is the acceleration of gravity.

2.

ABAQUS Model for Heat Transfer in Solids

A three-dimensional solid model of the square thin-walled steel was also established in ABAQUS, with geometry and material parameters fully consistent with the experimental specimen. The model was discretized using heat-transfer elements with a mesh size of 0.005 m. The heat-flux data obtained from the FDS simulation were applied as surface thermal-flow loads to the ABAQUS model, enabling subsequent heat-transfer analysis of the specimen.

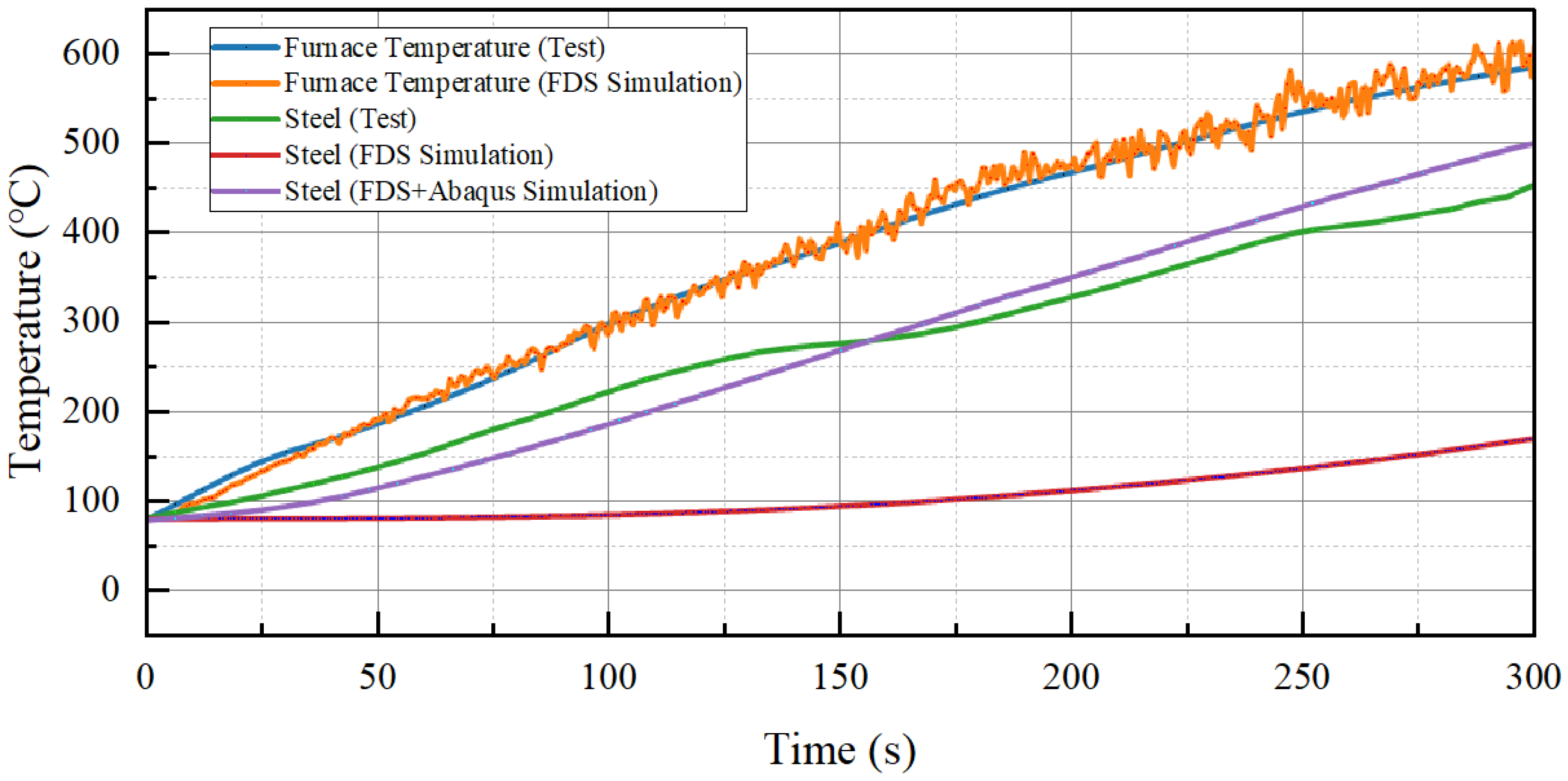
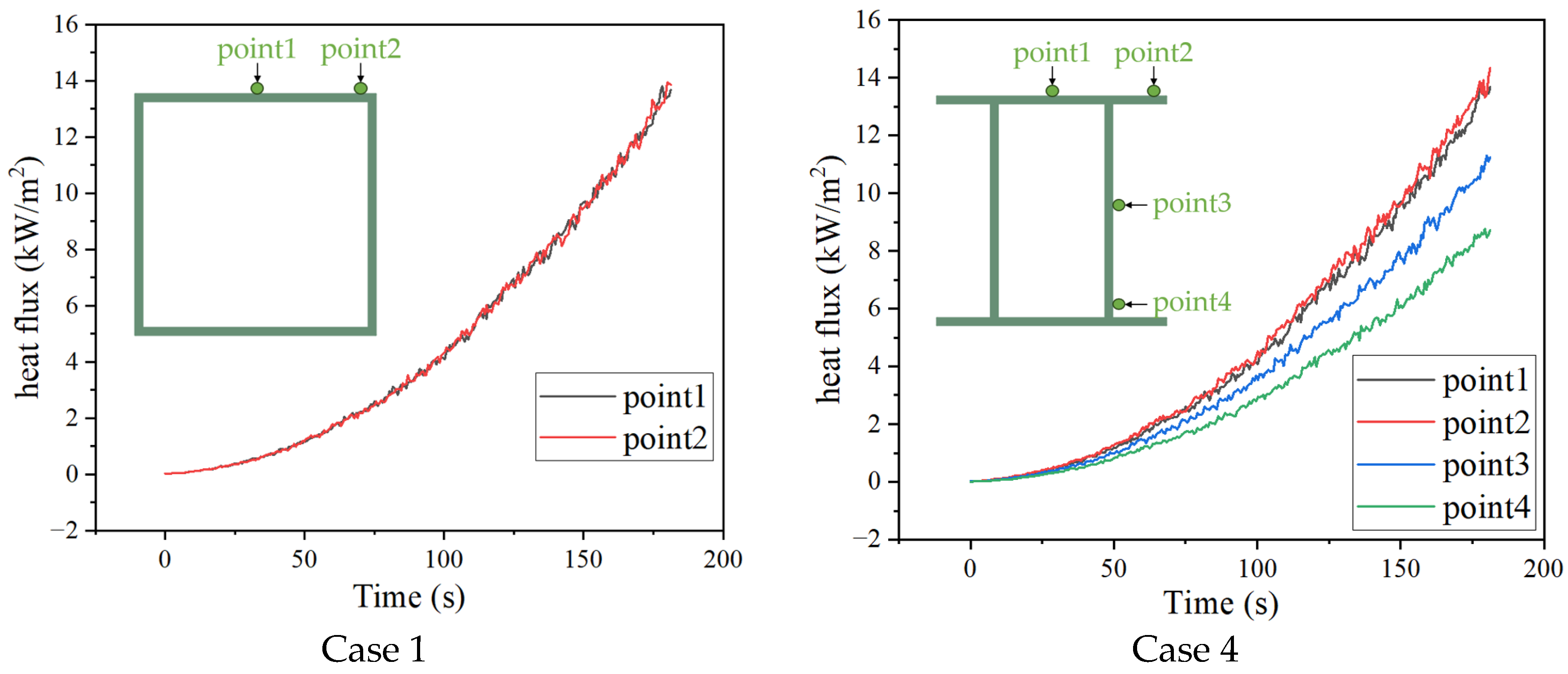
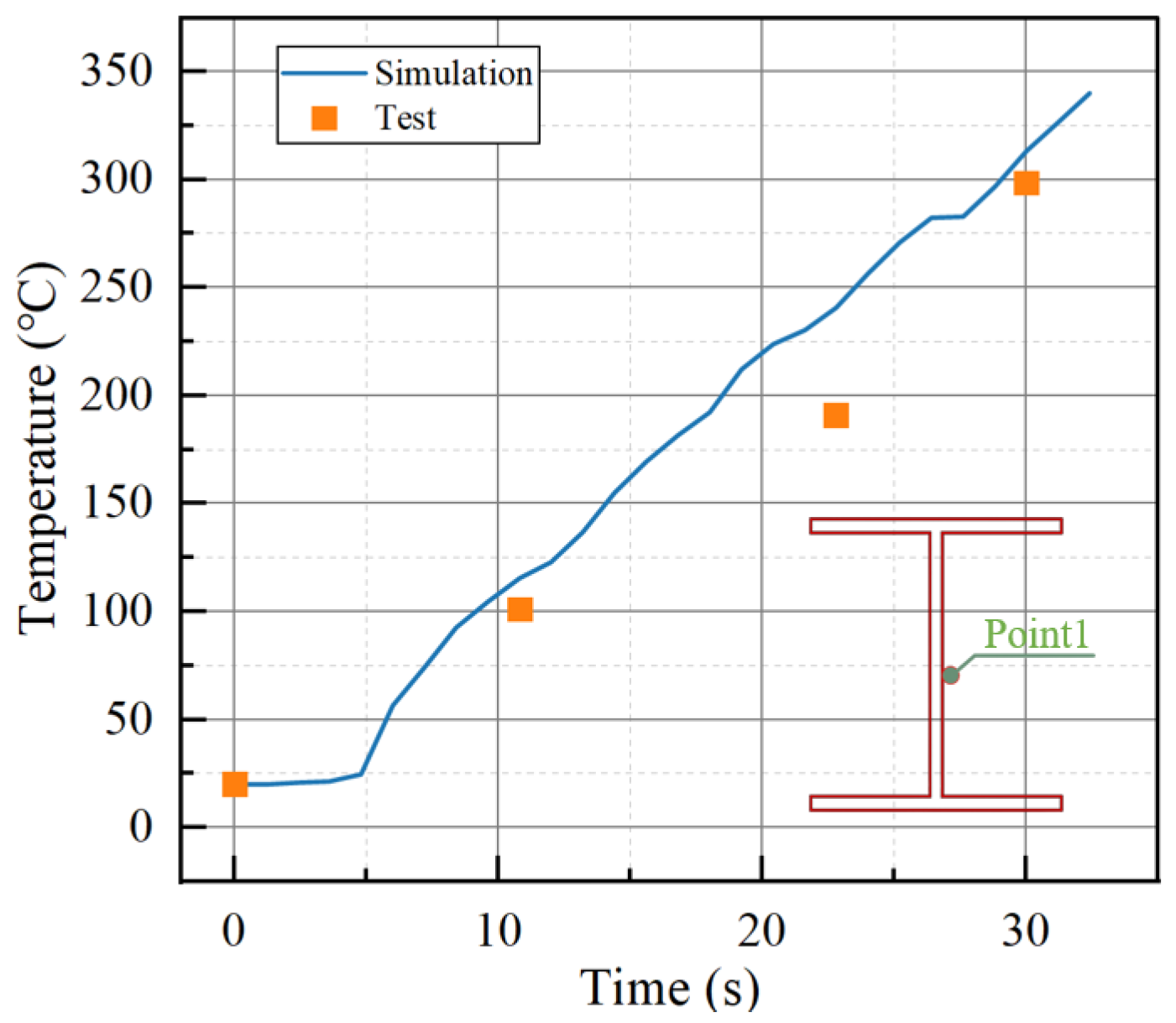
2.2.3. Results and Experimental Validation

1.

Accuracy Assessment of the Coupled Strategy

A comparison between the experimental and simulated results is presented in Figure 3. The close agreement between the measured and predicted furnace temperatures demonstrates that the FDS model accurately reproduces the internal thermal environment, confirming its reliability in simulating gas-phase heat transfer. For the structural thermal response, the proposed coupled strategy, which integrates FDS-derived heat-flux boundaries with the ABAQUS temperature-field solver, achieves higher computational accuracy than the standalone FDS approach. This improvement primarily stems from the inclusion of ABAQUS, which provides a more robust and versatile platform for handling multidimensional heat conduction problems, thereby compensating for the inherent limitations of the one-dimensional heat conduction solver in FDS. The comparative results indicate that the coupled framework can reliably predict the temperature evolution of steel structures under fire scenarios.

2.

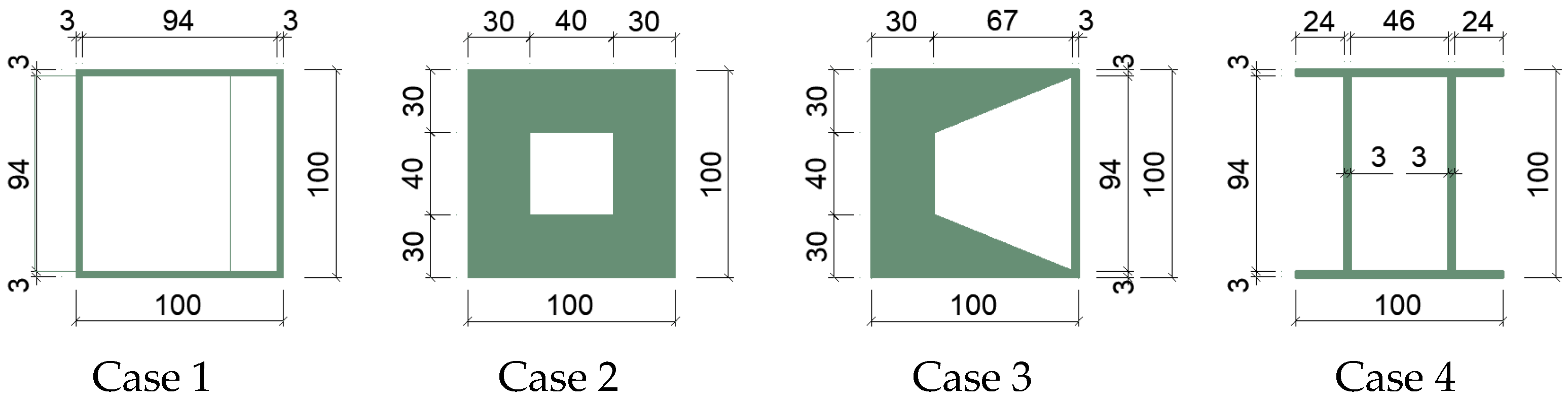
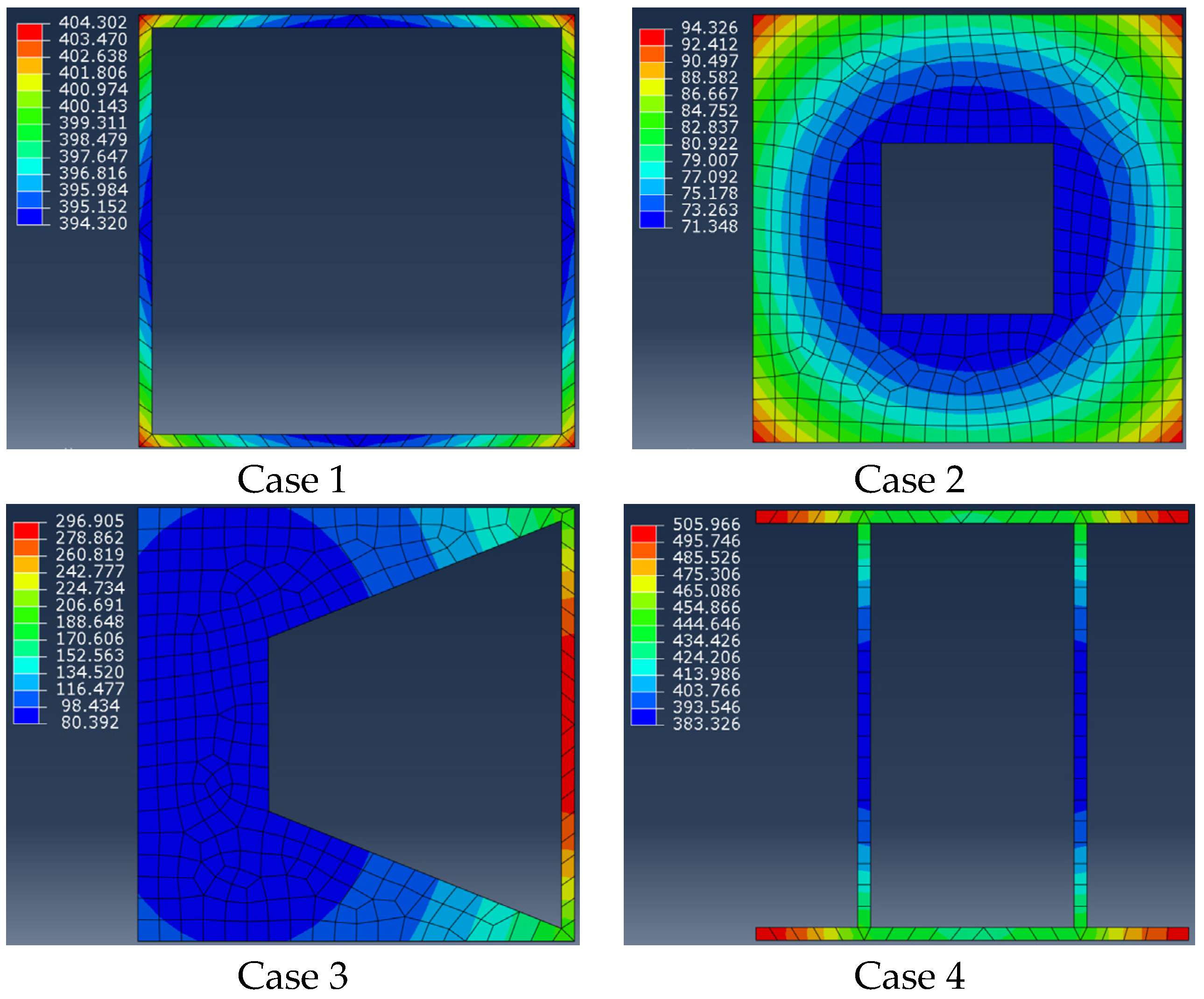
Generalizability Assessment of the Coupled Strategy

Given the limited availability of experimental data, the general applicability of the proposed coupled strategy for thermal analysis of thin-walled steel structures with varying geometric configurations was assessed through a comparative analysis of the cases discussed above and three additional numerical simulations. By varying external profile and wall-thickness distribution, three orthogonal comparison groups were established to validate the influences of size effects and shape effects. All cases are identical in all conditions except for the cross-sections of the steel members. The configurations of the steel member cross-sections are illustrated in Figure 4 and detailed below:

• Case 1: Thin-walled square steel tube with a 100 mm × 100 mm external square profile and a uniform wall thickness of 3 mm.
• Case 2: Thick-walled square steel tube with a 100 mm × 100 mm external square profile and a uniform wall thickness of 30 mm.
• Case 3: Square steel tube with a tapered wall thickness. The external profile is a 100 mm × 100 mm square, and the wall thickness varies linearly from 30 mm on the left side to 3 mm on the right side.
• Case 4: Thin-walled steel section with flanges. The overall external dimensions are 100 mm × 100 mm, and all walls have a uniform thickness of 3 mm.

Based on the results presented in Figure 5 and Figure 6, the generalizability of the coupled strategy is assessed through a three-step analysis.

First, to verify its ability to capture size effects in conduction, Cases 1 and 2 were compared. Owing to its larger heat capacity, the component in Case 2 required more heat input under the same heating power to reach thermal equilibrium, resulting in a significantly lower steady-state temperature level than in Case 1. The temperature field in Case 1 exhibited a nearly uniform concentric-band distribution, with a small radial temperature difference of only 10 °C, indicating efficient conductive heat transfer through the thin wall. In contrast, Case 2 displayed a pronounced radial temperature gradient of 23 °C from the outer to the inner surface, visually reflecting the nonlinear increase in thermal resistance with wall thickness. These results align perfectly with the predictions of Fourier’s law of heat conduction, confirming that the strategy accurately quantifies the influence of wall thickness on both the steady-state temperature level and the internal temperature gradient under a fixed external profile.

Second, to examine shape effects arising from non-uniform wall-thickness distribution, Cases 1 and 3 were compared. While Case 1 showed a centrosymmetric temperature distribution, the continuously varying wall thickness in Case 3 significantly modulated the heat conduction paths, creating an asymmetric temperature gradient field that developed directionally from the thin-walled side toward the thick-walled side. The thin-walled region, with its lower thermal resistance, acted as the primary heat-flow channel and exhibited higher temperatures, whereas the thick-walled region remained cooler due to higher resistance. This successfully reproduced the heat-flow redistribution and temperature-field distortion caused by macroscopic geometric non-uniformity, demonstrating the strategy’s effectiveness in handling complex conduction problems induced by such shape features under a constant external profile.

Third, to investigate the coupled heat-transfer response triggered by a change in the external profile while maintaining uniform, thin-wall properties, Cases 1 and 4 were compared. The heat flux profiles at monitored locations revealed distinct behaviors between the two cross-sectional configurations, as illustrated in Figure 6. In Case 1, Points 1 and 2 were nearly identical, both rising steadily to a plateau of approximately 14 kW/m² within 200 s, reflecting a relatively uniform and symmetric convective-radiative environment inside the furnace chamber. In Case 4, the responses clearly diverged: Points 1 and 2 on the top flanges followed a similar, high trend, while Points 3 and 4, located at the web center and bottom flange center, respectively, responded with significant delay and lower magnitude. Point 4 in particular showed a slow rise and a much lower steady value of 8 kW/m², illustrating a local thermal shielding effect induced by the geometric change. The underlying physical mechanism is clear: the outstanding flange physically partitions the originally continuous cavity, hindering the development of large-scale natural convection circulations and substantially altering the radiation view factors between internal surfaces. This shields points like Point 3 and Point 4 from direct radiation from high-temperature zones, forcing heat transfer to rely on more complex secondary convection and multiple-reflection radiation paths, thereby resulting in delayed and attenuated heat flux responses.

In summary, three case comparisons validate that the proposed couple strategy effectively captures size effects due to wall-thickness variation and shape effects arising from both non-uniform wall-thickness distribution and external-profile changes. These orthogonal verifications demonstrate the couple strategy’s capability to address thermal responses arising from dimensional, macroscopic, and detailed geometric variations in thin-walled steel structures. It reliably handles physical mechanisms spanning solid conduction to cavity-coupled convection-radiation, across geometric complexities from uniform to intricate sections. Therefore, the proposed coupled thermal-response analysis strategy is proven to be a robust and widely applicable numerical tool, capable of effectively supporting the assessment and prediction of the performance of thin-walled steel structures with complex geometric features under thermal exposure.

3. Fire Risk Analysis of the Anchor Rod–Sealant System

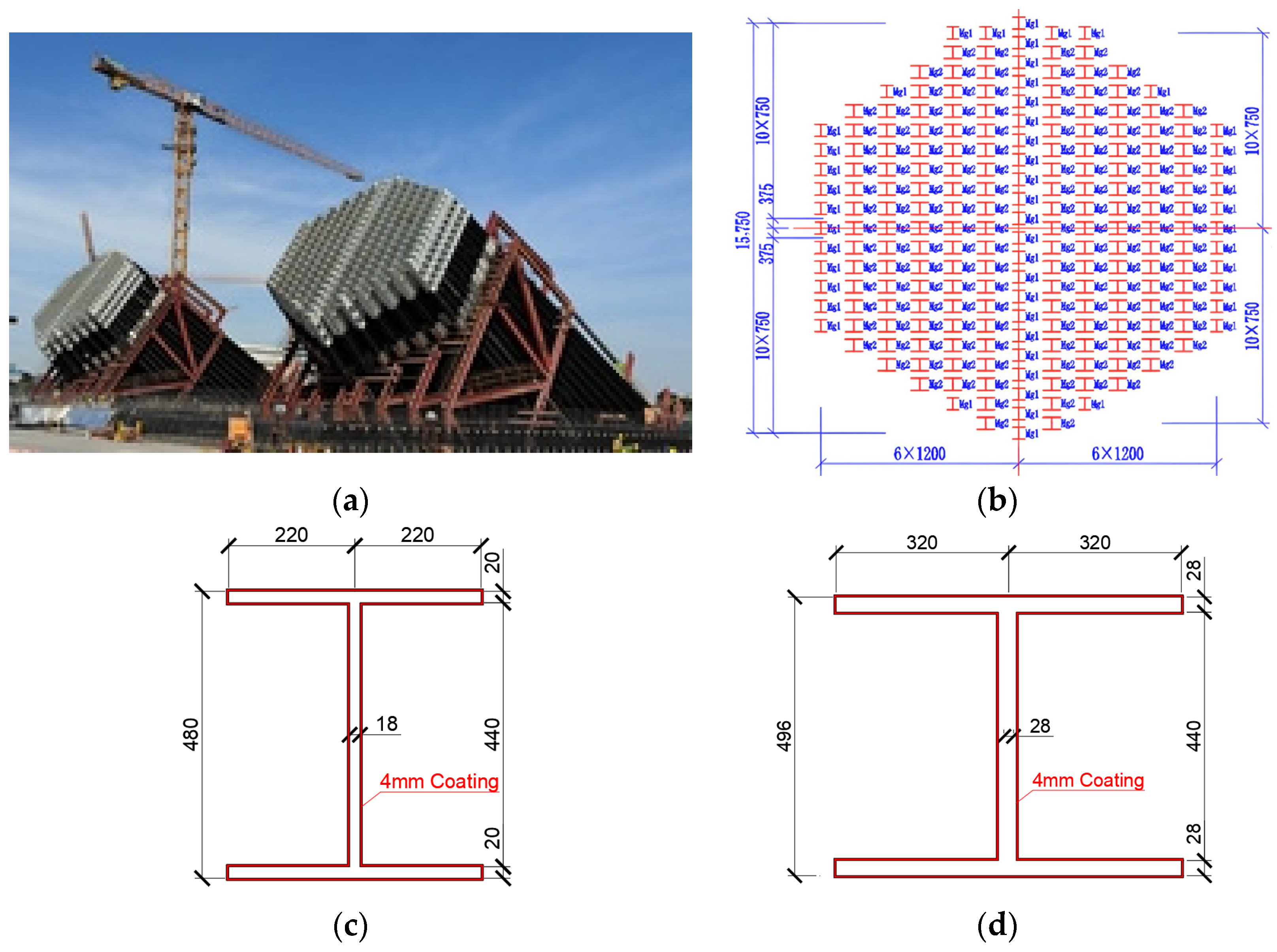
3.1. Engineering Background and System Description

The Shiziyang Grand Bridge is a double-deck steel truss suspension structure with a main span of 2180 m. The bridge employs a steel-frame anchorage system, with two anchorages positioned at each end, as shown in Figure 7a. Each anchorage contains a total of 636 anchor rods, consisting of 26 Mg1 rods and 610 Mg2 rods, arranged as illustrated in Figure 7b. The cross-sections of the Mg1 and Mg2 rods are shown in Figure 7c,d, respectively. Both rod types are coated with a 4-mm-thick layer of sealant, which provides corrosion protection and ensures deformation compatibility with the encasing concrete. However, the sealant is flammable and can be ignited by sparks during riveting operations. Such ignition may degrade the mechanical properties of the steel, posing risks to both construction safety and long-term structural integrity. Accordingly, this study focuses on assessing the fire risk of the anchor rod–sealant system, with particular emphasis on the Mg2 rod configuration as the predominant anchor type.

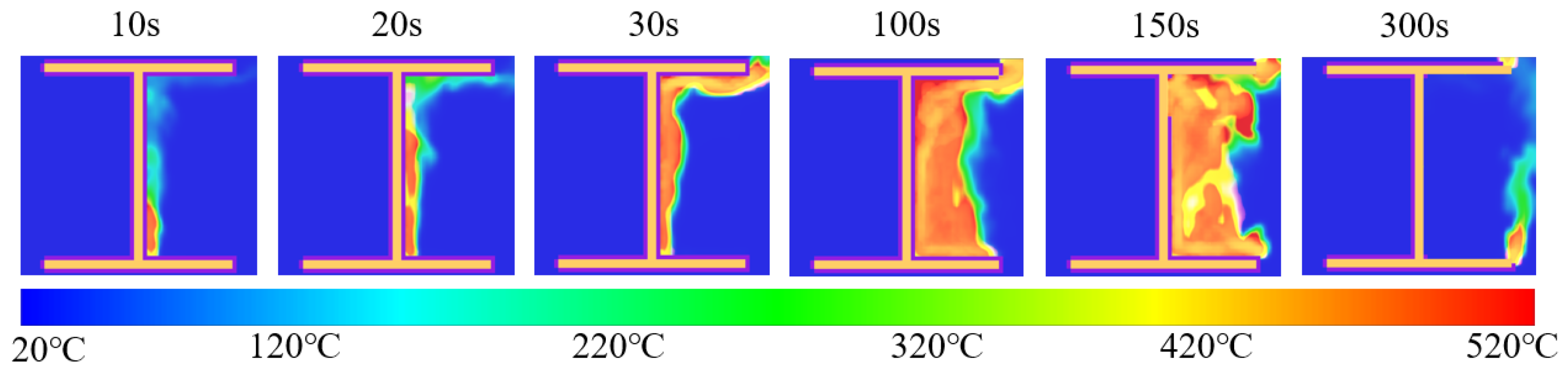
3.2. Thermal Response of a Single Anchor Rod Configuration

A 6-m-long Mg2 anchor rod was subjected to an open-flame test and numerical simulation to investigate the flammability of its sealant coating and the effects of combustion on the steel component.

3.2.1. Open-Flame Test

The test was conducted under wind-free conditions at an ambient temperature of 20 °C. A propane torch (flame-core temperature ≈ 1000 °C, heat flux density ≈ 110 kW/m²) was used to locally heat the sealant layer on the lower side of the web. The sealant ignited promptly upon contact with the heat source, and the flame propagated along the bonded interface on the component surface. Distinct oxidation scale formation and carbonization of the sealant were observed in the combustion zone. For safety reasons, the test was terminated 30 s after ignition. Owing to on-site limitations, only three temperature readings taken near the mid-web within the combustion zone were recorded at 10 s, 20 s, and 30 s.

3.2.2. Numerical Simulation

A numerical model of the 6 m long Mg2 anchor rod was built using the proposed coupled FDS-ABAQUS strategy. The material parameters of the anchor steel were assigned according to Section 2.2.2, while the key thermal parameters of the sealant were determined experimentally, with the results presented in

Table 2. Thermophysical parameters of sealant.

Density	Heat Release Rate	Ignition Temperature	Combustion Heat	Mass Burning Rate	Specific Heat Capacity	Thermal Conductivity
1300 kg/m3	897 kW	200 °C	14.80 MJ/kg	0.664 g/s	1 kJ/(kg·K)	0.1 W/(m·K)

.

Based on the thermal parameters of the sealant and Equation (1), the characteristic fire diameter D* was calculated as 0.827 m, which implies a maximum permissible mesh size of 0.16 m for the computational domain. However, since the sealant layer is only 0.004 m thick, the mesh dimension in the thickness direction must be limited to ≤0.004 m. To maintain mesh quality, the element sizes in the other two directions should also remain suitably refined. Accordingly, A mesh size of 0.005 × 0.005 × 0.004 m was therefore adopted in the simulations. A mesh sensitivity analysis confirmed that further refinement did not significantly affect the predicted temperature field.

The work zone was modeled as a partially enclosed space with restricted ventilation. Based on the typical mesh size of safety netting, approximately 25 mm × 25 mm, and the estimated enclosed volume, the effective opening factor was calculated to be 0.02 m^1/2, indicating a ventilation-limited environment. To conservatively represent the worst-case scenario with minimal heat dissipation, still air conditions, and zero wind speed at the boundaries were applied in the simulation.

Ignition was simulated using two distinct planar heat sources to assess the sensitivity of the results to the ignition parameters. The first source measured 0.01 m × 0.01 m with a prescribed temperature of 1600 °C, representing a hot particle. The second source measured 0.005 m × 0.005 m at 1000 °C, representing a localized spark. Both sources were applied to the same anchor-rod model and deactivated 5 s after ignition to reflect the transient nature of riveting spark exposure. A comparison of the simulation results revealed that the predicted peak anchor temperature differed by less than 1% between the two cases. This close agreement demonstrates that the thermal response of the system is dominated by the combustion and heat transfer characteristics of the sealant itself, rather than by the specific size or temperature of the ignition source within the tested ranges. Therefore, the simulation outcomes can be considered robust and not sensitive to reasonable variations in these ignition parameters. Based on the above, the first ignition configuration was employed in all subsequent analyses.

3.2.3. Results and Comparisons

The results indicate that the numerical simulation and the full-scale open-flame test exhibit similar evolutionary paths of thermal response. As shown in Figure 8, combustion in both cases initiates at the ignition point located beneath the web, rapidly propagates upward along the vertical direction to the bottom of the top plate, and subsequently spreads toward both ends of the member over time, with the burning area continuously expanding. Furthermore, Figure 9 compares the experimental measurements and numerical results at point 1, showing agreement between the measured temperature profiles and the simulated data. These comparisons demonstrate that the simulation effectively captures the transient thermal response of the structure.

The simulation results indicate that once ignited, the sealant undergoes sustained combustion with rapid, uncontrolled flame spread. Figure 10 illustrates the main combustion process of the sealant (purple region in the figure) following ignition. The sealant ignites 5 s after heat-source contact, with flames propagating upward along the web surface. By 20 s, the flames reach the top of the web, and by 30 s, the sealant on the bottom of the upper flange is ignited. Over time, the flames continue to spread, expanding their coverage and initiating thermal decomposition of the sealant. At 150 s, the fire extends across the entire right side of the anchor rods, accompanied by pronounced thermal degradation and shrinkage of the sealant; the sealant near the bottom of the upper flange and the upper part of the web is largely consumed. By 300 s, as the sealant on the bottom of the upper flange, the top of the lower flange, and the web has been completely depleted, the fire intensity diminishes significantly, leaving only residual flames along the edges of the upper and lower flanges.

During this process, the ambient air temperature peaks at 520 °C as presented in Figure 11, and the anchor rod temperature exceeds 900 °C. These extreme temperatures lead to a severe reduction in the mechanical properties of the steel. Furthermore, the combination of high thermal loads and persistent flaming poses a significant hazard for fire propagation to adjacent components.

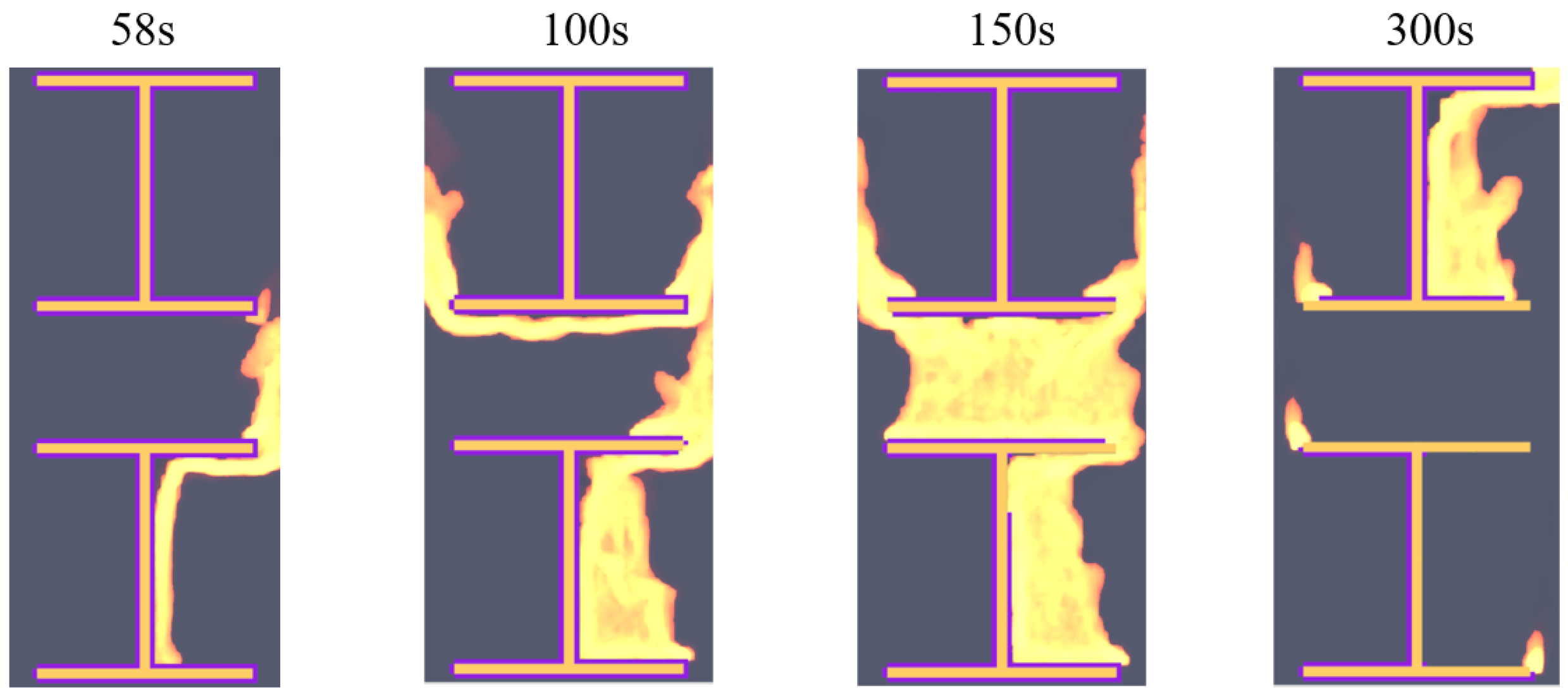
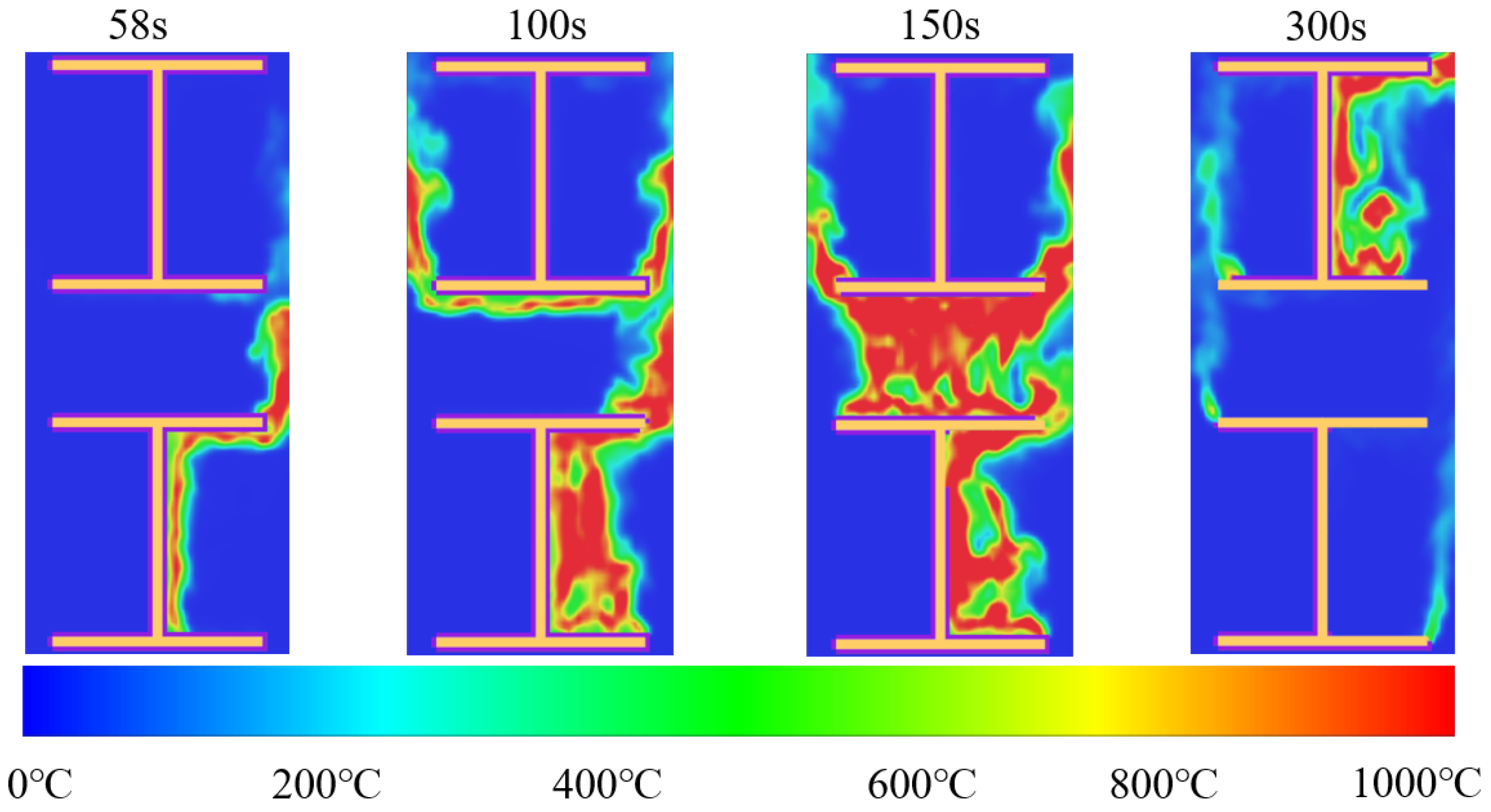
3.3. Flame Propagation in a Double Anchor Rod Configuration

Building upon the findings that highlight the sealant’s high combustibility and the associated risk of fire spread to adjacent materials, this study further investigates a critical practical scenario: fire propagation between closely spaced anchor rods. As shown in Figure 7a, anchor rods are frequently installed in groups, raising a key safety concern as to whether a fire initiated on one rod can propagate to its neighbors, potentially escalating into a larger conflagration. To address this, a numerical model of a double-anchor-rod system was developed specifically to simulate and analyze inter-rod flame spread behavior.

3.3.1. Model of the Double-Anchor-Rod System

The double-anchor-rod system was modeled by replicating the validated single-rod configuration established in Section 3.2.2. An identical second Mg2 anchor rod was positioned vertically above the first rod with a clear spacing of 270 mm. The same coupled FDS-ABAQUS strategy, mesh settings, and confined environmental boundary conditions were applied to this extended model.

3.3.2. Results and Discussion

The simulation results indicate that the combustion behavior of the sealant on the lower anchor rod during the first 50 s after ignition is largely consistent with that observed in the single-rod scenario. As shown in Figure 12, ignition is observed at the edge of the lower flange of the upper rod at 58 s. Subsequently, driven by buoyancy and radiative heating, the flame spreads along the underside of the flange and extends toward its left-side region. During this process, flammable gases generated by pyrolysis of the sealant accumulate near the lower surface of the flange, providing the necessary fuel supply for sustained flame propagation and allowing the flame to grow continuously. By 150 s, a distinct flame zone develops between the upper and lower rods and to the right of the lower rod, where the local air temperature reaches approximately 1000 °C as illustrated in Figure 13. The intense thermal environment accelerates the pyrolysis and combustion of the sealant, and the additional heat released further intensifies the flame. After the sealant in this zone is consumed, the flame gradually weakens and the temperature declines. However, as the sealant on the top surface of the lower flange of the upper rod is ignited, the main combustion zone shifts to the right side of the upper rod.

If a third anchor rod were present above, its sealant would likely be ignited by the rising hot plume, thereby triggering a progressive upward chain-reaction of fire spread. The described process demonstrates that densely arranged anchor-rod arrays are susceptible to systemic fire-spread risks.

4. Sensitivity Analysis and Identification of Fire-Safe Thermophysical Thresholds

The sealant readily promotes flame propagation between anchor rods, increasing the fire hazard. To mitigate its flammability and suppress flame spread, it is essential to understand how key thermal parameters govern fire development. This section examines the influence of three critical parameters, ignition temperature, thermal conductivity and specific heat capacity, on the thermal response under fire conditions. A single-factor sensitivity analysis is performed to identify suitable parameter ranges that meet engineering requirements for fire-safe sealants, providing theoretical guidance for material selection.

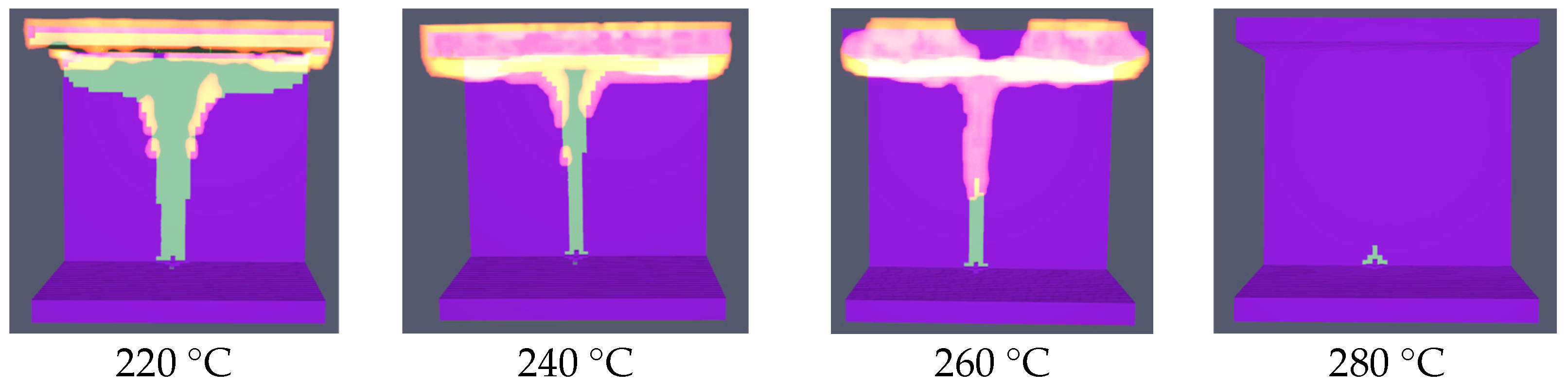
4.1. Model and Parameter Settings

To optimize computational efficiency without compromising the accuracy of the observed flame-spread phenomena, a half-section model of the anchor rod was employed. This simplification is justified as the flame is predominantly concentrated on the web near the ignition source during the critical early and middle stages of combustion, while the opposite side remains largely thermally unaffected.

A single-factor sensitivity analysis was conducted, systematically varying one parameter while keeping the others constant. The specific parameter settings for each simulation group are as follows:

(1)

Ignition Temperature: Four simulation nodes were uniformly defined within the range of 220 °C to 280 °C. Thermal conductivity and specific heat capacity were held constant at 0.10 W/(m·K) and 1.1 kJ/(kg·K), respectively.

(2)

Thermal Conductivity: Five simulation nodes were uniformly distributed within the range of 0.14 W/(m·K) to 0.26 W/(m·K). Ignition temperature and specific heat capacity were fixed at 280 °C and 1.1 kJ/(kg·K), respectively.

(3)

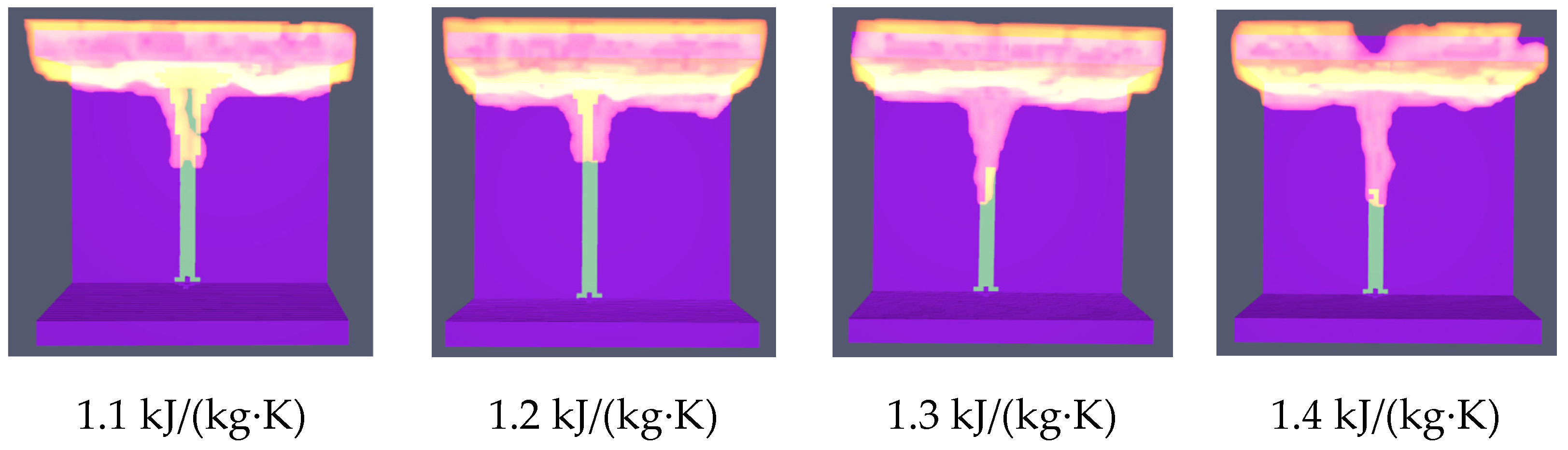
Specific Heat Capacity: Six simulation cases were uniformly established within the range of 1.1 kJ/(kg·K) to 1.5 kJ/(kg·K). Ignition temperature and thermal conductivity were maintained at 240 °C and 0.10 W/(m·K), respectively.

4.2. Results

4.2.1. Effect of Ignition Temperature

Figure 14 illustrates the flame spread patterns of the sealant at 60 s under different ignition temperature conditions. It can be observed that as the ignition temperature increases, the flame coverage gradually decreases, and less sealant is consumed by combustion within the same time period. This indicates that a higher ignition temperature can delay the rate of flame development. Furthermore, when the ignition temperature reaches or exceeds 280 °C, the flame exhibits self-extinguishing behavior.

4.2.2. Effect of Thermal Conductivity

The influence of thermal conductivity on flame spread at 60 s is shown in Figure 15. Similar to the effect of ignition temperature, an increase in thermal conductivity retards flame progression. The enhanced heat dissipation away from the flame front likely reduces the temperature of the pyrolysis zone, slowing fuel gas production. A significant finding is that a thermal conductivity of ≥0.26 W/(m·K) is sufficient to induce self-extinguishment under the studied conditions.

4.2.3. Specific Heat Capacity

Figure 16 presents the results for varying specific heat capacity. An increase in specific heat capacity provides only a modest retardation of flame spread and does not, within the tested range (up to 1.5 kJ/(kg·K)), lead to self-extinguishing behavior. The higher heat capacity increases the thermal inertia of the material, slowing its temperature rise and thus the rate of pyrolysis, but this effect alone is insufficient to halt the combustion process once initiated.

5. Conclusions

This study provides a multi-physics analysis of the thermal response characteristics and fire risks of anchor rod–sealant systems by integrating a coupled simulation framework with systematic parametric analysis. The main findings are as follows:

(1)

A robust coupled FDS–ABAQUS simulation strategy was developed and validated. By integrating fire-driven fluid dynamics with radiative/convective heat transfer and three-dimensional solid conduction, this framework effectively bridges key multi-physics gaps in structural fire analysis. The strategy reliably predicts temperature-field evolution under fire exposure, as demonstrated through validation against standard fire-resistance tests. Furthermore, it shows good robustness across varying geometric scales, and the capability to capture coupled convection-radiation-conduction phenomena in confined spaces. Consequently, the proposed approach provides a reliable numerical tool for analyzing thermal responses in such structural systems.

(2)

The fire risk of the anchor rod–sealant system was assessed through simulations of both single- and double-rod configurations. The results show that the sealant coating on the rod surface is readily ignited by hot particles or localized sparks and sustains continuous combustion, a process that generates extreme local temperatures capable of raising the rod temperature above 900 °C. Furthermore, the simulations reveal that when one rod is on fire, the rising hot plume is highly likely to ignite the sealant on the adjacent upper rod, triggering a progressive upward chain-reaction of fire spread. These findings indicate that densely arranged anchor-rod arrays are subject to a systemic risk of fire propagation.

(3)

A single-factor sensitivity analysis identified ignition temperature and thermal conductivity as the primary material properties controlling self-extinguishing behavior. For reliable suppression of flame spread and promotion of self-extinction, sealants should meet or exceed the following dual thresholds: an ignition temperature ≥280 °C and a thermal conductivity ≥0.26 W/(m·K). While specific heat capacity can retard flame growth, its role in achieving self-extinction is secondary.

The limitations of this study primarily lie in the scarcity of full-scale experimental data on sealant ignition by actual riveting sparks and the lack of consideration for coupling effects among multiple parameters in the analysis. Future work should focus on conducting well-instrumented experiments to validate the model, performing multi-parameter synergistic optimization to screen flame-retardant formulations, thereby enhancing the reliability of fire-safe design in engineering applications.