Mechanical Performance of Joints with Bearing Plates in Concrete-Filled Steel Tubular Arch-Supporting Column-Prestressed Steel Reinforced Concrete Beam Structures: Numerical Simulation and Design Methods

Abstract

Research on the configuration and mechanical performance of arch-column-tie beam joints, which combine features of arch-tie beam joints and tubular joints, remains limited, particularly for long-span structures subjected to heavy loads at high building stories. This study focuses on a joint in an engineering structure comprising a circular arch beam, a square-section inclined column, and a tie beam, where both the arch and the inclined column are concrete-filled steel tube (CFST) members. A novel joint configuration was proposed, then a refined finite element model was established. The joint’s mechanical mechanism and failure mode under axial compression in the arch beam were investigated, considering two conditions: the presence of prestressed high-strength rods and the failure of the rods. Subsequently, a parametric study was conducted to investigate the influence of variations in the web thickness of the tie beam, the steel tube wall thickness of the arched beam, the steel tube wall thickness of the supporting inclined column, and the strength grades of steel and concrete on the bearing capacity behavior and failure modes. Numerical simulation results indicate that the joint remains elastic under the design load for both conditions, meeting the design requirements. The joint reaches its ultimate capacity when extensive yielding occurs in the tie beam along the junction region with the circular arch beam, as well as in the steel tube of the arch beam. At this stage, the steel plates and concrete within the joint zone remain elastic, ensuring reliable load transfer. The maximum computed load of the model with prestressed rods was 2.28 times the design load. The absence of prestressed rods could lead to a significant increase in the high-stress area within the web of the tie beam, decreasing the joint’s stiffness by 12.4% at yielding, but have a limited effect on its maximum bearing capacity. Gradually increasing the wall thickness of the arch beam’s steel tube shifts the failure mode from arch-beam-dominated yielding to tie-beam-dominated yielding along the junction region. Increasing the steel strength grade is more efficient in enhancing the bearing capacity than increasing the concrete strength grade. Finally, a design methodology for the joint zone was established based on three aspects: local stress transfer at the bottom of the arch beam, force equilibrium between the arch beam and the tie beam, and the biaxial compression state of the concrete in the joint zone. Furthermore, the construction process and mechanical analysis methods for various construction stages were proposed.

1. Introduction

As the critical connecting unit in steel tube structures and concrete-filled steel tube structures, the multi-member connection joints exhibit a more complex construction and mechanical mechanism compared to conventional beam-column joints, along with diverse structural forms. Common types of multi-member connection joints include the intersecting joints in trusses or spatial grid structures, and the arch-tie rod joints.

Multi-member intersecting joints typically consist of a continuous chord and multiple braces directly welded along the intersecting lines onto the chord [1]. Based on the spatial arrangement of the components, they can be categorized into planar joints and space joints. Depending on whether the chord is filled with concrete, they are further classified as hollow tubular joints and concrete-filled steel tubular (CFST) composite joints. Multi-member intersecting joints are widely used in long-span spatial structures and have long been a focus of research for scholars globally. Their mechanical behavior and design methods have been extensively and intensively investigated. Regarding static performance, numerous studies have employed numerical simulations and experimental methods to investigate the mechanical behavior and design approaches for various joints. The main research findings are summarized below. Choo, Y.S. et al. [2] investigated thick-walled K-joints with a diameter-to-thickness ratio smaller than 10. Through finite element parametric analysis, they examined the effects of different boundary conditions and chord stresses on the static strength. They proposed a modified formula for calculating joint strength under static loading, based on the maximum chord stress ratio. Hamid Ahmadi et al. [3] studied internally ring-stiffened KT-joints in bridges under four types of out-of-plane bending loads. Using experiments and finite element parametric analysis, they analyzed the influence of geometric parameters on the stress concentration factor (SCF) and proposed an SCF calculation formula. Zhihua Zhong et al. [4] focused on overlapped asymmetric K-joints of square hollow sections (SHS) with internal stiffeners. Combining experimental and finite element methods, they revealed the enhancement mechanism of the stiffeners on the joint’s mechanical performance. It was demonstrated that the stiffeners improve ductility and bearing capacity by altering the failure mode. Junping Liu et al. [5] investigated joints in CFST truss arch bridges. Their experimental and numerical study identified that interface debonding weakens shear transfer efficiency. They confirmed that embedded studs can significantly enhance this efficiency by more than 30% and quantified the relationship between shear transfer length and member inclination angle. Kangkang Yang et al. [6] analyzed a novel steel-concrete truss joint for bridges. Through a 1/5 scale model test and nonlinear finite element analysis, they verified that the joint remained elastic under 1.5 times the design load. Their study also confirmed that reducing the concrete corner inclination effectively mitigates stress concentration. Zafimandimby et al. [7] proposed a novel CFST K-joint with box sections using members of different cross-sections. Their finite element simulation and multi-parameter comparative analysis indicated that the typical failure mode is fracture of the tensile brace. The joint exhibited higher initial stiffness and ultimate strength compared to traditional rectangular hollow section and rectangular CFST joints. Jiachang Wang et al. [8] studied a spatial truss joint where H-section and box-section web members converge. Utilizing a multi-member simultaneous loading test and finite element analysis, they elucidated the joint’s mechanical behavior. Design strategies were proposed, including employing gradual transitions, using box-section web members, and thickening the joint plate to improve performance.

The fatigue performance of multi-member intersecting joints has also attracted significant research attention. Lie et al. [9] employed finite element parametric analysis and full-scale fatigue tests to validate the calculation accuracy of stress intensity factors for circular hollow section (CHS) K-joints with surface cracks under combined axial and in-plane bending loads, and proposed a hybrid-mode assessment method for stress intensity factors based on integral and displacement extrapolation techniques. Ann Schumacher et al. [10] investigated welded K-joints in bridge trusses through large-scale planar truss fatigue tests, revealing that the measured hot-spot stress was significantly lower than the code-calculated value, yet the joint fatigue strength still fell below the current design curve, highlighting the dominant influence of size effects on fatigue performance. Nussbaumer et al. [11] studied the fatigue size effect of welded CHS K-joints in bridge structures using full-scale tests and three-dimensional boundary element crack propagation simulations, finding that the fatigue strength decreased with increasing chord wall thickness, and the influence of non-proportional size variations on the stress intensity factor could be quantified by a geometric correction factor. Hamid Ahmadi et al. [12] conducted a systematic study based on 81 finite element parametric analyses and nonlinear regression fitting, examining the influence of geometric parameters on the bending capacity of tubular K-joints under out-of-plane bending moments, and proposed a formula directly applicable for fatigue life assessment of K-joints under out-of-plane loading. Lei Jiang et al. [13] combined experimental and finite element simulations to develop a stress concentration factor formula for concrete-filled welded spatial K-joints, clarifying the contribution of concrete infill to enhancing fatigue performance.

Regarding the influence of concrete infill on the mechanical performance of multi-member intersecting joints, researchers have drawn the following main conclusions. Yoshinaga Sakai et al. [14] conducted static and fatigue tests on tubular K-joints strengthened with concrete infill, demonstrating that the concrete infill could approximately double the ultimate bearing capacity of the joint, and verified that joints with stiffeners and centered butt welds exhibited excellent fatigue performance. Wenjin Huang et al. [15,16] investigated CFST K-joints in truss structures where only the chord was concrete-filled while the braces remained hollow tubes. Comparative tests with hollow tubular joints showed that the concrete infill completely suppressed local buckling of the chord, changing the failure mode from chord face plastic failure in hollow joints to punch shear failure of thick-walled braces or yield failure of thin-walled braces, with the peak strain reduced by over 50% compared to hollow joints. Yinping Ma et al. [17] studied concrete-filled steel tubular T-joints through theoretical modeling and finite element analysis, finding that the concrete infill resulted in significantly higher compressive stiffness than tensile stiffness in the chord, and proposed a theoretical calculation method. These studies indicate that filling the joint region with concrete or adding stiffeners according to the force transmission mechanism are effective methods for enhancing mechanical performance. However, since chords in spatial trusses generally withstand larger forces than braces, further investigation into joint detailing is necessary for cases where both chord and brace members are subjected to significant forces, considering their spatial arrangement.

Another major category of multi-member connection joints is found in arch-tie rod structures, which primarily form a self-balancing system through the interaction of the arch and the tie member and are widely used in bridge engineering. Tobias Mansperger et al. [18] investigated the dynamic response and fatigue performance of the hanger joints in a long-span bridge under high-speed railway loads, using finite element analysis and field monitoring. Dai et al. [19] studied the stress distribution and mechanical behavior of the arch-girder joint in a bridge under complex loading conditions through finite element analysis. Yan Yang et al. [20] examined the mechanical performance of an arch-girder joint via scaled model testing and finite element analysis. In contrast, the application of arch-tie rod structural systems in building structures is relatively limited. In such cases, the arches and ties often need to connect to columns, resulting in the joint configurations and force-transfer mechanisms that are more complex than those in typical arch-tie joints. Therefore, it is necessary to study appropriate joint detailing based on the geometric relationships of the members and load-transfer mechanisms. For instance, Chen Qingjun et al. [21] conducted static tests and finite element analysis on a CFST arch transfer structure under vertical loading. The structural layout consisted of an arch, side columns, and multi-story beams suspended by hangers. The joints were specifically designed with stiffening measures, and the force-transfer characteristics were analyzed by varying parameters such as beam and hanger stiffness. Zhao Wenyan et al. [22] performed a full-process simulation analysis of an arch-tie structure with complex joints, including arch rib and hanger connections, and summarized key construction technologies for long-span arch-tie corridors. Guo Wenfeng et al. [23] adopted a structural system with a partial frame-supported shear wall and a large-span top corridor designed as an arch-tie structure. In this system, the tie member functioned both as an arch abutment tie and as the main load-carrying beam of the floor system, resulting in small structural deformations and enhanced progressive collapse resistance. In-plane and out-of-plane stability of arches is also one of the key challenges in design. Guo, Yanlin et al. [24] established an analytical solution for the out-of-plane elastic buckling load of steel tubular truss arches, proposed a design equation for elastoplastic stability-bearing capacity, and developed a threshold stiffness theory for braces in solid-web arches. Wang Yuyin et al. [25] derived an analytical solution for the in-plane elastic buckling load of concrete-filled steel tubular circular arches, and proposed a practical calculation formula for the elastoplastic stability coefficient based on normalized slenderness ratio, revealing the influence of initial imperfections and geometric nonlinearity on stability-bearing capacity.

Multi-member connection joints, characterized by complex force transfer mechanisms, often serve as critical components in structural systems. Although various types of multi-member joints have been developed, limited research has been conducted on the structural detailing and mechanical behavior of arch-column-tie beam joints, which combine features of both arch-tie systems and intersecting connections. The configuration of such joints is closely related to architectural design requirements, resulting in diverse structural forms. The design of arch-foot joints for long-span, high-load-bearing elevated structures remains a significant challenge. Conventional solutions—including ground-supported arches, elevated arches relying on adjacent buildings, and self-balancing arches with pure steel tie beams—are often challenged by insufficient load capacity, limited applicability, or negative impacts on surrounding structures, particularly in heavy-load, large-span applications. Regarding the joint configuration, conventional cast steel joints or simple welded connections are not optimal for arch-foot joints subjected to exceptionally high internal forces. If such schemes were adopted, the enormous compressive force in the joint region would be entirely borne by the steel, potentially leading to excessively thick steel plates. This would introduce severe issues including significant welding residual stresses, a high risk of lamellar tearing, and substantial economic costs. Consequently, developing a novel joint configuration that fully utilizes the compressive capacity of concrete and promotes composite action between steel and concrete becomes an essential requirement for achieving both structural safety and economic efficiency.

To enhance the understanding of rational detailing and mechanical performance for arch-tie joint systems, this study focuses on a specific elevated joint in a museum structure comprising a circular arch beam, a square-section inclined supporting column, and a prestressed steel reinforced concrete tie beam—all made of CFST members. A novel joint detailing scheme was proposed. Previously, Li Chongyang et al. [26] conducted static loading tests and preliminary finite element numerical simulations on a 1:3 scale model of this joint. However, limited by the loading capability of the loading devices and the testing costs, the tests failed to obtain the joint’s ultimate bearing capacity and failure mode. Furthermore, research on the joint’s mechanical mechanism, the influence laws of parameters, and design methods still requires further in-depth investigation. In this paper, a refined finite element model validated against the previous experimental results was first established. Through finite element simulation, a detailed analysis of the joint’s mechanical mechanism and failure mode was carried out. Subsequently, a parametric study was conducted to investigate the influence of variations in the web thickness of the tie beam, the steel tube wall thickness of the arched beam, the steel tube wall thickness of the supporting inclined column, and the strength grades of steel and concrete on the bearing capacity behavior and failure modes. Finally, design methods for the joint zone, along with the construction process and mechanical analysis methods for various construction stages, were propose. The findings can provide theoretical foundations and practical references for the design and application of similar CFST joints.

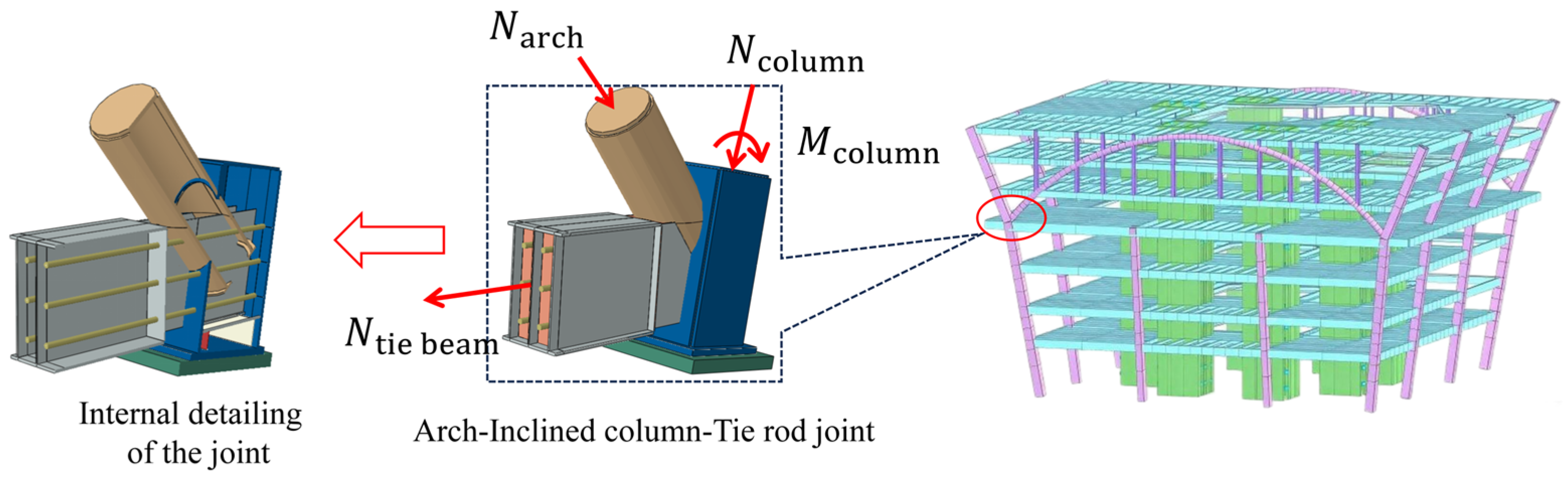
2. Research Object

2.1. Project Background

The museum project is located in Shenzhen, China, with a design service life of 100 years and a maximum building height of 67.5 m. The structural design employs an innovative steel frame-reinforced concrete core tube hybrid system. Above the fifth floor, a large-span CFST arch frame with a span of 94.8 m is incorporated, creating a distinctive architectural form and spatial effect, as shown in Figure 1.

Above the fifth floor of the building, the arch foot of the large-span CFST arch frame is a complex joint where the circular CFST arch beam, the lower chord steel-concrete prestressed tie beam, and the square CFST inclined column converge. A schematic diagram of the joint’s location within the overall structure is shown in Figure 2. This joint must not only transfer the vertical load from the CFST inclined column but also withstand the axial compression from the circular arch beam and provide a tension-balancing mechanism for the tie beam and prestressed cables. Its load-bearing mechanism is more complex than that of traditional CFST joints. The mechanical performance of this joint directly affects the safety and reliability of the overall structure. Therefore, it is essential to investigate the rational configuration of the joint and conduct an in-depth study on its load-bearing capacity performance.

In the arch-column-tie beam joint, the load-bearing relationships among the inclined column, tie beam, and circular arch beam are as follows. (1) The CFST circular arch beam transfers the weight of the 6th to 8th floor structures, primarily transmitting axial force. Under the most critical design condition, which is dominated by the dead load and live load, the axial compressive force is 95,736 kN. (2) The horizontal component of the force from the circular arch beam is mainly balanced by the tie beam, which is primarily subjected to tension. (3) The CFST inclined column bears the axial force and bending moment transferred from the upper structure. However, the axial compressive force, 36,408 kN, transmitted from the upper structure is less than that in the circular arch beam. Meanwhile, the inclined column can provide a certain horizontal force component. Nevertheless, due to the significant story height of the structure, the slenderness ratio of the inclined column is 19.7. Under the most critical design condition, the horizontal shear force in the column is 13,199 kN, which is only 0.29 times of the force in the tie beam.

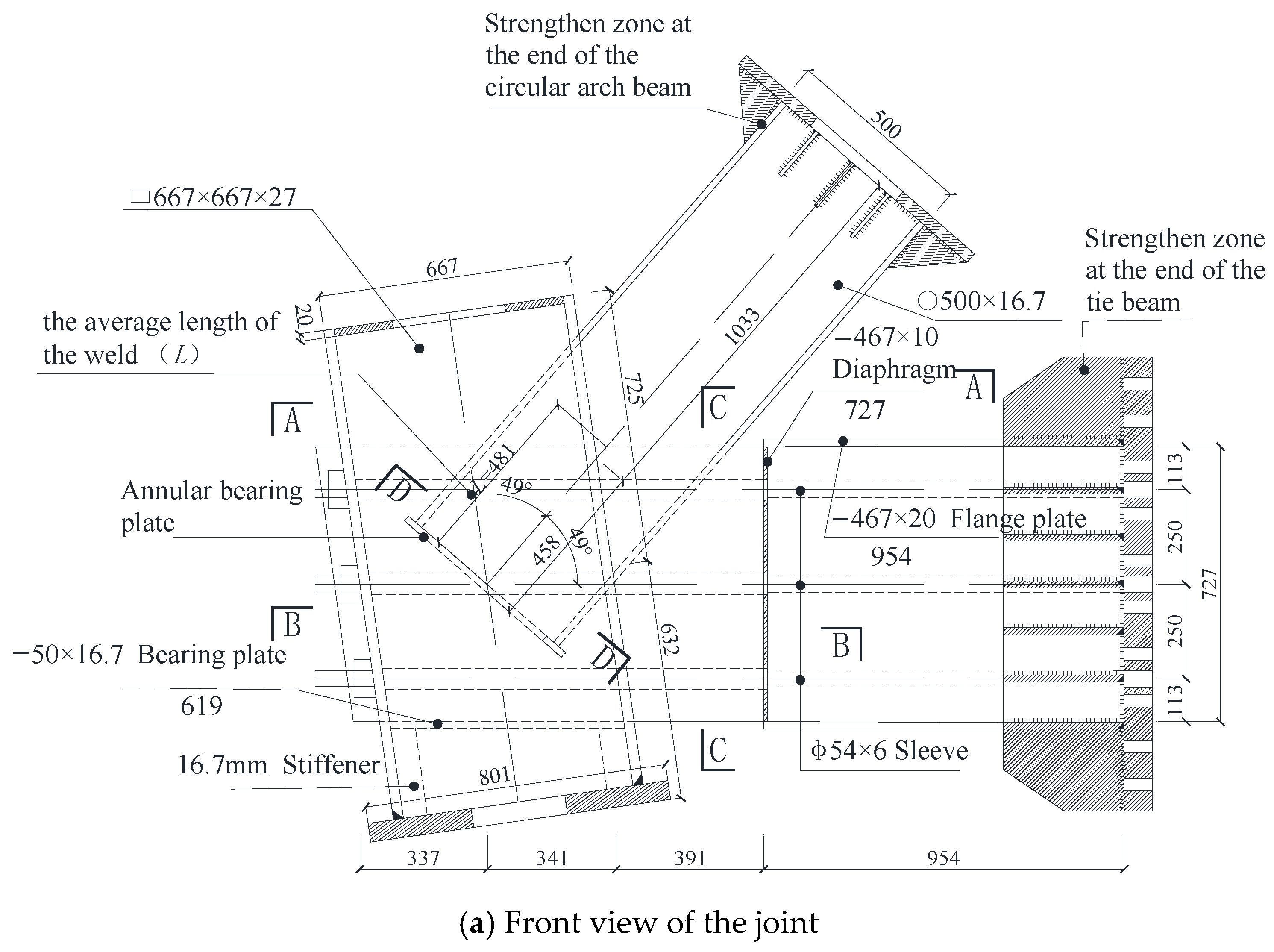
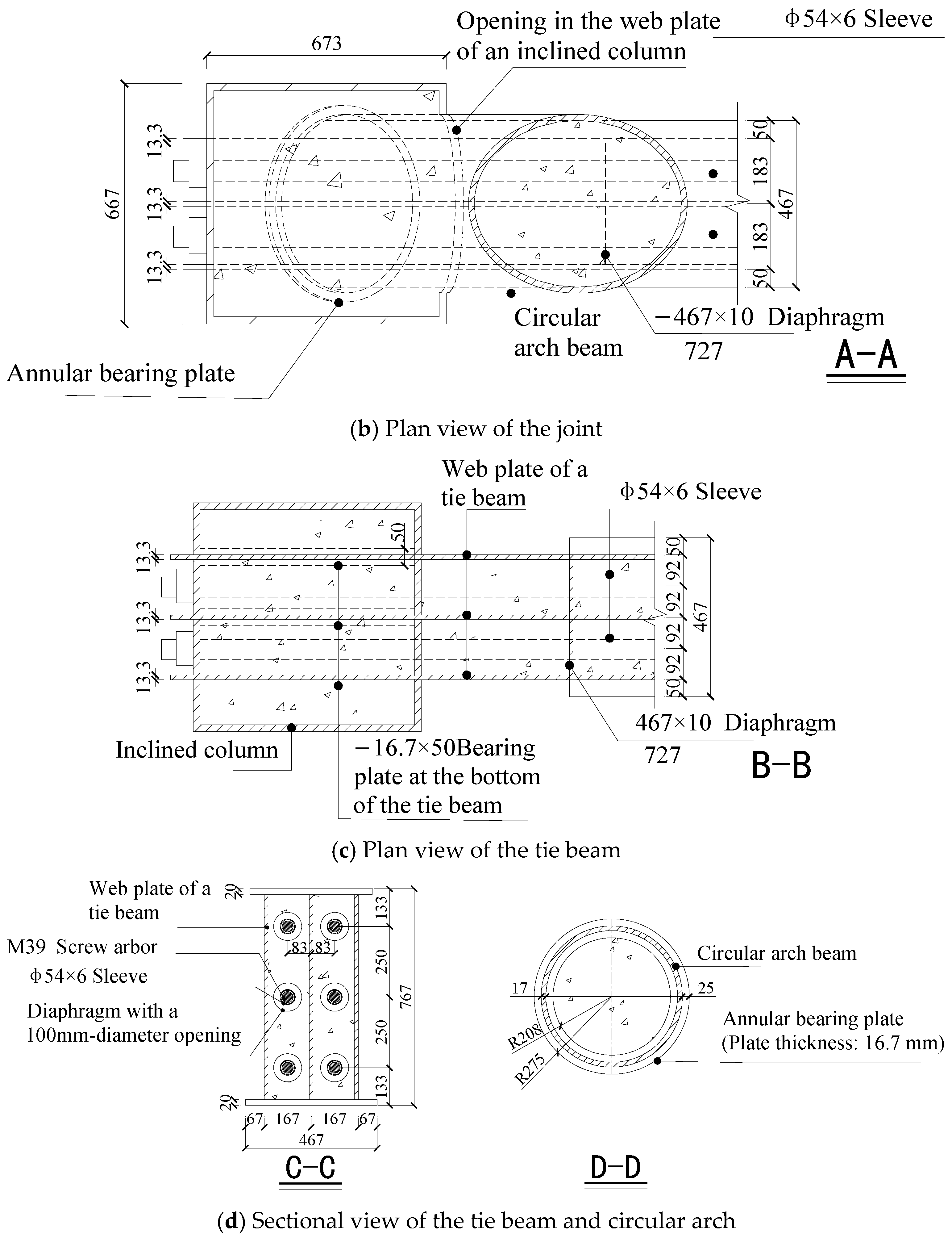
2.2. Construction and Design Concept of the Joint

Based on the 1:3 scale joint model fabricated by Li Chongyang et al. [26], with its detailed construction drawing shown in Figure 3, the construction features and design concept of the joint are summarized as follows.

The joint primarily comprises three components: a square CFST inclined supporting column tilted at an angle of 7.78°, a circular CFST arch beam with a horizontal inclination of 49°, and a steel-concrete prestressed tie beam. The tie beam consists of three steel web plates, six prestressed cables or rods, and flange plates that support the floor slab. The construction of the joint forms the basis for its functional realization, with key design aspects including:

(1)

Connection design at the arch beam-tie beam intersection: The circular CFST arch beam is inserted into the joint zone. Slots are cut into the circular steel tube to allow the three web plates of the tie beam to pass through. The web plates are connected to the steel tube using groove full-penetration welds, forming an engagement segment with an average length of L. This design transfers part of the axial force from the arch to the tie beam’s web plates via shear through the welds.

(2)

Setting of an annular bearing plate at the arch beam end: An annular plate is installed at the end of the circular steel tube to increase the contact area between the tube and the concrete in the joint zone. This action disperses the concentrated axial force from the steel tube more uniformly into the concrete, thereby preventing concrete splitting and ensuring a more uniform local stress transfer.

(3)

Connection design at the tie beam-inclined column intersection: Slots are opened in the inclined column to allow the three web plates of the tie beam to pass through. After passing through the inclined column, the tie beam’s web plates are welded to the steel tube of the inclined column.

(4)

Arrangement of tie beam flanges and prestressed cables: To ensure thorough compaction of the concrete, the upper and lower flanges of the tie beam are discontinued outside the joint zone, thus avoiding intrusion into the joint core during casting. The prestressed cables are arranged horizontally between the web plates of the tie beam, passing through the joint zone and anchored outside the supporting column. Horizontal bearing plates are provided at the bottom of the web plates within the joint zone to assist in transferring the prestressing force.

(5)

Integrated concrete casting: Concrete is cast continuously in a single operation for the circular steel tube, the joint zone, and the tie beam, forming an integral concrete core. This ensures continuous force transfer and maintains the integrity of the joint.

2.3. Preliminary Validation of the Rationality of Joint Construction

Li Chongyang et al. [26] conducted a static loading test on a 1:3 scale model of the joint to preliminary verify its reliability under design loads, as shown in Figure 4. The test included two loading conditions: one with the prestressed high-strength rods installed and another with them removed. The experimental results indicated that the area of maximum stress in the joint occurred at the interface between the tie beam and the arch beam. For both conditions, with and without prestressed high-strength rods, the specimen remained essentially within the elastic range under the design load. Its bearing capacity reached 1.66 times the design load without exhibiting obvious signs of damage. However, this value had reached the maximum loading capacity of the system. Moreover, at this load level, the presence of the prestressed high-strength rods reduced the elongation of the tie beam to 68% of that observed in the condition without prestressed rods. It correspondingly helped reduce the displacement of arch structure.

3. Numerical Simulation

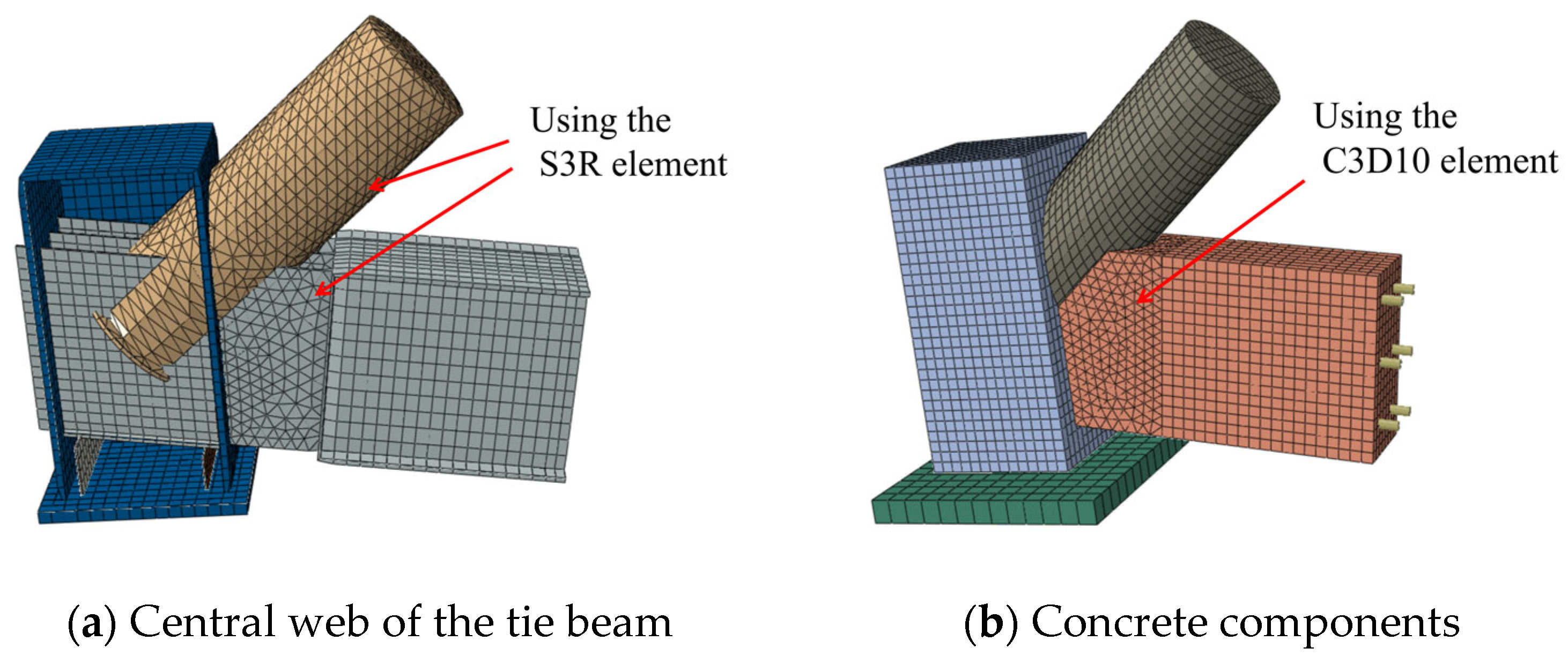
3.1. Geometric Modeling

The modeling was conducted using the finite element software ABAQUS 2024. Based on Figure 3, a finite element model of the 1:3 scale joint specimen was developed. The model was divided into the following components: the steel structure (including the inclined column, circular arch beam, and tie beam), the concrete parts (including the concrete inside the inclined column, circular arch beam, and tie beam), and the prestressed rods.

3.2. Material Properties

The steel material properties in the model were set to be identical to those of the steel used in the tests, as listed in

Table 1. Mechanical properties of steel.

Plate Thickness or Nominal Diameter/mm	Strength Grade	Yield Stress/N/mm2	Peak Stress/N/mm2	Elastic Modulus/N/mm2
20	Q420	491	631	196,333
16.7	Q420	528	682	179,875
10	Q420	498	662	217,666
13.3	Q420	449	579	219,666
39 (Steel rods)	12.9	1080	1200	210,000

[26]. An elastic-hardening bilinear uniaxial stress–strain relationship [27] was adopted, in which the slope of the hardening segment is 0.01 times the elastic modulus, and the isotropic hardening criterion was used. The mass density of the steel was taken as 7.85 × 10³ kg/m³, and Poisson’s ratio was set as 0.3.

The concrete used in the model had a design strength grade of C60, with a measured cube compressive strength of 59 MPa [26]. Concrete is filled inside the inclined column and circular arch beam, where it is confined by the external steel tubes. Therefore, the enhancement in peak strain and bearing capacity of the concrete due to this confinement should be considered. The uniaxial stress–strain relationship of the concrete adopted the equivalent uniaxial stress–strain model for core concrete confined by circular or square steel tubes, as proposed by Liu Wei et al. [28]. This constitutive model incorporates the confinement effect coefficient ξ to account for the composite action in CFST sections. The coefficient ξ is calculated as follows:

$$\xi = {\displaystyle \frac{A_{\mathrm{s}}{f}_{\mathrm{y}}}{A_{\mathrm{s}}{f}_{\mathrm{c}}}} = \alpha \times {\displaystyle \frac{f_{\mathrm{y}}}{f_{\mathrm{c}}}}$$

(1)

where a is the steel ratio of the CFST section; f_y is the yield strength of the steel; f_c is the axial compressive strength of concrete. The equivalent stress–strain relationship of the core concrete is categorized into two conditions: concrete under tension and concrete under compression. For concrete under compression, the stress–strain curve is defined by the following equations:

$$y = \left\{\begin{array}{c}2·x{-x}^2 (x \le 1)\\ {\displaystyle \frac{x}{{\beta }_0·{\left(x-1\right)}^{\eta }+x}} (x > 1)\end{array}\right.$$

(2)

where

$$x={\displaystyle \frac{{\epsilon }_{\mathrm{c}}}{{\epsilon }_0}},y={\displaystyle \frac{{\sigma }_{\mathrm{c}}}{{\sigma }_0}}$$

$${\sigma }_0=f_{\mathrm{c}}, {\epsilon }_0={\epsilon }_{\mathrm{c}}+800·{\xi }^{ 0.2}·{10}^{-6}$$

$${\epsilon }_{\mathrm{c}}=1300+12.5·f_{\mathrm{c}}·{10}^{-6}$$

$$\eta =\left\{\begin{array}{ll} 2& (\mathrm{circular} \mathrm{CFST})\\ 1.6+{\displaystyle \frac{1.5}{x}}& (\mathrm{square} \mathrm{CFST})\end{array}\right.$$

$${\beta }_0=\left\{\begin{array}{ll}{(2.36 \times 10^{-5})}^{[0.25+\xi (-0.5{)}^7]}·{f }_{\mathrm{c}}^{0.5}·0.5 ⩾ 0.12& (\mathrm{circular} \mathrm{CFST})\\ {\displaystyle \frac{{f }_{\mathrm{c}}^{0.1}}{1.2\sqrt{1+\xi }}}& (\mathrm{square} \mathrm{CFST})\end{array}\right.$$

For concrete under tension, the stress–strain curve is defined by the following equations:

$$y=\left\{\begin{array}{ll}1.2·x-0.2·x^6& (x \le 1)\\ {\displaystyle \frac{x}{0.31·{{\sigma }_{\mathrm{p}}}^2\cdot (x-1{)}^{1.7}+x}}& (x > 1)\end{array}\right.$$

(3)

where

$$x={\displaystyle \frac{{\epsilon }_{\mathrm{t}}}{{\epsilon }_{\mathrm{p}}}},y={\displaystyle \frac{{\sigma }_{\mathrm{t}}}{{\sigma }_{\mathrm{p}}}}$$

$${{\sigma }_{\mathrm{p}} \mathrm{is} \mathrm{the} \mathrm{peak} \mathrm{stress} \mathrm{under} \mathrm{tension}, \sigma }_{\mathrm{p}}=0.26·{(1.25·f_{\mathrm{c}})}^{{\displaystyle \frac{2}{3}}}$$

$${{\epsilon }_{\mathrm{p}} \mathrm{is} \mathrm{the} \mathrm{strain} \mathrm{at} \mathrm{the} \mathrm{peak} \mathrm{load}, \epsilon }_{\mathrm{p}}=43.1·{\sigma }_{\mathrm{p}} (\mathsf{\mu }\mathsf{\epsilon })$$

For the multiaxial constitutive relationship, the concrete damaged plasticity (CDP) model in ABAQUS was adopted, with the parameter values listed in

Table 2. Parameter values for the concrete damaged plasticity model.

Ψ	ϕ	fbo/fco	K	Viscosity Parameter	Ec	ρ (kg/m3)	υ
30	0.1	1.16	0.6667	0.0005	36,000	2.5 × 103	0.2

. The selection of the concrete constitutive model and the calibration of its parameters are crucial for the accuracy of finite element analysis results of concrete-filled steel tubular (CFST) structures. Bilal et al. [29] addressed this issue through systematic parameter sensitivity analysis and model calibration, establishing a set of parameter values for the CDP model in ABAQUS. Additionally, referring to the research by Wosatko et al. [30] on the CDP model, a dilation angle between 25° and 35° is recommended. In this study, a dilation angle of 30° was adopted based on the agreement between the calculated and experimental results, while the remaining parameters are based on the recommendations of Bilal et al. [29].

In Table 2, Ψ denotes the dilation angle, ϕ represents the flow potential eccentricity, f_bo/f_co is the ratio of biaxial compressive strength to uniaxial compressive strength, K is the ratio of the second stress invariant on the tensile meridian to that on the compressive meridian, E_c stands for the elastic modulus of concrete, ρ indicates the density of concrete, and υ is Poisson’s ratio. To ensure convergence of the computational results, the damage factor is calculated with reference to the energy equivalence principle-based method proposed by Sidoroff [31], using the following expression:

$$d_{\mathrm{c}}=1-\sqrt{{\displaystyle \frac{{\sigma }_{\mathrm{c}}}{E_{\mathrm{c}}{\epsilon }_{\mathrm{c}}}}}$$

(4)

$$d_{\mathrm{t}}=1-\sqrt{{\displaystyle \frac{{\sigma }_{\mathrm{t}}}{E_{\mathrm{c}}{\epsilon }_{\mathrm{t}}}}}$$

(5)

3.3. Boundary Conditions and Contact Interactions

Taking into account the test conditions [26] and the load-bearing characteristics of each member in the joint, the boundary conditions of the model were defined as follows.

(1)

The end of the tie beam was designed as a fixed support.

(2)

The end of the circular arch beam was free, and axial compression was applied at this location.

(3)

The top of the inclined column was free, and the relatively small load transferred from the upper floors was neglected.

(4)

As mentioned above, under the most critical design condition, the horizontal shear force in the column is only 0.29 times of the force in the tie beam. Therefore, the horizontal resistance of the inclined column was neglected, with only the balance between the horizontal components of the tie beam and the circular arch beam considered in the analysis. This approach results in a more critical load condition for the tie beam and represents a conservative simplification, and it is also adopted in the design method. In the numerical model, the bottom of the inclined column was provided with a sliding support.

As shown in Figure 5, “Tie” constraints were applied at the connection between the concrete of the circular arch beam and the concrete of the inclined column, as well as at the steel connections between the inclined column, tie beam, and circular arch beam. A frictional contact interface, with a coefficient of 0.6, was defined in the tangential direction between the following components and the internal concrete: (1) the steel tube of the inclined column, (2) the steel tube of the circular arch beam. The value of the friction coefficient is determined with reference to the research findings of Rabbat, B.G. et al. [32] on the interfacial friction behavior between steel and concrete. Their study recommends a friction coefficient ranging from 0.57 to 0.65 when lateral pressure exists at the interface. In the joint discussed in this paper, the concrete within the concrete-filled steel tubular component exerts a compressive effect on the steel tube wall. Therefore, a friction coefficient of 0.6 is adopted, aligning with the recommended range while accounting for the specific mechanical interaction in such composite structures. A friction coefficient of 0.3 was adopted for the interfaces involving the web/flange plates of the tie beam. “Hard contact” was specified in the normal direction. The portions of the steel components of the circular arch beam and the tie beam that extend into the inclined column were embedded into the concrete of the inclined column. The central web and transverse diaphragms of the tie beam were embedded within its own concrete, while the portion of the web inserted into the circular arch beam was embedded within the arch beam’s concrete.

One end of the prestressed high-strength rods was tied to the outer surface of the inclined column, while the other end was coupled to a reference point located at the centroid of the tie beam end section. No constraints or contacts were defined between the rods and the concrete.

A steel plate was incorporated at the bottom of the inclined column to simulate the sliding boundary condition between the inclined column and the base. The contact between the bottom of the inclined column and the base steel plate was modeled as “hard contact” in the normal direction, while a frictional contact with a coefficient of 0.05 was defined in the tangential direction. The bottom surface of the base steel plate was assigned a fixed constraint, and the reference point at the end of the tie beam was also assigned a fixed constraint.

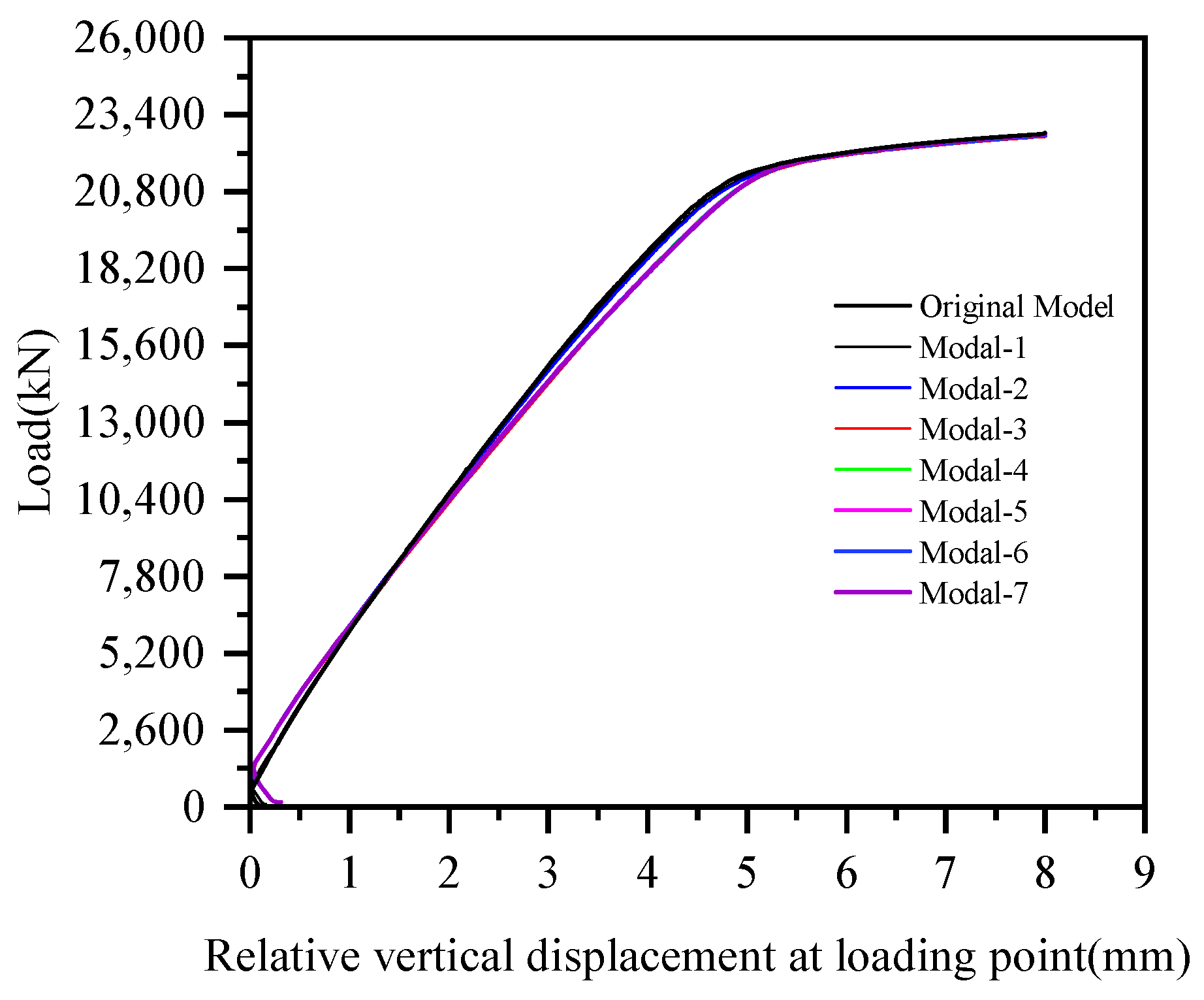
3.4. Element Selection and Meshing

The selection of mesh division schemes and element types significantly influences the accuracy of calculation results, computational speed and convergence. The components in the model were meshed as shown in Figure 6. For the web of the tie beam, the S3R element type was employed in the region between its vertical diaphragm and the outer edge of the inclined column. The S3R element was also used for the arched beam. For the remaining steel components, the S4R was adopted. A global element size of 50 mm was specified for all these aforementioned elements. The concrete in the inclined columns and the arched beam was modeled using the C3D8R element type, with a global element size of 45 mm. For the concrete inside the tie beam, the C3D10 element was used in the region between its vertical diaphragm and the outer edge of the inclined column, while the C3D8R element was applied to the remaining areas, with a global element size of 45 mm. The screws were modeled as three-dimensional truss elements (T3D2), with a global element size of 50 mm. To ensure the accuracy of stress results in critical regions (e.g., weld intersections), a mesh sensitivity analysis was conducted. Grid sizes ranging from 10 mm to 100 mm were compared. The results indicated that the computed peak stress values converged when the mesh was refined below 30 mm. The finally adopted 50 mm mesh, while ensuring computational efficiency, yielded predictions for the joint’s overall mechanical behavior and ultimate bearing capacity that were essentially consistent with those obtained from finer meshes.

3.5. Loading Protocol

Axial compression was applied at the end of the circular arch beam. To compare with existing experimental results [26], the loading protocol involved two conditions:

(1)

Condition 1: Loading was applied up to the design value of 9967 kN, corresponding to 1/9 of the original structural design load. It was then increased from 9967 kN to the test system’s maximum capacity of 16,500 kN, and further continued until significant failure characteristics were observed in the model.

(2)

Condition 2: After removing the six prestressed high-strength rods to simulate the unfavorable condition of prestress loss, the same loading protocol as in Condition 1 was applied.

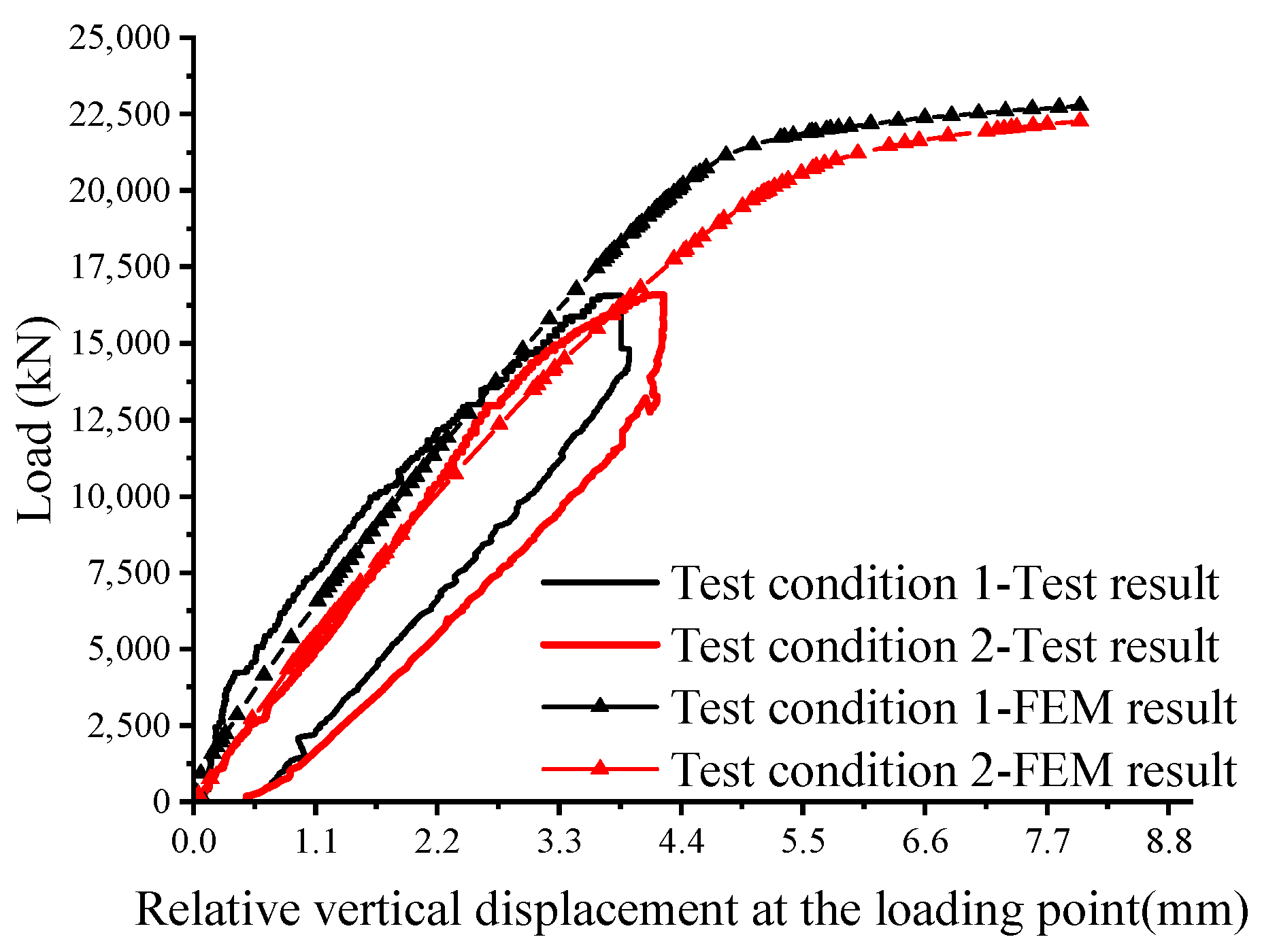
3.6. Validation

Figure 7 shows a comparison of load versus relative displacement curves at the loading point between the experimental data [26] and refined finite element model. The relative displacement at the loading point (top of the circular arch beam) was defined as, and calculated by, the difference between the axial displacement at that point and the displacement component along the loading direction at the tie beam’s fixed support. This relative displacement could reflect the global deformation characteristics of the joint.

It can be seen that when the relative displacement at the loading point reached 8 mm, the calculation failed to converge due to excessive deformation of elements in the high-stress region. At this stage, the load-relative displacement curve transitioned to a plateau, accompanied by yielding of the circular arch beam’s steel tube outside the nodal zone. Therefore, the calculation was terminated, and the load at this point was defined as the maximum computed load. As can be observed from the figure, the results from the finite element model show good agreement with the experimental results, indicating that the computational model can be used for further analysis of the joint’s load-bearing mechanism.

To ensure the accuracy of the computational results, the refined finite element model described above comprehensively accounted for all detailed structural features. However, this refined model required excessively long computation times, and exhibited poor convergence. Therefore, it was used only for analyzing the joint’s load-bearing mechanism and validating the rationality of the design scheme. To facilitate subsequent parametric studies, the refined finite element model was simplified.

To understand the impact of the simplifications on the computational results, a stepwise simplification approach was adopted. This involved simplifying one component at a time and comparing the results of the simplified model against the refined model. As shown in Figure 8, a total of six simplified models were explored: (1) Model 1: considering the low tensile strength of concrete, the concrete inside the tie beam was removed; (2) Model 2: regarding that the critical region of the tie beam is the three web plates connected to the nodal zone, the upper and lower flange plates and the vertical stiffeners located a certain distance from the joint were removed; (3) Model 3: the additional loading plate at the top of the inclined column, which was installed to meet testing requirements, was removed; (4) Model 4: the additional loading plate at the top of the circular arch beam, which was installed to meet testing requirements, was removed; (5) Model 5: the two internal stiffener plates inside the inclined column were removed; (6) Model 6: The bearing plate beneath the tie beam web inside the inclined column was removed.

The load versus relative displacement at the loading point curves of the models from the simplification process are compared with those of the refined model, as shown in Figure 9. Compared to the refined model, the seven simplified models exhibited only minor variations in the ascending branch of the curve within the pre-5.2 mm displacement range. However, the difference in the maximum computed load at a displacement of 8 mm did not exceed 1%. Therefore, the simplified model, obtained through this stepwise simplification process, retained sufficient accuracy and was used for subsequent parametric simulation analyses.

4. Analysis of the Force Mechanism

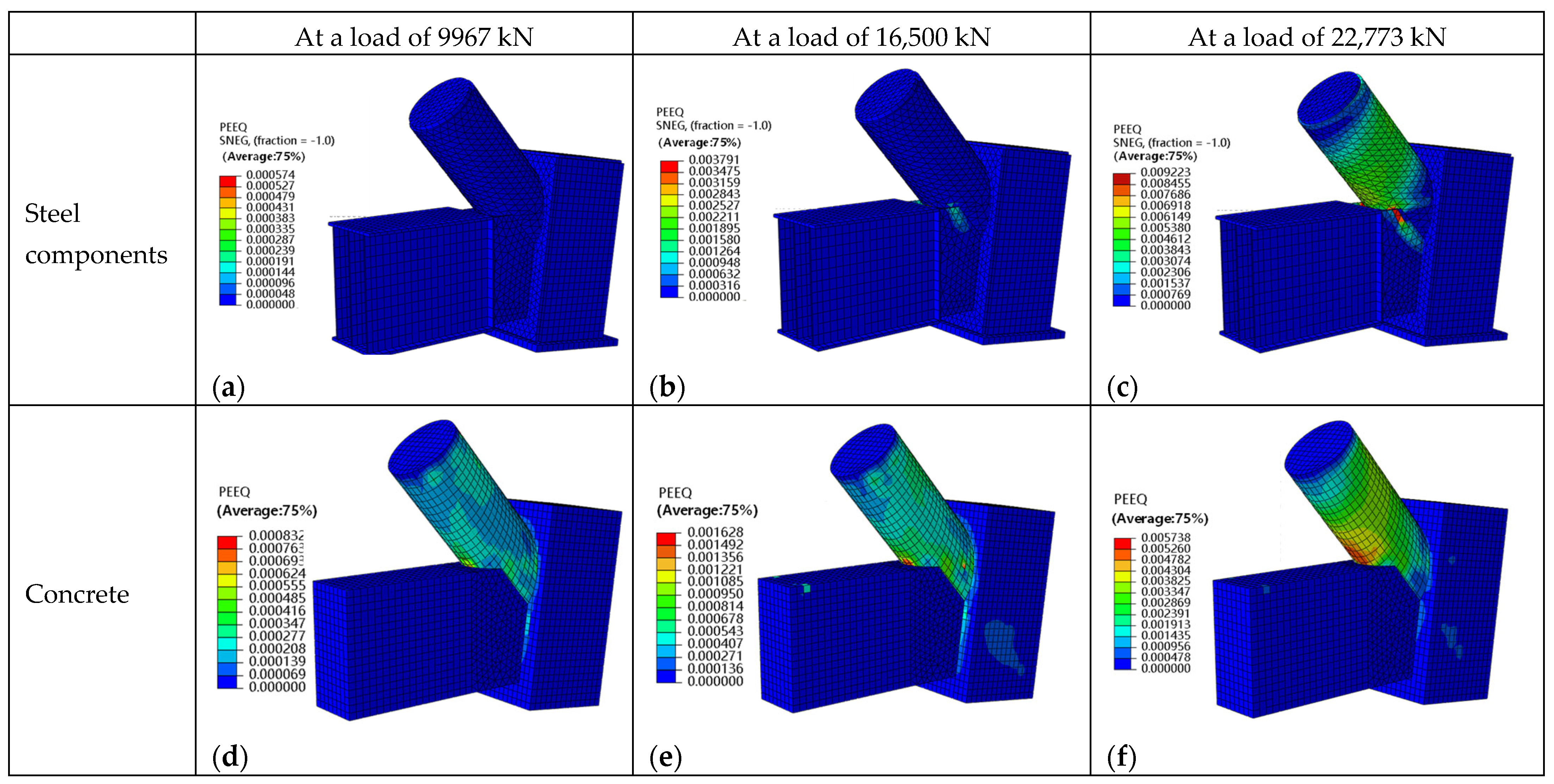
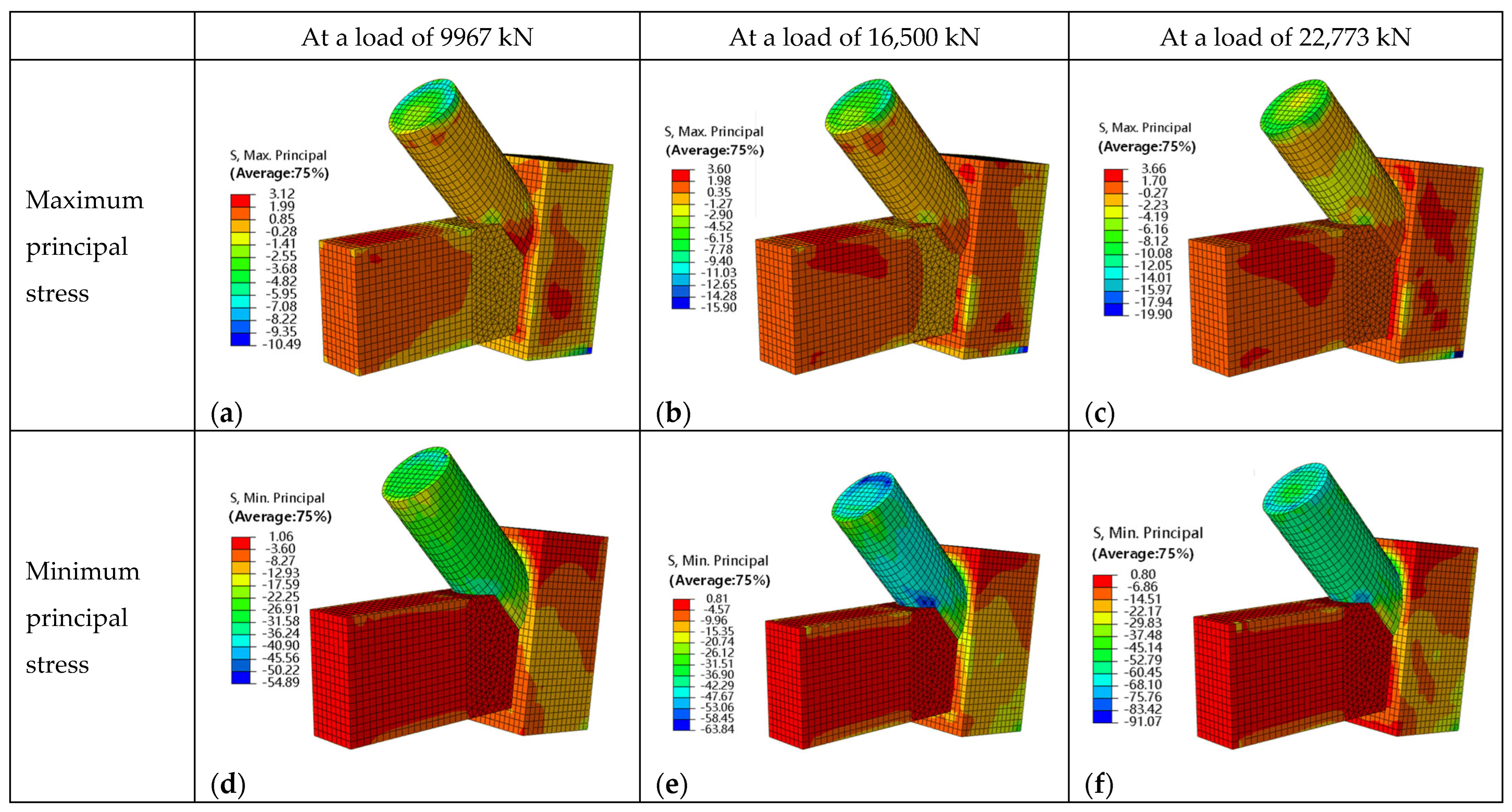
4.1. The Load-Bearing Capacity and Deformation Characteristics

Comparing the load versus relative displacement curves at the loading point from the refined model, as shown in Figure 7. It is observed that, the maximum computed load of the model with prestressed rods (22,773 kN) was 2.28 times the design load (9967 kN). The absence of prestressed rods led to only a 2.2% reduction in the maximum computed load. However, the yield load decreased by 6.8%, the relative displacement at yielding increased by 6.4%, and the stiffness at yielding decreased by 12.4%. This indicated that the presence of prestressed rods could contribute to increasing the joint’s stiffness, but had a limited effect on its maximum bearing capacity.

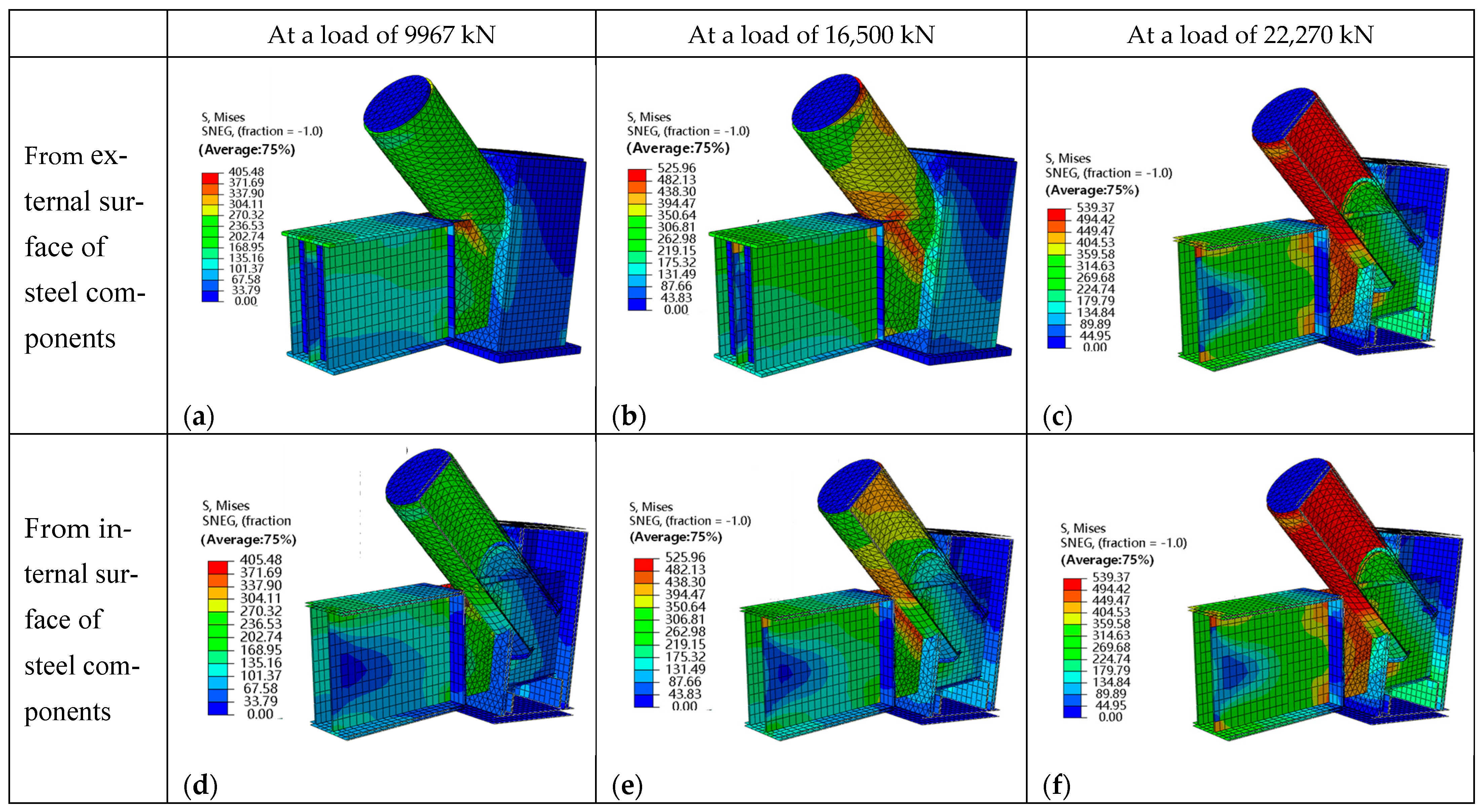
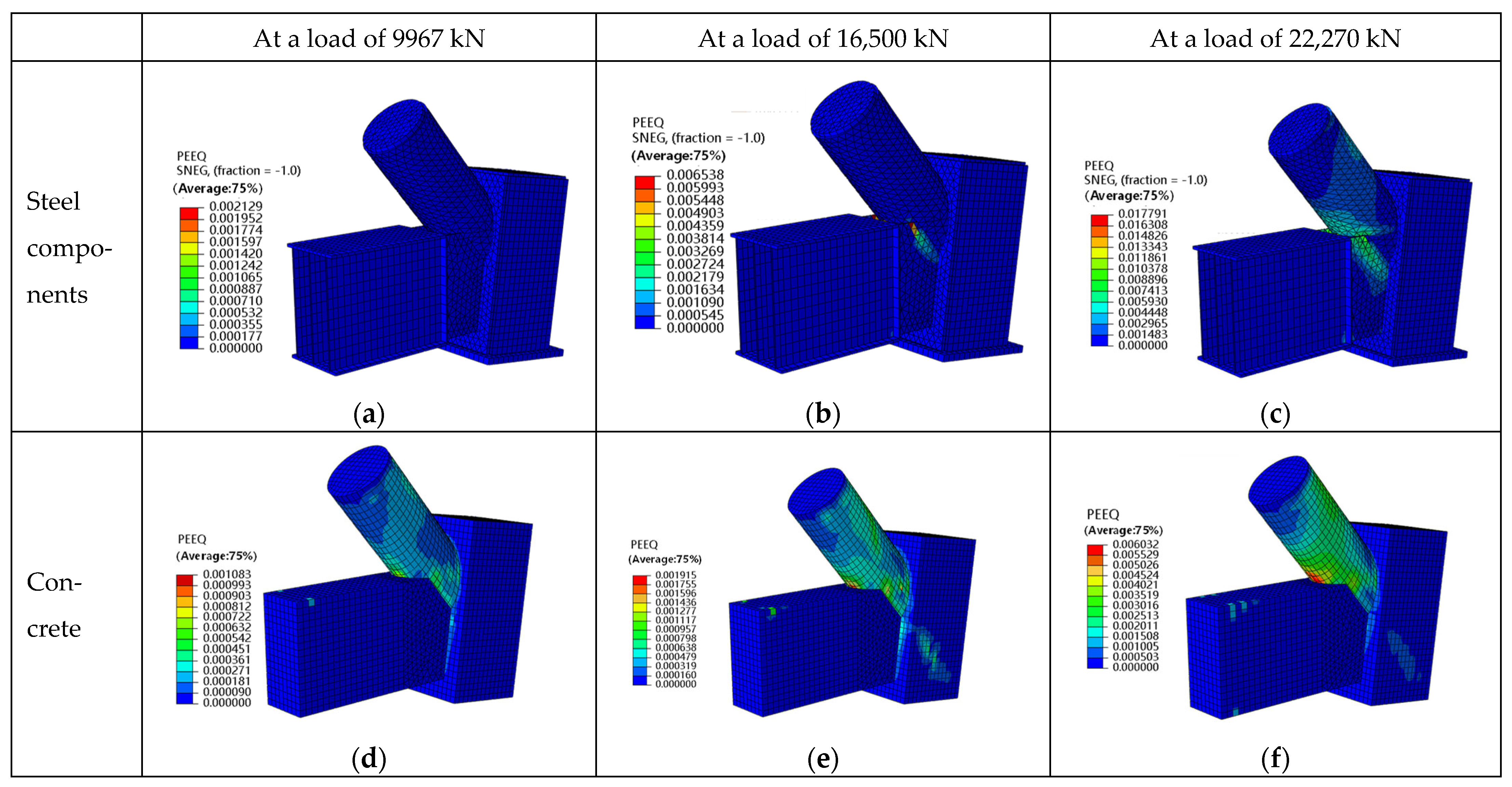
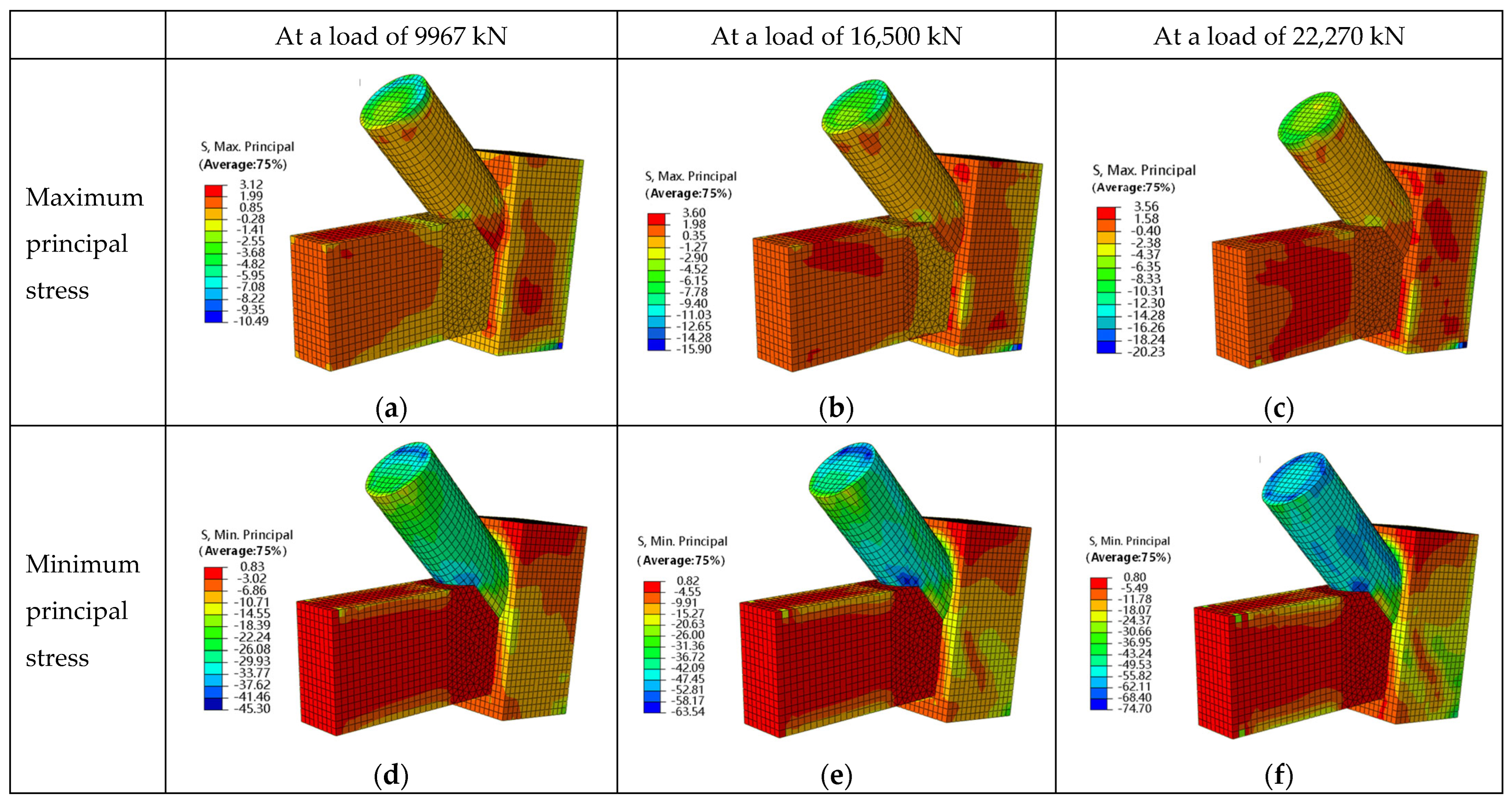
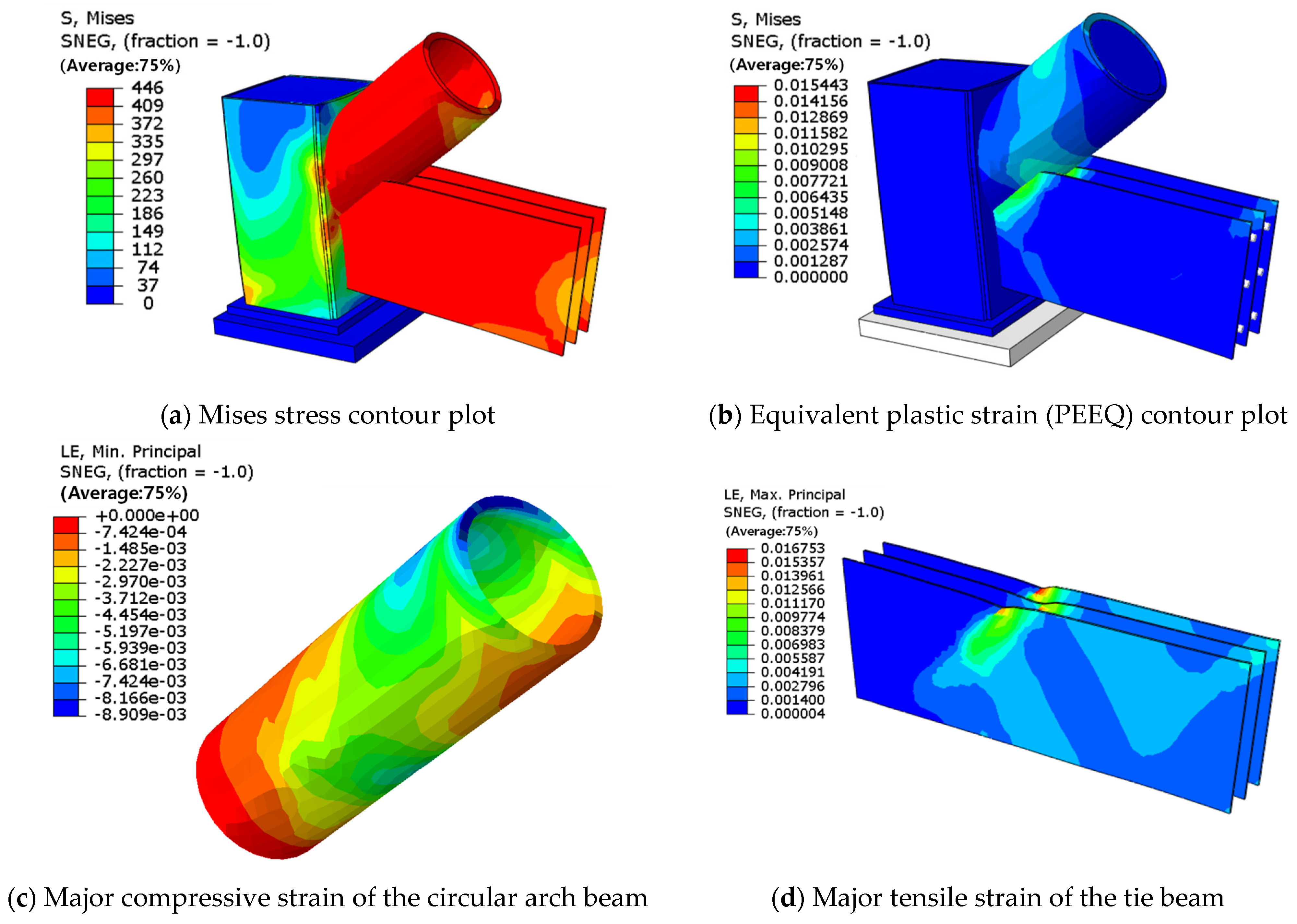
4.2. Effect of Prestressed Rods on Joint Stress Distribution and Plastic Zone Development

Figure 10 shows the von Mises stress contours of the steel component under Condition 1 at the design load of 9967 kN, the maximum test load of 16,500 kN, and the maximum computed load of 22,773 kN. The numerical values in the figure represent equivalent stress in MPa, with higher values indicating a greater stress level in the region, which is a potential failure risk zone. From Figure 10a–c, under Condition 1, when the design load of 9967 kN was reached, all steel components remained in the elastic state. However, stress concentrations were observed in the steel tube of the circular arch beam and the web of the tie beam at their intersection. As the load increased, the stress development in these concentration zones progressed significantly faster than in other regions. Subsequently, the high-stress area in the steel tube of the circular arch beam expanded circumferentially, while the high-stress area in the tie beam extended along the interface between the arch beam and the tie beam. When the maximum computed load of 22,773 kN was reached, most of the steel tube of the circular arch beam (outside the inclined column) and the tie beam web at the junction with the arch beam had reached the yield stress of the steel. Furthermore, while the yielded region in the tie beam did not extend through its full section height, the high-stress zone in the circular arch beam was more extensive. This stress distribution suggests that the circular arch beam acted as the critical component of the joint.

From Figure 10d–f, it could be seen that the stress was higher in the steel tube of the inclined column and the web of the tie beam within the joint zone along the load path extending from the circular arch beam. The stress decreased with increasing distance from this load path, reflecting the force transfer mechanism from the circular arch beam to the inclined column and the tie beam.

From Figure 10g–i, for the prestressed high-strength rods, the stress in the rods located in the upper part of the tie beam was 5.9% to 13.4% higher than that in the rods in the lower part, indicating that the tie beam was subjected to eccentric tension. This eccentric loading primarily resulted from the inclined sliding displacement at the inclined column’s support during loading, which thereby induced a relative inclined displacement at the root of the tie beam. The stress in the rods increased from the initial prestress level of 183 MPa to 614 MPa at the maximum computed load, demonstrating that the rods worked compositely with the tie beam in resisting the applied loads.

Figure 11 presents the contour plots of the equivalent plastic strain (PEEQ) in both the steel components and concrete for Condition 1 at the design load of 9967 kN, the maximum test load of 16,500 kN, and the maximum computed load of 22,773 kN. The numerical values represent equivalent plastic strain, which indicates the extent of irreversible plastic deformation in the material [33]. Higher values indicate more severe plastic deformation in the region. As observed in Figure 11a–c, the significant PEEQ in the steel components was primarily located in the steel tube of the arched beam and the web of the tie beam near the joint region. The maximum plastic strain occurred at the intersection between the root of the arched beam and the web of the tie beam. Furthermore, the steel tube of the arched beam above the tie beam exhibited an extensive area of high plastic strain, which further confirmed that the arched beam was a critical component. From Figure 11d–f, it can be seen that the concrete with relatively high PEEQ was mainly distributed in the arched beam section above the tie beam. A minor area of plastic strain was also observed in the concrete of the inclined column along the extension of the arched beam. In contrast, the concrete within the tie beam was predominantly in tension, resulting in a comparatively lower equivalent plastic strain.

Figure 12 shows the contour plots of the maximum and minimum principal stresses in the concrete for Condition 1 at the design load of 9967 kN, the maximum test load of 16,500 kN, and the maximum computed load of 22,773 kN. The numerical values in the maximum and minimum principal stress contour plots are in MPa. Positive values represent tensile stress, while negative values represent compressive stress. As shown in Figure 12a–c, regions of relatively high maximum principal stress (i.e., principal tensile stress) in the concrete were primarily distributed within the tie beam as the load increased. The concrete in the tie beam was not continuous with that in the arched beam or the inclined column’s steel tube. The tensile stress in the tie beam’s concrete was transferred through the bond with the tie beam’s web. Consequently, the area of high tensile stress developed from the fixed end towards the joint zone, while a significant region of high principal tensile stress also formed at the intersection between the root of the arched beam and the web of the tie beam. In the inclined column, the region of high principal tensile stress in the concrete initially developed from the upper and lower sides of the arched beam root (Figure 12a). This was likely due to the splitting tensile stresses generated on both sides of the compression zone as the local pressure from the arched beam was transferred to the inclined column. This corresponded to the development path of the high principal compressive stress zone observed in the inclined column in Figure 12d. Figure 12d–f show that regions of high maximum principal compressive stress were primarily concentrated in the arched beam, with the highest stress occurring specifically in the section above the tie beam. This area corresponded to the region of maximum equivalent plastic strain (PEEQ) in the concrete shown in Figure 11f, indicating a localized compression zone.

Figure 13 shows vector diagrams of principal compressive and tensile stresses in the steel and concrete at key locations of the joint. Figure 13a depicts the principal compressive stress in the concrete core of the inclined column and the circular arch beam, demonstrating direct load transfer through the continuous concrete. The higher stress at the arch beam’s connection interface indicates force transfer from the steel tube to the core concrete via the bearing plate. Figure 13b, showing the principal compressive stress in the middle web of the tie beam, illustrates load transfer from the arch beam’s steel tube through the interfacial welds. Figure 13c, illustrating the principal tensile stress in the same web, confirms the effective transfer of loads—carried by both the arch beam’s steel tube and concrete—to the tie beam web, which penetrates the concrete core and is fixed to the inclined column’s outer wall.

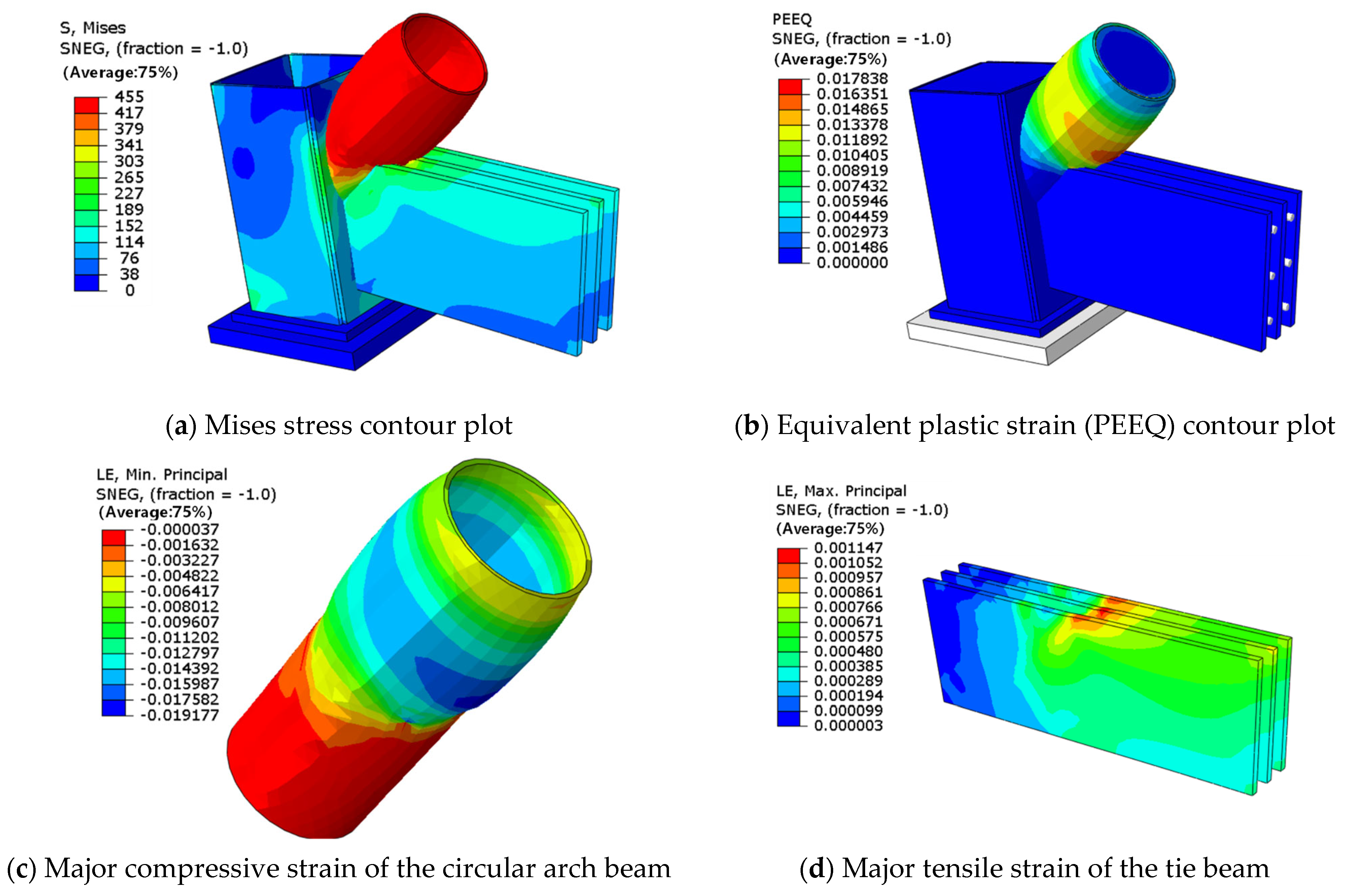
4.3. Joint Stress Distribution and Plastic Zone Propagation Under Failure of Prestressed Rods

Figure 14 presents the von Mises stress contours of the steel components for Condition 2 at the design load of 9967 kN, the maximum test load of 16,500 kN, and the maximum computed load of 22,270 kN. Figure 14a showed that in the absence of prestressed rods, all steel components remained in the elastic state when the design load of 9967 kN was reached. The maximum stress in the steel components still initially occurred in the steel tube of the circular arch beam and the web of the tie beam at their intersection. However, at the design load, the stress in the tie beam at the junction was greater than that in the arch beam, and the maximum stress in the tie beam was approximately 16.3% higher than that in condition 1.

A comparison of Figure 10b with Figure 14b indicated that when the load reached 16,500 kN, the high-stress zone in the tie beam under Condition 2 was larger than that in Condition 1, while the high-stress zone in the circular arch beam was smaller. This reflected that after the removal of the prestressed rods in Condition 2, the tie beam became relatively weaker compared to the circular arch beam.

A comparison of Figure 10c and Figure 14c at the ultimate load of 22,270 kN reveals that the high-stress areas in the tie beam web were significantly more extensive under Condition 2 than under Condition 1. Notably, the regions that had reached yield stress in the outer web extended through the full section height in Condition 2.

A comparison of Figure 10f with Figure 14f revealed that the stress in the tie beam web within the joint zone was greater in Condition 2 than in Condition 1, with the high-stress zone extending from outside the joint zone into the joint zone itself.

Figure 15 presents the equivalent plastic strain (PEEQ) contours of the steel components and concrete for Condition 2 at the design load of 9967 kN, the maximum test load of 16,500 kN, and the maximum computed load of 22,270 kN. A comparison between Figure 11c and Figure 15c revealed that the distribution of regions with significant PEEQ in the steel components was generally consistent with that in Condition 1. However, the high-strain zone was more concentrated in the intersection area between the root of the tie beam and the arched beam. Moreover, at the maximum computed load, the maximum PEEQ value increased by 93% (a factor of 1.93) compared to Condition 1. From Figure 15d–f, the regions with larger concrete equivalent plastic strains were generally consistent with those in Condition 1, but the maximum plastic strain at the maximum computed load increased by 5.1%.

Figure 16 shows the contour plots of the maximum and minimum principal stresses in the concrete at the design load of 9967 kN, the maximum test load of 16,500 kN, and the maximum computed load of 22,270 kN. As observed in Figure 16a–c, the development of principal tensile stresses with increasing load followed a pattern similar to that in Condition 1. However, at the design load of 9967 kN, the region of high principal tensile stress in the tie beam was more extensive than in Condition 1. A larger area of high stress was also evident in the inclined column. From Figure 16d–f, it can be seen that for the arched beam, which experienced high principal compressive stresses, the stress concentration in the section above the tie beam was reduced by 18% compared to Condition 1. This reduction was attributed to the larger deformation and consequent decrease in stiffness of the tie beam in Condition 2, which alleviated the local stress concentration at the intersection between the arched beam and the tie beam.

The comparison between Conditions 1 and 2 thus indicates that while the joint can meet design requirements even under complete failure of the prestressed rods, the composite action of these rods with the tie beam significantly benefits the structure by reducing local stress and increasing the load-bearing capacity reserve.

5. Parametric Analysis

Based on the simplified finite element model, a parametric study was conducted to investigate the influence of various parameters on the joint’s failure mode and bearing capacity behavior. The parameters varied include: thickness of the tie beam web plates, wall thickness of the circular arch beam steel tube, wall thickness of the inclined column steel tube, and the strength grades of steel and concrete.

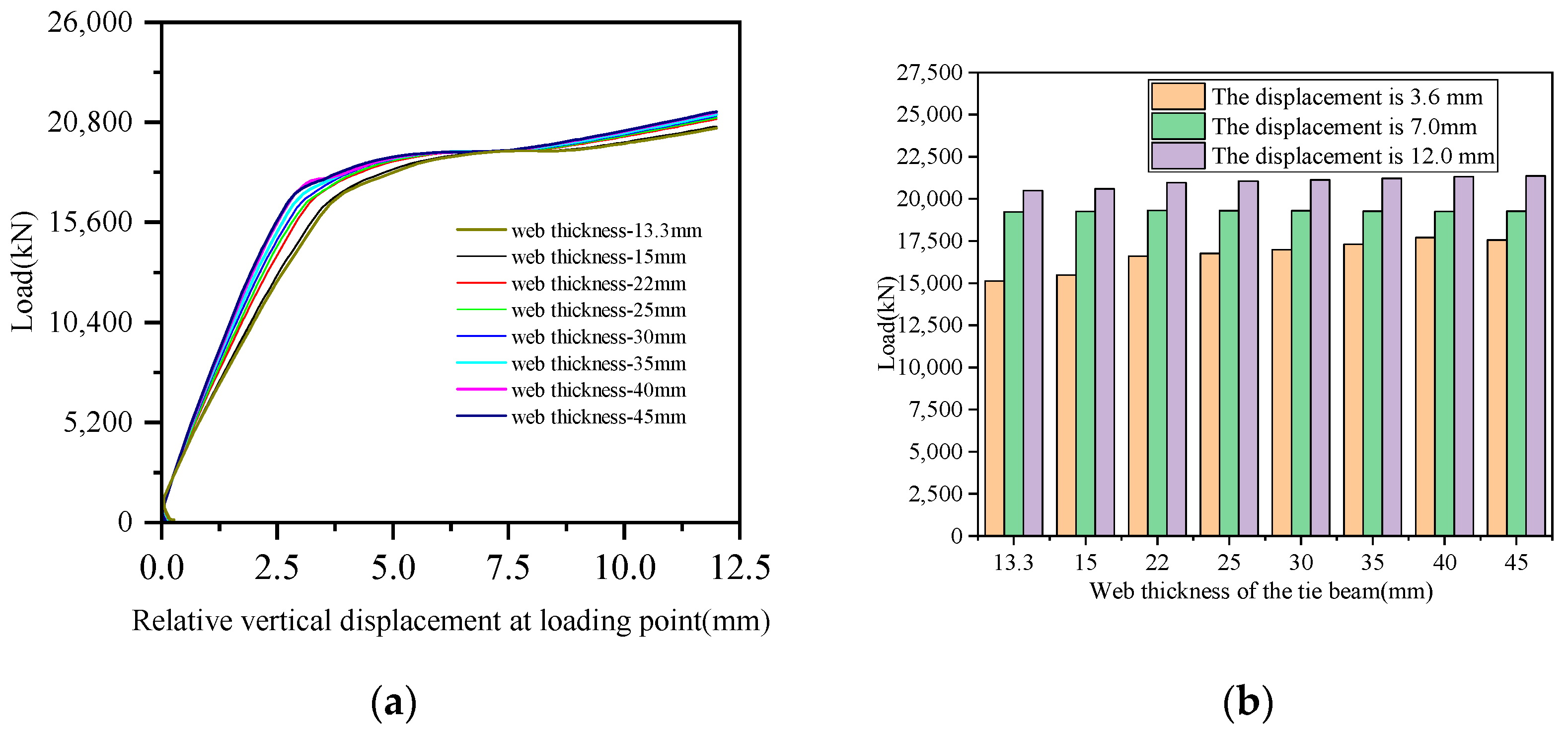
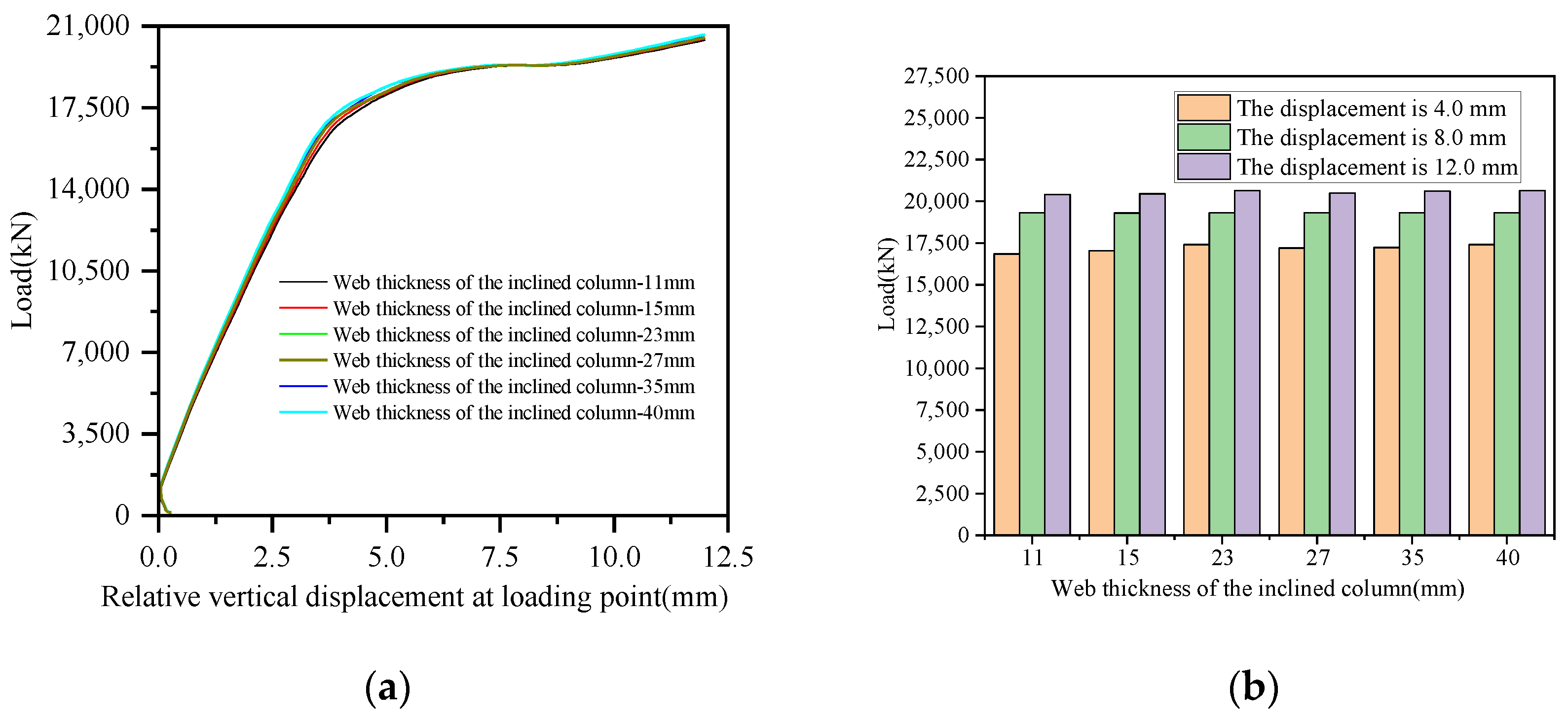
5.1. Thickness of Tie Beam Web Plates

During the testing, multiple yield points were observed on the tie beam. Consequently, the influence of the tie beam web plate thickness on the mechanical performance of the joint was investigated. Based on the original design thickness of the tie beam web plates (13.3 mm), additional analyses were conducted for web plate thicknesses of 15 mm, 22 mm, 25 mm, 30 mm, 35 mm, 40 mm, and 45 mm. The load versus relative displacement at the loading point curves for the different web plate thicknesses are shown in Figure 17. The slopes of the load–displacement curves in the elastic stage differed significantly among models with different web plate thicknesses. When the web thickness increased from 13.3 mm to 45 mm approximately a 3.38-fold increase, the bearing capacity improved by only 1.1%. This indicates that within this joint design, the strength of the tie beam web plates is sufficient, and the joint’s bearing capacity is primarily governed by other members, such as the circular arch beam. Nevertheless, increasing the thickness of the tie beam web plates reduced the deformation of the tie beam, thereby enhancing the stiffness of the joint.

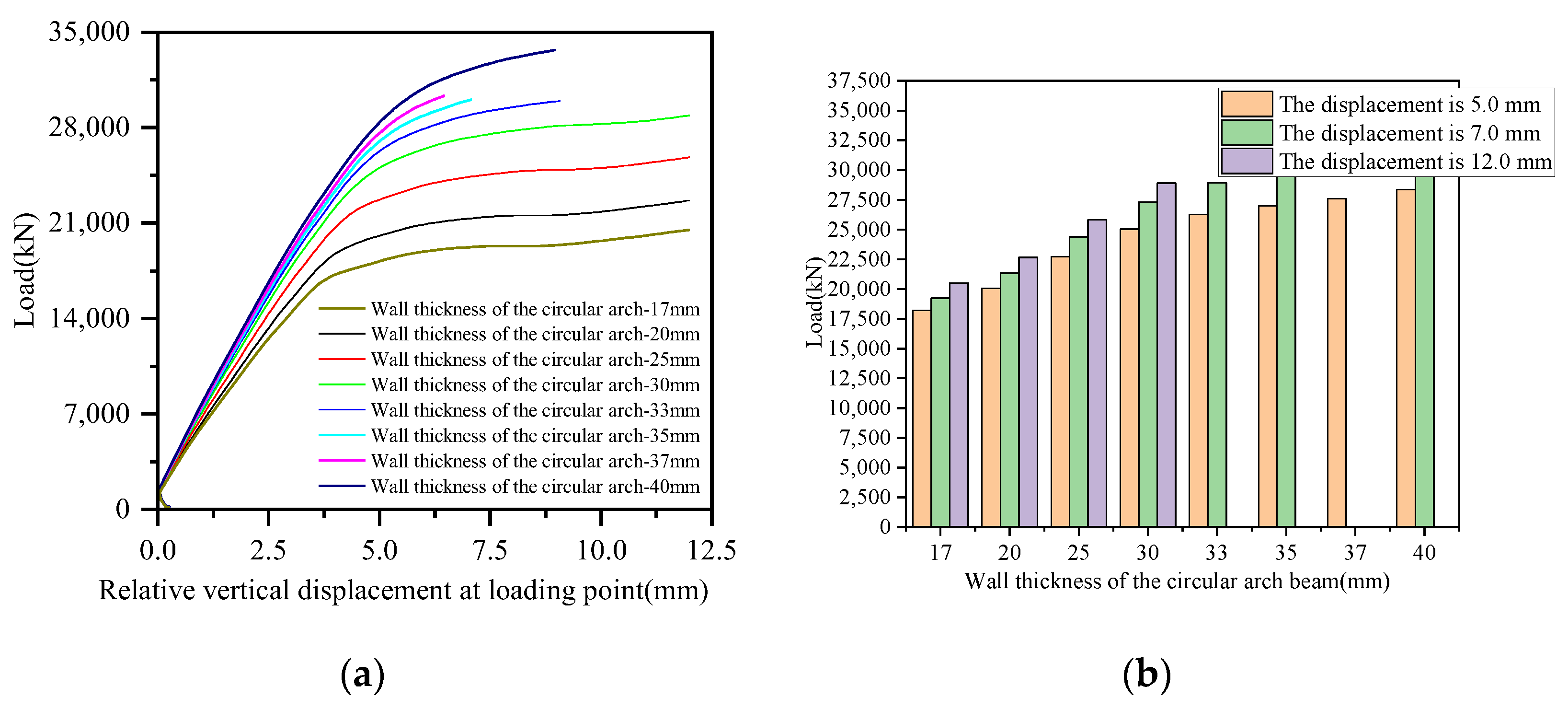
5.2. Wall Thickness of the Circular Arch Beam Steel Tube

Based on the previous analysis of the force mechanism of joints, the steel tube of the circular arch beam was identified as the critical component governing the joint’s bearing capacity, since most of its regions had yielded at the ultimate load. Using the wall thickness of the circular arch beam steel tube as a parameter and starting from the original design thickness of 17 mm, eight models with thicknesses of 20 mm, 25 mm, 30 mm, 33 mm, 35 mm, 37 mm, and 40 mm were established. The load versus relative displacement at the loading point curves for the different wall thicknesses are shown in Figure 18. When the wall thickness of the circular arch beam increases from the minimum value of 17 mm to the maximum of 40 mm (an increase by approximately 135%), the maximum computed load (peak load) significantly improves from about 19,000 kN to about 33,000 kN, representing an increase of approximately 74%.

The circular arch beam and the tie beam are the two most critical components of this joint, representing the key members where yielding occurs during the loading process. Analysis of the test results indicated that during loading, localized regions of the tie beam yielded first, while stress development in the circular arch beam was relatively slower [26]. However, the analysis of the joint’s force mechanism, based on finite element simulations, revealed that as the load increased, the yielded regions in the circular arch beam gradually expanded. This expansion ultimately led to a larger yielded area in its steel tube than in the tie beam, as shown in Figure 10c. If the strength of the circular arch beam was significantly greater than that of the tie beam (corresponding, for instance, to the 40 mm wall thickness condition mentioned above), the tie beam yielded first at its intersection with the arch beam during loading. Upon reaching the maximum computed load, as shown in Figure 19, only the tube wall near the loading point of the circular arch beam reached the yield strain, while the strain in the tie beam was substantially greater than that in the arch beam.

If the tie beam was strengthened (corresponding, for instance, to the 45 mm tie beam web plate thickness condition mentioned above), another failure mode emerged where the circular arch beam yielded and failed first. As shown in Figure 20, the enhanced load-bearing capacity of the tie beam resulted in severe deformation of the circular arch beam’s steel tube at the calculated ultimate load, whereas the tie beam itself remained elastic without yielding.

5.3. Wall Thickness of the Inclined Column Steel Tube

The wall thickness of the inclined column steel tube was set to 11 mm, 15 mm, 23 mm, 27 mm, 35 mm, and 40 mm. The load versus relative displacement at the loading point curves for the different wall thicknesses were calculated, as shown in Figure 21. When the web thickness of the inclined column increased from the minimum value of 11 mm to the maximum of 40 mm (approximately a 2.64-fold increase), the maximum computed load (peak load) improved marginally from about 20,000 kN to 20,500 kN, representing an increase in merely 2.5%. This indicates that within this joint design, the inclined column possesses a high safety margin.

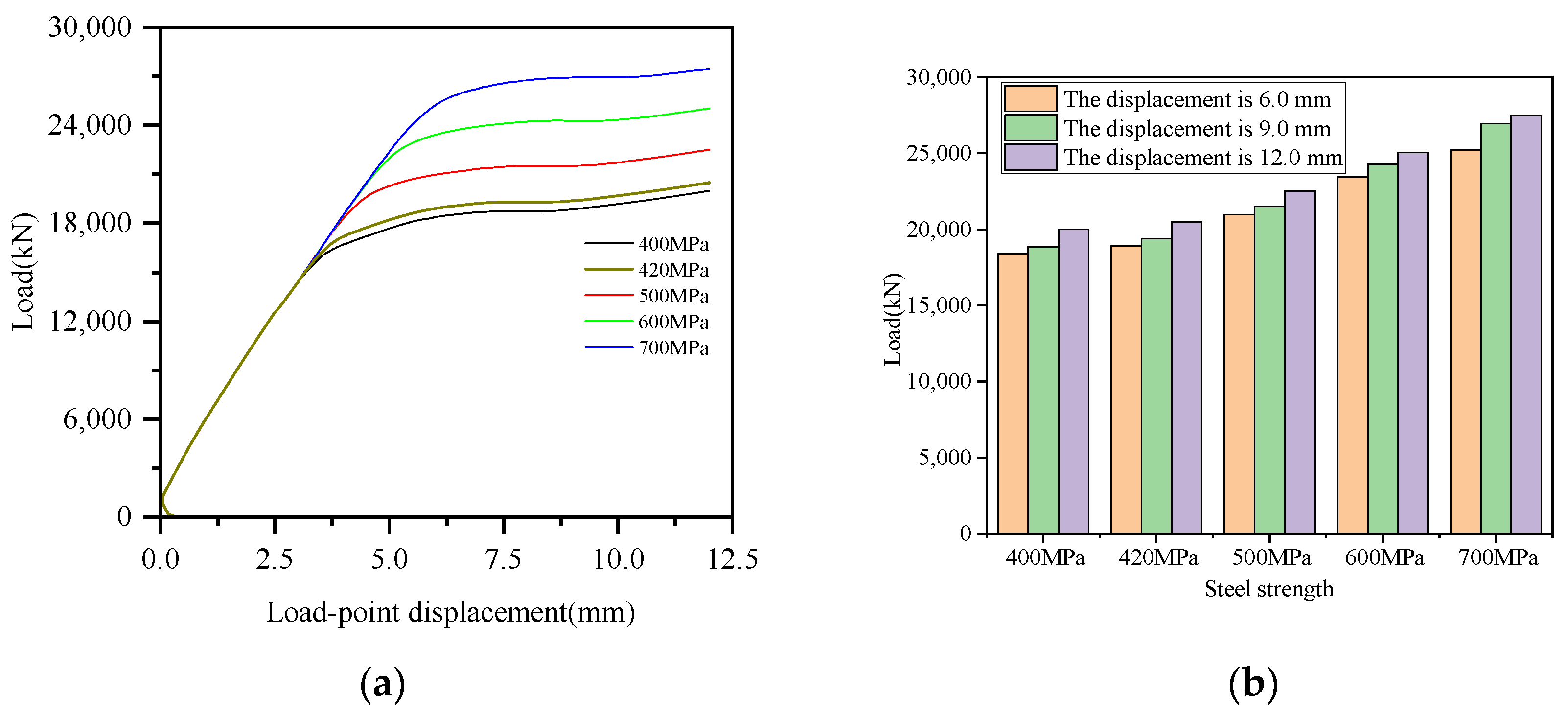
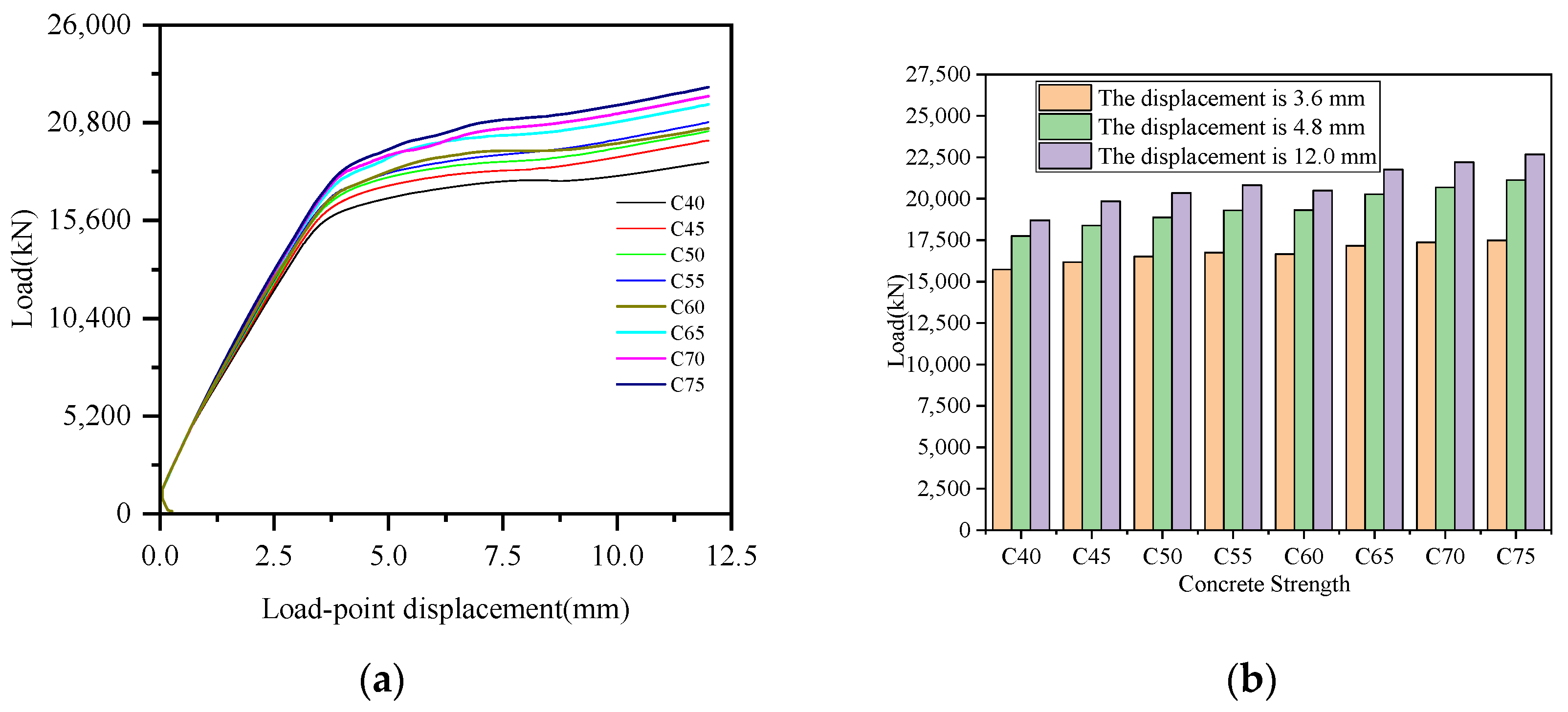
5.4. Strength Grade of Steel and Concrete

As illustrated by the joint force mechanism in Section 4, when the joint fails, both the steel tube of the circular arch beam and the web of the tie beam reach the yield strength. Therefore, enhancing the steel strength is one effective approach to improve the joint-bearing capacity. By setting the yield strength of the steel in the model to 400 MPa, 500 MPa, 600 MPa, and 700 MPa, the load versus loading-point relative displacement curves for different steel strength grades are shown in Figure 22. It can be observed that the stiffness of the joint during the elastic stage remains essentially unchanged as the steel yield strength increases. However, after the elastic stage, when the material strength increased from the minimum value of 400 MPa to the maximum of 700 MPa (a 75% increase), the maximum computed load (peak load) improved significantly from about 18,000 kN to 27,000 kN, representing an increase of approximately 50%. The joint-bearing capacity increases approximately linearly with the improvement in steel strength, indicating that the bearing capacity is significantly influenced by the steel strength.

The concrete strength is another crucial factor affecting the joint-bearing capacity. In particular, the joint design should ensure that the concrete in the joint zone has sufficient compressive capacity to facilitate effective force transfer. When the concrete strength grade in the model is varied from C40 to C75, the corresponding load versus loading-point relative displacement curves are shown in Figure 23. When the concrete strength grade increased from the minimum C40 to the maximum C75 (an increase of approximately 87.5%), the maximum computed load (peak load) under three-point bending improved from about 19,000 kN to 22,000 kN, representing an increase of approximately 15.8%. Increasing the concrete strength grade has a certain beneficial effect on the stiffness during the elastic stage and also enhances the bearing capacity after the steel yields. However, the efficiency in improving the bearing capacity is lower compared to increasing the steel strength grade. This is because the concrete in the tie beam contributes relatively little to the overall bearing capacity. Consequently, once the compressive capacity of the circular arch beam and the joint zone is enhanced, the tie beam becomes the weak link governing the joint’s bearing capacity.

6. Design Method

This paper presents a novel joint connecting a concrete-filled circular steel tubular arch, a prestressed steel-concrete composite tie beam with prestressing tendons, and concrete-filled square steel tubular supporting columns. The design philosophy is centered on achieving efficient force transfer among the various components through an internal bearing plate and mechanical design, thereby forming a self-balancing system. This system is capable of supporting heavy loads without imposing horizontal force on the adjacent structures on either side. The design procedure of the joint is as follows.

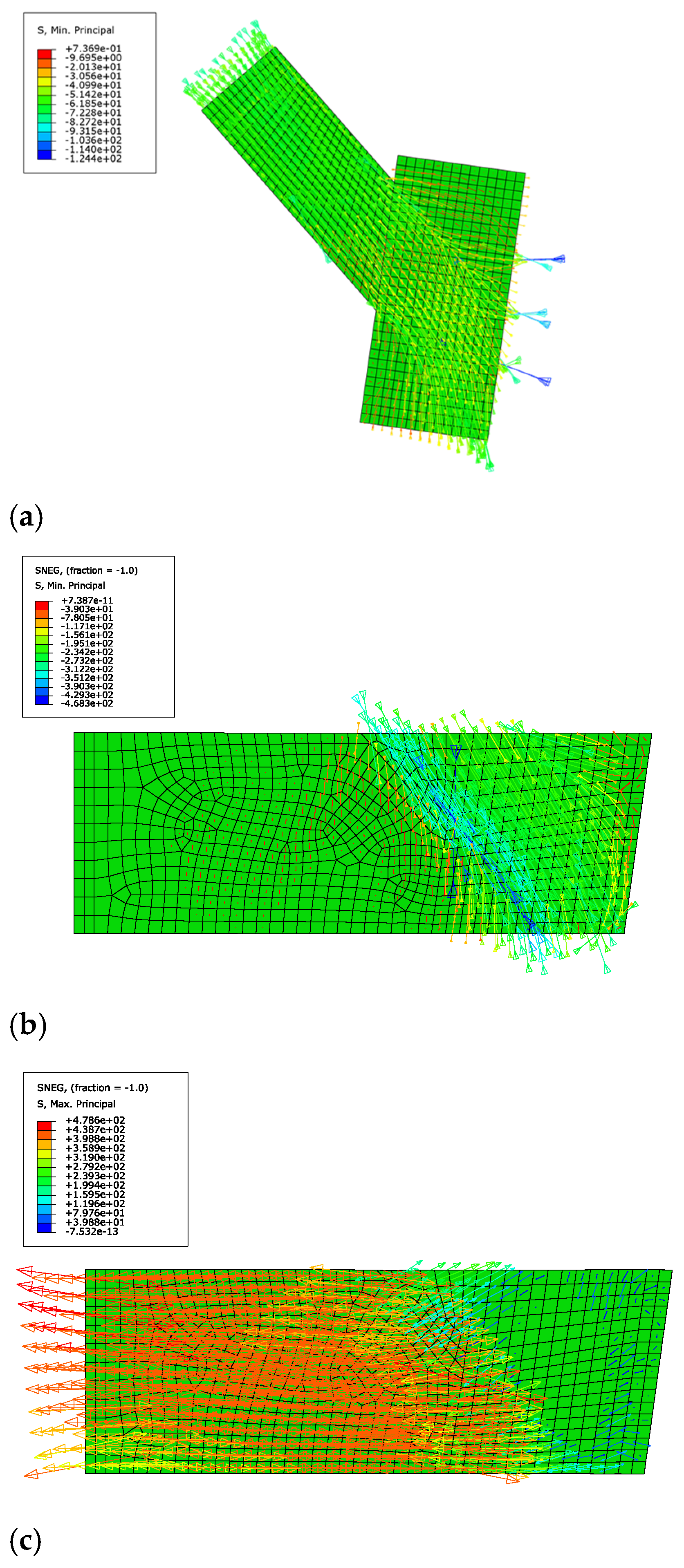
6.1. Local Bearing Capacity

Based on the design philosophy of the joint, the horizontal component of the axial force from the arched beam must be transferred to the tie beam (which contains prestressing tendons), while the vertical component is transferred to the supporting column. The transfer of the axial force within the joint should adhere to the principle of “uniform local bearing pressure transmission.” Accordingly, a bearing plate is provided at the bottom of the arched beam. Based on the force transfer mechanism of the axial force into the joint region, the design methodology is established as follows.

The axial force $N_0$ in the arched beam is resisted by both the steel and concrete within its cross-section. The portions of the axial force carried by the steel tube and the concrete are denoted as $N_{0\mathrm{s}}$ and $N_{0\mathrm{c}}$, respectively. This axial force is transferred into the arch-foot joint through three primary paths: (i) via welds between the steel tube of the arched beam and the web plates of the tie beam that penetrate into the joint, (ii) via an annular bearing plate installed at the bottom of the arched beam, and (iii) via the concrete within the circular steel tube, which transfers force directly to the concrete in the core joint region.

(1) Calculate the shear strength of the weld connecting the circular steel tube to the tie beam web, based on the force transferred from the tube. The arched beam extends into the joint region by an average length $L$, as shown in Figure 3. Slots are cut into the steel tube, allowing the three web plates of the tie beam to pass through. These web plates are then connected to the steel tube using full-penetration groove welds. Consequently, there are a total of 6 weld lines. The total effective length of the welds is denoted as 6L, the thickness of a single web plate is $t_{\mathrm{b}}$, and the design shear strength of the welds is $f_{\mathrm{v}}$. The total horizontal force that can be resisted by the three web plates via these welds is calculated as:

$$N_{\mathrm{b}\mathrm{s}}=6{Lf}_{\mathrm{v}}{t}_{\mathrm{b}}\mathrm{c}\mathrm{o}\mathrm{s}\alpha$$

(6)

The corresponding axial force in the arched beam is

$$N_{0\mathrm{s}\mathrm{s}}=N_{\mathrm{b}\mathrm{s}}/\mathrm{c}\mathrm{o}\mathrm{s}\alpha$$

(7)

where α is the angle between the arched beam and the tie beam.

(2) A portion of the axial force $N_{0\mathrm{s}}$ of the circular steel tube is transferred to the tension beam web through welds, while the remaining portion is transferred to the joint-zone concrete via the contact surface between the steel tube and the joint-zone concrete:

$$N_{0\mathrm{s}\mathrm{c}}=N_{0\mathrm{s}}-N_{0\mathrm{s}\mathrm{s}}$$

(8)

For a circular steel tube with diameter D and steel plate wall thickness t, when no end bearing plate is added, the local pressure along the axis of the circular arch beam is:

$${{\sigma }_{0\mathrm{s}\mathrm{c}\mathrm{d}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}}=N}_{0\mathrm{s}\mathrm{c}}/\mathsf{\pi }Dt$$

(9)

Since the steel tube wall thickness is usually between 20–60 mm (relatively thin), it will generate a concentrated stress and cause a splitting effect on the concrete. To increase the contact area with the joint-zone concrete, a ring-shaped bearing plate is used. The bearing plate is arranged at the end of the steel tube, with a width of ${\mathrm{w}}_{\mathrm{c}}$ and a thickness of ${\mathrm{t}}_{\mathrm{c}}$. The contact area between the steel tube and the concrete is increased to:

$$A_{0\mathrm{s}\mathrm{c}}=\mathsf{\pi }/4[{\left(D+{\displaystyle \frac{w_{\mathrm{c}}}{2}}\right)}^2-{\left(D-{\displaystyle \frac{w_{\mathrm{c}}}{2}}\right)}^2]$$

(10)

The compressive stress transferred to the concrete is:

$${{\sigma }_{0\mathrm{s}\mathrm{c}}=N}_{0\mathrm{s}\mathrm{c}}/A_{0\mathrm{s}\mathrm{c}}$$

(11)

Based on this, the width of the bearing plate can be calculated. The thickness of the bearing plate is usually determined by construction requirements and should be sufficient in stiffness to maintain the rigidity of the pressure-bearing ring plate.

(3) The concrete in the circular arch beam is connected and densely cast as a whole with the concrete in the joint zone. The compressive stress of the concrete inside the steel tube is:

$${{\sigma }_{0\mathrm{c}\mathrm{c}}=N}_{0\mathrm{c}}/A_{0\mathrm{c}}={\displaystyle \frac{N_{0\mathrm{c}}}{\frac{\mathsf{\pi }}{4}{\left(D-2t\right)}^2}}$$

(12)

This stress is also transmitted to the concrete in the joint zone along the axis of the circular arch beam, with a plane-included angle of $\alpha$. In the ideal state, the stress transferred to the joint-zone concrete from the circular steel tube after pressure reduction by the bearing plate is equal to the stress transferred to the joint-zone concrete from the concrete inside the steel tube, realizing the uniform force transfer of the entire cross-section of the circular arch beam, i.e., ${\sigma }_{0\mathrm{s}\mathrm{c}}={\sigma }_{0\mathrm{c}\mathrm{c}}$. In summary, this section provides the specific design basis for the width and thickness of the bearing plate at the circular arch beam end, as well as for the size of the connecting weld to the tie beam web, through local bearing and force transfer analysis.

6.2. Force Equilibrium of the Joint

This section establishes the force equilibrium relationship of the joint to determine the required total cross-sectional area of the tie beam web (stiffeners) and the amount of prestressed tendons needed to balance the horizontal thrust at the arch springing, thereby providing the core basis for their dimensional design. The arch component exerts an outward horizontal force at the arch-foot. If this horizontal force is borne by the adjacent buildings at both ends, additional lateral-resistance strengthening measures need to be arranged for these buildings, which will affect the building functions. The joint in this paper is designed to achieve horizontal force equilibrium between the circular arch beam and the tie beam at the arch-foot joint. The resultant of these horizontal forces is a vertical force acting on the support column, disregarding the transfer of horizontal force to the adjacent buildings at both ends. Thus, the horizontal force at the arch foot is borne by the tension beam composed of a steel-concrete composite beam with prestressed tendons. Mathematically, this equilibrium relationship is expressed as:

$$N_0\times \mathrm{c}\mathrm{o}\mathrm{s}\alpha =N_{\mathrm{p}}+N_{\mathrm{s}}$$

(13)

where $N_{\mathrm{s}}$ is the tensile force borne by the steel-concrete composite beam, and $N_{\mathrm{p}}$ is the tensile force of the prestressed tendon. The tensile force of the prestressed tendon is calculated as:

$$N_{\mathrm{p}}=n\times A_{\mathrm{p}}\times f_{\mathrm{p},\mathrm{c}\mathrm{o}\mathrm{n}}$$

(14)

where $A_{\mathrm{p}}$ is the cross-sectional area of a single tendon, $n$ is the number of tendons, and $f_{\mathrm{p},\mathrm{c}\mathrm{o}\mathrm{n}}$ is the tension control stress of the tendon. To ensure anchoring safety, the design adopts half of the standard strength of the prestressed anchorage as its bearing capacity, providing ample safety margin. After tensioning is completed, the anchorage self-locks, and its end is sealed for protection. Given the structural characteristics of its embedded joint, this anchorage is a permanent component designed to be non-replaceable. The tensile force of the composite beam is given by:

$$N_{\mathrm{s}}=A_{\mathrm{s}}\times f_{\mathrm{y},\mathrm{c}\mathrm{o}\mathrm{n}}$$

(15)

where $A_{\mathrm{s}}$ is the steel area of the web of the composite beam, and $f_{\mathrm{y},\mathrm{c}\mathrm{o}\mathrm{n}}<f_{\mathrm{y}}$ ($f_{\mathrm{y}}$ is the design control stress of the steel). A certain design margin should be reserved.

To ensure the connectivity of the joint area for concrete pouring, the flange of the tension beam does not extend into the arch-foot joint. Inside the arch-foot joint, vertical stiffeners are set to correspond one-to-one with the webs of the tension beam, so as to achieve force transfer with equal strength. The horizontal bearing capacity provided by the web of the tension beam is the sum of the tensile capacities of multiple webs. Among them, m is the number of webs of the tension beam, the height of the vertical stiffener is the same as the height H of the tension beam, and the thickness is t₂. That is:

$$N_{\mathrm{s}}\le m\times \left(H\times t_2\right)\times f_{\mathrm{y},\mathrm{c}\mathrm{o}\mathrm{n}}$$

(16)

In the preliminary design, the cross-section $A_{\mathrm{s}}$ of the tension beam and the thickness t₂ of the vertical stiffener can be determined according to engineering experience. Then, the tensile force borne by the tension beam can be calculated according to the pre-defined steel stress ratio $f_{\mathrm{y},\mathrm{c}\mathrm{o}\mathrm{n}}$. If this tensile force is insufficient to balance the horizontal force at the arch foot, the remaining part is supplemented by the prestressed tendons, and thus the number of prestressed tendons can be determined. If the thickness of the stiffener exceeds the commonly used processable thickness, the tensile force borne by the tension beam should be reduced, and the number of prestressed tendons should be increased simultaneously.

Although the joint can still meet the design requirements under extreme conditions such as Condition 2, the prestress losses induced by effects including concrete shrinkage and creep should be considered in the design of prestressed components. Furthermore, in the practical engineering, the design of this joint embodies the principle of structural redundancy by providing dual load paths to ensure safety. The primary load path is assigned to the prestressed tendons, which are designed to balance the full horizontal thrust of the arch under the standard load combination of 1.0 Dead Load + 1.0 Live Load. A redundant load path is provided by the steel web and stiffeners of the tie beam. The cross-section of the tie beam steel components is designed such that, in the extreme event of a complete loss of prestress, it can independently sustain the total arch thrust. This creates an effective backup load-transfer mechanism, significantly enhancing the robustness of both the joint and the overall structure, in compliance with safety guidelines for important public buildings.

6.3. Stress State of Concrete in the Joint Core Region

In the core area of the joint, the concrete is under biaxial compression, and its actual compressive strength can be calculated based on the concrete strength theory.

(1) The circular steel tube wall and the concrete inside the tube of the circular beam jointly transfer the inclined compressive force $N_0$, which causes the concrete in the joint area to bear a compressive stress at an angle $\mathsf{\alpha }$ to the plane:

$${\sigma }_{\mathsf{\alpha }}={\sigma }_{0\mathrm{s}\mathrm{c}}={\sigma }_{0\mathrm{c}\mathrm{c}}$$

(17)

(2) During the prestressing process, the tensile force $N_{\mathrm{p}}$ applied to the prestressing tendon is converted into a horizontal compressive force acting on the arch-foot joint. This compressive force is jointly borne by the web of the extended beam (penetrating into the joint area) and the concrete in the joint area. Among them, the horizontal compressive stress of the concrete in the joint area is ${\sigma }_{\mathrm{x}}$. The value of ${\sigma }_{\mathrm{x}}$ can be approximately calculated according to the compressive modulus of the concrete cross-section within the height range of the beam web (in the joint area). Here, A_tc represents the cross-sectional area of the concrete within the height range of the beam web in the joint area, and E_c and E_s are the elastic module of concrete and the beam web, respectively.

$${\sigma }_{\mathrm{x}}={\displaystyle \frac{N_{\mathrm{p}}{\times E}_{\mathrm{c}}}{E_{\mathrm{s}}\times m\times H\times t_2+E_{\mathrm{c}}\times A_{\mathrm{t}\mathrm{c}}}}$$

(18)

(3) According to the Mohr–Coulomb criterion, the concrete in the core area of the joint is under biaxial compression, which can fully exert the compressive capacity of the concrete and improve the bearing capacity of the arch-foot joint. Let the maximum compressive principal stress be ${\sigma }_1$, and it should be less than the design compressive strength of concrete f_c:

$${\sigma }_1={\displaystyle \frac{-\left({\sigma }_{\mathrm{x}}+{\sigma }_{\mathsf{\alpha }}\right)+\sqrt{{\sigma }_{\mathrm{x}}^2+2{\sigma }_{\mathrm{x}}{\sigma }_{\mathsf{\alpha }}\mathrm{c}\mathrm{o}\mathrm{s}2\alpha +{\sigma }_{\mathsf{\alpha }}^2}}{2}}\le f_{\mathrm{c}}$$

(19)

The direction angle of the maximum compressive stress is:

$$\beta ={\displaystyle \frac{1}{2}}\arctan \left({\displaystyle \frac{{\sigma }_{\mathsf{\alpha }}\sin 2\alpha }{{\sigma }_{\mathrm{x}}+{\sigma }_{\mathsf{\alpha }}\cos 2\alpha }}\right)$$

(20)

This stress check ensures that the selected concrete strength grade for the joint core area can meet the bearing capacity requirements under its complex stress state.

6.4. Analysis of Construction Sequence and Corresponding Load Stages

The design of this joint follows a clear mechanical logic: first, the member-end internal forces are determined based on the overall structural analysis; subsequently, the key dimensions of each component and part are determined one by one based on the criteria of local force transfer, global equilibrium, and stress state described below; finally, the design intent is realized through a rational construction sequence.

The construction sequence of this arch-foot joint must be specially designed to ensure that all components can work in coordination along the predetermined force-transfer path step by step. The entire process can be divided into five main stages, and the corresponding structural force-bearing states will also undergo critical transitions. The core of the construction process lies in first establishing a prestressed self-balancing system, then installing the main load-bearing arch, and finally applying the service load.

(1)

First Stage

In this stage, component installation and preliminary joint connection are carried out. When construction reaches the floor where the arch foot is located, first lift and position the tension beam. Subsequently, the prefabricated arch-foot joint segment is hoisted into place and connected to the tension beam. The key construction measure involves two steps. First, the multiple web plates of the tie beam are inserted into the preset slots on the arch-foot circular steel pipe. Then, a full-penetration bevel-edge welding process is applied to firmly weld the web plates to the pipe wall, thereby forming a preliminary steel frame. At this stage, concrete has not been poured in the joint area, the overall integrity of the structure has not been formed, and all components are in a stress-free state. Quality control at this stage is critical for the main load-bearing welds. It is imperative that the steel members for the arch footing node section are prefabricated in a factory. Full-penetration groove welds between the tubular arch beam and the tie beam web shall undergo non-destructive testing and receive approval before shipment.

(2)

Second Stage

After the steel structure welding is completed, concrete pouring in the joint area and prestressed cable installation are carried out. The pouring scope includes the cavity of the tension beam, the circular steel pipe concrete, and the entire arch-foot joint core area. It is ensured that the three are continuously poured at one time to form a complete steel-concrete composite structure. When pouring the tension beam concrete, holes for the prestressed cables to pass through need to be pre-embedded. After the concrete reaches the design strength, the prestressed cables are inserted into the pre-embedded holes to prepare for the subsequent tensioning operation. The primary quality control goals here are achieving thorough concrete compaction and measuring the actual cast-in-place strength. The use of self-consolidating concrete in the node area is mandatory.

(3)

Third Stage

In this stage, prestressing is carried out to establish a self-balancing system. The prestressed cables are tensioned, and the design control tension $N_{\mathrm{p}}$ is applied. The tension force is transmitted to the arch-foot joint through the anchor, and then transformed into pressure on the entire lower-chord system. At this time, the pressure is borne by the steel of the web plates extending into the joint area and the concrete in the joint core area. As a result, the concrete in the joint area will produce a horizontal prestress ${\sigma }_{\mathrm{x}}$. At the same time, prestressing will cause elastic compression deformation ${\delta }_{\mathrm{p}}$ of the lower-chord system, and this deformation can be used as an important reference value for construction monitoring. So far, a self-balancing system with initial stress has been initially established, and the lower-chord system is in a compressed state. After the prestressing tension was completed, pressure grouting was carried out on the prestressing ducts to protect the prestressing cables.

(4)

Fourth Stage

In this stage, the arch is installed to form the structure. After the prestressed system is established, the remaining arch components are installed in sections from the arch foot to the arch top, and finally closed at the arch top to form a complete arch structure. At this stage, the self-weight of the arch and the construction loads are carried by the arranged vertical temporary supports. The arch-foot joint does not yet participate in the overall load-bearing mechanism. When closed, the pressure provided by the prestress and the internal force generated by the arch installation reach an initial balance at the arch-foot joint. At this time, the arch structure has the overall stiffness to bear the load, but it has not yet borne other service loads except its own weight.

(5)

Fifth Stage

With the construction of the upper structure, the axial force $N_0$ of the arch gradually increases from zero to the design value. This loading process causes the redistribution of internal forces at the joint. The key turning point is that when the pressure of the lower-chord system is completely offset, the horizontal force of the arch foot is only balanced by the prestressed cable force, that is:

$$N_0\times \mathrm{c}\mathrm{o}\mathrm{s}\alpha =N_{\mathrm{p}}$$

(21)

When the load continues to increase, the lower-chord system will change from a compressed state to a tensile state, and finally balance the thrust of the arch together with the prestressed cable:

$$N_0\times \mathrm{c}\mathrm{o}\mathrm{s}\alpha =N_{\mathrm{p}}+N_{\mathrm{s}}$$

(22)

Throughout the process, the concrete in the joint core area is in a biaxial compressive state composed of the prestress ${\sigma }_{\mathrm{x}}$ and the inclined compressive stress ${\sigma }_{\mathsf{\alpha }}$ caused by the arch axial force, and the material properties can be fully exerted. Regarding stages three through five, the key quality control procedure is the real-time measurement of tie beam deflection and stress–strain readings at critical locations throughout the tensioning and loading process. These measurements are to be compared with theoretical values for verification.

7. Conclusions

(1)

A novel configuration for a concrete-filled steel tube arch-column-tie beam joint is proposed. The joint exhibits a rational design and reliable mechanical performance. Through finite element simulation, it can be observed that the joint remains elastic under the design load for both conditions, including the presence of prestressed high-strength rods and the failure of the rods, meeting the design requirements. The joint reaches its ultimate capacity when extensive yielding occurs in the tie beam along the junction region with the circular arch beam, as well as in the steel tube of the arch beam. At this stage, the steel plates and concrete within the joint zone remain elastic, ensuring reliable load transfer.

(2)

The maximum computed load of the model with prestressed rods is 2.28 times the design load. The absence of prestressed rods leads to a significant expansion of the high-stress zone within the web of the tie beam. At the ultimate state, the maximum equivalent plastic strain increases by 1.93 times, whereas the stress at the stress concentration point on the circular arch beam above the tie beam decreases by 18%. Consequently, the absence of the rods decreases the joint’s stiffness at yielding by 12.4%, but its effect on the maximum bearing capacity is limited, resulting in merely a 2.2% reduction.

(3)

The wall thickness of the circular arch beam steel tube is the key parameter controlling the bearing capacity of this joint. Gradually increasing the wall thickness of the arch beam’s steel tube shifts the failure mode from arch-beam-dominated yielding to tie-beam-dominated yielding along the junction region. Increasing the steel strength grade is more efficient in enhancing the bearing capacity than increasing the concrete strength grade.

(4)

The joint zone should be designed based on three aspects: local stress transfer at the bottom of the arch beam, force equilibrium between the arch beam and the tie beam, and the biaxial compression state of the concrete in the joint zone. The rational construction process lies in first establishing a prestressed self-balancing system, then installing the main load-bearing arch, and finally applying the service load. The stress state of the arch structure should be calculated step by step based on the arch forming process to ensure construction safety and achieve the arch structure’s function.