Abstract
Vortex-induced vibration (VIV) is a common fluid–structure interaction phenomenon in practical engineering with significant research value. Traditional methods to solve VIV issues include experimental studies and numerical simulations. However, experimental studies are costly and time-consuming, while numerical simulations are constrained by low Reynolds numbers and simplified models. Deep learning (DL) can successfully capture VIV patterns and generate accurate predictions by using a large amount of training data. The Physics-Informed Neural Network (PINN), a subfield of DL, introduces physics equations into the loss function to reduce the need for large data. Nevertheless, PINN loss functions often include multiple loss terms, which may interact with each other, causing imbalanced training speeds and a potentially inferior overall performance. To address this issue, this study proposes an Adaptive Weight Physics-Informed Neural Network (AW-PINN) algorithm built upon a gradient normalization method (GradNorm) from multi-task learning. The AW-PINN regulates the weights of each loss term by computing the gradient norms on the network weights, ensuring the norms of the loss terms match predefined target values. This ensures balanced training speeds for each loss term and improves both the prediction precision and robustness of the network model. In this study, a VIV dataset of a cylindrical body with different degrees of freedom is used to compare the performance of the PINN and three PINN optimization algorithms. The findings suggest that, compared to a standard PINN, the AW-PINN lowers the mean squared error (MSE) on the test set by 50%, significantly improving the prediction accuracy. The AW-PINN also demonstrates an enhanced stability across different datasets, confirming its robustness and reliability for VIV modeling. Compared with existing methods in the literature, the AW-PINN achieves a comparable lift prediction accuracy using merely 1% of the training data, while simultaneously improving the prediction accuracy of the peak lift.
1. Introduction
Vortex-induced vibration (VIV) is a common phenomenon in various engineering structures, including the cables of long-span bridges [1,2,3], wind turbine towers [4,5], and risers of offshore platforms [6,7]. When a bluff body is placed in a flowing fluid, alternating vortex shedding occurs downstream of the bluff body. This vortex shedding causes periodic variations in the lift and drag forces acting on the body, and thereby induces vibrations in the structure. The interaction between the fluid and the structure is referred to as VIV [8]. When the vortex-shedding frequency approaches the structure’s natural frequency, the vibration amplitude may increase dramatically. This may cause fatigue failure, threaten structural integrity, and reduce the structure’s service life [9].
Researchers have studied VIV using various methods, including experimental research [10,11], semi-empirical models [12,13], and numerical simulations [14,15]. Experimental studies enable the observation of phenomena through physical models and the collection of data. However, this approach is costly and time-consuming due to the requirement for model fabrication. Based on experimental data and theoretical studies, researchers have developed many semi-empirical models to predict the characteristics of VIV. Representative models include the wake oscillator model [16,17], the single-degree-of-freedom model [18,19], and the force decomposition model [20,21]. With advancements in computational technology, numerical simulations have become a crucial tool for VIV research. Common methods include Direct Numerical Simulation (DNS) [22,23], Large Eddy Simulation [24,25], as well as Reynolds-Averaged Navier–Stokes (RANS) models [26,27,28]. Numerical simulations offer a cost-effective means to address most VIV problems and can precisely predict both the flow field and structural motion. Nevertheless, numerical simulations require substantial computational resources, particularly for high Reynolds number turbulent flows and complex geometries [29]. Therefore, the accurate and efficient solution of VIV problems remains a highly demanding task.
Deep learning (DL), as one of the core research areas in AI, is widely applied across various industries [30]. Compared to traditional machine learning, deep learning offers superior data processing capabilities. As the volume of data increases, the performance of deep learning models improves substantially, whereas traditional models plateau after a threshold and show no further gains [31]. Deep learning is particularly effective at nonlinear fitting, enabling adjustments to network architectures by combining linear and nonlinear modules. In theory, it can map any function and solve complex problems in high-dimensional data [32]. In fluid dynamics, the application of deep learning has grown, offering approximate solutions to a range of fluid dynamics problems [33]. Jin et al. [34] proposed a data-driven model integrating a Convolutional Neural Network (CNN) that uses pressure data around a cylinder at different Reynolds numbers to predict the velocity field. Sekar et al. [35] built a data-driven method combining the CNN and Multi-Layer Perceptron (MLP) for rapid flow field prediction. Kim et al. [36] utilized existing experimental data and deep neural networks to model the VIVs of a cylinder, significantly reducing the need for experimental data. However, data-driven models require large amounts of training data to ensure predictive accuracy and perform poorly with noisy data [37]. Moreover, these models lack interpretability and convergence guarantees due to ignoring prior knowledge [38].
To enhance the interpretability and robustness of data-driven models and reduce their reliance on large datasets, Raissi et al. [38] introduced prior knowledge into the DL framework, proposing the Physics-Informed Neural Network (PINN) to solve problems about partial differential equations. By incorporating a physical information loss term into the loss function, the PINN remarkably improves model performance in data-scarce scenarios. This approach enables the PINN to capture and simulate physical phenomena with fewer training data. Raissi et al. [39] incorporated the incompressible Navier–Stokes equations as physical constraints in the PINN. They utilized the spatiotemporal data of the velocity field and structural motion to reconstruct the fluid’s velocity and pressure fields, as well as to infer the lift and drag forces acting on the structures. Cheng et al. [40] integrated the RANS equations (with additional viscosity parameters) into the loss function. This addressed VIV and wake-induced vibrations across turbulent flow velocities. Tang et al. [41] proposed a transfer learning-physics informed neural network(TL-PINN) to study the VIVs of cylinders, leveraging transfer learning to reduce the PINN’s dependence on large datasets and thus lower training costs. Zhu et al. [42] applied the PINN to learn VIV response data under varying stiffness conditions, enabling the prediction of VIV responses and the inference of structural stiffness. The PINN loss function combines data loss and various physical information losses with fixed weights. This approach enables the PINN to simultaneously learn from data while embedding physical laws, improving both its predictive capability and generalization. However, the gradients of the various loss terms in the PINN loss function can vary significantly during backpropagation. This gradient imbalance leads to an uneven optimization of the multi-component loss function. Wang et al. [43] identified this issue and explored potential solutions.
To improve the performance and robustness of the PINN in solving complicated problems, many researchers have proposed different optimization algorithms. Xiang et al. [44] introduced an optimization algorithm for the PINN that automatically updates the weights during training. This method constructs a Gaussian probabilistic model, defines the loss function based on a maximum likelihood estimation, and validates its effectiveness and robustness by solving classical partial differential problems. Chen et al. [45] investigated the impact of various weightings on the PINN’s solution of the Richards–Richardson equation (RRE) and proposed a principled loss function-based method. The method automatically adjusts the loss function weights without needing any hyperparameters, thus lowering the PINN’s reliance on the initial weight settings. Tarbiyati et al. [46] trained and determined the initial weights of the PINN by solving partial differential equations with finite difference methods and used the equation solutions to enhance the performance. In the application of PINNs to solve the Navier–Stokes equations, researchers have also proposed optimization algorithms. Li et al. [47] proposed a dynamic weighting strategy inspired by minmax algorithms. It addresses forward and inverse Navier–Stokes problems. This strategy identifies the difficulty level of the training data and adjusts the weights of more difficult data to accelerate the training process, balancing the contributions of various data loss terms to the network. Hou et al. [48] proposed an adaptive loss balance PINN (LB-PINN) to reconstruct the propeller wake flow field. Through introducing adaptive weights, this method balances the different losses in the network, elevating the flow field reconstruction accuracy. Shi et al. [49] framed the PINN as a multi-task learning problem and introduced a method that automatically adjusts loss weights, balancing the training speed of different loss components and stabilizing the network’s training process.
In this study, we propose an Adaptive Weight Physics-Informed Neural Network (AW-PINN) incorporating the principles of multi-task learning. The AW-PINN enhances neural network training by integrating gradient normalization (GradNorm) to enhance the model’s capacity to predict complex phenomena in fluid dynamics. In the AW-PINN, we use the gradient norm of the weighted loss with respect to the hidden layer weights of the network as the indicator for the training speed. The average of the gradient norm of all the weighted loss serves as a common scale. The AW-PINN adjusts the weights of different loss components to control their training speeds and contributions to the overall training. When the gradient norm of a loss term’s weight exceeds the target gradient norm, the network reduces the weight of that specific loss term to slow down its training speed. The adjustment ensures that all loss terms are trained at comparable rates. We apply the PINN, AW-PINN, and other optimization algorithms to different VIV datasets. Through comparisons of the test errors across multiple datasets, we demonstrate that the AW-PINN outperforms the other algorithms in performance and exhibits a superior stability compared to other PINN optimization methods. The remainder of this research is organized as follows: Section 2 provides a detailed description of the cylinder VIV problem, along with the principles behind the PINN, GradNorm, and AW-PINN; Section 3 presents the training of various network models using datasets generated from numerical simulations and verifies the stability of these models using additional datasets; and Section 4 concludes this study.
2. Problem and Model
2.1. Research Problem
This study focuses on cylindrical structures, which are widely used in engineering, and investigates the application of the AW-PINN to solve the problem of VIV in cylinders. As illustrated in Figure 1, this study considers a two-dimensional elastically supported cylindrical structure and analyzes the two-dimensional VIV problem. The cylinder is simplified as a mass–spring–damping system that can move freely in both the streamwise direction (x-direction) and the transverse direction (y-direction).
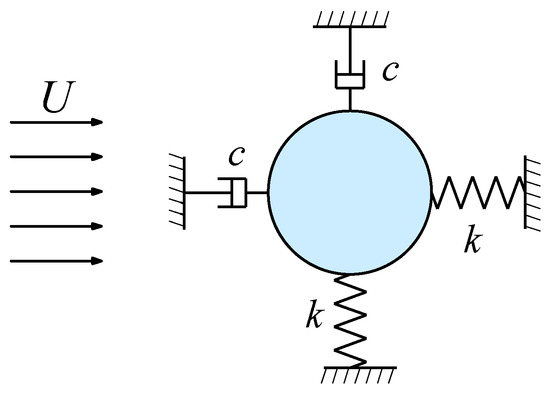
Figure 1.
Physical model of two-degree-of-freedom (2-DOF) vortex-induced vibration.
In the rectangular coordinate system, the origin is set at the center of the cylinder, and a moving reference frame that moves with the cylinder is defined. The continuity equation for incompressible fluid and the momentum conservation equation (Navier–Stokes equations) [50] in the moving reference system are given by
where u and v represent the streamwise and transverse velocities of the flow field; p is the pressure in the flow field; and and are the streamwise and transverse displacements of the cylinder. Re represents the Reynolds number, a dimensionless parameter that characterizes the fluid flow behavior.
The structural dynamics governing equation for the motion of the cylinder is given by
where FD and FL denote the drag and lift forces acting on the cylinder; m signifies the mass of the cylinder; c and k denote the damping and stiffness of the cylinder.
After reconstructing the velocity and pressure fields, the lift and drag forces acting on the cylinder can be inferred from the velocity gradients and the pressure field, as expressed in the following equation:
where nx and ny are the outward normal components of the cylinder’s surface; ds is the arc length of the cylinder’s surface.
2.2. Physics-Informed Neural Network (PINN)
A PINN is essentially a deep neural network (DNN) augmented with prior physical knowledge, enabling it to accurately approximate any continuous function. During the training of the PINN, the residuals of partial differential equations (PDEs) at specified points in the computational domain, along with initial and boundary conditions, are incorporated into the loss function. This ensures that the predicted results align with the prior knowledge embedded in physical laws. The training of a PINN combines data-driven learning with physical constraints, improving the model accuracy and reliability. Compared to traditional DNNs, PINNs reduce the dependence on the training dataset, enhance the network interpretability, and improve the generalization performance. Leveraging the widely used automatic differentiation technique in DNNs, PINNs can accurately compute the derivatives of network outputs with respect to input variables. This capability enables precise PDE residual calculations for physical constraints.
The objective of this research is to reconstruct the flow field of two-dimensional VIVs and predict the displacement of a cylindrical structure in the absence of flow field pressure data. The prior physical knowledge of the PINN consists of the continuity equation and the momentum conservation equation (Navier–Stokes equations) for incompressible fluids, as shown in Equations (8), (9), and (10). Here, , , and represent the residuals of the three physical equations, as detailed below.
where x and y are spatial variables and t is the time variable. The spatial and temporal derivatives of the velocity and pressure fields are nonlinear differential terms, which are evaluated using automatic differentiation in the neural network.
Figure 2 illustrates the architecture of the PINN employed for a two-dimensional VIV of a cylindrical body. The physical constraints of the continuity equation and the Navier–Stokes equations are incorporated into a fully connected network. The network inputs include the spatial coordinates (x, y) and time t of the fluid elements in the flow field. The network outputs consist of the streamwise velocity , transverse velocity , and pressure of the fluid elements. Additionally, the streamwise displacement and transverse displacement of the cylinder are also predicted. The loss function consists of two components: the data loss and the equation loss. The data loss is the error between the predicted values of the neural network and the dataset, which includes four components: downstream velocity u, lateral velocity v, downstream displacement , and lateral displacement . Network outputs and partial derivatives are substituted into the governing equations to compute PDE residuals , , and . The PINN loss function is as follows:
where N is the number of training data points in the dataset; M is the number of configuration points for the equation losses. represents the data loss, and represents the equation losses for the three physical equations.
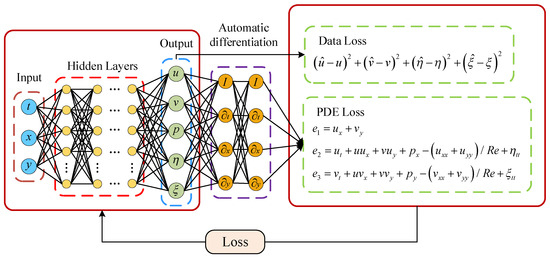
Figure 2.
Network architecture of PINN for solving vortex-induced vibration problems.
2.3. GradNorm Algorithm
The loss function of the PINN encompasses both the data loss and the residual losses of different physical equations. Significant variations in the backpropagation gradients of different losses can cause the model to overemphasize certain losses and overlook others. This can lead to a slow convergence and poor prediction accuracy. To improve the model’s learning capacity, we need to properly weight these different losses. Therefore, it is essential to balance the gradients of each component to ensure consistent and stable training. As a result, the multi-task learning algorithms from the computer vision can be utilized during the training of the PINN to improve the training stability and convergence of the network.
In multi-task learning, simply summing the losses of varying tasks to form the total loss does not account for the varying contributions of each task’s backpropagation gradients to the network model. When there are significant discrepancies between the gradients of different tasks, tasks with smaller gradients may not receive sufficient learning, preventing a balance in the losses across tasks. Introducing fixed weights in the loss function can help balance these gradient differences, but assigning small weights to high-gradient tasks will unnecessarily limit the learning of tasks, which ultimately impedes the effective learning of tasks with larger gradients. To solve this issue in multi-task learning optimization, regarding the task weights as trainable parameters enables the model to automatically adjust the weights during training in response to variations in task gradients, ensuring a more balanced learning process for all tasks.
In this study, we propose a PINN with adaptive weights for solving the vortex-induced vibration problem, building on the GradNorm algorithm for multi-task optimization in computer vision [51]. The GradNorm algorithm adjusts the weight of each task dynamically in the process of training. This adjustment balances the contributions of different loss components in the total loss function, enabling uniform learning across tasks. In particular, the GradNorm algorithm compares the actual gradient norm of a task with the target gradient norm of each task and accordingly scales the task weights. When the actual gradient norm of a task exceeds the target gradient norm, the algorithm reduces the weight of that task, allowing tasks with larger actual gradients to receive smaller weights, while tasks with smaller gradients are assigned larger weights. This approach allows the model to balance the gradient norm across all tasks, so that all tasks learn at a similar rate. The implementation of the GradNorm algorithm’s loss function is as follows.
In the algorithm, the multi-task loss function is a linear function of the single-task losses, and the loss function is as follows:
where N is the number of tasks, and w and Li are the single-task weights and losses.
The gradient norm of the weighted loss for a single task and the average gradient norm across all tasks are defined as follows:
where represents the gradient norm of the weighted loss with respect to the network weights , a subset of the full network parameters. To save computational resources, only the weights of the last shared layer are considered when computing the gradients. denotes the average gradient norm of all tasks at iteration t and is used as a unified scale for gradient magnitudes.
The target gradient norm of each task at iteration t is calculated as follows:
where and denote the current and initial losses of task I, respectively, and is the corresponding loss ratio. represents the relative inverse training rate of task i, which is used to balance the gradients. A larger indicates a slower training rate for the task, so a larger weighted gradient is allocated to accelerate its learning. α is a hyperparameter that regulates how strongly the training rates are balanced. A larger α imposes a stronger constraint on balancing the training speeds.
The gradient loss function of GradNorm is defined as the difference between the actual gradient norm and the target gradient norm across all tasks, as shown in the following formula:
The weight updates are computed using the following rules:
where k represents the learning rate for the weight updates, and T is the number of tasks. When the gradient norm of a particular task is significantly higher than the target gradient norm, the algorithm reduces its weight , promoting balance across tasks. Conversely, if the gradient norm is lower than target gradient norm, the weight is increased to accelerate convergence.
2.4. Adaptive Weight Physics-Informed Neural Network (AW-PINN)
Building on the work presented in this study, we introduce an improved version of the GradNorm algorithm, which is applied as a multi-loss training method for the PINN. The proposed model, the AW-PINN, automatically adjusts the weights of each task during training, ensuring that the learning rates are balanced across tasks without favoring any single one. By adopting this approach, we enhance the overall capability of the model to learn effectively. The implementation of the AW-PINN is outlined as follows.
After the initialization, the task losses of a PINN show considerable uncertainty. Directly employing the initial task losses as for computing the relative inverse training rates may prevent the algorithm from accurately determining these rates. This leads to an unstable predictive accuracy in the AW-PINN. To address this, we perform pretraining with equal weights before applying the GradNorm algorithm, which stabilizes the network initialization. Employing task losses after pretraining, represented as , effectively reduces the uncertainty caused by initialization. Moreover, appropriate pretraining can improve the model’s learning ability and predictive performance.
In the GradNorm algorithm, the task weights are updated by computing and then employing backpropagation to update the weight of task i. This weight update approach does not impose any constraints on the sign of the weights. Therefore, the AW-PINN’s unconstrained weights can turn negative, potentially leading to unstable gradients and disrupting the training process. To ensure that the task weights remain non-negative throughout training, we define the weights as an exponential function, as follows:
where is set as a learnable parameter in the network and updated in each iteration. The loss weights are defined as exponential functions of , ensuring that all weights remain non-negative.
The update rule for is given as follows:
where the computation of follows the same formulation as in the GradNorm algorithm. After updating the value of for task i, the task weight for the next iteration can be obtained accordingly. The total sum of the loss weights is normalized to the number of tasks using Equation (27). This weight update method can balance the contribution of losses and avoid training instability. The AW-PINN algorithm is summarized in Algorithm 1.
| Algorithm 1. Adaptive weight optimization algorithm for PINN (AW-PINN) |
| Step 1: Initialization Initialize network weights and biases. Initialize task weights . Select the value of α and designate the shared layer (the last hidden layer). Step 2: Pretraining with Equal Weights For iteration from the first to the n-th iteration: Calculate . Train the network with equal weights. Step 3: Training with Adaptive Weighting Method At the n-th iteration, proceed as follows: Compute the total loss . Compute , , and . Compute and . Update and . Update using . Renormalize , and set . End. |
Figure 3 shows the AW-PINN’s network architecture. After completing the PINN training, the data loss and equation loss are obtained. The hidden layers of the network serve as shared layers, with the last hidden layer selected to compute the gradient norm loss. This loss is then used to update the task weights for the subsequent iteration. The loss function of the AW-PINN is as follows:
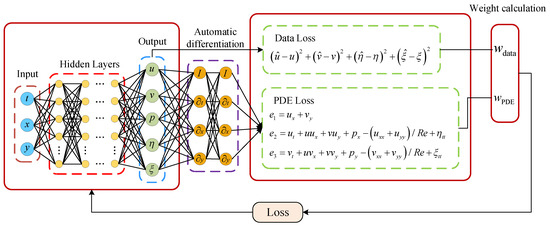
Figure 3.
Network architecture of AW-PINN for solving vortex-induced vibration problem.
3. Results and Discussion
3.1. Obtaining the Training Dataset
To obtain a high-resolution dataset, we perform a 2-DOF cylinder VIV simulation. The simulated data are then selected as the training data for the neural network. As illustrated in Figure 4, the computational domain of the model is a rectangular region with a length of 40D and a width of 20D, where D is the diameter of the cylinder. The initial position of the cylinder’s center is at the origin of the coordinate system. The inlet boundary condition is a velocity inlet, located 10D from the cylinder’s center. The outlet boundary condition is a pressure outlet, positioned 30D from the cylinder’s center. The upper and lower side walls are treated as slip walls, each situated 10D from the cylinder’s center. The flow parameters are as follows: a Reynolds number (Re) of 150, fluid density (ρ) of 1.5 kg/m3, and inlet velocity (U) of 1 m/s.
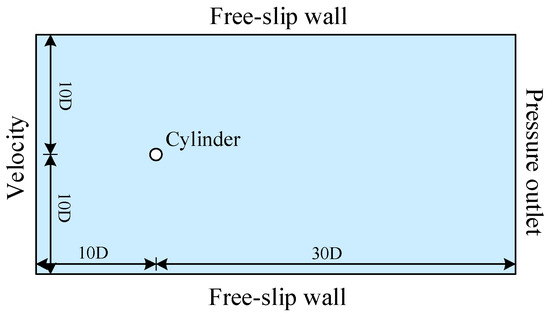
Figure 4.
Computational domain and boundary conditions of flow field.
The flow field varies with changes in the cylinder’s boundary. To simulate the motion of the cylinder boundary within the flow field, a nested grid technique [52] is employed. Based on fluid simulation software and structural dynamics principles, we construct a 2-DOF VIV numerical model using User-Defined Functions (UDFs) and nested grids. The nested grid system is divided into a foreground grid that encloses the cylinder and a background grid that spans the surrounding flow field. Subsequently, the overlapping regions between the foreground grid boundary and the background grid are removed and interpolated. The foreground and background grids are then integrated into a coupled grid system, as depicted in Figure 5.

Figure 5.
Meshing for computational domains.
As presented in Table 1, to validate the reliability of the simulation results, we compare the simulation data with the findings from Bao et al. [53]. Key parameters include the transverse displacement , the downstream displacement , the root mean square value of the lift coefficient , and the average value of the drag coefficient . The errors between the two sets of results are minimal, confirming that the simulation results are suitable for use as the neural network dataset. Table 1 uses a reduced velocity of , where U is the fluid velocity and f is the natural frequency of the structure. The displacements in the x- and y-directions from the simulation results exhibit periodic variations, with the amplitude stabilizing after the fluctuations. Consequently, the simulation results are considered appropriate for training the neural network. For the 15-s simulation data, we select 150 snapshots of the flow field, with a time interval of 0.1 s between consecutive snapshots. We extract flow field data within the coordinate range x ∈ [−2D, 8D] and y ∈ [−4D, 4D]. Based on the extracted data, 40,000 random samples are selected to form the training dataset.

Table 1.
Comparison of numerical simulation results with other studies.
3.2. Reconstructing the Flow Field Using Velocity Data
In the VIV problem of the cylinder, four types of PINN models were selected for comparative analysis, as detailed in Table 2. These four models share the same network architecture and learning rate to compare their performance and stability. The baseline PINN model employs equal weighting in its loss function during training. The LB-PINN constructs a Gaussian probabilistic model by treating the weight coefficients of each loss term as learnable uncertainty parameters. These weights are dynamically updated via a maximum likelihood estimation to balance the influence of different loss components during optimization. The GNPINN utilizes the backpropagated gradients of each loss term to assess their respective training speeds and adjusts the loss weights through a dedicated weighting loss function. This approach reduces the sample weights for fast-learning tasks while increasing those for slower-learning tasks, thereby promoting balanced training across tasks. The AW-PINN introduces improvements based on the GradNorm algorithm for multi-task learning, incorporating a pretraining phase and a negative weight constraint mechanism to enhance the stability of the optimization process. The four network models were implemented in Python using the PyTorch deep learning framework. The compilation environment was Python 3.8.17 and PyTorch 2.0.1.

Table 2.
Description of different models.
The network architecture employed in the present study is built upon the design proposed by Cheng et al. [40]. The PINN consists of a 14-layer neural network, encompassing an input layer, an output layer, and 12 hidden layers, with each hidden layer containing 64 neurons. The network weights are initialized via Xavier initialization, while the biases are initialized to 0. The activation function chosen is the sine function to introduce nonlinearity.
The fixed weights for the PINN model are set to , while the initial weights for the LB-PINN, GNPINN, and AW-PINN are also initialized to . All models are trained for 600 epochs, with 100 iterations per epoch. The initial learning rate of the network model is 0.002. For the first 200 epochs, the learning rate remains 0.002, after which it decays to 0.1 times the previous value every 200 epochs.
Figure 6 illustrates the evolution of the data loss weights and equation loss weights during the training process. In the early stages of training, the equation loss weight in the LB-PINN increases rapidly, becoming significantly larger than the data loss weight. This asymmetric weight allocation causes the optimization process to be heavily biased toward the physical constraints, rendering the data-driven component ineffective and ultimately leading to training failure. Similarly, due to the absence of a pretraining mechanism for parameter initialization, the GNPINN exhibits comparable abnormal behavior under gradient competition. The data loss weight gradually decreases to near zero after approximately 2500 iterations, while the equation loss weight dominates. In contrast, the AW-PINN effectively mitigates this issue through a two-phase optimization strategy. This model first employs an equal-weight strategy during the pretraining phase to establish stable baseline loss values through preliminary network parameter training, then implements a dynamic weight adjustment via the GradNorm algorithm in the formal training phase. Following pretraining, the data loss weight rapidly escalates to approximately 1.8, gradually converging around 1.5 after 2500 iterations, while the equation loss weight stabilizes near 0.5. Figure 7 depicts the changes in the training loss and test error for the four models during the training process. Throughout training, the PINN and AW-PINN effectively reduce the training loss, demonstrating robust performances, with final training losses of 7.8 × 10−3 and 9.7 × 10−3, respectively. On the test set, the AW-PINN achieves a 29% reduction in the test error compared to the PINN. However, both models exhibit signs of overfitting in the final 200 epochs, with the test error increasing abruptly upon the learning rate adjustment. The LB-PINN struggles to effectively train and minimize the loss function. The GNPINN performs poorly, with a training loss of 1.8 × 10−2 and a test error twice that of the PINN. Figure 8 illustrates the convergence behavior of the test errors in the later stages of training for different models. Under the combined influence of data-driven supervision and physical constraints, the total prediction errors for supervised network outputs (streamwise flow velocity u, crossflow flow velocity v and cylinder displacement n) exhibit a sustained downward trend. In contrast, the prediction error of the unsupervised flow pressure (p) experiences a sudden increase around the 400th epoch. This divergent convergence behavior suggests that the physical constraints on the flow pressure gradually weaken during the middle-to-late stages of training, leading to an increased prediction error for the flow pressure.
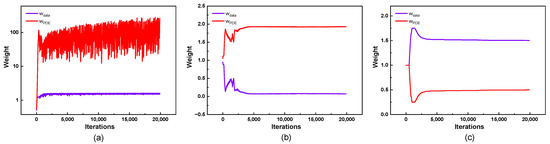
Figure 6.
Adaptive weight changes in 2-DOF cylinder: (a) LB-PINN; (b) GNPINN; and (c) AW-PINN.
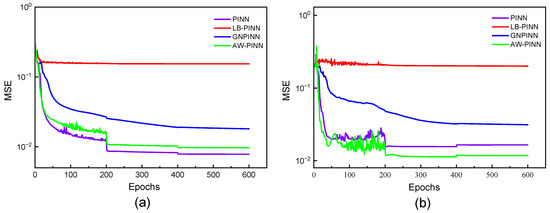
Figure 7.
Mean square error of four models in 2-DOF cylinder: (a) training loss curves (including data loss and equation loss) and (b) test error curves (error for all output variables).
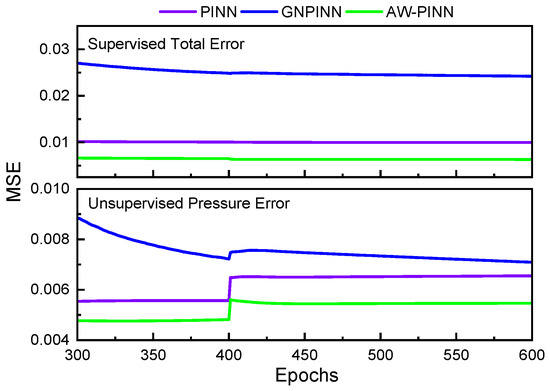
Figure 8.
Comparison of late-stage training errors across models in 2-DOF cylinder.
Figure 9, Figure 10, Figure 11 and Figure 12 present the velocity and pressure fields predicted by the four network models, along with the errors between the numerical simulations and the model predictions. The LB-PINN fails to accurately predict the flow field velocity and pressure, resulting in significant prediction errors. The GNPINN provides relatively accurate predictions but still exhibits considerable errors. The PINN and AW-PINN effectively infer the velocity and pressure fields across the entire flow field with reasonable accuracy. Compared to other models, the AW-PINN achieves the highest prediction accuracy among all models. Table 3 lists the mean squared errors (MSEs) for the various predictions of the four models on the validation set. The PINN and AW-PINN achieve velocity field prediction accuracies to the order of 10−3, while the LB-PINN and GNPINN converge only to the order of 10−2, with the LB-PINN’s downstream velocity MSE reaching 0.105. For the pressure field, the PINN, AW-PINN, and GNPINN achieve prediction accuracies to the order of 10−3, whereas the LB-PINN converges to 4.23 × 10−2. All four models provide reasonably accurate predictions for the displacement of the cylindrical structure, with accuracies approximating 10−4. Figure 13 shows the predicted and simulated displacement values of the cylindrical structure. Compared to the simulation values, the GNPINN’s predicted peak displacement is approximately 7% higher, while the other three models exhibit a relatively accurate prediction.
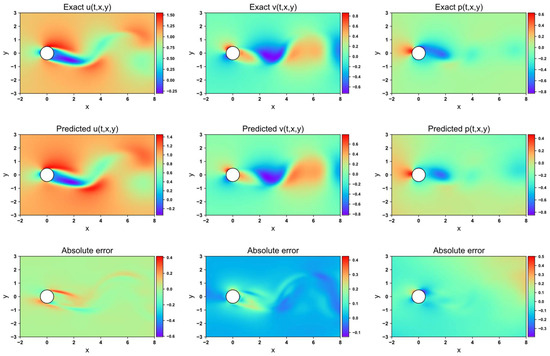
Figure 9.
Flow field prediction for PINN in 2-DOF cylinder.
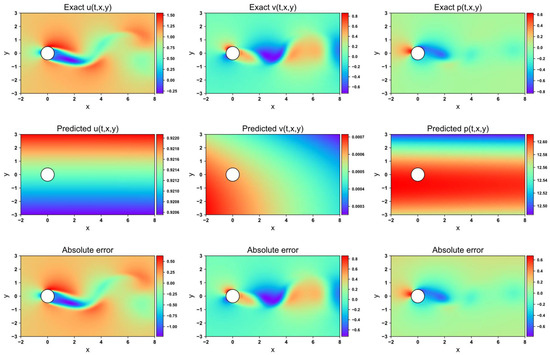
Figure 10.
Flow field prediction for LB-PINN in 2-DOF cylinder.
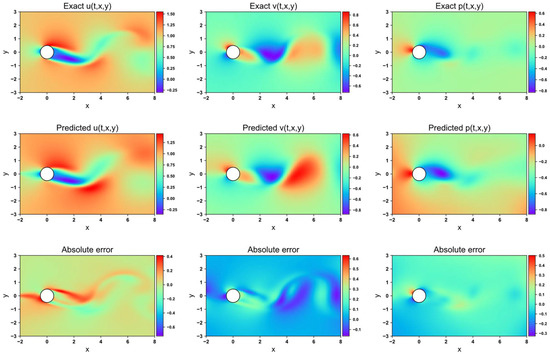
Figure 11.
Flow field prediction for GNPINN in 2-DOF cylinder.
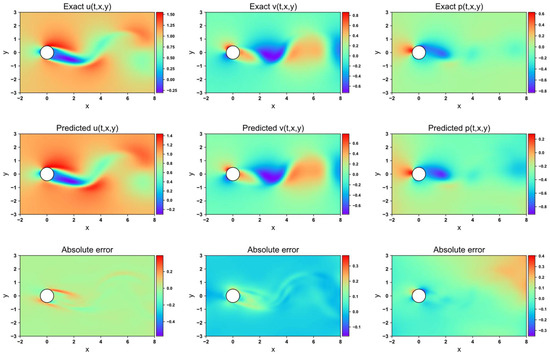
Figure 12.
Flow field prediction for AW-PINN in 2-DOF cylinder.

Table 3.
Mean squared errors of predictions by different models.
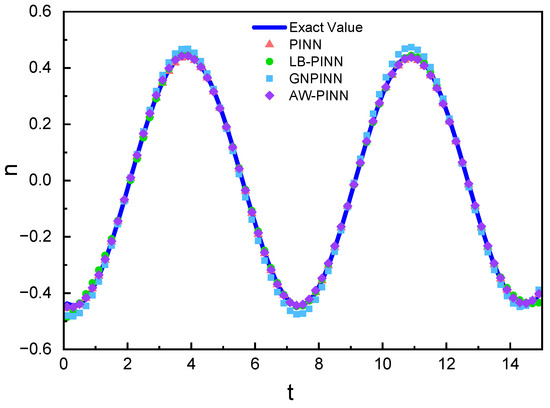
Figure 13.
Transverse structural displacement prediction in 2-DOF cylinder.
3.3. Stability Verification of AW-PINN
To assess the stability of the optimization algorithm, we train the four models using the dataset from Raissi et al. [39]. This dataset consists of simulated data for a single-degree-of-freedom (1-DOF) cylinder undergoing VIV, analyzed via Direct Numerical Simulation (DNS). The dataset consists of 280 flow field time steps after vibration stabilization. Each step has a 0.05 s interval, totaling 14 s of simulation.
Figure 14 presents the variations in the data loss weight and equation loss weight throughout the training process. Before 5000 iterations, the LB-PINN tends to prioritize the equation loss in training. Beyond this threshold, the data loss weight gradually outweighs the equation loss weight. Both the GNPINN and AW-PINN focus primarily on minimizing the data loss, though during the first 1500 iterations, the GNPINN tends to assign higher weights to the equation loss during training. Figure 15 illustrates the loss function curves and test set error curves for the four models during the training process. In terms of the training loss convergence performance, all four models exhibit similar trends, effectively reducing the loss values to the order of 10−4. Among the four network models, the PINN exhibits the highest test error, while the GNPINN and AW-PINN show comparable prediction errors, both lower than those of the other two models. Figure 16 shows the convergence of the test set errors for different models in the later stages of training. Under the combined influence of data-driven components and physical constraints, the total output error with labeled data (u, v, n) and the pressure error with unlabeled data for the four models show a downward trend. However, the PINN, GNPINN, and AW-PINN exhibit a similar phenomenon of two-degree-of-freedom vortex-induced vibration, while the prediction error of the flow field pressure suddenly increases at the 400th epoch.
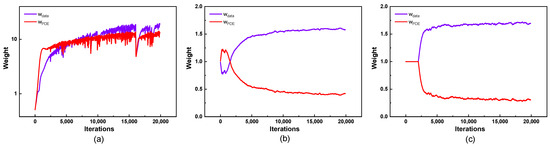
Figure 14.
Adaptive weight changes in 1-DOF cylinder: (a) LB-PINN; (b) GNPINN; and (c) AW-PINN.
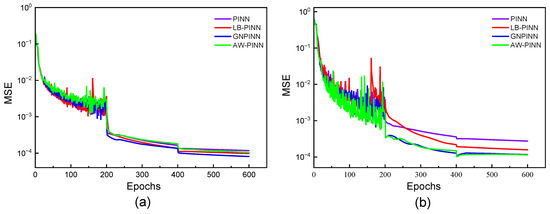
Figure 15.
Mean square error of four models in 1-DOF cylinder: (a) training loss curves (including data loss and equation loss) and (b) test error curves (error for all output variables).
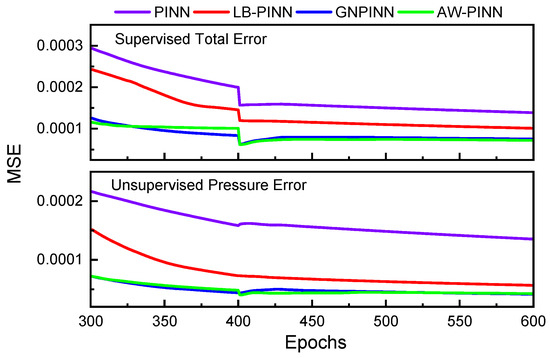
Figure 16.
Comparison of late-stage training errors across models in 1-DOF cylinder.
Figure 17, Figure 18, Figure 19 and Figure 20 depict the velocity and pressure fields predicted by the four network models, along with the errors between the numerical simulations and model predictions, using the 1-DOF dataset. In the velocity field prediction, the PINN exhibits the largest absolute error among the models, while the other three optimization algorithms demonstrate a superior prediction performance. All models accurately predict the flow field pressure. Table 4 lists the mean squared errors for the four models on the validation set. The MSE for both the velocity field and structural displacement predictions across all models reaches the order of 10−5. Three of the optimization algorithms achieve an MSE for the flow field pressure in the order of 10−5, while PINN has an MSE of 1.35 × 10−4.
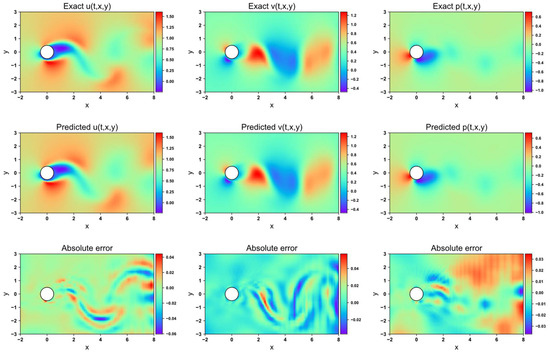
Figure 17.
Flow field prediction for PINN in 1-DOF cylinder.
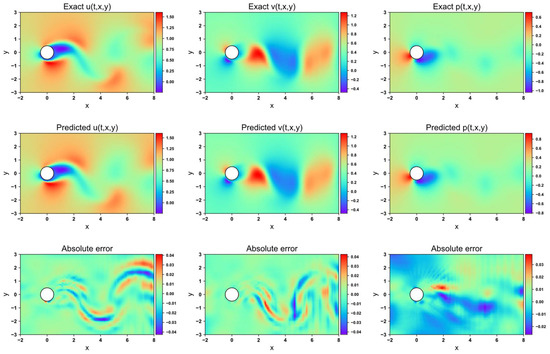
Figure 18.
Flow field prediction for LB-PINN in 1-DOF cylinder.
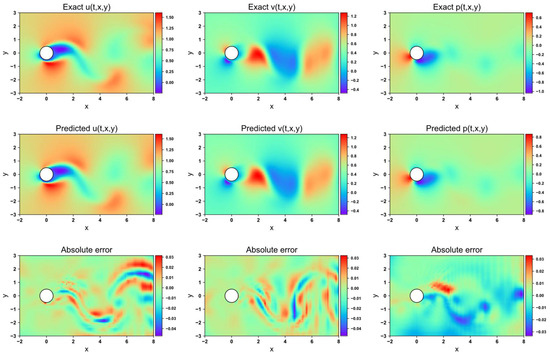
Figure 19.
Flow field prediction for GNPINN in 1-DOF cylinder.
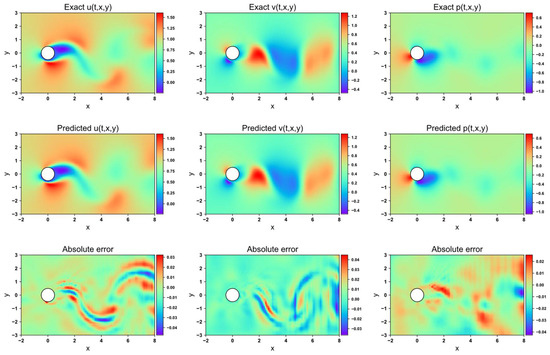
Figure 20.
Flow field prediction for AW-PINN in 1-DOF cylinder.

Table 4.
Mean squared error using validation dataset.
Figure 21 shows the structural displacement predictions and simulation values for the four models. All models accurately predict the cylindrical structure’s displacement. Figure 22 compares the lift and drag inferred from the pressure field by the four models with the simulation results. In the drag prediction, all four models exhibit a high accuracy, with the peak error not exceeding 4%. Among these models, the AW-PINN achieves the highest accuracy, with a peak error of only 1.4%. In the lift prediction, the PINN and LB-PINN exhibit larger prediction errors, with the predicted lift deviating significantly at peak values, with maximum errors of 40.0% and 39.2%, respectively. The GNPINN has a maximum peak prediction error of 22.7%, while the AW-PINN demonstrates a superior accuracy compared to other models, with a maximum error of 8.2%. The network models in this study embed physical constraints into deep neural networks, regressing the training data while enforcing the corresponding partial differential equations. Due to the lack of training data at and , the prediction accuracy for the start and end times in lift and drag predictions is relatively low, particularly for lift. Figure 23 presents a comparison of the lift predictions between this study and the existing literature. The AW-PINN achieves a comparable lift prediction accuracy using only 1% of the data amount used in reference [39], and the predicted lift magnitude is more accurate.
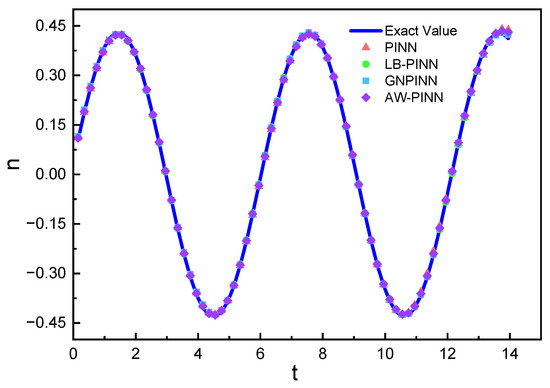
Figure 21.
Transverse structural displacement prediction in 1-DOF cylinder.
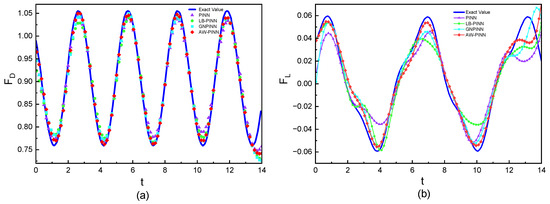
Figure 22.
Force prediction of cylinder: (a) drag of cylinder and (b) lift of cylinder.
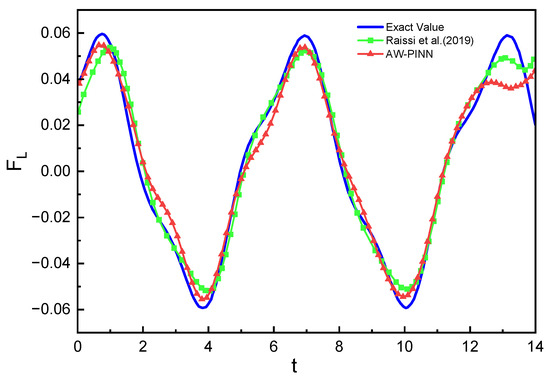
Figure 23.
Comparison with existing literature on lift prediction [39].
4. Conclusions
This study presents an Adaptive Weight Physics-Informed Neural Network (AW-PINN). It is designed to enhance the overall performance of the network model by adjusting the training speed of different loss terms, thereby balancing the model’s learning process. The model optimizes the training speed of various loss terms by automatically adjusting the weight values. This study applies four models to different datasets and compares their results with numerical simulation data, leading to the following conclusions:
(1) The PINN model can utilize a limited amount of velocity data as the training set to accurately reconstruct the velocity and pressure fields of the VIV problem. Due to the absence of pressure data and the characteristics of the Navier–Stokes equations, the pressure field reconstructed by the PINN exhibits a constant difference in the mean pressure. However, it is capable of accurately predicting the distribution trend of the pressure. Additionally, the mean squared errors of the reconstructed velocity and pressure fields by the PINN both converge to the order of 10−3.
(2) When addressing the single-degree-of-freedom vortex-induced vibration problem, both the LB-PINN and GNPINN demonstrate strong performances. The GNPINN achieves a mean squared error that is half of the PINN model in predicting the flow field velocity and structural displacement. Moreover, it reduces the flow field pressure prediction error to one-third, significantly improving the model performance. Although the LB-PINN also enhances the model performance, the improvement in the flow field velocity prediction accuracy is limited. However, in the case of the two-degree-of-freedom VIV problem, both models tend to prioritize the equation loss during training. This leads to larger prediction errors compared to the PINN, and they fail to effectively address the two-degree-of-freedom VIV problem.
(3) Among all the models, the AW-PINN exhibits the best performance in the single-degree-of-freedom VIV problem, significantly improving the prediction accuracy. Compared to the other two optimization models, the AW-PINN shows better stability in the two-degree-of-freedom VIV problem. It improves the prediction accuracy of the flow field velocity, structural displacement, and flow field pressure.
In vortex-induced vibration (VIV) problems, the PINN can reconstruct the entire flow field’s velocity and pressure distributions, as well as the structural vibration displacements, using only minimal data through the incorporation of the governing equations of the VIV system. Although the AW-PINN demonstrates superior performance compared to the original PINN, several issues remain to be addressed. For instance, the AW-PINN is generally unable to train without any labeled data. While the AW-PINN requires less labeled data than the PINN, it still relies on some labeled data to assist the training process. Additionally, the AW-PINN employs a shared equation loss weight for different governing physical equations. In practical applications, the network often needs to balance a more diverse range of loss components. Therefore, further studies are needed to evaluate the model’s performance and stability when balancing multiple loss terms, as well as to improve the AW-PINN’s convergence speed. In the later stages of training, the model exhibits signs of overfitting. To address this issue, future work will explore the interaction mechanisms between data-driven components and physical constraints and employ techniques such as residual-based adaptive sampling and transfer learning to alleviate overfitting. The AW-PINN has shown promising results in vortex-induced vibration problems. In future research, we plan to explore its applications in three-dimensional incompressible flows, compressible flows, and biomedical flow problems to further validate and enhance the model’s capabilities.
Author Contributions
Writing—review and editing, Validation, Supervision, Methodology, Investigation, Funding acquisition, Formal analysis, P.Z.; Writing—original draft, Visualization, Investigation, Formal analysis, Data curation, Conceptualization, Z.L.; Software, Data curation, Formal analysis, Z.X.; Investigation, Formal analysis, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was made possible with the support of the Natural Science Foundation of Chongqing, China (CSTB2024NSCQ-MSX1206). The authors would like to express their gratitude for the financial support.
Data Availability Statement
Data will be made available on request. The PINN model presented in this paper is publicly available on GitHub at https://github.com/Liuzhonglingg/AW-PINN (7 April 2025).
Conflicts of Interest
Author Junxue Lv was employed by the company Guangxi Communications Design Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Matsumoto, M.; Yagi, T.; Shigemura, Y.; Tsushima, D. Vortex-induced cable vibration of cable-stayed bridges at high reduced wind velocity. J. Wind Eng. Ind. Aerodyn. 2001, 89, 633–647. [Google Scholar] [CrossRef]
- Liu, Z.; Shen, J.; Li, S.; Chen, Z.; Ou, Q.; Xin, D. Experimental study on high-mode vortex-induced vibration of stay cable and its aerodynamic countermeasures. J. Fluids Struct. 2021, 100, 103195. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.; Kim, H.-K. High-mode vortex-induced vibration of stay cables: Monitoring, cause investigation, and mitigation. J. Sound Vib. 2022, 524, 116758. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, J.-w.; Li, F.; Gong, D. Nonlinear vortex-induced vibration of wind turbine towers: Theory and experimental validation. Mech. Syst. Signal Process. 2023, 204, 110772. [Google Scholar] [CrossRef]
- Chizfahm, A.; Yazdi, E.A.; Eghtesad, M. Dynamic modeling of vortex induced vibration wind turbines. Renew. Energy 2018, 121, 632–643. [Google Scholar] [CrossRef]
- Han, X.; Lin, W.; Qiu, A.; Feng, Z.; Wu, J.; Tang, Y.; Zhao, C. Understanding vortex-induced vibration characteristics of a long flexible marine riser by a bidirectional fluid–structure coupling method. J. Mar. Sci. Technol. 2020, 25, 620–639. [Google Scholar] [CrossRef]
- Hong, K.-S.; Shah, U.H. Vortex-induced vibrations and control of marine risers: A review. Ocean Eng. 2018, 152, 300–315. [Google Scholar] [CrossRef]
- Williamson, C.H.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Kumar, N.; Kolahalam, V.K.V.; Kantharaj, M.; Manda, S. Suppression of vortex-induced vibrations using flexible shrouding—An experimental study. J. Fluids Struct. 2018, 81, 479–491. [Google Scholar] [CrossRef]
- Trim, A.; Braaten, H.; Lie, H.; Tognarelli, M. Experimental investigation of vortex-induced vibration of long marine risers. J. Fluids Struct. 2005, 21, 335–361. [Google Scholar] [CrossRef]
- Zhang, C.; Kang, Z.; Stoesser, T.; Xie, Z.; Massie, L. Experimental investigation on the VIV of a slender body under the combination of uniform flow and top-end surge. Ocean Eng. 2020, 216, 108094. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, T.; Dai, H.; Ni, Q. Three-dimensional vortex-induced vibrations of supported pipes conveying fluid based on wake oscillator models. J. Sound Vib. 2018, 422, 590–612. [Google Scholar] [CrossRef]
- Meng, S.; Chen, Y.; Che, C. Slug flow’s intermittent feature affects VIV responses of flexible marine risers. Ocean Eng. 2020, 205, 106883. [Google Scholar] [CrossRef]
- Rahman, M.A.A.; Leggoe, J.; Thiagarajan, K.; Mohd, M.H.; Paik, J.K. Numerical simulations of vortex-induced vibrations on vertical cylindrical structure with different aspect ratios. Ships Offshore Struct. 2016, 11, 405–423. [Google Scholar] [CrossRef]
- Wu, W.; Wang, J. Numerical simulation of VIV for a circular cylinder with a downstream control rod at low Reynolds number. Eur. J. Mech.-B/Fluids 2018, 68, 153–166. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F.; Øiseth, O. Aerodynamic damping models for vortex-induced vibration of a rectangular 4: 1 cylinder: Comparison of modeling schemes. J. Wind Eng. Ind. Aerodyn. 2020, 205, 104321. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, H.; Ying, X. Incorporation of subcritical Reynolds number into an aerodynamic damping model for vortex-induced vibration of a smooth circular cylinder. Eng. Struct. 2021, 249, 113325. [Google Scholar] [CrossRef]
- Iwan, W.D.; Blevins, R.D. A Model for Vortex Induced Oscillation of Structures. J. Appl. Mech. 1974, 41, 581–586. [Google Scholar] [CrossRef]
- Goswami, I.; Scanlan, R.H.; Jones, N.P. Vortex-induced vibration of circular cylinders. II: New model. J. Eng. Mech. 1993, 119, 2288–2302. [Google Scholar] [CrossRef]
- Morse, T.; Williamson, C. Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 2009, 634, 5–39. [Google Scholar] [CrossRef]
- Zhang, M.; Song, Y.; Abdelkefi, A.; Yu, H.; Wang, J. Vortex-induced vibration of a circular cylinder with nonlinear stiffness: Prediction using forced vibration data. Nonlinear Dyn. 2022, 108, 1867–1884. [Google Scholar] [CrossRef]
- Evangelinos, C.; Lucor, D.; Karniadakis, G. DNS-derived force distribution on flexible cylinders subject to vortex-induced vibration. J. Fluids Struct. 2000, 14, 429–440. [Google Scholar] [CrossRef]
- Chen, W.; Ji, C.; Xu, D.; Zhang, Z. Three-dimensional direct numerical simulations of vortex-induced vibrations of a circular cylinder in proximity to a stationary wall. Phys. Rev. Fluids 2022, 7, 044607. [Google Scholar] [CrossRef]
- Wang, X.; Xu, F.; Zhang, Z.; Wang, Y. 3D LES numerical investigation of vertical vortex-induced vibrations of a 4: 1 rectangular cylinder. Adv. Wind Eng. 2024, 1, 100008. [Google Scholar] [CrossRef]
- Al-Jamal, H.; Dalton, C. Vortex induced vibrations using large eddy simulation at a moderate Reynolds number. J. Fluids Struct. 2004, 19, 73–92. [Google Scholar] [CrossRef]
- Pan, Z.; Cui, W.; Miao, Q. Numerical simulation of vortex-induced vibration of a circular cylinder at low mass-damping using RANS code. J. Fluids Struct. 2007, 23, 23–37. [Google Scholar] [CrossRef]
- Khan, N.B.; Ibrahim, Z.; Nguyen, L.T.T.; Javed, M.F.; Jameel, M. Numerical investigation of the vortex-induced vibration of an elastically mounted circular cylinder at high Reynolds number (Re = 104) and low mass ratio using the RANS code. PLoS ONE 2017, 12, e0185832. [Google Scholar] [CrossRef]
- Dobrucali, E.; Kinaci, O. URANS-based prediction of vortex induced vibrations of circular cylinders. J. Appl. Fluid Mech. 2017, 10, 957–970. [Google Scholar] [CrossRef]
- Liu, G.; Li, H.; Qiu, Z.; Leng, D.; Li, Z.; Li, W. A mini review of recent progress on vortex-induced vibrations of marine risers. Ocean Eng. 2020, 195, 106704. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Mathew, A.; Amudha, P.; Sivakumari, S. Deep Learning Techniques: An Overview. In Advanced Machine Learning Technologies and Applications: Proceedings of AMLTA 2020; Springer: Singapore, 2021; pp. 599–608. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Lino, M.; Fotiadis, S.; Bharath, A.A.; Cantwell, C.D. Current and emerging deep-learning methods for the simulation of fluid dynamics. Proc. R. Soc. A 2023, 479, 20230058. [Google Scholar] [CrossRef]
- Jin, X.; Cheng, P.; Chen, W.-L.; Li, H. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder. Phys. Fluids 2018, 30, 047105. [Google Scholar] [CrossRef]
- Sekar, V.; Jiang, Q.; Shu, C.; Khoo, B.C. Fast flow field prediction over airfoils using deep learning approach. Phys. Fluids 2019, 31, 057103. [Google Scholar] [CrossRef]
- Kim, G.-y.; Lim, C.; Kim, E.S.; Shin, S.-C. Prediction of dynamic responses of flow-induced vibration using deep learning. Appl. Sci. 2021, 11, 7163. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, D.; Wang, N. Deep-learning based discovery of partial differential equations in integral form from sparse and noisy data. J. Comput. Phys. 2021, 445, 110592. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2019, 861, 119–137. [Google Scholar] [CrossRef]
- Cheng, C.; Meng, H.; Li, Y.-Z.; Zhang, G.-T. Deep learning based on PINN for solving 2 DOF vortex induced vibration of cylinder. Ocean Eng. 2021, 240, 109932. [Google Scholar] [CrossRef]
- Tang, H.; Liao, Y.; Yang, H.; Xie, L. A transfer learning-physics informed neural network (TL-PINN) for vortex-induced vibration. Ocean Eng. 2022, 266, 113101. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, Y.; Zhang, Y.; Zhou, Y.; Zhao, Q.; Liu, T.; Xie, X.; Liang, Y. Application of Physics-Informed Neural Network (PINN) in the Experimental Study of Vortex-Induced Vibration with Tunable Stiffness. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Ottawa, Canada, 19–23 June 2023; pp. ISOPE–I-23-305. [Google Scholar]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and mitigating gradient pathologies in physics-informed neural networks. arXiv 2020, arXiv:2001.04536. [Google Scholar] [CrossRef]
- Xiang, Z.; Peng, W.; Liu, X.; Yao, W. Self-adaptive loss balanced physics-informed neural networks. Neurocomputing 2022, 496, 11–34. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Y.; Wang, L.; Li, T. Modeling water flow in unsaturated soils through physics-informed neural network with principled loss function. Comput. Geotech. 2023, 161, 105546. [Google Scholar] [CrossRef]
- Tarbiyati, H.; Nemati Saray, B. Weight initialization algorithm for physics-informed neural networks using finite differences. Eng. Comput. 2024, 40, 1603–1619. [Google Scholar] [CrossRef]
- Li, S.; Feng, X. Dynamic weight strategy of physics-informed neural networks for the 2d navier–stokes equations. Entropy 2022, 24, 1254. [Google Scholar] [CrossRef]
- Hou, X.; Zhou, X.; Liu, Y. Reconstruction of ship propeller wake field based on self-adaptive loss balanced physics-informed neural networks. Ocean Eng. 2024, 309, 118341. [Google Scholar] [CrossRef]
- Shi, S.; Liu, D.; Huo, Z. Simulation of thermal-fluid coupling in silicon single crystal growth based on gradient normalized physics-informed neural network. Phys. Fluids 2024, 36, 053610. [Google Scholar] [CrossRef]
- Yin, G.; Janocha, M.J.; Ong, M.C. Physics-Informed Neural Networks for Prediction of a Flow-Induced Vibration Cylinder. J. Offshore Mech. Arct. Eng. 2024, 146, 061203. [Google Scholar] [CrossRef]
- Chen, Z.; Badrinarayanan, V.; Lee, C.-Y.; Rabinovich, A. Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 794–803. [Google Scholar]
- Zhao, G.; Xu, J.; Duan, K.; Zhang, M.; Zhu, H.; Wang, J. Numerical analysis of hydroenergy harvesting from vortex-induced vibrations of a cylinder with groove structures. Ocean Eng. 2020, 218, 108219. [Google Scholar] [CrossRef]
- Bao, Y.; Huang, C.; Zhou, D.; Tu, J.; Han, Z. Two-degree-of-freedom flow-induced vibrations on isolated and tandem cylinders with varying natural frequency ratios. J. Fluids Struct. 2012, 35, 50–75. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).