Hybrid Machine Learning Model for Predicting the Fatigue Life of Plain Concrete Under Cyclic Compression
Abstract
1. Introduction
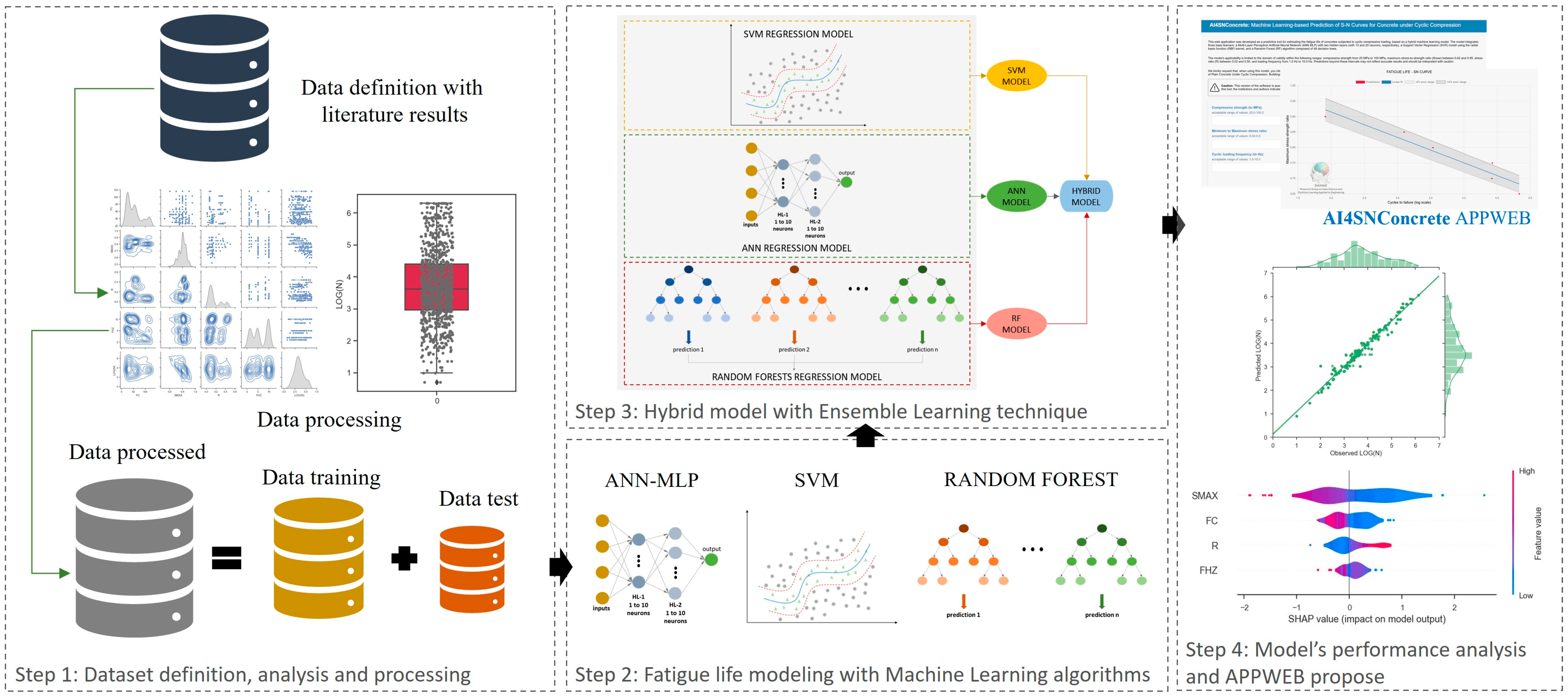
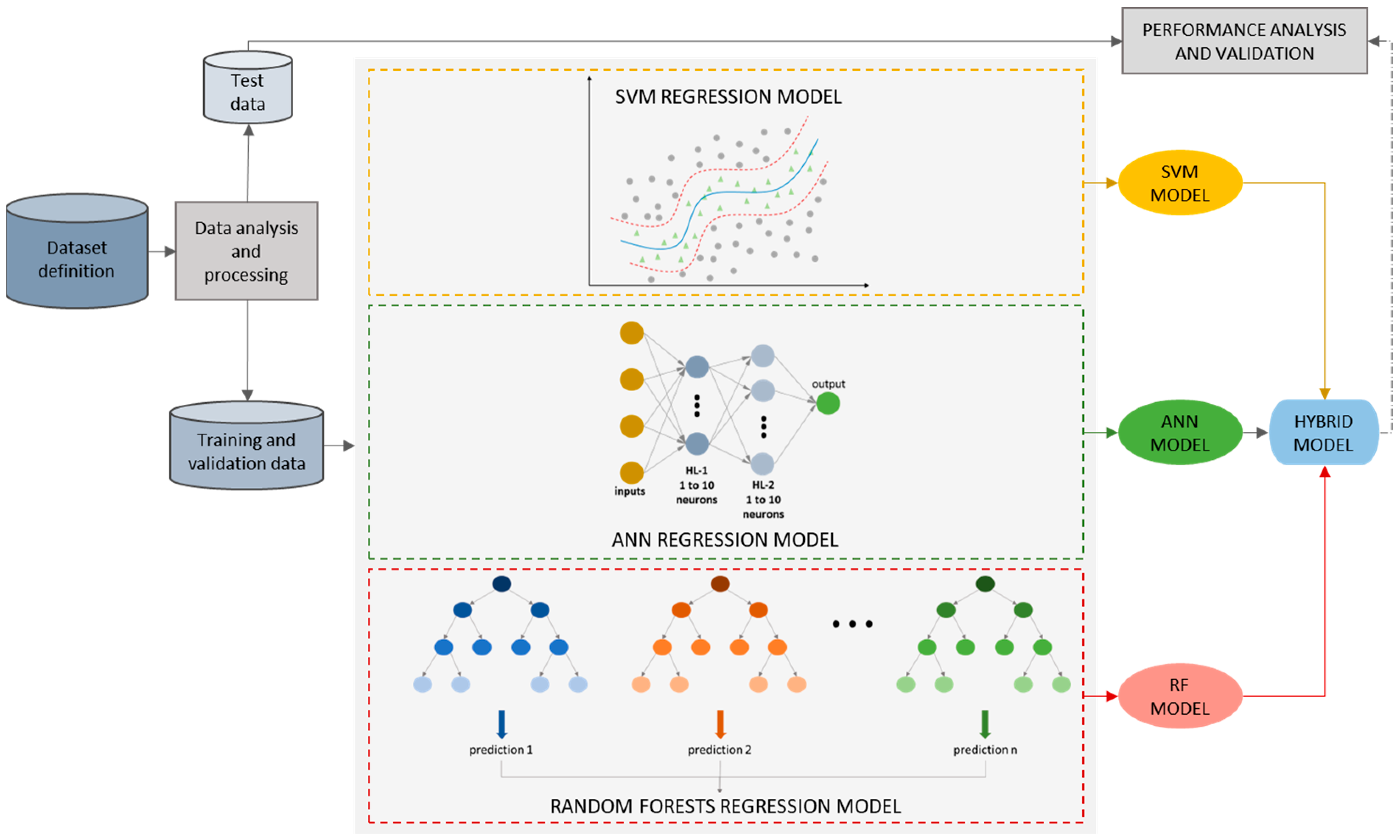
2. Data Processing and Modeling
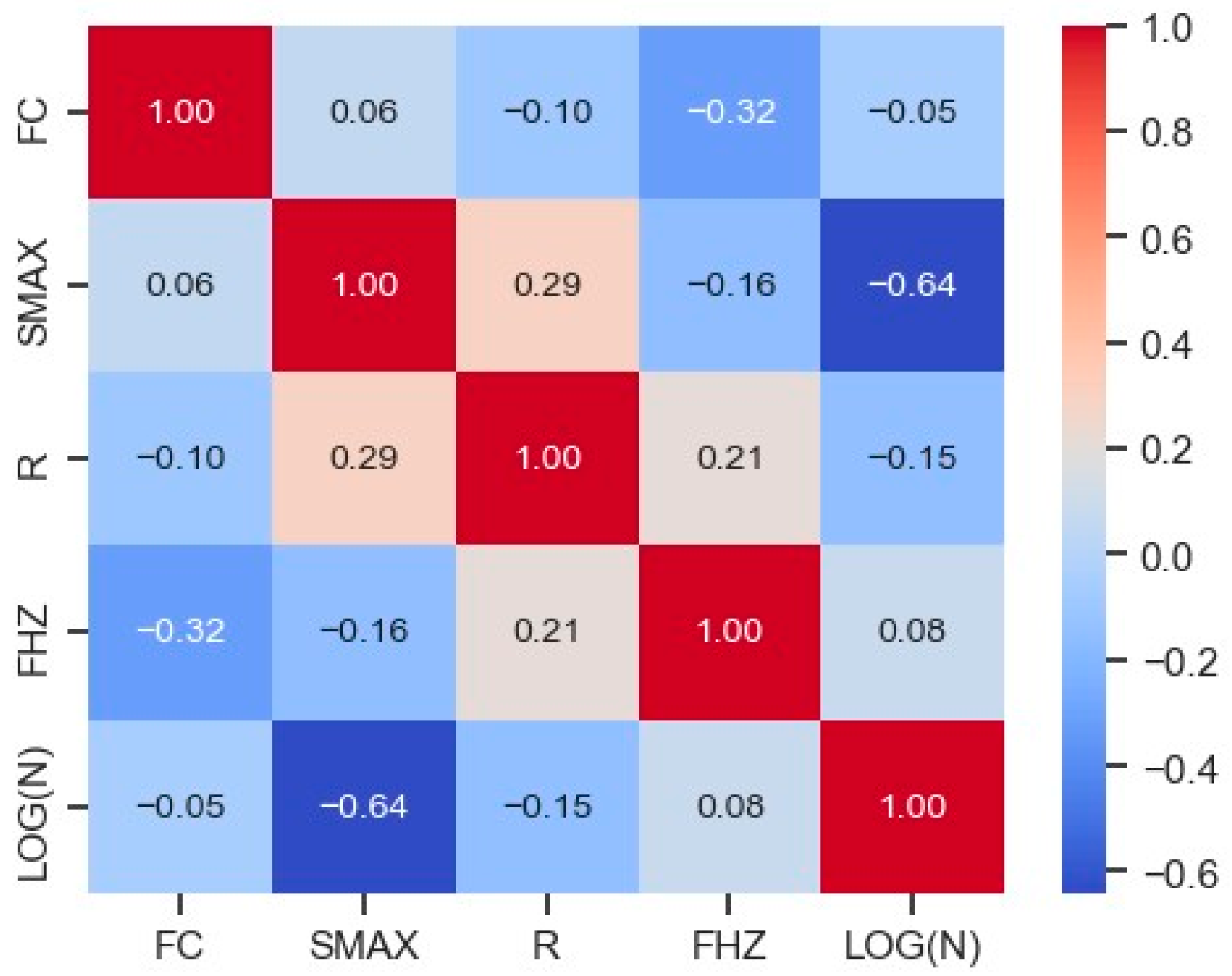
2.1. Dataset Definition, Analysis, and Processing
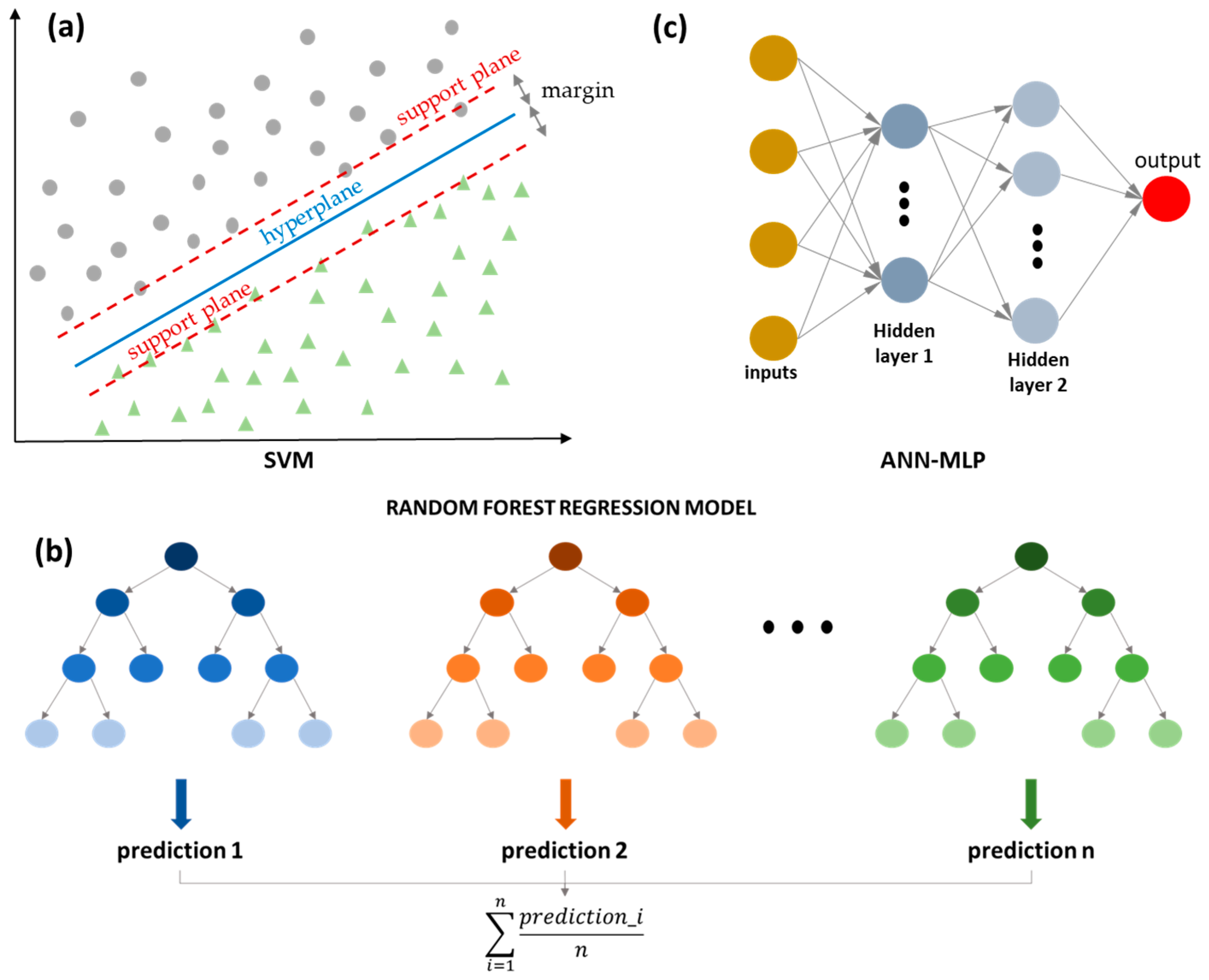
2.2. Machine Learning Algorithms
2.3. Hybrid Model Development
2.4. Performance Analysis
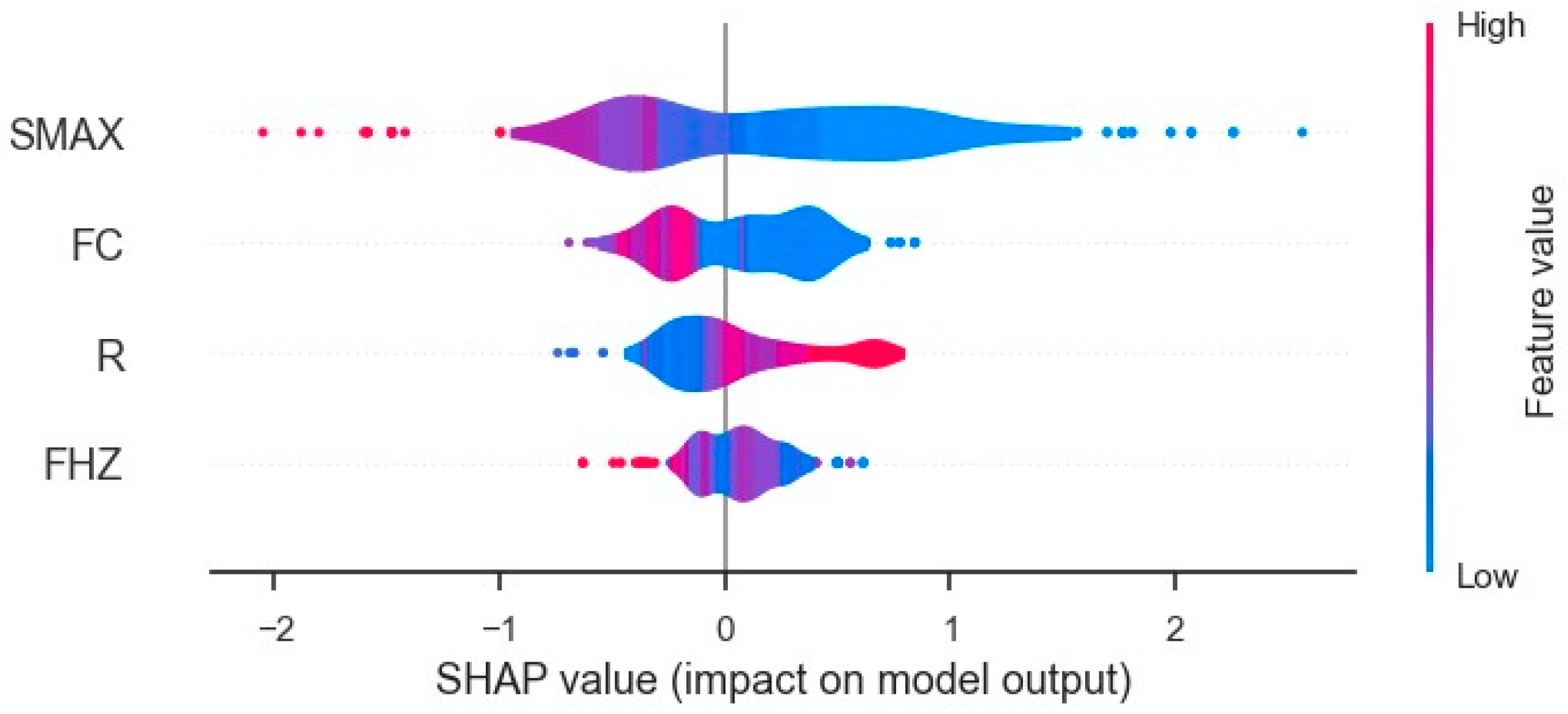
2.5. SHAP Analysis
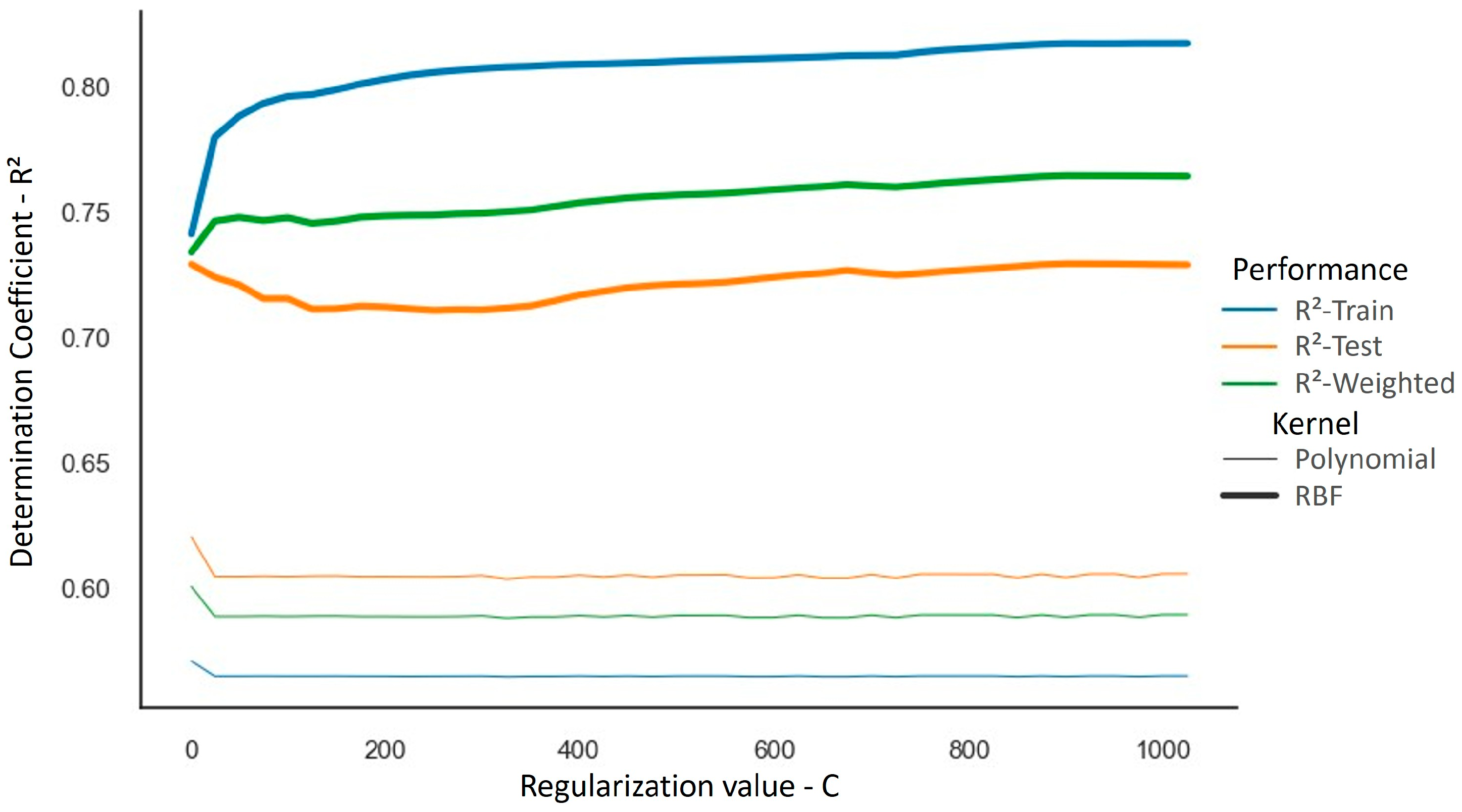
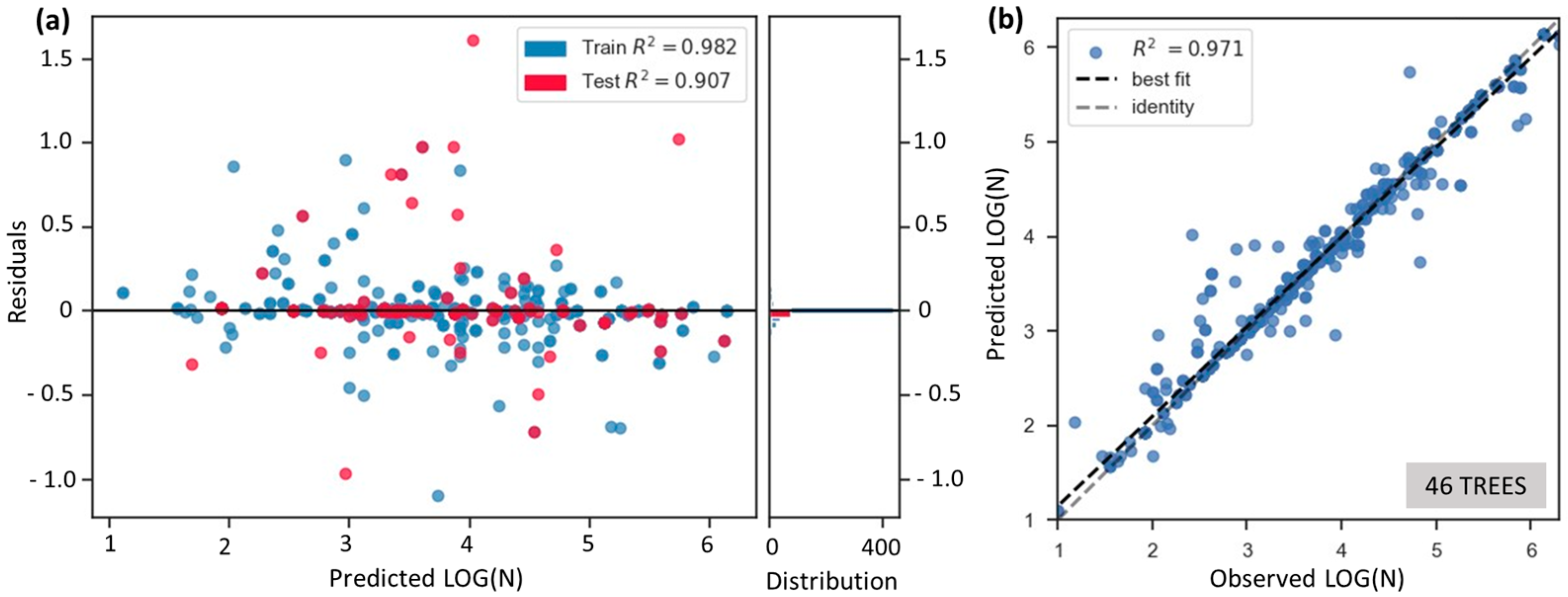
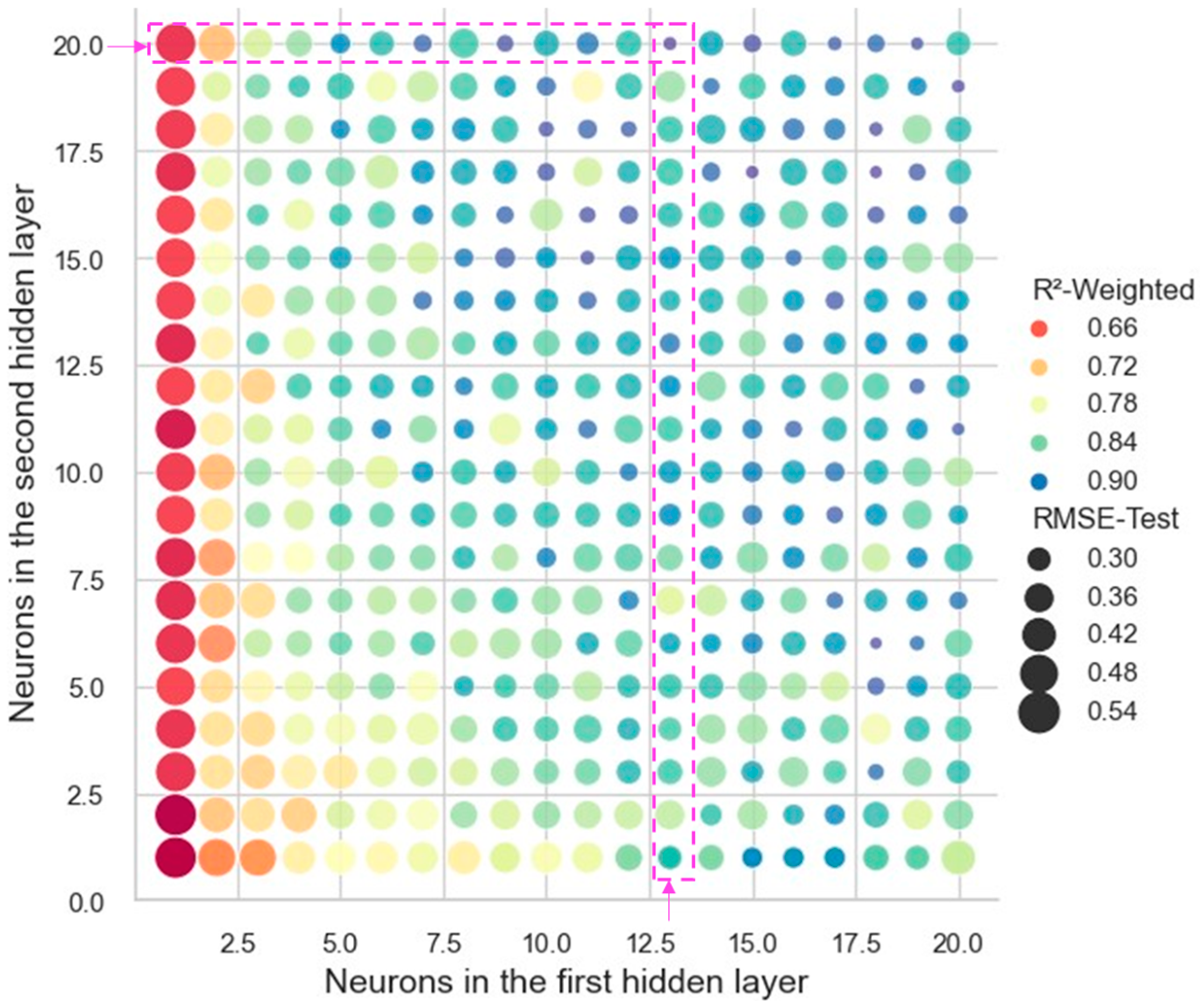
3. Results and Discussion
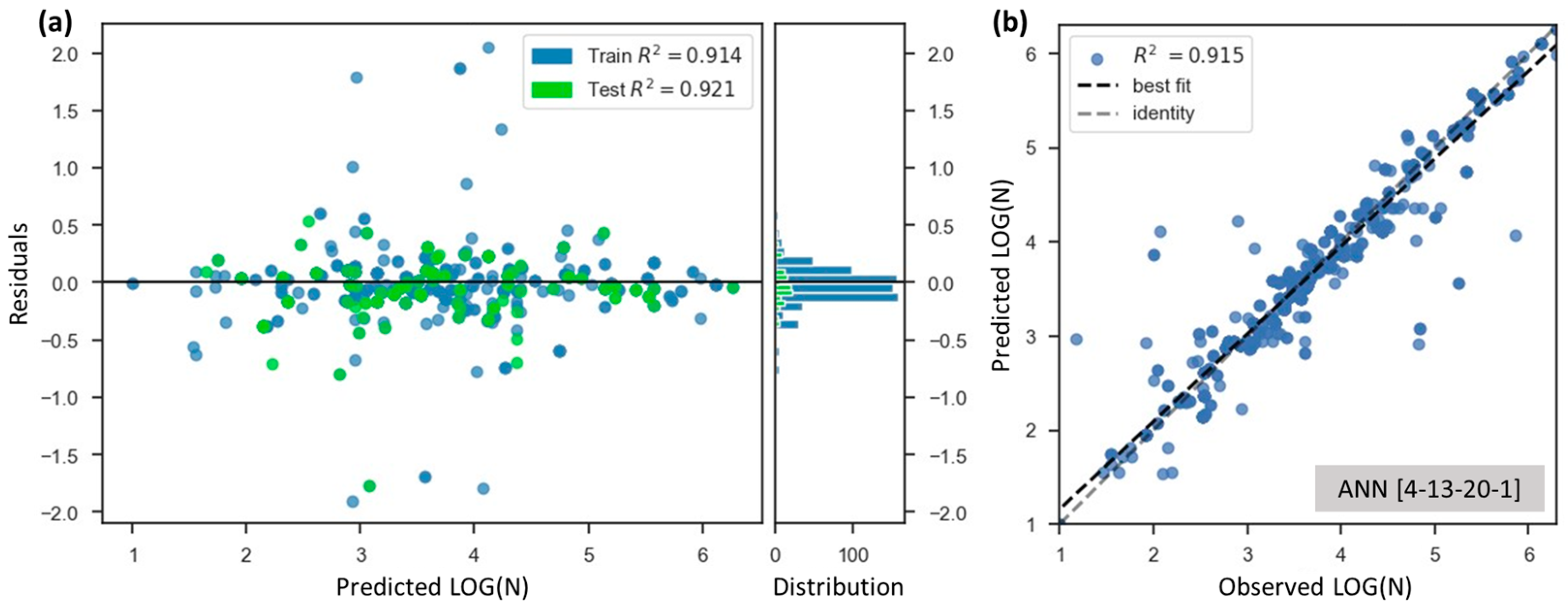
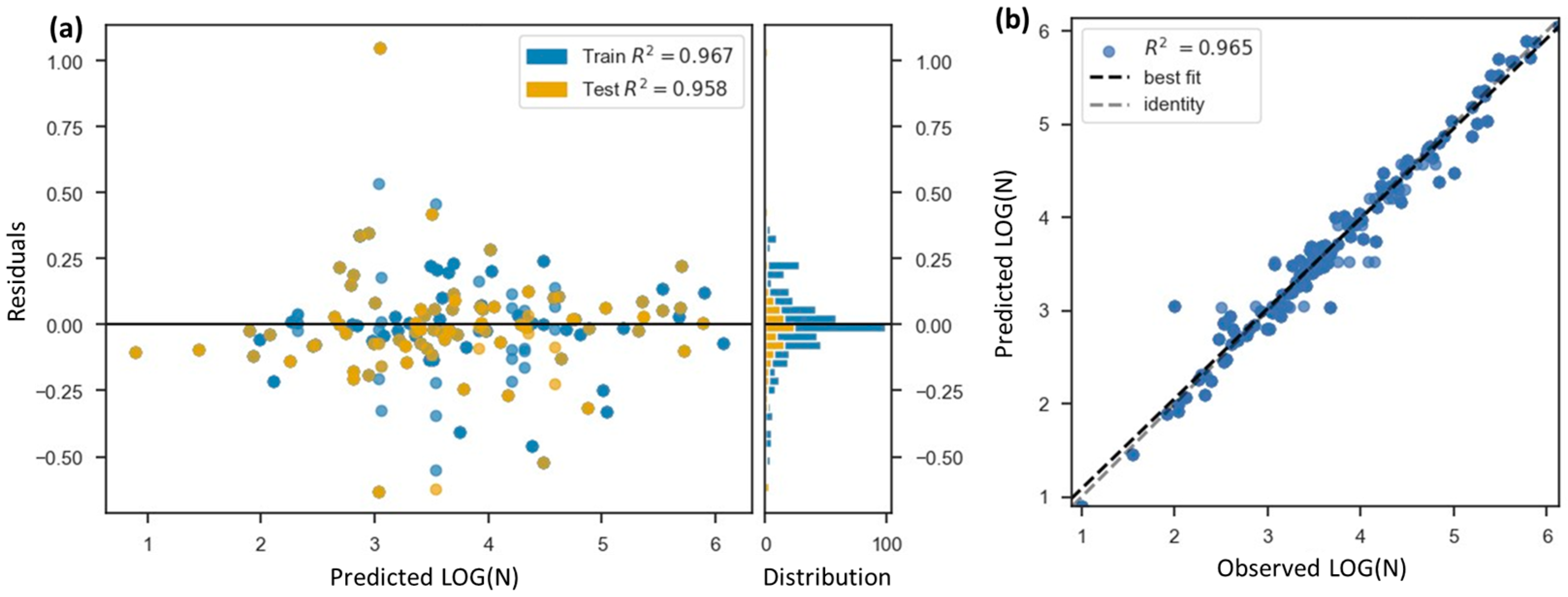
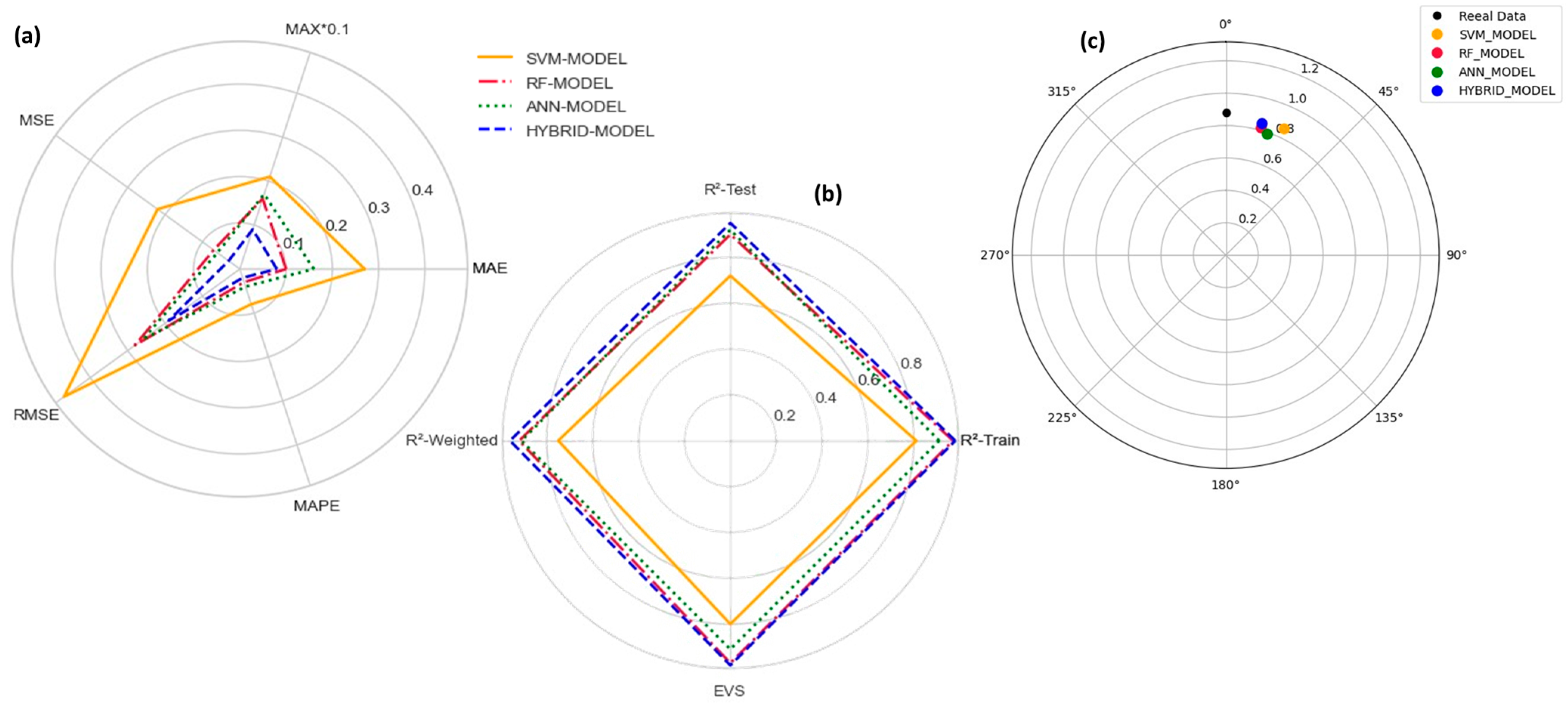
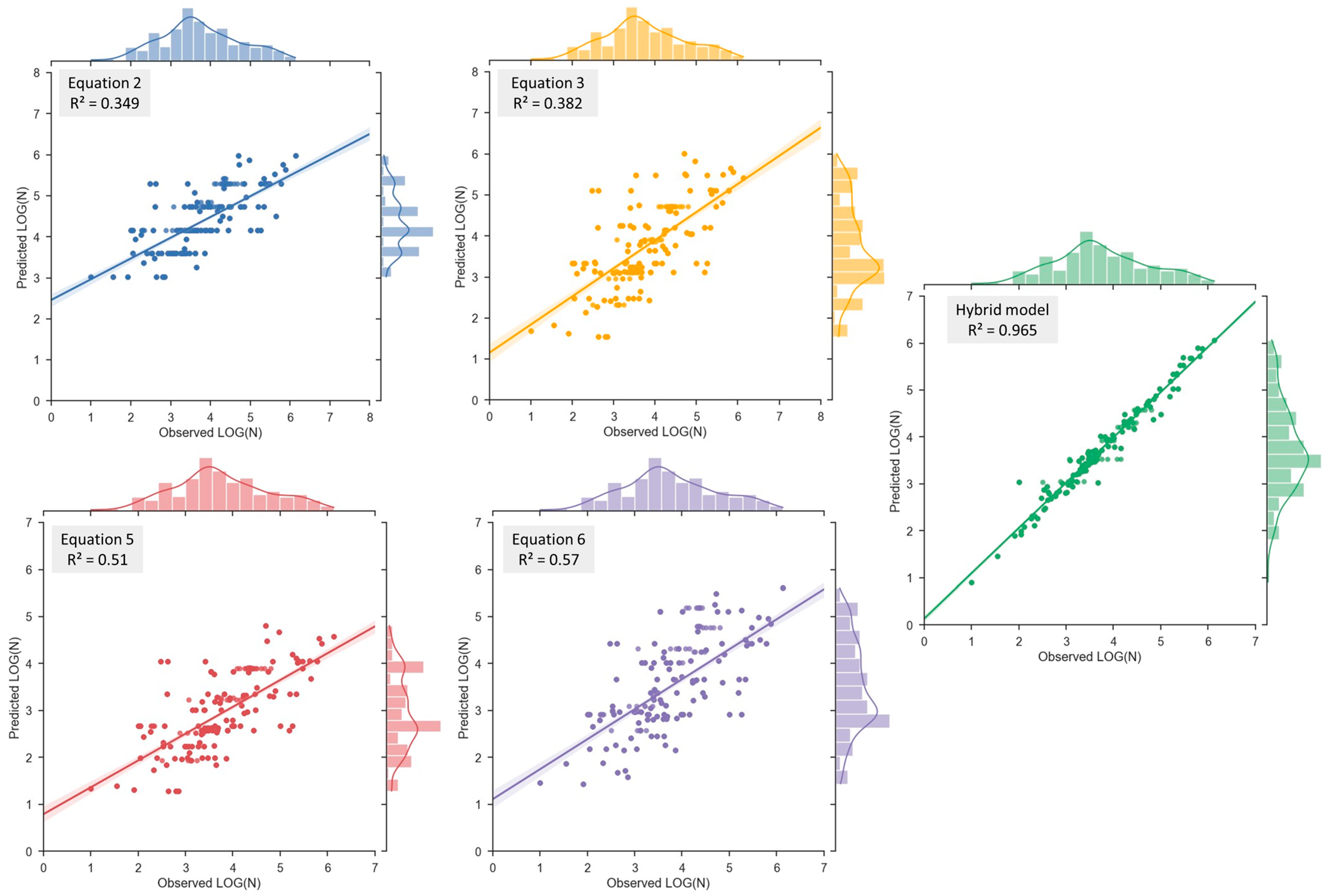
3.1. Models’ Performance
3.2. AI4SNConcrete App with Graphical Interface and Model Analysis
4. Conclusions
- Development of a highly accurate stacking-based hybrid model combining SVR, RF, and ANN approaches to predict the fatigue life of plain concrete, achieving R2 = 0.965 and RMSE = 0.19.
- Identification that only four input variables—compressive strength (FC), maximum stress ratio (SMAX), stress ratio (R), and loading frequency (FHZ)—are sufficient to model concrete’s fatigue behavior accurately.
- Applying SHAP analysis to interpret the model, confirming SMAX as the most influential variable, followed by FC, with R and FHZ also playing significant, albeit secondary, roles.
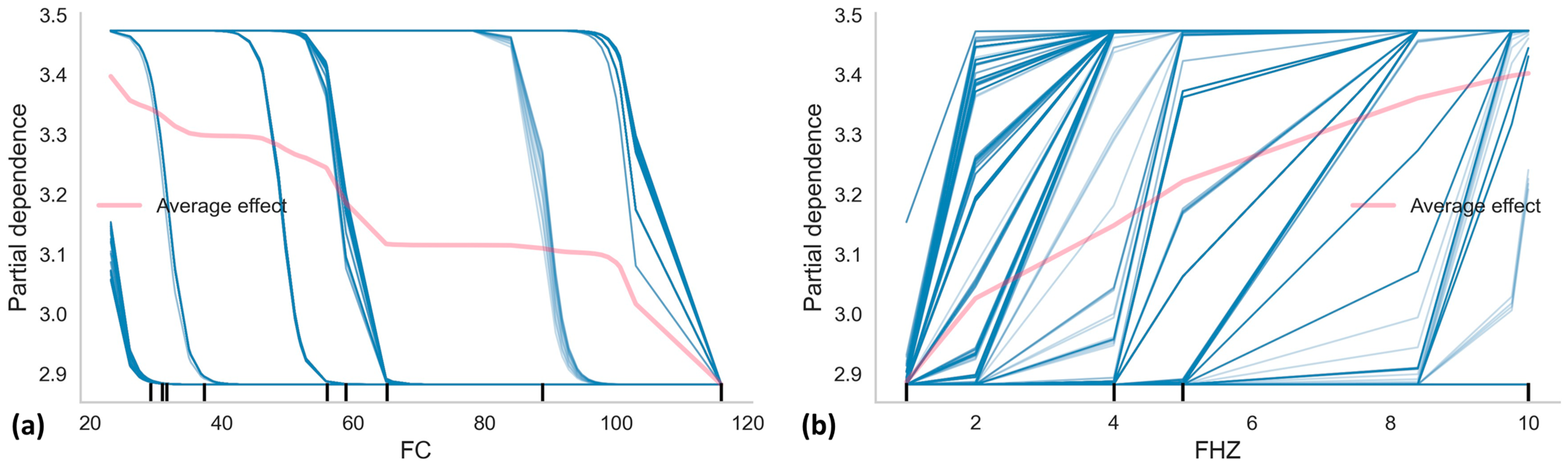
- Generation of Partial Dependence Plots (PDPs) and Individual Conditional Expectation (ICE) curves for FC and FHZ, providing a detailed and physically interpretable understanding of how these features affect the predicted fatigue life.
- Developing and publicly releasing a user-friendly web application based on the proposed hybrid model, allowing engineers and practitioners to easily generate S-N curves for plain concrete under cyclic loading. This tool simplifies the application of machine learning techniques in practice and can be accessed at https://ai4snconcrete.dasmae.com/ (accessed on 20 April 2025).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Clemmer, H.F. Fatigue of Concrete. Proc. Am. Soc. Test. Mater. 1922, 22, 408–419. [Google Scholar]
- Hsu, T.T.C. Fatigue of Plain Concrete. ACI J. Proc. 1981, 78, 292–305. [Google Scholar] [CrossRef]
- Do, M.; Chaallal, O.; Aïtcin, P. Fatigue Behavior of High-Performance Concrete. J. Mater. Civ. Eng. 1993, 5, 96–111. [Google Scholar] [CrossRef]
- Kolluru, S.V.; O’Neil, E.F.; Popovics, J.S.; Shah, S.P. Crack Propagation in Flexural Fatigue of Concrete. J. Eng. Mech. 2000, 126, 891–898. [Google Scholar] [CrossRef]
- Subramaniam, K.V.; Shah, S.P. Biaxial Tension Fatigue Response of Concrete. Cem. Concr. Compos. 2003, 25, 617–623. [Google Scholar] [CrossRef]
- Cornellissen, H.A.W. Fatigue Failure of Concrete in Tension. Heron 1984, 29, 2–67. [Google Scholar]
- Callister, W.D., Jr.; Rethwisch, D.G. Materials Science and Engineering: An Introduction, 10th ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Fédération Internationale du Béton. Model Code 2010: Final Draft; Fib Bulletin 65-66. International Federation for Structural, 2012. Available online: https://www.fib-international.org/publications/fib-bulletins/model-code-2010-final-draft,-volume-1-detail.html (accessed on 5 April 2025).
- Raithby, K.D.; Galloway, J.W. Effects of Moisture Condition, Age, and Rate of Loading on Fatigue of Plain Concrete. In Proceedings of the ABELES Symposium: Fatigue of Concrete; ACI Publication: Farmington Hills, MI, USA, 1974; pp. 15–34. [Google Scholar]
- Sparks, P.R. The Influence of Rate of Loading and Material Variability on the Fatigue Characteristics of Concrete. ACI J. 1982, 75, 331–342. [Google Scholar]
- Tepfers, R.; Kutti, T. Fatigue Strength of Plain, Ordinary and Lightweight Concrete. ACI J. 1979, 76, 635–652. [Google Scholar]
- Code Committee 351 001. Technical Foundations for Structures. In Regulations for Concrete-Bridges-Structural Requirements and Calculation Methods, NEN 6723:2009; Nederlands Normalisatie Instituut: Gouda, The Netherlands, 2009. [Google Scholar]
- Lee, M.K.; Barr, B.I.G. An Overview of the Fatigue Behaviour of Plain and Fibre Reinforced Concrete. Cem. Concr. Compos. 2004, 26, 299–305. [Google Scholar] [CrossRef]
- Ortega, J.J.; Ruiz, G.; Yu, R.C.; Afanador-García, N.; Tarifa, M.; Poveda, E.; Zhang, X.; Evangelista, F. Number of Tests and Corresponding Error in Concrete Fatigue. Int. J. Fatigue 2018, 116, 210–219. [Google Scholar] [CrossRef]
- Son, J.; Yang, S. A New Approach to Machine Learning Model Development for Prediction of Concrete Fatigue Life under Uniaxial Compression. Appl. Sci. 2022, 12, 9766. [Google Scholar] [CrossRef]
- Lee, H.; Lee, H.-S.; Suraneni, P. Evaluation of Carbonation Progress Using AIJ Model, FEM Analysis, and Machine Learning Algorithms. Constr. Build. Mater. 2020, 259, 119703. [Google Scholar] [CrossRef]
- Felix, E.F.; Carrazedo, R.; Possan, E. Vida Útil à Fadiga Do Concreto: Estudo Experimental Da Influência Das Condições de Carregamento e Da Resistência Do Material. Rev. ALCONPAT 2022, 12, 1–15. [Google Scholar] [CrossRef]
- Felix, E.F.; Carrazedo, R.; Possan, E. Análise Experimental Da Vida Útil à Fadiga de Concretos Submetidos à Compressão Cíclica de Baixa Frequência. Matéria 2022, 27, e202145017. [Google Scholar] [CrossRef]
- Medeiros, A.; Zhang, X.; Ruiz, G.; Yu, R.C.; Velasco, M.d.S.L. Effect of the Loading Frequency on the Compressive Fatigue Behavior of Plain and Fiber Reinforced Concrete. Int. J. Fatigue 2015, 70, 342–350. [Google Scholar] [CrossRef]
- Sain, T.; Chandrakishen, J. Residual Fatigue Strength Assessment of Concrete Considering Tension Softening Behavior. Int. J. Fatigue 2007, 29, 2138–2148. [Google Scholar] [CrossRef]
- Liang, J.; Ding, Z.; Li, J. A Probabilistic Analyzed Method for Concrete Fatigue Life. Probabilistic Eng. Mech. 2017, 49, 13–21. [Google Scholar] [CrossRef]
- Li, J.; Gao, R. Fatigue Reliability Analysis of Concrete Structures Based on Physical Synthesis Method. Probabilistic Eng. Mech. 2019, 56, 14–26. [Google Scholar] [CrossRef]
- Cui, K.; Xu, L.; Li, L.; Chi, Y. Mechanical Performance of Steel-Polypropylene Hybrid Fiber Reinforced Concrete Subject to Uniaxial Constant-Amplitude Cyclic Compression: Fatigue Behavior and Unified Fatigue Equation. Compos. Struct. 2023, 311, 116795. [Google Scholar] [CrossRef]
- Zhang, W.; Lee, D.; Lee, J.; Lee, C. Residual Strength of Concrete Subjected to Fatigue Based on Machine Learning Technique. Struct. Concr. 2022, 23, 2274–2287. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, W.; Zhao, Y. ANN Prediction Model of Concrete Fatigue Life Based on GRW-DBA Data Augmentation. Appl. Sci. 2023, 13, 1227. [Google Scholar] [CrossRef]
- Adeli, H.; Yeh, C. Perceptron Learning in Engineering Design. Comput.-Aided Civ. Infrastruct. Eng. 1989, 4, 247–256. [Google Scholar] [CrossRef]
- Williams, T.P.; Gucunski, N. Neural Networks for Backcalculation of Moduli from SASW Test. J. Comput. Civ. Eng. 1995, 9, 1–8. [Google Scholar] [CrossRef]
- Goh, A.T.C. Neural Networks for Evaluating CPT Calibration Chamber Test Data. Comput.-Aided Civ. Infrastruct. Eng. 1995, 10, 147–151. [Google Scholar] [CrossRef]
- Bonini Neto, A.; dos Santos Batista Bonini, C.; Santos Bisi, B.; Rodrigues dos Reis, A.; Sommaggio Coletta, L.F. Artificial Neural Network for Classification and Analysis of Degraded Soils. IEEE Lat. Am. Trans. 2017, 15, 503–509. [Google Scholar] [CrossRef]
- Xie, J.; Huang, J.; Zeng, C.; Huang, S.; Burton, G.J. A Generic Framework for Geotechnical Subsurface Modeling with Machine Learning. J. Rock. Mech. Geotech. Eng. 2022, 14, 1366–1379. [Google Scholar] [CrossRef]
- Puri, N.; Prasad, H.D.; Jain, A. Prediction of Geotechnical Parameters Using Machine Learning Techniques. Procedia Comput. Sci. 2018, 125, 509–517. [Google Scholar] [CrossRef]
- Lin, S.; Liang, Z.; Zhao, S.; Dong, M.; Guo, H.; Zheng, H. A Comprehensive Evaluation of Ensemble Machine Learning in Geotechnical Stability Analysis and Explainability. Int. J. Mech. Mater. Des. 2024, 20, 331–352. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Hong, L.; Han, L.; Wang, L. Comprehensive Review of Machine Learning in Geotechnical Reliability Analysis: Algorithms, Applications and Further Challenges. Appl. Soft Comput. 2023, 136, 110066. [Google Scholar] [CrossRef]
- Jenkins, W.M. A Neural Network for Structural Re-Analysis. Comput. Struct. 1999, 72, 687–698. [Google Scholar] [CrossRef]
- Babiker, S.A.; Adam, F.M.; Mohamed, A.E. Design Optimization of Reinforced Concrete Beams Using Concrete Beams Using Artificial Neural Network. Green. Bookee 2012, 1, 07–13. [Google Scholar]
- Ge, K.; Wang, C.; Guo, Y.T.; Tang, Y.S.; Hu, Z.Z.; Chen, H.B. Fine-Tuning Vision Foundation Model for Crack Segmentation in Civil Infrastructures. Constr. Build. Mater. 2024, 431, 136573. [Google Scholar] [CrossRef]
- Félix, E.F.; Falcão, I.d.S.; dos Santos, L.G.; Carrazedo, R.; Possan, E. A Monte Carlo-Based Approach to Assess the Reinforcement Depassivation Probability of RC Structures: Simulation and Analysis. Buildings 2023, 13, 993. [Google Scholar] [CrossRef]
- Felix, E.F.; Carrazedo, R. Análise Probabilística Da Vida Útil de Lajes de Concreto Armado Sujeitas à Corrosão Por Carbonatação via Simulação de Monte Carlo. Matéria 2021, 26, e13043. [Google Scholar] [CrossRef]
- Felix, E.F.; Lavinicki, B.M.; Bueno, T.L.G.T.; de Castro, T.C.C.; Cândido, R.A. Integrating Machine Learning and Monte Carlo Simulation for Probabilistic Assessment of Durability in RC Structures Affected by Carbonation-Induced Corrosion. J. Build. Pathol. Rehabil. 2024, 9, 143. [Google Scholar] [CrossRef]
- Mangalathu, S.; Hwang, S.-H.; Jeon, J.-S. Failure Mode and Effects Analysis of RC Members Based on Machine-Learning-Based SHapley Additive ExPlanations (SHAP) Approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Li, G.; Luo, R.; Yu, D.-H. A Framework for Developing a Machine Learning-Based Finite Element Model for Structural Analysis. Comput. Struct. 2025, 307, 107617. [Google Scholar] [CrossRef]
- Adeli, H. Advances in Design Optimization; Adeli, H., Ed.; CRC Press: Boca Raton, FL, USA, 1994; ISBN 9780429082245. [Google Scholar]
- Al-Suhaili, R.H.S.; Ali, A.A.M.; Behaya, S.A.K. Artificial Neural Network Modeling for Dynamic Analysis of a Dam-Reservoir-Foundation System. Int. J. Eng. Res. Appl. 2014, 4, 10–32. [Google Scholar]
- Ge, K.; Wang, C.; Guo, Y.-T.; Tang, Y.-S.; Fan, J.-S. A Multitask Fourier Transformer Network for Seismic Source Characterization Estimation From a Single-Station Waveform. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Ge, K.; Guo, Y.T.; Wang, C.; Hu, Z.Z. AI-Based Prediction of Seismic Time-History Responses of RC Frame Structures Considering Varied Structural Parameters. J. Build. Eng. 2025, 106, 112643. [Google Scholar] [CrossRef]
- Neves, A.C.; González, I.; Karoumi, R.; Leander, J. The Influence of Frequency Content on the Performance of Artificial Neural Network–Based Damage Detection Systems Tested on Numerical and Experimental Bridge Data. Struct. Health Monit. 2021, 20, 1331–1347. [Google Scholar] [CrossRef]
- Gomes, G.F.; Mendez, Y.A.D.; da Silva Lopes Alexandrino, P.; da Cunha, S.S.; Ancelotti, A.C. A Review of Vibration Based Inverse Methods for Damage Detection and Identification in Mechanical Structures Using Optimization Algorithms and ANN. Arch. Comput. Methods Eng. 2019, 26, 883–897. [Google Scholar] [CrossRef]
- Bakhary, N.; Hao, H.; Deeks, A.J. Damage Detection Using Artificial Neural Network with Consideration of Uncertainties. Eng. Struct. 2007, 29, 2806–2815. [Google Scholar] [CrossRef]
- Jeyasehar, C.A.; Sumangala, K. Damage Assessment of Prestressed Concrete Beams Using Artificial Neural Network (ANN) Approach. Comput. Struct. 2006, 84, 1709–1718. [Google Scholar] [CrossRef]
- Bonifácio, A.L.; Mendes, J.C.; Farage, M.C.R.; Barbosa, F.S.; Barbosa, C.B.; Beaucour, A.-L. Application of Support Vector Machine and Finite Element Method to Predict the Mechanical Properties of Concrete. Lat. Am. J. Solids Struct. 2019, 16, e205. [Google Scholar] [CrossRef]
- Jueyendah, S.; Lezgy-Nazargah, M.; Eskandari-Naddaf, H.; Emamian, S.A. Predicting the Mechanical Properties of Cement Mortar Using the Support Vector Machine Approach. Constr. Build. Mater. 2021, 291, 123396. [Google Scholar] [CrossRef]
- Saha, P.; Debnath, P.; Thomas, P. Prediction of Fresh and Hardened Properties of Self-Compacting Concrete Using Support Vector Regression Approach. Neural Comput. Appl. 2020, 32, 7995–8010. [Google Scholar] [CrossRef]
- Abambres, M.; Lantsoght, E.O.L. Lantsoght ANN-Based Fatigue Strength of Concrete under Compression. Materials 2019, 12, 3787. [Google Scholar] [CrossRef]
- Fathalla, E.; Tanaka, Y.; Maekawa, K. Remaining Fatigue Life Assessment of In-Service Road Bridge Decks Based upon Artificial Neural Networks. Eng. Struct. 2018, 171, 602–616. [Google Scholar] [CrossRef]
- Rabin Gani, B.; Simon, K.M.; Bharati Raj, J. Development of Artificial Neural Network for the Fatigue Life Assessment of Self Compacting Concrete. In International Conference on Structural Engineering and Construction Management; Springer International Publishing: Cham, Switzerland, 2023; pp. 695–704. [Google Scholar]
- Zheng, D.; Ozbayoglu, E.; Miska, S.Z.; Liu, Y.; Li, Y. Cement Sheath Fatigue Failure Prediction by ANN-Based Model. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 25 April 2022. [Google Scholar]
- Al-Saraireh, M.A. Predicting Compressive Strength of Concrete with Fly Ash, Metakaolin and Silica Fume by Using Machine Learning Techniques. Lat. Am. J. Solids Struct. 2022, 19, e454. [Google Scholar] [CrossRef]
- Endzhievskaya, I.G.; Endzhievskiy, A.S.; Galkin, M.A.; Molokeev, M.S. Machine Learning Methods in Assessing the Effect of Mixture Composition on the Physical and Mechanical Characteristics of Road Concrete. J. Build. Eng. 2023, 76, 107248. [Google Scholar] [CrossRef]
- Khodaparasti, M.; Alijamaat, A.; Pouraminian, M. Prediction of the Concrete Compressive Strength Using Improved Random Forest Algorithm. J. Build. Pathol. Rehabil. 2023, 8, 92. [Google Scholar] [CrossRef]
- Li, H.; Lin, J.; Lei, X.; Wei, T. Compressive Strength Prediction of Basalt Fiber Reinforced Concrete via Random Forest Algorithm. Mater. Today Commun. 2022, 30, 103117. [Google Scholar] [CrossRef]
- Alabduljabbar, H.; Khan, K.; Awan, H.H.; Alyousef, R.; Mohamed, A.M.; Eldin, S.M. Modeling the Capacity of Engineered Cementitious Composites for Self-Healing Using AI-Based Ensemble Techniques. Case Stud. Constr. Mater. 2023, 18, e01805. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Shahjalal, M.; Islam, K.; Mahmood, S.M.F.; Billah, A.H.M.M.; Nehdi, M.L. Explainable Ensemble Learning Data-Driven Modeling of Mechanical Properties of Fiber-Reinforced Rubberized Recycled Aggregate Concrete. J. Build. Eng. 2023, 76, 107279. [Google Scholar] [CrossRef]
- Jiao, H.; Wang, Y.; Li, L.; Arif, K.; Farooq, F.; Alaskar, A. A Novel Approach in Forecasting Compressive Strength of Concrete with Carbon Nanotubes as Nanomaterials. Mater. Today Commun. 2023, 35, 106335. [Google Scholar] [CrossRef]
- Sapkota, S.C.; Saha, P.; Das, S.; Meesaraganda, L.V.P. Prediction of the Compressive Strength of Normal Concrete Using Ensemble Machine Learning Approach. Asian J. Civ. Eng. 2023, 25, 583–596. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, X. Predicting the Fracture Characteristics of Concrete Using Ensemble and Meta-Heuristic Algorithms. KSCE J. Civ. Eng. 2023, 27, 2940–2951. [Google Scholar] [CrossRef]
- Huo, Z.; Wang, L.; Huang, Y. Predicting Carbonation Depth of Concrete Using a Hybrid Ensemble Model. J. Build. Eng. 2023, 76, 107320. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pham, A.-D. Enhanced Artificial Intelligence for Ensemble Approach to Predicting High Performance Concrete Compressive Strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Moussa, H.; Elabeidy, A.B.; Akçaoğlu, T. Predicting the Compressive Strength of Rubberized Concrete Containing Silica Fume Using Stacking Ensemble Learning Model. Constr. Build. Mater. 2024, 449, 138254. [Google Scholar] [CrossRef]
- Alshboul, O.; Almasabha, G.; Shehadeh, A.; Al-Shboul, K. A Comparative Study of LightGBM, XGBoost, and GEP Models in Shear Strength Management of SFRC-SBWS. Structures 2024, 61, 106009. [Google Scholar] [CrossRef]
- Suenaga, D.; Takase, Y.; Abe, T.; Orita, G.; Ando, S. Prediction Accuracy of Random Forest, XGBoost, LightGBM, and Artificial Neural Network for Shear Resistance of Post-Installed Anchors. Structures 2023, 50, 1252–1263. [Google Scholar] [CrossRef]
- Abdulalim Alabdullah, A.; Iqbal, M.; Zahid, M.; Khan, K.; Nasir Amin, M.; Jalal, F.E. Prediction of Rapid Chloride Penetration Resistance of Metakaolin Based High Strength Concrete Using Light GBM and XGBoost Models by Incorporating SHAP Analysis. Constr. Build. Mater. 2022, 345, 128296. [Google Scholar] [CrossRef]
- Li, Q.; Song, Z. Prediction of Compressive Strength of Rice Husk Ash Concrete Based on Stacking Ensemble Learning Model. J. Clean. Prod. 2023, 382, 135279. [Google Scholar] [CrossRef]
- Tanga, Y.M.P.; Simanjuntak, R.P.R.; Rofik, R.; Muslim, M.A. Improving Car Price Prediction Performance Using Stacking Ensemble Learning Based on Ann and Random Forest. J. Soft Comput. Explor. 2024, 5, 290–298. [Google Scholar] [CrossRef]
- Satish, N.; Anmala, J.; Rajitha, K.; Varma, M.R.R. A Stacking ANN Ensemble Model of ML Models for Stream Water Quality Prediction of Godavari River Basin, India. Ecol. Inf. 2024, 80, 102500. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kim, J.-K.; Kim, Y.-Y. Experimental Study of the Fatigue Behavior of High Strength Concrete. Cem. Concr. Res. 1996, 26, 1513–1523. [Google Scholar] [CrossRef]
- Saucedo, L.; Yu, R.C.; Medeiros, A.; Zhang, X.; Ruiz, G. A Probabilistic Fatigue Model Based on the Initial Distribution to Consider Frequency Effect in Plain and Fiber Reinforced Concrete. Int. J. Fatigue 2013, 48, 308–318. [Google Scholar] [CrossRef]
- Lv, J.; Zhou, T.; Du, Q.; Li, K. Experimental and Analytical Study on Uniaxial Compressive Fatigue Behavior of Self-Compacting Rubber Lightweight Aggregate Concrete. Constr. Build. Mater. 2020, 237, 117623. [Google Scholar] [CrossRef]
- Fan, Z.; Sun, Y. Detecting and Evaluation of Fatigue Damage in Concrete with Industrial Computed Tomography Technology. Constr. Build. Mater. 2019, 223, 794–805. [Google Scholar] [CrossRef]
- Vicente, M.A.; González, D.C.; Mínguez, J.; Tarifa, M.A.; Ruiz, G.; Hindi, R. Influence of the Pore Morphology of High Strength Concrete on Its Fatigue Life. Int. J. Fatigue 2018, 112, 106–116. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Ma, A. Investigation into the Fatigue Damage Process of Rubberized Concrete and Plain Concrete by AE Analysis. J. Mater. Civ. Eng. 2011, 23, 953–960. [Google Scholar] [CrossRef]
- Dyduch, K.; Szerszeń, M.; Destrebecq, J.-F. Experimental Investigation of the Fatigue Strength of Plain Concrete under High Compressive Loading. Mater. Struct. 1994, 27, 505–509. [Google Scholar] [CrossRef]
- Tepfers, R.; Hedberg, B.; Szczekocki, G. Absorption of Energy in Fatigue Loading of Plain Concrete. Matériaux Et. Constr. 1984, 17, 59–64. [Google Scholar] [CrossRef]
- Tue, N.V.; Mucha, S. Ermüdungsfestigkeit von Hochfestem Beton Unter Druckbeanspruchung. Bautechnik 2006, 83, 497–504. [Google Scholar] [CrossRef]
- Mu, B.; Subramaniam, K.V.; Shah, S.P. Failure Mechanism of Concrete under Fatigue Compressive Load. J. Mater. Civ. Eng. 2004, 16, 566–572. [Google Scholar] [CrossRef]
- Isojeh, B.; El-Zeghayar, M.; Vecchio, F.J. Concrete Damage under Fatigue Loading in Uniaxial Compression. ACI Mater. J. 2017, 114, 225–235. [Google Scholar] [CrossRef]
- Mun, J.-S.; Yang, K.-H.; Kim, S.-J. Tests on the Compressive Fatigue Performance of Various Concretes. J. Mater. Civ. Eng. 2016, 28, 04016099. [Google Scholar] [CrossRef]
- Oneschkow, N. Fatigue Behaviour of High-Strength Concrete with Respect to Strain and Stiffness. Int. J. Fatigue 2016, 87, 38–49. [Google Scholar] [CrossRef]
- Almeida, T.A.d.C.; Felix, E.F.; de Sousa, C.M.A.; Pedroso, G.O.M.; Motta, M.F.B.; Prado, L.P. Influence of the ANN Hyperparameters on the Forecast Accuracy of RAC’s Compressive Strength. Materials 2023, 16, 7683. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T. Ensemble Learning. In An Introduction to Materials Informatics; Springer Nature: Singapore, 2025; pp. 141–165. [Google Scholar]
- Riyar, R.L.; Mansi; Bhowmik, S. Fatigue Behaviour of Plain and Reinforced Concrete: A Systematic Review. Theor. Appl. Fract. Mech. 2023, 125, 103867. [Google Scholar] [CrossRef]
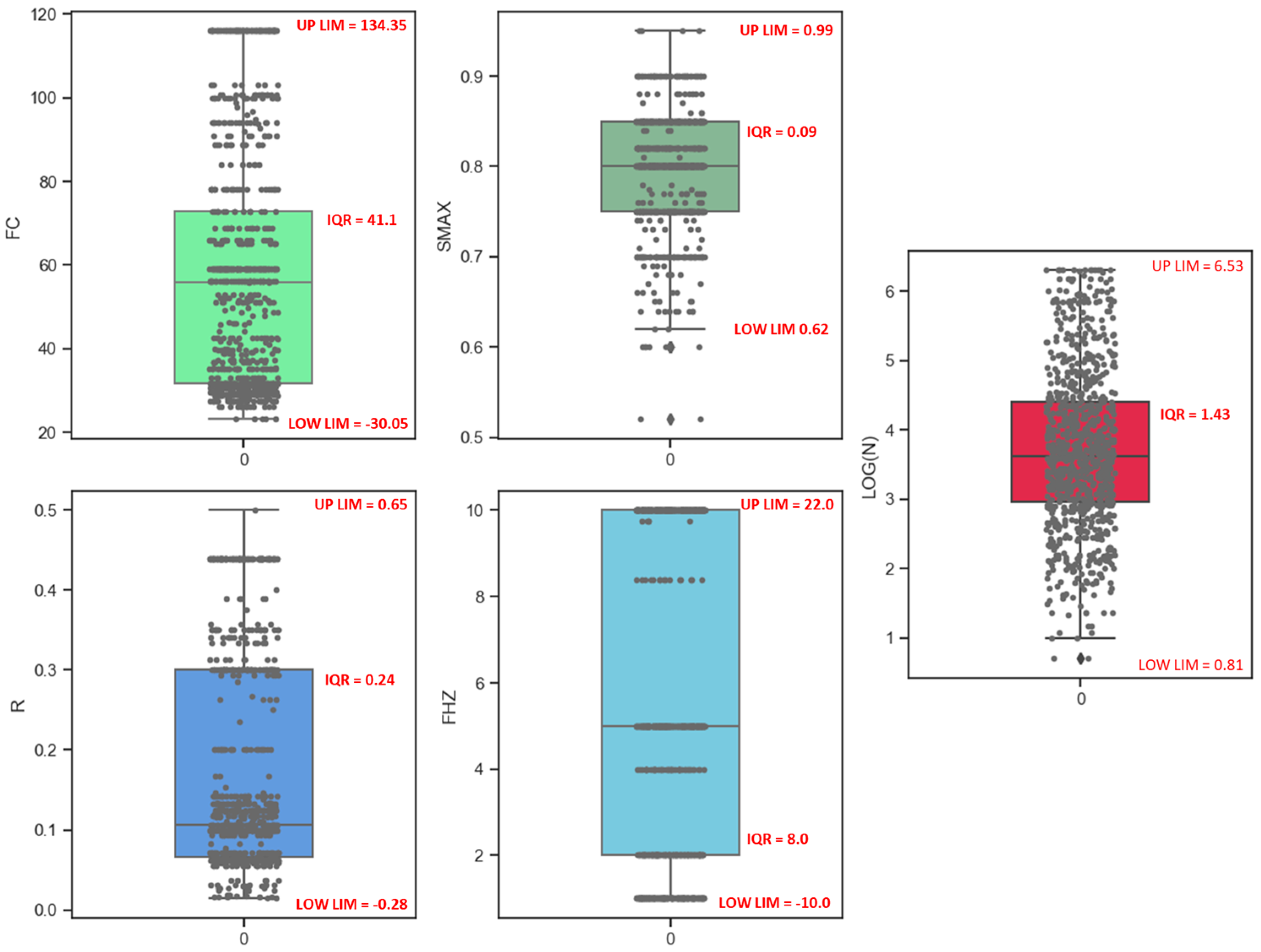




| Feature | Minimum | Maximum | Standard Deviation | Mean | Q1 (25%) | Q2 (50%) | Q3 (75%) |
|---|---|---|---|---|---|---|---|
| FC (MPa) | 23.10 | 116.00 | 29.02 | 57.47 | 31.60 | 55.80 | 72.70 |
| SMAX | 0.52 | 0.95 | 0.06 | 0.79 | 0.75 | 0.80 | 0.84 |
| R | 0.01 | 0.50 | 0.13 | 0.17 | 0.06 | 0.10 | 0.30 |
| FHZ (Hz) | 1.00 | 10.00 | 3.65 | 5.84 | 2.00 | 5.00 | 10.00 |
| N (cycles) | 5.00 | 2.00E6 | 3.31E5 | 1.09E5 | 9.18E2 | 4.20E3 | 2.50E4 |
| LOG(N) | 0.69 | 6.30 | 1.14 | 3.72 | 2.96 | 3.62 | 4.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lunardi, L.R.; Cornélio, P.G.; Prado, L.P.; Nogueira, C.G.; Felix, E.F. Hybrid Machine Learning Model for Predicting the Fatigue Life of Plain Concrete Under Cyclic Compression. Buildings 2025, 15, 1618. https://doi.org/10.3390/buildings15101618
Lunardi LR, Cornélio PG, Prado LP, Nogueira CG, Felix EF. Hybrid Machine Learning Model for Predicting the Fatigue Life of Plain Concrete Under Cyclic Compression. Buildings. 2025; 15(10):1618. https://doi.org/10.3390/buildings15101618
Chicago/Turabian StyleLunardi, Lucas Rodrigues, Paulo Guilherme Cornélio, Lisiane Pereira Prado, Caio Gorla Nogueira, and Emerson Felipe Felix. 2025. "Hybrid Machine Learning Model for Predicting the Fatigue Life of Plain Concrete Under Cyclic Compression" Buildings 15, no. 10: 1618. https://doi.org/10.3390/buildings15101618
APA StyleLunardi, L. R., Cornélio, P. G., Prado, L. P., Nogueira, C. G., & Felix, E. F. (2025). Hybrid Machine Learning Model for Predicting the Fatigue Life of Plain Concrete Under Cyclic Compression. Buildings, 15(10), 1618. https://doi.org/10.3390/buildings15101618






