Constrained Optimization for the Buckle and Anchor Cable Forces Under One-Time Tension in Long Span Arch Bridge Construction
Abstract
1. Introduction
2. Full-Process Constrained Optimization Method
2.1. Initial Cable Force Calculation
2.2. Barrier Function Interior-Point Method
2.3. Cable Force Optimization
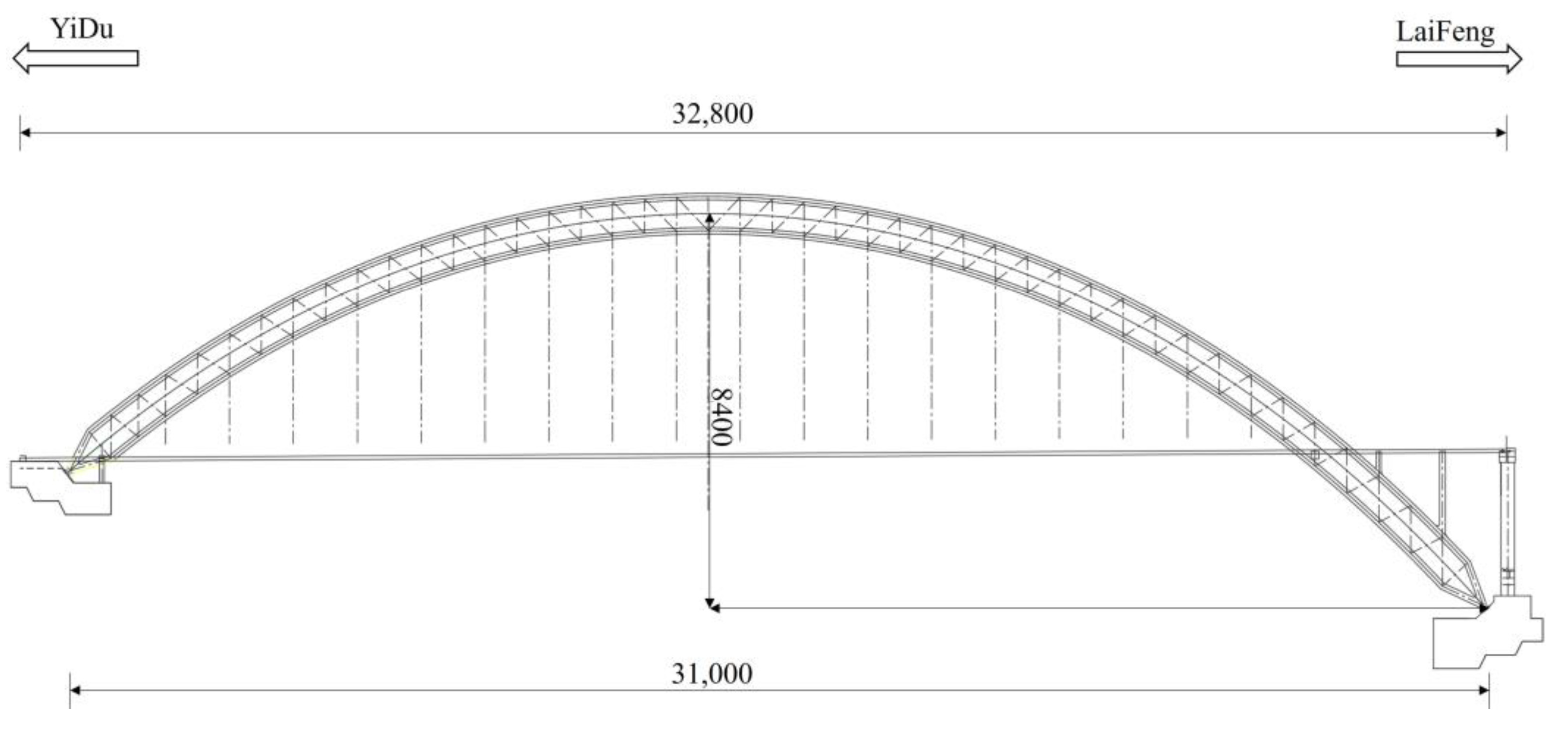
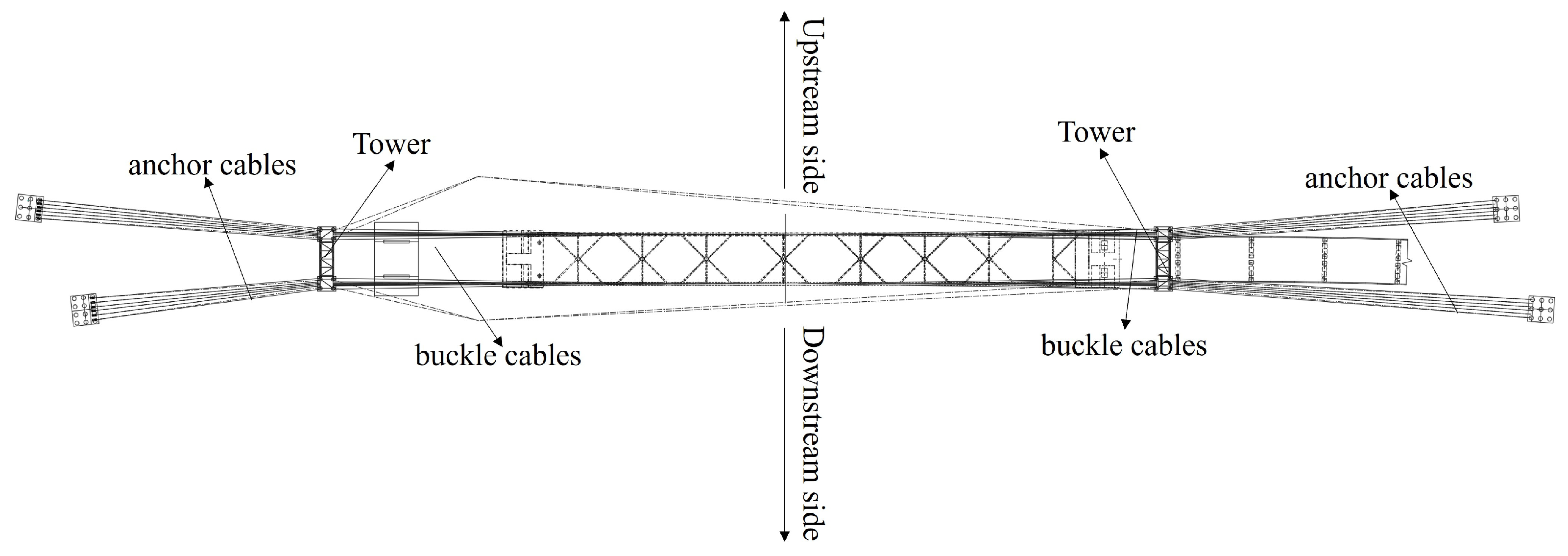
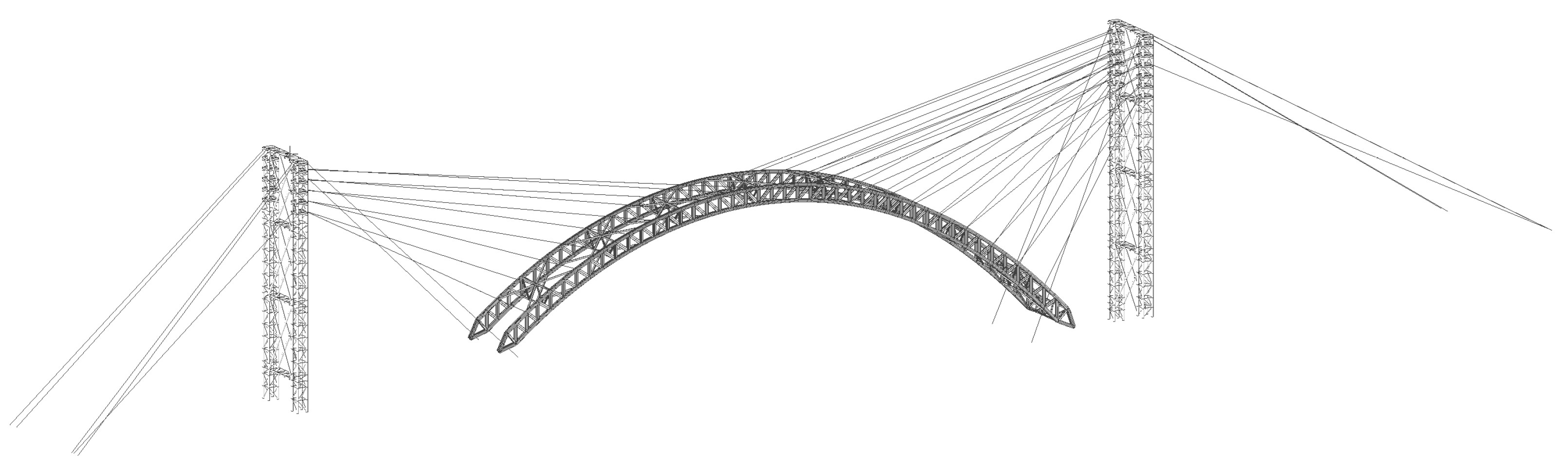
3. Engineering Application
3.1. Engineering Situations
3.2. Structural Calculation Model
3.3. Optimization Results
3.4. Control Results
4. Conclusions
- (1)
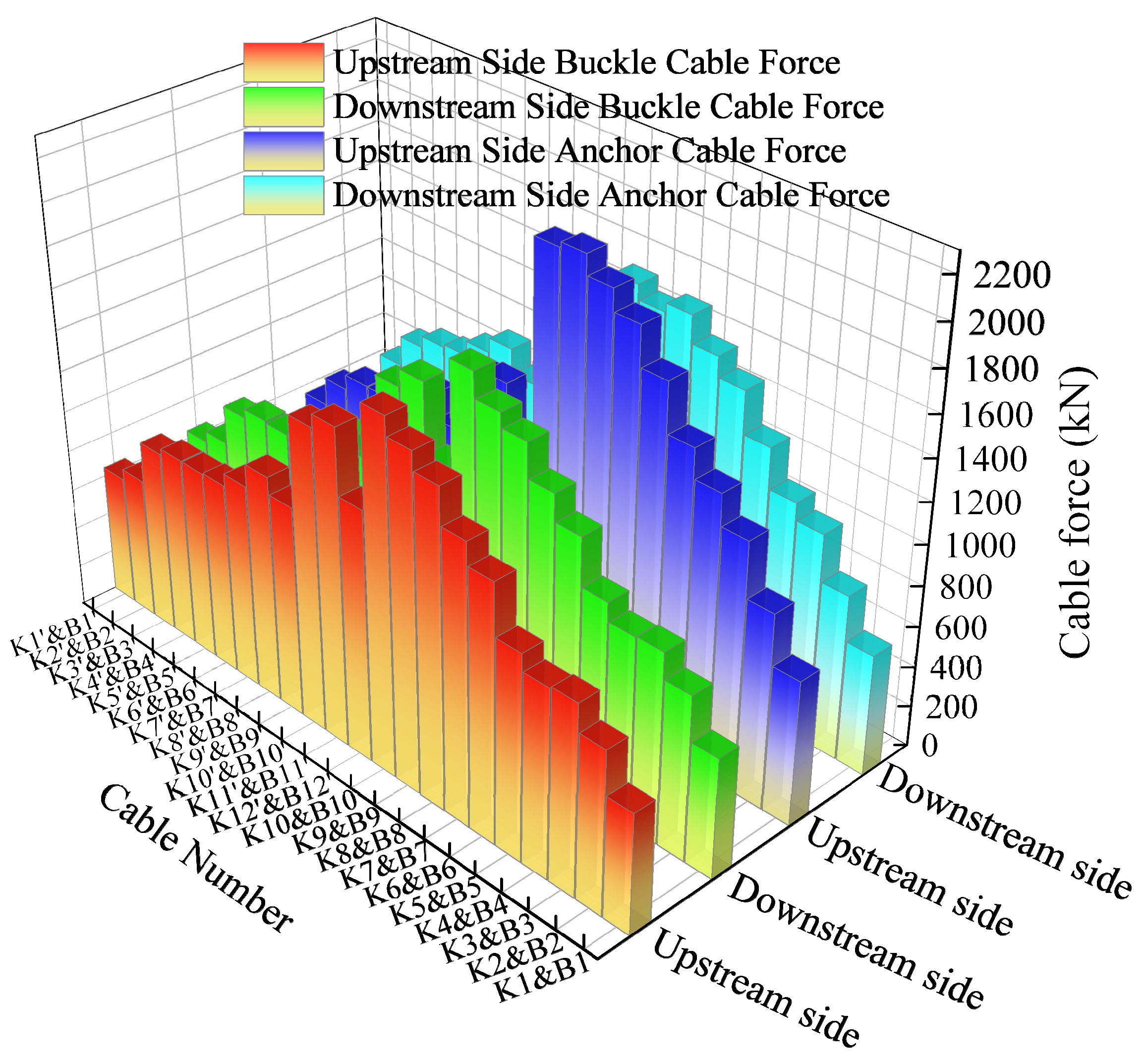
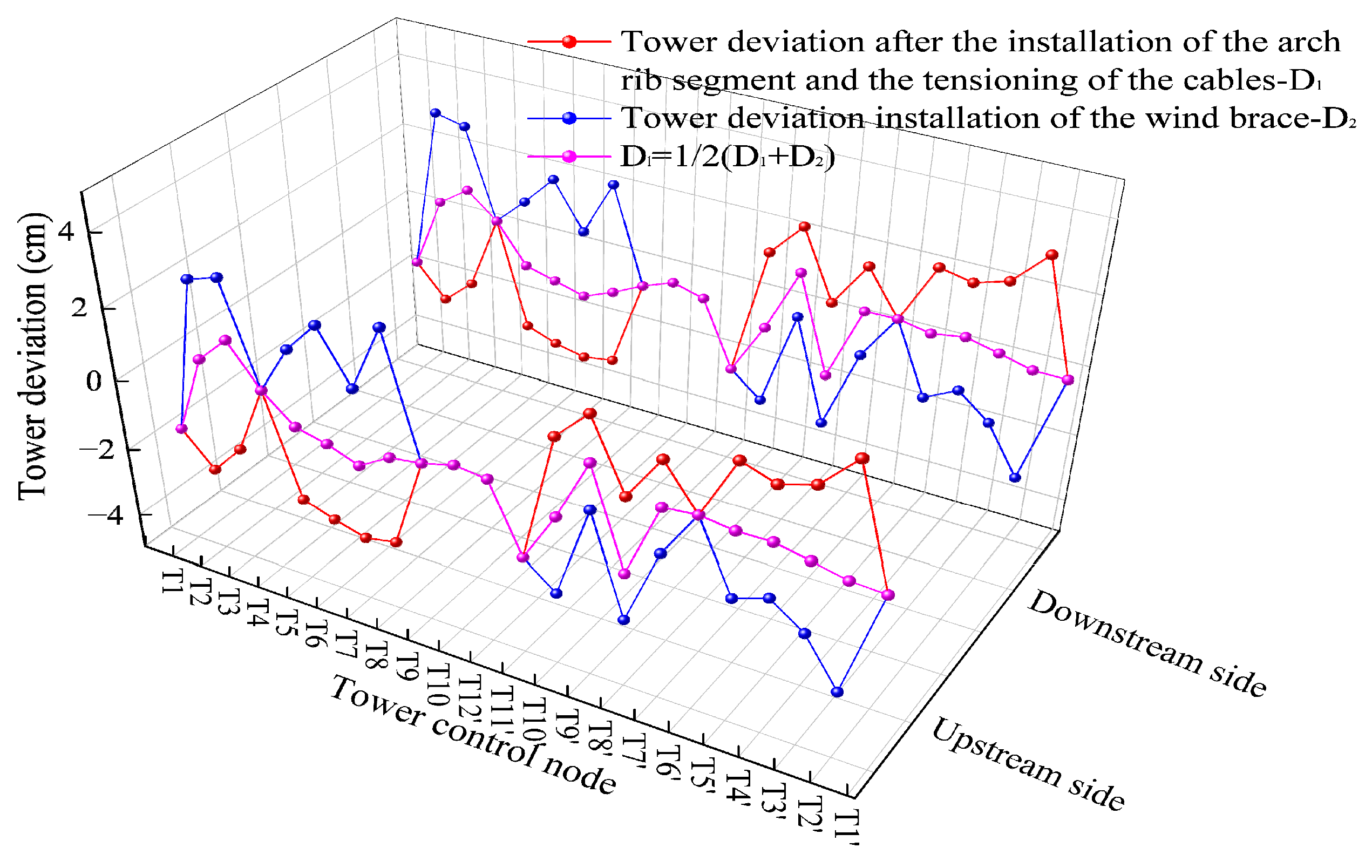
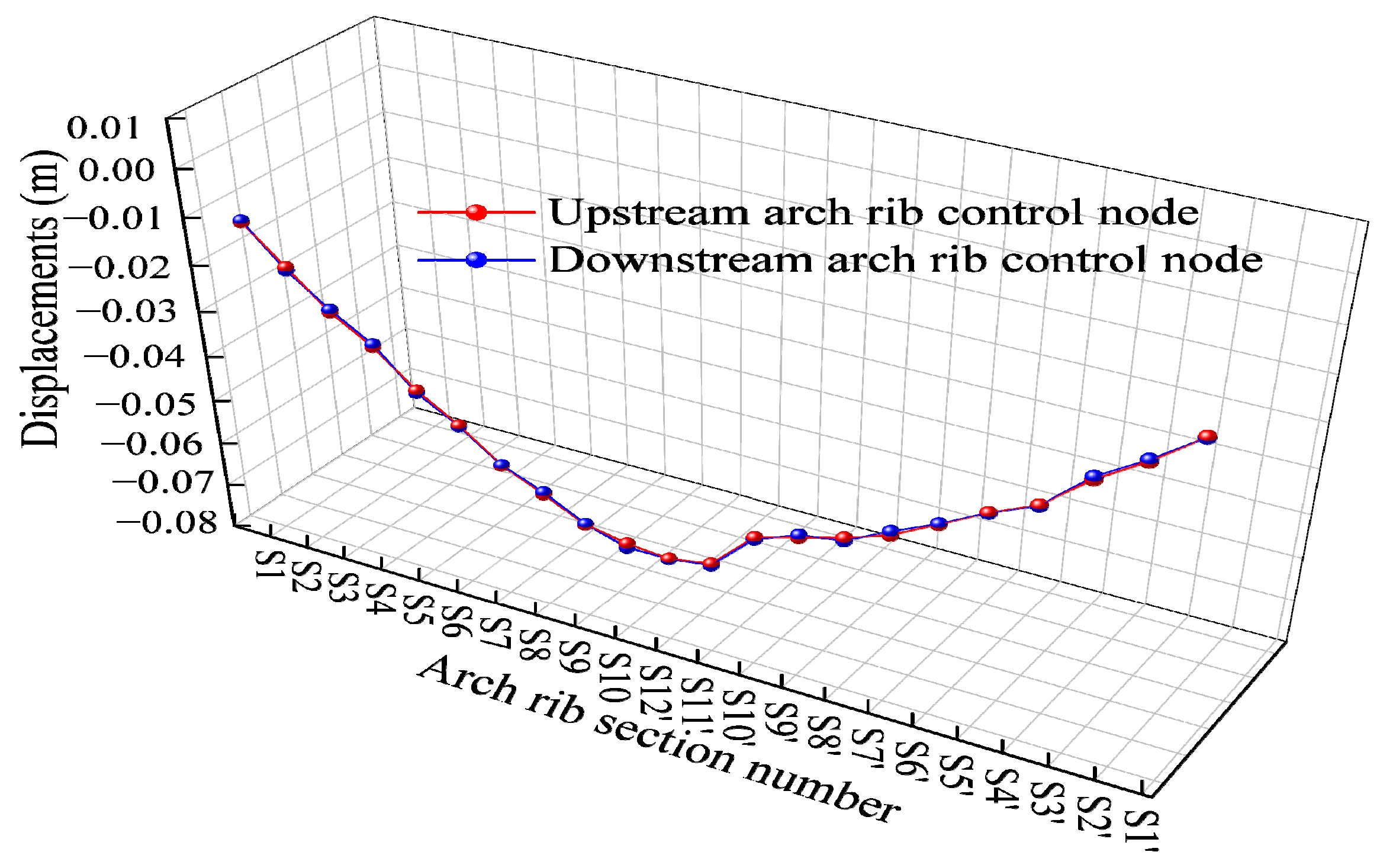
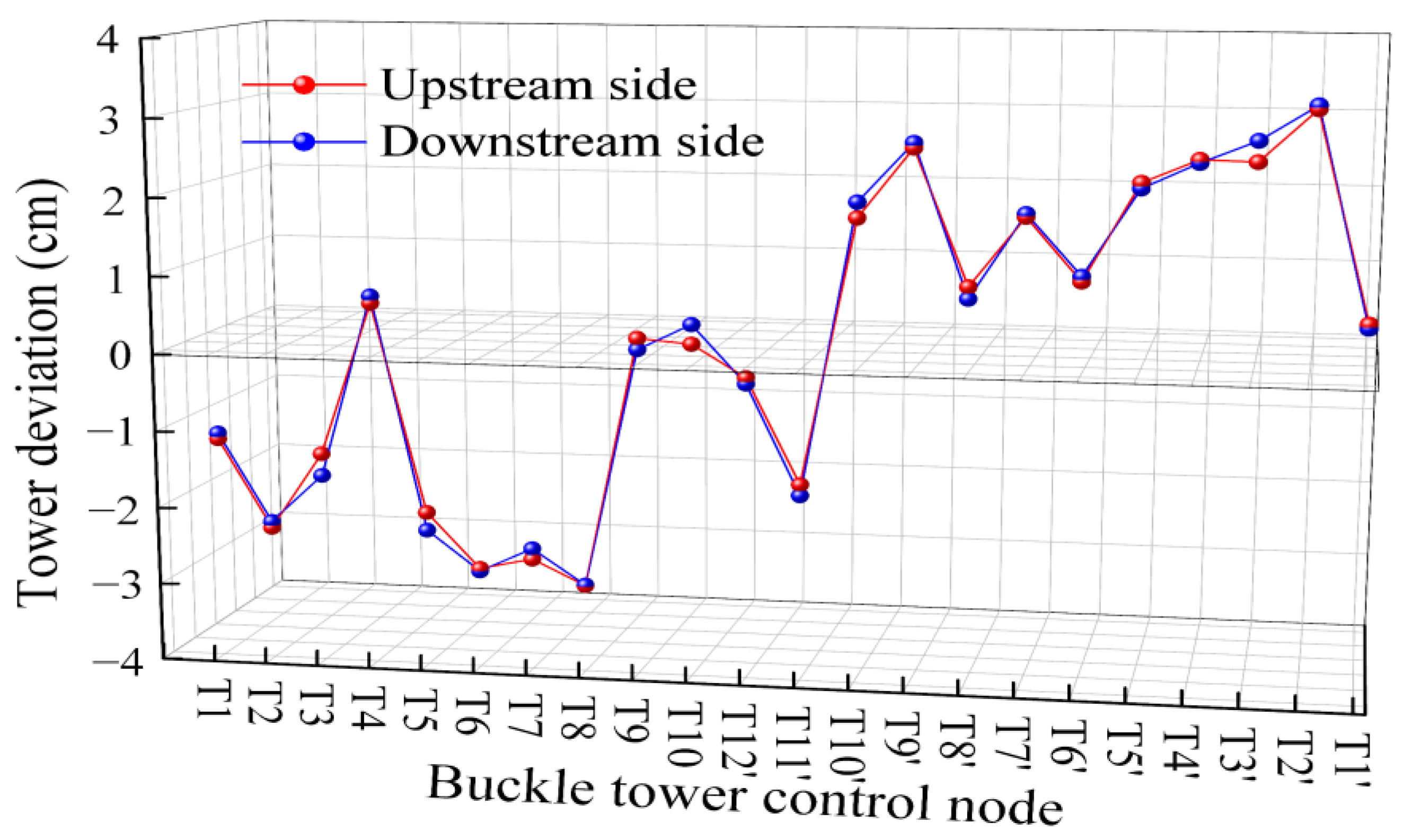
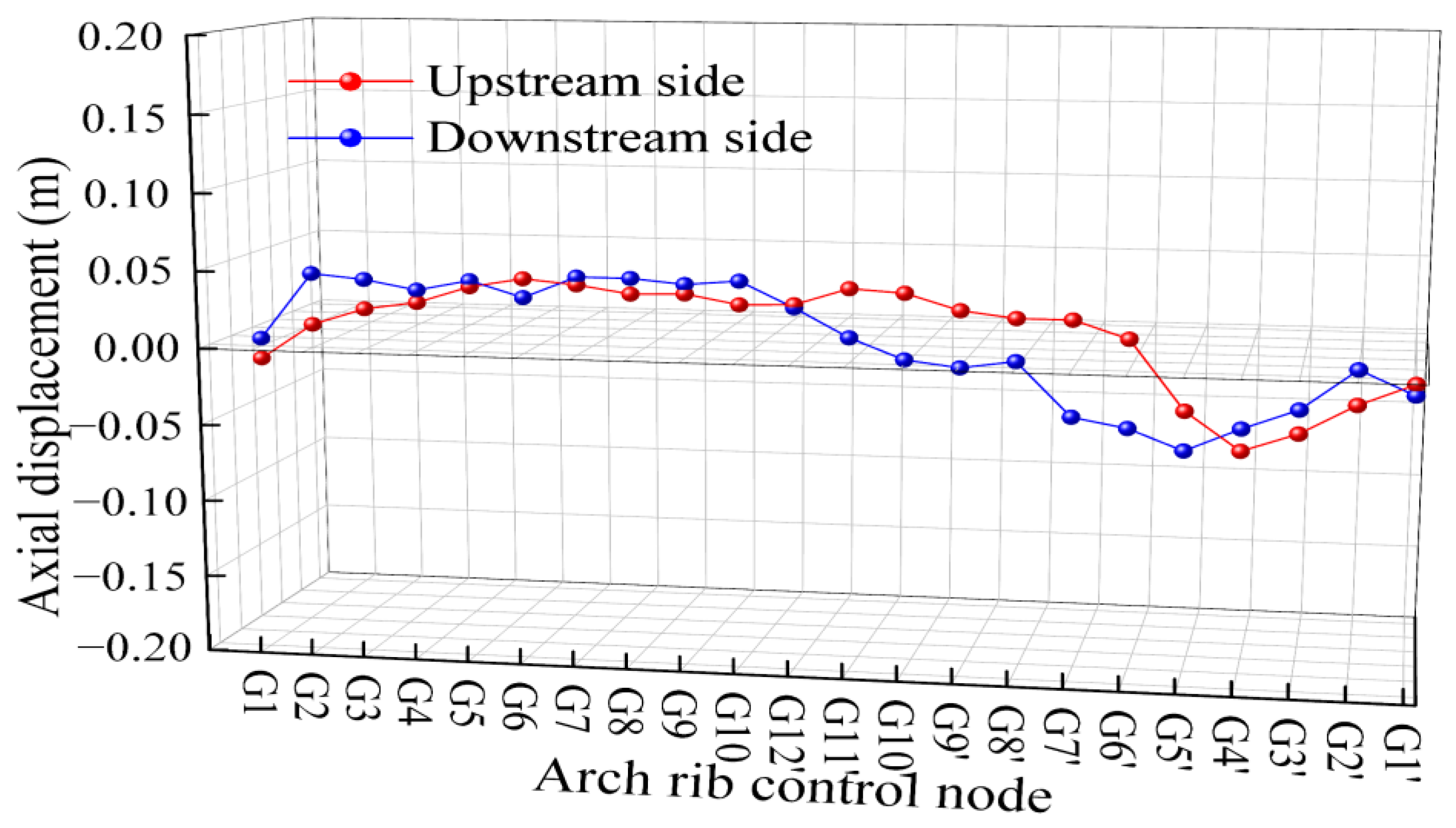
- The experimental results show that the maximum deviation between the measured and theoretical cable forces during construction is 4.81%; the maximum difference in the measured and theoretical arch displacements after tensioning is 3.4 cm; and the maximum axial displacement of the arch rib is 5 cm. These findings indicate that the measured alignment, as well as the buckle and anchor cable forces, closely match theoretical values, meeting design and specification requirements.
- (2)
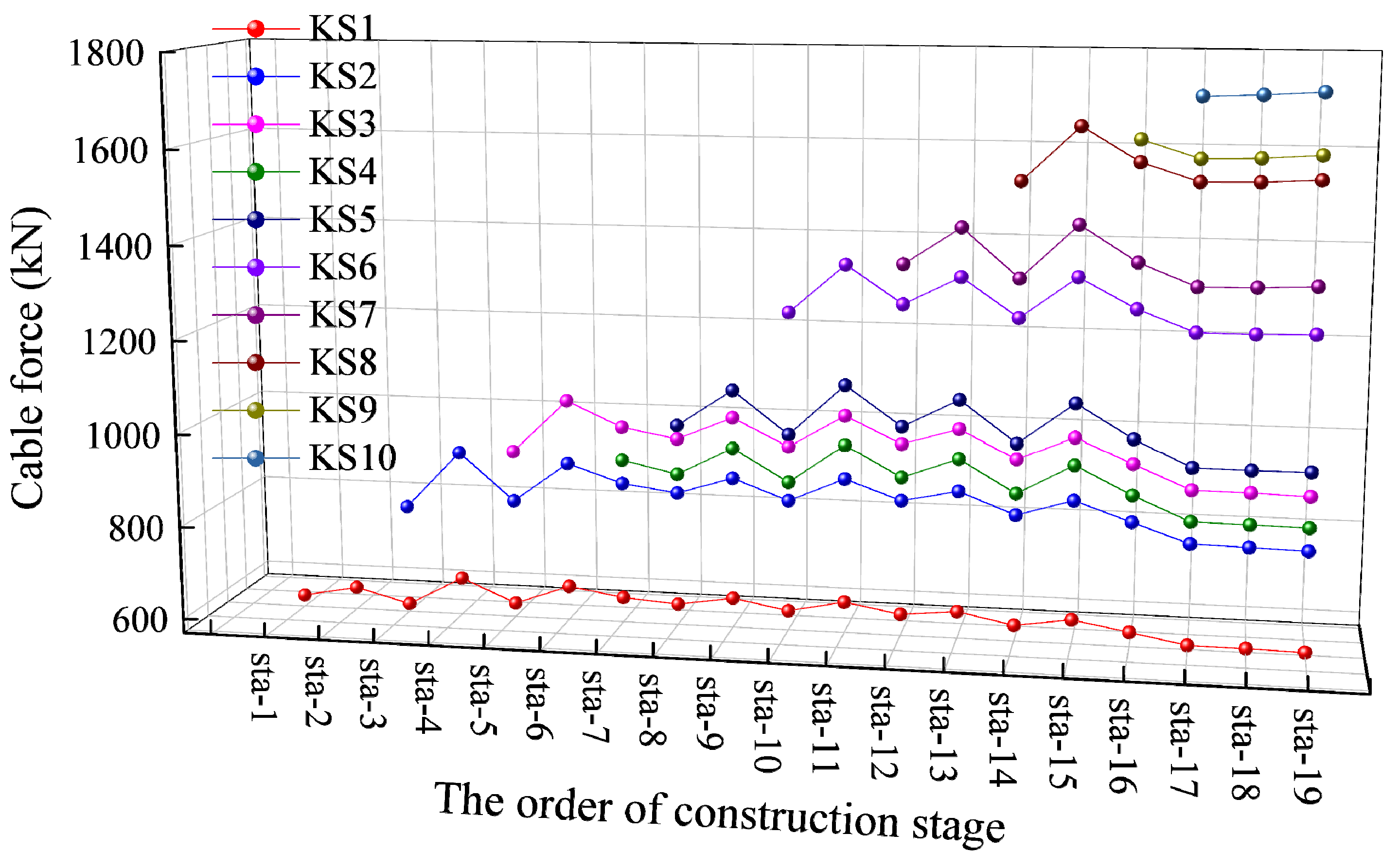
- The proposed optimization method effectively controls fluctuations in arch rib alignment, tower deviation, and cable forces during construction, ensuring a stable arch shape. It enables a one-time calculation of buckle and anchor cable forces, eliminating iterative computations and simplifying the analysis process while enhancing the accuracy of theoretical arch alignment.
- (3)
- In this study, the constraint conditions did not account for the stress state of the arch rib during construction, nor did they comprehensively consider the bridge’s in-service stress conditions. Future research could incorporate arch rib axial forces during construction as optimization objectives, impose constraints on the bridge’s in-service stress state to enhance the model’s comprehensiveness and practical applicability, and perform a systematic sensitivity study of key parameters (e.g., cable tension and section stiffness) to further verify robustness.
- (4)
- The method proposed in this paper introduces a versatile workflow for extracting influence matrices and mapping constraints applicable to any staged finite-element model, offering a portable tool for construction control of arch bridges with diverse structural forms. It also lays the theoretical foundation for incorporating in-service axial forces, temperature effects, and other stress states into construction control and for developing real-time adaptive tensioning control systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, B.C.; Liu, J.P. Review of construction and technology development of arch bridges in the world. J. Transp. Eng. 2020, 20, 27–41. [Google Scholar]
- Liang, Y.; He, W.; Tang, M.L. State of The Art Review of Bridge Aesthetics in 2020. J. Civ. Environ. Eng. 2021, 43, 234–241. [Google Scholar]
- Xia, H.; Xu, H.; Yi, Y.J. Main Bridge Design of Wujiang River Bridge of Dejiang-Yuqing Expressway. World Bridges 2023, 51, 14–21. [Google Scholar]
- Rajagopalan, G.; Karnik, M.; Pulkkinen, P. Chenab Bridge-Constructing the World’s Tallest Railway Bridge. Struct. Eng. Int. 2023, 33, 232–237. [Google Scholar] [CrossRef]
- Liu, X.H.; Chen, F.M.; Zeng, Y.Z. Overall Design of Fenglai Bridge in Chongqing. Bridge Constr. 2023, 53, 101–107. [Google Scholar]
- Zhou, S.X. The Study of Effect on Capacity of CFST Arch Bridge with Steel Tube Initial Stress; Chongqing University: Chongqing, China, 2007. [Google Scholar]
- Wang, P.H.; Tang, T.Y.; Zheng, H.N. Analysis of Cable-Stayed Bridges during Construction by Cantilever Methods. Comput. Struct. 2004, 82, 329–346. [Google Scholar] [CrossRef]
- Sun, S. Study on Determination Method of Reasonable Construction State in Hoisting Process of Long-Span Concrete Filled Steel Tube Arch Bridge; Changsha University of Science and Technology: Changsha, China, 2017. [Google Scholar]
- Wu, H.J.; He, L.; Wang, S.R. Geometry Control Method Based on Stress-Free State Theory For Long Span Concrete Filled Steel Tube Arch Bridge. Bridge Constr. 2020, 50, 20–26. [Google Scholar]
- Yao, G.W.; Chao, Y.; Wu, H.J. Construction Control of Hoisting and Installation of Arch Rib of a Half-Through CFST Stiff Skeleton Arch Bridge. Bridge Constr. 2017, 47, 107–111. [Google Scholar]
- Xu, Y.; Shen, C.Y.; Zhu, Y.B. Improved iteration algorithm for determination of tension of buckle stays for cantilever construction of Arch Bridge. Bridge Constr. 2016, 46, 65–69. [Google Scholar]
- Yu, Y.J.; Luo, Y.Q.; Zhou, W. A Combined Algorithm for the Buckle Stay Force Determinations in Cantilever Construction by Synthesizing the Zero-Displacement and Zero-Stress State Control Methods. Adv. Eng. Sci. 2024, 3–4, 1–8. [Google Scholar]
- Li, Y.; Wang, J.L.; Ge, S.S. Optimum calculation method for cable force of concrete filled steel tube arch bridge in inclined cable-stayed construction. J. Highw. Transp. Res. Dev. 2017, 11, 42–48. [Google Scholar] [CrossRef]
- Gu, Y.; Yao, C.R.; Li, Y.D. Study of alignment control method for installation of arch ribs of long span CFST arch bridge. Bridge Constr. 2014, 44, 107–113. [Google Scholar]
- Jia, Y.; Wei, C.; Huang, Z. Cable Force Calculation of Cable Hoisting of CFST Arch Bridge Research. Buildings 2023, 13, 2370. [Google Scholar] [CrossRef]
- Liu, Z.W.; Zhou, S.X.; Zou, K.R. A numerical analysis of buckle cable force of concrete arch bridge based on stress balance method. Sci. Rep. 2022, 12, 12451. [Google Scholar] [CrossRef]
- Tian, Z.C.; Peng, W.P.; Zhang, J.R. Determination of initial cable force of cantilever casting concrete arch bridge using stress balance and influence matrix methods. J. Cent. South Univ. 2019, 26, 3140–3155. [Google Scholar]
- Li, Y.D.; Yao, C.R.; Liang, Y. On Technical Advancement and Challenge of Arch Bridges. Bridge Constr. 2012, 42, 13–20. [Google Scholar]
- Zheng, J.L.; Wang, J.J.; Mou, T.M. The Design and Construction Feasibility Study of 700m Scale Concrete Filled Steel Tubular Arch Bridge. Eng. Sci. 2014, 16, 33–36. [Google Scholar]
- Zhang, Z.C.; Ye, G.R.; Wang, Y.F. Optimization of Stayed-Buckle Cable Forces During Adjustment of the Line-Shape on Long Span Arch Bridge. Eng. Mech. 2004, 6, 187–192. [Google Scholar]
- Zhang, J.M.; Zheng, J.L.; Xiao, R.C. Calculation Method for Optimizing the Installation Process of Concrete-Filled Steel Tube Arch Bridge. China J. Highw. Transp. 2005, 18, 40–44. [Google Scholar]
- Zhou, Q.; Zhou, J.T.; Ma, H. Improved algorithm of cable force for one-time cable tension on Steel tube arch ribs with segmental hoisting. J. Traffic Transp. Eng. 2020, 20, 92–101. [Google Scholar]
- Qin, D.Y.; Zheng, J.L.; Du, H.L. Optimization Calculation Method for Stayed-Buckle Cable Force under One-Time Tension by Buckle Stay Method and Its Application. China Railw. Sci. 2020, 41, 52–60. [Google Scholar]
- Zhou, Y.; Wang, Y.; Zhou, J.T. Arch Forming Calculation Theory and Control Method of 500m Steel Tube Arch Bridge, China. J. Highw. Transp. 2022, 35, 60–72. [Google Scholar]
- Song, C.L.; Xiao, R.C.; Sun, B. Cable force optimization of cable-stayed bridges: A surrogate model-assisted differential evolution method combined with B-Spline interpolation curves. Eng. Struct. 2023, 283, 115856. [Google Scholar] [CrossRef]
- Tian, Z.; Zhang, Z.; Ning, C. Multi-objective optimization of cable force of arch bridge constructed by cable-stayed cantilever cast-in-situ method based on improved NSGA-II. Structures 2024, 59, 105782. [Google Scholar] [CrossRef]
- Dai, Y.W.; Wang, Y.Y. A research to cable force optimizing calculation of cable-stayed arch bridge. Procedia Eng. 2012, 37, 155–160. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; M. Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Huang, Y.; Xu, Y.; Chen, S. Research on Solution Method for Cable-Stayed Bridge Formation Based on Influence Matrix and Interior Point Method. Buildings 2025, 15, 673. [Google Scholar] [CrossRef]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A Trust Region Method Based on Interior Point Techniques for Nonlinear Programming. Math. Program. 2000, 89, 149–185. [Google Scholar] [CrossRef]
- Waltz, R.A.; Morales, J.L.; Nocedal, J.; Orban, D. An interior algorithm for nonlinear optimization that combines line search and trust region steps. Math. Program. 2006, 107, 391–408. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An Interior Point Algorithm for Large-Scale Nonlinear Programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Mohammadzadeh, S.; Miri, A.; Nouri, M. Enhancing the structural performance of masonry arch bridges with ballast mats. J. Perform. Constr. Facil. 2017, 31, 04017089. [Google Scholar] [CrossRef]
- Lonetti, P.; Pascuzzo, A. Optimum Design Analysis of Hybrid Cable-Stayed Suspension Bridges. Adv. Eng. Softw. 2014, 73, 53–66. [Google Scholar]
- Dan, Q.L.; Qin, S.Q.; Wei, K. Equation for Geometric Shape Control of Structure Formed in Stages Based on Plane Beam Elements. Bridge Constr. 2017, 47, 42–47. [Google Scholar]
- Yuan, R.A.; Qin, S.Q. Application of Unstressed State Method to Construction of Steel Strand Stay Cable. Bridge Constr. 2012, 42, 75–79. [Google Scholar]
- GB50017-2020; Code for Design of Steel Structure. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2020.
- JTG/TF50-2011; Technical Specification for Construction of Highway Bridge and Culvert. Ministry of Transport of China: Beijing, China, 2011.
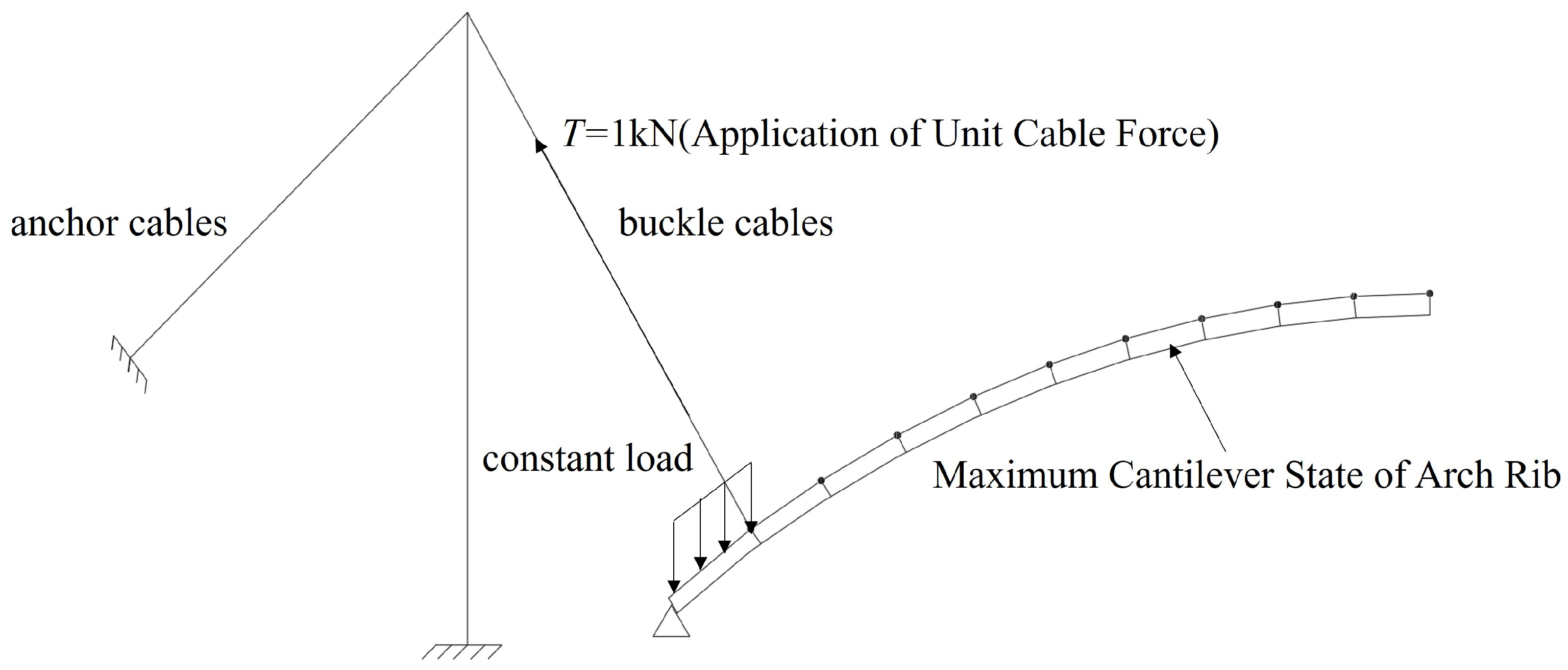
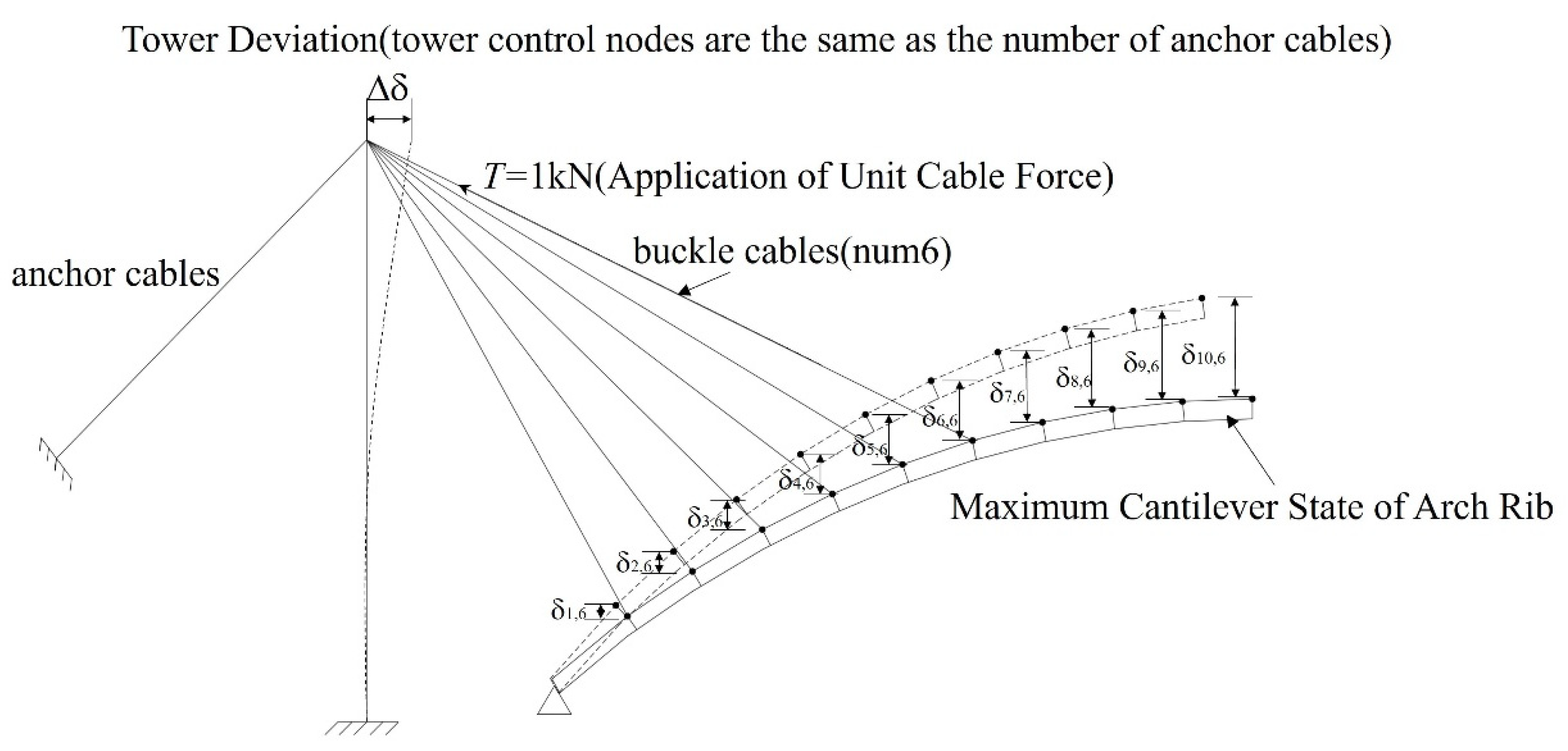

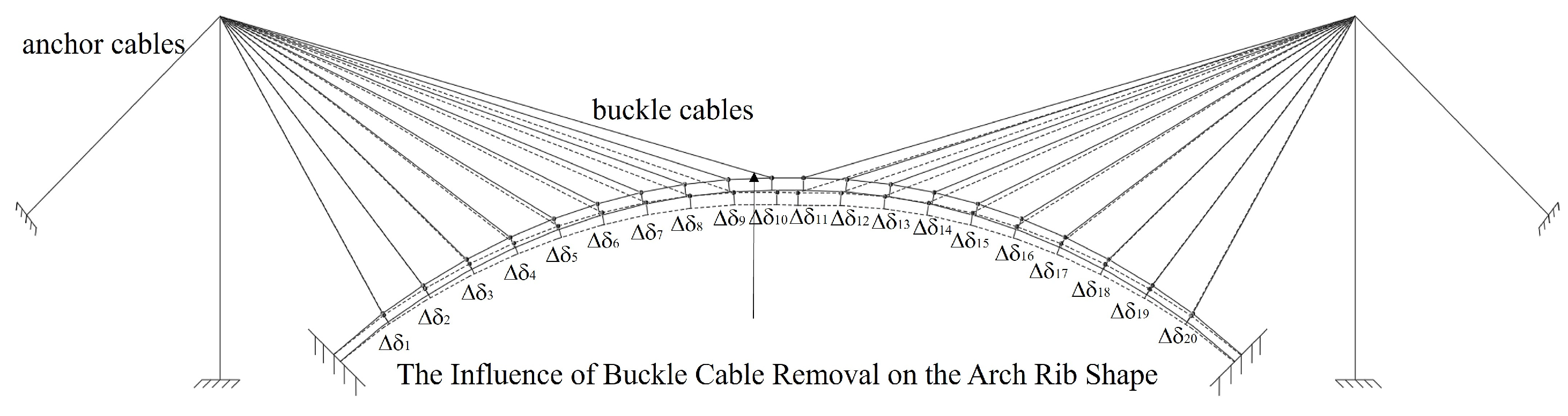
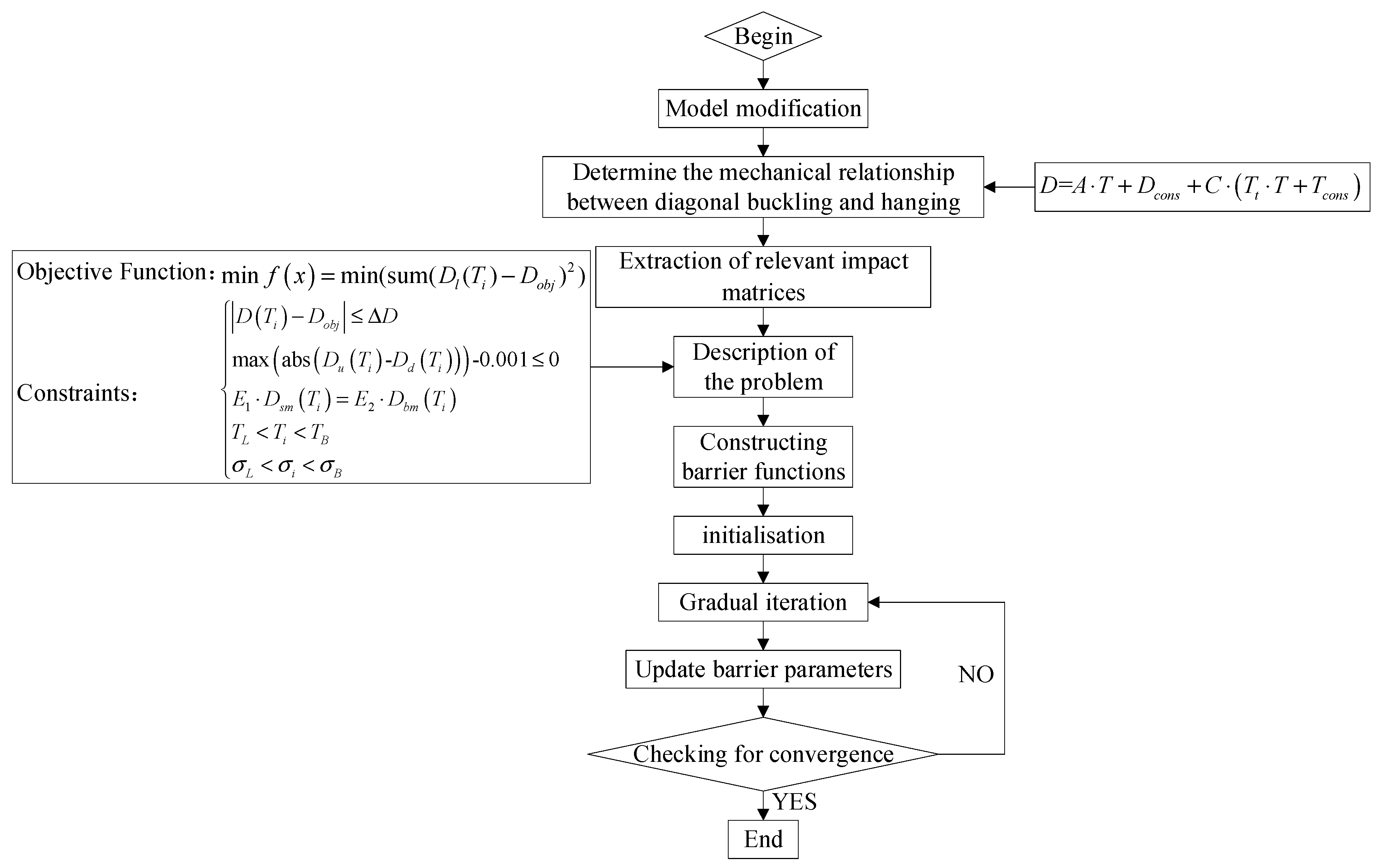
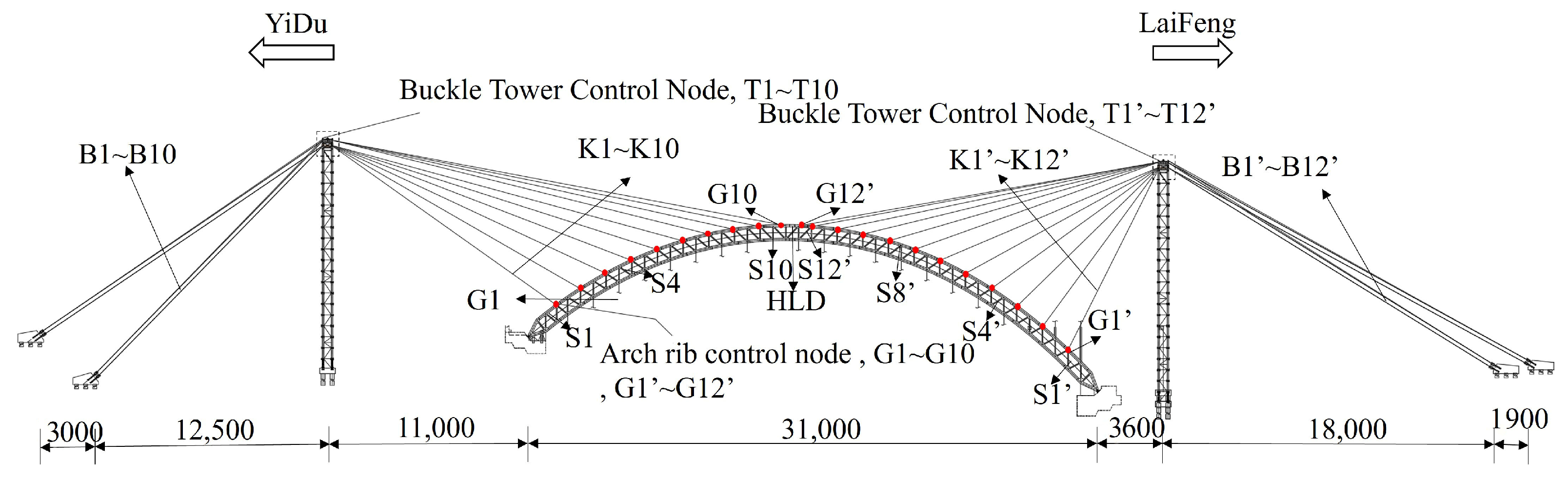


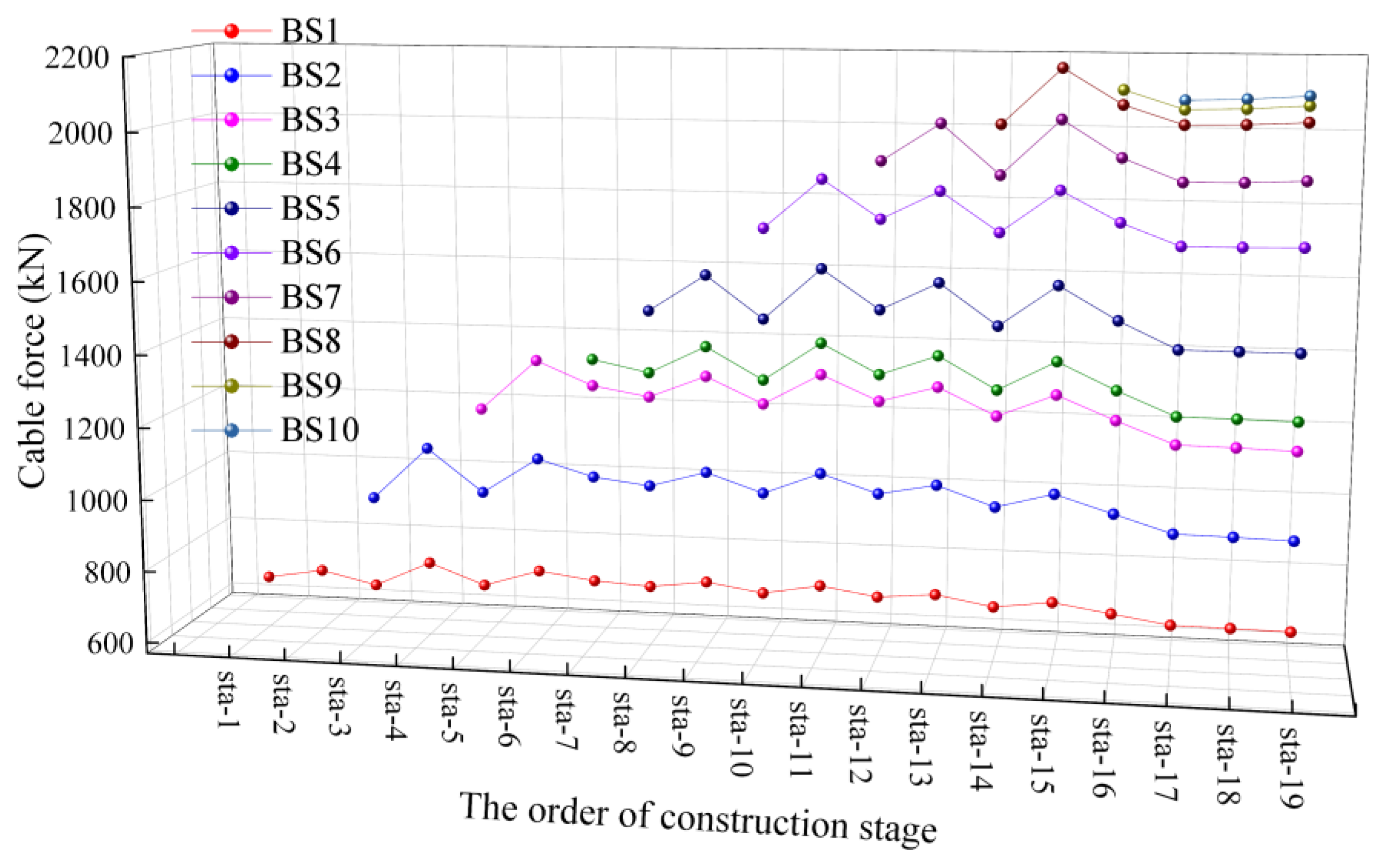
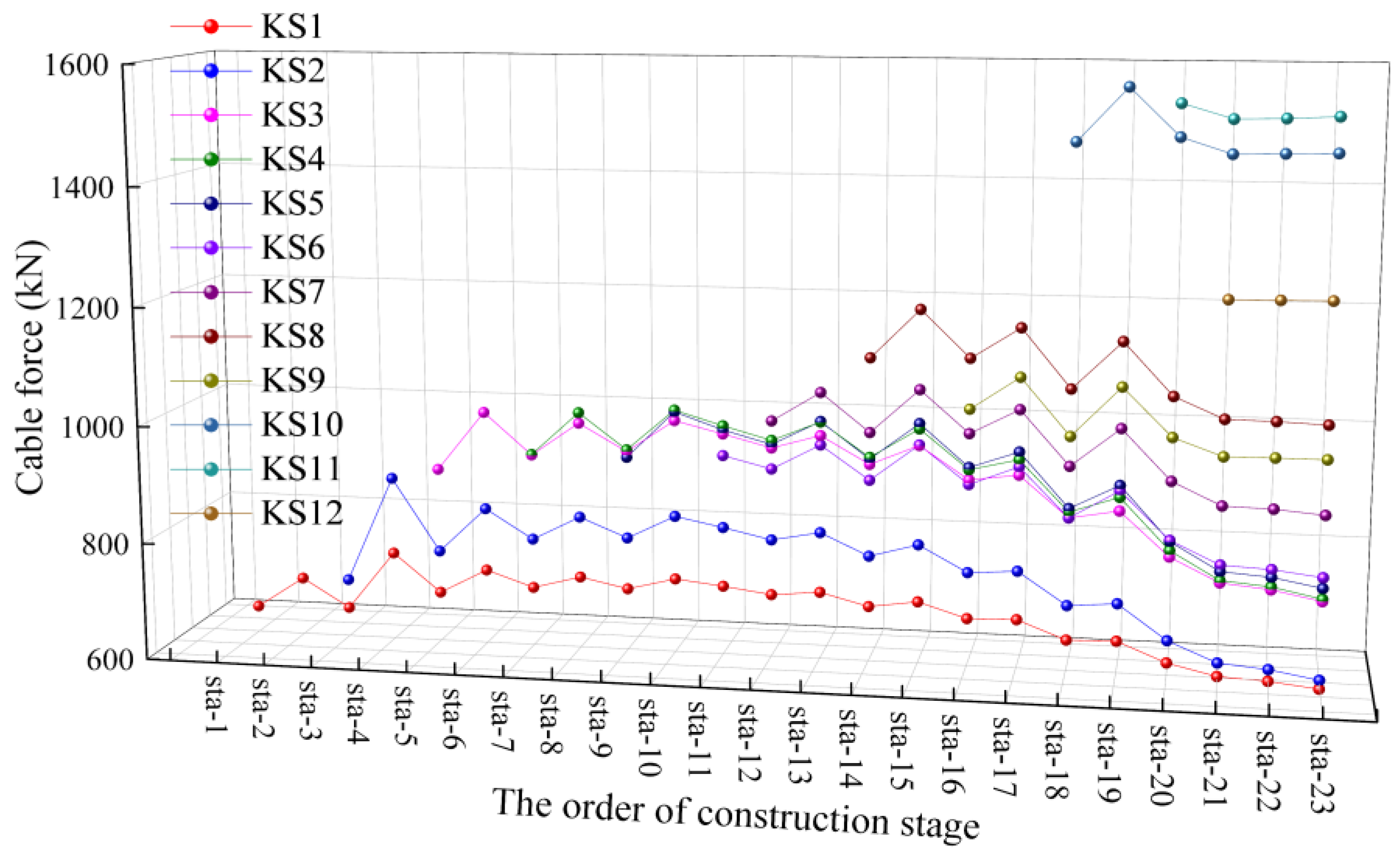
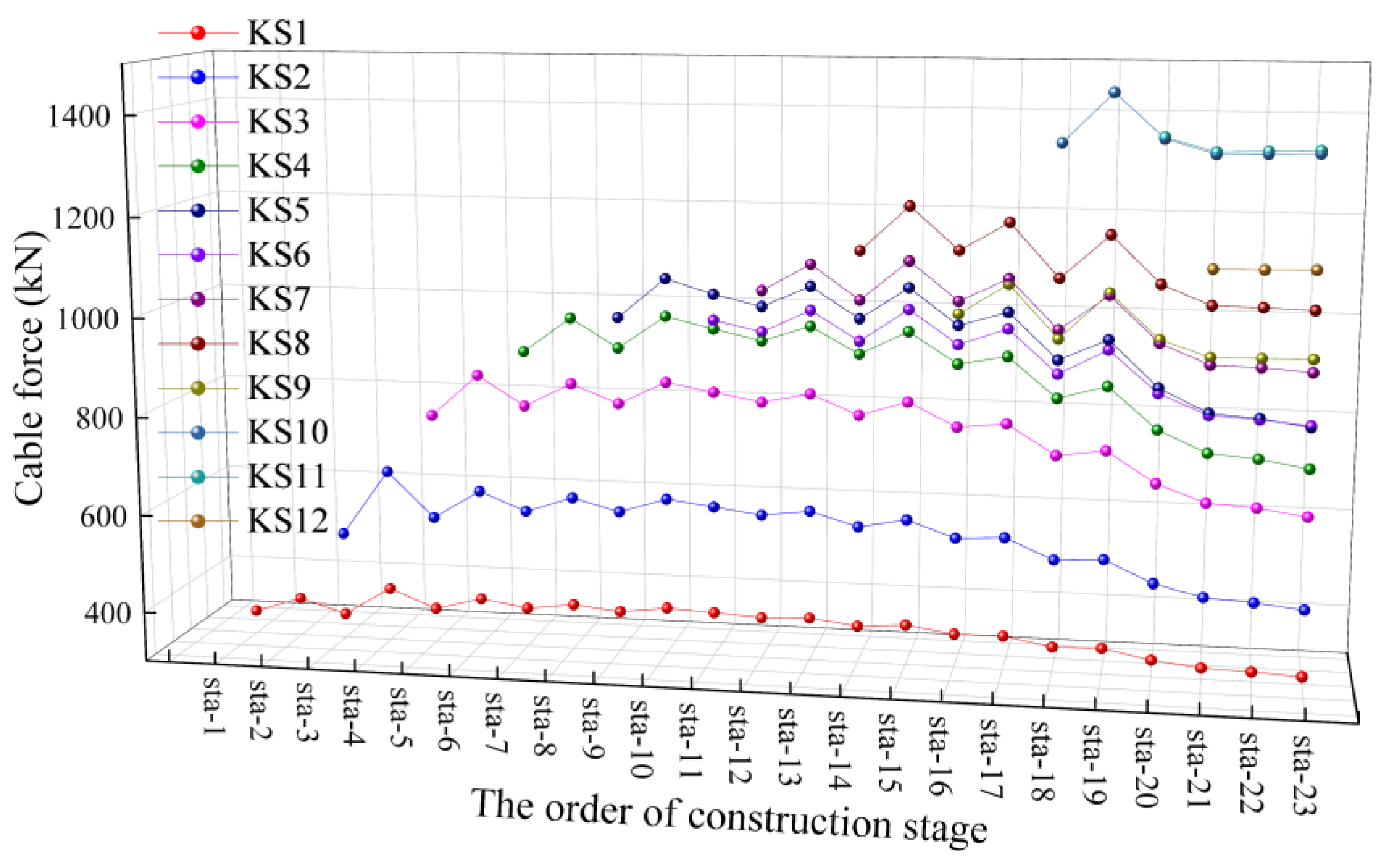
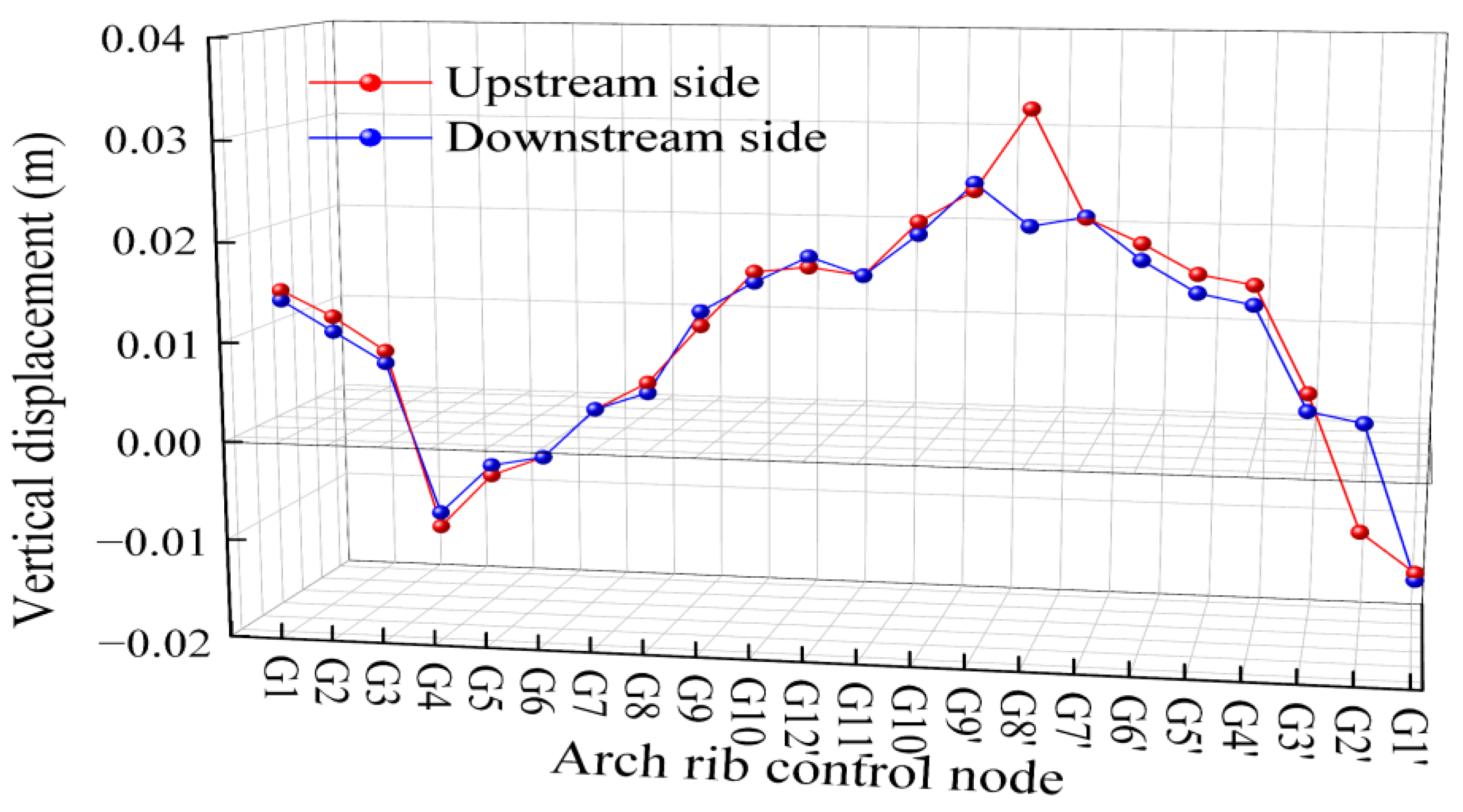
| Working Condition | Construction State | Working Condition | Construction State |
|---|---|---|---|
| 1 | Tower Construction | 20 | Segment 10 + Buckle and Anchor Cable 10 |
| 2 | Wind-Resistant Cable Installation | 21 | Remaining Diagonal Braces of the Second Section of Wind Brace |
| 3 | Segment 1 + Buckle and Anchor Cable 1 | 22 | Segment 11 + Buckle and Anchor Cable 11 |
| 4 | Removal of Temporary Support of Arch Rib | 23 | Segment 12 + Buckle and Anchor Cable 12 |
| 5 | Segment 2 + Buckle and Anchor Cable 2 | 24 | Closure Segment Assembly |
| 6 | The Sixth Section of Wind Brace | 25 | The First Section of Wind Brace |
| 7 | Segment 3 + Buckle and Anchor Cable 3 | 26 | Remove Buckle and Anchor Cable 12 |
| 8 | The Fifth Section of Wind Brace | 27 | Remove Buckle and Anchor Cable 11 |
| 9 | Segment 4 + Buckle and Anchor Cable 4 | 28 | Remove Buckle and Anchor Cable 10 |
| 10 | Transverse Connections and Oblique Web Members of the Fourth Section of Wind Brace | 29 | Remove Buckle and Anchor Cable 9 |
| 11 | Segment 5 + Buckle and Anchor Cable 5 | 30 | Remove Buckle and Anchor Cable 8 |
| 12 | Remaining Diagonal Braces of the Fourth Section of Wind Brace | 31 | Remove Buckle and Anchor Cable 7 |
| 13 | Segment 6 + Buckle and Anchor Cable 6 | 32 | Remove Buckle and Anchor Cable 6 |
| 14 | Segment 7 + Buckle and Anchor Cable 7 | 33 | Remove Buckle and Anchor Cable 5 |
| 15 | Transverse Connections and Oblique Web Members of the Third Section of Wind Brace | 34 | Remove Buckle and Anchor Cable 4 |
| 16 | Segment 8 + Buckle and Anchor Cable 8 | 35 | Remove Buckle and Anchor Cable 3 |
| 17 | Remaining Diagonal Braces of the Third Section of Wind Brace | 36 | Remove Buckle and Anchor Cable 2 |
| 18 | Segment 9 + Buckle and Anchor Cable 9 | 37 | Remove Buckle and Anchor Cable 1 |
| 19 | Transverse Connections and Oblique Web Members of the Second Section of Wind Brace |
| Number | Theoretical Cable Force (kN) | Measured Cable Force (kN) | Error |
|---|---|---|---|
| K-1 | 595 | 614 | 3.20% |
| B-1 | 713 | 722 | 1.30% |
| K-2 | 805 | 824 | 2.40% |
| B-2 | 956 | 970 | 1.42% |
| K-3 | 937 | 945 | 0.81% |
| B-3 | 1220 | 1232 | 1.01% |
| K-4 | 927 | 919 | −0.82% |
| B-4 | 1369 | 1355 | −1.00% |
| K-5 | 1007 | 1019 | 1.15% |
| B-5 | 1508 | 1544 | 2.42% |
| K-6 | 1257 | 1292 | 2.78% |
| B-6 | 1741 | 1761 | 1.14% |
| K-7 | 1365 | 1425 | 4.38% |
| B-7 | 1927 | 1975 | 2.51% |
| K-8 | 1542 | 1588 | 3.01% |
| B-8 | 2029 | 2059 | 1.48% |
| K-9 | 1631 | 1675 | 2.70% |
| B-9 | 2123 | 2145 | 1.02% |
| K-10 | 1720 | 1765 | 2.61% |
| B-10 | 2098 | 2146 | 2.31% |
| Number. | Theoretical Cable Force (kN) | Measured Cable Force (kN) | Error |
|---|---|---|---|
| K-1′ | 645 | 640 | −0.71% |
| B-1′ | 347 | 341 | −1.71% |
| K-2′ | 700 | 694 | −0.90% |
| B-2′ | 521 | 521 | −0.07% |
| K-3′ | 902 | 892 | −1.09% |
| B-3′ | 777 | 759 | −2.37% |
| K-4′ | 934 | 940 | 0.68% |
| B-4′ | 915 | 918 | 0.28% |
| K-5′ | 935 | 962 | 2.93% |
| B-5′ | 990 | 1011 | 2.16% |
| K-6′ | 944 | 972 | 2.99% |
| B-6′ | 990 | 1023 | 3.35% |
| K-7′ | 1006 | 1019 | 1.28% |
| B-7′ | 1052 | 1063 | 1.00% |
| K-8′ | 1118 | 1064 | −4.81% |
| B-8′ | 1136 | 1090 | −4.05% |
| K-9′ | 1037 | 1026 | −1.04% |
| B-9′ | 1016 | 993 | −2.23% |
| K-10′ | 1480 | 1445 | −2.39% |
| B-10′ | 1354 | 1319 | −2.61% |
| K-11′ | 1544 | 1528 | −1.04% |
| B-11′ | 1368 | 1351 | −1.23% |
| K-12′ | 1230 | 1188 | −3.39% |
| B-12′ | 1116 | 1087 | −2.61% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Ma, X.; Chen, W.; Xu, W.; Kang, Y.; Wu, Y. Constrained Optimization for the Buckle and Anchor Cable Forces Under One-Time Tension in Long Span Arch Bridge Construction. Buildings 2025, 15, 1529. https://doi.org/10.3390/buildings15091529
Zhang X, Ma X, Chen W, Xu W, Kang Y, Wu Y. Constrained Optimization for the Buckle and Anchor Cable Forces Under One-Time Tension in Long Span Arch Bridge Construction. Buildings. 2025; 15(9):1529. https://doi.org/10.3390/buildings15091529
Chicago/Turabian StyleZhang, Xiaoyu, Xuming Ma, Wei Chen, Wei Xu, Yuan Kang, and Yonghong Wu. 2025. "Constrained Optimization for the Buckle and Anchor Cable Forces Under One-Time Tension in Long Span Arch Bridge Construction" Buildings 15, no. 9: 1529. https://doi.org/10.3390/buildings15091529
APA StyleZhang, X., Ma, X., Chen, W., Xu, W., Kang, Y., & Wu, Y. (2025). Constrained Optimization for the Buckle and Anchor Cable Forces Under One-Time Tension in Long Span Arch Bridge Construction. Buildings, 15(9), 1529. https://doi.org/10.3390/buildings15091529






