Safety Risk Assessment of Jacking Renovation Construction for Aging Bridges Based on DBN and Fuzzy Set Theory
Abstract
1. Introduction
2. Risk Analysis Methods
2.1. Bayesian Network and Dynamic Bayesian Network
2.2. Leaky Noisy-OR Gate Extension Model and Fuzzy Set Theory
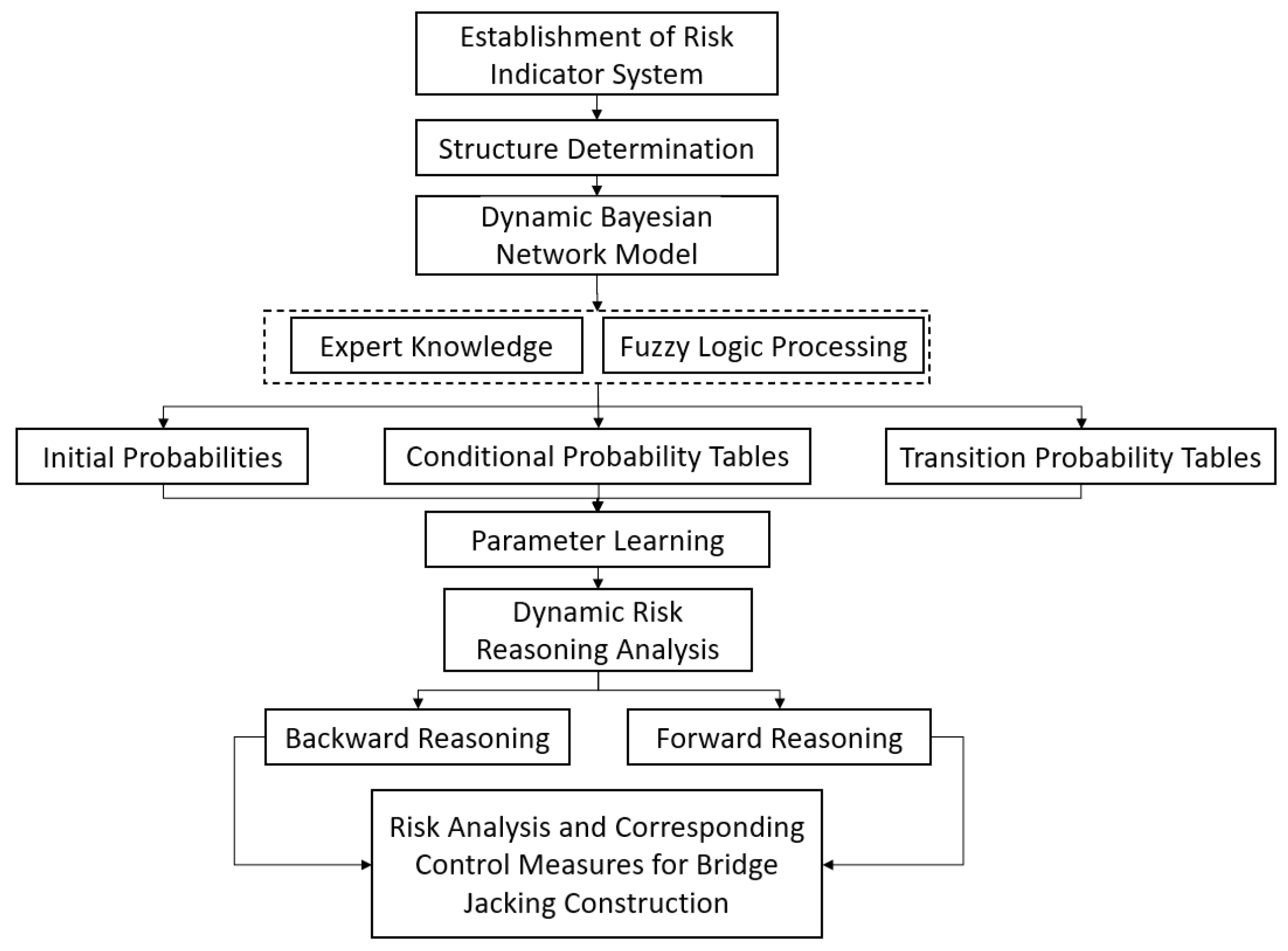
3. Safety Risk Analysis of Bridge Jacking Construction Based on DBN
3.1. Establishment of the Risk Indicator System
3.2. DBN Network Model Construction
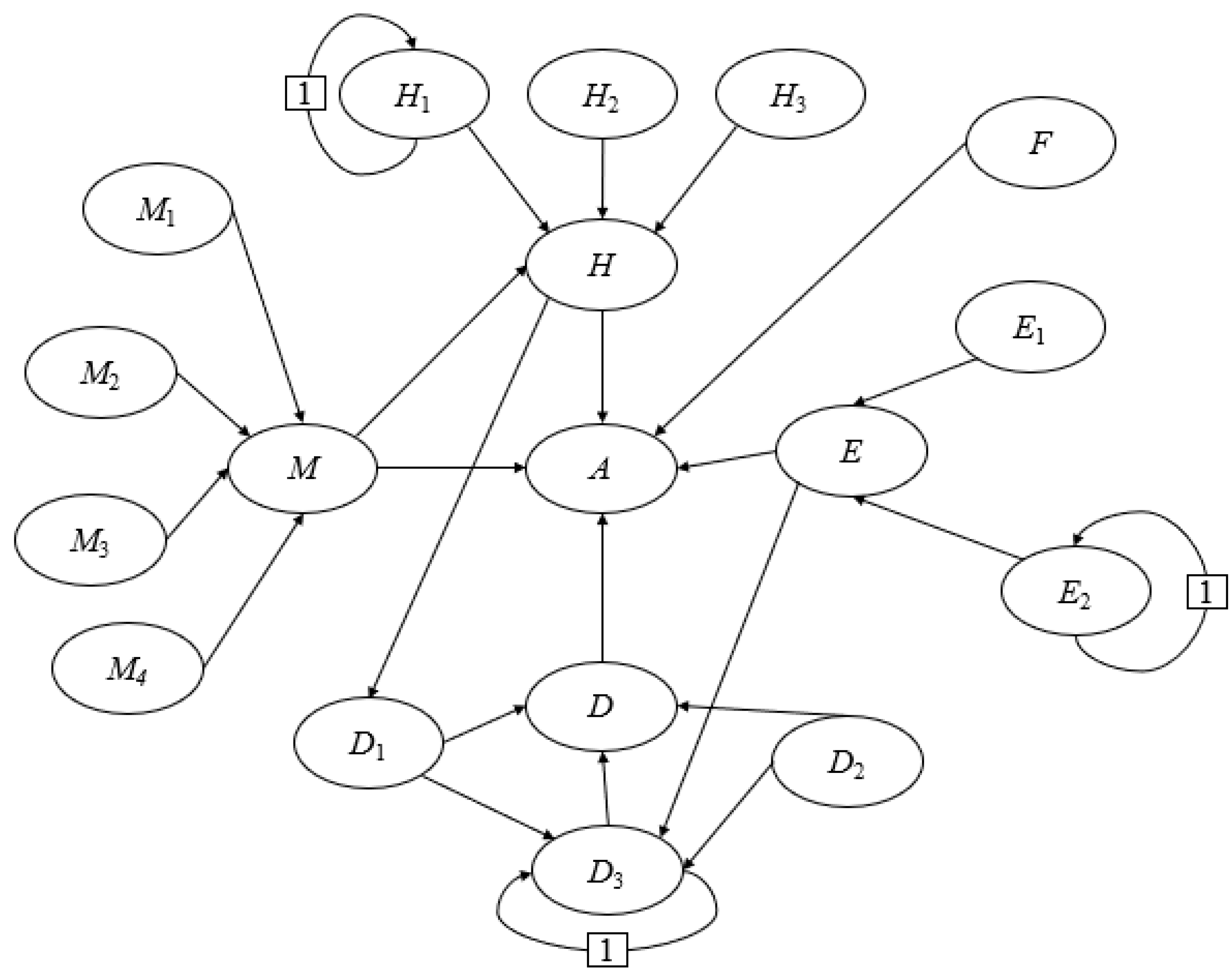
3.2.1. Network Structure Design
3.2.2. Parameter Learning
4. Application of the DBN Model in Bridge Jacking Construction
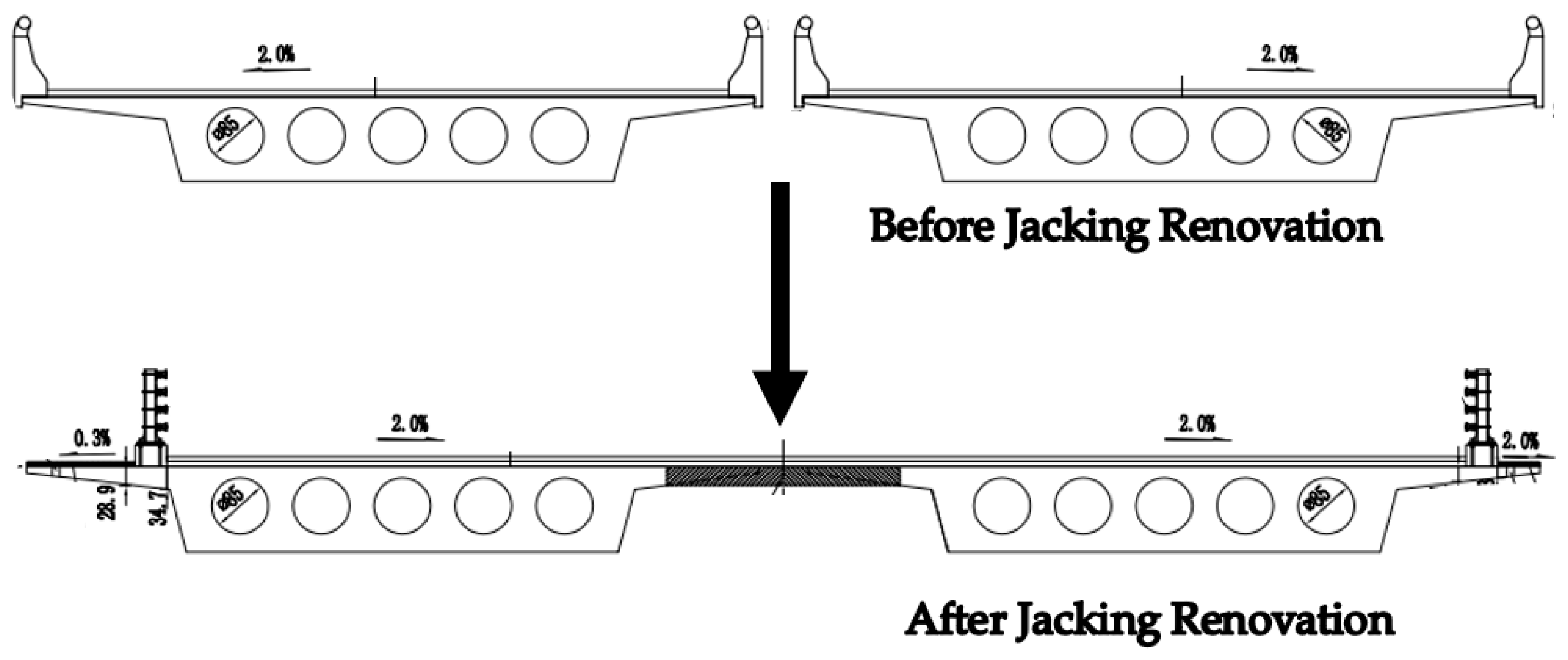
4.1. Project Overview
4.2. Establishment and Parameter Determination of the DBN Model
4.3. Risk Analysis
4.4. Discussion on DBN Model
5. Conclusions
- (1)
- A dynamic risk assessment model was developed by integrating the temporal inference capabilities of DBN with the uncertainty handling mechanisms of fuzzy set theory. The DEMATEL method was employed to quantify interactions among risk factors, coupled with expert scoring and Gaussian membership functions, effectively addressing parameter learning challenges in data-scarce scenarios and enhancing the model’s robustness and adaptability.
- (2)
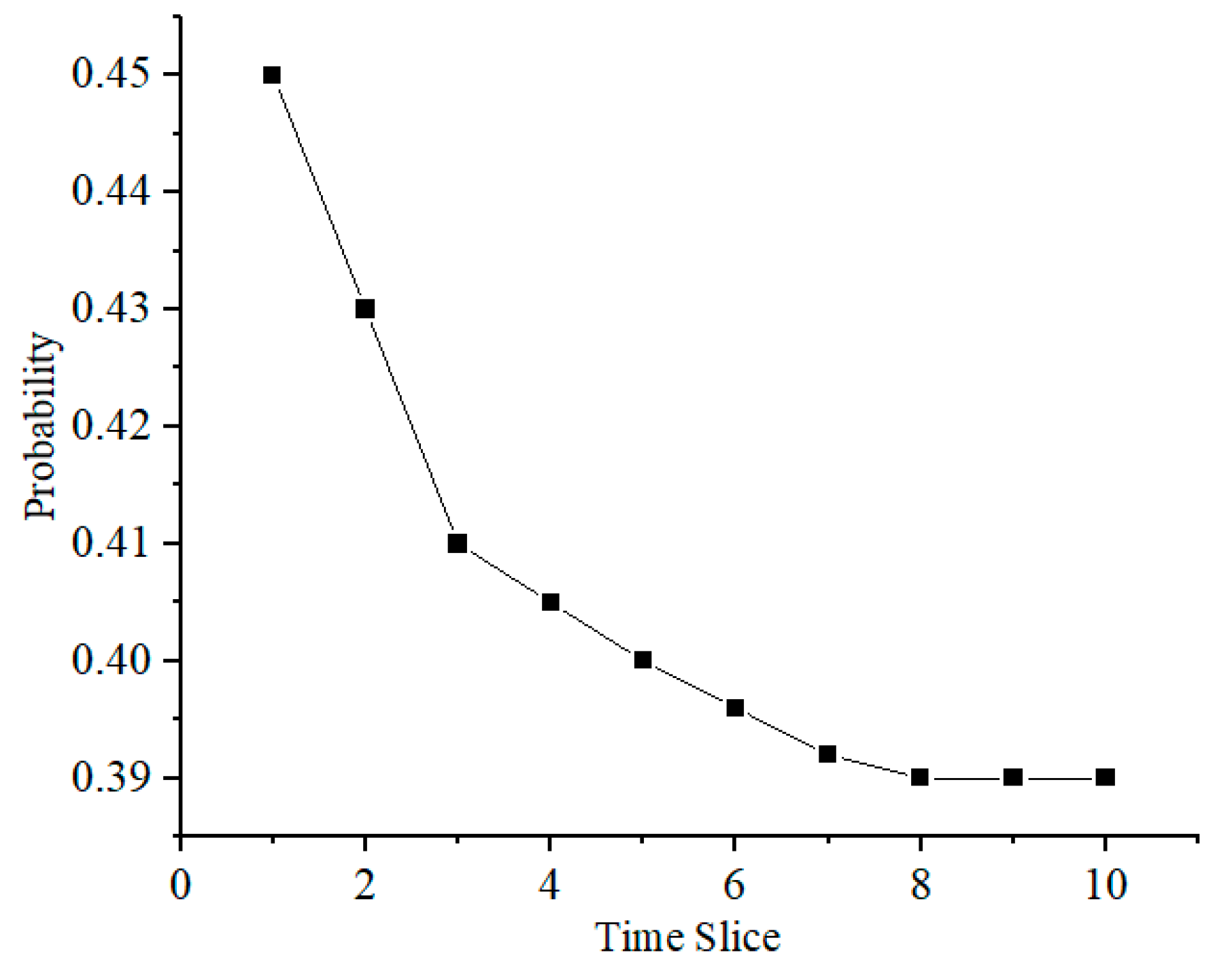
- Using an elevated bridge jacking project in Qingdao, China, as a case study, the practical engineering value of the model was validated. Forward inference results show that the overall construction risk probability decreased from 0.45 to 0.39 (a reduction of 13.3%), highlighting the need to prioritize the high-risk initial phase. Backward inference precisely identified poor foundation (ROV = 0.306), inadequate safety technical briefing (ROV = 0.305), and substructure instability (ROV = 0.298) as critical sensitive factors, uncovering the dominant driving mechanisms in the dynamic evolution of risks.
- (3)
- Based on the analysis results, targeted risk prevention measures were proposed, encompassing detailed foundation surveys and reinforcement, redundant support system design, enhanced operational standardization, and integration of real-time monitoring technologies. Future research could incorporate digital twin technology to further optimize the model’s dynamic updating capabilities and explore collaborative decision-making frameworks under multi-risk coupling scenarios, thereby improving risk management efficiency in complex engineering environments.
- (4)
- The DBN model presented in this study was specifically designed for a particular bridge jacking construction project, effectively capturing project-specific risk factors. However, the fixed nature of its structure and parameters limits its applicability across different bridge types (e.g., arch bridges, suspension bridges), locations (e.g., urban, mountainous), or project conditions (e.g., scale, duration). To transform it into a universal risk analysis tool capable of accommodating diverse bridge jacking scenarios, systematic modifications are required in three key areas: model structure, parameter estimation, and data acquisition.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DBN | Dynamic Bayesian Network |
| BN | Bayesian Network |
| FST | Fuzzy Set Theory |
| DEMATEL | Decision Making Trial and Evaluation Laboratory |
| CPT | Conditional Probability Table |
| ROV | Relative Operating Value |
| TVFEMD | Time-Varying Filter Empirical Mode Decomposition |
| ED | Encoder–Decoder |
| LSTM | Long Short-Term Memory |
| BIM | Building Information Modeling |
| CNN | Convolutional Neural Networks |
| AHP | Analytic Hierarchy Process |
| FTA | Fault Tree Analysis |
| SEM | Structural Equation Modeling |
References
- American Road & Transportation Builders Association (ARTBA). 2023 Bridge Report; ARTBA: Washington, DC, USA, 2023. [Google Scholar]
- Kumamoto, H.; Henley, E.J. Automated Fault Tree Synthesis by Disturbance Analysis. Ind. Eng. Chem. Fundam. 1986, 25, 233–239. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making—The Analytic Hierarchy and Network Processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Fang, S.E.; Yu, Q.K. Bayesian Networks-Based Hierarchical Vulnerability Evaluation of Long-Span Structures. Eng. Struct. 2024, 306, 117867. [Google Scholar] [CrossRef]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers; World Scientific: Singapore, 1996. [Google Scholar]
- Lee, R.C.T. Fuzzy Logic and the Resolution Principle. J. ACM 1972, 19, 109–119. [Google Scholar] [CrossRef]
- Chen, S.M. A Fuzzy Reasoning Approach for Rule-Based Systems Based on Fuzzy Logics. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 769–778. [Google Scholar] [CrossRef]
- Pearl, J. Fusion, Propagation, and Structuring in Belief Networks. In Probabilistic and Causal Inference: The Works of Judea Pearl; ACM Books: New York, NY, USA, 2022; pp. 139–188. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Wu, W.J.; Wang, Y.F. Bridge Life Cycle Assessment with Data Uncertainty. Int. J. Life Cycle Assess. 2016, 21, 569–576. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Soleimani, F. Analytical Seismic Performance and Sensitivity Evaluation of Bridges Based on Random Decision Forest Framework. Structures 2021, 32, 1234–1245. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, Y.; Zhu, W.; Li, T.; Zhang, L. Real-Time Early Safety Warning for Personnel Intrusion Behavior on Construction Sites Using a CNN Model. Buildings 2023, 13, 2206. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, Y.; Wang, X.; Chen, L. Predicting Bridge Longitudinal Displacement from Monitored Operational Loads with Hierarchical CNN for Condition Assessment. Mech. Syst. Signal Process. 2023, 200, 110623. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Li, C.; Yan, M.; Wang, J.; Zhang, K. Research on Deformation Safety Risk Warning of Super-Large and Ultra-Deep Foundation Pits Based on Long Short-Term Memory. Buildings 2024, 14, 1464. [Google Scholar] [CrossRef]
- Xin, J.; Li, H.; Wang, T.; Liu, Y. A Signal Recovery Method for Bridge Monitoring System Using TVFEMD and Encoder-Decoder Aided LSTM. Measurement 2023, 214, 112797. [Google Scholar] [CrossRef]
- Yue, Z.; Wang, J.; Li, X.; Zhang, K. Mechanics-Guided Optimization of an LSTM Network for Real-Time Modeling of Temperature-Induced Deflection of a Cable-Stayed Bridge. Eng. Struct. 2022, 252, 113619. [Google Scholar] [CrossRef]
- Liao, Y.; Chen, X.; Zhang, Q.; Liu, H. Attention-Based LSTM (AttLSTM) Neural Network for Seismic Response Modeling of Bridges. Comput. Struct. 2023, 275, 106915. [Google Scholar] [CrossRef]
- You, Y.; Zhang, Y.; Wang, X.; Chen, L. Postfire Performance of Thread-Anchored Blind-Bolted Connection. J. Struct. Eng. 2023, 149, 04023173. [Google Scholar] [CrossRef]
- You, Y.; Li, H.; Wang, T.; Liu, Y. Study on Tensile Behavior and Design Methods of Thread-Fixed One-Side Bolted Joints to Concrete-Filled Steel Tubes. J. Constr. Steel Res. 2024, 222, 108958. [Google Scholar] [CrossRef]
- Eastman, C.M. BIM Handbook: A Guide to Building Information Modeling for Owners, Managers, Designers, Engineers and Contractors, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Liu, J.; Ergan, S.; Zhang, Q. An AprilTags-Based Approach for Progress Monitoring and Quality Control in Modular Construction. Buildings 2024, 14, 2252. [Google Scholar] [CrossRef]
- Zou, Y.; Kiviniemi, A.; Jones, S.W. Developing a Tailored RBS Linking to BIM for Risk Management of Bridge Projects. Eng. Constr. Archit. Manag. 2016, 23, 727–750. [Google Scholar] [CrossRef]
- Civera, M.; Calamai, G.; Fragonara, L.Z. System Identification via Fast Relaxed Vector Fitting for the Structural Health Monitoring of Masonry Bridges. Structures 2021, 30, 1234–1245. [Google Scholar] [CrossRef]
- Civera, M.; Mugnaini, V.; Fragonara, L.Z. Machine Learning-Based Automatic Operational Modal Analysis: A Structural Health Monitoring Application to Masonry Arch Bridges. Struct. Control Health Monit. 2022, 29, e3028. [Google Scholar] [CrossRef]
- Mugnaini, V.; Fragonara, L.Z.; Civera, M. A Machine Learning Approach for Automatic Operational Modal Analysis. Mech. Syst. Signal Process. 2022, 170, 108813. [Google Scholar] [CrossRef]
- Civera, M.; Wang, Y.; Fragonara, L.Z.; Ceravolo, R. A DBSCAN-Based Automated Operational Modal Analysis Algorithm for Bridge Monitoring. Measurement 2023, 208, 112451. [Google Scholar] [CrossRef]
- Civera, M.; Fragonara, L.Z.; Ceravolo, R.; Surace, C. The Teager-Kaiser Energy Cepstral Coefficients as an Effective Structural Health Monitoring Tool. Appl. Sci. 2019, 9, 5064. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, T.; Yu, Y. Evaluation of the Durability of Bridge Tension Cables Based on Combination Weighting Method-Unascertained Measure Theory. Sustainability 2022, 14, 7147. [Google Scholar] [CrossRef]
- Yue, J.; Lu, H.; Qian, R.; Tang, J. Application of Combined Weighting–Fuzzy Hierarchical Model in Condition Assessment of Concrete Continuous Girder Bridges. Buildings 2025, 15, 993. [Google Scholar] [CrossRef]
- Xu, J.; Li, Z.; Wang, H.; Chen, X.; Liu, Y. Construction Safety Influencing Factor Analysis of Bridge-Erecting Machines Based on Structural Equation Modeling. Heliyon 2024, 10, e25062. [Google Scholar] [CrossRef]
- Diez, A.; Khoa, N.L.D.; Makki Alamdari, M.; Wang, Y.; Chen, F.; Runcie, P. A Clustering Approach for Structural Health Monitoring on Bridges. J. Civ. Struct. Health Monit. 2016, 6, 429–445. [Google Scholar] [CrossRef]
- She, Y.; Pu, N.; Wang, Y.; Li, J.; Peng, X.; Lv, Q.; Ma, M. Drivers for the Acceptance of Green Housing Insurance from the Perspective of House Owners. Buildings 2025, 15, 1241. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Wang, X. An Investigation into the Risk Assessment of Building-Integrated Photovoltaic Residential Project Development Utilizing the DEMATEL-ANP Methodology: A Chinese Case Study. Buildings 2024, 14, 623. [Google Scholar] [CrossRef]
- He, C.; Yu, B.; Liu, M.; Guo, L.; Tian, L.; Huang, J. Utilizing Large Language Models to Illustrate Constraints for Construction Planning. Buildings 2024, 14, 2511. [Google Scholar] [CrossRef]
- Eker, H. Natural Language Processing Risk Assessment Application Developed for Marble Quarries. Appl. Sci. 2024, 14, 9045. [Google Scholar] [CrossRef]
- You, Y.; Wang, J.; Chen, X.; Zhang, Q. Post-Fire Behavior of Square Hollow Section Column Connections Using Thread-Anchored Blind Bolts. Structures 2024, 59, 1234–1245. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). AASHTO LRFD Bridge Construction Specifications, 3rd ed.; AASHTO: Washington, DC, USA, 2010. [Google Scholar]
- Neitzel, D.K. Electrical Safety Update—OSHA 29 CFR 1910.269 and NFPA 70E-2015 Revisions. IEEE Trans. Ind. Appl. 2016, 52, 2753–2758. [Google Scholar] [CrossRef]
- JGJ59-99; Standard for Construction Safety Inspection. China Architecture & Building Press: Beijing, China, 1999.
- GB/T51256-2017; Technical Code for Bridge Jacking-up and Reposition. China Standards Press: Beijing, China, 2017.


| Risk Category | Risk Description |
|---|---|
| Structural Stability and Integrity Risks |
|
| Complex Stress States and Mechanical Analysis |
|
| Constraints and Risks of the On-Site Work Environment |
|
| Technical and Operational Challenges |
|
| Time and Economic Pressures |
|
| Unpredictable Incidents |
|
| Category | Code | Risk Factor |
|---|---|---|
| Material Factors | D1 | Jack Failure |
| D2 | Temporary Support Failure | |
| D3 | Substructure Instability | |
| Environmental Factors | E1 | Adverse Weather |
| E2 | Poor Foundation Conditions | |
| Human Factors | H1 | Improper Operation |
| H2 | Poor Communication | |
| H3 | Low Safety Awareness of Construction Personnel | |
| Management and Planning Factors | M1 | Risk Emergency Plan |
| M2 | On-Site Construction Management Level | |
| M3 | Safety Technical Briefing and Training | |
| M4 | Investment in Safety Measures | |
| Unpredictable Incidents Ambiguous Factors | F | Fuzzy factor |
| Linguistic Variable | Mean (μ) | Standard Deviation (σ) | |
|---|---|---|---|
| 1 | Very High | 0.95 | 0.05 |
| 2 | High | 0.8 | 0.10 |
| 3 | Moderately High | 0.7 | 0.15 |
| 4 | Medium | 0.5 | 0.15 |
| 5 | Moderately Low | 0.3 | 0.15 |
| 6 | Low | 0.2 | 0.10 |
| 7 | Very Low | 0.05 | 0.05 |
| Indicator | Description | Scoring Criteria |
|---|---|---|
| Educational Background (W1) | Level of academic training and depth of theoretical knowledge | PhD: 0.4, Master’s: 0.3, Bachelor’s: 0.2 |
| Years of Experience (W2) | Duration of practice in civil engineering | Baseline of 5 years: 0.2, +0.1 per additional 5 years, maximum 0.6 |
| Number of Relevant Projects (W3) | Experience in bridge jacking or similar projects | Baseline of 5 projects: 0.2, +0.1 per additional 5 projects, maximum 0.5 |
| Professional Title (W4) | Professional standing and technical authority in the industry | Professor/Researcher: 0.3, Senior Engineer: 0.2, Engineer/Assistant Engineer: 0.1 |
| Domain Relevance (W5) | Alignment of expertise with jacking construction | Directly relevant: 0.3, Generally relevant: 0.2, Indirectly relevant: 0.1 |
| Influence (W6) | Contributions to academic research or engineering practice | High (10 papers/major projects): 0.3, Medium (5–10 papers/medium projects): 0.2, Low (<5 papers/ordinary projects): 0.1 |
| Expert | Academic Degree (W1) | Years of Experience (W2) | Number of Projects (W3) | Professional Title (W4) | Field Relevance (W5) | Influence (W6) | Initial Weight (Si) | Normalized Weight (Wi) |
|---|---|---|---|---|---|---|---|---|
| Expert 1 | 0.4 (PhD) | 0.5 (21 years) | 0.3 (12 bridge projects) | 0.3 (Professor) | 0.3 (Bridge Structural Design Expert) | 0.3 (Published over 10 papers) | 0.350 | 0.186 |
| Expert 2 | 0.3 (Master’s) | 0.4 (16 years) | 0.2 (6 bridge projects) | 0.2 (Senior Engineer) | 0.3 (Construction Technology Expert) | 0.2 (Published 7 papers) | 0.267 | 0.142 |
| Expert 3 | 0.4 (PhD) | 0.6 (33 years) | 0.4 (18 bridge projects) | 0.3 (Researcher) | 0.3 (Geotechnical Engineering Expert) | 0.3 (Published over 10 papers) | 0.383 | 0.203 |
| Expert 4 | 0.3 (Master’s) | 0.3 (14 years) | 0.2 (7 bridge projects) | 0.1 (Engineer) | 0.3 (Equipment Management Expert) | 0.2 (Published 5 papers) | 0.233 | 0.124 |
| Expert 5 | 0.2 (Bachelor’s) | 0.5 (24 years) | 0.2 (10 bridge projects) | 0.2 (Senior Engineer) | 0.2 (Safety Management Expert) | 0.2 (Published 5 papers) | 0.250 | 0.133 |
| Expert 6 | 0.3 (Master’s) | 0.4 (16 years) | 0.2 (5 bridge projects) | 0.2 (Senior Engineer) | 0.2 (Project Management Expert) | 0.2 (Published 6 papers) | 0.250 | 0.133 |
| Expert 7 | 0.3 (Master’s) | 0.2 (7 years) | 0.1 (3 bridge projects) | 0.1 (Assistant Engineer) | 0.1 (Digital Technology Expert) | 0.1 (Published 2 technical papers) | 0.150 | 0.080 |
| Root Nodes | Expert 1 | Expert 2 | Expert 3 | Expert 4 | Expert 5 | Expert 6 | Expert 7 |
|---|---|---|---|---|---|---|---|
| D1 | Medium | Moderately Low | Medium | Moderately High | Moderately Low | Medium | Low |
| D2 | Moderately Low | Medium | Moderately Low | Medium | Low | Moderately Low | Moderately Low |
| D3 | Moderately High | Medium | High | Medium | Moderately High | Medium | Medium |
| E1 | Medium | Medium | Moderately Low | Medium | Moderately High | Moderately Low | Medium |
| E2 | High | Moderately High | Very High | Moderately High | Medium | High | Moderately High |
| H1 | Moderately High | Medium | Medium | High | Medium | Moderately High | Moderately Low |
| H2 | Moderately Low | Low | Moderately Low | Medium | Moderately Low | Medium | Low |
| H3 | Medium | Moderately Low | Medium | Moderately Low | Medium | Moderately Low | Low |
| M1 | Medium | Moderately High | Medium | Medium | Moderately High | Medium | Medium |
| M2 | Moderately Low | Medium | Moderately Low | Medium | Moderately Low | Medium | Moderately Low |
| M3 | Moderately High | Medium | Moderately High | Medium | Medium | Moderately High | Medium |
| M4 | Medium | Moderately Low | Medium | Moderately Low | Medium | Moderately Low | Medium |
| F | Moderately Low | Low | Moderately Low | Medium | Low | Moderately Low | Low |
| Root Nodes | Fuzzy Values | Initial Probabilities P (X = 1) | Fuzzy Values | ||
|---|---|---|---|---|---|
| t | t − 1 | ||||
| 1 | 0 | ||||
| D1 | (0.45,0.15) | 0.45 | |||
| D2 | (0.32,0.14) | 0.32 | |||
| D3 | (0.62,0.14) | 0.62 | 1 | 0.75 | 0.25 |
| 0 | 0.22 | 0.78 | |||
| E1 | (0.47,0.14) | 0.47 | |||
| E2 | (0.77,0.12) | 0.77 | 1 | 0.85 | 0.15 |
| 0 | 0.10 | 0.90 | |||
| H1 | (0.58,0.14) | 0.58 | 1 | 0.72 | 0.28 |
| 0 | 0.21 | 0.79 | |||
| H2 | (0.29,0.13) | 0.29 | |||
| H3 | (0.39,0.14) | 0.39 | |||
| M1 | (0.54,0.15) | 0.54 | |||
| M2 | (0.38,0.15) | 0.38 | |||
| M3 | (0.59,0.15) | 0.59 | |||
| M4 | (0.43,0.15) | 0.43 | |||
| F | (0.25,0.12) | 0.25 | |||
| Root Nodes | Risk Factor | Prior Probability | Posterior Probability | ROV Value |
|---|---|---|---|---|
| E2 | Poor Foundation Conditions | 0.49 | 0.64 | 0.306 |
| M3 | Safety Technical Briefing and Training | 0.59 | 0.77 | 0.305 |
| D3 | Substructure Instability | 0.47 | 0.61 | 0.298 |
| H1 | Improper Operation | 0.41 | 0.53 | 0.293 |
| D2 | Temporary Support Failure | 0.32 | 0.36 | 0.125 |
| F | Fuzzy factor | 0.25 | 0.28 | 0.12 |
| M4 | Investment in Safety Measures | 0.43 | 0.48 | 0.116 |
| D1 | Jack Failure | 0.45 | 0.5 | 0.111 |
| M1 | Risk Emergency Plan | 0.54 | 0.6 | 0.111 |
| E1 | Adverse Weather | 0.47 | 0.52 | 0.106 |
| M2 | On-Site Construction Management Level | 0.38 | 0.42 | 0.105 |
| H2 | Poor Communication | 0.29 | 0.32 | 0.103 |
| H3 | Low Safety Awareness of Construction Personnel | 0.39 | 0.43 | 0.103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Y.; You, Y. Safety Risk Assessment of Jacking Renovation Construction for Aging Bridges Based on DBN and Fuzzy Set Theory. Buildings 2025, 15, 1493. https://doi.org/10.3390/buildings15091493
Ge Y, You Y. Safety Risk Assessment of Jacking Renovation Construction for Aging Bridges Based on DBN and Fuzzy Set Theory. Buildings. 2025; 15(9):1493. https://doi.org/10.3390/buildings15091493
Chicago/Turabian StyleGe, Yanhui, and Yang You. 2025. "Safety Risk Assessment of Jacking Renovation Construction for Aging Bridges Based on DBN and Fuzzy Set Theory" Buildings 15, no. 9: 1493. https://doi.org/10.3390/buildings15091493
APA StyleGe, Y., & You, Y. (2025). Safety Risk Assessment of Jacking Renovation Construction for Aging Bridges Based on DBN and Fuzzy Set Theory. Buildings, 15(9), 1493. https://doi.org/10.3390/buildings15091493






