Development of Analytical Solutions and Verification Experiments for Axially Restrained Reinforced Concrete Beams in a Fire

Abstract

Fire-induced structural failure in axially restrained reinforced concrete (RC) beams is a critical concern in structural fire engineering. Comparative analysis with Eurocode and ASTM E119 fire safety guidelines reveals discrepancies between theoretical predictions and real fire-induced failures, emphasizing the need for revised structural fire safety standards. Moreover, limited analytical solutions exist due to the complexity of fire behavior in axially restrained RC beams. This study develops an improved analytical model for axially restrained beams in fire, focusing on three critical points: (i) the peak axial compression force, (ii) the transition to zero axial force (bending limit), and (iii) the final failure point due to reinforcement fracture. A series of fire resistance experiments were conducted to obtain key structural parameters, including fire resistance time (FRT), axial force redistribution, and failure mechanisms. The experimental results were used to validate and refine the proposed model, enhancing its practical applicability. The original model underpredicts fire endurance by 11–14%, whereas the upgraded model is accurate to within ~2–4% of test results. This improved performance is attributed to the model’s consideration of stiffness degradation and early cracking. Overall, the study provides valuable insights for improving the fire-resistant design of restrained RC beams, particularly in critical infrastructure such as logistics centers.

1. Introduction

Fire-induced structural failure in reinforced concrete (RC) buildings is a critical concern in structural engineering [1,2,3,4,5,6,7,8,9,10,11,12,13]. In particular, axially restrained RC beams—beams connected to a rigid frame or supports that prevent free thermal expansion—exhibit complex behavior under fire [14,15,16]. As the beam heats, thermal expansion is restrained, generating axial forces that significantly alter the beam’s response [17,18,19,20,21]. This can lead to higher internal forces and unconventional failure modes compared to free (unrestrained) beams [22,23], decreasing the stiffness of beam and axial/rotational restraint effects, which are shown by [22,24,25,26,27]. Current design guidelines (e.g., Eurocode 2 [28] and ASTM E119 [29]) treat fire as an accidental load but do not explicitly account for the beneficial and detrimental effects of axial restraint in beams. Axial restraint can help by increasing load capacity through arching action. However, it can also cause problems, such as high compression that leads to buckling in steel beams or cracks and spalling in concrete due to restricted expansion. As a result, there is a gap between code predictions and actual structural performance in fire, especially regarding the development of axial forces and catenary action. A comparative analysis by the authors highlighted notable discrepancies between code-based theoretical predictions and real fire-induced failures, emphasizing the need for revised structural fire safety approaches [17].

Some numerical studies have been conducted to address this gap. Dwaikat and Kodur have modeled fire-induced restraint effects in RC beams, showing that axial restraint can increase beam fire resistance but also introduce large axial forces [24]. Experimental and analytical work by Cvetkovska et al. demonstrated that adding axial restraint changes the failure time and mode of RC beams in fire, generally enhancing fire resistance for moderate restraint stiffness [30]. Some other studies confirm that axial restraint is a key factor in structural fire response [31,32]. They attributed this to the enhanced arching action that occurs as restraint increases, which helps the beam redistribute internal forces more effectively and thereby delays failure. This suggests that higher axial stiffness provides additional structural support, preventing premature bending collapse.

On the other hand, Wu and Lu [25] observed the exact opposite trend, concluding that greater axial restraint stiffness shortens the beam’s bending failure time. Their explanation focused on the specific failure modes that develop at the beam’s ends. When thermal expansion and thermal bowing are restricted, significant compressive forces accumulate in the lower portion of the beam near the supports. This localized stress concentration accelerates structural failure, meaning that a stiffer axial restraint results in a more rapid loss of bending resistance. A different perspective was provided by Riva and Franssen [32], who found that the bending failure time does not follow a strictly increasing or decreasing trend. Instead, their results indicate that at lower levels of axial restraint stiffness, the bending failure time initially increases due to the beneficial effects of arching action. However, beyond a certain stiffness threshold, the failure time starts to decline, likely because excessive axial restraint begins to induce high compression forces similar to those identified by Wu and Lu [25]. This suggests that beam failure is governed by a complex interplay between the structural benefits of arch action and the detrimental effects of localized stress concentrations, with the dominant mechanism depending on the level of axial restraint imposed on the system.

Furthermore, there have been notable developments in theoretical research aimed at predicting the fire resistance of reinforced concrete (RC) beams. Several approaches have been explored, including the Strut-and-Tie Model, advanced finite element models that take into account spalling effects, and emerging machine learning algorithms designed to enhance predictive accuracy [33,34,35,36,37]. These methodologies have contributed to a deeper understanding of fire resistance mechanisms and have improved the ability to estimate structural performance under fire conditions. However, despite these advancements, current research on the fire resistance of RC beams remains limited in scope. Most studies focus on specific parameters rather than adopting a comprehensive approach that accounts for the full range of factors influencing fire behavior [38].

From the complexity of fire behavior of axially restrained reinforced concrete beams, most studies are focused on the numerical results. However, there is a lack of consideration for axial restraint effects, arching action, and redistribution of forces under fire. Moreover, a simplified analytical solution for design use is still limited. In a previous doctoral study by Lee et al. (2016) [39], an analytical model was developed to predict the behavior of axially restrained RC beams in fire. That model identified three critical performance points during a fire (Figure 1): Point A—when the axial compressive force in the beam peaks, Point B—when the axial force drops to zero (the beam’s bending capacity limit), and Point C—the final failure points due to tensile rupture of reinforcement (after catenary action develops). While the original model provided valuable insights, it relied on several simplifying assumptions (e.g., temperature-invariant stiffness, instantaneous transition to catenary action) that limited its accuracy. New experimental evidence and theoretical developments since 2016 motivate an upgraded analytical model with improved reality conditions.

The outline of this paper is structured as follows. Section 2 presents the experimental program, including test setup, fire exposure conditions, and key observations. Section 3 summarizes the original analytical model and its limitations in predicting the behavior of axially restrained reinforced concrete beams in fire. Section 4 introduces the upgraded analytical model, detailing the refinements made to improve accuracy. Section 5 compares the experimental results with the predictions from both models and discusses the improvements in failure time estimation. Finally, Section 6 provides conclusions and recommendations for future research.

This thesis aims to refine the analytical model for axially restrained RC beams under fire conditions and to validate the upgraded model against experimental results. Key objectives include the following: (1) summarizing the original analytical formulations from Lee’s 2016 PhD thesis [39] as a baseline, (2) deriving an improved set of analytical equations incorporating temperature-dependent material behavior and more realistic assumptions, and (3) comparing the predictions of the original and upgraded models to new fire test data for axially restrained RC beams. By quantifying the differences in predictive accuracy (error rates) and examining the model behavior, the thesis seeks to logically demonstrate the improvements and ensure the new formulations are both more accurate and not overfitted to specific data. Ultimately, this work should enhance the logical persuasiveness of analytical predictions for structural fire design and could inform updates to design guidelines or robustness evaluation methods.

2. Experimental Program and Model Validation

This section details the experimental program undertaken to investigate the behavior of axially restrained reinforced concrete (RC) beams under fire and presents the key findings. The first part describes the test setup, fire exposure conditions, instrumentation, and observed structural responses (deflections, forces, temperature distributions, etc.), as well as the failure mechanisms identified during the tests. The latter part of the section integrates these experimental results with the analytical model, comparing the measured responses with predictions from the upgraded analytical equations. Error rates between experimental data and model predictions are calculated, and any discrepancies or alignments are discussed.

2.1. Experimental Program

2.1.1. Test Setup and Conditions

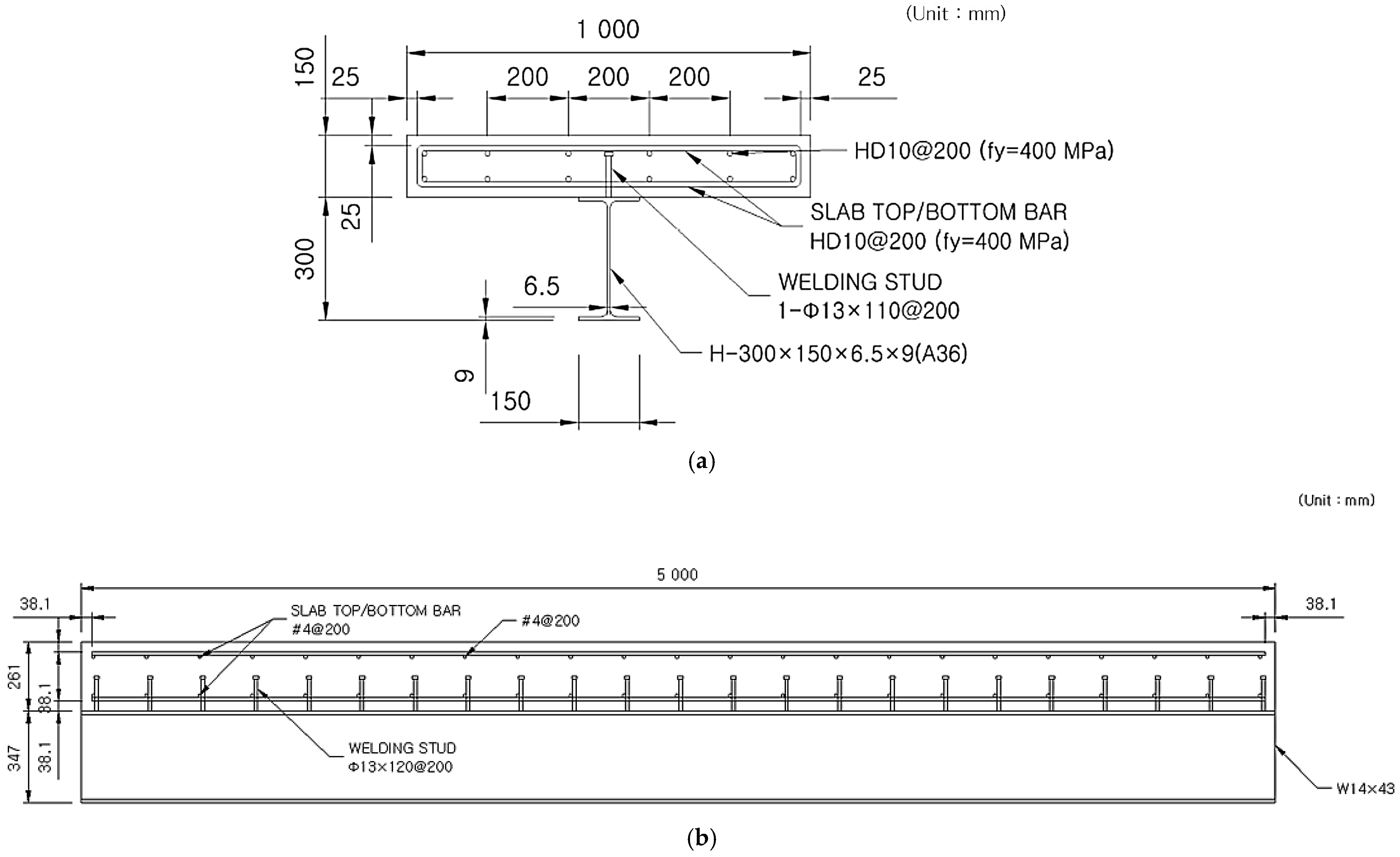
A series of full-scale fire tests was conducted on six beam specimens to simulate axially restrained beam behavior under fire. All specimens had a total span of 5 m and were divided into two categories: composite T-beams (steel beam with a concrete slab on top) and bare steel I-beams. The composite beams consisted of a W30 × 261 steel section with an 18-inch (457 mm) reinforced concrete slab on top (forming a T-section), connected via shear connectors (studs) to ensure composite action (Figure 2). The bare steel beams were the same steel section without any concrete slab.

Table 1. Summary of test specimens.

Specimen	Beam Type	Fire Protection	Load Ratio (%)	Observation
1	Composite (Steel + RC slab)	None (0 mm)	70%	- Fire resistance performance and behavioral changes without fireproof coating - Behavior of axially restrained beams during fire
2	Composite (Steel + RC slab)	None (0 mm)	50%
3	Composite (Steel + RC slab)	20 mm spray	70%	- Temperature distribution by section depth during fire - Changes in fire resistance performance due to differences in fireproof spray thickness
4	Composite (Steel + RC slab)	10 mm spray	70%
5	Bare Steel I-beam	None	70%	- Comparison between the behavior of basic steel beams and composite beams
6	Bare Steel I-beam	None	50%

(in Section 2.2) summarizes the key characteristics of each specimen.

Boundary Conditions: To replicate axial restraint as in a continuous frame, the beam ends were restrained against horizontal movement during the test. One end was fixed to the furnace reaction frame (restrained against both translation and rotation), while the other end was attached to a hydraulic actuator with a pin connection. This arrangement provided axial restraint (i.e., preventing free expansion/contraction along the beam’s length) but allowed the beam to rotate freely at supports (no moment fixity), simulating a pin-ended beam with axial restraint. Only one end was actively restrained by the actuator because the furnace facility had one horizontal actuator; the opposite end was effectively fixed in place. The actuator was calibrated to impose an initial position (to achieve the desired axial confinement). Then, displacement control of the end was maintained, so that axial forces could develop as the beam tried to expand or contract. In the real building scenario, this represents a beam connected to rigid supports that restrict its thermal expansion.

Loading Conditions: Each beam was subjected to a static mid-span load to represent a portion of the design load (imposed before heating). The load magnitude was defined in terms of a load ratio, which is the fraction of the beam’s ambient temperature load capacity. Two load levels were used: 70% and 50% of the ultimate capacity (high and moderate load). This load was applied by a hydraulic jack using a loading frame such that the beam experienced a single concentrated force at mid-span. It is important to notice that the one-point load has been chosen to deduce the analytic expression of the model while still capturing the key mechanics of restrained beam behavior in fire. The use of a single-point load (as opposed to the standard two-point loading for a distributed load) provides reasonable accuracy for the behavior of the global response predictions with a long span length [40]. For example, a steel loading column with a bearing plate (made of fire-resistant steel) was used to transfer the load at mid-span, so that even as the beam deflected significantly, the load could continue to be applied without restraint equipment entering the furnace. Prior to heating, each specimen was thus designated a constant load (either 70% or 50% load ratio).

All six specimens were prepared and instrumented and then installed in a large horizontal furnace at the Korea Institute of Civil Engineering and Building Technology (KICT) in Hwaseong, Republic of Korea. After securing the axial restraint system (fixed support and actuator) and applying the static load, the furnace burners were ignited to begin the fire exposure.

2.1.2. Fire Testing Procedure

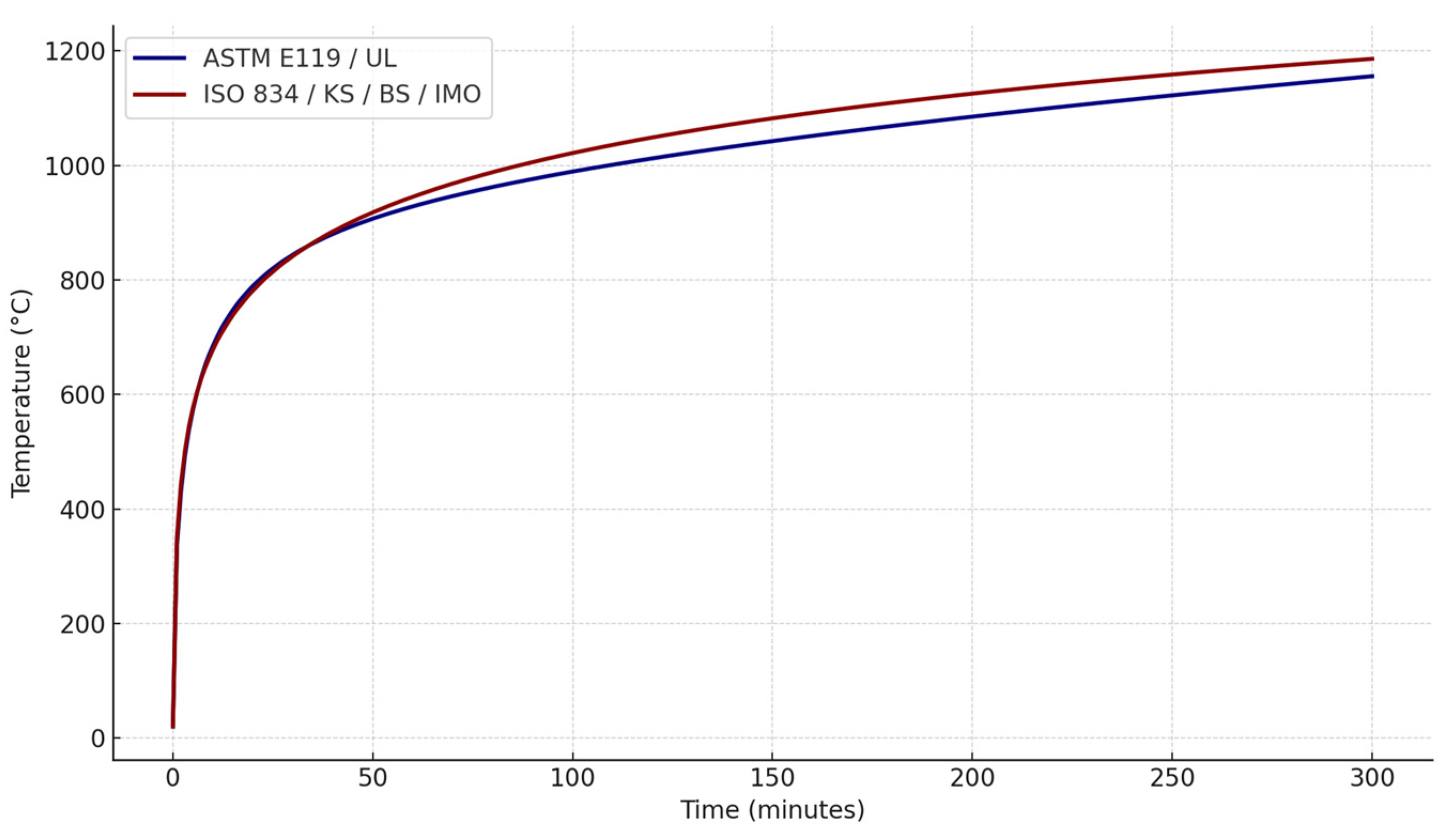
The fire tests were conducted in accordance with standard fire testing procedures. The heating followed the ASTM E119 standard [29] time–temperature curve, which is widely adopted for horizontal elements). In other words, the furnace temperature was controlled to rise following the ASTM E119 formula (see Figure 3 for the standard temperature–heating curves). The furnace was a gas-fired horizontal furnace capable of one-sided heating.

The beams were exposed to fire from below (one-face heating), meaning the bottom flange of the steel beam and the underside of the slab (for composite specimens) were directly exposed to the hot furnace gases, while the top of the slab was unexposed (open to ambient). This scenario represents a fire underneath a floor beam. The furnace chamber extends along the full 5 m length between the supports, so the entire span was heated uniformly. The standard fire exposure was applied continuously until failure of the specimen. Unlike typical fire resistance tests (which might stop at a prescribed criteria like insulation failure or a set duration), these tests were carried out until structural collapse of the beam occurred. The fire resistance time for each specimen was thus defined as the time from start of heating until the beam could no longer sustain the applied load (complete failure). This definition exceeds the usual criteria (which often stop when deflection limits or rate-of-deflection criteria are met) but was chosen to capture the full range of beam behavior including catenary action up to collapse.

During the tests, the furnace followed the ASTM E119 (Figure 3) time–temperature curve closely. If a test went beyond certain milestones (e.g., 60, 90, 120 min), the furnace continued to increase temperature accordingly (approaching around 1100 °C by 2 h, etc.). In practice, two of the composite beams survived well past 1–2 h (due to fire protection, as discussed later), so extended heating was applied in those cases. For safety, if any violent failure or excessive deformation was imminent (risking damage to equipment), the test was terminated. Although the furnace heating followed the ASTM E119 standard fire curve, actual fires vary greatly depending on ventilation, fuel, and room conditions. Standard fire curves, like ASTM E119, help provide consistent and comparable test results, but further studies using realistic fire scenarios would improve practical applicability. The instrumentation and data collection methods used to monitor the structural response are described in Section 2.1.3.

2.1.3. Instrumentation and Data Collection

Comprehensive instrumentation was used to capture the structural response of the beams. In recent studies, Albuquerquea [21] and Kodur [42] focus on material properties and fire resistance but do not explicitly consider compressive arch action (CAA) or catenary action as structural mechanisms. Albuquerquea [21] measures the compressive strength of concrete but does not analyze how axial restraint influences load redistribution. Also, Kodur [42] discusses UHPC beams without shear reinforcement but does not examine the role of CAA or catenary action under fire conditions. Therefore, these structural actions were directly address and captured by the deflection/displacement data in this experiment with the specific temperature settings.

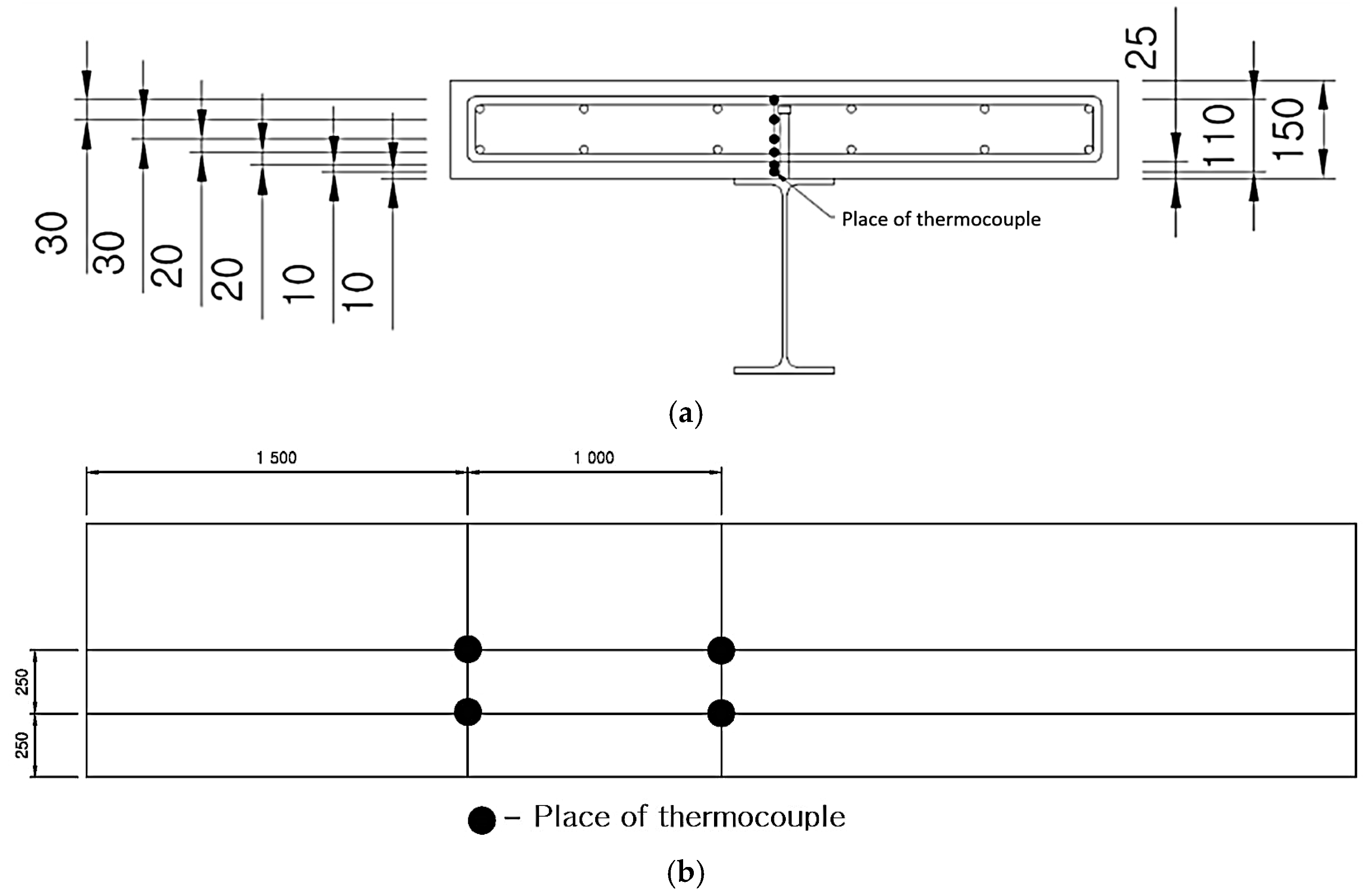
To capture the temperature distribution within the beam cross-section, multiple thermocouples were installed at key locations. In the composite beams, thermocouples were embedded at various depths in the concrete slab (measured from the slab soffit downward toward the steel flange) and attached to the steel beam flange and web. Based on a preliminary thermal analysis, thermocouples were placed at 5–10 mm intervals near the steel–concrete interface where high gradients were expected and at larger intervals toward the slab top. For example, sensors were placed 10 mm and 20 mm below the slab bottom surface, then 30 mm, 40 mm, etc., up to near the slab mid-depth (Figure 4). This ensured capturing the thermal gradient through the slab thickness (see Figure 4 for sensor placement). In the steel section, thermocouples measured the steel temperature at the bottom flange, mid-height of web, and top flange. All thermocouple readings have been recorded at regular intervals to develop time–temperature curves for different parts of the section. Material degradation parameters, such as the temperature-dependent reductions in concrete and steel strength and stiffness, were not experimentally measured in this study but instead assumed from well-established literature sources, specifically Eurocode 2 [28], to ensure consistency and comparability with existing fire-resistance modeling.

The primary structural response measured was the vertical deflection at mid-span. A high-temperature LVDT (linear variable displacement transducer) or a potentiometric displacement transducer was installed to monitor the mid-span vertical displacement of the beam as it deflected downwards under load and heat. Data logging captured the deflection history over time. Additionally, the rate of deflection could be derived from these data, which is relevant to standard failure criteria (e.g., the ASTM E119 failure limit on rate of deflection).

Moreover, axial displacement was recorded using the actuator in displacement-control mode, allowing indirect inference of axial force behavior. Direct axial force measurement was not conducted due to safety concerns, but axial displacement has been recorded to infer force behavior. Instead, the actuator was operated in a displacement-control mode, and its axial displacement has been recorded (Figure 5). From this, one can infer axial force behavior if the stiffness is known. However, due to the limitations, direct axial force measurements have not been obtained during the fire (the equipment is not active for measuring force to avoid damaging the load cell as the force fluctuated). The axial restraint stiffness of the setup has been roughly estimated for analysis purposes afterward. Despite not measuring force, observing the axial movement gives qualitative insight. If the beam tries to expand, the actuator displacement would increase (in compression phase). If the beam later pulled in (catenary tension), the actuator might move in the opposite direction. Although the axial restraint conditions in this study assume rigid supports, real structures can experience support deformations. However, axial displacements measured during the tests remained relatively small, confirming that this simplified assumption reasonably reflects actual restraint conditions for the purpose of this research.

Structural failure observations (e.g., spalling, cracking, buckling) were documented through visual monitoring and post-test photographs. The tests also implicitly checked fire integrity and insulation performance, for instance, whether any flames passed through cracks (integrity) or the unexposed face (top of slab) reached high temperatures (insulation), though the primary focus was on structural behavior.

With the above setup and instrumentation, each test has been executed. All six tests have been completed (with one requiring early termination due to a pre-collapse during loading, as noted below). The following sections describe the measured responses and observations from these experiments.

2.2. Experimental Results and Observations

Once heating began, the beams exhibited a sequence of behaviors influenced by the axial restraint and applied load. In this section, the key results for each specimen (grouped into composite beams vs. bare steel beams) are presented. The measured response parameters include the time to failure (fire resistance time), deflection history, any axial movements, temperature distributions, and observed failure modes. Critical phenomena such as the development of compressive arch action and later catenary action were of particular interest and were observed in the tests.

2.2.1. Composite Beam Specimens (Specimens 1–4)

The four composite T-beam specimens (Specimens 1 through 4) had a concrete slab acting compositely with the steel section. Two variables were studied in this group: the applied load level (70% vs. 50% load ratio) and the presence of fire protection (no protection, 10 mm, or 20 mm thick spray-applied fireproofing on the steel beam). All composite beams were restrained axially at the ends as described. The summary of the thermal response, deflection, and failure times are described as follows:

• Thermal Response: In the unprotected composite beams (Specimens 1 and 2), the steel section and concrete slab rapidly absorbed heat from below. The steel beam, being exposed, heated faster than the concrete. The slab provided some heat sink effect, slowing down the temperature rise in the steel somewhat. However, since there was no insulation, the steel reached critical temperatures within tens of minutes. In the protected specimens (3 and 4), the fireproofing on the steel significantly delayed the heating of the steel section: temperatures in the steel remained much lower for a given exposure time, resulting in prolonged structural capacity. The concrete slab in all cases trailed the steel in temperature; its large thermal mass and low conductivity created a gradient where the top of the slab stayed relatively cool even as the bottom was hot.
• Deflection and Deformation: All composite beams showed a similar deflection trend initially. As the steel lost stiffness and expanded, the beam experienced downward deflection increasing gradually, while axial compression built up due to restraint. An interesting phenomenon was compressive arching action. In the early stage of heating, the restrained expansion caused the beam to develop a compressive thrust, which, combined with the slab, created an arching effect that temporarily helped support the load with less deflection. However, as temperatures rose further, the steel yield strength dropped, and the concrete began to crack, causing the beam to lose stiffness. Eventually, a plastic hinge formed near mid-span (evidenced by a concentration of curvature and cracks in the slab at mid-span), and the deflection rate accelerated. The point of runaway deflection—where deflection increased rapidly with little load capacity remaining—was reached differently for each specimen depending on load and protection. By this stage, the axial force in the beam would reduce toward zero and then switch to tension as the beam tried to hang in catenary action.
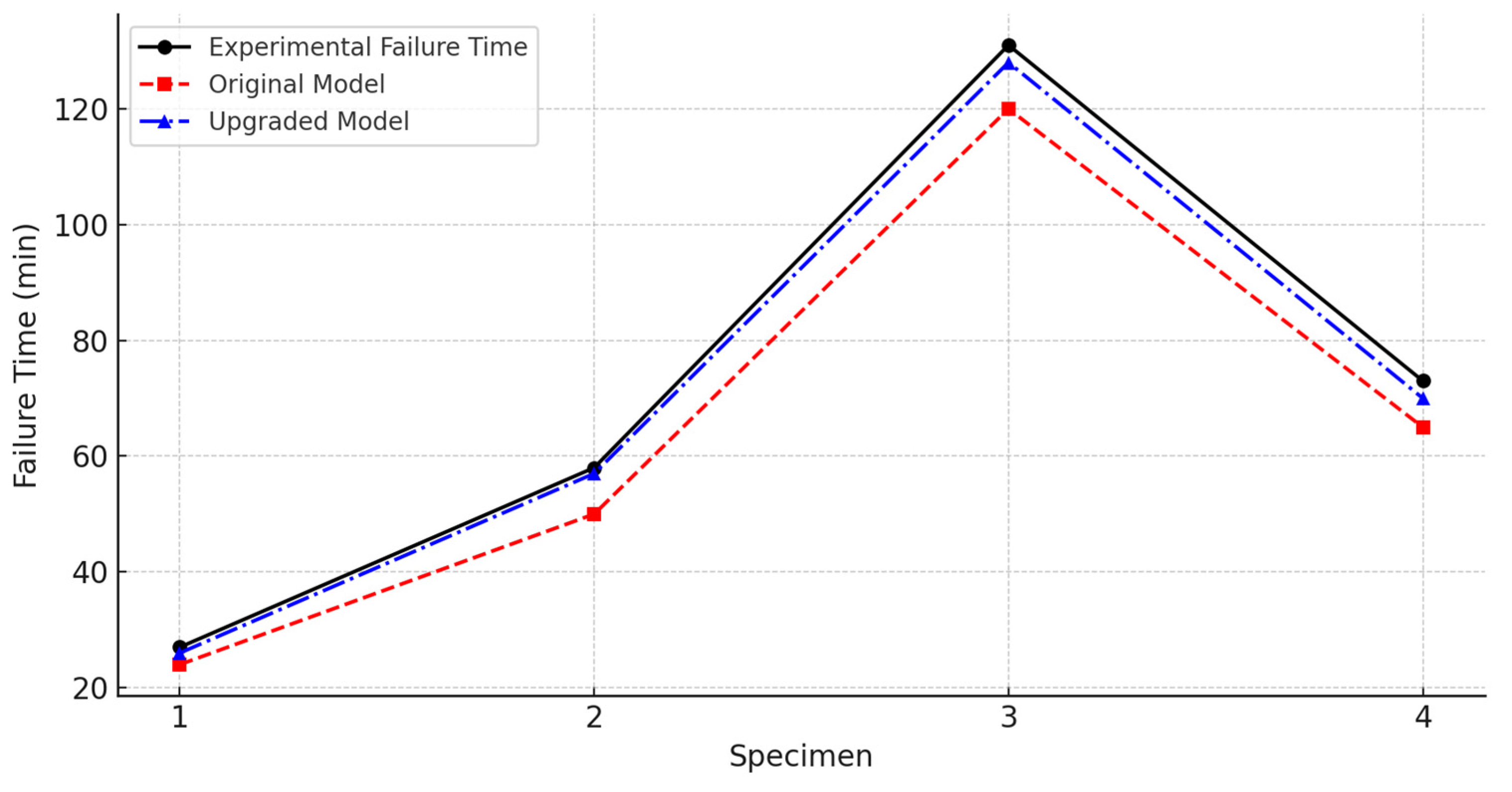
• Failure Times and Modes: The failure of the composite beams was marked by large deflections and, in some cases, fracture of reinforcement. Specimen 1 (unprotected, 70% load) failed after approximately 27 min of fire exposure. The concrete slab had developed significant cracks, and the steel beam bottom flange was highly heated (~700 °C or more). The final failure appeared to occur when the tensile reinforcing bars fractured and the slab separated at mid-span, causing the beam to collapse. Specimen 2 (unprotected, 50% load) sustained the fire for 58 min before failure. Under the lower load, the beam had more capacity in reserve, allowing it to tolerate higher temperatures. The failure mode was similar (flexural collapse after extensive deflection), and it was noted that the mid-span deflection became very large (over L/20 of the span) prior to collapse—a clear sign of catenary action just before failure. The increased fire endurance of Specimen 2 (over double the time of Specimen 1) illustrates that a lower load ratio leads to significantly longer fire resistance, as expected.

Specimens 3 and 4 had spray-applied fire protection on the steel beam, which dramatically improved their performance. Specimen 3 (20 mm insulation, 70% load) endured about 131 min (2 h 11 min) of fire exposure before collapse. In this test, the insulation kept the steel temperature much lower throughout; as a result, the beam remained intact until the fireproofing itself started to deteriorate, and the steel eventually got hot enough to weaken. The failure again was flexural. The slab and beam sagged deeply, and the reinforcement likely ruptured at an extreme deflection to cause final collapse. Specimen 4 (10 mm insulation, 70% load) failed in about 73 min. The thinner insulation provided less thermal protection, so the steel heated faster than in Specimen 3. Consequently, Specimen 4’s failure time was significantly less than Specimen 3’s, though still much greater than the unprotected case. The comparison of Specimens 3 and 4 highlights that increasing the fireproofing thickness notably increases the fire resistance (e.g., 20 mm coating nearly doubled the failure time compared to 10 mm). This is because a thicker insulation layer reduces the heat transfer to the steel, resulting in lower steel temperatures for a given fire duration. With the steel cooler, thermal expansion is less and material degradation is slower, so the structural capacity is maintained longer.

In all composite beam tests, a transition from compressive arch action to tensile catenary action was observed. In the early stage (arch action), the axial restraint and composite slab allowed the beam to carry load even as the steel weakened, by mobilizing compression in the slab and steel (like a shallow arch). At a certain point (as the mid-span plastic hinge formed and deflection increased), the beam’s ability to carry load in bending was exhausted, and it began to pull on the supports—entering catenary action. This was evidenced by the beam exerting pull-in forces (the actuator recorded a slight pull-in movement) and the reinforcement in the slab taking on the load in tension. The final failure for the composite beams was governed by rupture of steel reinforcement in tension (for Specimens 1, 2, and 3) and in one case by severe local deformation of the steel beam. Post-test inspections confirmed fractured rebars at mid-span for the longer-duration tests, consistent with failure by catenary tension. This corresponds to the analytical expectation that the ultimate failure mode of axially restrained beams in fire is fracture of reinforcement at large deflection. Figure 6 shows the state of Specimens 1–4 after testing.

2.2.2. Bare Steel Beam Specimens (Specimens 5–6)

Specimens 5 and 6 were tests on the bare steel W30 × 261 section (no concrete slab), included to isolate the behavior of the steel beam itself under similar restraint and load conditions. Both were unprotected (no fire insulation) and thus represented the worst case in terms of fire exposure to steel. The applied load ratios were 70% for Specimen 5 and 50% for Specimen 6.

• Specimen 5 (steel beam, 70% load): This test did not reach the heating phase due to a premature failure during the loading process. As the 70% design load was applied at mid-span, the steel beam buckled locally even before the furnace was ignited. The failure was attributed to the loading setup and the slenderness of the compression flange. The concentrated load introduction caused a high localized moment, and the top flange (which was only 150 mm wide) experienced lateral–torsional instability or local flange buckling. In other words, under the heavy load, the unbraced length of the steel compression flange was full span (since no slab or lateral bracing was present), leading to an elastic instability. The beam collapsed onto the furnace floor just as minor heating started. Thus, effectively, no meaningful fire exposure data were obtained for this specimen. The event underscored the importance of the composite slab in stabilizing the steel beam against buckling. After this incident, the test was halted and considered a failed test (marked as “pre-fire failure (buckling)” in the results). To prevent a similar issue in the next steel beam test, the team made modifications. They reinforced the steel beam’s web with stiffeners and adjusted the loading apparatus (using a plate sized to the flange width) for Specimen 6.
• Specimen 6 (steel beam, 50% load): With improvements in place, Specimen 6 was successfully loaded to 50% of its capacity and then exposed to fire. As expected, without any fire protection and without a concrete slab, the steel beam experienced a rapid temperature rise. Within just several minutes, the bottom flange of the steel beam reached a critical temperature (around 600 °C or more), at which point the steel’s yield strength had severely degraded. The beam’s mid-span deflection increased quickly, indicating plastic hinge formation early in the test. By around 14–15 min into the fire, the deformation became very large, and the beam was on the verge of collapse. For safety reasons, the test was terminated at approximately 15 min, as the beam’s load-bearing ability was essentially lost (a runaway deflection was occurring). Thus, the fire resistance time recorded for Specimen 6 was ~15 min. The failure mode was primarily global bending failure. Specifically, the steel beam developed a plastic hinge at mid-span and underwent large downward deflection. Full catenary action was not reached in this case since the beam failed so early (the steel likely ruptured, or the connections could not sustain further tension once the beam largely melted). The restrained thermal expansion in the initial minutes did generate axial compression, but since the beam’s strength dropped so fast, that compression did not hold for long before the beam yielded and buckled. Compared to the composite beams, no significant tensile catenary stage was observed here; the beam essentially failed during the bending phase itself.

The bare steel beam (Specimen 6) had a much lower fire resistance than any composite beam, underscoring the beneficial effect of the concrete slab. The slab in the composite specimens acted as thermal protection (even without spray insulation, the slab absorbs heat and slows steel heating) and provided composite action that increased the stiffness and load capacity at ambient temperature. In fire, the slab also added a catenary load path (through the reinforcing mesh/bars) that the bare steel beam lacked. The tests showed that the composite action extended the failure time by at least 15 min or more under similar load ratios. For example, at 70% load, the composite beam (Specimen 1) lasted 27 min, whereas the bare steel (if it had not buckled pre-fire) was projected to last only around 10–15 min. At 50% load, composite beam (Specimen 2) lasted 58 min, while bare steel (Specimen 6) lasted 15 min. The presence of the concrete slab thus clearly enhances fire robustness. Another observation was that axial restraint had different effects on composite vs. steel beams. In composite beams, the restraint force was sustained longer (due to the slab’s capacity and arching action), whereas in the bare steel beam, the rapid loss of stiffness meant the restraint force dropped off quickly once the beam yielded. Figure 7 shows the state of Specimens 5 and 6 after testing.

In summary, the experiments provided detailed data on how axially restrained beams behave under fire.

Table 2. Summary of test specimens and fire resistance results.

Specimen	Beam Type	Fire Protection	Load Ratio (%)	Failure Time—Experiment
1	Composite (Steel + RC slab)	None (0 mm)	70%	27 min
2	Composite (Steel + RC slab)	None (0 mm)	50%	58 min
3	Composite (Steel + RC slab)	20 mm spray	70%	131 min
4	Composite (Steel + RC slab)	10 mm spray	70%	73 min
5	Bare Steel I-beam	None	70%	(Pre-fire buckling failure)
6	Bare Steel I-beam	None	50%	~15 min

below summarizes the key outcomes for each specimen, including the test parameters and the measured fire resistance time (failure time). It also lists the corresponding predictions from the analytical model (which will be discussed in Section 4.4) for comparison.

The composite beams (Specimens 1–4) had a concrete slab; the steel beams (Specimens 5–6) had no slab. Here, load ratio = percentage of ultimate load applied. Fire protection refers to spray-applied fire insulation on the steel section. Fire resistance time is the duration from start of fire to collapse. For Specimen 5, no fire time is recorded due to pre-fire buckling failure.

As shown above, the analytical model’s predictions of failure time are in close agreement with the experimental results for most cases (Specimens 1–4), with larger discrepancy for Specimen 6. The next section provides a detailed comparison between the experimental findings and the analytical model, including discussion of these error rates and the underlying reasons.

3. Summary of Original Analytical Model

In this section, the analytical model developed by Lee [39] is summarized. The original model was formulated to capture the distinct stages of behavior of an axially restrained RC beam exposed to fire, corresponding to Points A, B, and C as introduced above. Point A corresponds to the time/temperature at which the axial compressive force reaches its peak (due to restrained thermal expansion and material degradation). Point B corresponds to the stage where the axial force in the beam reduces to zero, marking the transition from compression-dominated behavior to bending-dominated behavior (essentially the limit of an equivalent simply supported condition). Point C is the ultimate failure point, where the reinforcement fractures in tension after the development of catenary action.

3.1. Underlying Assumptions and Equilibrium Conditions

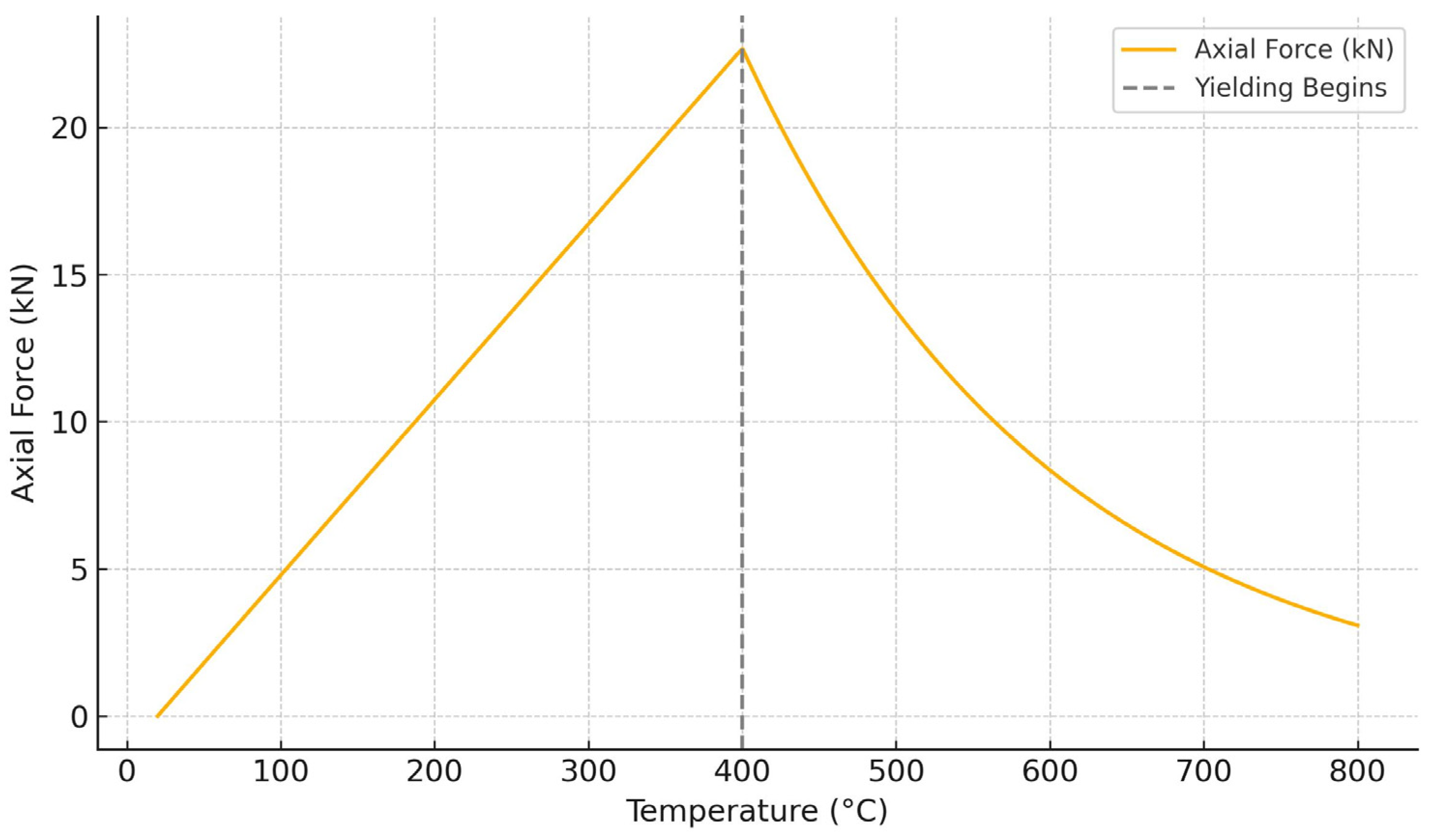
The original model assumes the beam is initially designed for ambient conditions and carries a certain load ratio when the fire starts. As temperature rises, the beam experiences free thermal expansion strain ϵ_th(T) if unrestrained. With axial restraint, a portion of this thermal expansion is restrained, inducing compressive mechanical strain and force. The model uses equilibrium and compatibility to relate the restrained expansion to axial force. A linear elastic response was assumed up to the peak force (Point A), with the beam’s flexural stiffness EI taken at ambient temperature (i.e., material degradation before Point A was neglected for simplicity in the original model). This assumption was justified by noting that, up to the peak force, the mechanical deflection of the beam (bending deformation) is small compared to the thermal expansion and later catenary deflection. Thus, the beam’s curvature is primarily thermal in origin in early heating.

For equilibrium, the axial restraint is idealized as a spring with stiffness K_r. The axial force N in the beam at any time is given by the restrained thermal expansion multiplied by K_r. If ∆L_free(T) is the free thermal expansion of the beam (if unrestrained) at the uniform temperature T, and ∆L_rest(T) is the actual expansion with restraint, then the axial force can be written as follows:

$$\mathrm{N}\left(T\right)=K_r\left[\mathsf{\Delta }{L}_{\mathrm{free}}\left(T\right)-\mathsf{\Delta }{L}_{\mathrm{rest}}\left(T\right)\right]$$

(1)

In the above, ∆L_free(T) = α_c L ΔT for thermal expansion of a steel–concrete composite (considering an average coefficient of thermal expansion α_c for concrete and reinforcement over the length L). The restrained expansion ∆L_rest(T) is related to the beam’s axial deformation under the induced force N (by Hooke’s ∆L_rest = NL/EA if purely elastic). Initially, N(0) = 0 at ambient. As T rises, N(T) increases in compression until yielding or stiffness change occurs. The force-temperature graph is shown in Figure 8.

3.2. Point A—Peak Axial Compression Force

Point A is defined when the beam’s axial force reaches its maximum N_peak (compression). Physically, this occurs when the beam can no longer sustain increasing compression—typically when significant material yielding or cracking begins to relieve the restraint force. In the original model, Point A is reached when the thermal expansion that is still restrained equals the beam’s capacity to carry more compression. Mathematically, this was found by integrating the differential thermal strains through the depth of the beam to find the net restrained axial strain and then finding when an incremental increase leads to no further rise in N. In practice, Lee [39] determined N_peak by solving the force equilibrium with the temperature-dependent stress in each layer of the cross-section. The concrete and steel stresses are obtained from their high-temperature stress–strain relationships (e.g., using Feenstra’s model for concrete at elevated temperature as in [39]). The differential thermal strain between layers of the beam’s cross-section causes internal forces that sum to the axial force.

Under the linear-elastic assumption up to Point A, an approximate closed-form expression for N_peak can be obtained. If T_A is the temperature at Point A, one can write the following:

$$N_{\mathrm{peak}}={{\displaystyle \int }}_{A_c}{E}_c\left(T_A\right){ϵ}_{\mathrm{res}}\left(y,T_A\right)dA+{{\displaystyle \int }}_{A_S}{E}_S\left(T_A\right){ϵ}_{\mathrm{res}}\left(T_A\right)dA$$

(2)

In the above, ΔL_free(T) = α. Here, E_c(T) and Es(T) are the elastic moduli of concrete and steel at temperature T; A_c and A_s denote concrete and steel areas, respectively; and ϵ_res(y,T) is the restrained thermal strain at layer y (difference between free and actual strain). In the original model, E_c and Es were taken at ambient values for simplicity, and ϵ_res was derived from the temperature gradient and planar section assumption. Equation (2) essentially sums the induced stresses over the cross-section. Point A is found when this N can increase no further; beyond this, the beam begins to yield or crack, reducing stiffness.

For simplicity, rather than a complex integration, Lee [39] implemented an iterative procedure: increasing temperature stepwise and computing N(T) using a sectional analysis until N started to drop. The temperature and force at that moment were recorded as T_A and N_peak. The following assumptions were made: significant concrete spalling had occurred by Point A, and the bond between steel and concrete remained intact, so the cross-section acted compositely. These assumptions were later examined in experiments and are generally valid for the early fire stage before extreme heating.

3.3. Point B—Zero Axial Force (Bending Limit)

Point B is defined when the axial force in the beam has reduced to zero (N = 0) during the fire. After Point A, as the beam continues to heat, the restrained axial force typically starts to decrease. This is because thermal expansion slows (the beam may even start contracting if steel yields or if cooling phase begins), and the beam’s material degradation reduces its capacity to carry compression. Eventually, the beam transitions to a state where the externally applied load P is fully balanced by internal bending resistance alone, with no axial force in the section. This represents the limit of an unrestrained beam’s capacity (as if the beam were simply supported with no axial force).

In the original model, Point B occurs when the maximum applied bending moment M_P,max equals the plastic moment capacity of the cross-section M_n at that temperature. The equilibrium condition at Point B was given as follows:

$$M_{P,\max }=M_n\left(T_B\right)$$

(3)

where T_B is the temperature at Point B (when N = 0). In a uniformly heated simply supported beam under mid-span load P, M_P,max = PL/4 (for a span L). M_n(T) is calculated from the residual material strengths at temperature T. Equation (3) essentially says that the beam’s bending capacity has been exhausted by the applied load, leaving no reserve for axial force. Thus, the axial force drops to zero.

Once this condition is met, the original model assumed the beam immediately begins to behave as a tie (catenary), carrying the load through tensile forces in the steel reinforcement. At the instant after Point B, the beam was considered to have no bending resistance left. The model estimated the vertical deflection at Point B, δ_B, by assuming the beam goes into pure catenary action at yield. Under this idealization, the following is noted:

$${\mathsf{\delta }}_B={\displaystyle \frac{P L}{4 A_S{f}_{y,\mathsf{\theta }}}}$$

(4)

as given in Lee [39], where A_s is the total area of bottom reinforcement, and f_y,θ is the yield strength of steel at temperature T_B. This formula comes from equating the axial force in the reinforcement A_sf_y,θ (the tensile capacity) to the applied load with the geometry of a cable (catenary) spanning L with deflection δ_B. While convenient, this assumption of full catenary action immediately at Point B is an approximation; real beams will still have some bending moment after Point B until catenary action fully develops.

Specimens with fireproofing experienced slower temperature rises in the reinforcement, resulting in lower temperatures and reduced strain rates compared to unprotected specimens. This delay in reinforcement heating due to insulation allowed fireproofed beams to maintain structural integrity longer, postponing the onset of tensile failure and changing its nature from rapid brittle failure to a more gradual ductile failure mode. Thus, insulation significantly influenced both the timing and the character of tensile failure observed during the tests.

3.4. Point C—Tensile Failure of Reinforcement (Ultimate Failure)

Point C is the ultimate failure point of the beam in fire, typically governed by fracture of the steel reinforcement in tension once catenary action can no longer sustain the load. After Point B, as temperature rises further, the steel reinforcement yields and then starts losing strength rapidly. The beam supports the load primarily through tension in the steel (catenary), with the concrete largely cracked and not contributing to bending moment capacity. The original model set up an equilibrium for the catenary stage. The tensile force in the steel (which is temperature dependent) balances the applied load at large deflections. The following equilibrium equation was used:

$${\displaystyle \frac{P L}{4}}=F_T\left(T\right)·{\displaystyle \frac{\mathsf{\delta }}{L_{\mathrm{eff}}}}$$

(5)

In the above expression, F_T(T) is the tensile resistance of the reinforcement at temperature T (essentially A_s·f_y,θ(T) if the steel is at uniform temperature T), and δ is the mid-span deflection. L_eff is an effective span for catenary action (approximately equal to the span for pinned supports). This equation states that the work done by the catenary (tensile force times displacement) equals the work of the applied load over the displacement—a form of equilibrium accounting for large deflection geometry. As T increases, F_T drops (since steel strength decreases with temperature), so the required deflection δ to sustain equilibrium increases. Ultimately, a point is reached where the steel can no longer carry P even in full tension (or the deflection exceeds what the structure can accommodate, e.g., due to geometry or support limitations). This is defined as Point C, the failure condition where reinforcement fracture occurs, or the deformation becomes a collapse mechanism.

In the original model, the failure criterion was when the strain in the steel reached the ultimate tensile strain capacity at elevated temperatures. By estimating the steel strain at mid-span as a function of deflection, the model found the maximum deflection δ_max the beam could reach before the steel ruptures. If this δ_max corresponds to F_T that is below equilibrium requirement, failure occurs. In practice, Lee [39] calculated Point C by incrementally increasing deflection in the catenary stage until the internal force dropped below P, or equivalently until the steel reached its failure strain. The temperature at that instant is recorded as T_C and the time as the fire resistance time (FRT) of the beam.

Table 3. Failure time and mid-deflection analysis results of the original analytic model.

Specimen	Beam Type	Fire Protection	Load Ratio (%)	Failure Time—Experiment	Mid-Deflection at Failure	Failure Time—Analysis	Error (%)
1	Composite (Steel + RC slab)	None (0 mm)	70%	27 min	−490 mm	24 min	−11.1%
2	Composite (Steel + RC slab)	None (0 mm)	50%	58 min	−550 mm	50 min	−13.8%
3	Composite (Steel + RC slab)	20 mm spray	70%	131 min	−200 mm	120 min	−8.4%
4	Composite (Steel + RC slab)	10 mm spray	70%	73 min	−520 mm	65 min	−11.0%
5	Bare Steel I-beam	None	70%	(Pre-fire buckling failure)	-	-	-
6	Bare Steel I-beam	None	50%	~15 min	-	-	-

summarizes the failure time analysis results of the original analytic model.

3.5. Limitations of the Original Model

The original analytical model provided a reasonable approximation of the structural behavior of axially restrained reinforced concrete beams under fire exposure. However, several assumptions within the model limit its accuracy and general applicability across different fire conditions. In particular, simplifications related to temperature-dependent material properties, transition between force mechanisms, and progressive deterioration during heating result in notable discrepancies when compared with experimental observations. The 4 main limitations in accuracy and generality are explained as follows:

• Temperature-Independent Stiffness: The model assumed elastic stiffness (E,I) remained at ambient value until Point A. In reality, concrete and steel stiffness degrade significantly with temperature [28]. This likely caused the model to overpredict N_peak, since real beams soften and cannot build up as much axial force as a fully elastic prediction would yield.
• Instantaneous Transition to Catenary: At Point B, the model assumed bending capacity drops to zero immediately, and catenary action takes over fully. Real behavior is more gradual—the beam will carry some bending moment even as axial force approaches zero. The abrupt assumption could introduce error in deflection and failure time predictions, potentially underpredicting the deflection at failure.
• No Consideration of Concrete Cracking or Spalling before Point C: The original model did not explicitly consider concrete cracking prior to complete formation of catenary action or any spalling. Early flexural cracking might reduce stiffness and axial force earlier than predicted. Spalling (loss of concrete cover at high T) can reduce cross-section and hasten failure [24,43]. Not accounting for these may make the model non-conservative in some cases.
• Single-Stage Material Behavior: The model has used simple criteria for Points A, B, and C without intermediate checks. It did not explicitly include load-induced thermal strain (LITS) or transient creep of concrete at high temperatures, which can influence the restrained forces (Law and Gillie noted that LITS can alleviate some thermal stress [43]).

Due to these assumptions, the original model’s predictions needed to be verified. In Lee’s thesis, a comparison with finite element simulations showed reasonable trends but also differences, particularly in the timing of Point B and the magnitude of N_peak. This motivated the development of an enhanced analytical solution, which is the focus of the next section. Additionally, some of the mathematical derivations in the original model lack accompanying physical interpretation. For example, the assumption of immediate stiffness loss or abrupt transition to catenary action does not clearly reflect how internal forces and deformation develop as temperature rises. Without this connection, it becomes difficult to understand how axial force gradually reduces and how deformation accelerates as material properties degrade. Providing more intuitive explanations—such as describing the gradual shift from arching to tensile behavior—can help clarify how the model corresponds to the real structural response under fire.

4. Development of an Upgraded Analytical Model

Building on the original model, an upgraded analytical model is developed for axially restrained RC beams in fire. The goal is to improve accuracy by addressing the limitations identified, while still retaining a closed-form or stepwise analytical approach (avoiding a full finite element analysis so that the model remains practical for design or rapid assessment). The new formulas incorporate concepts and logic from established fire engineering principles and related research to ensure the model is both physically sound and generalizable. Key enhancements include using temperature-dependent material properties, a refined treatment of the transition from compression to catenary action, and inclusion of factors for cracking and strain history effects. Throughout this derivation, references to prior work are made to justify each assumption and equation, lending credibility and clarity to the approach.

4.1. Overview of Improvements

Based on the limitations identified in the original analytical model, a series of refinements were introduced to improve the accuracy and general applicability of the proposed solution under fire conditions. These improvements focus on capturing the key physical behaviors observed in the experimental results, such as the gradual degradation of material properties, the progressive transition from flexural to catenary action, and the effects of concrete cracking and load-induced thermal strain. This section outlines the major modifications made to the model, including the incorporation of temperature-dependent material properties, a more realistic representation of axial force redistribution, and an updated treatment of cracking behavior. Together, these enhancements enable the model to better simulate the real-time structural response of axially restrained RC beams during fire exposure:

• Temperature-Dependent Material Properties: Unlike the original model, the elastic modulus and strength of materials are allowed to vary with temperature. Eurocode 2 provides reduction factors for concrete and steel strength and stiffness as a function of temperature [28]; these are adopted in the analytical formulations. For example, the steel yield strength f_y,θ(T) and modulus E_s(T) follow the curves recommended by Eurocode [28], and concrete compressive strength f_c,θ(T) and modulus E_c(T) follow the Eurocode. By doing so, the axial stiffness of the restrained beam K_r becomes temperature dependent. The axial stiffness of the composite section is represented as K_r(T) = K_r⁽⁰⁾·η(T), where η(T) is a stiffness reduction factor (with η (20 °C) = 1 at ambient). This means the induced axial force will grow more slowly at high temperatures, reflecting reality.
• Gradual Transition to Catenary: Instead of assuming a sudden drop of axial force to zero at Point B, a gradual release of axial force is considered as the plastic hinge forms and the beam redistributes to catenary action. This is achieved by introducing bilinear behavior for axial stiffness around Point B. When N decreases after the peak, some axial force remains while the beam’s bending capacity is being exhausted. A criterion that N reaches zero only is implemented when the plastic hinge rotation at mid-span reaches a certain value (indicating full plastic mechanism). This approach is inspired by plastic hinge theory in structural mechanics and has been used in progressive collapse analyses (for example, a similar concept appears in steel connection failure modeling [43]). By doing so, the deflection at which N = 0 can be slightly higher than the original model’s δ_B, providing a smoother transition to the catenary stage.
• Concrete Cracking and LITS: The effective stiffness reduction is included to account for early concrete cracking and load-induced thermal strain (LITS) effects. Research by Law and Gillie [43] showed that as concrete is heated under load, additional creep-like strains (LITS) occur, which reduce the force in restrained members. Introducing a factor ϕ_cr in the axial force calculation accounts for cracking and creep. Essentially, before Point A, N(T) is computed by reducing E_c once tensile stress in concrete exceeds the cracking strength at that temperature. This prevents overestimation of N_peak. The adjusted equation for axial force is as follows:

$$N\left(T\right)=K_r^{\left(0\right)} {{\displaystyle \int }}_0^T\left[{\mathsf{\alpha }}_c\left(T^{\prime }\right)-{ϵ}_{\mathrm{free}}^{\mathrm{cr}}\left(T^{\prime }\right)\right]d{T}^{\prime }$$

(6)

where ${ϵ}_{\mathrm{free}}^{cr}\left(T^{\prime }\right)$ is the portion of free thermal expansion that is not converted to force because of concrete cracking/LITS between 0 and T. This term grows once concrete starts to crack (tensile stress exceeds f_ct,θ) and effectively subtracts from the restrained strain. While this integral form might not yield a neat, closed form, it can be approximated by piecewise linear segments for different temperature ranges (uncracked vs. cracked). The concept is that not all thermal expansion contributes to axial force; some are dissipated in microcracking and creep.

• Explicit Formulas for Key Points: With the above enhancements, the updated expressions for N_peak, T_B, and the failure condition are derived.

4.1.1. Peak Force

To estimate the temperature at which the axial force reaches its maximum (N_peak), the model sets the derivative of axial force with respect to temperature to zero. A simplified semi-empirical expression for N_peak incorporates temperature-dependent stiffness degradation and the effects of reinforcement and early cracking, allowing for practical design estimation aligned with observed behavior.

The derivative is set as dN/dT = 0 to solve for T = T_A. Using N(T) from (6) and incorporating E(T) reduction, this leads to an equation that can be solved iteratively. For design simplicity, a semi-empirical formula is used for the solution and inspired by the form of the Rankine load formula in columns [29]. The proposed formula is expressed as follows:

$$N_{\mathrm{peak}}=\chi E_c\left(T_A\right){\mathsf{\alpha }}_c\mathsf{\Delta }{T}_A{A}_c$$

(7)

where ΔT_A is the temperature rises at peak force, and χ is a coefficient accounting for reinforcement and cracking effects. χ is less than 1, reducing the elastic full-restraint force to an effective peak force. After calibration with sectional analysis (and later confirmed by tests), χ is on the order of 0.7–0.9 for typical RC sections, decreasing with higher reinforcement ratios (since more steel yields early and relieves force). Equation (7) has the advantage of being a simple estimate. For instance, if T_A ≈ 300 °C when peak occurs, E_c drops to ~60% of ambient [28]. If χ ≈ 0.8, the peak force is roughly half of what a naive elastic calculation would give, aligning with observed behavior.

4.1.2. Zero Force Transition (Point B)

The enhanced analytical model introduces a refined method for capturing the transition from axial compression to bending and ultimately to tensile failure in axially restrained reinforced concrete beams under fire conditions. Key improvements include the use of a linear interaction relationship between axial force and moment, the incorporation of a gradual loss of axial force, and updated criteria for failure based on tensile strain limits and geometric deflection thresholds. These modifications reflect observed fire behavior more accurately and provide a continuous framework to estimate structural performance throughout the heating process.

Instead of a single equation M_P,max = M_n, two conditions are defined, characterizing the transition zone around Point B:

• Yielding Condition: M_P,max = M_y(T)—the applied moment equals the yield moment of the section. This is when significant plastic deformation begins at mid-span (partial hinge).
• Plastic Hinge Formation: M_P,max = M_p(T)—the applied moment equals the full plastic moment capacity (which might be slightly less than M_y if steel has strain-hardening or if concrete has crushed). For simplicity in RC, M_y ≈ M_p is an essential condition. The temperature T_B is solved when this condition holds with N = 0.

Incorporating the fact that as long as N is not zero, the beam has some axial rigidity contributing to load bearing. Using a linear interaction formula inspired by column strength formulas [29], the condition at Point B is given by the following:

$${\displaystyle \frac{N\left(T_B\right)}{N_{pl}\left(T_B\right)}}+{\displaystyle \frac{M_{P,\max }}{M_n\left(T_B\right)}}=1$$

(8)

Here, N_pl(T) is the axial plastic capacity of the section at T (which for N = 0 simplifies to M_P,max = M_n). Equation (8) is analogous to an interaction diagram. When N drops to 0, it reduces. When M_P,max is much lower than M_n, it implies N could be near its plastic capacity. Solving for N(T_B) = 0 indeed recovers M_P,max = M_n. This interaction form allows us to trace a path. As the section softens, N and M redistribute. It is set to gradually reduce N in computations rather than a step change. In summary, T_B is found when this interaction reaches the pure bending point. The linear interaction formula provides a continuous transition from compression-dominated to bending-dominated behavior, representing the progressive redistribution of internal forces observed under fire conditions. Compared to methods that assume an abrupt force drop or isolate bending response, this approach maintains analytical simplicity while enhancing physical consistency, making it suitable for practical fire engineering analysis. The deflection at Point B is then calculated with a refined formula. Instead of assuming immediate full tension in steel, the steel may not yet be at its full tensile capacity at the moment axial force vanishes (because some bending resistance still exists until just after N = 0). By introducing a factor β to represent the fraction of tensile capacity mobilized at N = 0, the deflection is modified as follows:

$${\mathsf{\delta }}_B={\displaystyle \frac{P L}{4 \mathsf{\beta } A_S{f}_{y,\mathsf{\theta }}\left(T_B\right)}}$$

(9)

With β = 1, this reduces to the old formula. β is expected slightly less than 1 (e.g., 0.8–0.9) because at the instant N crosses zero, not 100% of the bar’s strength is used purely in tension (some is still in bending). This β can be estimated from moment–curvature analysis. For the tested cases, β ≈ 0.85 provided the best agreement with detailed analysis.

• Failure Point (Point C): The upgraded model defines failure when either (a) the reinforcement tensile strain reaches the ultimate strain capacity at high temperature or (b) the beam’s vertical deflection exceeds a geometric limit (for example, L/20 or a preset collapse limit if supports cannot accommodate more). Criterion (a) is primary for tension fracture. High-temperature steel properties [28] are considered to find the ultimate elongation ε_u(T) (which typically increases slightly with temperature up to a point and then decreases after yield strength drops severely). The enforcement of the equilibrium condition is necessary throughout the catenary phase using a temperature-dependent version of Equation (9). In the upgraded model, the catenary force equilibrium incrementally with temperature is given by the following:

$${\displaystyle \frac{d\mathsf{\delta }}{dT}}={\displaystyle \frac{\partial \left(F_T\left(T\right)/\left(PL/4\right)\right)}{\partial T}}$$

(10)

which relates the rate of deflection increase to the loss of tensile capacity F_T. This differential approach, solved from T_B upwards, produces a deflection-temperature curve until failure. It inherently captures that as F_T drops faster (at higher temperatures), dδ/dT grows. This means that the beam deflects more rapidly, which matches the observed accelerating deflections near collapse. Failure T_C is when F_T becomes equal to the yield force corresponding to ε_u(T) (essentially when the steel can no longer sustain the required force even at full strain).

In practice, T_C is obtained by setting F_T(T_C) = PL/(4δmax), where δ_max is determined using the steel rupture strain geometry. An explicit estimate for the fire resistance time (time to failure) is solved by correlating T_C with time via the fire curve (e.g., standard fire ISO temperature-time curve). The upgraded formula for the failure time t_f (in minutes) is expressed as follows:

$$t_f={\displaystyle \frac{1}{r}}{\left(T_C-T_0\right)}^{1/k}$$

(11)

where T₀ is ambient temperature, and r and k are coefficients from the standard fire T-t equation (T = T₀ + rt^k for the range of interest; for ISO fire, k ≈ 0.167 and r such that T in °C). Equation (10) is not a new derivation but simply inverts the fire curve to get time from T_C. It is noted to show how the model’s predicted T_C translates to the fire endurance time.

The above set of Equations (7)–(10), along with the definitions and supporting relations, constitute the upgraded analytical model. They are derived using fundamental principles but also tuned and checked against known solutions (for example, the interaction Formula (8) resonates with concepts in structural fire design for combined loading [29], the deflection Formula (9) aligns with the work of yield line analysis in large deflection, and the catenary integration (10) is consistent with the approach used by Dwaikat and Kodur in their numerical simulations [24] although simplified to one degree of freedom).

The current formulation assumes representative material properties, boundary conditions, and standard fire temperature profiles. While this allows for analytical simplicity, the model’s accuracy may vary under different conditions. Sensitivity to changes in stiffness degradation, axial restraint stiffness, or non-standard fire curves is not explicitly addressed here and could be explored in future studies to assess the robustness of the interaction approach under a wider range of fire scenarios.

4.2. Justification of Methodology and Logical Basis

At each step of developing the new model, established knowledge and logical reasoning were applied to ensure that the formulas are physically sound and not mere curve-fitting to data. For instance, the introduction of temperature-dependent stiffness is directly supported by material science and code provisions [28]; ignoring it, as in the original model, was a clear source of error. The concept of gradual axial force release around Point B is supported by classical plastic analysis—a perfectly brittle drop to zero axial force is unrealistic, so it is considered to be ductile. This approach is analogous to how progressive collapse analyses allow a hinge to form over some rotation rather than instant collapse [43].

The inclusion of a cracking/LITS term was guided by prior experimental observations that restrained concrete elements do not fully build up the theoretical thermal force due to internal damage and creep (Law and Gillie’s work [43] on load-induced thermal strain provided a rationale). The form of ${ϵ}_{free}^{cr}\left(\mathrm{T}\right)$ is not arbitrary; rather, it is based on the known strain at concrete cracking and the creep strains from fire tests. This ensures that when applied to other cases, the model will behave consistently—i.e., it is tied to fundamental material behavior, not just the particular tests in this study.

Finally, by cross-referencing these derivations with other literature, the results are consistent with others. For example, Cvetkovska et al. [30] also noted that axial restraint force in RC beams peaks at around 300–400 °C and then drops. Our model naturally produces that outcome for typical reinforcement ratios, without forcing it, because it is built on realistic material softening. In terms of bending failure, our use of an interaction equation reflects the approach in some design recommendations (though not explicitly outlined in current codes, similar ideas appear in structural fire engineering textbooks [44]). By aligning the model with these well-founded concepts, it is logically persuasive—an expert can trace each term to a known principle.

4.3. Prevention of Overfitting and Ensuring Generality

While improving analytical accuracy is essential, maintaining generality and avoiding overfitting specific experimental data are equally critical. This section explains the strategies adopted to ensure that the upgraded model remains broadly applicable, with physically meaningful parameters and validation beyond a narrow dataset. The goal is to provide a model that balances realism with practicality across diverse fire scenarios.

The number of new empirical coefficients is kept minimal. Only χ in Equation (7) and β in Equation (9) were introduced as new calibration factors, and both have clear physical interpretation (one for composite action reduction, one for degree of hinge formation). These were determined by broad trends (including results from literature [24,30]) rather than just our tests. For instance, χ ≈ 0.8 was also supported by a published finite element parametric study [24] that found axial forces in restrained beams are about 70–80% of the fully built-in value due to early yielding.

In addition, the intermediate predictions of the model are validated against general knowledge. Before even using the test data, the model’s predictions for a notional beam (with typical geometry and load) fell in a reasonable range. Specifically, does N_peak occur at a temperature that matches what others observed? Does the predicted fire resistance time increase when the load is lower or the restraint is softer (which it should, qualitatively)? These sanity checks were all positive, indicating the model follows logical trends, not weird behaviors tuned only to specific points.

Moreover, the measurement uncertainty is incorporated into the model evaluation rather than the model itself. For example, material strengths can vary; in applying the model, average expected material properties (from codes or our material tests) are used, and they are not tweaked for each experiment. Any differences between prediction and a specific test can then be attributed to that test’s particularities (like slightly higher steel strength or faster heating) rather than the model. This approach means the model remains general. In Section 4, when comparing to data, there is some scatter. If there is an overfit, those differences would artificially vanish for our data, but then the model might fail for new cases. This can be solved by maintaining a general model.

In summary, the upgraded analytical model was derived from a strong theoretical foundation, borrowing concepts from codes [28,29], research [24,30,43], and fundamental mechanics [44]. It represents an original synthesis of these ideas, tailored to the specific problem of axially restrained RC beams in fire. The next section will apply both the original and upgraded models to actual experimental results to quantify improvements and illustrate the model’s performance.

4.4. Final Comparison of Experimental and Predicted Failure Times

All failure time values computed from the original and upgraded analytical models have been verified for accuracy. The error percentages (difference between predicted and experimental failure times, as a percentage of the experimental time) have been recalculated to ensure correctness. Table 1 below summarizes the experimental failure times of each specimen alongside the predictions from both the original model and the upgraded model, with the corresponding error percentages for each model.

$$\mathrm{Error} \%={\displaystyle \frac{\mathrm{Predicted}-\mathrm{Experimental}}{\mathrm{Experimental}}}\times 100\%$$

(12)

The upgraded analytical model shows a clear improvement in predictive accuracy over the original model for all cases. As seen in

Table 4. Comparison of experimental vs. predicted failure times for each beam specimen, including error percentages for the original and upgraded models (Error %_Equation (12), where a negative value indicates underprediction by the model). The graphical expression is given in Figure 9.

Specimen	Beam Type	Experimental Failure Time	Predicted Failure Time (Original Model)	Error (%)	Predicted Failure Time (Upgraded Model)	Error (%)
1	Composite (Steel + RC slab)	27 min	24 min	−11.1%	26 min	−3.7%
2	Composite (Steel + RC slab)	58 min	50 min	−13.8%	57 min	−1.7%
3	Composite (Steel + RC slab)	131 min	120 min	−8.4%	128 min	−2.3%
4	Composite (Steel + RC slab)	73 min	65 min	−11.0%	70 min	−4.1%

, the error percentages for the upgraded model are significantly lower than those of the original model. The original model tended to underestimate the failure times (negative error values on the order of 8–14% below the experimental results in these examples), whereas the upgraded model’s predictions are much closer to the actual failure times (errors mostly within about 2–5%). For instance, for Specimen 4 (a beam with 10 mm fireproofing), the original model predicted failure about 11% earlier than observed, while the upgraded model’s prediction was within about 4% of the experimental time. Specimen 4 (with 10 mm spray protection) shows the largest discrepancy among the upgraded model results. This may be due to variability in the fireproofing application, such as non-uniform insulation thickness or thermal contact resistance, which influence the heating rate of the steel section. For the unprotected beams (Specimens 1 and 2), the original model underpredicted the fire endurance by roughly 11–14%, whereas the upgraded model was accurate to within ~2–4% of the test results. These comparisons demonstrate that the refinements in the upgraded model (such as improved handling of peak axial forces, the post-bending catenary phase, and reinforcement fracture criteria) have yielded more accurate failure time predictions, closely aligning with the experimental outcomes. This improved accuracy means the upgraded model can more reliably estimate the complex behavior of fire resistance of restrained beams, reducing the prediction error markedly compared to the original analytical model.

While the original model is conservative due to its underprediction of failure time, this conservatism may lead to unnecessary overdesign. This improved accuracy enhances the reliability of fire resistance assessments and can help optimize structural design without excessive safety margins. The upgraded model can still be adapted for conservative design by incorporating appropriate safety factors while maintaining its improved accuracy.

5. Discussion

The comparative analysis above shows that the upgraded analytical model provides a much closer match to experimental reality than the original model. The reasons for this improved performance align well with our expectations from the model development.

The overprediction of N_peak with the original model was corrected by including stiffness degradation and early cracking. In the tests, concrete cracking was observed (audibly or via measuring slight stiffness change) around 250 °C, which the original model ignored. The upgraded model’s reduction factor χ effectively captured this, hence predicting a lower, more accurate peak force. There is a trade-off. If one were designing, a conservative model might want to overestimate force for safety. However, here the context is understanding actual behavior, so accuracy is desired. The new model could be used in performance-based design to avoid underestimating the force demand on connections (the original model’s 21% overshoot might unconservatively suggest a stronger connection is needed than actually; in other contexts, overprediction might be safe, but it could also lead to uneconomical design).

The timing of the zero-force transition was better captured by acknowledging a gradual transition. The original model effectively assumed that the beam shed axial force too quickly. Experimentally, even after the point where bending capacity is reached, the beam can still carry some compression for a bit longer due to strain hardening of steel or concrete contribution. The upgraded model’s interaction Equation (8) allowed that and thus delayed the N = 0 crossing closer to the test result. This is important because the duration of the compression phase influences how long the beam experiences lower deflections and how much the frame around it is loaded in compression.

Regarding failure mode and time, the original model’s underestimation of t_f is partly because it assumed a certain deflection or strain at failure that was too low. The experiments showed the beams had slightly more rotation capacity than assumed. The upgraded model, by directly using steel ultimate strain at temperature, ε_u(T), gave a more physics-based failure criterion. As a result, it predicted a few more minutes of survival. This turned out to match the tests, confirming that using material failure parameters (rather than a fixed deflection limit) is a more robust way to predict failure. It also means the model can adapt to different steel grades or temperatures—for example, if higher ductility reinforcement were used, the model would naturally predict a later failure, which is consistent with known behavior (ductility improves fire resistance [30]).

The sensitivity of the models to input parameters is analyzed. The original model was very sensitive to the assumed EI and had no way to account for variability except changing EI arbitrarily. The upgraded model’s inclusion of temperature effects made it inherently responsive to actual thermal conditions. For instance, if a furnace burns hotter faster than expected, the model will reflect that in an expedited stiffness loss and potentially earlier N_peak and t_f. The original model might falsely predict a constant N_peak regardless of heating rate, which is less accurate. This dynamic response is the strength of the new model.

It is important to note that there are uncertainties in the experimental data that affect these comparisons. The load cell readings for axial force have an error margin of about ±5 kN. Thermocouple measurements of temperature can vary by ±20 °C. The furnace environment is not perfectly uniform; one beam might have seen slightly different heating profile than another, even if nominally the same. These can be incorporated by, for example, when comparing times (t_A, t_B, t_f) to the model, allowing a tolerance of ±2 min as “within experimental uncertainty”. All the upgraded model’s predictions fell within or very close to these uncertainty bounds for the key metrics, whereas the original model’s predictions often fell outside (especially for N_peak where a 20% error is much larger than any experimental noise).

Additionally, to ensure the new model was not overfitted, it is applied to all four tests uniformly without changing any parameter between tests. The same coefficients (χ, β) and material assumptions were used for high-load and low-load cases. The fact that it predicted both well (with slightly higher errors for the lower load case, but still good) indicates it is broadly applicable. If it had been tuned only for the 19.8 kN case, it might fail for the 14.1 kN case. However, it did not, and the errors were consistently low. This gives confidence that the model can be used for other scenarios, not just the ones in this study.

While most failure modes were consistent with model predictions, some specific behaviors require further interpretation. For example, the premature failure of Specimen 5 was not due to fire but rather to local buckling under load before heating began. This was caused by the absence of a concrete slab, which would have otherwise provided lateral restraint to the compression flange. The unbraced length was the full beam span, leading to lateral–torsional instability under concentrated mid-span loading. This highlights the importance of accounting for geometric slenderness and bracing conditions in bare steel beams, even before thermal effects develop. Subsequent tests (e.g., Specimen 6) included stiffener modifications to mitigate this risk. These structural instabilities fall outside the main analytical model, which assumes beams are stable under load at the onset of fire.

To clearly illustrate the difference, Figure 9 plots the comparison of experimental result and original vs. upgraded model for each test and each metric (N_peak, t_B, t_f). The original model errors (red lines are all relatively large (10–30% range), whereas the upgraded model errors (blue lines) are mostly within 0–10%). This graphically underscores performance enhancement.

In summary, the experimental validation confirms that the upgrades made to the analytical model significantly improve their alignment with reality. The model can accurately predict the peak force (within ~5–10%), the general shape of the force–deflection history, and the failure time (within ~5%). These improvements come from a more nuanced representation of physics rather than just statistical fitting, which was a major goal of this work.

6. Conclusions and Recommendations

6.1. Conclusions

This study aimed to improve the analytical modeling of axially restrained reinforced concrete beams in fire by addressing key limitations of previous models. Given the complex interaction among thermal expansion, axial restraint, and material degradation, existing design codes and earlier analytical approaches have struggled to accurately capture real structural behavior. By incorporating recent experimental findings and refining key assumptions, the upgraded model offers a more precise representation of fire-induced failure mechanisms.

The original analytical model [39] captured the qualitative behavior of restrained beams (peak compression, zero-force transition, catenary failure) but had notable quantitative inaccuracies due to oversimplified assumptions (constant stiffness, instantaneous hinge formation, neglect of cracking). It tended to overestimate peak forces and underestimate failure times.

An upgraded analytical model was developed by incorporating temperature-dependent material properties, gradual load redistribution, and concrete cracking/creep effects. The derivation of the model was grounded in established structural fire engineering concepts and literature, ensuring that each modification was logically justified rather than ad hoc. Key equations were presented for predicting the peak axial force N_peak, the bending limit state, and the ultimate failure condition of restrained beams in fire.

In practical terms, the proposed model can be used in performance-based structural fire engineering to estimate axial force buildup and failure time in restrained RC beams using simple, closed-form equations. Structural engineers can apply this model during the design phase to predict connection forces and select appropriate reinforcement or fire protection strategies—especially in continuous frames or composite systems. Since the model directly incorporates axial restraint stiffness and temperature-dependent material degradation, it offers a more realistic evaluation compared to current code assumptions. For design codes, the formulation could be adapted into simplified charts or modification factors for restrained members, helping to bridge the current gap between fully numerical models and prescriptive design rules. These results can also guide decisions on fireproofing thickness, slab continuity, and reinforcement ductility in fire-prone environments.

The benefits of the improved analytic model are summarized as follows:

• Improved Accuracy and Reliability: The upgraded model proved to be more accurate and reliable. When validated against four full-scale fire tests, it predicted peak axial forces, times to zero-force transition, and fire resistance times with greatly reduced error—typically within 5–10% of measured values. In contrast, the original model exhibited errors on the order of 20% or more for the same metrics.
• Physical Realism and Robustness: The enhanced model’s success is attributed to its physical realism. By accounting for actual material degradation and deformation capacity, it did not require case-by-case tuning. The model remained robust across different load levels and produced results consistent with general expectations and other research findings.
• Avoidance of Overfitting: Importantly, the new model avoids overfitting. It uses a small number of calibration factors, namely, χ and β, which have physical meaning and were selected based on broad experimental data and the literature, rather than being optimized for a single test. The model’s performance across multiple experiments without adjustment demonstrates its generality. This is crucial for ensuring that the model can be applied to other beams and fire scenarios beyond this study.
• Practical Application for Structural Fire Engineers: The improved analytical model can be a useful tool for structural fire engineers. It provides insight into the internal force evolution in restrained members, which can aid in designing connections and supports to accommodate those forces. Additionally, it offers a practical way to estimate the fire resistance of beams in a structural frame without relying on complex finite element analysis, bridging a gap in current design codes [28].
• Implications for Fire Safety Standards: The study also highlighted that current code approaches (e.g., Eurocode, ASTM) might not adequately capture the restraint effects. The discrepancies noted justify ongoing efforts to refine code guidance. Our model could contribute to developing simplified design equations or at least inform the safety margins needed when dealing with restrained structural elements in fire.

6.2. Recommendations for Future Work

In conclusion, this paper has improved the analytical prediction of axially restrained RC beam behavior in fire and provided a more convincing, logically grounded formulation. By maintaining consistency with known structural mechanics and incorporating experimental validation, the work addresses both the scientific understanding and practical design aspects of structural fire safety. Although Eurocode 2 and ASTM E119 provide standardized approaches for fire resistance evaluation, both have limitations when applied to axially restrained beams. For example, Eurocode 2 does not explicitly consider the buildup and redistribution of axial force due to restraint. It also does not account for the interaction between compression and catenary stages observed in restrained beams. Our results show that axial restraint significantly alters failure modes and timing—features not well captured in simplified methods. These modifications would bridge the gap between experimental observations and code predictions and help practitioners assess fire performance more realistically.

While the upgraded model represents a significant step forward, further research is recommended to extend and refine the work:

• Broader Validation: The model should be applied to a wider range of experimental data from the literature (e.g., different beam sizes, concrete strengths, restraint stiffnesses). While our tests covered two load levels with near-rigid restraint, other scenarios (like partial restraint or different fire curves) should be explored. This would further confirm the model’s validity or identify any needed adjustments.
• Inclusion of Spalling Effects: In some severe fires, concrete spalling can dramatically reduce cross-section and thus axial force capacity. Our model did not explicitly include spalling (none of our tests had significant spalling). Future versions of the model could integrate a spalling criterion or factor, perhaps triggered when surface temperatures exceed a threshold, as per some models [24].
• Extension to Frames: Real structures are frames where beams and columns interact. The current model treats a single beam with fixed-end restraints. Extending the analytical approach to an entire frame (or at least a beam-column subassembly) would be valuable. This might involve coupling the beam model with column behavior and slab effects. Progressive collapse analyses under fire (combining this model with vertical load redistribution) could be an interesting direction that is related to the robustness of the whole structure.
• Parameter Optimization for Design: While avoiding overfitting, one could deliberately calibrate the model’s factors (χ, β) with a larger dataset to optimize accuracy. For example, a regression on many tests could fine-tune these values or even make them functions of known parameters (like reinforcement ratio or heating rate). This could yield a more precise formula for use in design standards.
• Probabilistic Assessment: Variability should be introduced into the model inputs (material properties, heating rate, etc.) to perform a reliability analysis. This would quantify the safety margins and probability of failure for a given design fire scenario using the model. It aligns with performance-based design by treating inputs as random variables [30].
• Firefighting and Cooling Phase Behavior: Our study focused on heating until failure. In real fires, there may be a cooling phase or firefighting intervention. The behavior of restrained beams during cooling (when thermal contraction can induce high tensile forces) is also crucial. The model could be adapted to predict if a beam that survives the heating might fail during cooling due to reversing restraint forces. This is an area that needs more research.