Critical Region Identification of Cable-Stayed Bridges Based on Eigensensitivity
Abstract
1. Introduction
2. Eigensensitivity-Based Critical Region Identification
2.1. Eigenvalue Sensitivity
2.2. Eigenvector Sensitivity
2.3. Criterion of Critical Region Determination
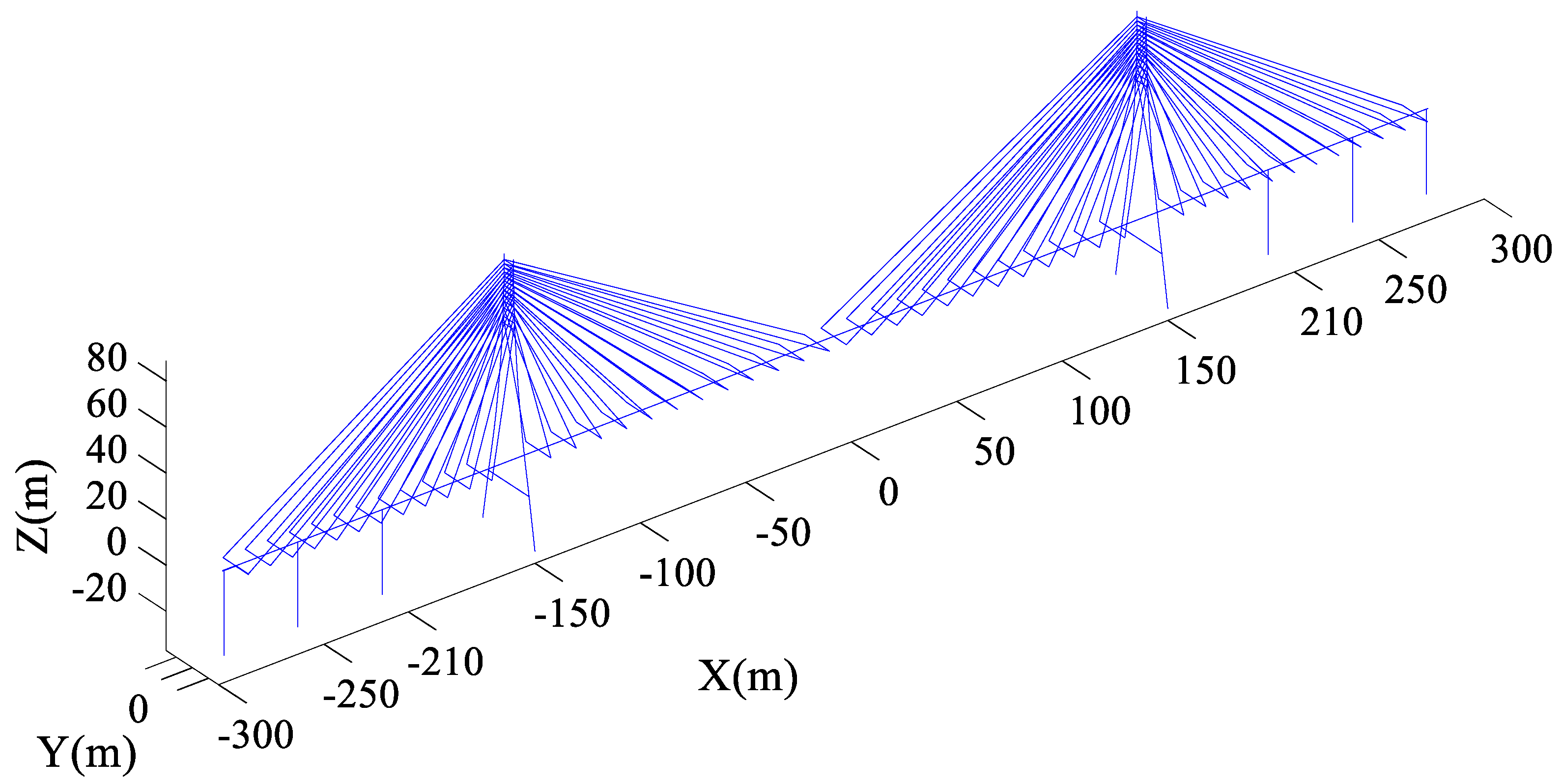
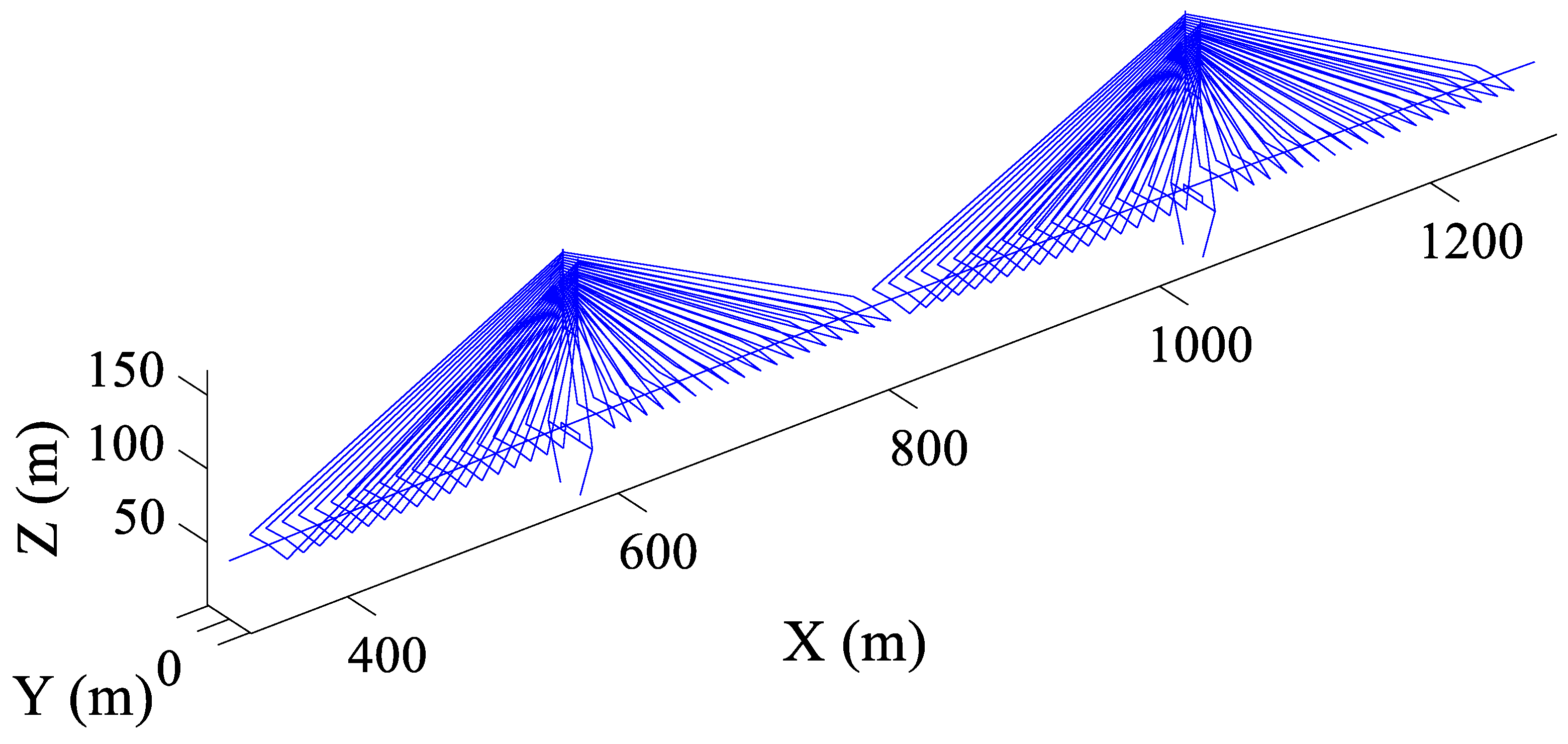
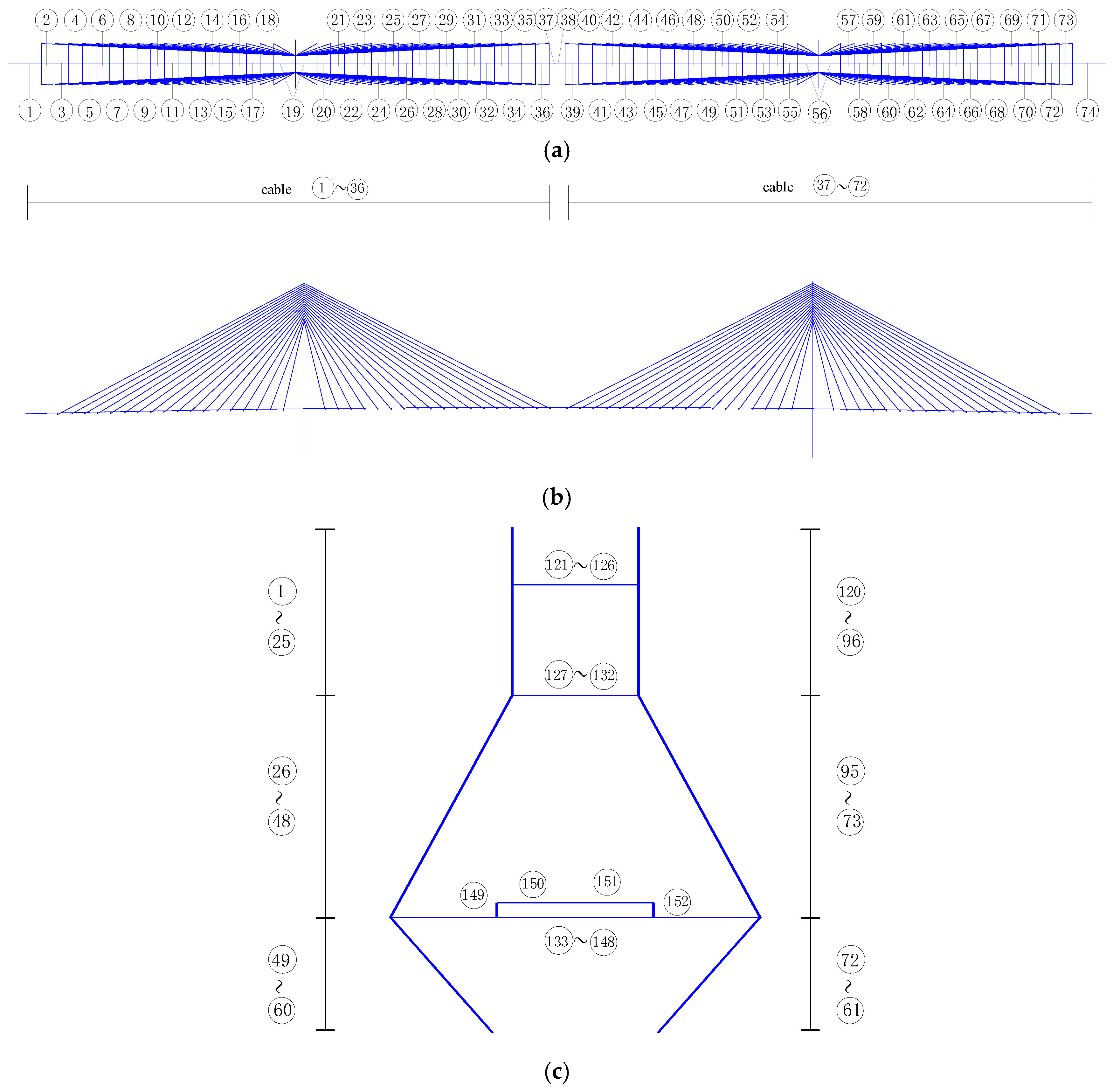
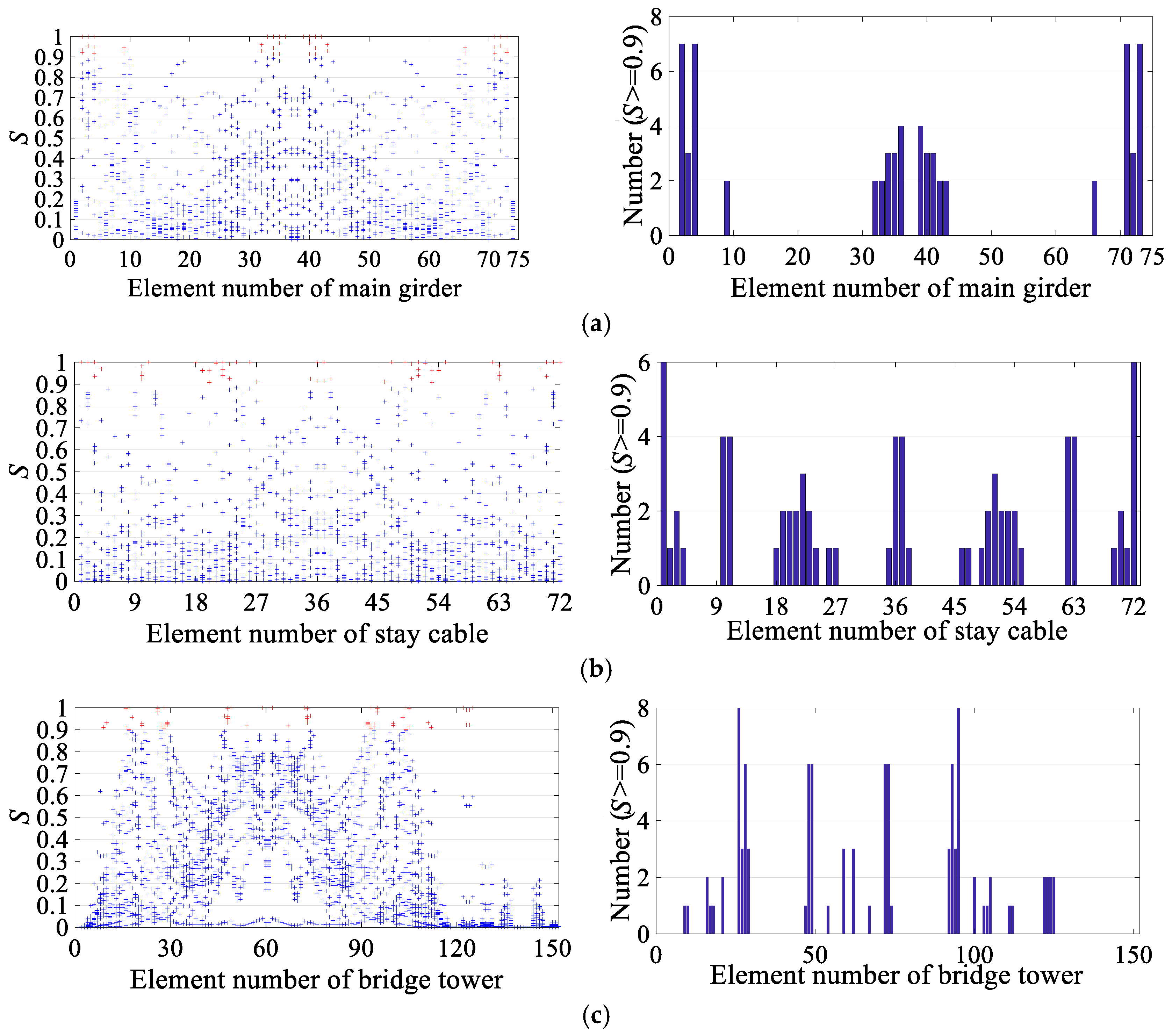
3. Numerical Simulation: Two Cable-Stayed Bridges
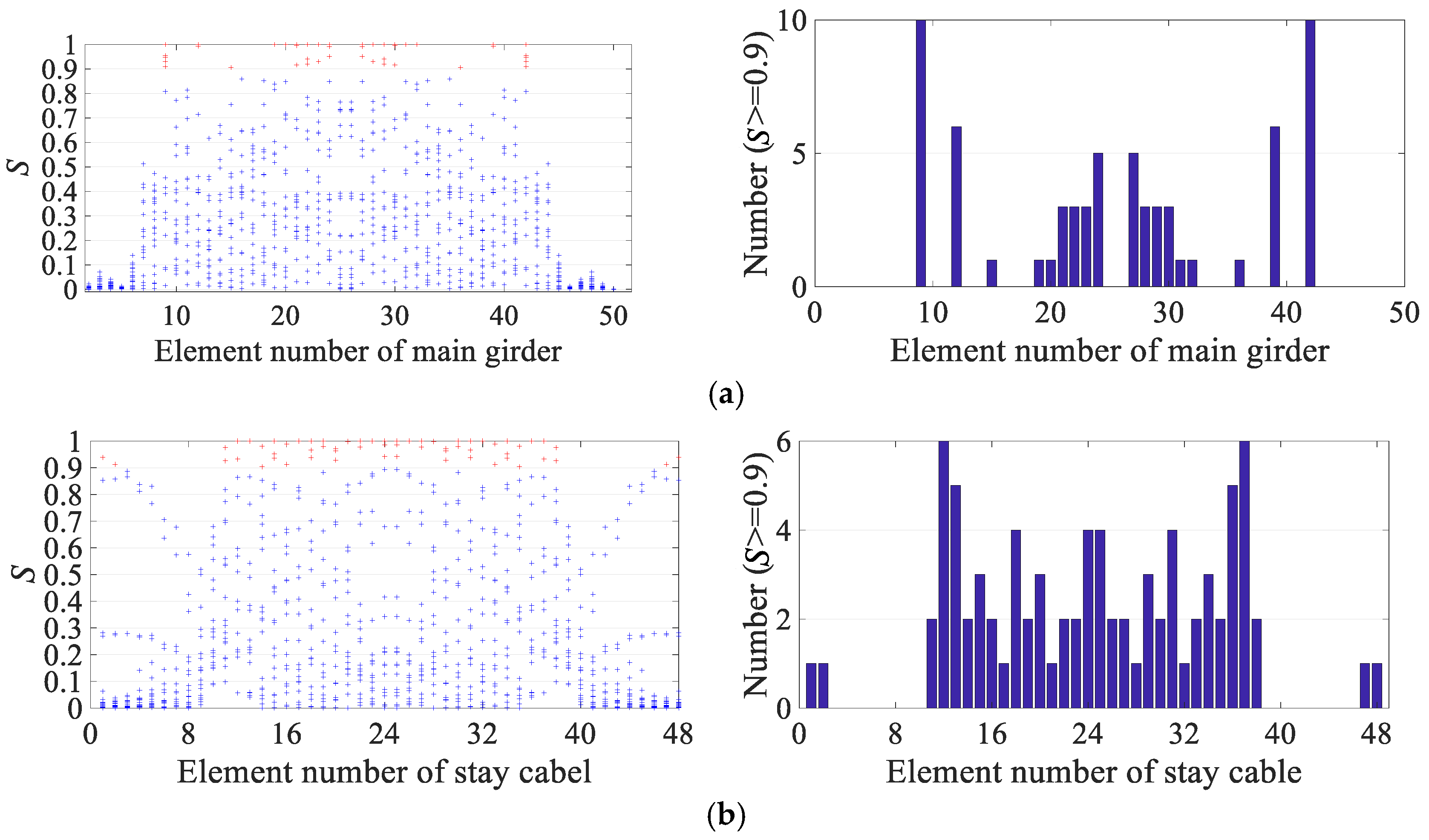
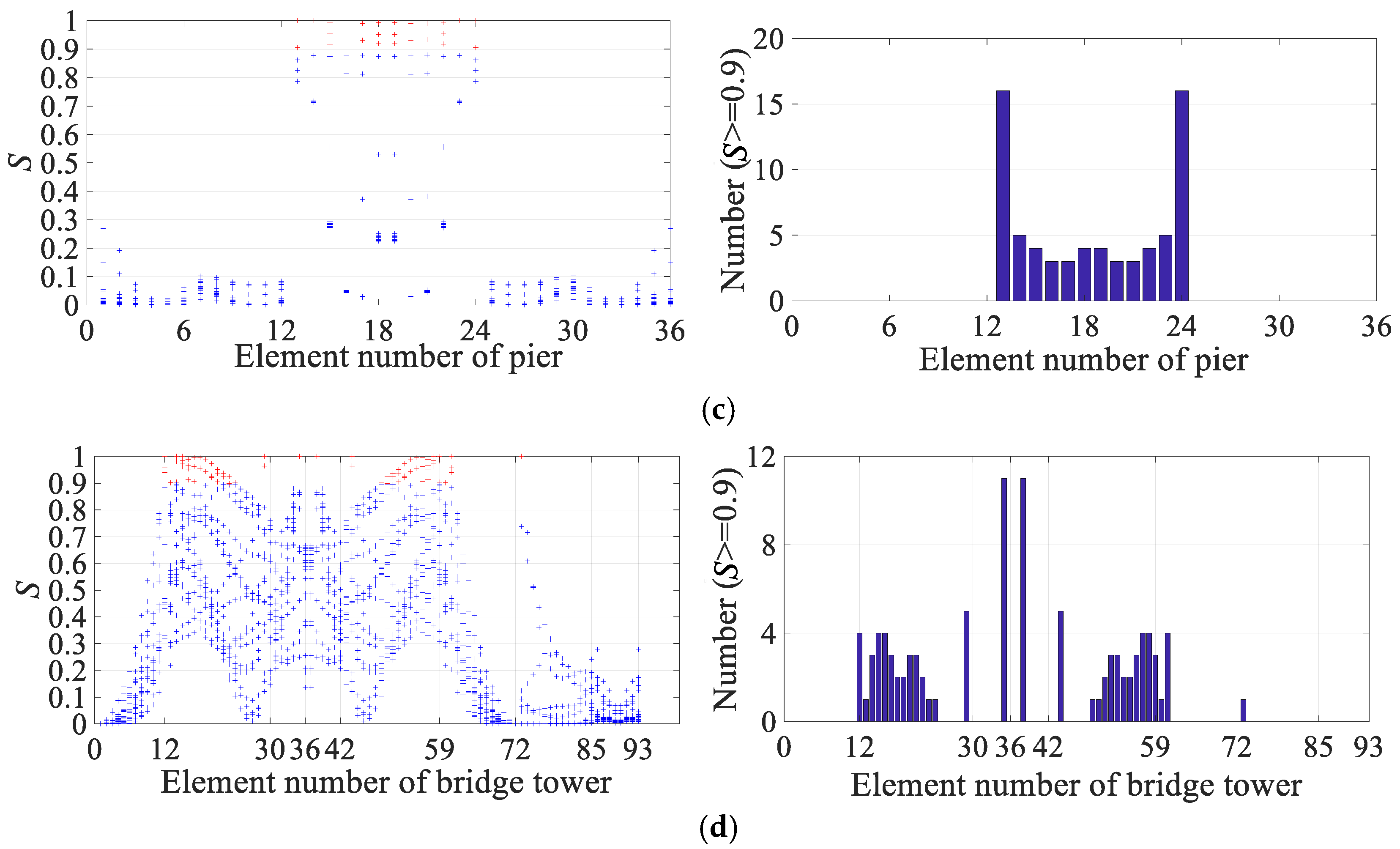
3.1. Ganjiang Bridge
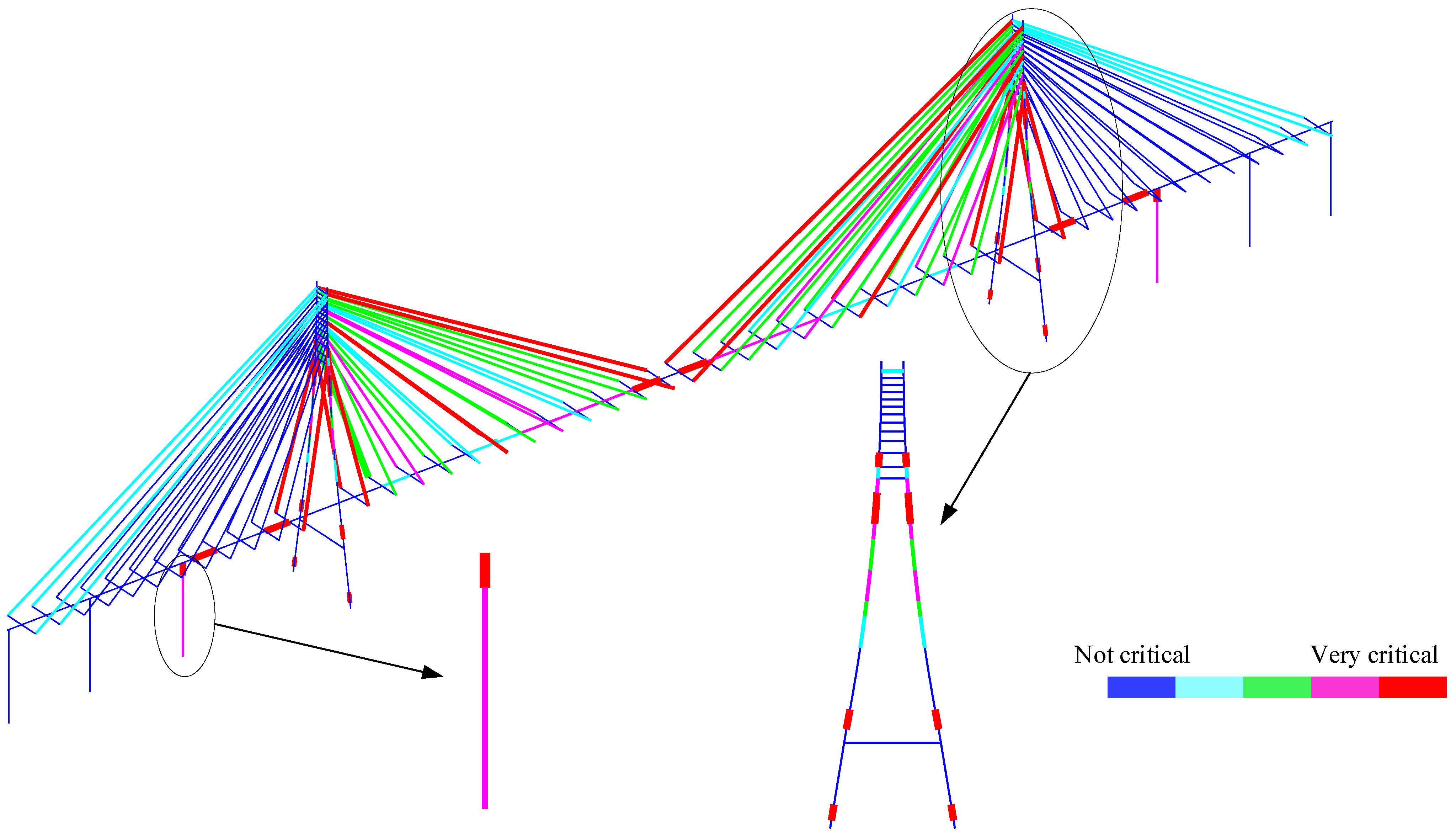
3.2. Junshan Bridge
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOFs | Degrees of freedom |
References
- Qin, J.G.; Zhang, W.W.; Huang, T.; Qian, K.; Deng, X.F. Effect of steel reinforcement corrosion on progressive collapse resistant of beam-slab structure with interior column failure. Eng. Struct. 2024, 312, 118257. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Yan, S.; Chen, Y.Y.; Xu, Z.Y.; Lu, Y. Experimental study on progressive collapse-resistant behavior of planar trusses. Eng. Struct. 2017, 135, 104–116. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Chen, G.; Cai, Q.; Feng, R.Q. Robustness study of fabricated single-layer grid shell structures based on component sensitivity and vulnerability. Thin-Walled Struct. 2022, 180, 109753. [Google Scholar] [CrossRef]
- Calvi, G.M.; Moratti, M.; O’Reilly, G.J.; Scattarreggia, N.; Monteiro, R.; Malomo, D.; Calvi, P.M.; Pinho, R. Once upon a time in Italy: The tale of the Morandi Bridge. Struct. Eng. Int. 2019, 29, 198–217. [Google Scholar] [CrossRef]
- Farneti, E.; Cavalagli, N.; Costantini, M.; Trillo, F.; Minati, F.; Venanzi, I.; Ubertini, F. A method for structural monitoring of multispan bridges using satellite InSAR data with uncertainty quantiffcation and its pre-collapse application to the Albiano-Magra Bridge in Italy. Struct. Health Monit. 2022, 22, 353–371. [Google Scholar] [CrossRef]
- Calό, M.; Ruggieri, S.; Buitrago, M.; Nettis, A.; Adam, J.M.; Uva, G. An ML-based framework for predicting prestressing force reduction in reinforced concrete box-girder bridges with unbonded tendons. Eng. Struct. 2025, 325, 119400. [Google Scholar] [CrossRef]
- Gao, K.; Weng, S.; Zhu, H.P.; Chen, C.J. Recovery of missing strain data under multiple time-varying effects using IMM Kalman filtering. Eng. Struct. 2025, 329, 119830. [Google Scholar] [CrossRef]
- Weng, S.; Xia, Y.; Xu, Y.L.; Zhu, H.P. Substructure based approach to finite element model updating. Comput. Struct. 2011, 89, 772–782. [Google Scholar] [CrossRef]
- Sun, L.M.; Shang, Z.Q.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of bridge structural health monitoring aided by big data and artificial intelligence: From condition assessment to damage detection. J. Struct. Eng. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- He, Z.G.; Li, W.T.; Salehi, H.D.; Zhang, H.; Zhou, H.Y.; Jiao, P.C. Integrated structural health monitoring in bridge engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Abiona, Q.O.; Head, H.M. Determination of bridge elements’ weights using the random forest algorithm. J. Perform. Constr. Facil. 2025, 39, 04024056. [Google Scholar] [CrossRef]
- Inkoom, S.; Sobanjo, J. Availability function as bridge element’s importance weight in computing overall bridge health index. Struct. Infrastruct. Eng. 2018, 14, 1598–1610. [Google Scholar] [CrossRef]
- Lin, Y.J.; Zhang, X.Z.; Xu, W.Q.; Zhou, M. Importance assessment of structural members based on elastic-plastic strain energy. Adv. Mater. Sci. Eng. 2019, 2019, 8019675. [Google Scholar] [CrossRef]
- Feng, J.; Li, C.T.; Xu, Y.X.; Zhang, Q.; Wang, F.; Cai, J.G. Analysis of key elements of truss structures based on the tangent stiffness method. Symmetry 2020, 12, 1008. [Google Scholar] [CrossRef]
- Cai, J.G.; Jia, W.W.; Feng, J.; Wang, F.; Xu, Y.X. Applications of stiffness-based evaluation method to element importance of truss systems. J. Civ. Eng. Manag. 2017, 23, 562–572. [Google Scholar] [CrossRef]
- Ma, S.Y.; Chun, Q.; Zhang, C.W.; Yang, L.; Qian, Y.C.; Cao, G.; Dong, Q.C. Quantitative evaluation method for the structural safety status of traditional courtyard-style timber buildings. Int. J. Archit. Herit. 2024, 18, 1323–1345. [Google Scholar] [CrossRef]
- Inkoom, S.; Sobanjo, J.O. Reliability importance as a measure of bridge element condition index for deteriorating bridges. Transp. Res. Rec. 2019, 2673, 327–338. [Google Scholar] [CrossRef]
- Liu, W.H.; Zeng, B.; Zhou, Z.; Zheng, Y.F. Multi-indicator evaluation method of important members of truss string structure. Struct. Des. Tall Spec. Build. 2024, 33, e2085. [Google Scholar] [CrossRef]
- Xia, J.W.; Wu, X.S. Evaluating the stiffness of cable-bar tensile structures based on subspaces of zero elastic stiffness and demand stiffness. Eng. Struct. 2020, 206, 110167. [Google Scholar] [CrossRef]
- Yuan, P.F.; He, B.Y.; Nie, R.; Zhang, L.H.; Yu, H.B.; Wang, G.B.; Ma, X.F. Member importance prediction and failure response analysis for cable network antennas. Eng. Struct. 2022, 266, 114642. [Google Scholar] [CrossRef]
- Lin, R.M.; Mottershead, J.E.; Ng, T.Y. A state-of-the-art review on theory and engineering applications of eigenvalue and eigenvector derivatives. Mech. Syst. Signal Process. 2020, 138, 106536. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhang, Y.; Weng, S. Damage identification of mono-coupled periodic structures based on driving-point anti-resonance frequency and sensitivity analysis. J. Sound Vib. 2025, 597 Pt B, 118819. [Google Scholar] [CrossRef]
- Yin, X.F.; Yan, W.L.; Liu, Y.; Zhou, Y.; Li, L.Y. Structural damage detection based on improved sensitivity function of modal flexibility and iterative reweighted lp regularization. Int. J. Struct. Stab. Dyn. 2024, 24, 2450111. [Google Scholar] [CrossRef]
- Weng, S.; Zhu, H.P.; Xia, Y.; Li, J.J.; Tian, W. A review on dynamic substructuring methods for model updating and damage detection of large-scale structures. Adv. Struct. Eng. 2020, 23, 584–600. [Google Scholar] [CrossRef]
- Weng, S.; Tian, W.; Zhu, H.P.; Xia, Y.; Gao, F.; Zhang, Y.T.; Li, J.J. Dynamic condensation approach to calculation of structural responses and response sensitivities. Mech. Syst. Signal Process. 2017, 88, 302–317. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Li, Y.C.; Wang, S.Q.; Xu, M.Q. A novel multistage approach for structural model updating based on sensitivity ranking. Smart Struct. Syst. 2020, 25, 657–668. [Google Scholar] [CrossRef]
- Cong, S.; Hu, S.L.J.; Li, H.J. Model updating methods using complex eigenvalues: Sensitivity-based versus cross-model cross-mode. J. Eng. Mech. ASCE 2021, 147, 04021013. [Google Scholar] [CrossRef]
- Chai, W.H.; Yang, Y.X.; Yu, H.B.; Yang, F.L.; Yang, Z.K. Optimal sensor placement of bridge structure based on sensitivity-effective independence method. IET Circ. Devices Syst. 2022, 16, 125–135. [Google Scholar] [CrossRef]
- Gonen, S.; Demirlioglu, K.; Erduran, E. Optimal sensor placement for structural parameter identification of bridges with modeling uncertainties. Eng. Struct. 2023, 292, 116561. [Google Scholar] [CrossRef]
- Kodur, V.K.R. Strategies for improving the performance of high-strength concrete columns under fire hazard. Struct. Control Health Monit. 2008, 15, 921–938. [Google Scholar] [CrossRef]
- Nelson, R.B. Simplified calculation of eigenvector derivatives. AIAA J. 1976, 14, 1201–1205. [Google Scholar] [CrossRef]
- Chen, Q.X. Model Updating and Elaborate Simulation of Multi-Type Bridges. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2021. [Google Scholar] [CrossRef]
- Zhu, T.Y.; Tian, W.; Weng, S.; Ge, H.B.; Xia, Y.; Wang, C. Sensitivity-based finite element model updating using dynamic condensation approach. Int. J. Struct. Stab. Dyn. 2017, 45, 1840004. [Google Scholar] [CrossRef]
- JT/T 1037-2022; Technical Specifications for Structural Monitoring of Highway Bridges. China Communications Press: Beijing, China, 2022.



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Meng, M.; Wu, Q. Critical Region Identification of Cable-Stayed Bridges Based on Eigensensitivity. Buildings 2025, 15, 1038. https://doi.org/10.3390/buildings15071038
Li J, Meng M, Wu Q. Critical Region Identification of Cable-Stayed Bridges Based on Eigensensitivity. Buildings. 2025; 15(7):1038. https://doi.org/10.3390/buildings15071038
Chicago/Turabian StyleLi, Jiajing, Meng Meng, and Qiaoyun Wu. 2025. "Critical Region Identification of Cable-Stayed Bridges Based on Eigensensitivity" Buildings 15, no. 7: 1038. https://doi.org/10.3390/buildings15071038
APA StyleLi, J., Meng, M., & Wu, Q. (2025). Critical Region Identification of Cable-Stayed Bridges Based on Eigensensitivity. Buildings, 15(7), 1038. https://doi.org/10.3390/buildings15071038





