Seismic Behavior of a Timber Structure Based on a Soft-Kill BESO Optimization Algorithm ^†

Abstract

The seismic performance assessment of timber structures and topology optimization have been widely researched in recent years. Furthermore, the use of wood as a construction material has increased due to new sustainability challenges. This research assesses the seismic performance of a topologically optimized timber building located in Concepcion, Chile. The structure is a five-story glulam braced frame, designed following current Chilean standards. The structural configuration was obtained through a topology optimization process using a variation of a soft-kill BESO algorithm implemented in MATLAB R2015a, obtaining topologies with low structural redundancy. For the analysis, a full 3D nonlinear model was prepared using OpenSees (Version 3.7.1), and the nonlinear behavior of the structure was only considered at joints using the backbone curves introduced in ASCE 41-13. Six different study cases were analyzed, varying joint strengths and ductility. The fragility curves were determined from a static pushover analysis (SPO) using SPO2FRAG (V1.1), considering the performance levels established in ASCE 41-13. The seismic hazard of the building’s site is estimated through a probabilistic seismic hazard analysis (PSHA), and the seismic performance of each case is determined by computing the probabilities of exceedance of the considered limit states. Analysis results show that wood braced-frame structures with low structural redundancy (and fewer main joints to dissipate energy), such as those obtained from topology optimization algorithms, exhibit a markedly brittle behavior with almost no displacement ductility. This undesirable behavior does not improve by providing more deformation capacity to this structure’s reduced number of main joints. Currently, the Chilean standard for seismic design requires a unique response modification factor R for wood structures. This research suggests that this requirement should be revisited, specifying different R values depending on the wood structure’s redundancy, considering that its displacement ductility comes almost exclusively from the nonlinear deformation capacity of joints.

1. Introduction

In 2015, the United Nations adopted the 2030 Agenda of Sustainability Development, which seeks to protect the planet and improve the lives and prospects of everyone [1]. Goal 9 is related to civil engineering because it refers to building resilient infrastructure, promoting sustainable industrialization, and fostering innovation. The approach is the development of resilient and sustainable infrastructure, that is, being able to recover from natural disasters and be environmentally friendly.

The construction sector had a total CO₂ emission of 5.7 billion tons in 2009, contributing 23% of the total carbon emission produced by global economic activities. Of these 5.7 billion tons, 94% are indirect emissions [2]. Indirect emissions are related to indirect energy use, the energy required to provide products and services for construction operations [2]. Building materials are one of the most critical parts of the indirect CO₂ emissions in the construction sector because each material has to be extracted, processed, and finally transported to its place of use [3].

On that basis, timber takes an advantageous position as an alternative construction material to solve this problem. According to Buchanan and Levine [4], carbon emissions from the manufacturing of construction are far more critical than the carbon stored in the materials, so wood is a much better building material because of the lower fossil fuel energy required for processing it compared to other energy-intensive materials such as steel or concrete.

However, a sustainable increase in wood usage is completely subjected to sustainable management of natural resources to keep safe the natural environment and ensure its long-term stability [4,5]. These challenges have led to the increased use of wood as a construction material and are currently a widely researched topic.

Timber structures generally have lower seismic demands because they are lighter than equivalent reinforced concrete (RC) or steel buildings. According to [6], the ductility of the structures depends on the selected constructive system and design. Ductile behavior in timber frames is mainly provided by the joints, which implies more hysteretic energy dissipation due to their nonlinear response and, thus, larger values of damping coefficients and reductions of the seismic demands over the structure.

Nowadays, a widely implemented method to evaluate the seismic performance of structures is developing fragility curves obtained from incremental dynamic analysis (IDA) [7]. To do so, several earthquake records are used, and each response is obtained by performing a response history analysis (RHA) at increasing values of a given intensity measure (IM). Then, the response value of a given engineering demand parameter (EDP) is obtained. With the previous data, finding the number of records for a given IM value that causes the EDP to exceed a given threshold, usually related to a specific limit state, is possible. Finally, the probability of exceedance conditional to given values of the IM is obtained directly and presented as fragility curves.

As mentioned, this method requires many RHAs, hundreds or even more, which implies a high computational cost. Therefore, alternative methods to obtain these curves with lower costs have been studied to handle this problem. One of these methods is the SPO2IDA [8], which estimates the IDA curves from the results of an SPO analysis using empirical equations. In addition, there is the SPO2FRAG [9] extension, which estimates fragility curves considering some limit state thresholds and sources of uncertainty. SPO2FRAG reasonably estimates the fragility curves compared to those obtained from traditional IDAs [10].

This paper evaluates the performance of a topologically optimized glulam (pinus radiata) five-story braced building to be located in Concepción, Chile, through a fragility-based analysis carried out using SPO2FRAG (V1.1), extending our previous work presented in [11]. A full 3D nonlinear model was prepared in the software OpenSees (Version 3.7.1) and then analyzed by a static pushover (SPO) analysis. Several fragility curves were obtained considering different values of ductility and strength for the building’s main joints, and the influence of these parameters on the probability of exceedance (POE) of different limit states on the building’s life cycle (50 years) was then evaluated.

2. Review of Seismic Performance of Timber Structures

Timber structures have gained significant attention due to their sustainability, energy efficiency, and favorable seismic performance. The seismic behavior of these structures is influenced by various factors, such as material properties, structural systems, and connection design. This section reviews the seismic performance of timber structures, highlighting key findings from experimental studies, numerical modeling, design principles, and implications for seismic strengthening.

One of the main advantages of timber structures in seismic performance is their high strength-to-weight ratio, which leads to lower inertia forces during seismic events. This characteristic is particularly beneficial in earthquake-prone areas, as it reduces the seismic demand on the structure [12]. However, timber’s brittle nature, particularly perpendicular to the grain, presents challenges in seismic design. To address this, modern timber structures are designed to maintain the elasticity of timber members, with energy dissipation and post-elastic behavior concentrated in the connections [13]. This approach aligns with the capacity design philosophy, which aims to localize plastic deformations in ductile components (e.g., steel connectors) while preventing brittle failures in the timber elements [14].

The seismic performance of timber structures is highly dependent on the type of structural system used. Light-frame timber structures, which are common in residential buildings, have been widely studied through full-scale shaking table tests. These tests demonstrate that light-frame structures exhibit highly dissipative behavior, with plastic deformations primarily occurring in the sheathing-to-framing joints, while anchoring devices (such as hold-downs and angle brackets) remain elastic [12]. In contrast, recent research has focused on Cross-Laminated Timber (CLT) structures, which offer superior in-plane stiffness and load-carrying capacity compared to light-frame systems. CLT structures can be divided into two groups based on their dissipative capacity: monolithic walls and segmented walls with vertical step joints. Monolithic walls rely on anchoring connections for energy dissipation, whereas segmented walls enhance ductility through vertical step joints, which allow for more widespread energy dissipation [13].

Experimental testing has played a crucial role in understanding the seismic behavior of timber structures. Full-scale shaking table tests on CLT buildings have shown that CLT panels behave almost like rigid bodies, with the connections providing the necessary ductility and energy dissipation [12]. For instance, the SOFIE project conducted shaking table tests on a seven-story CLT building, demonstrating that the structure could withstand significant seismic forces without collapse, with damage primarily localized around the connections [13]. Similarly, tests on light-frame structures underscore the importance of connections in achieving ductile behavior, with the sheathing-to-framing joints serving as the main source of energy dissipation.

Numerical modeling has also been instrumental in predicting the seismic performance of timber structures. Finite element (FE) models are commonly used to simulate the non-linear behavior of timber structures, with timber panels modeled as elastic elements and the non-linear response focused on the connections [12]. Advanced models incorporate the interaction between axial and lateral loads in connections, allowing for a more accurate representation of the hysteretic behavior observed in experimental tests. Pushover analyses and non-linear dynamic simulations are frequently employed to assess seismic behavior, aiding in scaling down the elastic response spectrum to the design spectrum in seismic design.

The seismic design of timber structures is governed by principles that emphasize redundancy, ductility, and the capacity design approach. Redundancy enables the redistribution of forces in the event of localized damage, while ductility ensures that the structure can undergo significant deformations without collapsing [14]. The capacity design approach ensures that plastic deformations are concentrated in selected ductile components, such as connections, while brittle elements are designed with sufficient overstrength to remain elastic [13].

Seismic strengthening of existing timber structures often involves improving the in-plane stiffness of floor and roof diaphragms and enhancing the connections between timber elements. Traditional carpentry joints, which rely on direct contact and friction, are commonly reinforced with metal connectors to prevent disassembly under seismic loads [15]. However, it is crucial to avoid excessive stiffness, which could lead to brittle failures. Recent research has explored using advanced materials, such as Fiber-Reinforced Polymers (FRPs), to strengthen timber structures. FRPs offer high strength and stiffness with minimal weight, making them suitable for seismic strengthening without significantly increasing the structure’s mass [15].

Several studies have contributed to advancing seismic resilience in timber structures. For example, Quizanga et al. [16] assessed the effectiveness of Impact Resilient Double Concave Frictional Pendulum (IR-DCFP) isolators in protecting Light Frame Timber Buildings (LFTBs) from extreme seismic events. Shaking table tests on a scaled model demonstrated that the superstructure remained undamaged, with peak acceleration ratios below 0.75 and story drift ratios under 0.52%. This finding confirms that IR-DCFP isolators provide a cost-effective seismic protection solution for LFTBs. Wenzel et al. [17] introduced the Energy and Structural Timber Building Optimization (ESTIBO) methodology, which integrates energy efficiency and seismic–structural design variables in light-frame timber buildings. Simulations revealed that key parameters, such as stud spacing, wall insulation thickness, insulation type, and floor concrete thickness, significantly influence both thermal and structural performance. Optimizing these variables improves energy efficiency while maintaining structural feasibility.

Further research has focused on improving energy-dissipating joints. Dang et al. [18] studied timber frames with novel energy-dissipating joints through quasi-static tests, demonstrating improvements in load-bearing capacity, lateral stiffness, and energy dissipation compared to traditional mortise–tenon joints. This study confirms that energy-dissipating joints enhance seismic resilience by delaying structural yield and providing additional lateral support. Similarly, Cao et al. [19] conducted full-scale cyclic loading tests on timber frames to assess seismic performance, focusing on semirigid joints. The study found that deformation and energy dissipation were concentrated in these joints, with wood splitting occurring near bolt holes. A simplified numerical model was developed and validated, revealing that gravity loading significantly affects structural capacity, while increased aspect ratios reduce stiffness and load capacity.

Chen et al. [20] reviewed recent advancements in self-centering (SC) mass timber structures, highlighting experimental, numerical, and analytical developments. Although SC technology has shown success in shear walls, further research is needed for multi-story applications and composite actions. Key challenges include toe crushing in PT wall systems, connection detailing for compression perpendicular to the grain, and inefficient energy dissipation connections. Shake table tests confirm the feasibility of SC systems, but additional research is necessary on long-term performance, fire safety, and velocity dampers. Alarcón et al. [21] implemented a low-cost seismic instrumentation system (LCSIS) to monitor the structural health of South America’s first six-story experimental light-frame timber building, the Peñuelas Tower (Chile). The system tracked natural frequency variations due to environmental changes, suggesting that LCSIS can enhance monitoring of timber structures, though further research is needed on damage quantification and environmental effects.

In summary, a combination of material properties, structural systems, and connection design significantly influences the seismic performance of timber structures. Experimental testing and numerical modeling have provided valuable insights into timber’s behavior under seismic loads, emphasizing the importance of ductile connections and the capacity design approach. Seismic strengthening requires careful consideration of stiffness and ductility, focusing on enhancing the in-plane behavior of diaphragms while preventing brittle failures. Ongoing research into innovative materials and design strategies will further improve the seismic resilience of timber structures.

3. Fundamentals of Topology Optimization (TO)

In general, the traditional structural design process mainly depends on the designer’s experience to obtain structures that fulfill all the requirements regarding response and costs. The structural characteristics, such as the form and dimensions, are mainly related to this experience, subjected to a trial-and-error process to obtain solutions with better results but not necessarily the optimal structure.

According to Sigmund [22], structural optimization is developed to find methods to obtain optimal structures. It is divided into four categories: sizing optimization, material optimization, shape optimization, and topology optimization (TO). The difference between the four categories is mainly related to the design variables.

The topology optimization method solves the most general structural optimization problem of distributing a given amount of material freely in the design space to obtain an optimal performance [22], combining all the structural optimization methods. The structures are analyzed by dividing them into numerous small elements, called finite elements, and the optimization problem is typically stated considering the density of material in each element as the design variable. The procedure starts once the design domain, boundary conditions, and loads are defined [22].

In TO, there are two main models to solve the optimization problem: discrete and continuous variable optimization parameters to interpolate material properties. Discrete parameters consider values equal to 0 or 1, and continuous variables consider values between 0 and 1. Among the most extended methods are the solid isotropic material with penalization (SIMP) model in continuous variables and the bi-directional evolutionary optimization (BESO) in discrete variables.

This paper applies a modified soft-kill BESO model presented by Uarac [23]. The model modifies the original method introduced by Huang and Xie [24], which combines SIMP and BESO schemes into one model to avoid some numerical problems typical of the previous ones. A comprehensive discussion of this model’s main characteristics is presented later.

4. SPO2IDA and SPO2FRAG Methods

SPO2IDA is a methodology presented by Vamvatsikos and Cornell [8] that provides estimations of incremental dynamic analysis (IDA) based on the results obtained through static pushover (SPO) analysis of single-degree-of-freedom (SDoF) systems. The capacity curve of the analyzed structure is simplified into a piecewise curve defined with a few parameters. A set of semi-empirical equations was obtained by analyzing numerous SDoF systems through IDA. These equations use the system’s natural vibration period and the capacity curve parameters as predictors to estimate the SDoF 16, 50, and 84% fractile IDA curves, assuming a Gaussian distribution.

SPO2FRAG is a procedure presented by Baltzopoulos et al. [9], developed to estimate the fragility functions of buildings based on the results of SPO analysis as a complement to SPO2IDA methodology. This software, coded in MATLAB^® R2015a, estimates the fragility functions considering different limit states and sources of uncertainty.

This method uses an equivalent SDoF system whose force-displacement relationship is a simplified piecewise curve obtained from the original capacity curve. Once the three fractile IDA curves are obtained, defining the limit-state thresholds for the considered engineering demand parameter (EDP) is necessary to estimate the fragility curves. These limit-state thresholds are defined as vertical lines to determine the intensity measure (IM) values obtained from the intersection with the 16%, 50%, and 84% fractiles, resulting in $I{M}_{16\%}^{LS}, I{M}_{50\%}^{LS}$ and $I{M}_{84\%}^{LS}$, respectively [9]. Then, the lognormal fragility parameters, that is, mean and standard deviation ($\eta ,\beta )$, are obtained as follows:

$$\eta =\ln \left(I{M}_{f,50\%}^{LS}\right)$$

(1)

$$\beta =\ln \left({\displaystyle \frac{I{M}_{f,50\%}^{LS}}{I{M}_{f,16\%}^{LS}}}\right) or \beta ={\displaystyle \frac{1}{2}}\ln \left({\displaystyle \frac{I{M}_{f,84\%}^{LS}}{I{M}_{f,16\%}^{LS}}}\right)$$

(2)

One modification to the mean can be implemented for structural damping different than $\zeta =5\%$. It is considered sufficient to modify the mean only for the limit states nearing collapse [9]. To do so, a modification factor, $C_{\zeta }$, proposed by Han et al. [25], is applied to the mean of the limit states defined by EDP thresholds near collapse, that consider $\zeta =5\%$ by default (${\eta }_{\zeta =5\%}^{LS}$):

$$C_{\zeta }=1-{\displaystyle \frac{0.07·\ln \zeta +0.20}{{\left(T_{eq}\right)}^{0.38}·{\left|{\alpha }_c\right|}^{-0.26}\cdot {\mu }_c^{-0.44}}}$$

(3)

$${\eta }_{\zeta }^{LS}={\eta }_{\zeta =5\%}^{LS}-\ln C_{\zeta }$$

(4)

with ${\alpha }_c$, ${\mu }_c$ parameters of the piecewise curve obtained from the capacity curve and $T_{eq}$ the period of natural vibration of the SDoF equivalent system. Additional sources of uncertainty, such as the record-to-record variability at nominal yield due to the higher mode effects (${\beta }_y$) or the modeling uncertainty (${\beta }_U$) may be included, increasing the total value of $\beta$.

5. Development of an Optimized Five-Story Timber Building

As presented before, TO methods are divided into continuous and discrete variable methods. SIMP and BESO are well-known continuous and discrete variables models, respectively.

The SIMP model works considering that each finite element of the mesh has a relative density ($x_i$) varying into the [0, 1] interval, obtained as the ratio of the element’s density at the $i$^th iteration to the initial density (iteration 0). This variation also modifies the modulus of elasticity of the element ($E_i$) [26], considering the following interpolation scheme: $E_i=x_i^p\cdot E_0,$ where $E_0$ is the initial element’s elastic modulus and $p$ a penalty factor. These intermediate densities may imply problems to be materialized, and some restrictions on the density field variation are usually required to ensure the existence of solutions [24].

The BESO model uses a discrete design variable. It defines the element’s modulus of elasticity and stiffness as E and K, respectively, when $x_i=1$ and both equal to 0 when $x_i=0$. It has been discussed that the BESO model can present numerical instability due to this discrete definition of the design variables [24].

The soft-kill BESO method [24] provides a blended model that works by carrying out an optimization process without deleting the inefficient elements $\left(x_i=0\right)$ but applying an interpolation based on the SIMP method to assign low values to the element’s densities, trying to avoid the defects of both previous methods.

This paper applies an algorithm developed by Uarac [23] based on the soft-kill BESO method, which allows the incorporation of multiple displacement restrictions and load combinations into the problem. These conditions are widespread requirements that must be considered in the structural design process.

In this case, the problem is a maximization of the structural stiffness or, equivalently, a minimization of the strain energy or mean compliance for a given volume of material. Equation (5) states the optimization problem,

$$\begin{gathered} \min c\left(x\right)={\displaystyle \frac{1}{2}}{U}^{T}KU={\displaystyle \frac{1}{2}}{\displaystyle \sum }_{i=1}^n{x}_i^p u_i^T{k}_i{u}_i \\ Subject to: \left\{\begin{array}{c}\mathrm{K}\mathrm{U}=\mathrm{F}\\ \mathrm{V}\left(x\right)-f\cdot {\mathrm{V}}_0=0\leftrightarrow {\displaystyle \frac{\mathrm{V}\left(x\right)}{{\mathrm{V}}_0}}=f\\ {\mathrm{u}}_{\mathrm{j}}\le {\mathrm{u}}_{\mathrm{j}}^{\ast }\end{array}\right. \\ {x}_i=x_{min} \mathrm{or} 1 \end{gathered}$$

(5)

where U and K are the displacement vector and stiffness matrix, respectively. The natural value $n$ is the number of finite elements, $u_i$ and $k_i$ the displacement vector and stiffness matrix of the $i$^th element, $p$ is a penalty factor, and $x_i$ denotes the density of the $i$^th element, where $x_{min}=0.001$ is the value used to denote the void elements to avoid the singularity of the stiffness matrix [24].

The first restriction is the equilibrium equation, where F is the force vector. The second one is the volume restriction, where $V_0$ is the initial design domain volume, $V\left(x\right)$ is the prescribed total volume of material, and $f$ is the volume ratio. Finally, the third one is the displacement restriction, where $u_j$ is the displacement of the $j$^th degree of freedom (DoF) and $u_j^{\ast }$ the maximum allowed displacement.

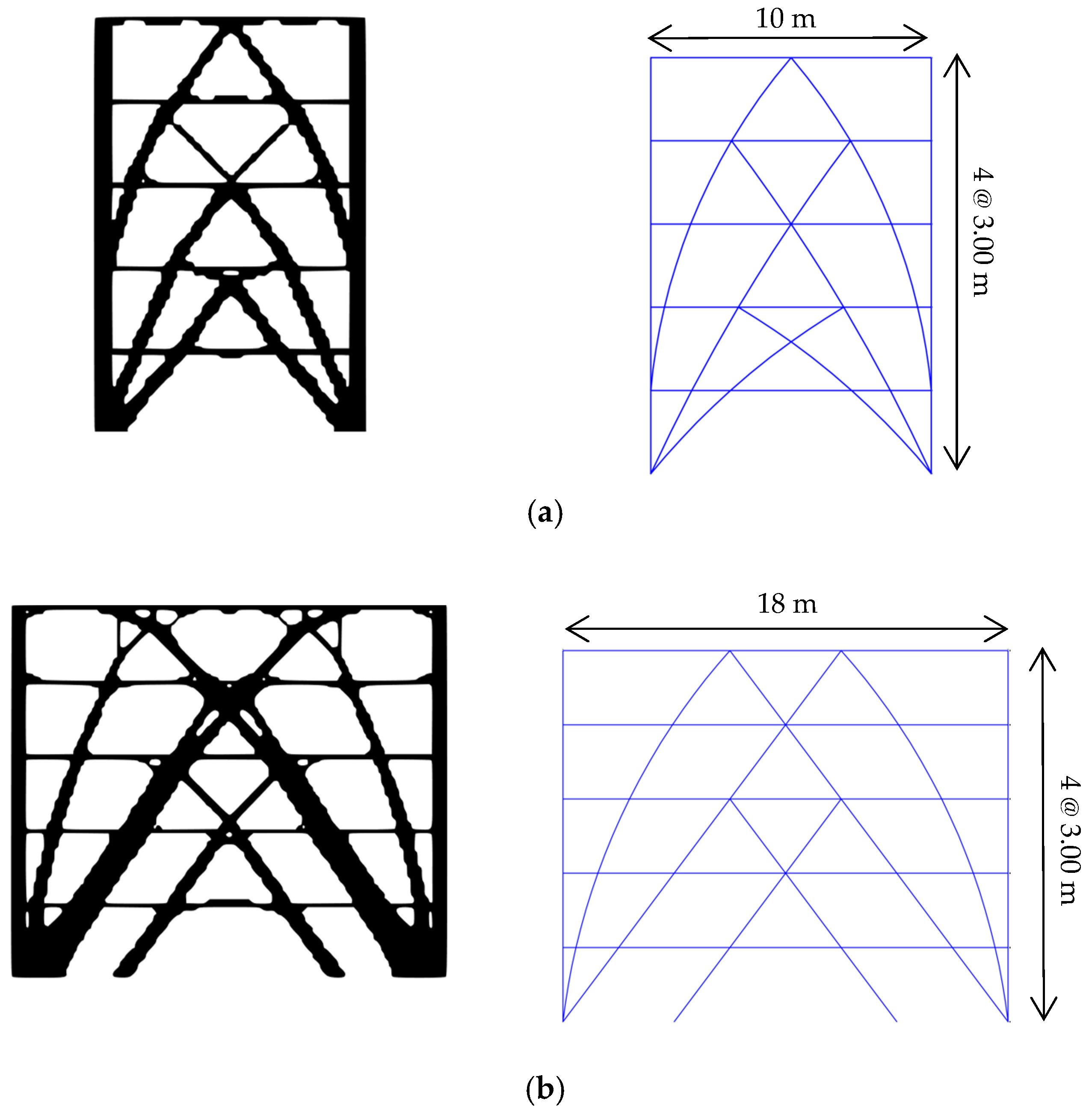
Figure 1 presents the archetype building before applying the TO algorithm. The structure has five stories of 3 m height and 10 × 18 m plan dimensions. The whole structure considers glued laminated (glulam) timber elements of pinus radiata. The first iteration considers solid domains at the axes where the frames will be located. This is only required to start the optimization process. Later, the algorithm introduced in Equation (5) will optimize these solid domains, obtaining the tree-like frames typically found by TO algorithms. Design loads were defined according to current Chilean standards NCh1537 [27] and NCh433 [28], as appropriate.

Dead loads (D) considered the self-weight (450 kg/m³) of the glulam elements plus a superimposed load of 150 kg/m² on each story. Live loads (L) considered 250 kg/m² at typical levels and a roof live load (Lr) of 64 kg/m². The design of timber members followed the ASD procedure required in NCh1198 [29]. Load combinations were obtained from NCh3171 [30].

In the TO algorithm, some non-optimizable zones were defined to prescribe beams at each floor level and boundary columns (Figure 2). Timber was considered an isotropic material with a Young’s modulus (E) of 10,500 MPa, that is, the parallel-to-fiber elastic modulus of NCh1198, and a Poisson’s ratio equal to 0.2.

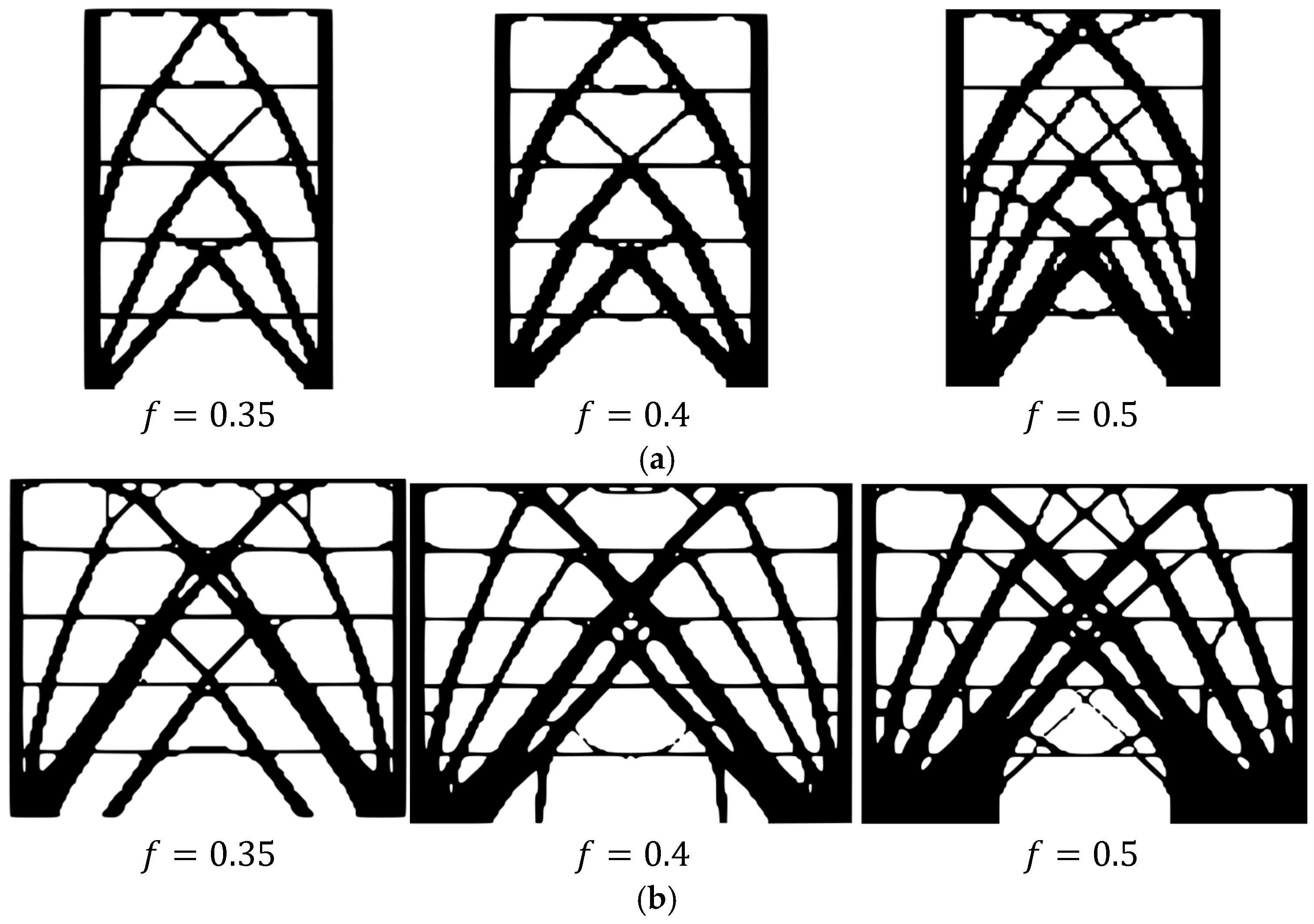
Each building wall was optimized using the TO algorithm implemented in MATLAB, considering a planar model for each one, with the corresponding load and displacement restrictions imposed by local standards. Three different volume ratios ($f$) were considered: 0.35, 0.40, and 0.50. Figure 2 depicts the resultant topologies in both directions.

All the topologies presented interstory drift ratios (IDR) lower than the NCh433 restriction of 2‰, so $f=0.35$ was selected in both cases to minimize the material usage. The final topologies were then post-processed and exported to the structural analysis software. Figure 3 depicts the selected topologies and the structural model, with prismatic elements, used in the final analysis/design.

The structural design followed the NCh1198, complemented by the NCh2165 [31], to compute the allowable stresses of pinus radiata’s glulam elements. The material’s elastic properties are the same as in the previous section, and the humidity was defined according to NCh1198. Timber was considered an isotropic linear elastic material for modeling purposes, and all joints were pinned. The seismic analysis followed the modal response spectrum analysis method of NCh433 for seismic zone 3 and soil type D.

Figure 4 shows the final model used in the analysis/design, where some changes were added to the structural configuration. An elevator space was included in the floor plan, following the requirements of local standards [32].

Table 1. Final dimensions of glulam elements.

Line Color	Height [mm]	Width [mm]	N° of Layers
Orange	480	240	12
Blue	440	240	11
Green	280	180	7
Red	240	180	6
Yellow	240	140	8
Pink	240	140	8
Grey	160	160	4

presents the final element’s dimensions.

Table 2. Direction-dependent building properties.

Direction	Period [s]	Code Reduction Factor R	Effective Reduction Factor Reff	Design Base Shear Coefficient
Short	0.22	3.30	4.99	0.19
Long	0.26	3.06	4.94	0.19

summarizes the building’s direction-dependent properties, showing that the maximum base shear coefficient controls the design in both analysis directions.

6. Nonlinear Modeling of Timber Building

An OpenSees full 3D nonlinear model was prepared for the archetype building to assess its seismic performance. In timber elements, ductile failures can only occur under perpendicular and parallel-to-fiber compression because the failure is brittle under shear and tension. Therefore, timber elements are preferred to remain linear elastic, and thus, the members should be designed with more strength than their connections to ensure a full nonlinear incursion at joints. Therefore, the OpenSees model considers linear-elastic structural members and nonlinear behavior only at joints, as typically done in nonlinear analysis of timber structures [33]. The model considers linear frame members with isotropic timber material. Only the connections of diagonal braces were modeled with a nonlinear behavior [34], considering the backbone curves introduced in ASCE 41-13 [35] (Figure 5), due to the lack of information about the hysteretic behavior of the specific timber joints. Considering all diagonal joints were pinned, backbone curves were provided only for axial and shear behavior, using ZeroLength elements and MultiLinear Material.

Table 3. Modeling parameters and numerical acceptance criteria for nonlinear procedures obtained from ASCE41-13 [35].

Connection Type	Modeling Parameters			Acceptance Criteria Δ/Δy
	Δ/Δy		Residual Strength	Performance Level
	d	e	c	IO	LS	CP
Bolts—metal to wood	2.8	3.3	0.2	1.5	2.8	3.3

presents the modeling parameters.

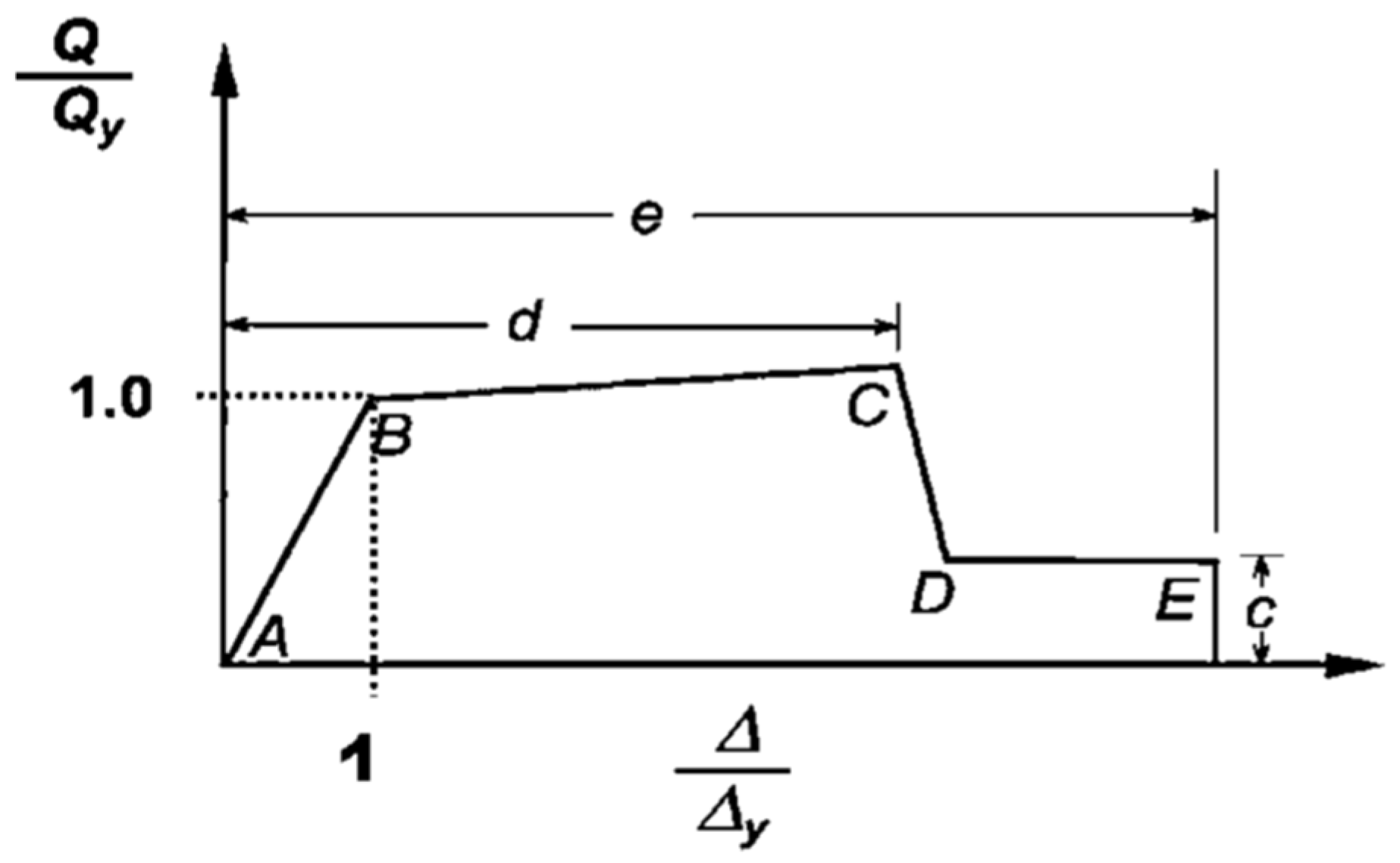
Figure 5 depicts the backbone curve introduced by ASCE 41-13. This constitutive law considers the non-deformed condition (A), yielding point (B), the beginning of softening (C), the beginning of residual strength (D), and finally, the ultimate point (E).

A sensitivity study was performed to assess the influence of the primary joints’ strength and ductility on the whole building’s seismic behavior. Analyzed cases included joints designed to have 67%, 80%, and 90% of the connected member strength, defined as strength ratio (SR), to ensure full nonlinear incursion at joints before member failure. In addition, three more cases were defined, considering the same strength ratios but increasing 30% of the modeling parameters d and e (Table 3) of the backbone curves to provide more ductility at joints.

7. Pushover Analysis (SPO) and Seismic Fragilities

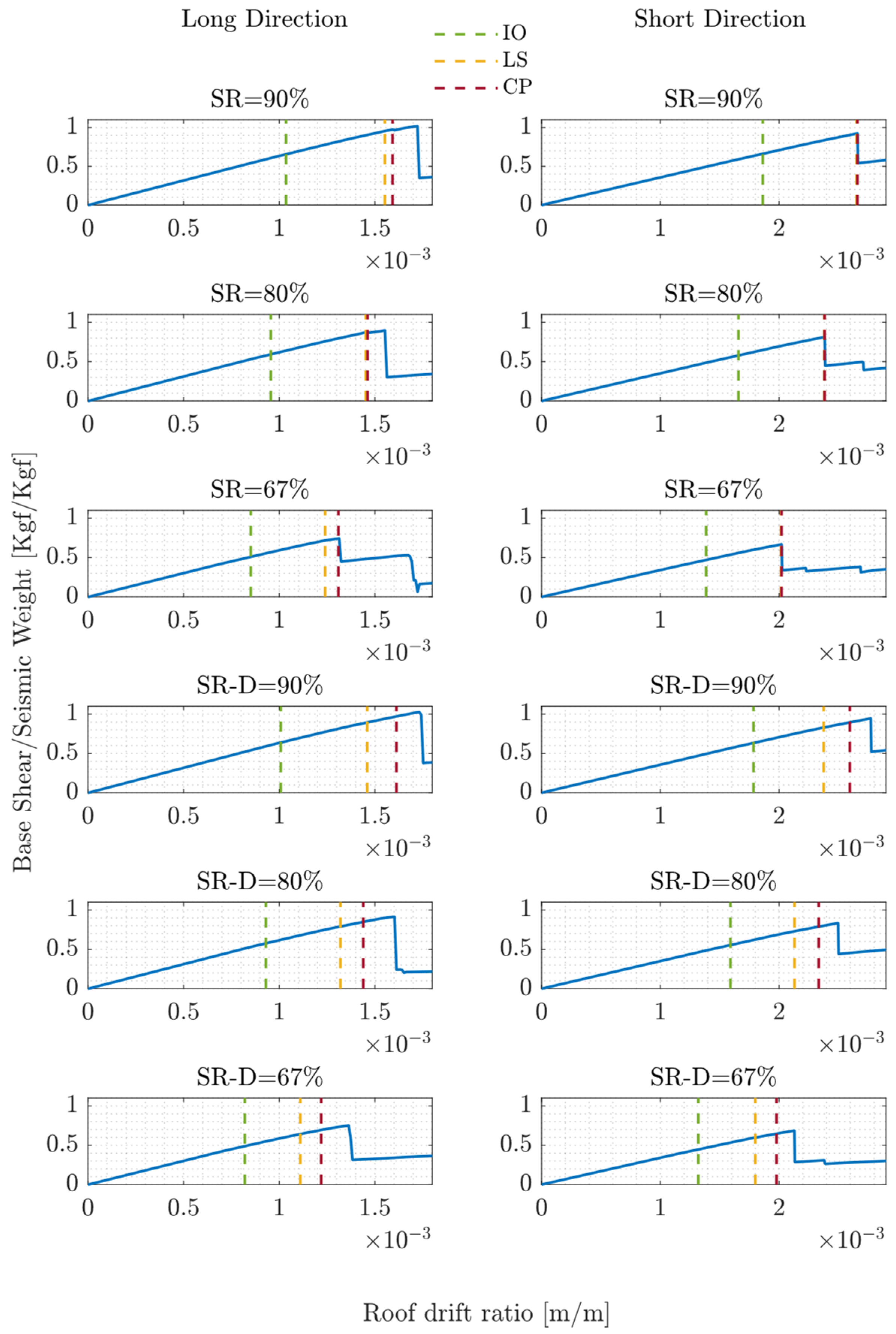
Six SPO analyses were carried out in each building direction (twelve analyses in total), one for each of the previously defined cases, using a lateral load pattern proportional to the first mode of the structure. Figure 6 depicts the capacity curves obtained from each analysis (SR-D represents the cases with increased joint ductility).

For all cases, the peak of the pushover curve correlates well with the defined strength ratio (SR) of each analysis case, confirming the expected relationship between joint and global strength. When increasing the ductility of the connections by 30%, a slight increase in the roof drift at the peak of the pushover curve is observed. However, the behavior remains brittle, as evidenced by the abrupt post-peak strength degradation. This response does not exhibit a smoother softening, which would indicate some level of ductile behavior desirable in seismic-resistant design.

Timber buildings rely on the nonlinear behavior of their joints to develop ductility, requiring a sufficiently high number of connections to achieve an adequate global ductile response. In frame buildings with low redundancy—such as the one analyzed in this study, due to the topology optimization (TO) design process—the nonlinear demands at joints must be unreasonably high to obtain a globally ductile behavior. Higher joint strengths lead to greater overall structural strength but do not result in improved ductility.

In addition, backbone curves introduced by ASCE 41 intend to provide a tool for a conservative evaluation of existing buildings rather than accurately determining the behavior of actual buildings. Following the Chilean standards, this structure was designed with an effective R factor close to 5, meaning that some ductile behavior was expected but not obtained [36]. Therefore, the response modification factor R specified for timber buildings must be carefully reviewed in the current Chilean seismic design standard to specify that some timber topologies with low structural redundancy should use a lower reduction factor.

The capacity curve provides the input data for SPO2FRAG (V1.1). With this information, the software automatically defines the piecewise backbone curve of the SDoF equivalent system. SPO displacements at each story, story heights, and masses are also needed to obtain an internal approximation of the modal participation factor of the first mode (Γ₁) and the first mode period ($T_1$). From the piecewise curve is also estimated the period of vibration of the equivalent SDoF system ($T_{eq}$).

Table 4. Equivalent SDoF periods $T_{eq}$ [s] and limit state thresholds for different SR cases.

Case	Direction	${\mathit{T}}_{\mathit{e}\mathit{q}}$ [s]	Limit State Threshold (RDR)
			IO [%]	LS [%]	CP [%]
SR = 90%	Long	0.29	0.10	0.16	0.16
	Short	0.30	0.19	0.27	0.27
SR = 80%	Long	0.29	0.10	0.15	0.15
	Short	0.30	0.17	0.24	0.24
SR = 67%	Long	0.28	0.09	0.12	0.13
	Short	0.31	0.14	0.20	0.20
SR-D = 90%	Long	0.27	0.10	0.15	0.16
	Short	0.30	0.18	0.24	0.26
SR-D = 80%	Long	0.30	0.09	0.13	0.14
	Short	0.31	0.16	0.21	0.23
SR-D = 67%	Long	0.27	0.08	0.11	0.12
	Short	0.31	0.13	0.18	0.20

presents the $T_{eq}$ obtained in each case.

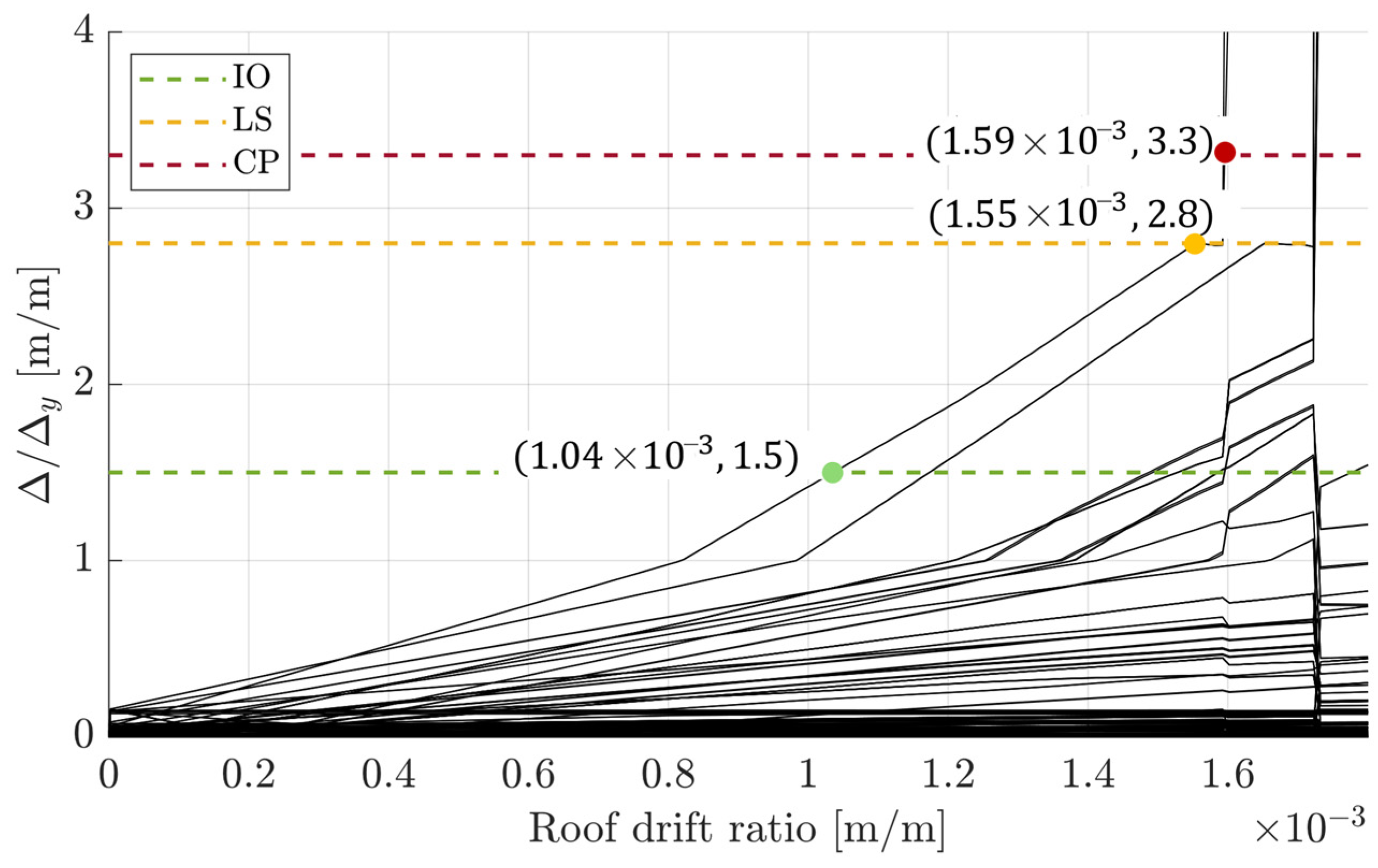
In SPO2FRAG, limit state thresholds for immediate occupancy (IO), life safety (LS), and collapse prevention (CP) are defined in terms of roof drift ratio (RDR), but in ASCE 41-13, they are defined in terms of relative deformation at joints ($\Delta /{\Delta }_y$). The limit state thresholds in terms of RDR were obtained by plotting the relative deformation of each nonlinear connection versus the RDR of the building. The horizontal lines with the acceptance criteria for each limit state, according to values presented in Table 3, were also plotted. The adopted criterion is that the first joint reaching each limit state threshold defines the limit state threshold of the whole structure in terms of RDR. Figure 7 shows an example of this process for SR = 90% in the building’s long direction, and Table 4 presents the obtained limit state thresholds for all the SR cases. Figure 6 also compares these values in terms of RDR with the capacity curves.

With the previous data, the software computes the 16%, 50%, and 84% fractile IDA curves in EDP (RDR) versus IM ($S_a$($T_{eq}$)) format, and then, the limit state thresholds are included for the fragility curve estimation. Additional sources of uncertainty are included, considering ${\beta }_y$ and ${\beta }_U$. The value of the last one was set according to Table 5-3 of FEMA P-695 [37], as recommended in [9]. Consequently, ${\beta }_U$ was set equal to 0.35 (side-way collapse), and the value of ${\beta }_y$ was automatically computed by the software. 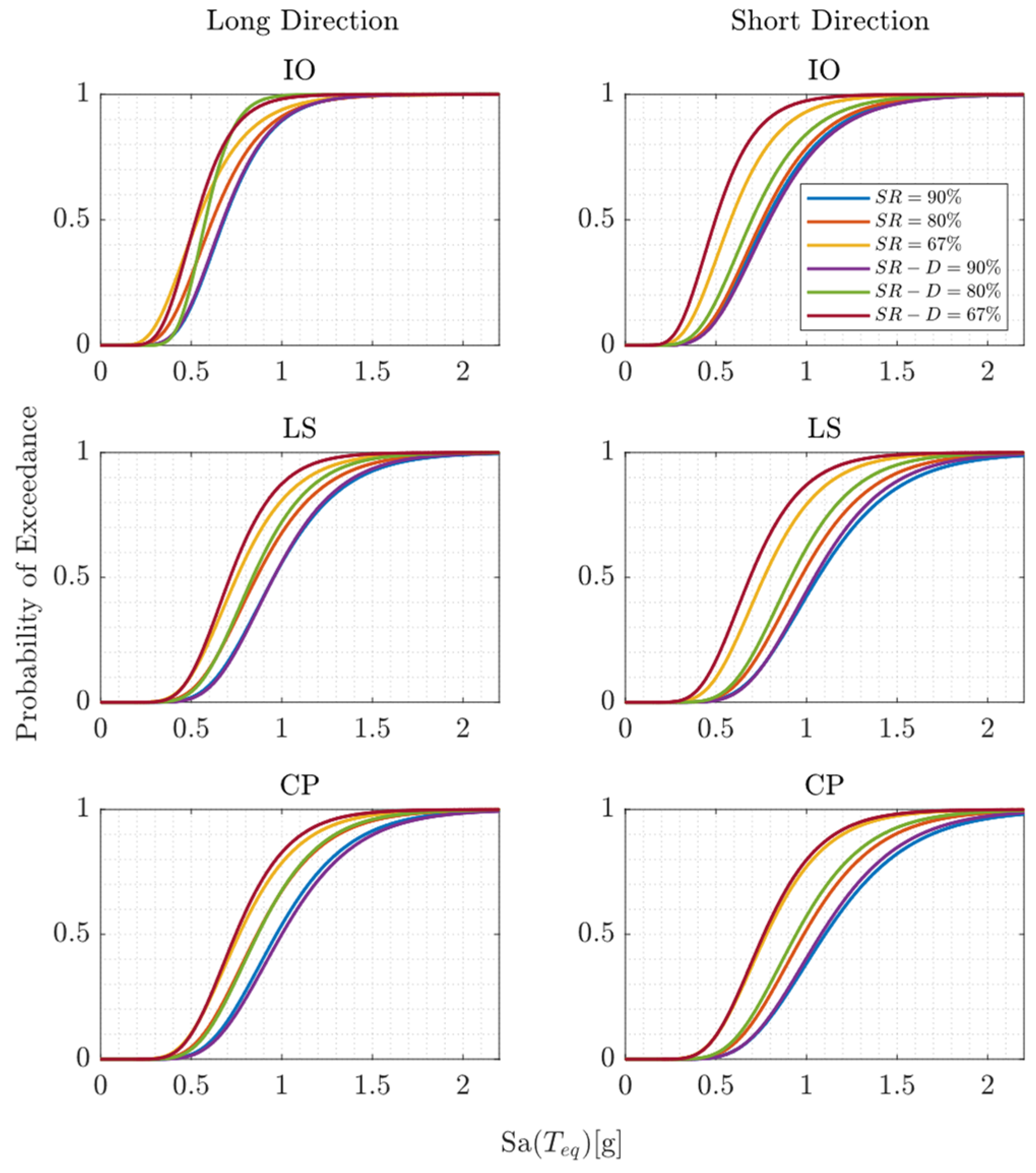Finally, Figure 8 depicts the fragility curves for the different SR cases, showing that fragilities increase when the joint strength ratio decreases.

Later, the probabilities of exceedance (POE) of limit states in the structure’s life cycle (50 years) were evaluated using the seismic hazard curve at the building site and the fragility curves.

8. Seismic Hazard and Probability of Exceedance of Limit States

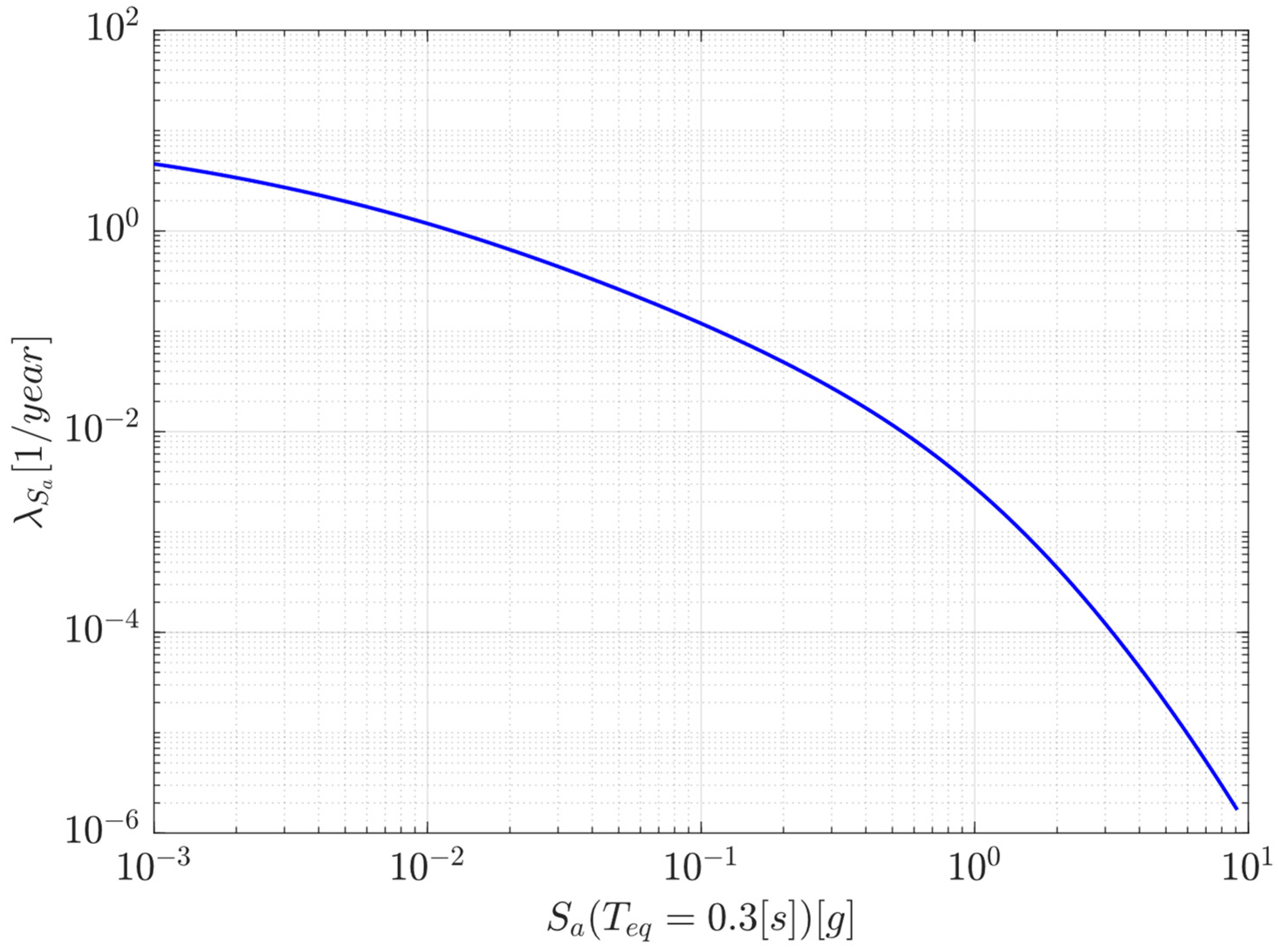
The mean annual rate of exceedance of $S_a\left(T_{eq}\right)$ is estimated by a probabilistic seismic hazard analysis (PSHA) using the software R-CRISIS V20.0 [38]. Chile is located along the boundary between the subducting Nazca plate and the South American plate, extending approximately 3500 km. This zone is characterized by M_w 8.0–8.5 megathrust earthquakes with 68–80 mm/year convergence rates and an average recurrence of ~80 years [39]. Crustal faults are much less frequent but can generate destructive earthquakes [40]. Therefore, this project only considers subduction earthquakes for hazard analysis.

The geometry and magnitude recurrence relationships for faults were obtained from Martin [41]. The ground motion intensity at the considered site was determined using the ground motion prediction equations (GMPE) proposed by Montalva et al. [42], Abrahamson et al. [43], and Youngs et al. [44]. Figure 9 depicts the hazard curve obtained for $T_{eq}=0.3$ [s], which shows the mean annual rate of exceedance (${\lambda }_{S_a}$) as function of $S_a\left(T_{eq}\right)$ at the building’s site.

The mean annual frequency of exceedance of a limit state (${\lambda }_{LS}$) can be stated as

$${\lambda }_{LS}={{\displaystyle \int }}_0^{\infty }P\left(LS|im\right)\cdot \left|{\displaystyle \frac{d{\lambda }_{IM}\left(im\right)}{d\left(im\right)}}\right|d\left(im\right)$$

(6)

where $P(LS|im)$ is the conditional probability of exceedance of a limit state when subjected to an earthquake with intensity level $im$, and ${\lambda }_{IM}$ is the mean annual frequency of exceedance of the ground motion intensity im.

If the occurrence of earthquakes in time is assumed to follow a Poisson process, the probability of exceedance of a limit state over $t$ years can be computed as

$$P_{LS}\left(in t years\right)=1-\exp \left(-{\lambda }_{LS}t\right)$$

(7)

Table 5. Mean annual frequencies and probabilities of exceedance in 50 years for the SR cases at IO, LS, and CP limit states.

Case	Direction	${\mathit{\lambda }}_{\mathit{I}\mathit{O}}\mathit{·}{10}^{-3}$	${\mathit{\lambda }}_{\mathit{L}\mathit{S}}\mathit{·}{10}^{-3}$	${\mathit{\lambda }}_{\mathit{C}\mathit{P}}\mathit{·}{10}^{-3}$	${\mathit{P}}_{\mathit{I}\mathit{O}}\left[\mathit{\%}\right]$	${\mathit{P}}_{\mathit{L}\mathit{S}}\left[\mathit{\%}\right]$	${\mathit{P}}_{\mathit{C}\mathit{P}}\left[\mathit{\%}\right]$
SR = 90%	Long	6.82	3.43	3.34	28.89	15.75	15.39
	Short	5.58	2.74	2.56	24.35	12.79	12.00
SR = 80%	Long	8.64	4.36	4.33	35.07	19.59	19.49
	Short	5.85	3.33	3.25	25.37	15.34	14.98
SR = 67%	Long	11.71	5.77	5.61	44.31	25.05	24.47
	Short	9.77	5.56	5.41	38.64	24.28	23.68
SR-D = 90%	Long	6.96	3.37	3.13	29.38	15.51	14.47
	Short	5.33	2.78	2.64	23.40	12.99	12.35
SR-D = 80%	Long	8.68	4.45	4.22	35.22	19.94	19.03
	Short	6.88	3.72	3.55	29.10	16.96	16.27
SR-D = 67%	Long	11.12	6.15	5.75	42.65	26.48	25.00
	Short	12.77	6.87	5.53	47.19	29.08	24.17

summarizes the mean annual frequency of exceedance and probability of exceedance in 50 years (life cycle considered for the building) for the three limit states considered in this research. Analysis results show that the SR value is crucial in the seismic performance of the building, and the probability of reaching each LS limit state increases when SR decreases. On the other hand, the 30% increment in the joint ductility of the structure seems to have minor impact on the structural performance in terms of POE of limit states during the life cycle. Table 5 also shows that the POE of a limit state in 50 years in the building’s long direction is higher than the POE in the short direction.

The results in Table 5 reveal a clear correlation between the strength ratio (SR) and the probability of exceedance for the different limit states. As SR decreases, the exceedance probabilities for immediate occupancy (IO), life safety (LS), and collapse prevention (CP) increase significantly, indicating a higher seismic vulnerability for structures with weaker connections. For instance, in the long direction, the probability of reaching CP in 50 years rises from 15.39% (SR = 90%) to 24.47% (SR = 67%), a 59% increase, while in the short direction, it jumps from 12.00% to 23.68%, almost doubling. This suggests that the seismic risk escalates disproportionately as joint strength decreases, likely due to higher stress concentrations and the inability to redistribute seismic forces efficiently in a structure with low redundancy.

The comparison between structural directions further highlights anisotropic seismic behavior, with higher exceedance probabilities in the long direction across all cases. For example, for SR = 80%, the probability of CP exceedance in 50 years is 19.49% in the long direction compared to 14.98% in the short direction, and for SR = 67%, the values increase to 24.47% and 23.68%, respectively. This trend suggests that the long direction may be experiencing greater lateral demands, possibly due to uneven stiffness distribution or topology-induced vulnerabilities.

A crucial observation is that increasing joint ductility by 30% has a negligible impact on the exceedance probabilities. For SR = 90%, the probability of CP only decreases from 15.39% to 14.47% in the long direction and from 12.00% to 12.35% in the short direction. Similarly, for SR = 67%, the probability remains nearly unchanged at 24.47% vs. 25.00% and 23.68% vs. 24.17%. This suggests that merely increasing ductility is insufficient to counteract the lack of redundancy, as the structure still exhibits a brittle post-peak response, with a sudden loss of strength rather than a gradual degradation typical of ductile systems.

These findings strongly indicate that topologically optimized structures with low redundancy may not meet the expected seismic performance levels, particularly if designed under current seismic codes that assume higher ductility. The results suggest a potential overestimation of the response modification factor (R-factor) for these types of structures, as the observed exceedance probabilities are significantly higher than those expected for traditional timber systems. To mitigate this, design modifications should focus on increasing structural redundancy rather than solely enhancing joint ductility, potentially through modifications to the optimization process or the inclusion of secondary bracing elements.

9. Conclusions

This research assessed the seismic performance of a five-story glulam frame building in Chile’s high seismicity region. Current sustainability challenges have led to increased use of timber in construction, even in tall structures in high seismicity regions. The analyzed structure was topologically optimized using a variation of the soft-kill BESO algorithm and designed according to local standards. The resulting building from the TO process was a tree-like structure with low redundancy. The seismic performance was assessed through an SPO analysis, considering a state-of-the-art nonlinear model developed in OpenSees. Nonlinear behavior was included only at joints of diagonal braces, using the backbone curves introduced in ASCE 41, while structural members were considered linear-elastic. Six different cases of backbone curves were analyzed in the building, considering three different strength ratios (90%, 80%, and 67%) and increasing d and e values by 30%. All the capacity curves showed high strength and stiffness behavior without ductility. It was observed that higher joint strength produces higher strength in capacity curves, but increasing ductility at joints had limited effects on global ductility, at least in the analyzed range.

Using SPO2FRAG, fragility curves for each case were estimated. The hazard curve of the building’s site was determined through a PSHA for $T_{eq}=0.3 \left[s\right],$ and probabilities of exceedance of each limit state were also obtained. The probability of exceedance in 50 years of IO, LS, and CP limit states increases when joint strength decreases, while increasing ductility at joints has no relevant variations. Thus, for buildings with low structural redundancy, joint strength has more influence than ductility at joints in terms of the seismic performance of the whole structure.

As a structural design tool, topology optimization provides structures with low structural redundancy, meaning that a few connections have considerable relevance in the structural performance. To address the issue of low redundancy, future designs should incorporate additional structural elements or alternative load paths that enhance energy dissipation and distribute seismic forces more effectively. One possible approach is to introduce strategically placed secondary bracing elements that complement the primary load-bearing members without significantly increasing material usage. Another potential solution is modifying the optimization constraints to ensure a minimum level of connectivity and redundancy, thereby reducing the likelihood of brittle failure modes during seismic events. These enhancements could significantly improve the overall resilience of topologically optimized timber structures in high-seismicity regions. Furthermore, the study underscores the importance of balancing material efficiency with structural performance, particularly in seismic-prone areas. While topology optimization aims to minimize material usage, seismic resilience must not be compromised in the process. Implementing hybrid optimization strategies that integrate redundancy constraints while still achieving efficient material distribution could be a viable path forward. Future research should investigate the interplay between redundancy and seismic performance through experimental testing and advanced numerical simulations to establish best practices for the design of optimized timber structures that align with both sustainability and safety objectives. The response modification factor R specified for timber buildings with low structural redundancy must be carefully reviewed in the current Chilean design standard because ductility is expected but not obtained in those buildings.

The results presented in this study provide a significant contribution to the understanding of seismic performance in topologically optimized timber structures. While our investigation is based on a specific five-story glulam braced frame building located in Concepción, Chile, the findings offer valuable insights into the challenges associated with structural redundancy and ductility in timber frames. The study highlights the need for further research to validate these observations across various seismic contexts and different timber structural typologies. Future work should focus on expanding the scope of topological optimization applications while incorporating more diverse design configurations and regional seismic hazard considerations to improve the generalizability of the results.