Validated and Optimized Strategies for Preserving Historical Heritage Towards Natural and Anthropic Risks: Insights from the DETECT-AGING Project

Abstract

This paper summarizes simple and practically attractive new methodologies based on validated and optimized strategies for preserving historical heritage towards natural or anthropic risks in order to assist public administrations and stakeholders involved at various levels in the protection of cultural heritage. This represents the outcome of the PRIN 2017 project DETECT-AGING—degradation effects on structural safety of cultural heritage constructions through simulations and health monitoring. Results were built on recent advances in structural performance modelling of historical masonry structures, interpretation of effects of degradation, advanced numerical simulations, and structural health monitoring, with the final aim to go beyond the state of the art in regard to assessing and establishing: (i) degradation effects from the level of materials to the scale of components; (ii) methodologies able to transfer information on mechanical behaviour from a micro-scale to a macro-scale; (iii) the use of ambient vibration measurements to address epistemic modelling uncertainties in historical masonry buildings; (iv) structural health monitoring (SHM) to detect the occurrence of damage and locate/quantify damage; (v) the capability of equivalent frame models (EFMs) to support the SHM of masonry structures in place of more refined 3D finite element models (FEMs); (vi) variations in the structural response that can be monitored by sensor networks as a function of simulated degradation.

1. Introduction

This paper outlines simple and practically attractive new methodologies for protecting historical sites from natural and anthropic risks. Cultural heritage encompasses the totality of expressions characterizing the lifestyles of past generations, including inherited traditions, habitual practices, significant places, material artefacts, and artistic productions. Not least, this definition involves all the built environments and existing constructions that are considered to have historical, cultural, architectural, archeological, or social significance, together with the associated values that live and develop within the community. The study of built heritage by means of theoretical and experimental research is critical, not only for the advancement of knowledge within the humanities and sciences but also for the implementation of effective strategies that ensure its preservation for the future [1,2]. The longevity of these manufacts, achieved with nascent technological solutions, underscores the sophistication of historical engineering practices. Safeguarding cultural heritage and ensuring its conveyance to future generations thus represent paramount research in current engineering disciplines. The profound significance of built heritage is highlighted, systematically, by the extensive cultural and economic losses caused by natural hazards, particularly earthquakes [3,4]. This is extremely relevant for seismically active regions characterized by rich architectural heritage, such as for many countries in Europe, thereby reinforcing the urgent imperative for proactive risk mitigation strategies. Building upon these foundational principles, the methods presented in this paper are based on validated and optimized strategies, whose goal is to be a valuable resource for government agencies and anyone involved in protecting cultural heritage at all levels. These outcomes address the goals of the PRIN 2017 project DETECT-AGING—degradation effects on structural safety of cultural heritage constructions through simulation and health monitoring [5]. PRIN is a programme funded by the Italian Ministry of University and Research (MUR) that aims to support high-quality research projects in all scientific and technological fields.

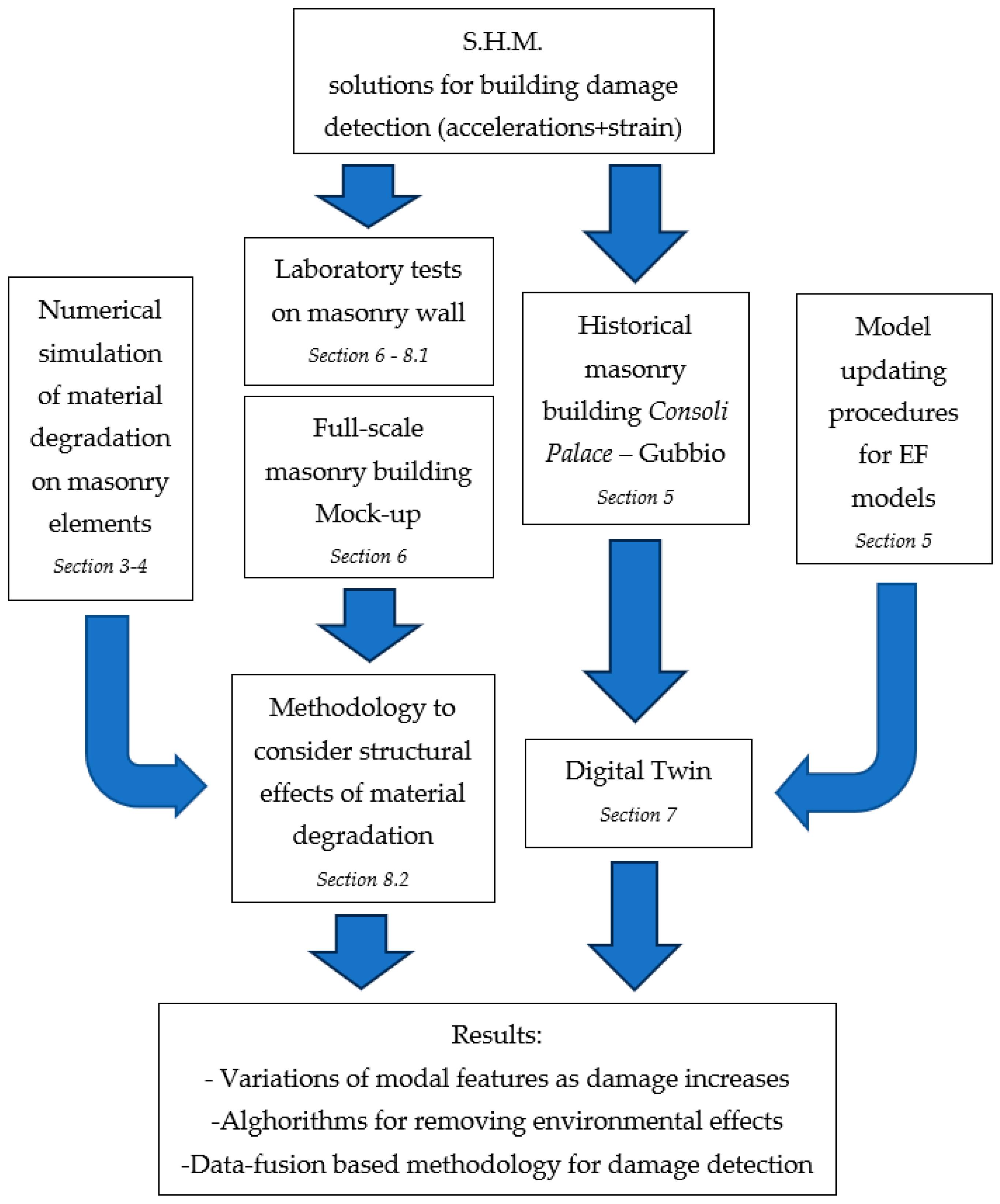
The main purpose of the project was to develop a new analytical–instrumental approach aimed at the quantitative assessment of the effects of ageing and material degradation (Figure 1) on the structural safety of cultural heritage, with particular reference to masonry structures. Through the combined use of structural models and health monitoring, indications and operative tools are provided for the identification and quantification of structural damage which can improve the management of built cultural heritage.

The main outcomes of the project were built on recent advances in the structural performance modelling of historical masonry structures, the interpretation of effects of degradation, advanced numerical simulations and structural health monitoring (SHM), with the final aim to provide simple and practically attractive new methodologies going beyond the state of the art in regard to assessing and establishing the following:

• Degradation effects from the level of material to the scale of component;
• Methodologies that are able to transfer information on mechanical behaviour from a micro-scale to a macro-scale through coherent variables;
• Structural element modelling of historical masonry buildings via the use of ambient vibration measurements to address epistemic modelling uncertainties;
• SHM to detect the occurrence of damage and locate/quantify damage by relying upon denser sensor networks in most critical structural parts;
• Capability of equivalent frame models (EFMs) to support SHM in place of more refined 3D finite element modelling (FEMs);
• Variations in the structural response that can be monitored by sensor networks as a function of degradation simulated by structural models.

Each one of these aspects is discussed in the next paragraphs. The referenced research papers deepen the disseminated results of the research activity.

The research (Figure 2) emphasizes the crucial need for understanding degradation mechanisms and employing minimally invasive SHM techniques to effectively leverage modern technologies for the preservation of cultural heritage. While seismic vulnerability of these structures has been extensively researched, the effects of the formers remain understudied. This work addresses this knowledge gap, focusing on the development and evaluation of robust predictive methodologies for assessment in the context of the cited PRIN project.

2. The State of the Art

2.1. Performance of Historical Cultural Heritage Masonry Structures, Effects of Degradation, and Wrong Past Interventions

Natural and man-made events induce serious threats to cultural heritage constructions, most of them consisting of masonry structures such as buildings, churches, bell towers, and arch bridges. In the case of natural events, the World Bank has reported that the number of disasters and affected people worldwide has been rapidly raising, attaining a percentage increase approximately equal to 400% and 500% from 1975 to 2005 [6,7]. In addition, the rise in population and urbanization has produced a dramatic increase in exposure, resulting in catastrophic consequences even after relatively minor events. Italy, which has the highest number of UNESCO World Heritage Sites in the world, has suffered a huge toll in terms of earthquake damage affecting cultural heritage. In this context, wrong retrofit interventions have been found to be an additional source of structural vulnerability [8].

Masonry constructions also show poor structural performance and suffer heavy damages under man-made actions, such as ground settlements induced by excavations for new lifelines and shallow tunnelling for new metro lines in historical urban centres [9]. Such an issue stimulated a number of experimental and theoretical investigations [10,11,12]. The degradation of materials is a major cause of structural damage [13] and, in the archeological field [14], often resulted in significant reductions in safety levels or even catastrophic collapses.

2.2. Structural Analysis of Historical Cultural Heritage Masonry Structures

Monumental masonry structures are usually characterized by huge dimensions and complex and irregular geometries that make numerical modelling a challenging task. Among available strategies [15,16], the use of FEMs represents one of the most common choices for safety assessment, as well as in an SHM perspective. Although recent generation procedures facilitate their implementation [17,18], the required computational effort is often not feasible at the level of engineering practices and for real-time damage identification through inverse analysis. On the other hand, synthetic modelling strategies working at the structural element scale, such as EFMs, are able to significantly reduce the computational effort thanks to a dramatic reduction in the model dimensions compared to FEMs [19,20]. At the current stage of development, EFM validation has been essentially limited to the seismic engineering field and mostly oriented to ordinary residential buildings [21,22]; among various software available at the commercial and research levels, the Tremuri programme [23], which was adopted in this research, has been employed in several applications in the last decade, testifying its reliability in the nonlinear regime. Recent studies have been oriented to verify the reliability of EFMs in the presence of flexible diaphragms [24] and irregular layouts of the openings [25,26], features that often characterize historical buildings. Nevertheless, the assessment of EFM limits and potentials in the elastic regime typical of SHM applications, related to some of the intrinsic assumptions on which the method is based on, represents a major challenge that this research has contributed addressing.

2.3. Structural Health Monitoring

SHM stands for systems able to provide real-time information on the actual performance of a structure based on instrumental data [27]. SHM systems typically rely upon the continuous acquisition of static and dynamic response data in operational conditions and in the application of suitable statistical or machine learning tools to extract damage-sensitive features from data [28,29], removing the effects of changing environmental conditions and revealing, in an automated way, the formation and localization of small damage in the structure. While the literature counts several application studies of similar SHM systems on bridges and infrastructural systems [30,31,32], the documented validations of SHM effectiveness in the case of historic masonry structures are quite rare and essentially limited to the detection and localization of damages caused by earthquakes in slender buildings, such as civic and masonry towers [33,34]. The application of SHM systems for detecting and localizing degradation effects in masonry buildings is quite a challenge that this project has contributed to addressing. Compared to the case of earthquake-induced damage, degradation effects are more difficult to detect and localize because they typically develop over a long time period and might have quite limited effects on the overall stiffness properties of the structure. At the same time, other challenges in the application of SHM systems to masonry structures are related to the complex behaviour of the material and the possible activation of both global and local failure mechanisms.

2.4. Estimation of Uncertainties and Their Impact on Evaluations

Decision makers are interested in estimates of structural safety modifications due to damage. The determination of safety, as well as its uncertainty, is an open issue in many fields. A great deal of research has been focused on quantifying the effects of uncertainties on the seismic performances of masonry structures [35,36,37], given that high variability in material properties—the assignment of physical properties is a difficult task even in the presence of regular layouts—and epistemic uncertainties related to the structural behaviour (e.g., the effectiveness of connections between walls, the stiffness of slabs, and more) could have a significant impact also on safety against non-seismic loads [38,39,40]. Researchers have developed various procedures for uncertainty propagation such as Monte Carlo simulation methods, the perturbation method, the quadrature method, spectral methods, Bayesian methods, and metamodel-based approaches [35,41]. These are particularly appealing when dealing with complex structures that require long computational times for their simulation, because they approximate the relationship between their response and a set of uncertain variables with statistical (analytical) models that are fitted based on a limited set of simulations. These models can then be easily combined with simulation methods for uncertainty propagation given their analytical form [42,43,44].

3. Degradation Effects from the Level of Materials to the Scale of Components

Recent studies have shown that variations in the strength of bricks, mortar, and stones (i.e., material properties) can make the nonlinear behaviour of unreinforced masonry (URM) walls more difficult to predict. This is a serious concern for preserving historical buildings because their URM walls weaken over time, and ideally, quickly predicting how weak these URM walls become as they become older and deteriorate would help to manage risks and preserve these historic structures. Currently, researchers use conservative estimates (safe but not very accurate) to assess the safety of old buildings. These estimates come from models designed for new buildings, not old ones. More detailed models that consider cracks and material degradation are available, but they are too expensive for practical use on complex buildings. A comprehensive degradation model considers alterations across three key domains: dimensional (abrasion and the loss of integrity), chemical/physical (material changes due to infiltration, etc.), and mechanical (damage and cracking from overloading). Additionally, the inherent uncertainties in the spatial distribution and severity of degradation must be factored in for an accurate assessment. To move from the material properties of single constituents to the global structural capacity of masonry walls, an investigation was performed by means of validated numerical FEM analyses based on full-scale URM wall testing [45]. The focus is on evaluating the impact of material (single constituents) property degradation on macroscopic descriptors like the peak strength and stiffness of global masonry walls. The inherent uncertainties in material property estimation are also considered. Here, the physical ageing process itself is not modelled, but rather, different degradation levels are assumed, and their effects on structural response and capacity are analyzed. Force–displacement curves generated through validated FEMs and failure modes are linked to the overall nonlinear response of masonry walls undergoing progressive material deterioration. Regression models are proposed to predict variations in peak load-bearing capacity and in-plane lateral stiffness due to changes in constituent mechanical properties, from the initial tested values of compressive strength of 4.13 MPa and 2.5 MPa, respectively, for tuff stones and a mortar [46].

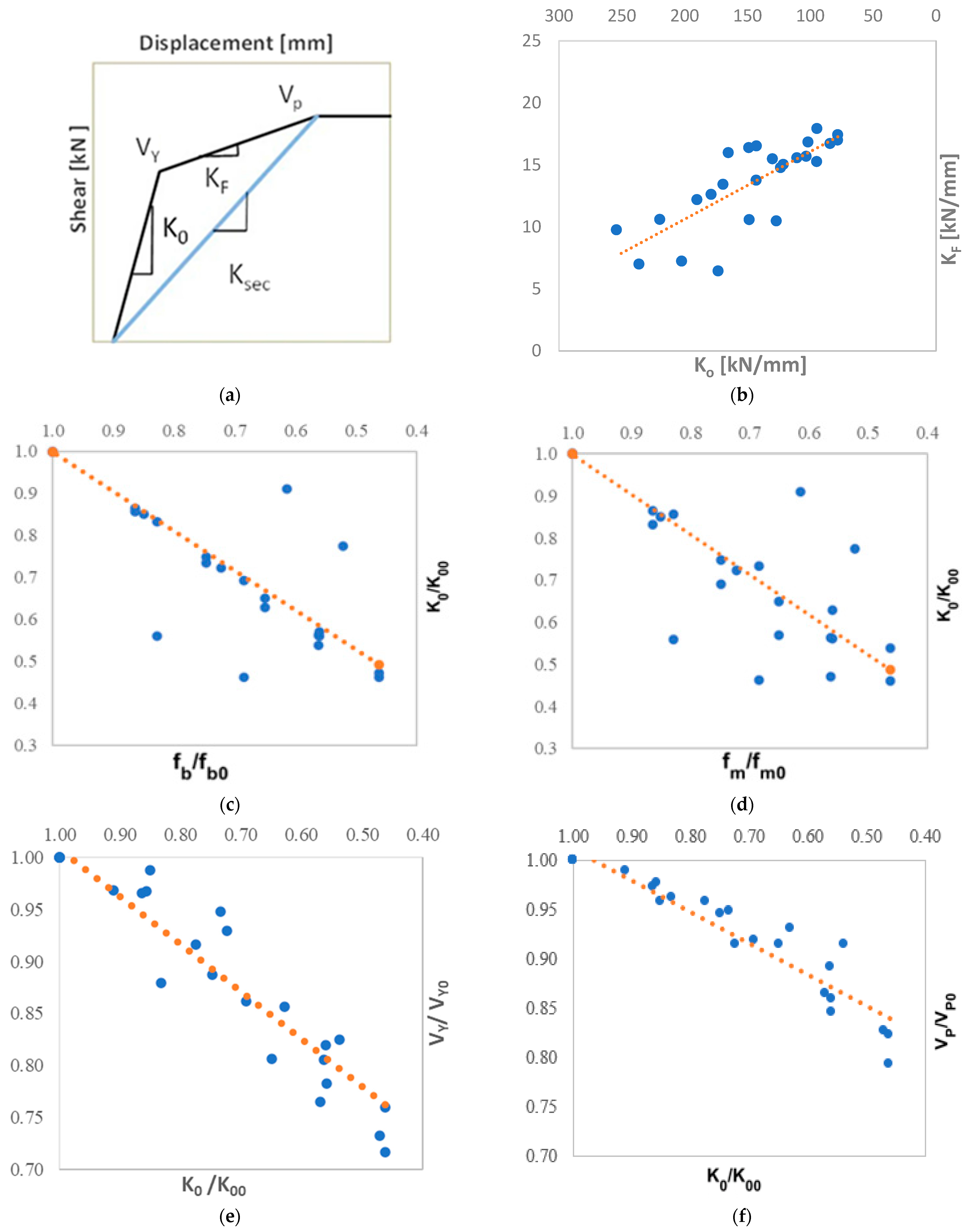
To assess the influence of material property variability on tuff stone masonry, nonlinear analyses were performed in the DIANA FEA software simulating unreinforced walls subjected to compression and in-plane shear loading. A statistics-based sensitivity analysis followed by regression analysis was conducted to quantify the degradation effect at the wall scale. Typical results of this approach [46] are shown in Figure 3a, where each parameter of the curve can be related to others; in Figure 3b, attention is focused on the relationship between cracked stiffness, K_F, and the wall’s initial stiffness, K₀, but in Figure 3c,d, we focus on the relationship between the degradation of stone, f_b, and mortar, f_m, compressive strengths, and in Figure 3e,f, we focus on the elastic limit shear force, V_Y, and peak shear force, V_P. Similarly, K₀₀, f_b0, f_m0, V_Y0, and V_P0 indicate the initial values of properties, and these regressions can be used for interpolation only, never for data extrapolation. The proposed equations are as follows:

$${\displaystyle \frac{K_0}{K_{00}}}=1.0033 {\displaystyle \frac{f_b}{f_{b0}}}-0.0040$$

$${\displaystyle \frac{K_0}{K_{00}}}=0.9943 {\displaystyle \frac{f_m}{f_{m0}}}+0.0022$$

$$K_F=0.1228 K_0+19.146$$

$${\displaystyle \frac{V_Y}{V_{Y0}}}=0.4574 {\displaystyle \frac{K_0}{K_{00}}}+0.5517$$

$${\displaystyle \frac{V_P}{V_{P0}}}=0.2481{\displaystyle \frac{K_0}{K_{00}}}-0.7519.$$

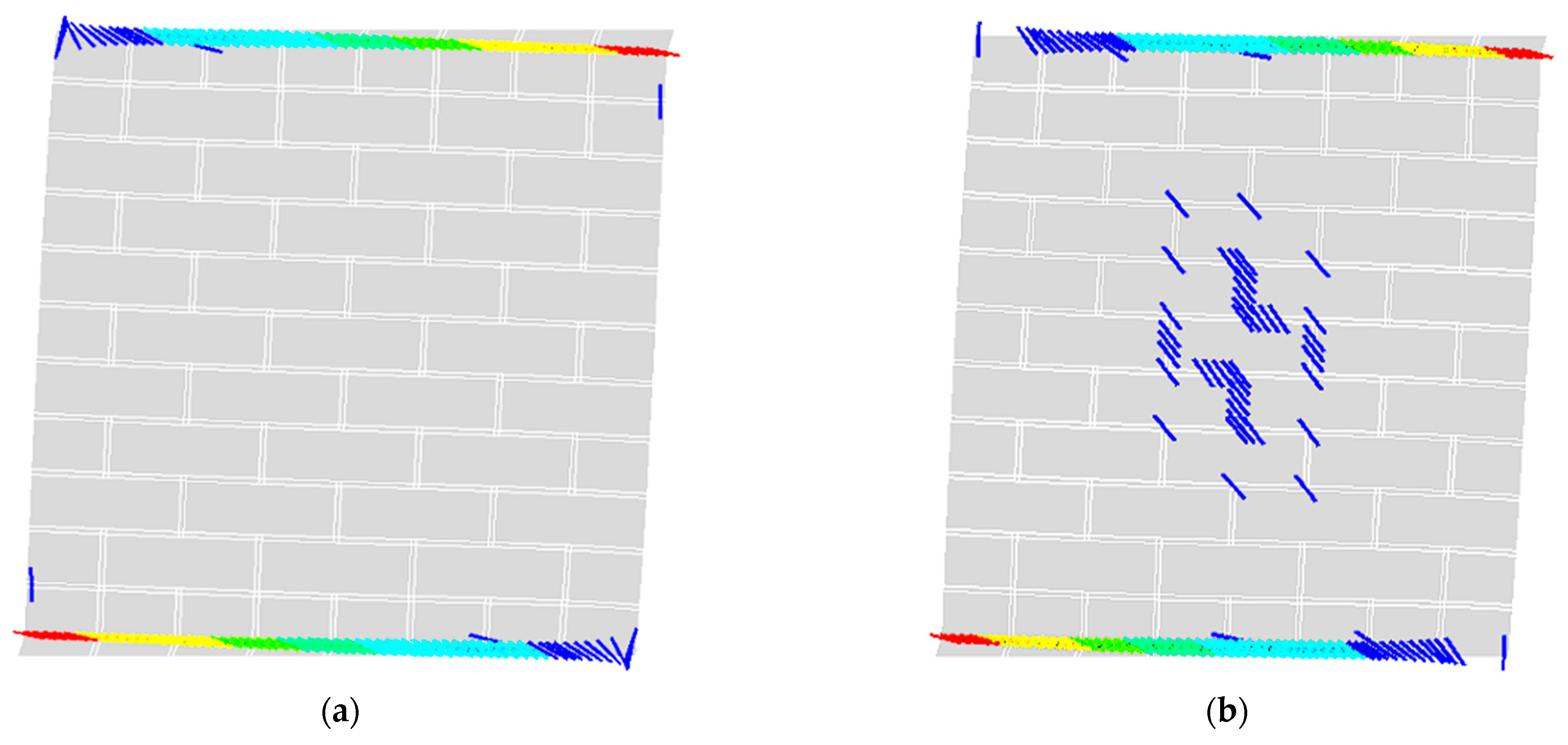
To obtain these results, micro-scale modelling was used to simulate FEM bidimensional walls, considering the individual units and mortar joints of masonry (Figure 4). On the contrary, macro-scale models consider masonry as a homogeneous material and are less computationally expensive than micro-scale models but require global masonry properties to simulate bidimensional walls [15]. In this case, the goal was to move directly to macroscopic descriptors like the peak strength and stiffness of individual masonry walls to be modelled as one-dimensional members, for instance, in EFMs.

The impact of material property variability becomes most evident when the compressive strength of blocks or stones is set to its minimum value. In such cases, variability leads to either a sudden increase in cracked stiffness or a decrease in the wall’s initial stiffness, without affecting the overall response regardless of mortar strength or degradation level. Similarly, assigning extreme values (minimum or maximum) to both mortar and stone properties while assuming early degradation levels showed no significant change in peak shear force. This observation holds true even when considering the transition from mean to minimum mortar strength and from mean to maximum stone strength at the two highest degradation levels. When masonry compressive strength is lower than initially assumed due to material decay, this approach allows for the rapid estimation of the expected reduction in elastic stiffness. This information helps assess the overall performance of the wall and determine the urgency of intervention.

Regression equations can be used by initially establishing the influence of constituent ageing on the elastic stiffness of the masonry wall (Figure 3c,d); subsequent correlations were derived, linking elastic stiffness to other relevant mechanical properties. These properties include cracked stiffness (Figure 3b), elastic limit shear (Figure 3e), and peak shear (Figure 3f) force. This methodology enables a stepwise characterization of the complete structural response of the wall (Figure 3a) under varying conditions resulting from alterations in the mechanical properties of its constituent materials due to ageing.

4. Methodologies to Transfer Information on Mechanical Behaviour from a Micro-Scale to a Macro-Scale Through Consistent Variables

A critical aspect lies in establishing a correlation between material degradation at the micro-scale and its impact on component behaviour at the meso-scale. This can be achieved through the use of well-defined, consistent variables. By bridging the micro-to-meso scales, global parameters for masonry elements (macro-scale), such as force–displacement curves, can be defined. These curves should account for degradation effects under various loading conditions, including gravitational loads, settlements, and horizontal actions (shear, axial load, and bending moment).

An integrated approach utilizing numerical analysis (with the DIANA FEA software, described in detail in [46]) not only offers predictive capabilities for performance decay but also holds a significant value for the SHM of historical masonry buildings. These analyses based on micro-scale modelling with nonlinear, constitutive relationships for constituent materials, accounting for strain softening both in tension and compression through fracture energies, reveal that degradation not only reduces stiffness and strength but also influences the probable failure mode of tuff masonry walls subjected to compression and in-plane shear loading. Structural failure may shift from flexural failure (cracks concentrated at wall ends) to less desirable mixed or shear failure modes (crack patterns extending through mortar joints in the wall’s centre), see Figure 4a,b.

Saviano et al. [46] presented five regression models for efficiently predicting the initial stiffness loss, cracked stiffness, and reductions in elastic and load-bearing capacities of tuff stone masonry walls. These models demonstrate a good correlation between capacity features and material strength, which serves as a degradation measure.

Furthermore, the research highlights the role of monitoring tools in identifying and quantifying degradation phenomena. When stiffness reductions are detected, these tools can locate the position and extent of the damage. This allows for setting alarm thresholds based on the connection between stiffness loss and reduced load-bearing capacity, which ultimately increases the collapse risk. However, broader analyses are required to understand the global structural behaviour.

The proposed regression models pave the way for structural health monitoring and damage detection in historical masonry buildings. They enable the estimation of degradation effects based on the loss of natural frequency, which often translates to stiffness reduction in load-bearing walls. Potential areas for future research include the following:

• Establishing correlations between masonry wall capacity and geometrical alterations, such as mortar loss from joints;
• Utilizing stochastic FEMs informed by data on masonry degradation and material property variations. These data could be obtained through future accelerated degradation tests and could consider the early-age effects of hardened mortar, including pozzolana-based or cement-based mortars;
• Implementing stiffness and strength degradation properties into FEMs and equivalent frame models to assess response variations under horizontal loads. This would enable the monitoring of complex masonry buildings using both FEMs and equivalent frame approaches, with the regression models serving as a tool for the rapid estimation of key material properties.

Similar studies could be conducted on other types of masonry walls, considering their unique material properties and potential for different degradation processes and failure modes.

5. Structural Element Modelling of Historical Masonry Buildings: The Use of Ambient Vibration Measurements to Address Epistemic Modelling Uncertainties

Historical masonry buildings challenge engineers with the complex task of assessing their current health conditions and ensuring their future preservation. This objective can be accomplished through the synergic use of structural models and monitoring systems, which allow for the fine-tuning of the model and enhancing the interpretation of experimental data [47,48], finally providing a deeper understanding of the underlying physical phenomenon.

The modelling of existing buildings comes with several epistemic uncertainties [49] arising from the necessity to develop a model which is representative and, at the same time, synthetic. This ambitious goal guides the expert judgement in choosing the most suitable modelling approach. Vibration data acquired via on-site testing and SHM systems can be, in this respect, a decisive tool to orient the modelling choices. The use of ambient vibration measurements for structural assessment and identification is becoming increasingly common, driven by its non-destructive nature and ability to capture the crucial dynamic characteristics of existing structures. Some of the key advantages include the minimal disruption to the building’s normal operations, the possibility of testing under operational conditions, and the ability to assess the overall dynamic response without the need for artificial excitation. On the other hand, several challenges exist, including the relatively low amplitude of ambient vibrations, which can lead to noisy data and necessitate careful signal processing. Furthermore, the accuracy of results is highly dependent on proper sensor placement, data acquisition parameters, and careful analysis to separate the structural response from background noise and other external excitations. The interpretation of results can also be complex, especially for structures with coupled or closely spaced modes, as well as in the case of damage. In this context, the project investigated the reliability of EFMs in supporting the vibration-based evaluation of damage and degradation of historical masonry structures, pointing out new fields of applications of this modelling technique, its inherent limitations, and how to optimize its practical application.

The EFM approach is now widely recognized as a consolidated technique for the seismic analysis of ordinary masonry buildings. Structural element models such as the EFM are particularly appreciated for their computational efficiency in simulating the structural response to earthquake actions, even in the strongly nonlinear regime. On the other hand, their application as an SHM tool in operative conditions, i.e., ambient vibrations and environmental actions, is still in an exploratory phase. Moreover, the peculiar aspects of heritage masonry structures, such as the irregularity in inter-storey heights, the presence of vaulted floors, and the irregular distribution of the openings, can question the reliability of the equivalent frame idealization. Different strategies can be adopted, for example, for mesh generation in the case of irregular opening arrangements [50,51], to account for the out-of-plane response of masonry walls, to model the deformability of horizontal diaphragms, and to reproduce the wall-to-wall and wall-to-diaphragms connections. The first result achieved by this project showed, for masonry palaces, how the choice of the proper EFM discretization rules and the tuning of the mechanical parameters can be supported by the use of ambient vibration measurements. In Cattari et al. [52], the EFM of the Consoli Palace of Gubbio, Italy, has been dynamically calibrated based on the experimental modal properties identified from ambient vibration tests (AVTs), providing a satisfying accordance with a more refined FEM companion. As a starting point of this research, the referenced paper highlights how some of the basic assumptions of the EFM approach—the in-plane response of masonry walls, the lumping of wall masses at the floor level, and the presence of rigid nodes—may alter the calibration of the model mechanical parameters. These aspects are addressed in detail in the following paragraphs.

5.1. In-Plane Stiffness of Floor Diaphragms: Modelling Assumptions and Calibration

Vibration measurements can be of great help in validating the EFM simplifying modelling assumptions and calibrating the unknown mechanical parameters, in particular those that determine the global dynamic response of the building and would be difficult to quantify via classical in situ tests. This is the case of the floor in-plane shear stiffness, a parameter that is difficult to estimate locally and can vary significantly from modern rigid-behaving diaphragms (reinforced concrete) to flexible diaphragms often encountered in heritage structures (masonry vaults, timber floors, and roofs). A reliable calibration of the floor shear stiffness is fundamental to correctly capture, globally, all the structural modes that are involved the in-plane diaphragm behaviour, both the rigid translational and torsional modes and the non-rigid shear and flexural ones. Recent research on this topic [53] shows how ambient vibration data allow for discrimination between two common modelling assumptions, perfectly rigid-behaving diaphragms and flexible ones. 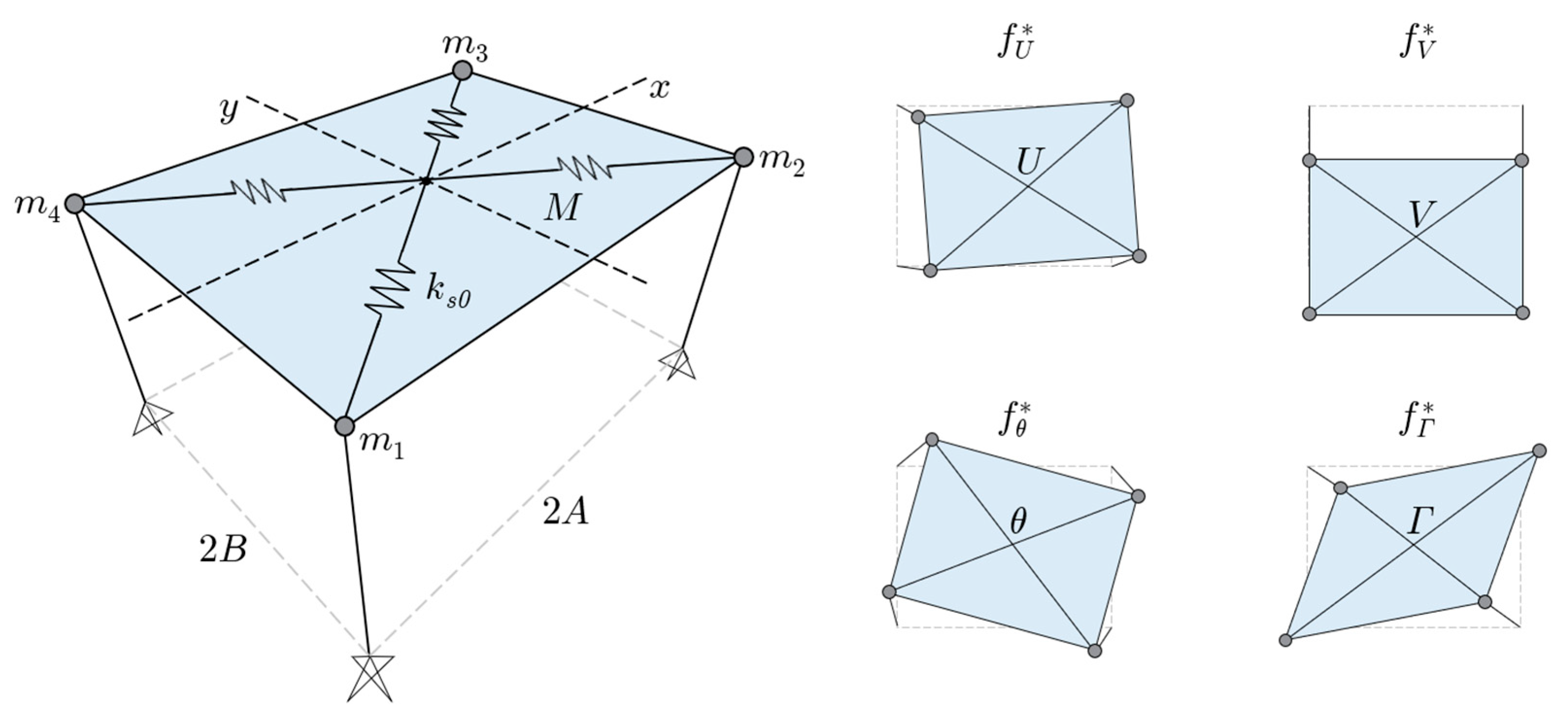Starting from this original idea, the same authors derived a novel proposal regarding a closed-form analytical expression to estimate the in-plane shear stiffness of diaphragms from its experimental modal properties [54]. The equivalent shear stiffness $G_{eq}$, which is the physical stiffness of a diaphragm with in-plane shear modulus G and thickness S, can be estimated as

$$G_{eq}=GS={\displaystyle \frac{2AB{k}_{s0}}{A^2+B^2}}, k_{s0}={\displaystyle \frac{\left(M+m_1+m_2+m_3+m_4\right)\left(\left(B^2{\lambda }_U^{*}+A^2{\lambda }_V^{*}\right){\lambda }_{\Gamma }^{*}-\left(A^2{\lambda }_U^{*}+B^2{\lambda }_V^{*}\right){\lambda }_{\theta }^{*}\right)}{8\left(A^2+B^2\right){\lambda }_{\theta }^{*}}}$$

where $A \mathrm{a}\mathrm{n}\mathrm{d} B$ are the semi-lengths of the sides of the rectangular diaphragm along x and y, respectively, $M$ is the total distributed mass, $m_1,m_2,m_3, \mathrm{a}\mathrm{n}\mathrm{d} m_4$ are the masses lumped at the four corners, and ${\lambda }^{*}={\omega }^{*2}={\left(2\pi f^{*}\right)}^2$ are the eigenvalues of the experimentally identified eigenfrequencies $f^{*}$ of the two (rigid) translational modes U and V (developing along x and y, respectively), of the (rigid) rotational mode $\theta$, and of the shear deformability mode $\Gamma$ (Figure 5).

The formulation was validated using pseudo-experimental simulations and full-scale tests on laboratory structures and existing masonry buildings, proving its effectiveness in improving the dynamic calibration of EFMs. A case study shows, for the town hall building of the Pizzoli (AQ) municipality permanently monitored by the Italian structural seismic monitoring network (OSS), that employing the identified diaphragm shear stiffness in the EFM grants the best agreement between the mode shapes simulated and those experimentally identified [54]. The same calibrated model is employed, in another research work [55], to investigate the accelerations induced by the earthquake at the floor level by means of floor spectra, reproducing with good accuracy the amplifications measured on the building during a seismic event. Such an approach has also been adopted in the context of the DETECT-AGING project for the mock-up realized in the laboratory with quite satisfying results [56,57].

5.2. Quality of Wall-to-Wall Connections and the “Flange Effect”

Another topic of relevant interest in calibrating EFMs is the so-called “flange effect”, which refers to the influence of orthogonal walls on the in-plane response of walls loaded with seismic forces. The research developed in this framework [58] proposes a practice-oriented analytical formulation to calibrate the connection between intersecting walls in EFMs. For two orthogonal piers of width l and thickness t, depending on the direction of the horizontal load, one will act as a web (behaving in-plane) and the other as a flange. Their connection is simulated by a beam whose stiffness is a function of the geometrical dimensions of the intersecting walls and the effectiveness of their connection, as observed in situ. The transversal area A_B of the equivalent beam, assumed to be made with the same material as the web (shear modulus G_W, Poisson coefficient ν_W), can be estimated as

$$A_B=l_B\omega {\displaystyle \frac{12(1+{\nu }_W)A_W}{5h\left(\frac{1+\zeta }{\zeta }+\frac{12d^2}{l_W^2\left(1+\frac{E_F{J}_F}{E_W{J}_W}\right)}\right)}}\cong l_B\omega {\displaystyle \frac{12\left(1+{\nu }_W\right)A_W}{5h\left(\frac{1+\zeta }{\zeta }+\frac{12d^2}{l_W^2}\right)}},$$

where h is the inter-story height, A_W and J_W are the area and moment of inertia of the web ($t_W{l}_W$ and ${\displaystyle \frac{1}{12}}{t}_W{l}_W^3$, respectively), J_F is the moment of inertia of the flange (equal to ${\displaystyle \frac{1}{12}}{l}_F{t}_F^3$), E_W and E_F are the Young’s Moduli of masonry characterizing the two piers, d is the distance between the centroid of the web and the middle plane of the flange, and finally, $\zeta ={\displaystyle \frac{E_F{A}_F}{E_W{A}_W}}$ is a dimensionless factor. On the right hand side, the ratio $E_F{J}_F/E_W{J}_W$ is reasonably assumed equal to 0 since the thickness of the web is usually limited when compared to the width of piers whose flange effect may be relevant ($E_F{J}_F\ll E_W{J}_W$).

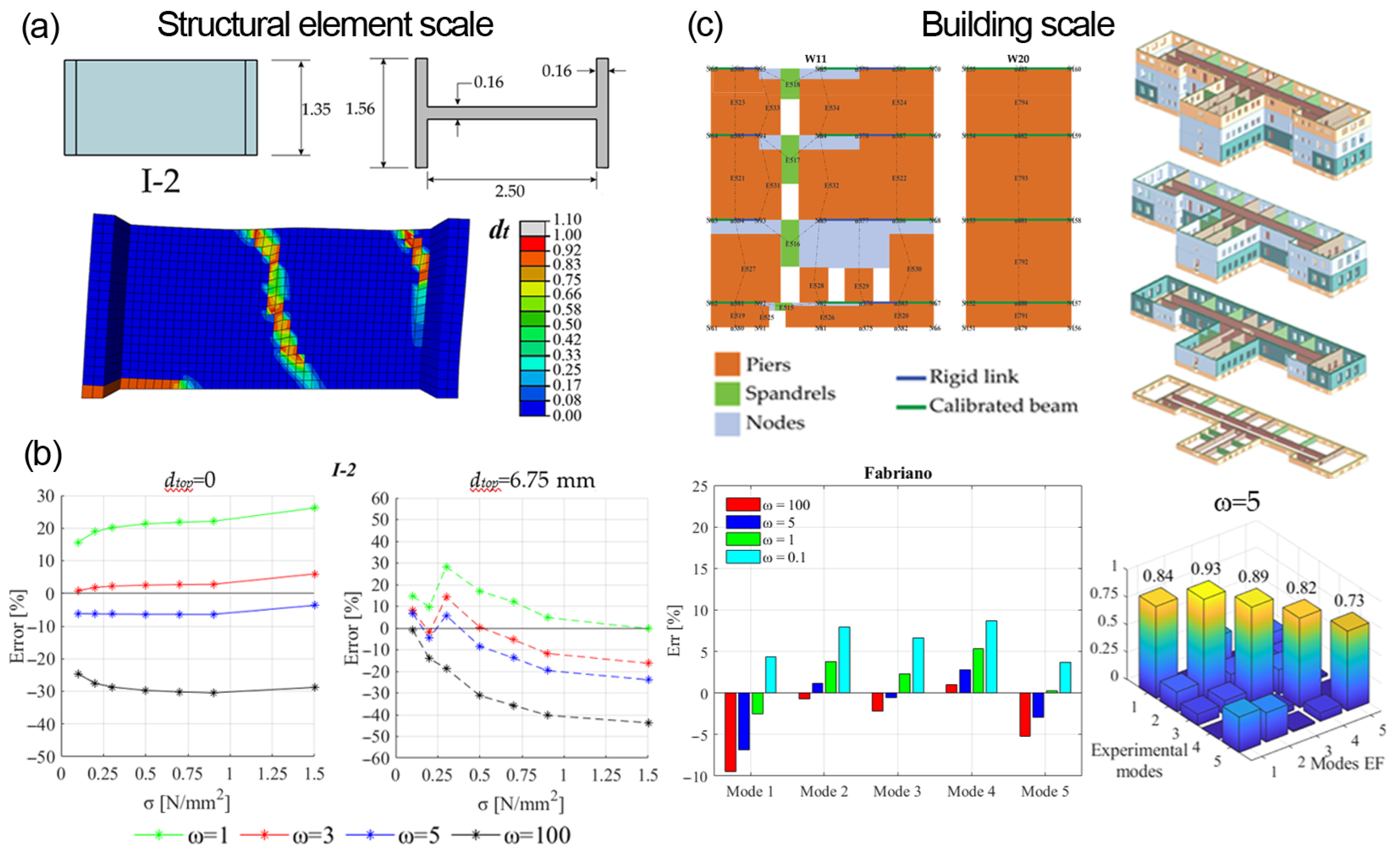
The degree of connection is governed by the dimensionless parameter ω, which assumes the limit values of 0.1 for a complete decoupling and of 100 for a perfectly rigid connection. Intermediate values of practical interest are proposed in this paper, resulting from the comparison between 3D FEM and EFM parametrical nonlinear analyses (Figure 6a,b). In the presence of a good connection, assuming ω equal to 5 grants the proper redistribution of the vertical loads between the web and the flange. Conversely, poor connections (for example due to an irregular masonry) can be reproduced by values close to 1.

The procedure is validated by the comparison between calibrated EFMs of complex buildings and high-fidelity FE analyses on simple 3D assemblies, showing that the proposed formulation can reproduce the actual behaviour of masonry walls with flanges in terms of failure modes, maximum strength, and displacement capacity. Moreover, reference values are provided to reproduce the flange effect in EFMs depending on the quality of the wall-to-wall connections. The practical application to two existing buildings permanently monitored by OSS (see Figure 6c for the Fabriano building) shows that only a proper calibration of the flange allows for the obtainment of a satisfying agreement between the natural modes simulated by the EFM and those experimentally identified, in particular for what concern mode shapes.

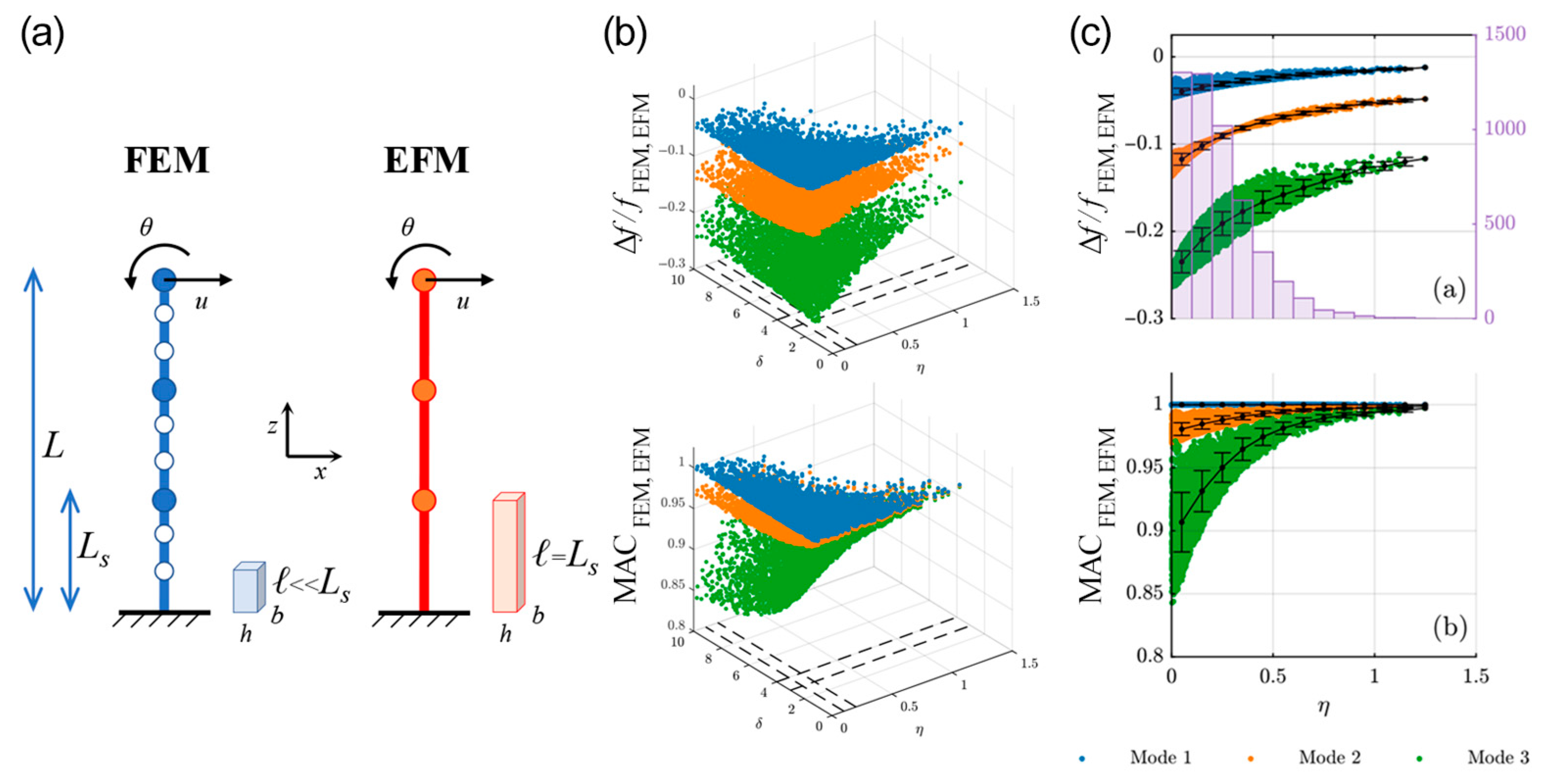
5.3. Mass Lumping at the Floor Level

The simplified EFM mass distribution along the height of the building, in which wall masses are concentrated at the floor level, can deviate significantly from the actual mass distribution of the real structure. This is evident for thick walls or large inter-storey heights, peculiarities that are often encountered in monumental masonry palaces. This assumption tends to overestimate the importance of inertial effects, lowering the natural frequency predicted by the EFM. This alteration can be relevant when modelling old palaces with thick walls and inter-story heights, but it is mitigated when the floor mass is much greater than the wall mass, for example, in the case of vaulted floors. The repercussions can affect, among others, the model-based inverse procedures typical of structural monitoring such as model updating and digital twinning, the structural identification of mechanical parameters, and damage quantification. In the process of model calibration, for example, this effect can increase the apparent value of the elastic parameters of the masonry, which may be not directly linked to the quality of the material itself. Based on these motivations, the research carried out in the project [59], which is still ongoing [60], is focused on identifying a reduced-order EFM with lumped parameters sharing the same natural frequencies with a high-fidelity FEM (or with an experimental modal model), with distributed mass ideally representing the physical system. Achieving such a goal can provide a quantitative measure of the unwanted effects on direct (modal analysis) and inverse (structural identification) procedures, suggesting at the same time possible strategies to mitigate them in seismic applications and structural monitoring. The preliminary results of this study show how this effect, which is the underestimation of natural frequencies, is mainly governed by the ratio between the floor mass and the inter-story wall mass η (Figure 7); it becomes important for ratios lower than unity and is contrasted by the opposite effect of rigid nodes, as discussed in the next section. Finally, the research presents some practical recommendations related to the EF modelling of typical structural configurations of existing masonry buildings, considering low-, mid-, and high-rise structures with light or heavy floor diaphragms. The procedure quantifies the impact of mass lumping on the fundamental frequency for various mass ratios η and, through an inverse structural identification procedure, estimates the alteration of the mass distribution which compensates this effect, achieving the dynamic calibration of the EFM model with respect to the FEM.

5.4. Equivalent Frame Idealization Rules (The Dimension of Rigid Nodes and the Irregular Layout of Openings)

Different rules are available to discretize masonry walls according to the EFM idealization. These rules determine not only the shape of the wall deformable portions, piers, and spandrels but also those of the connecting rigid nodes. Most of such rules have been proposed based on the evidence of damage after seismic events, thus mainly referring to the activation of a strong nonlinear response usually concentrated in the abovementioned piers and spandrels. Up until now, no unique and scientifically consensus-based criteria are available neither for the case of regular nor for irregular opening layouts, with the latter being even more problematic. In [50], the issue is discussed by referring to the implications that such choices may produce when nonlinear static analyses are performed for addressing seismic assessment. However, the issue is relevant also in the case of SHM application or for operational condition assessments.

In fact, in the case of irregular opening arrangements or large inter-storey heights typical of heritage masonry buildings, the rigid portions tend to become bigger and bigger with respect to deformable ones, with the consequence of overestimating the stiffness of the wall. The results of numerical simulations [59] and experimental calibrations [52] suggest that solutions with smaller rigid nodes should be generally favoured to reproduce more reliably the elastic behaviour of the structure. Such an impact on the global stiffness needs to be carefully considered also in the case of nonlinear analyses, in which usually secant values of Young’s moduli are adopted for piers and spandrels; in fact, these two effects are to some extent counterbalanced.

Moreover, the case of irregular opening layouts may imply additional tricky issues associated with the use of rigid links usually adopted to couple the behaviour of adjacent piers that may lead to unrealistic redistributions of the axial actions.

6. Structural Health Monitoring (SHM) to Detect the Occurrence of Damage and Locate/Quantify Damage by Relying upon Denser Sensor Networks in the Most Critical Structural Parts

Diffuse and continuous strain monitoring in masonry buildings can allow for the early identification of the formation of cracks and collapse mechanisms before the occurrence of severe consequences. In practical applications, achieving this goal by using traditional sensing technologies, such as piezoresistive strain gauges, is often a challenging task, in which the main limitations stem from issues with the scalability and deployment of the sensors themselves. A new class of strain-sensing sensors, called smart bricks, has been recently developed to achieve diffuse SHM of masonry buildings [61]. Smart bricks are burnt clay bricks made from an engineered composite material consisting of a mixture of clay and stainless-steel microfibers. Their sensing principle leverages the piezoresistive behaviour developed with the doping of the clay matrix. Resembling conventional clay bricks in shape and esthetics, smart bricks can be embedded anywhere within masonry load-bearing structures [62,63].

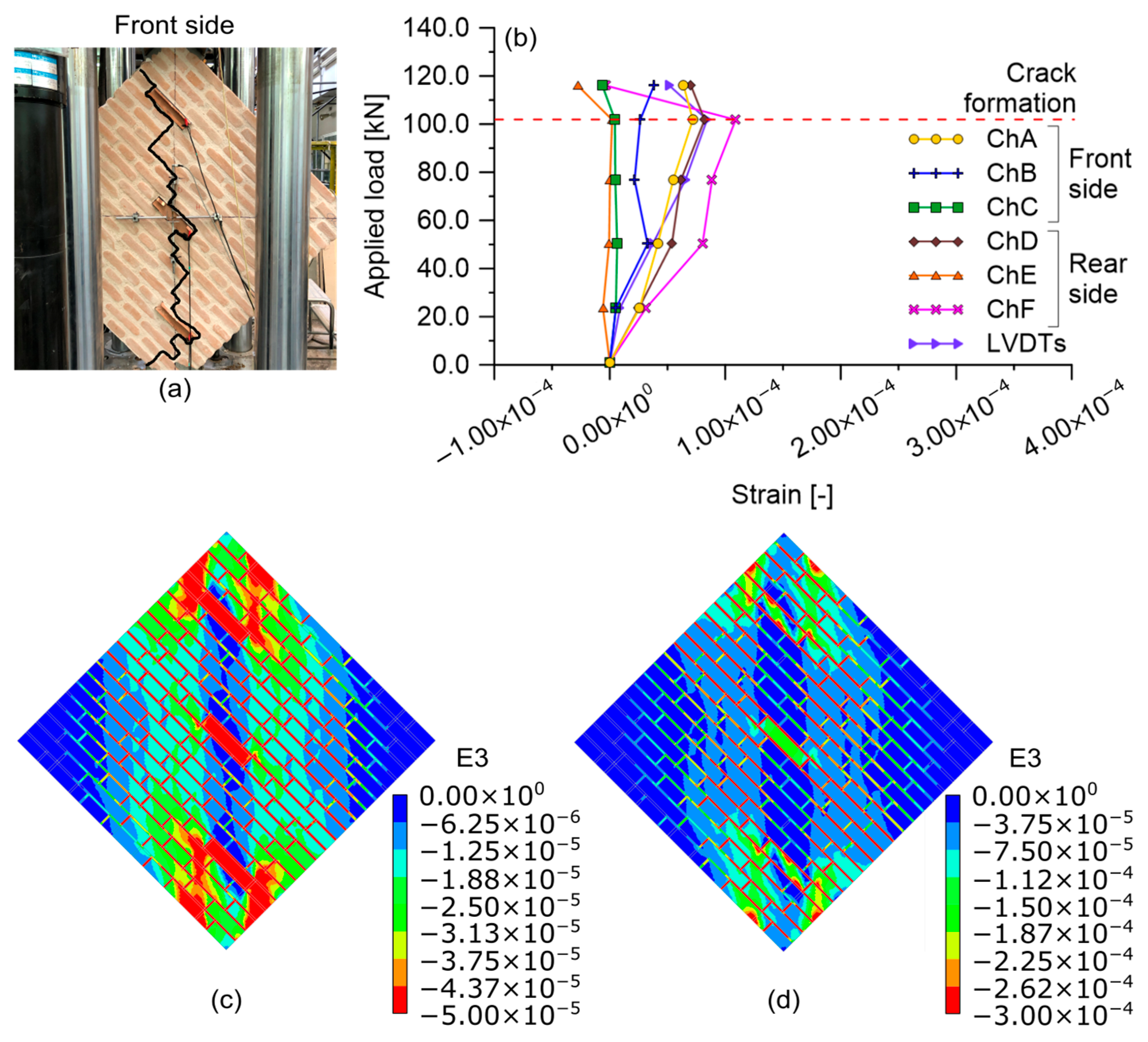
In this research, the effectiveness of smart bricks for monitoring strain in masonry structures was first investigated by testing two masonry wall specimens under diagonal compression (please refer to [64] for further details). Both the samples, with dimensions of 1.29 × 0.25 × 1.29 m³, were constructed by arranging conventional clay bricks with mortar layers of about 10 mm thickness and by placing smart bricks along the compressed diagonals. Linear variable differential transformers (LVDTs) were also mounted on the masonry specimens, on both their front and rear sides, to measure displacements that occurred parallel and orthogonal to the applied loads. Diagonal compression tests were conducted under displacement control by applying displacements with increasing magnitude until failure of the wall specimens occurred. Strains outputted by smart bricks were compared with those retrieved from the processing of the displacement outputs from LVDTs for comparative purposes. Nonlinear FE models of the two wall specimens were also defined to reproduce the tests and to interpret the outputs from the adopted sensing technologies. Numerical simulations were carried out using the TNO DIANA FE software, adopting a simplified micro-modelling approach to separately model brick elements and mortar layers as continuous isotropic materials without explicit contact interfaces. The interested reader can refer to [63] for further details as well as for the mechanical properties of the materials. The obtained results, shown in Figure 8 (only for one of the tested specimens), proved the effectiveness of smart bricks for monitoring strain and detecting shear-induced damage in masonry structural settings. The novel sensors outputted an increasingly compressive strain as the load applied on the tested wall specimens increased. Furthermore, the smart bricks provided variations in the trend of their strain outputs that were clearly attributable to crack initiation in wall specimens. A good agreement in terms of strain magnitude and trend was found by comparing the smart brick and LVDT outputs, as well as the smart brick and numerical model outputs. Regarding the latter comparison, numerical simulations indicated greater strain concentrations at the edges of the compressed diagonals in the tested wall specimens compared to their central areas. Similar findings were experimentally confirmed through the outputs of the smart bricks.

A second research step involved the use of smart bricks for monitoring strain in a full-scale masonry building prototype subjected to controlled damage (more details can be found in [56,57]). The building had plan dimensions of 4.72 × 3.50 m² and a total height of 4.67 m. Smart bricks were fully integrated within the load-bearing structure of the building specimen during the construction phase by adopting the same methodology used for conventional clay bricks, thus enabling the monitoring of strain at strategical positions of the construction during its service life (see Figure 9). Modifications in the entity of the live loads, changes in the coupling between walls, and differential foundation settlements were among the simulated damage scenarios to which the building prototype was subjected. Smart bricks monitored strain in a continuous fashion since the completion of the mock-up construction phase; the SHM system was active for more than two years. The novel sensors were able to detect the induced progressive damage through variations in their strain measurements [65]. The experiment highlighted the critical importance of removing environmental effects due to changes in air temperature and humidity from strains measured by the novel sensors. To this purpose, tailored algorithms, developed through previous research experience in the field [66], were adopted to process the strain measurements of the smart bricks.

7. Capability of EFMs to Support SHM in Place of More Refined 3D FEMs

Digital twins (DTs) are emerging as a comprehensive solution to support the SHM of built structures, enhancing the decision-making process for their management and conservation. DT methodologies rely on the use of a digital structural model which continuously exchanges information with the real structure through sensors, providing real-time feedback on the structural behaviour and detecting the effects of underlying physical processes that could alter it, such as ageing, degradation, and damage. The flux of information coming from sensors is particularly heavy for large and complex structures, such as monumental palaces, and employing refined FEMs is often computationally unfeasible. In this context, the project investigated the viability of using a light EFM as a DT to support the seismic SHM of masonry palaces, in particular, to carry out the damage assessment after the earthquake. The findings of the research [67] show the possibility of employing the EFM as an efficient physics-based surrogate, which can reproduce in quasi-real-time the operational behaviour of the palace and quickly estimate the damage that occurred after the earthquake while drastically reducing the computational effort required by more refined FE models (Figure 10a). The EFM twin developed for the case study of the Consoli Palace, a monumental building in Gubbio, Italy, has been continuously updated based on modal information identified from the SHM system in May 2021, achieving a similar accuracy as the FE modal-surrogate companion in both the model updating (Figure 10b) and damage assessment phases. The true strength of the EFM twin resided in its nonlinear simulation capabilities, which allows it to quickly predict the expected seismic response of the building to an earthquake that struck the structure and its evolution during aftershocks, finally enhancing the classical data-based damage assessment. The online updating procedure closely reproduces the permanent decrease in natural frequencies observed after a minor seismic event in May 2021, quantifying the corresponding reduction in the modulus of elasticity of the masonry from 3% to 8%. Employing offline static and dynamic nonlinear simulations, the physics-based EFM forecasts in a short time frame the reduction in strength and capacity caused by structural damage, confirming the earthquake has not compromised the structural integrity and residual capacity of the palace to aftershocks. The calibrated EFM twin can be then employed to develop a model-based behavioural chart of the building before the earthquake strikes [68]. This chart, represented in the form of frequency-based fragility curves developed through nonlinear dynamic analyses, establishing a connection between a permanent decrease in natural frequencies identified from vibration data and the estimated extent of seismic damage. Such a tool is readily deployable and can be used promptly in the aftermath of an earthquake to evaluate the expected operational status and the level of structural damage on monitored buildings, supporting the management of the post-earthquake emergency phase.

8. Variations in Responses That Can Be Monitored by Sensor Networks as a Function of Degradation Simulated by Structural Models

8.1. Vibration-Based Monitoring of Masonry Structures

Existing masonry buildings, such as towers, churches, and palaces, often develop a complex mechanical response due to the considerable material heterogeneity of the ancient masonry and the presence of structural pathologies. These responses, in most cases, are due to the occurrence of severe loading conditions, such as those caused by differential ground settlement and seismic events, as well as the inevitable ageing of the material and the resulting degradation. Operational modal analysis (OMA) methods are particularly well-suited SHM approaches for historical masonry buildings, given their non-destructive nature and global damage identification capabilities through the assessment of changes over time in the modal features of structures, namely natural frequencies, mode shapes, and damping ratios [69,70,71]. Despite the advantages, the low sensitivity of OMA methods to localized damage is often cited in the literature as a major limitation. In addition, difficulties in establishing robust correlations between changes in modal features and the residual load-bearing capacity of structures are a currently open field of research.

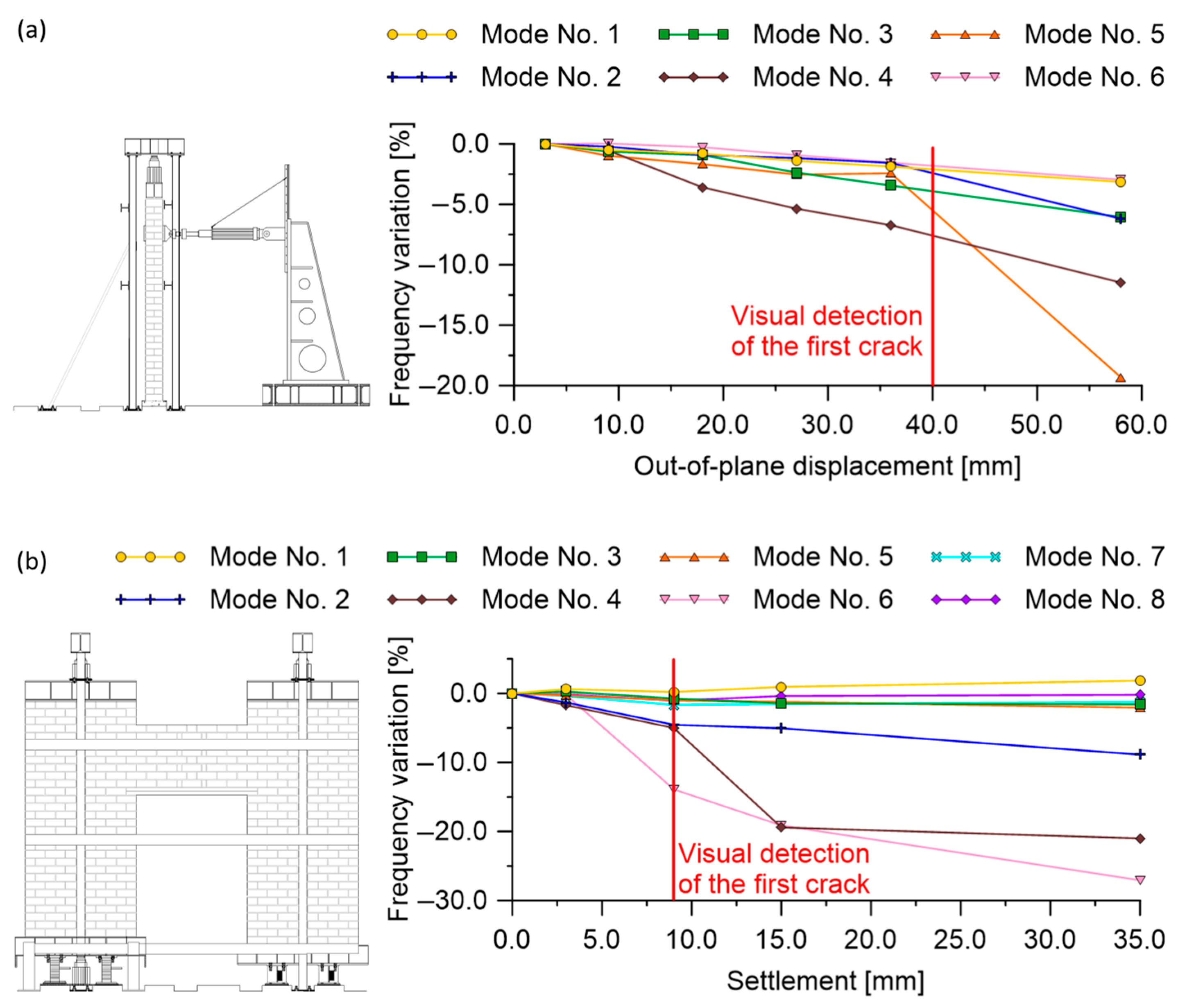
An experimental programme was conceived to systematically investigate these aspects in the framework of the research. Two full-scale masonry wall systems with a single opening were constructed in laboratory conditions by using tuff stones arranged with mortar layers, tested under controlled damage by considering diverse structural settings [72]. The first sample was tested by imposing increasing out-of-plane displacements to one of the two pillars, while the second sample was subjected to differential foundation settlements of incremental magnitude. AVTs were carried out on the structures at every step of the test sequences. The modal features of the wall systems were estimated through OMA methods, and the correlation between modifications in modal features and induced damage was assessed. The experiments were numerically reproduced through the definition of two structural models discretized according to the FE method, hence the execution of nonlinear modal analysis based on linear perturbation. The results obtained from this experimental programme point to clear variations in modal features as the level of structural damage increases (see Figure 11). In addition, findings from numerical simulations indicate that FE models, once properly tuned, can be used for SHM purposes, as they can faithfully reproduce the decay of modal features.

To extend the proposed investigation to real SHM scenarios (e.g., including the influence of environmental effects), the full-scale masonry building prototype, described previously, was first instrumented with a vibration-based SHM system including sixteen high-sensitivity piezoelectric accelerometers, tested under controlled damage while carrying out AVTs before and after every step of the test sequence (see [57]). Like before, the modal features of the building mock-up were estimated through OMA methods, and the correlation between modifications in modal features and induced damage was evaluated. Acceleration measurements, carried out continuously since the completion of the construction phase of the building for more than two years, using six of the sixteen accelerometers were processed to track changes in natural frequencies and corresponding mode shapes over time. Tailored algorithms were used for the removal of the environmental effects and the construction of control charts. An FE model of the building mock-up was also defined to replicate the performed experimental damage scenarios. The results obtained contributed to enriching the scientific community’s knowledge of real-world applications of vibration-based SHM systems to masonry construction.

8.2. Bayesian-Based Model Updating of Monumental Structures: The Case of the Consoli Palace

In the realm of SHM, the challenge of identifying damage can be viewed through a five-tiered hierarchical lens [29]: (i) detection, (ii) localization, (iii) classification, (iv) assessment, and (v) prediction. Traditional SHM systems, by and large, fall into the category of unsupervised learning. This is because they are primarily designed to discern alterations in the overall structural behaviour, essentially engaging in the task of novelty detection. Given the inherent ill conditioning of model-based approaches, it becomes imperative to intelligently annotate the data to establish priorities. This process aligns with the concept of transfer learning (TL), which is a semi-supervised learning technique that empowers the learning algorithm to autonomously construct a labelled training dataset. In this context, the study presented in [73] introduces a Bayesian-based TL methodology grounded in extensive long-term monitoring data, with the primary objective of assessing potential damage in monumental structures. Within this framework, the TL principles serve to alleviate the scarcity of labelled structural data, while a trained structural model assumes the role of a formal prior belief in the damage assessment process. The underlying idea is that it is feasible to glean valuable insights from data, which can be translated into the capability to assign a damage state or classification through a well-trained numerical model. Hence, to efficiently execute the model-based damage classification process within the TL framework, especially when dealing with a substantial number of damage-sensitive parameters, it becomes essential to train a numerical surrogate model (SM) with computational effectiveness as a paramount consideration [67,74].

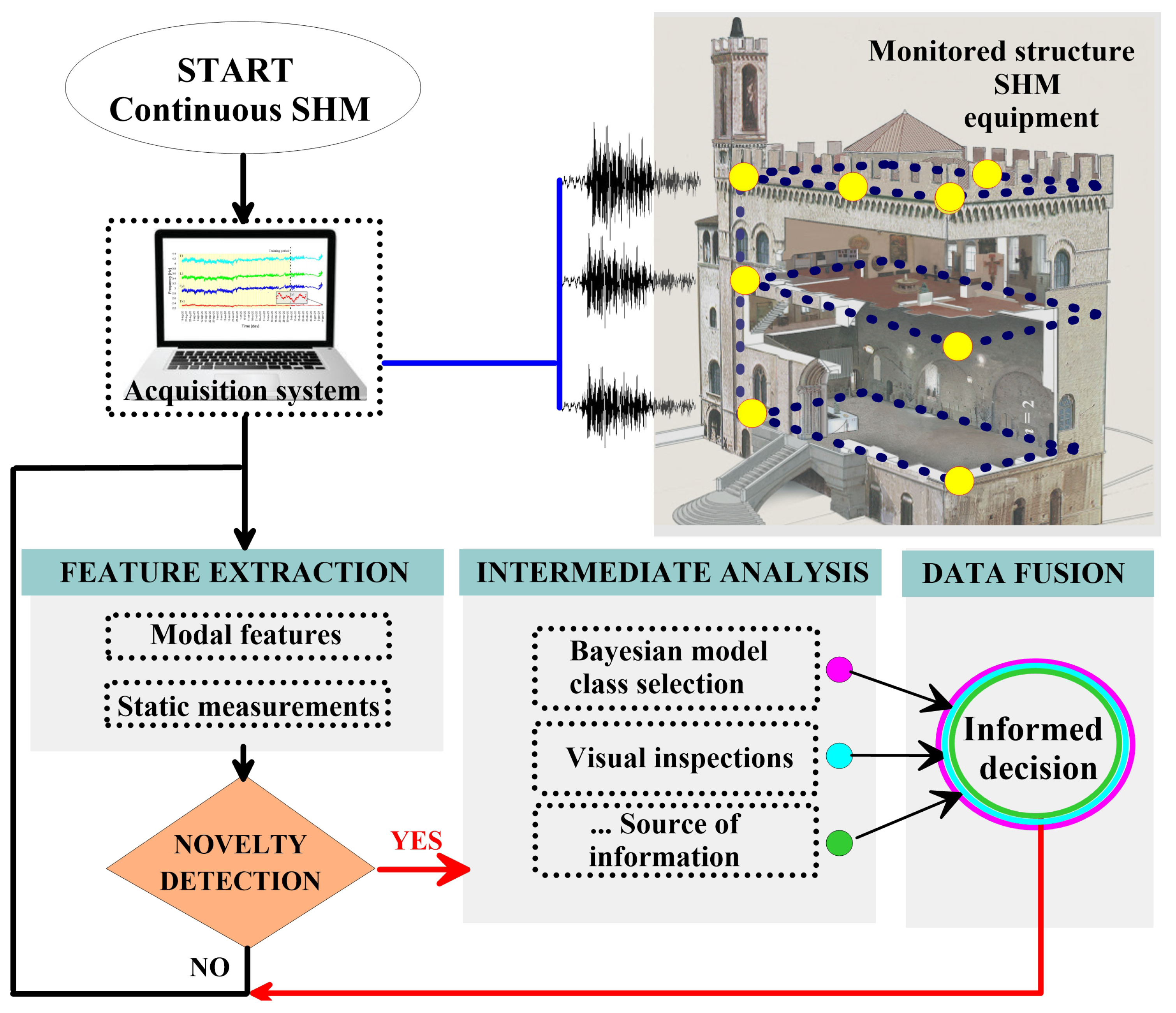
Furthermore, the work presented in [75] highlights the need for devising an efficient methodology capable of processing data by amalgamating diverse sources, e.g., data fusion, including visual inspections, to yield robust informed decisions. The main parts of a data fusion-based procedure for a correct interpretation of SHM data are summarized as follows (see Figure 12):

• Monitored structure and SHM equipment: based on the type of structure (construction material, architectural scheme, etc.), a network of sensors is installed in specific locations;
• Continuous SHM: the acquisition system enables the acquisition and storage of all the sensor data continuously over time;
• Feature extraction: Data recorded from the sensors are post-processed and tracked over time. For instance, vibration data enable the evaluation of the structural dynamic features;
• Novelty detection: statistical methods are used to detect anomalies in the data;
• Intermediate analysis: In this phase, all the possible information is stored. Concerning SHM data, if a novelty is detected, the features are used for a deeper investigation and damage prediction by means of numerical models previously reconstructed and calibrated (such as Bayesian model updating). Visual inspection results can also be used as a source of information;
• Data fusion: the amalgamation of all the information acquired in the previous steps enables a comprehensive and informed decision-making process.

The specific goal is to establish standardized protocols to bridge the existing gap between real-world inspection surveys, expert judgement, and numerical predictions derived from SHM data. Indeed, relying solely on numerical predictions can be problematic, as the solutions to detected anomalies may not be unique or may not exhibit continuous dependence on the data. On the other hand, exclusive reliance on visual inspections may overlook certain structural anomalies that are not readily apparent but can be captured through continuous SHM. This case study revolves around the Consoli Palace, situated in Gubbio, near Perugia, Italy, an intricate historical masonry building that is continuously monitored since 2017. The results underscore the advantages of augmenting long-term monitoring data with visual inspections to bolster confidence in damage identification by making use of Bayesian inference. Along the same line, it is also worth mentioning the work presented in [76] that highlighted how the SHM system installed on the Consoli Palace within this project allowed us to detect a small earthquake-induced damage in the building (see also previous sections devoted to the use of the EFM as a physics-based surrogate model in SHM) for which a robust procedure to handle outliers in the training period of the classification algorithm was found to be decisive.

Figure 12. A schematic representation of a data fusion-based methodology.

Figure 12. A schematic representation of a data fusion-based methodology.

9. Conclusions

This research programme addresses the critical issue of structural degradation in cultural heritage, with a specific focus on masonry structures, which constitute a significant portion of historic building stock. The rationale for this research stems from the documented evidence of damage and the loss of cultural heritage due to both natural ageing processes and extrinsic degradation factors. This vulnerability is recognized and officially documented by national and international bodies, such as the Italian Ministry of Cultural Heritage, which classifies various damage risks affecting cultural assets. The European Union has also consistently emphasized the importance of cultural heritage preservation through its research framework programmes, culminating in the declaration of 2018 as the European year of cultural heritage, underscoring the societal and economic value of these assets.

While substantial research has been conducted on the seismic vulnerability of historic masonry structures, a significant knowledge gap remains on the long-term effects of ageing and degradation on their structural behaviour and the application of effective structural health monitoring (SHM) techniques. This research aims to bridge this gap by promoting scientific and technical advancements in the development of proactive monitoring systems. These systems are intended to provide insights for formulating effective risk mitigation strategies against both natural hazards and anthropogenic risks.

A key practical objective of this research is the development and validation of reliable predictive methodologies for assessing the impact of degradation on the structural performance of masonry. This includes investigating the influence of degradation mechanisms on the mechanical properties from the level of constituent materials to macroscopic descriptors like peak strength and stiffness at the scale of components. This paves the way for structural health monitoring and damage detection by considering epistemic uncertainties. Concurrently, the research focuses on the validation of equivalent frame approaches (EFMs) as a computationally efficient tool for supporting SHM. EFMs offer a simplified yet reasonably accurate representation of complex masonry structures, enabling efficient structural analysis and damage identification with consistent idealization rules. The validation process involves comparing the results obtained from EFMs with those from more computationally intensive numerical models and/or experimental data and focusing on wall-to-wall connections, the “flange effect”, and mass lumping at the floor level.

SHM strategies using integrated sensing technologies that can effectively detect, localize, and quantify damage, thereby satisfying the principle of “minimum impact” on heritage structures, are in accordance with established conservation principles such as those articulated in the “Charter of Venice”. Finally, the monitorability of degradation was also checked by means of experimental tests and simulations with validated structural models.

The outlined integrated approach will enable the smart and effective use of available modern technologies for the long-term protection and conservation of cultural heritage buildings. And this research programme aims to establish a robust scientific basis for this.