The Application of a BiGRU Model with Transformer-Based Error Correction in Deformation Prediction for Bridge SHM

Abstract

Accurate deformation prediction is crucial for ensuring the safety and longevity of bridges. However, the complex fluctuations of deformation pose a challenge to achieving this goal. To improve the prediction accuracy, a bridge deformation prediction method based on a bidirectional gated recurrent unit (BiGRU) neural network and error correction is proposed. Firstly, the BiGRU model is employed to predict deformation data, which aims to enhance the modeling capability of the GRU network for time-series data through its bidirectional structure. Then, to extract the valuable information concealed in the error, a transformer model is introduced to rectify the error sequence. Finally, the preliminary and error prediction results are integrated to yield high-precision deformation prediction results. Two deformation datasets collected from an actual bridge health monitoring system are utilized as examples to verify the effectiveness of the proposed method. The results show that the proposed method outperforms the comparison model in terms of prediction accuracy, robustness, and generalization ability, with the predicted deformation results being closer to the actual results. Notably, the error-corrected model exhibits significantly improved evaluation metrics compared to the single model. The research findings herein offer a scientific foundation for bridges’ early safety warning and health monitoring. Additionally, they hold significant relevance for developing time-series prediction models based on deep learning.

1. Introduction

Structural health monitoring (SHM) technology is crucial in bridge management and maintenance [1,2]. In recent years, with the rapid development of SHM technology, intelligent sensor systems, such as wireless and optical fiber sensors, have been widely applied in bridge SHM systems [3]. In these systems, sensors are able to collect a large volume of real-time operational data of various types. Among them, deformation data, as a direct reflection of the bridge’s structural stress and damage state [4], provides valuable information for safety assessments and management decisions. By analyzing deformation data, potential issues in bridge operation can be identified, and future deformation trends can be predicted, thus providing effective early warnings for potential safety hazards. Furthermore, accurate deformation predictions provide a scientific basis for bridge maintenance, optimizing resource allocation and extending service life. Therefore, how to accurately predict the deformation behavior of bridges to achieve early warnings and optimize maintenance has become a key research topic in bridge health monitoring.

With the advancement of time-series analysis technology, many scholars use the time-series forecasting method to carry out forecasting research [5]. These prediction models can be roughly divided into two categories: one is the machine learning (ML) model, such as the long short-term memory (LSTM) neural network [6] and gated recurrent unit (GRU) neural network [7]; the other class is statistical models, such as vector auto-regressions models [8] and auto-regressive integrated moving average models [9]. Compared to traditional statistical models, the ML models are more adept at capturing nonlinear features in data due to their deeper network structures [10]. This capability renders them particularly suitable for analyzing and processing complex datasets. Thus, an increasing number of researchers opt for ML models, especially deep learning architectures, as their primary tools for time-series prediction. For example, Wang et al. considered the characteristics of time-series data and employed an LSTM network to predict deflection in real time [11]. Additionally, they proposed a bridge state assessment method, which was validated using monitoring data from the SHM system of the Chongqing Egongyan Rail Transit Bridge. Kisvari et al. developed a GRU model for predicting wind power and compared its performance with an LSTM model [12]. The results show that the GRU model outperforms the LSTM model in terms of both prediction accuracy and training efficiency. To enhance the prediction accuracy of the GRU model, She et al. developed a remaining useful life prediction method utilizing a bidirectional GRU (BiGRU) model, which they validated for reliability using bearing data [13]. Despite the superior predictive performance of the aforementioned models, the deformation data of bridges often exhibit significant nonlinear and non-stationary characteristics due to environmental complexities [14]. In this context, relying solely on a single model, such as a GRU or BiGRU, for time-series forecasting may result in large forecasting errors.

A hybrid model based on error correction has been proposed to address the aforementioned limitations [15,16]. This model effectively enhances prediction accuracy by mining potential features within the error sequence and adjusting the initial prediction results through an error correction mechanism. Xu et al. employed a convolutional neural network and an LSTM neural network to rectify the error sequence [17]. The results indicated that the prediction accuracy improved significantly compared to the model lacking error correction. Luo et al. predicted the error sequence using an LSTM neural network optimized by a genetic algorithm [18]. They validated the significance of error correction in enhancing prediction accuracy through experiments conducted on multiple sets of real data sequences. While hybrid models have demonstrated effectiveness in fields such as finance, hydrology, and wind speed prediction, research on their application in bridge health monitoring remains limited. Furthermore, error sequences frequently exhibit additional nonlinear components, necessitating the use of deeper models to capture these nonlinear features adequately [19]. The transformer model [20] utilizes a multi-head self-attention mechanism to assign varying weights to inputs at each time step, effectively modeling the complex nonlinear relationships within sequences. This approach is particularly well-suited for capturing the potential nonlinear dynamics present in error sequences [21]. Thus, this study employs the transformer model to predict the error sequence. At the same time, existing research on bridge deformation prediction primarily focuses on the accuracy of single-step prediction, which involves obtaining precise predictions of data changes at the next time step [4]. Unlike single-step prediction, multi-step prediction can forecast deformation data for multiple future time steps at once, thereby revealing the long-term evolution trends of the data [3,22] and providing decision-makers with more comprehensive information.

In this study, we propose a bridge deformation prediction method that integrates BiGRU and transformer error correction (BiGRU-Transformer). In particular, the BiGRU model is employed to generate preliminary predictions of deformation, which are then compared to the actual values to derive the error sequence. Subsequently, the transformer model is utilized to predict this error sequence for correction purposes. Ultimately, the final deformation prediction value is obtained by superimposing the preliminary and error prediction results. Taking the deformation data of a real bridge SHM system as an example, experiments with four different prediction steps are carried out, and the effectiveness of the proposed method is verified by comparing it with the model.

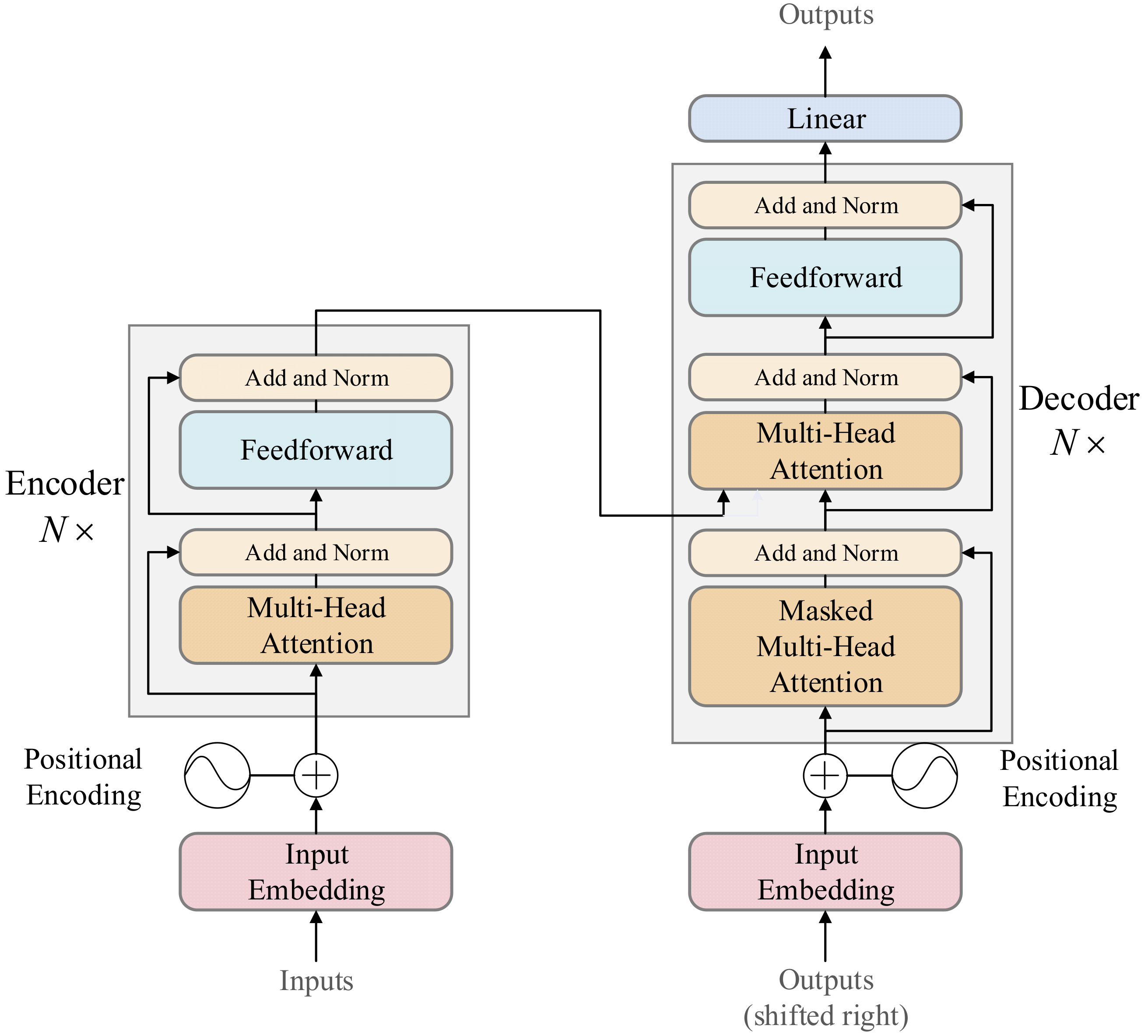
2. Methodology

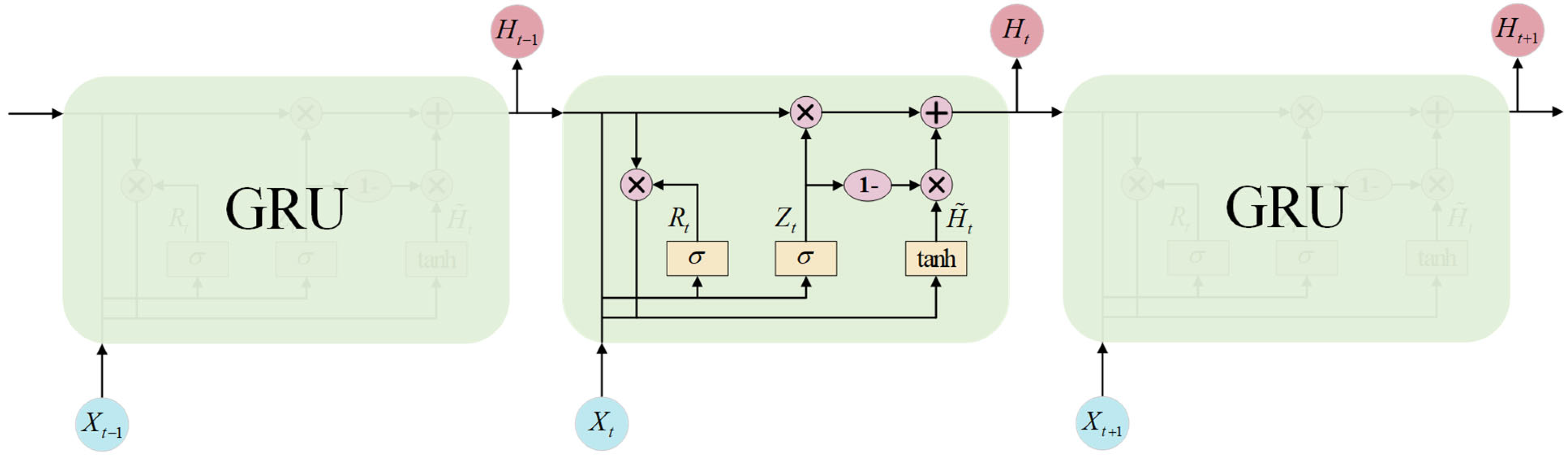
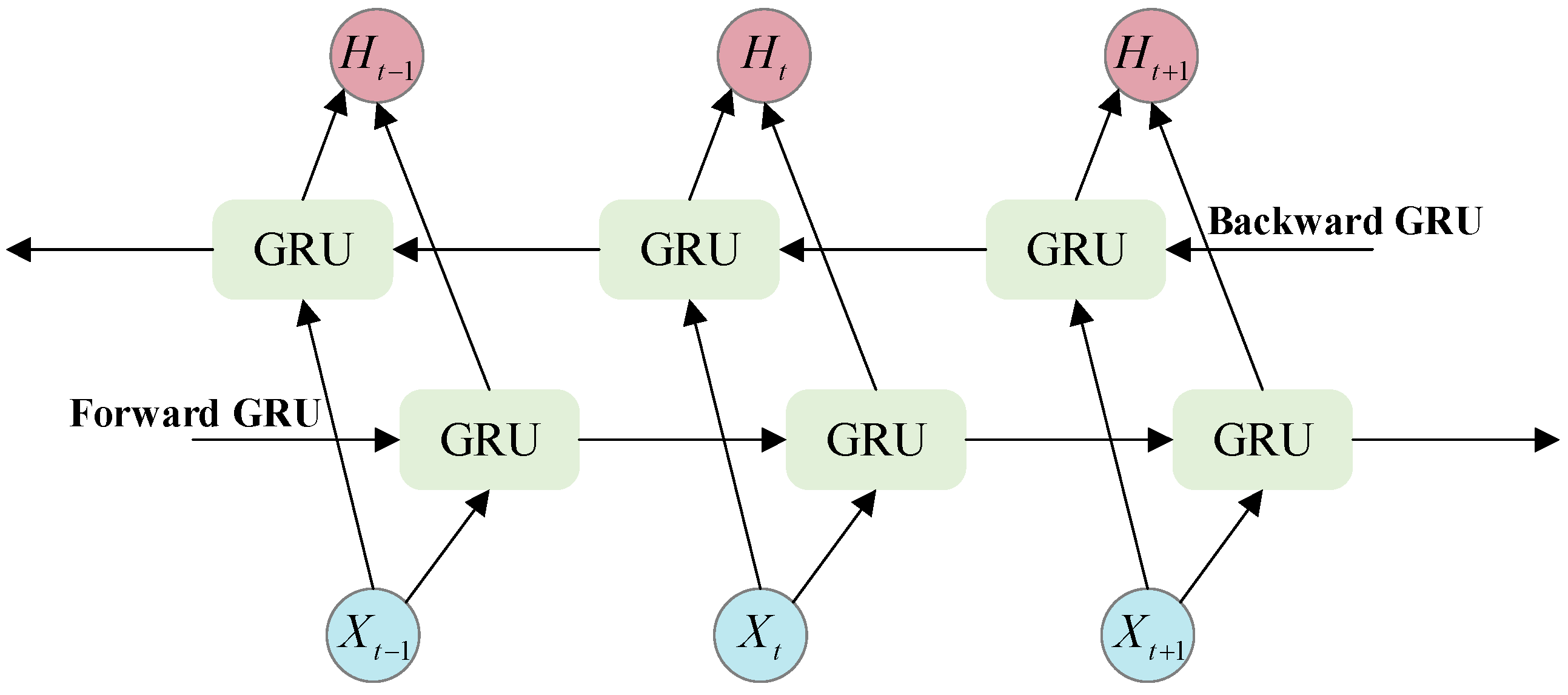
2.1. BiGRU Model

2.1.1. GRU Neural Network

Recurrent neural networks are extensively utilized in time-series prediction because they can capture dynamic features in sequential data. However, gradient disappearance and gradient explosion challenges constrain their ability to model long-term dependencies [23]. To address these issues, the LSTM networks facilitate effective learning and retention of long-term dependencies by incorporating a cell state and gate mechanisms [24].

The GRU is a simplified variant of the LSTM model, which preserves the ability to capture long dependencies while reducing the number of parameters by combining the forget and input gates into update gates and replacing the forget mechanism with reset gates [25]. Figure 1 shows the schematic diagram of the GRU module, and the calculation formula for the two gates is as follows:

$$R_t=\sigma (X_t{W}_{xr}+H_{t-1}{W}_{hr}+b_r)$$

(1)

$$Z_t=\sigma (X_t{W}_{xz}+H_{t-1}{W}_{hz}+b_z)$$

(2)

where $R_t$ is the reset gate; $Z_t$ is the update gate; $\sigma \left(\cdot \right)$ is the sigmoid activation function; $H_{t-1}$ is the hidden state at the last moment; $X_t$ is the input at the current moment; and $W$ and $b$ are the weight parameter matrix and bias vector, respectively.

Finally, the candidate hidden state ${\tilde{H}}_t$ and hidden state $H_t$ at the current moment are updated based on the calculation results of the update and reset gates:

$${\tilde{H}}_t=\tanh (X_t{W}_{xh}+(R_t\odot H_{t-1})W_{hh}+b_h)$$

(3)

$$H_t=Z_t\odot H_{t-1}+(1-Z_t)\odot {\tilde{H}}_t$$

(4)

where $\tanh \left(\cdot \right)$ is the hyperbolic tangent activation function and $\odot$ is the Hadamard product.

2.1.2. BiGRU Neural Network

The BiGRU neural network is a structure extended based on the GRU [26]. It is composed of a layer of forward GRU and a layer of reverse GRU, which aims to capture the forward and reverse dynamic features in time-series data at the same time to further improve the completeness and accuracy of the network’s time-series feature extraction. A diagram of the BiGRU model is shown in Figure 2.

2.2. Transformer Model

The transformer model was introduced by Vaswani et al. [20] in 2017, initially intended for natural language processing tasks. Due to its high performance and efficiency in dealing with complex time-series problems, it is also often used in time-series prediction tasks [27,28]. Central to the model is the self-attention mechanism, which allows the model to focus on information at any location while processing input sequences, thereby capturing global dependencies. Unlike traditional RNNs and their variants (such as GRU and BiGRU), the transformer model does not depend on sequential assumptions. Instead, it directly captures the relationships between key points in the sequence through a self-attention mechanism, thereby enhancing computational efficiency and modeling capability [29]. Furthermore, the transformer’s multi-head self-attention mechanism, combined with its feedforward network, creates a robust feature extraction system capable of identifying more complex nonlinear relationships.

The standard transformer model consists of an encoder and a decoder, each stacked with multiple layers of modules. Specifically, a single encoder layer computes the attention weights of each position in the input sequence relative to other positions through a multi-head self-attention mechanism. It then employs a feedforward network to independently and nonlinearly transform the features at each time step, enhancing feature representation. Furthermore, residual connections and layer normalization are incorporated after each sub-layer to ensure the training process’s robustness and effectiveness. A single decoder layer not only includes the mechanisms of the encoder layer but also employs the cross-attention mechanism to integrate the features extracted by the encoder with the target sequence, thereby establishing the dependency model between the sequences. A diagram of the standard transformer model is presented in Figure 3.

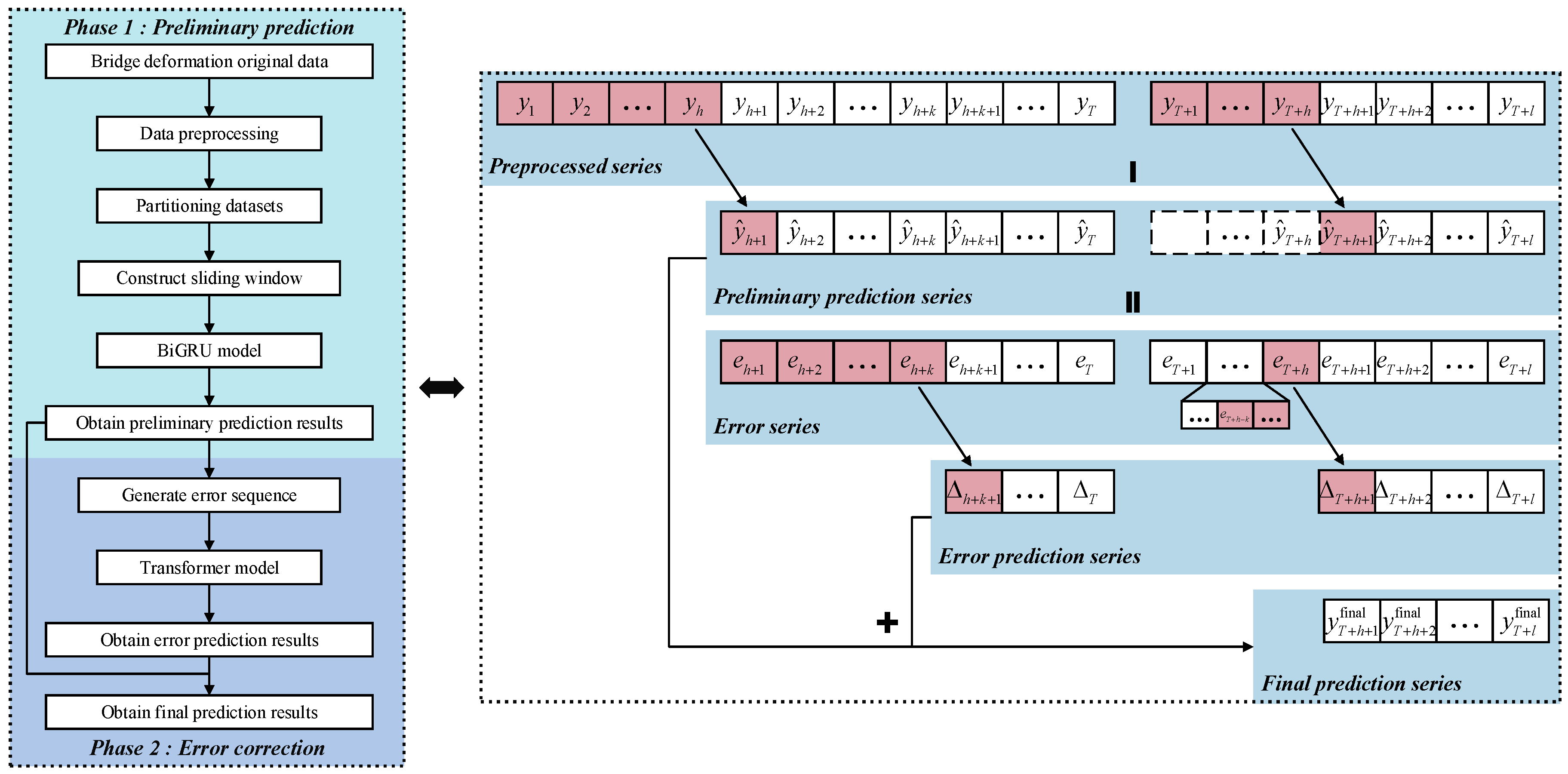
2.3. Bridge Deformation Prediction Method

This paper develops a method based on BiGRU and transformer models (BiGRU-Transformer) to enhance the accuracy and robustness of bridge deformation predictions. The process is structured into two distinct stages: the preliminary prediction stage and the error correction stage. This section will provide a detailed introduction to the specific research content associated with both stages of the proposed method.

2.3.1. Preliminary Forecasting Stage

Generally, future bridge deformation prediction trends rely on historical data [4]. Consequently, in the preliminary prediction stage, the objective is to estimate the future deformation trend using this historical data, thereby providing initial results for the subsequent error correction stage. Furthermore, considering that BiGRU can capture information from both past and future directions simultaneously and is better suited for handling the dynamic characteristics of time-series data, the BiGRU model is chosen as the core model for the preliminary prediction stage. The primary steps in this stage include:

Step 1: Data preprocessing. First, historical deformation data are obtained from the bridge SHM system. Then, the collected data undergo preprocessing, primarily including outlier removal, missing value imputation, and data normalization. Finally, 70% of the processed data are allocated as the training dataset, while the remaining 30% are used as the testing dataset.

Step 2: Train the BiGRU model. The training dataset is input into the established BiGRU model for training, where the model’s weight parameters are adjusted based on the historical data. It is important to note that the training dataset is constructed by defining a sliding window to generate the model’s inputs and outputs before training. The sliding step value during the training phase is set to 1.

Step 3: Preliminary prediction. The testing dataset is input into the trained BiGRU model to generate the preliminary prediction results. Similarly, the testing dataset is constructed by defining a sliding window to generate the model’s inputs and outputs. The sliding step value during the testing phase is consistent with the prediction step value.

2.3.2. Error Correction Stage

Based on the prediction results generated in the preliminary prediction stage, the error correction stage uses the transformer model for subsequent error correction. The core advantage of the transformer model lies in its powerful attention mechanism, which can capture complex nonlinear dependencies within the data, thereby effectively reducing the errors generated in the initial prediction. The main steps of the error correction stage include:

Step 1: Error calculation. According to the preliminary prediction value of the training set and the test set, the error sequence $e$ of the preliminary prediction stage is obtained by subtracting the preliminary prediction value from the real value. The calculation formula is as follows:

$$e_t=y_t-{\widehat{y}}_t$$

(5)

where $y_t$ and ${\widehat{y}}_t$ are the real and preliminary predicted values at time $t$, respectively. It should be noted that in order to ensure that the length of the error sequence of the test set is consistent with the length of the preliminary prediction sequence, the length of a sliding window is extended in the data of the test set, but this does not affect the division of the dataset in the previous section.

Step 2: Train the transformer model. Consistent with the construction of the dataset in the preliminary prediction stage, the training set and test set of the error sequence are also constructed by sliding window, and the constructed training set is substituted into the established transformer model for training.

Step 3: Error prediction. The trained transformer model is used to predict the test set of the error sequence. That is, the historical error data $\left\{e_{t-k},\cdots ,e_{t-1}\right\}$ are used to predict the error prediction value ${\Delta }_t$ at the current time $t$, where $k$ is the length of the sliding window constructed by the dataset in the error correction stage.

Step 4: Obtain the final forecast. By linear superposition of the preliminary predicted value and the error predicted value, the final predicted result is obtained. The calculation formula is as follows:

$${\widehat{y}}_t^{\mathrm{final}}={\widehat{y}}_t+{\Delta }_t$$

(6)

where ${\widehat{y}}_t^{\mathrm{final}}$ is the final predicted value at time $t$.

2.3.3. Bridge Deformation Prediction Framework

Based on the descriptions of the two distinct stages in the previous sections, the framework of the bridge deformation prediction method proposed in this study is shown in Figure 4. The left side of the figure represents the basic framework of the bridge deformation prediction method, while the right side illustrates the more detailed computational steps. For a comprehensive explanation of the model, please refer to Section 2.1 and Section 2.2.

3. Application

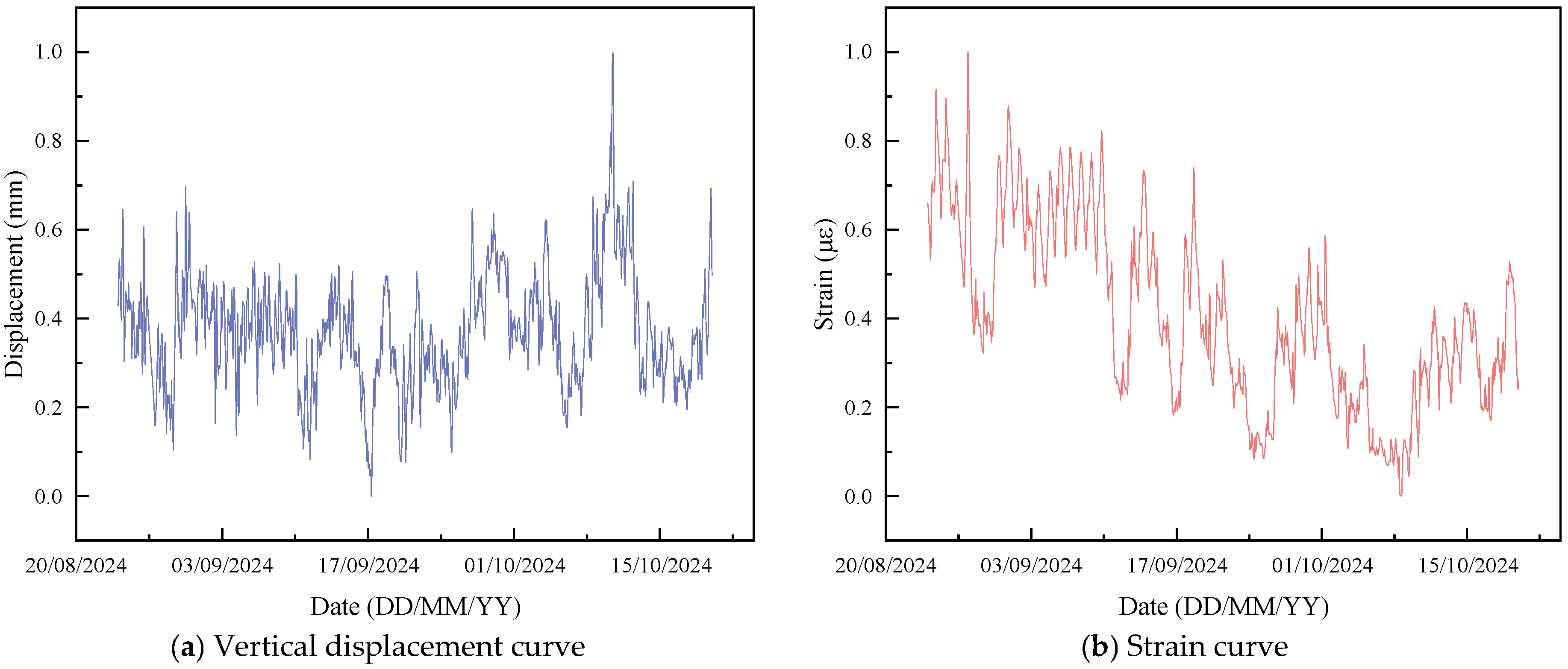
3.1. Data Source and Processing

The bridge deformation data used in this study are sourced from the SHM system of a steel tube concrete tied-arch bridge in Zhejiang Province, China. The system collects real-time deformation data of various types through sensors installed on the bridge, including vertical displacement, strain, and tie-rod displacement. For ease of subsequent analysis, vertical displacement and strain data recorded at the mid-span section of the main beam from 24 August 2024 to 19 October 2024 are selected as the research dataset. The data were recorded every hour, resulting in a total of 1369 data points. Additionally, some data in the dataset contain anomalies or missing values. To ensure data quality and that the requirements for subsequent model training are met, this paper uses the moving median method to identify outliers and the nearest-neighbor interpolation method to fill missing values. Furthermore, the data are normalized using the min–max normalization formula to eliminate dimensional discrepancies between different features. Figure 5 presents the vertical displacement and strain–curve plots after processing.

3.2. Model Setup

As mentioned earlier, the BiGRU and transformer models are the core components of bridge deformation prediction. The prediction performance and stability of the models are influenced by hyperparameters [30]. Therefore, to ensure the effectiveness of the BiGRU and transformer models, this study employs a trial-and-error method to determine the hyperparameters for both models during the training phase, as shown in

Table 1. The hyperparameter values of BiGRU and transformer models.

Model	Hyperparameter Name	Hyperparameter Value
BiGRU	Input length $h$ of BiGRU	12
	Number of BiGRU layers	2
	Hidden size of BiGRU	64, 128
Transformer	Input length $k$ of transformer	5
	Number of encoder layers	3
	Number of decoder layers	2
	Dimension of model	128
	Dimension of fcn	128
	Number of heads	8

. From the table, it can be seen that considering the temporal characteristics of bridge deformation, the sliding window length for the preliminary prediction stage is set to 12, while the sliding window length for the error correction stage is set to 5.

To ensure the model’s effectiveness and the stability of the training process, the learning rate for both the BiGRU and transformer models is set to 0.0005, the batch size is set to 32, and the training duration is 50 epochs. The Adam optimizer is used. Additionally, among the 50 training iterations, the model with the best performance is saved and used for testing in the next phase. The experiments are conducted in Windows 11, with the BiGRU and transformer models implemented in Python 3.9, using the PyTorch 1.12.0 deep learning framework.

3.3. Evaluation Metrics

To evaluate the effectiveness of the bridge deformation prediction method comprehensively, several commonly used error metrics are employed to assess model performance, including Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE). RMSE highlights the model’s sensitivity to large errors, while MAE provides an intuitive measure of the overall prediction error. MAPE reflects the magnitude of the prediction error relative to the true values. Smaller values of these metrics indicate better prediction performance.

4. Result and Discussion

4.1. Single-Step Prediction Results

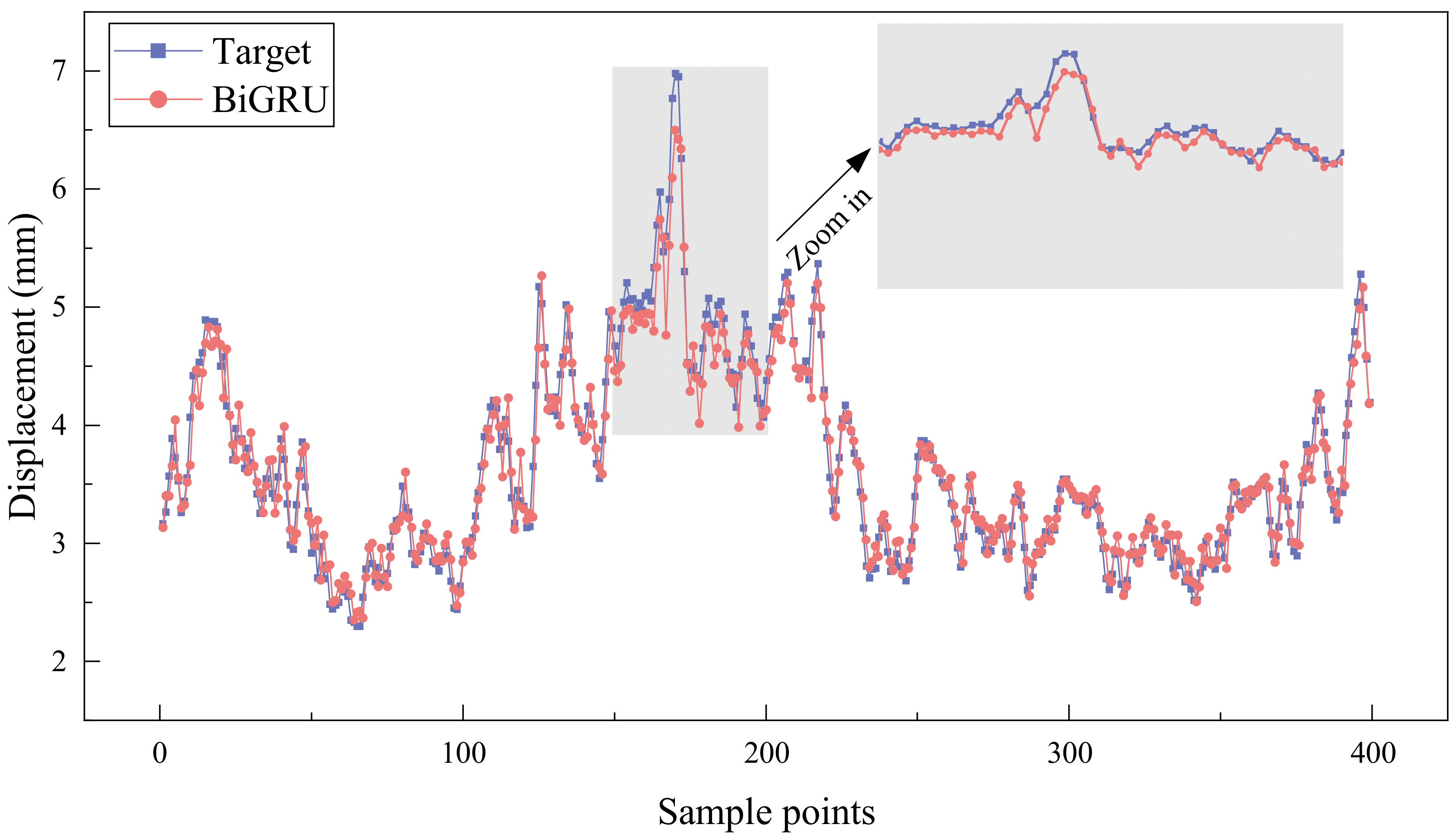
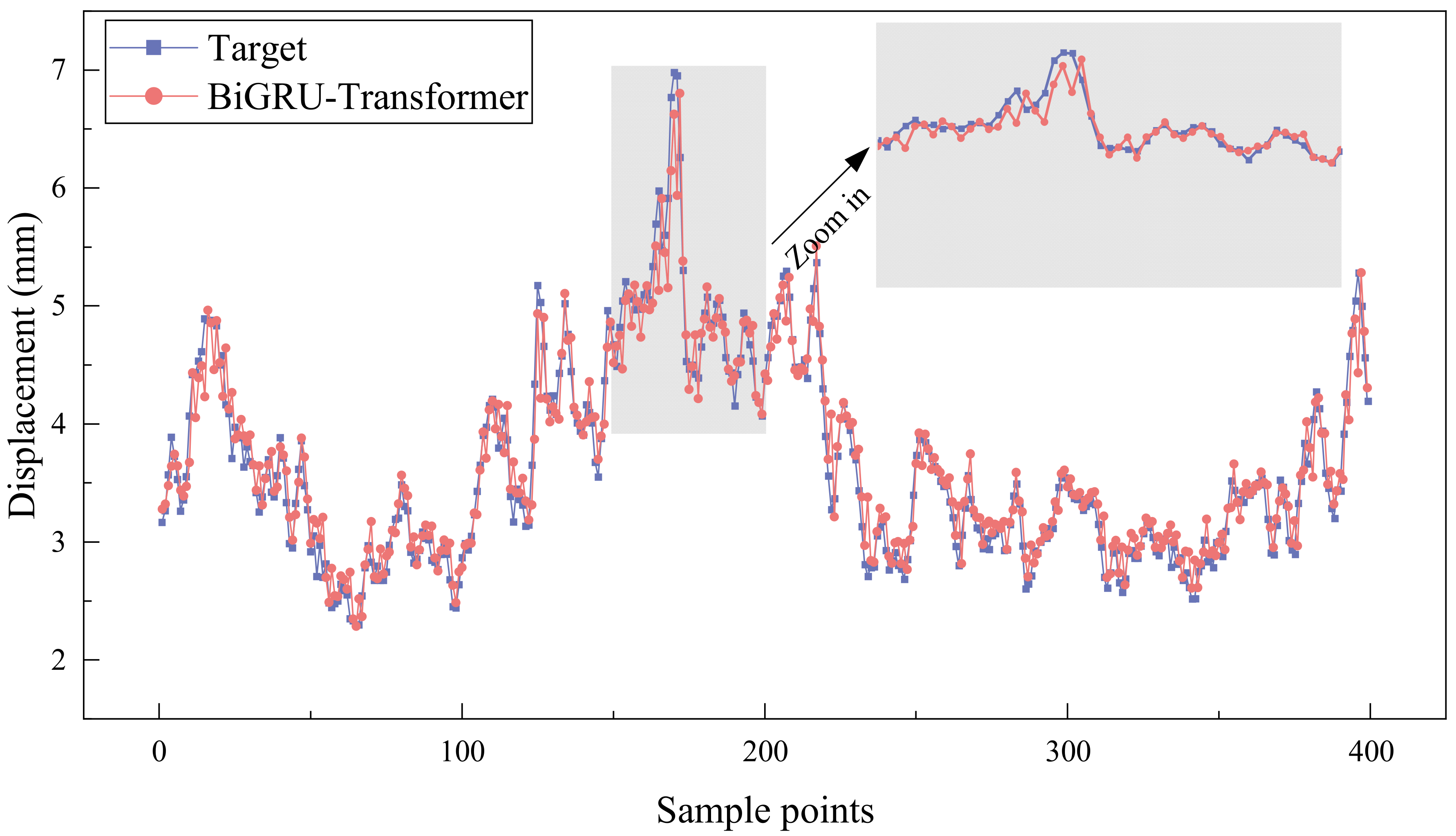
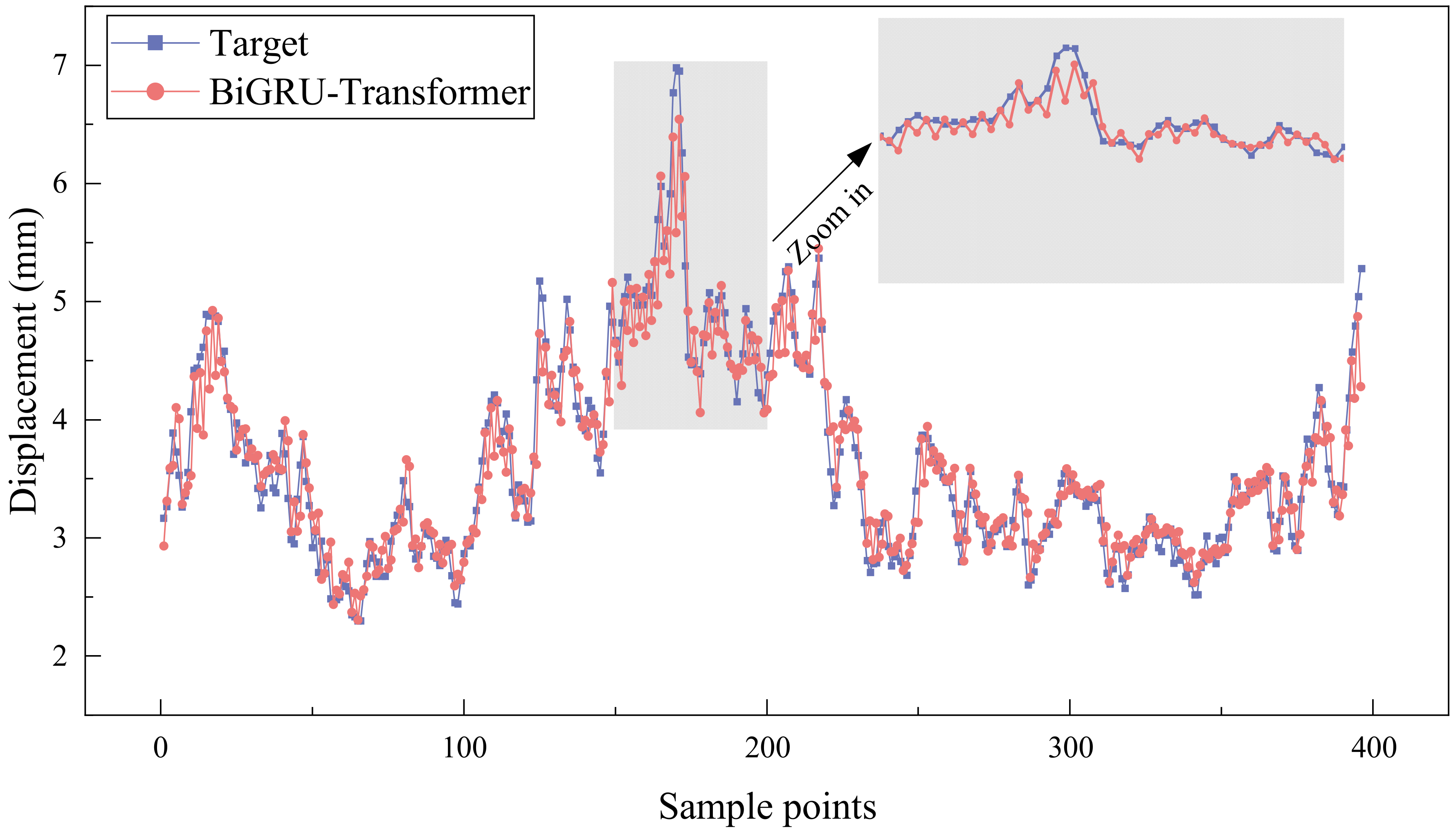
4.1.1. Bridge Deformation Prediction Results

As described in Section 2.3, this study develops a bridge deformation prediction method based on BiGRU and error correction. The method uses the BiGRU model for initial prediction and integrates the transformer model to correct the errors, achieving high-accuracy predictions. This section takes the vertical displacement data as an example and provides a detailed discussion of two aspects: the preliminary prediction results from the first stage and the error correction results from the second stage to evaluate the prediction performance and adaptability of the proposed method.

In the preliminary prediction stage, the BiGRU model performs one-step-ahead prediction of the vertical displacement data. The preliminary prediction results on the test set are shown in Figure 6. From the figure, it can be seen that the BiGRU model, by capturing the bidirectional dependencies in the time-series data, can accurately reflect the overall trend and some detailed features of the vertical displacement prediction. However, at specific points of sudden changes or peaks, the deviation between the predicted values and the actual values is relatively large, as indicated by the gray-shaded areas in the figure. This phenomenon can be attributed to external factors such as environmental disturbances, sensor noise, and time-series data’s inherent randomness and volatility [4]. These factors lead to discrepancies between the predicted and actual values, particularly in extreme variations and localized fluctuations. Furthermore, during the preliminary prediction stage, the evaluation metrics for the BiGRU model on the test set—RMSE, MAE, and MAPE—are 0.188, 0.142, and 3.840%, respectively. This further indicates that while the model is able to learn the deformation data characteristics reasonably well, there is still room for improvement in its performance.

To improve the prediction accuracy of bridge deformation, this study develops a transformer-based error correction model by learning the underlying patterns in the error sequences of the preliminary predictions. As described in Section 2.3.2, during the error correction phase, the error sequence of the vertical displacement preliminary prediction is first computed. Next, the transformer model is used to predict the error data one step ahead. Finally, the preliminary prediction result and the error prediction result are linearly combined to obtain the final prediction, as shown in Figure 7. From the figure, it is evident that the corrected predictions closely match the actual values, particularly at extreme and abrupt points where the errors are significantly reduced. This demonstrates the effectiveness of the transformer model in error correction.

To further demonstrate the effectiveness of the error correction mechanism, Figure 8 presents a comparison of the initial vertical displacement error and the corrected error. As shown in the figure, the initial vertical displacement error curve follows a similar trend to the original vertical displacement curve, indicating that there is still valuable information in the initial error that the BiGRU model did not capture. Moreover, after transformer-based error correction, the error curve fluctuates around zero, with small oscillations and no further similar features, suggesting that the transformer model has fully learned the effective information in the initial error. Meanwhile, after error correction, the evaluation metrics for vertical displacement prediction—RMSE, MAE, and MAPE—are 0.007, 0.002, and 0.054%, respectively. Upon observation, compared to the evaluation metrics from the preliminary prediction stage, all metrics are significantly reduced, indicating that the error correction effectively compensates for the limitations of the single model.

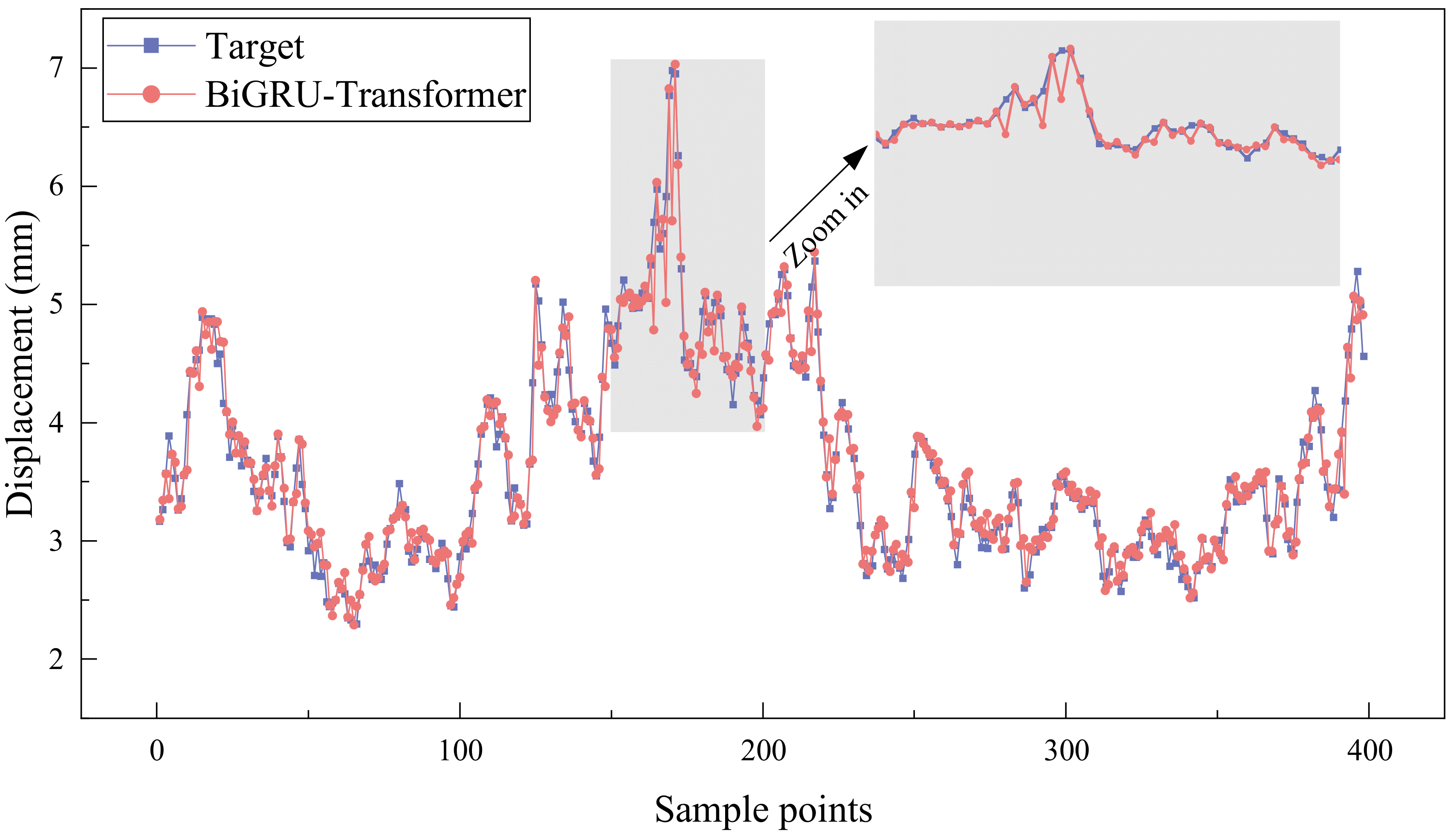
4.1.2. Model Comparison

Although the bridge deformation prediction method proposed in the previous section demonstrates good prediction performance, comparative experiments are still necessary to validate the model’s effectiveness and robustness. Thus, in this study, a one-dimensional convolutional neural network (1D-CNN) [31] and the GRU model are chosen as comparison models for the preliminary prediction stage, and their performance is compared with that of the BiGRU-Transformer model. The following will provide a comparative analysis of the performance of these models in both stages.

As described in Section 4.1.1, the vertical displacement is predicted one step ahead using the same calculation method, and the prediction performance metrics for the above models in the preliminary prediction stage are presented in

Table 2. The prediction performance metrics of different models in the preliminary prediction stage.

Preliminary Prediction Model	RMSE/mm	MAE/mm	MAPE/%
1D-CNN	0.224	0.169	4.516
GRU	0.195	0.149	3.985
BiGRU	0.188	0.142	3.840

. The table shows that the 1D-CNN performs the worst, with all evaluation metrics on the test set being higher than those of the GRU and BiGRU models. This is likely due to the lack of a memory mechanism in the 1D-CNN, making it difficult to capture long-term dependencies within the sequence, and thus, it shows significant limitations when dealing with the nonlinear dynamic characteristics of the data. The GRU outperforms the 1D-CNN, with RMSE, MAE, and MAPE decreasing by 12.946%, 11.834%, and 11.758%, respectively, compared to the 1D-CNN. This demonstrates that the GRU model, by incorporating a gating mechanism, can effectively capture temporal dependencies and dynamic changes in the data. The BiGRU performs the best, with RMSE, MAE, and MAPE improving by 3.590%, 4.698%, and 3.639%, respectively, compared to the GRU. This improvement is attributed to the bidirectional structure of the BiGRU, which enables it to simultaneously utilize both forward and backward information, thereby enhancing its ability to model time-series data more effectively.

To validate the effectiveness of the error correction model, the transformer model is used to correct further the preliminary prediction results of the models mentioned above. The prediction performance metrics of the corrected hybrid models are presented in

Table 3. The predictive performance metrics of different models are corrected by the transformer.

Hybrid Prediction Model	RMSE/mm	MAE/mm	MAPE/%
1D-CNN-Transformer	0.015	0.004	0.094
GRU-Transformer	0.010	0.006	0.165
BiGRU-Transformer	0.007	0.002	0.054

. By comparing Table 2 and Table 3, it is clear that the evaluation metrics for all hybrid models are significantly reduced, indicating that the error correction model based on the transformer can effectively learn useful information from the error sequence. Among the hybrid models, the model combining the BiGRU preliminary prediction model with the transformer error correction model shows the best prediction performance. Compared to the pre-error-correction results, the RMSE, MAE, and MAPE are reduced by 0.181, 0.140, and 3.786%, respectively. This demonstrates that the proposed prediction method has a significant advantage in capturing complex nonlinear dynamic characteristics and correcting errors, making it highly suitable for bridge deformation prediction.

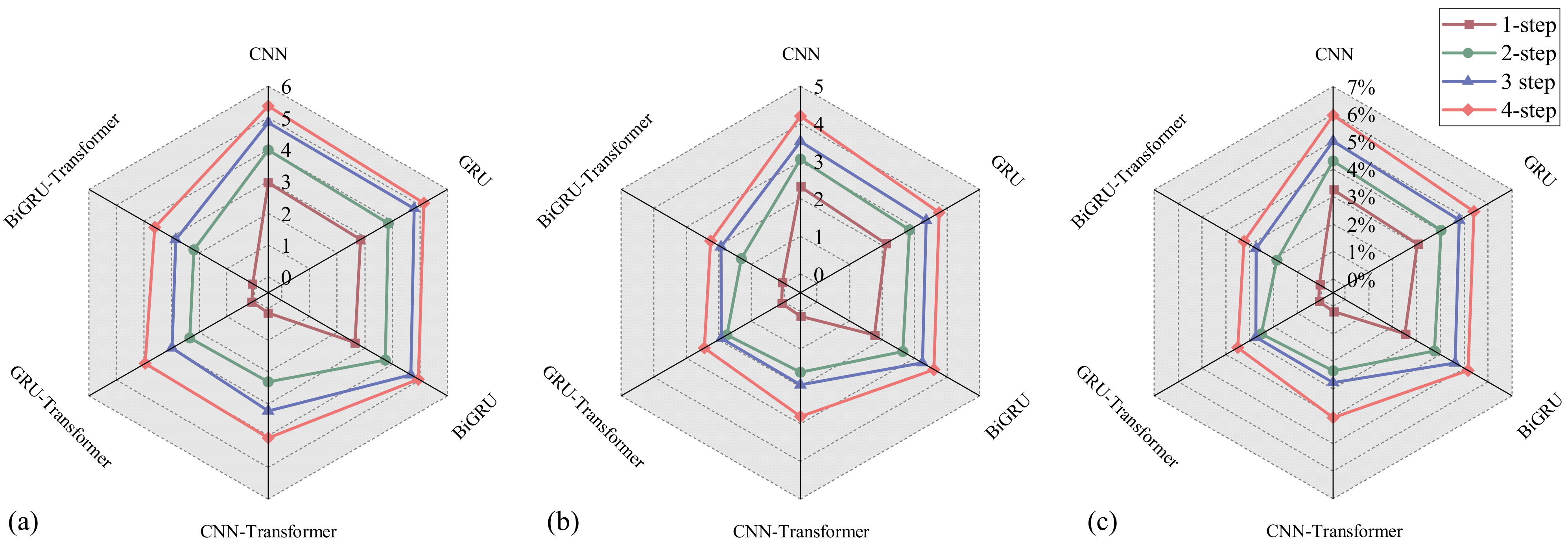
4.2. Multi-Step Prediction Results

The results above indicate that the proposed method provides high accuracy in single-step prediction for the bridge deformation task. However, its limitation lies in its ability to predict only the deformation value for the next time step, which may not fully satisfy the practical engineering need for forecasting deformation trends over multiple future time points. This is particularly critical in bridge health monitoring and risk early warning systems, where it is crucial to anticipate the deformation dynamics over a period of time to inform decision-making [3]. Therefore, this study attempts to apply the proposed method to the multi-step prediction of bridge deformation.

Experiments were designed for 2-step, 3-step, and 4-step prediction tasks to evaluate the method’s performance in multi-step prediction. The prediction results are shown in Figure 9, Figure 10 and Figure 11. It should be noted that in the preliminary prediction stage, a direct prediction approach is used, where all predicted values are output at once. The prediction results in the figures show that the proposed method still performs excellently in multi-step prediction. The predicted values consistently fluctuate around the actual values, with the prediction curves maintaining a high degree of trend alignment with the real deformation values.

To strengthen the argument,

Table 4. The performance comparison of different models under multi-step vertical displacement prediction.

Prediction Step	Model	RMSE/mm	MAE/mm	MAPE/%
2	1D-CNN	0.347	0.245	6.417
	GRU	0.301	0.212	5.536
	BiGRU	0.295	0.205	5.377
	1D-CNN-Transformer	0.218	0.145	3.912
	GRU-Transformer	0.204	0.116	3.034
	BiGRU-Transformer	0.181	0.100	2.687
3	1D-CNN	0.399	0.287	7.695
	GRU	0.376	0.268	7.024
	BiGRU	0.371	0.262	6.907
	1D-CNN-Transformer	0.240	0.154	4.046
	GRU-Transformer	0.227	0.154	4.110
	BiGRU-Transformer	0.215	0.145	3.968
4	1D-CNN	0.451	0.325	8.525
	GRU	0.386	0.279	7.355
	BiGRU	0.378	0.275	7.350
	1D-CNN-Transformer	0.288	0.196	5.303
	GRU-Transformer	0.242	0.170	4.705
	BiGRU-Transformer	0.248	0.168	4.515

Note: The bolded numbers in the table indicate that, at the corresponding prediction step, a particular model achieved the highest accuracy on that evaluation metric compared to the other prediction models.

presents the prediction performance metrics of different models for prediction horizons of 2, 3, and 4 steps. The experimental results show that, within all prediction step ranges, the proposed prediction model outperforms the other comparison models, with a few exceptions where the performance is slightly inferior. Notably, the BiGRU-Transformer model demonstrates even more significant advantages than single models, further validating the effectiveness and reliability of the proposed method. Additionally, it is observed that as the prediction step increases, the prediction accuracy of all models declines. This phenomenon can be attributed to the dilution or loss of the dynamic information contained in the input features over longer time steps and the increased influence of random factors on the long-term trend. Despite the increase in errors, the error growth rate of the proposed model is slower, demonstrating its superior robustness.

4.3. Generalization Performance of the Prediction Method

To further examine and validate the practicality and generalization ability of the proposed method, this study also applies the method to predict strain. The strain curve is shown in Figure 5b. It is clear from the figure that there are significant differences in the fluctuation patterns and trends of the strain curve compared to the vertical displacement curve. This discrepancy could lead to substantial deviations in the vertical displacement and strain prediction results. Thus, if the proposed model can accurately predict structural strain, it would effectively demonstrate its robustness and generalization capability.

Meanwhile, to evaluate the prediction performance of different models for strain, Figure 12 presents the visualization results of the evaluation metrics for each model at prediction horizons of 1, 2, 3, and 4 steps. It should be noted that the model parameters and training conditions in this experiment are consistent with those used in the vertical displacement prediction experiments. The figure shows that, with a few exceptions where some metrics perform poorly, the proposed model outperforms the other models. Additionally, the main findings align with the conclusions from the vertical displacement prediction experiments: (1) Among the single models, BiGRU performs better than 1D-CNN and GRU in prediction accuracy. (2) The two-phase prediction framework achieves higher accuracy than all single models. (3) The BiGRU-Transformer model performs the best among all models. (4) The prediction accuracy of all models decreases as the prediction step increases, but the BiGRU-Transformer still maintains good performance. These results strongly validate the excellent generalization and robustness of the proposed method across different datasets and multi-step prediction tasks, providing a scientific solution for the safety assessment and early warning of actual bridges.

5. Conclusions

To accurately predict bridge deformation, this study proposed a prediction method based on the BiGRU-Transformer. This method achieves high-precision deformation prediction through two stages: preliminary prediction and error correction. It not only provides accurate deformation forecasts but also offers an efficient and reliable technical solution for bridge monitoring. Using data collected from the SHM system of a real bridge as an example, BiGRU-Transformer models were established for different prediction steps, and a comparative analysis was conducted with 1D-CNN, GRU, BiGRU, 1D-CNN-Transformer, and GRU-Transformer models to verify the prediction performance and robustness of the proposed method. The main conclusions are as follows:

(1)

In the bridge deformation prediction experiments, BiGRU outperformed both 1D-CNN and GRU in all evaluation metrics. For example, in the vertical displacement prediction experiment, BiGRU improved prediction accuracy by approximately 11% compared to 1D-CNN and about 2% compared to GRU. This indicates that BiGRU, by learning both forward and backward features of the sequence, enhances its ability to capture complex patterns and long-term dependencies in the deformation data. Thus, its prediction accuracy is further improved compared to other single models.

(2)

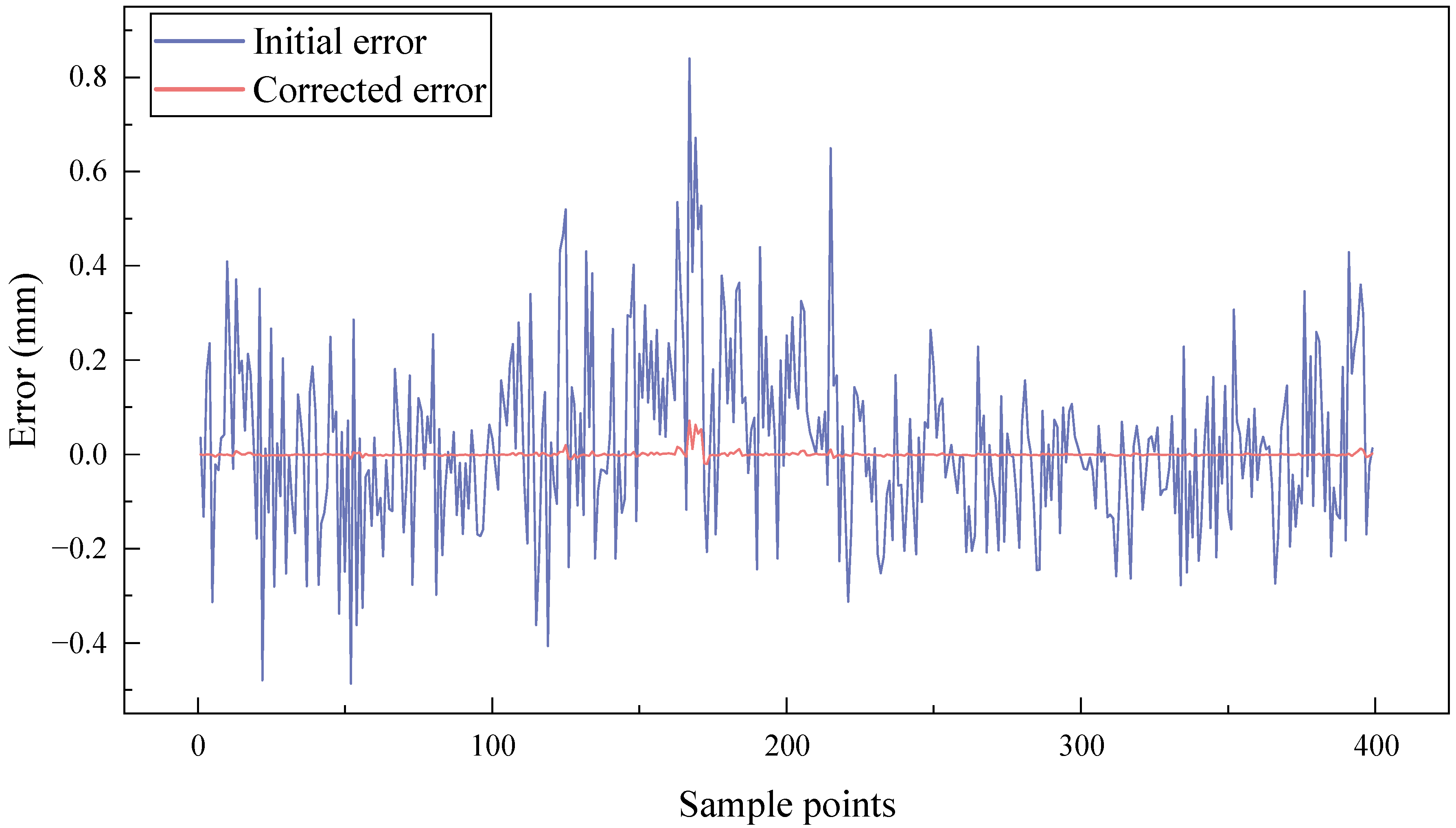
A comparison of single models and hybrid models incorporating transformer-based error correction was conducted for one-step prediction. The results show that the hybrid models significantly outperform the single models, with their prediction accuracy improving by up to 98.59%. Moreover, when the prediction steps are set to 2, 3, and 4, the hybrid models demonstrate more excellent stability and higher prediction accuracy than single models. This highlights the effectiveness of integrating error correction techniques into the bridge deformation prediction framework.

(3)

To improve prediction performance, the BiGRU-Transformer hybrid model employs a two-stage prediction approach, consisting of a preliminary BiGRU prediction followed by transformer-based error correction on SHM data. Compared to other models, the BiGRU-Transformer achieves the highest prediction accuracy, with its prediction error remaining within 5%. This demonstrates the advanced nature and superiority of the BiGRU-Transformer model.